Подготовка к ОГЭ по геометрии
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Модуль «Геометрия»
2. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между
Из точки А проведены две касательные к окружности сцентром в точке О. Найдите радиус окружности, если
угол между касательными равен 60°, а расстояние от
точки А до точки О равно 6.

3. Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в
Касательныев точках A и B к окружности
с центром в точке O пересекаются под углом 72°.
Найдите угол ABO. Ответ дайте в градусах.
4. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается нахорду АВ так, что угол ОАВ равен 60°.
Найдите длину хорды АВ, если радиус
окружности равен 8.
5. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания
Боковая сторона трапеции равна 3, а одиниз прилегающих к ней углов
равен 30°. Найдите площадь трапеции,
если её основания равны 2 и 6.
6. Точка О — центр окружности, ∠BOC=160° (см. рисунок). Найдите величину ∠BAC, ∠ОBC (в градусах).
Точка О — центр окружности, ∠BOC=160° (см. рисунок). Найдите величину ∠BAC, ∠ОBC (в
рисунок). Найдите величину ∠BAC, ∠ОBC (вградусах).
7. В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
В окружности с центром в точке О проведеныдиаметры AD и BC, угол ABO равен 75°.
Найдите величину угла ODC.
8. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность.Угол ABC равен 70°, угол CAD равен 49°.
Найдите угол ABD. Ответ дайте в градусах.
9. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность.Угол ABC равен 134°, угол CAD равен 81°.
Найдите угол ABD. Ответ дайте в градусах
.
10. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в
На окружности по разные стороны от диаметра ABвзяты точки M и N.
 Известно, что ∠NBA=36°.
Известно, что ∠NBA=36°.Найдите угол NMB. Ответ дайте в градусах.
11. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в
На окружности по разные стороны отдиаметра AB взяты точки M и N. Известно,
что ∠NBA=69°. Найдите угол NMB. Ответ дайте в
градусах.
12. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы,
Найдите угол АВС равнобедренной трапеции ABCD,если диагональ АС образует с основанием AD и
боковой стороной CD углы,
равные 20° и 100° соответственно.
13. В треугольнике ABC угол C равен 90°, AC=12, cosA=0,6. Найдите AB. В треугольнике ABC угол C равен 90°, AC=16, tg A=0,75.
В треугольнике ABC угол C равен 90°, AC=12, cosA=0,6.Найдите AB.
В треугольнике ABC угол C равен 90°, AC=16, tg A=0,75.
Найдите BC.
В треугольнике ABC угол C равен 90°, AC=15, tg A=0,2.
Найдите BC.

14. Найдите площадь треугольника АВС.
15. Медиана равностороннего треугольника равна 11√3. Найдите сторону этого треугольника. Сторона равностороннего треугольника
Медиана равностороннего треугольникаравна 11√3. Найдите сторону этого
треугольника.
Сторона равностороннего треугольника
равна 10√3. Найдите медиану этого
треугольника.
Высота равностороннего треугольника
равна 13√3. Найдите сторону этого
треугольника
16. В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
Сторона ромба равна 30, а острый угол равен 60°.Высота ромба, опущенная из вершины тупого угла,
делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол
равен 60°. Высота ромба, опущенная из вершины
тупого угла, делит сторону на два отрезка. Каковы
длины этих отрезков?
В треугольнике ABC известно, что AC=BC.

Найдите угол C. Ответ дайте в градусах.
Ответ: 9,5
Ответ: 30
Ответ: 7,5
Ответ: 294
English Русский Правила
Вариант 1 ОГЭ №16 | Вариант 2 ОГЭ №16 | ||||||
1 | К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см | 1 | Длина хорды окружности равна 96, а расстояние от центра окружности до этой хорды равно 20. | ||||
2 | Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK. | 2 | Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 60°. Найдите величину угла OMK. Ответ дайте в градусах. | ||||
3 | В треугольнике ABC угол C равен 45°, AB=6. Найдите радиус окружности, описанной около этого треугольника | 3 | К окружности с центром в точке О проведены касательная AB и секущая AO. | ||||
4 | Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. | 4 | Касательные в точках A и B к окружности с центром O пересекаются под углом 24°. Найдите угол ABO. Ответ дайте в градусах. | ||||
5 | Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах. | 5 | Радиус окружности, вписанной в трапецию, равен 20. | ||||
6 | Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах. | 6 | Радиус вписанной в квадрат окружности равен 4 . Найдите диагональ этого квадрата | ||||
7 | Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции. | 7 | В треугольнике ABC угол C равен 60°, AB=12. Найдите радиус окружности, описанной около этого треугольника. | ||||
8 | Радиус вписанной в квадрат окружности равен 2 . | 8 | Радиус окружности, описанной около квадрата, равен 8. Найдите радиус окружности, вписанной в этот квадрат. | ||||
9 | Радиус окружности, описанной около квадрата, равен 4. Найдите радиус окружности, вписанной в этот квадрат. | 9 | Радиус окружности, вписанной в равносторонний треугольник, равен 7. Найдите высоту этого треугольника. | ||||
10 | Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника. | 10 | Через точку A, лежащую вне окружности, проведены две прямые. | ||||
Вариант 3 ОГЭ №16 | Вариант 4 ОГЭ №16 | ||||||
1 | Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах. | 1 | Касательные в точках A и B к окружности с центром O пересекаются под углом 58°. Найдите угол ABO. Ответ дайте в градусах. | ||||
2 | Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности. | 2 | Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 12. Найдите AK | ||||
3 | Радиус окружности, вписанной в трапецию, равен 46. Найдите высоту этой трапеции. | 3 | Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 75°. | ||||
4 | Радиус вписанной в квадрат окружности равен 6 . Найдите диагональ этого квадрата | 4 | Длина хорды окружности равна 40, а расстояние от центра окружности до этой хорды равно 48. Найдите диаметр окружности. | ||||
5 | Радиус окружности, описанной около квадрата, равен 2. Найдите радиус окружности, вписанной в этот квадрат. | 5 | Радиус окружности, вписанной в трапецию, равен 38. Найдите высоту этой трапеции. | ||||
6 | Касательные в точках A и B к окружности с центром O пересекаются под углом 66°. | 6 | К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 40 см, AO = 85 см. | ||||
7 | В треугольнике ABC угол C равен 60°, AB=10. Найдите радиус окружности, описанной около этого треугольника. | 7 | Радиус вписанной в квадрат окружности равен 8 . Найдите диагональ этого квадрата | ||||
8 | К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 51 см, AO = 85 см. | 8 | В треугольнике ABC угол C равен 45°, AB=8. | ||||
9 | Радиус окружности, вписанной в равносторонний треугольник, равен 2. Найдите высоту этого треугольника. | 9 | Радиус окружности, описанной около квадрата, равен 10. Найдите радиус окружности, вписанной в этот квадрат. | ||||
10 | Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 27. Найдите AK. | 10 | Радиус окружности, вписанной в равносторонний треугольник, равен 15. | ||||
Круговая геометрия — касательные Задавать вопрос
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 231 раз
$\begingroup$
Всем добрый день. Я пытаюсь ответить на вопрос:
Пусть AB диаметр окружности K с центром O. Выберите точку P, внешнюю по отношению к K, на прямой, проходящей через A и B, и постройте касательные к K через P, пересекающиеся с K в точках X и Y. Пусть M будет пересечением AB и ХУ. Докажите, что касательные к K также касаются обеих окружностей с центром A и радиусом AM и окружности B и радиусом BM.
Контекст этого вопроса заключается в том, что я пытался выполнять эти задачи по обогащению математики чуть менее 3 месяцев, и они, наконец, подходят к концу, однако сложность вопросов увеличилась, и я начинаю иметь больше трудности с ответом, поскольку темы, обсуждаемые в дополнении, я не видел раньше. Что я узнал, чтобы ответить: я рассмотрел некоторые основные законы геометрии окружности, чтобы закончить этот вопрос, те, которые обычно изучаются на моем уровне математики: 1. если касательная встречается с радиусом, точка касания перпендикулярны, 2. две касательные из внешней точки равны, 3. если прямая проведена из центра к внешней точке двух касательных, то прямая делит угол пополам, 4. «теорема об альтернативном отрезке», 5. если 2 внешние окружности имеют 1 точку пересечения, прямая в этой точке является касательной. Я полагаю, что вопрос будет построен на основе этих правил, поскольку ожидается, что они будут изучены.
Любая помощь будет оценена по достоинству, и, пожалуйста, дайте мне знать, если есть что-то в вопросе, который мне нужно изменить, чтобы он был лучше отформатирован для будущих пользователей этого сайта.
- геометрия
- круги
- образование
$\endgroup$
3
$\begingroup$
Здесь мы хотим показать, что точки $B$ и $A$ являются соответственно центрами и эксцентрами, противоположными точкам $P$ в $\треугольнике PXY$. 92+2br}{b+r}$
Что такое $BM$?
$\frac{br}{b+r}$
Итак, почему окружность радиуса $BM$ также касается прямой?
Подсказка, используйте сходство.
$\endgroup$
геометрия — Докажите, что касательные и прямая параллельны
Хорошо, я серьезно думаю, что заслуживаю большой похвалы за написание этого доказательства! Я ожидаю много голосов и очень большое спасибо ! 😀
Пусть описанная окружность треугольника $XYZ$ равна $k_O$ с центром $O$. Пусть прямая $YO$ второй раз пересекает $k_O$ в точке $D$ (первая точка пересечения $Y$). Заметьте, что $DY$ — это диаметр $k_O$. Пусть $H$ — ортоцентр треугольника $XYZ$ (общая точка пересечения трех высот $XA, \, YB, \, ZC$). Пусть прямая $DH$ второй раз пересекает окружность $k_O$ в точке $E$ (первой точкой пересечения является точка $D$). Далее, пусть высота $YB$ пересекает ребро $XZ$ в точке $N$. Пусть две касательные к окружности $k_O$ в точках $X$ и $Z$ пересекаются в точке $S$, а окружность с центром в точке $S$ и радиусом $SX = SZ$ обозначается через $k_S$. 9{\circ}$.
Следовательно, точка $H$ является ортоцентром треугольника $RDY$, а четырехугольник $BHER$ вписан в окружность $k_G$ с центром $G$, являющимся серединой $HR$ (поскольку $HR$ является диаметром $ k_G$). Поскольку $BD$ ортогонален $BY$, а $BY$ ортогонален $XZ$ (как высота в $XYZ$), две прямые $BD$, которая совпадает с $DR$, и $XZ$ , проходящие через $N$, параллельны друг другу. Кроме того, это стандартный факт, что точка $N$ является серединой отрезка $HB$.
Пусть прямая $YO$ второй раз пересекает $k_O$ в точке $D$ (первая точка пересечения $Y$). Заметьте, что $DY$ — это диаметр $k_O$. Пусть $H$ — ортоцентр треугольника $XYZ$ (общая точка пересечения трех высот $XA, \, YB, \, ZC$). Пусть прямая $DH$ второй раз пересекает окружность $k_O$ в точке $E$ (первой точкой пересечения является точка $D$). Далее, пусть высота $YB$ пересекает ребро $XZ$ в точке $N$. Пусть две касательные к окружности $k_O$ в точках $X$ и $Z$ пересекаются в точке $S$, а окружность с центром в точке $S$ и радиусом $SX = SZ$ обозначается через $k_S$. 9{\circ}$.
Следовательно, точка $H$ является ортоцентром треугольника $RDY$, а четырехугольник $BHER$ вписан в окружность $k_G$ с центром $G$, являющимся серединой $HR$ (поскольку $HR$ является диаметром $ k_G$). Поскольку $BD$ ортогонален $BY$, а $BY$ ортогонален $XZ$ (как высота в $XYZ$), две прямые $BD$, которая совпадает с $DR$, и $XZ$ , проходящие через $N$, параллельны друг другу. Кроме того, это стандартный факт, что точка $N$ является серединой отрезка $HB$. Следовательно, середина $G$ треугольника $HR$, которая также является центром окружности $k_G$, лежит на $XZ$. Преследование прямого угла показывает, что $\угол \, GEH = 9{\circ}$, откуда следует, что окружности $k_G$ и $k_O$ ортогональны. Кроме того, мы показали, что $G$, центр $k_G$, лежит на $XZ$, которая является радикальной осью окружностей $k_O$ и $k_S$. Следовательно, по теореме о радикальной оси, если центр окружности лежит на радикальной оси двух других окружностей и ортогонален одной из них, то он ортогонален и другой. Следовательно, окружность $k_G$ ортогональна окружности $k_S$. Следовательно, окружность $k_S$ ортогональна как $k_G$, так и $k_O$. Таким образом, его центр $S$ лежит на радикальной оси $k_G$ и $k_O$, и этой радикальной осью является $BE$. 9{\circ}$ угол зрения из всех точек $A, C$ и $E$, пять точек $A, \, H, \, C, \, E$ и $Y$ лежат на одной окружности $ к_1$. Кроме того, по той же причине четверка $XZAC$ вписана в окружность $k_2$. По теореме о радикальных осях радикальные оси $EY, \, CA$ и $XZ$ между соответствующими парами из трех окружностей $k_1, \, k_2$ и $k_O$ совпадают, и пусть $Q$ — их общее пересечение.
Следовательно, середина $G$ треугольника $HR$, которая также является центром окружности $k_G$, лежит на $XZ$. Преследование прямого угла показывает, что $\угол \, GEH = 9{\circ}$, откуда следует, что окружности $k_G$ и $k_O$ ортогональны. Кроме того, мы показали, что $G$, центр $k_G$, лежит на $XZ$, которая является радикальной осью окружностей $k_O$ и $k_S$. Следовательно, по теореме о радикальной оси, если центр окружности лежит на радикальной оси двух других окружностей и ортогонален одной из них, то он ортогонален и другой. Следовательно, окружность $k_G$ ортогональна окружности $k_S$. Следовательно, окружность $k_S$ ортогональна как $k_G$, так и $k_O$. Таким образом, его центр $S$ лежит на радикальной оси $k_G$ и $k_O$, и этой радикальной осью является $BE$. 9{\circ}$ угол зрения из всех точек $A, C$ и $E$, пять точек $A, \, H, \, C, \, E$ и $Y$ лежат на одной окружности $ к_1$. Кроме того, по той же причине четверка $XZAC$ вписана в окружность $k_2$. По теореме о радикальных осях радикальные оси $EY, \, CA$ и $XZ$ между соответствующими парами из трех окружностей $k_1, \, k_2$ и $k_O$ совпадают, и пусть $Q$ — их общее пересечение. Затем, если мы еще раз применим теорему о радикальной оси, на этот раз ко всем трем парам окружностей $k_1, \, \hat{k}$ и $k_O$, соответствующие три радикальные оси $EY, \, AC $ и $BP$ также параллельны, и поскольку $Q$ уже является точкой пересечения $EY$ и $AC$, третья радикальная ось $BP$ также проходит через $Q$.
Затем, если мы еще раз применим теорему о радикальной оси, на этот раз ко всем трем парам окружностей $k_1, \, \hat{k}$ и $k_O$, соответствующие три радикальные оси $EY, \, AC $ и $BP$ также параллельны, и поскольку $Q$ уже является точкой пересечения $EY$ и $AC$, третья радикальная ось $BP$ также проходит через $Q$.
Следствие 3. Три прямые $BP, \, XZ$ и $EY$ пересекаются в общей точке $Q$.
Нарисуйте окружность $k_{BEQ}$, проходящую через три точки $B, \, Е$ и $Q$.
Лемма 3. Окружность $k_{BEQ}$ ортогональна окружности $k_S$.
Доказательство: Радикальная ось $k_{BEQ}$ и $k_O$ равна $BE$ и по
Лемма 1 проходит через центр $S$ окружности $k_S$. Опять же
одна из теорем о радикальной оси, поскольку $S$ находится на радикальной оси
$BE$ из $k_{BEQ}$ и $k_O$, а так как окружность $k_S$ ортогональна
к $k_O$, он также должен быть ортогонален окружности $k_{BEQ}$. (Что
Теорема гласит, что если центр окружности лежит на радикале
ось двух других окружностей и ортогональна одной из них, то
ортогонален и другому.

 Найдите диаметр окружности.
Найдите диаметр окружности. Найдите радиус окружности, если AB = 14 см, AO = 50 см.
Найдите радиус окружности, если AB = 14 см, AO = 50 см.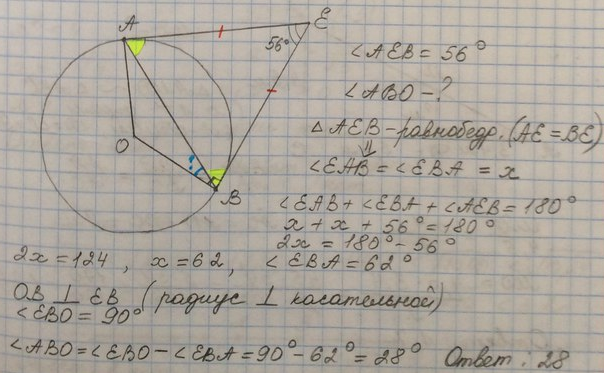 Найдите высоту этой трапеции.
Найдите высоту этой трапеции. Найдите диагональ этого квадрата
Найдите диагональ этого квадрата

 Найдите величину угла OMK. Ответ дайте в градусах.
Найдите величину угла OMK. Ответ дайте в градусах. Найдите угол ABO. Ответ дайте в градусах.
Найдите угол ABO. Ответ дайте в градусах.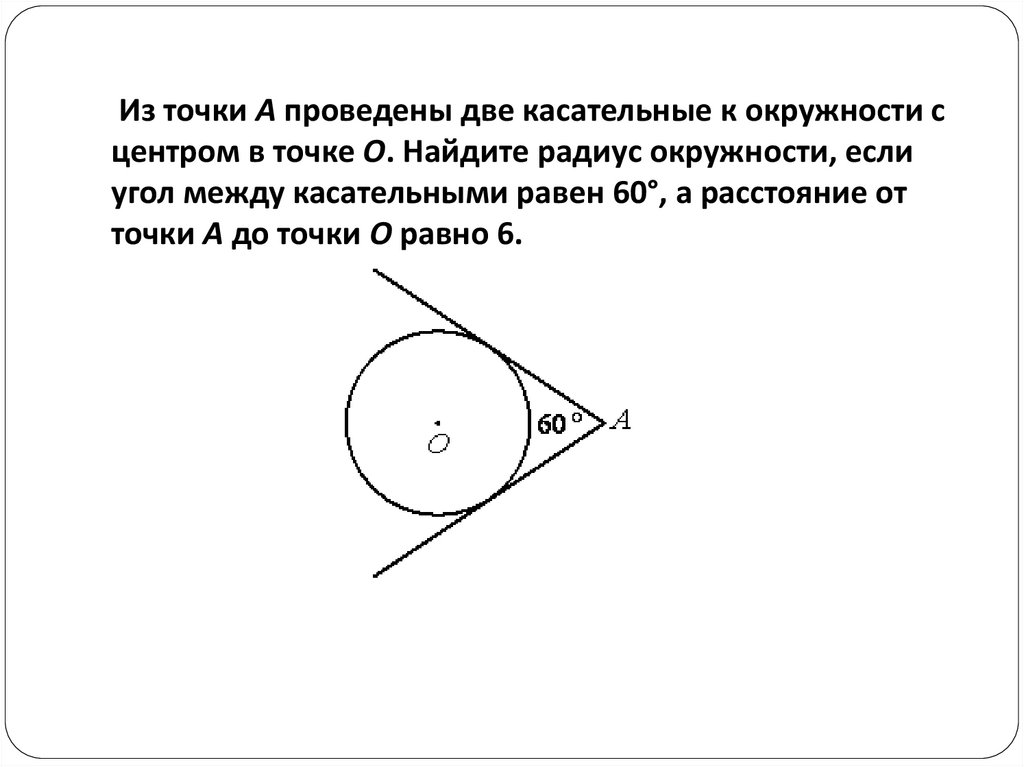 Найдите радиус окружности, описанной около этого треугольника
Найдите радиус окружности, описанной около этого треугольника Найдите высоту этого треугольника.
Найдите высоту этого треугольника.
Leave A Comment