Уравнение касательной
В этой статье мы разберем все типы задач на нахождение уравнения касательной.
Вспомним геометрический смысл производной: если к графику функции  в точке
в точке  проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси
проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси  ) равен производной функции в точке
) равен производной функции в точке 


Возьмем на касательной произвольную точку с координатами  :
:

И рассмотрим прямоугольный треугольник  :
:

В этом треугольнике 
Отсюда 
Или

Это и есть уравнение касательной, проведенной к графику функции  в точке
в точке  .
.
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти 
 .
.Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания 
2. Дан коэффициент наклона касательной, то есть значение производной функции 
 .
.3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1. Написать уравнение касательной к графику функции 
 .
.а) Найдем значение функции в точке  .
.
 .
.
б) Найдем значение производной в точке  . Сначала найдем производную функции
. Сначала найдем производную функции 


Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим: 
Ответ:  .
.
2. Найти абсциссы точек, в которых касательные к графику функции  параллельны оси абсцисс.
параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси  равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции
равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции  в точках касания равно нулю.
в точках касания равно нулю.
а) Найдем производную функции  .
.

б) Приравняем производную к нулю и найдем значения  , в которых касательная параллельна оси
, в которых касательная параллельна оси  :
:


Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5
3. Написать уравнения касательных к графику функции  , параллельных прямой
, параллельных прямой  .
.
Касательная параллельна прямой  . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
. Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция  и значение производной в точке касания.
и значение производной в точке касания.
а) Найдем точки, в которых производная функции  равна -1.
равна -1.
Сначала найдем уравнение производной.
Нам нужно найти производную дроби.


Приравняем производную к числу -1.


 или
или 
 или
или 
б) Найдем уравнение касательной к графику функции  в точке
в точке  .
.
Найдем значение функции в точке  .
.

 (по условию)
(по условию)
Подставим эти значения в уравнение касательной:
 .
.
б) Найдем уравнение касательной к графику функции  в точке
в точке  .
.
Найдем значение функции в точке  .
.

 (по условию).
(по условию).
Подставим эти значения в уравнение касательной:
 .
.
Ответ: 
4. Написать уравнение касательной к кривой  , проходящей через точку
, проходящей через точку 
Сначала проверим, не является ли точка  точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки
точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки  в уравнение функции.
в уравнение функции.

 . Мы получили под корнем отрицательное число, равенство не верно, и точка
. Мы получили под корнем отрицательное число, равенство не верно, и точка  не принадлежит графику функции и не является точкой касания.
не принадлежит графику функции и не является точкой касания.
Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.
Найдем значение  .
.
Пусть  — точка касания. Точка
— точка касания. Точка  принадлежит касательной к графику функции
принадлежит касательной к графику функции  . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
. Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
 .
.
Значение функции  в точке
в точке  равно
равно  .
.
Найдем значение производной функции  в точке
в точке  .
.
Сначала найдем производную функции  . Это сложная функция.
. Это сложная функция.

Производная в точке  равна
равна  .
.
Подставим выражения для  и
и  в уравнение касательной. Получим уравнение относительно
в уравнение касательной. Получим уравнение относительно  :
:


Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:


Приведем правую часть уравнения к общему знаменателю. Получим:

Упростим числитель дроби и умножим обе части на  — это выражение строго больше нуля.
— это выражение строго больше нуля.
Получим уравнение

Это иррациональное уравнение.
Решим его. Для этого возведем обе части в квадрат и перейдем к системе.


Решим первое уравнение.


Решим квадратное уравнение, получим
 или
или 
Второй корень не удовлетворяет условию 
 , следовательно, у нас только одна точка касания и её абсцисса равна
, следовательно, у нас только одна точка касания и её абсцисса равна  .
.
Напишем уравнение касательной к кривой  в точке
в точке  . Для этого подставим значение
. Для этого подставим значение  в уравнение
в уравнение 
 — мы его уже записывали.
— мы его уже записывали.
Получим:



Ответ: 
И.В. Фельдман, репетитор по математике.
Производная. Таблица производных. Связь функции с производной. Касательная. Первообразная
Факт 1.
Таблица производных: \[\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline
\textbf{1} & c & 0\\&&\\
\textbf{2} & x^a & a\cdot x^{a-1}\\&&\\
\textbf{3} & \ln x & \dfrac1x\\&&\\
\textbf{4} & \log_ax & \dfrac1{x\cdot \ln a}\\&&\\
\textbf{5} & e^x & e^x\\&&\\
\textbf{6} & a^x & a^x\cdot \ln a\\&&\\
\textbf{7} & \sin x & \cos x\\&&\\
\textbf{8} & \cos x & -\sin x\\
\hline
\end{array} \quad \quad \quad \quad
\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline &&\\
\textbf{9} & \mathrm{tg}\, x & \dfrac1{\cos^2 x}\\&&\\
\textbf{10} & \mathrm{ctg}\, x & -\,\dfrac1{\sin^2 x}\\&&\\
\textbf{11} & \arcsin x & \dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{12} & \arccos x & -\,\dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{13} & \mathrm{arctg}\, x & \dfrac1{1+x^2}\\&&\\
\textbf{14} & \mathrm{arcctg}\, x & -\,\dfrac1{1+x^2}\\[4ex]
\hline
\end{array}\]
Факт 2.
Пусть \(f=f(x), g=g(x)\) – функции.
\(\bullet\) Если \(c\) – число, то: \[(c\cdot f)’=c\cdot f’\] \(\bullet\) Производная суммы/разности двух функций: \[(f\pm g)’=f’\pm g’\] \(\bullet\) Производная произведения двух функций: \[(f\cdot g)’=f’\cdot g+f\cdot g’\] \(\bullet\) Производная частного двух функций: \[\left(\dfrac fg\right)’=\dfrac{f’\cdot g-f\cdot g’}{g^2}\] \(\bullet\) Производная сложной функции: \[\big(h(f(x))\big)’=h’_f(f)\cdot f’_x(x)\]
Факт 3.
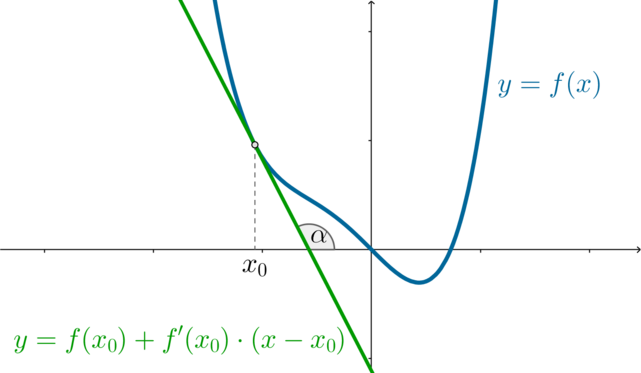
\(\bullet\) Если \(y=f(x)\) – некоторая функция, то касательная к ней в точке с абсциссой \(x_0\) имеет вид: \[y=f(x_0)+f'(x_0)\cdot (x-x_0)\] \(\bullet\) Следовательно, \(k=f'(x_0)=\mathrm{tg}\,\alpha\) – тангенс угла наклона касательной к положительному направлению оси \(Ox\), он же угловой коэффициент касательной, если ее уравнение записать как \(y=kx+b\).
Факт 4.
\(\bullet\) Если \(f'(x)>0\) на \((a;b)\), то \(f(x)\) возрастает на \((a;b)\).
\(\bullet\) Если \(f'(x)<0\) на \((a;b)\), то \(f(x)\) убывает на \((a;b)\).
\(\bullet\) Если \(f'(x_0)=0\) и в точке \(x_0\) производная меняет свой знак, то \(x_0\) — функции \(f(x)\):
— если производная меняет знак с “\(-\)” на “\(+\)” (считая слева направо), то \(x_0\) — ;
— если производная меняет знак с “\(+\)” на “\(-\)” (считая слева направо), то \(x_0\) — .
Факт 5.
\(\bullet\) \(F(x)\) – первообразная для \(f(x)\), если \(F'(x)=f(x)\).
\(\bullet\) Обозначение: \[\int f(x)\,dx=F(x)+c\] где \(c\in\mathbb{R}\) – некоторая константа.
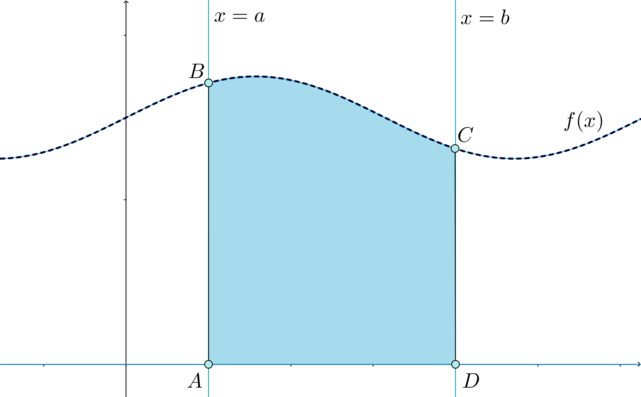
\(\bullet\) Формула Ньютона-Лейбница: \[\int \limits_a^b f(x)\,dx=F(b)-F(a)\] \(\bullet\) Тогда \(F(b)-F(a)\) равно площади закрашенной фигуры \(ABCD\), называемой криволинейной трапецией:
ПЗ. Производная: механический и геометрический смысл производной. Уравнение касательной в общем виде.
ПЗ. Производная: механический и геометрический смысл производной. Уравнение касательной в общем виде.
Задание:
1)Опорный конспект.
Механический смысл производной. Рассмотрим простейший случай: движение точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 +  точка перемещается на расстояние: x ( t0 +
точка перемещается на расстояние: x ( t0 +  ) — x ( t0 ) =
) — x ( t0 ) =  , а её средняя скорость равна: va =
, а её средняя скорость равна: va =  /
/  .
.
При 
 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0 ) материальной точки в момент времени t0 .
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0 ) материальной точки в момент времени t0 .
Но по определению производной мы имеем:

отсюда, v (t0) = x / (t0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v / ( t ).
Пример. Точка движется прямолинейно по закону S (t)= 2t3 – 0,5t2 + 3t (S – путь в метрах, t – время в секундах). Вычислить скорость движения точки в момент времени t=1с.
Решение: v( t ) = s / ( t ) = 6t2 – t + 3, v(1) = 6 – 1 + 3 = 8.
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Уравнение касательной. y = f ( x0 ) + f /( x0 ) · ( x – x0
2)Перепишите и заполните пропуски:
Пример 1. Найти угловой коэффициент касательной к графику функции y = f(x) в точке с
абсциссой х₀: а) y(x) = x³, x₀ = 1, б) y(x) = ln x, x₀ = 1, в) y(x) = 3x²  4x, x₀ = 2,
4x, x₀ = 2,
г) y(x) = х3 + 7x² 
Решение: угловой коэффициент k равен производной от функции в точке, т.е. k = y (x0) ,
найдем производные и вычислим их в точке x0
a)  б)
б) 

г) 
д) 
 7cos x,
7cos x,  7
7 cos 0 = 7
cos 0 = 7
ж)  е3 ln 4 = 3
е3 ln 4 = 3 43 = 3
43 = 3
Пример 2. а) Найти угловой коэффициент k, если 
 α = arctg 6, α = — arctg 8.
α = arctg 6, α = — arctg 8.
б) Найти α,если y(x) = 1/3 
Решение: а) k = tgα = tg  k = tgα = tg
k = tgα = tg  k = tgα = tg
k = tgα = tg 
k = tgα = tg  б)
б) 
Ответ: а)1, 
Пример 3. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Решение: Уравнение касательной: y = f / (x0) · (x − x0) + f(x0).
f (x0) = f (2) = 23 = …; f / (x) = (x3) = 3x2; f / (x0) = f / (2) = 3 · 22 = 3 4 = …;
4 = …;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16. Ответ: y = 12x − 16.
Пример 4. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.
Решение: f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = …; f / (x) = (2sin x + 5) / = 2cos x;
f / (x0) = f / (π/2) = 2cos (π/2) = 0; Уравнение касательной: y = 0 · (x − π/2) + 7 ⇒ y = … Ответ: y = 7.
Пример 5. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих  через точку M(– 3; 6).
через точку M(– 3; 6).
Решение: Точка M(– 3; 6) не является точкой касания, так как f(– 3) 6 (рис. ).
6 (рис. ).
1. a – абсцисса точки касания.
2. f(a) = – a2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a),a2 + 6a + 8 = 0 , D = 62  4
4 1
1 8 = 36
8 = 36  32 = …,
32 = …,
а1= ( 6
6  2) : 2 =
2) : 2 = 8 : 2 = …, а2 = (
8 : 2 = …, а2 = ( 6
6  2) : 2 =
2) : 2 =  4 : 2 = …,
4 : 2 = …,
Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение касательной имеет вид y = 6. Ответ: y = 4x + 18 или y = 6.
 Пример 6. Напишите уравнение касательной к графику функции y = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. ).
Пример 6. Напишите уравнение касательной к графику функции y = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. ).
Решение: Из условия f ‘(a) = tg 45°,  найдем a: a – 3 = 1 ,a = 3 + 1 = …
найдем a: a – 3 = 1 ,a = 3 + 1 = …
1. a = 4 – абсцисса точки касания. 2. f(4) = 8 – 12 + 1 = …
3. f ‘(4) = 4 – 3 = … 4. y = – 3 + 1(x – 4). y = x – 7 – уравнение касательной. Ответ: y = x – 7.
Пример 7. На параболе у = х2 взяты две точки с абсциссами 1 и 3. Через эти точки проведена прямая. В какой точке параболы касательная будет параллельна проведенной прямой?
Решение: у = х2 , (1;1), (3;9). Найдем уравнение прямой . 4х – 4 = у – 1. у = 4х – 3.
. 4х – 4 = у – 1. у = 4х – 3.
Прямые параллельны, если их угловые коэффициенты равны.
 — угловой коэффициент касательной в точке с абсциссой х0.
— угловой коэффициент касательной в точке с абсциссой х0.
 2х0 = 4. х0 = … ,
2х0 = 4. х0 = … ,  Ответ: в точке (2;4) касательная параллельна прямой.
Ответ: в точке (2;4) касательная параллельна прямой.
Пример 8. При каких b и c прямые y = x и y = – 2x являются касательными к графику
функции y = x2 + bx + c?
Решение: Пусть t – абсцисса точки касания прямой y = x с параболой y = x2 + bx + c;
p – абсцисса точки касания прямой y = – 2x с параболой y = x2 + bx + c.
Тогда уравнение касательной y = x примет вид y = (2t + b)x + c – t2, а уравнение
касательной y = – 2x примет вид y = (2p + b)x + c – p2. Составим и решим систему уравнений:
 ;
;
2t = 1,5; t = 0,75; p = – t = …, c =  =
=  = …, b = 1 – 2t = 1 – 2
= …, b = 1 – 2t = 1 – 2  0,75 = 1– 1,5 = …
0,75 = 1– 1,5 = …
Ответ: b = – 0,5; c = 0,562 5.
3)Решить задание ( по примерам):
- Найти угловой коэффициент касательной к графику функции y = f(x) в точке с
абсциссой х₀: а) y(x) = x4, x₀ = 1, б) y(x) = ln x, x₀ = 2, в) y(x) = 3x² — 4x, x₀ = 4,
г) y(x) = х3 + 7x² — 5x+3, x₀ =5, д) y(x) = ех, x₀ = ln 8, e) y(x) = 9sinx, x₀ = 0,ж) y(x) = е3х, x₀ = ln 6.
-
а) Найти угловой коэффициент k, если

 α = arctg 9, α = — arctg 11.
α = arctg 9, α = — arctg 11.
б) Найти α,если y(x) = 1/3  х3, x₀ = 4.
х3, x₀ = 4.
- Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 1.
- Составить уравнение касательной к графику функции f (x) = 4sin x + 5 в точке x0 = π/2.
- Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 9).
-
Напишите уравнение касательной к графику функции y = 0,5x2 – 5x + 1, проходящей
под углом 45° к прямой y = 0 . -
На параболе у=х2 взяты две точки с абсциссами 1 и 2. Через эти точки проведена прямая.
В какой точке параболы касательная будет параллельна проведенной прямой? -
При каких b и c прямые y = x и y = – 2x являются касательными к графику
функции y = x2 + 2bx + c? - Точка движется прямолинейно по закону S (t)= t5 – t4 + 6 (S – путь в метрах, t – время в секундах). Вычислить скорость движения точки в момент времени t=2с.
- Точка движется прямолинейно по закону S (t)= 2t3 – 0,5t2 + 3t (S – путь в метрах, t – время в секундах). Вычислить скорость движения точки в момент времени t= 2с.
- Какая из приведенных зависимостей описывает равноускоренное движение:
а) x = 4 + 2t; б) v = 5; в) x = 8 — 2t — 4t2; г) x = 10 + 5t2.
- Точка движется вдоль оси х согласно закону х = 8 – 2t – 4t2 . Определите начальную скорость и ускорение . Запишите уравнение для скорости.
4)Решить задание:
- Напишите уравнения касательных, проведенных к графику функции y = 2x2 – 4x + 3 в точках пересечения графика с прямой y = x + 3.
- При каких значениях a касательная, проведенная к графику функции y = x2 – ax в точке графика с абсциссой x0 = 1, проходит через точку M(2; 3)?
- Найдите все общие точки графика функции y = 3x – x3 и касательной, проведенной к этому графику через точку P(0; 16).
-
На кривой y = x2 – x + 1 найдите точку, в которой касательная к графику параллельна
прямой y – 3x + 1 = 0. - Найдите угол q между касательными к графику функции y = x3 – 4x2 + 3x + 1, проведенными в точках с абсциссами 0 и 1.
- Прямая y = 2x + 7 и парабола y = x2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.
- При каких значениях b касательная, проведенная к графику функции y = bx3 – 2x2 – 4 в точке с абсциссой x0 = 2, проходит через точку M(1; 8)?
-
Найти угол между касательными к графику функции
 , проведенными в точках с абсциссами 1 и 2.
, проведенными в точках с абсциссами 1 и 2.
- Является ли прямая у = х – 1 касательной к кривой у = х3 – 2х + 1?
-
Найдите уравнение касательной к графику функции
 в точке с абсциссой
в точке с абсциссой  .
.
-
К графику функции у = 3(х + 2) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х0 = – 1. Найдите абсциссу точки, в которой
другая касательная касается графика данной функции. - Напишите уравнение касательной к графику функции f(x) = x2 – 4x + 5, если эта касательная проходит через точку (0; 4) и абсцисса точки касания положительна.
- Напишите уравнение касательной к графику функции f(x) = x2 + 3x + 5, если эта касательная проходит через точку (0; 1) и абсцисса точки касания отрицательна.
-
Найдите уравнение параболы f(x) = ax2 + bx + 1 касающейся прямой у = 7х + 2
в точке М (1; 5). -
К графику функции
 провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
-
Из точки (0; 1) провести касательную к графику функции
 .
.
-
Составить уравнение касательной к графику функции
 в точке с абсциссой
в точке с абсциссой .
.
-
Составить уравнение касательной к графику функции
 в точке с абсциссой
в точке с абсциссой
-
Составить уравнение касательной к графику функции

в точке с абсциссой .
.
-
Составить уравнение касательной к графику функции
 > 0, отсекающей от осей координат треугольник, площадь которого равна
> 0, отсекающей от осей координат треугольник, площадь которого равна .
.
- Задача. Пусть X = 2 + 4t2 — sin2πt. Найти: а) мгновенную скорость, б) ускорение, если t = 0,5 c.
- Задача. Высота снежка, брошенного вертикально вверх со скоростью U0 с начальной высоты h0, меняется по закону h =h0+U0t-gt2/2, где g =10м/c – ускорение силы тяжести. Покажите, что энергия камня Е= mv2/ 2 + mgh, где m – масса снежка, не зависит от времени.
- Задача. Количество электричества, протекающее через проводник, задаѐтся формулой
q(t) = t+4/t. В какой момент времени ток в цепи равен нулю?
Уравнение касательной к графику функции
Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.
А что будет, если производная в точке x0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
- Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Задача. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x0) = f ’(π/2) = 2cos (π/2) = 0;
Уравнение касательной:
y = 0 · (x − π/2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
Смотрите также:
- Правила вычисления производных

- Вводный урок по вычислению производных степенной функции

- Пробный ЕГЭ-2011 по математике, вариант №6

- Площадь круга

- Иррациональные неравенства. Часть 1

- Задача B5: вычисление площади методом обводки

Производная функций,ее геометрический и физический смысл.Уравнение касательной .
Министерство образования и науки РД
МКОУ «Джибахнинская СОШ»
Открытый урок по математике для
6 класса
«Производная функций,ее геометрический и физический смысл.Уравнение касательной .»
Подготовила:
Магомедова П.М,
учитель математики
МКОУ «Джибахнинская СОШ»
2020
Тема: Производная функций, ее геометрический и физический смысл. Уравнение касательной
Задачи:
Обучающие: Обобщить и систематизировать свой знания умения и навыки нахождения производных функции ,ее геометрическом и физическом смысле и применить их к решению задач ЕНТ
Развивающие:Развитие познавательных интересов ,вычислительных навыков ,навыков устного счета , использование рациональных способов решения ,умения взаймопроверки и самооценки знаний
Воспитывающие: воспитание трудолюбия,чувства ответственности, рационального использование урочного времени
План урока.
I.Оганизационный момент
II.Проверка домашнего задания:
Работа в группах.
1.Проверить и оценить работу;
2. Разминка- знание формул 3 мин. нахождение соответствия « Найди пару».
III.Основной этап урока.
1. Повторение теоритического материала;
2.Выполнение задач ЕНТ, решаемых устно ;
3.Задание на соответствие;
4. Задание-2;
5. Тест
IV.Заверщающий этап
Домашнее задание.
Оценка знаний
Итог урока
Самооценочная карта
№ | Фамилия и имя уч-ся | Баллы | Оценка |
1 | Домашнее задание ( ) | ||
2 | Работа в парах «Найди пару»-(1балл) | ||
3 | Теория ( каждый правильный ответ по 1 баллу) | ||
4 | Устные задания (каждый правильный ответ по 1 баллу ) | ||
5 | Задачи | ||
6 | Тест | ||
9 | Итоговые баллы( ) | ||
Ход урока.
1.Организационный момент-(3-4мин)
-приветствие
-Девиз урока :
Урок начнем с девиза «Никогда не беритесь за последующее ,не усвоив предыдущее»
И.П. Павлов
Так как нам предстоит изучение темы «Применение производной,которая важна,так же как сама производная при подготовке и сдаче ЕНТ-ы,поэтому необходимо обобщить и закрепить наши знания по теме производная функций
И так тема урока:Производная функций,ее геометрический и физический смысл. Уравнение касательной в заданиях ЕНТ
Задачи урока:
Обучающие: Обобщить и систематизировать свой знания умения и навыки нахождения производных функции ,ее геометрическом и физическом смысле и применить их к решению задач ЕНТ
Развивающие:Развитие познавательных интересов ,вычислительных навыков ,навыков устного счета , использование рациональных способов решения ,умения взаймопроверки и самооценки знаний
Воспитывающие: воспитание трудолюбия,чувства ответственности, рационального использование урочного времени
2.Проверка домашнего задания-на дом были заданы 10 тестовых заданий из сборников ЕНТ-ы 2015
-«Проверь себя”
Ответы домашнего задания (3мин.)
3.А теперь разминка.(5мин)
-раздаточный материал
Найдите соответствие между функцией и ее производным.Напишите ответ. Например: 1функция – ? производная.
Ответы на соответствие:
Ответы: 1-9; 6-3; 11-14;
16-19; 2-4; 7-18; 12-19;
17-13; 3-5; 8-17; 4-19;
5-19; 15-16; 10-20.
Вопросы теоретического материала(7мин)
1.Определение производной функций и алгоритм ее нахождения
2.Правила вычисления производных
3.Физический смысл производной
4.Геометрический смысл производной
5.Уравнение касательной к графику функций в точке с абциссой х
6.Как найти уравнение касательной ,проведенной к графику функций у= f(x) параллельно прямой y=кх+в
7.Нахождение координаты точек пересечения производной и касательной проведенной в точку касания
8.Как найти уравнение касательной, если она пересекает ось ординат и ось абцисс
9.Как найти угол наклона между касательной и графиком функций
10.Как найти угловой коэффициент
11.Как найти скорость ,ускорение, силу и кинетическую энергию с помощью производной функций
Устные задания (5мин)
Некоторые задания ЕНТ расчитаны на устные выполнения,что позволяет сэкономить время для решения более сложных заданий:
1.у=
2. у=(х2+1) (х2-1)
3. у=-
4.у=cos2x+sin2x
5 y=cos2x-sin2x
6.y=(x-2) (x2+2х+4)
7.y=
Ответы:
1.y´=4x3— 3x2 2.y´=4x3 3. у/= 4.y´=0 5.y´=-2sin2x
6.y´=3x2 7. у/=
Тест
1.Найдите производную функций: f(x)=sin(x3+2)
A)3cos(x3+2) B)3sin(x3+2) C)x2(x3+2) D)3x2(x3+2) E) 3x2cos(x3+2)
2.В каких точках касательная,проведенная к графику функций у=
cостовляет с осью абцисс угол 60 0
A) ( ; ) B) ( 😉 C) (1 ; 1 ) D) ( ) E) ( )
3. Найдите производную функций f(x)=(x5+2x3)95
A)95(x5+2x3)94 B)95(x5+2x3)94 C)95(5x4+6x2)(x5+2x3)94
D) (x5+2x3)95 E)96(x5+2x3)96
4. Найдите производную функций: f(x)= (-5x2)32
A) -160(-5x2)32 B)-160(-5x2)32 C)-320(-5x2)32 D)8(-5x2)32 E)32(-5x2)32
5.Дана функция: у=найдите у/(х)
A) B — C) — D) E)
6. Найдите производную функций: f(x)=
A) B) C) D) E) —
7. Найдите производную функций:f(x)=(5x+6)8
A)5(5x+6)7 B)-8(5x+6)7 C)40(5x+6)7 D)13(5x+6)7 E)8(5x+6)8
8.Если y(x)=sin3x cos5x-cos3x sin5x,то y/()равно:
A)-1 B)- C) D)1 E) —
9.Если f(x)=sin3 . f/()
A) B) C)1 D)2 E)
10. Тело движется прямолинейно по закону S(t)=4t-t2 найдите скорость движения тела в момент времени t=1.75сек.
A)2,5м/с B)1м/с C)0,5м/с D)2м/с E)1,5м/с
Коды ответов:
1 | Е |
2 | А |
3 | С |
4 | С |
5 | В |
6 | В |
7 | С |
8 | Д |
9 | В |
10 | С |
Задачи :
Домашнее задание:задачи ЕНТ-2015год
Итог:
Изучение свойств и способов вычисления производных и их применение играет большую роль в развитий науки и техники.Это основа предмета ВУЗа –дифференциальное исчисления,механика.Необходимо для решения задач ЕНТ по физике, геометрии.
Материал этого урока поможет вам успешно выполнить задания при подготовке к ЕНТ.а также успешному усвоению следующего раздела: «Применение производных функций».
Урок окончен,
Спасибо за внимание!
Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
«Сегодня на уроке я познакомился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
Письменная работа
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
Карточка №2 (уровень сложности В)
1 Найдите производную функции:
у = —
у = sin(2х2 + 3)
3. Решите уравнение: f ‘ (x) = 0, если f (x) = —
Карточка №3 (уровень сложности С)
Найдите производную функции:
у =
у =
у = arctg 2x
Самооценочная карта
№ | Фамилия и имя уч-ся | Баллы | Оценка |
1 | Домашнее задание ( ) | ||
2 | Работа в парах «Найди пару»-(1балл) | ||
3 | Теория ( каждый правильный ответ по 1 баллу) | ||
4 | Устные задания (каждый правильный ответ по 1 баллу ) | ||
5 | Задачи | ||
6 | Тест | ||
9 | Итоговые баллы( ) | ||
Самооценочная карта
№ | Фамилия и имя уч-ся | Баллы | Оценка |
1 | Домашнее задание ( ) | ||
2 | Работа в парах «Найди пару»-(1балл) | ||
3 | Теория ( каждый правильный ответ по 1 баллу) | ||
4 | Устные задания (каждый правильный ответ по 1 баллу ) | ||
5 | Задачи | ||
6 | Тест | ||
9 | Итоговые баллы( ) | ||
Самооценочная карта
№ | Фамилия и имя уч-ся | Баллы | Оценка |
1 | Домашнее задание ( ) | ||
2 | Работа в парах «Найди пару»-(1балл) | ||
3 | Теория ( каждый правильный ответ по 1 баллу) | ||
4 | Устные задания (каждый правильный ответ по 1 баллу ) | ||
5 | Задачи | ||
6 | Тест | ||
9 | Итоговые баллы( ) | ||
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
——————————————————
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
——————————-
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
——————————————
Карточка №1 (уровень сложности А)
1 Найдите производную функции:
у = 4х4 — х5 + х2 -3х
у = (х + 4)3
у =
10 класс. Алгебра. Производная. Применение производной к исследованию функции. — Уравнение касательной к графику функции.
Комментарии преподавателя
Уравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую  (см. рис.1).
(см. рис.1).

Рис. 1. График функции  .
.
Зафиксируем точку  . Если
. Если  , то значение функции равно
, то значение функции равно  . Значит, имеем точку с координатами (
. Значит, имеем точку с координатами ( .
.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции  в точке с абсциссой
в точке с абсциссой  , в которой
, в которой  — существует.
— существует.
Уравнение касательной – это прямая, которая задается формулой 
Любая прямая, в том числе и касательная, определяется двумя числами: и
и  . Исходя из геометрического смысла производной
. Исходя из геометрического смысла производной  (тангенс угла наклона касательной) – это есть угловой коэффициент
(тангенс угла наклона касательной) – это есть угловой коэффициент  .
.
Параметр  найдем из условия, что касательная проходит через точку (
найдем из условия, что касательная проходит через точку ( , то есть
, то есть  .
.
 .
.
Стало быть  .
.
Запишем уравнение касательной
 .
.
Или,  .
.
Получили уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
– точка касания касательной и графика функции.
2)  — угловой коэффициент касательной к графику функции.
— угловой коэффициент касательной к графику функции.
3)  – произвольная точка на касательной.
– произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что  – это произвольная точка на касательной.
– это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Задача.
К кривой  в точке с абсциссой
в точке с абсциссой  провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).

Рис. 2. Касательная к графику функции  .
.
Зафиксируем точку  . Значение функции в этой точке равно 1.
. Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти  и точку касания.
и точку касания.
 — дано.Точка касания: (
— дано.Точка касания: ( ;
; .
.
2) Найти производную в любой точке  .
.
 .
.
3) Найти значение производной в точке с абсциссой  .
.
 .
.
4) Выписать и проанализировать уравнение касательной.
 .
.
Упрощаем и получаем:  .
.
Ответ:  .
.
Задача 1.
Пусть дано уравнение касательной  .
.
Найдите точки пересечения касательной с осями координат.
Если  , то
, то  .
.  – это первая точка.
– это первая точка.
Если  , то
, то  .
.  — вторая точка.
— вторая точка.
Итак, первая точка – это точка  с координатами
с координатами  . Вторая точка – точка пересечения с осью
. Вторая точка – точка пересечения с осью  , точка
, точка  с координатами
с координатами  (см. рис.3).
(см. рис.3).

Рис.3. Точки пересечения касательной к графику функции  с осями координат. Задача 2.
с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка  .
.
Рассмотрим прямоугольный треугольник  (Рис. 3). Длина катета
(Рис. 3). Длина катета  равна 1. Длина катета
равна 1. Длина катета  . Длину отрезка
. Длину отрезка  из прямоугольного треугольника найдем по теореме Пифагора:
из прямоугольного треугольника найдем по теореме Пифагора:

Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника  (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
(Рис. 3) — площадь треугольника, образованного касательной и осями координат.

Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник  . Радиус окружности, описанной около треугольника
. Радиус окружности, описанной около треугольника  .
.
Рассмотрим пример.
Дана функция  . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
. Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).

Рис. 4. Касательная к графику функции  .
.
Нахождение точки касания.
1.  Точка касания имеет координаты
Точка касания имеет координаты
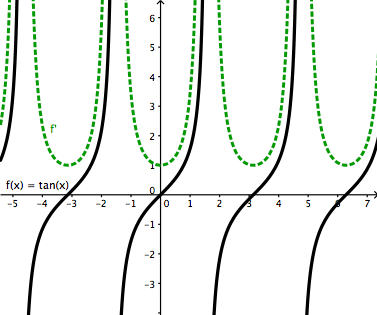
Производная tan (x) | Ресурсы Wyzant
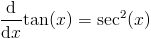
Производное доказательство tan (x)
Мы можем доказать эту производную, используя производные sin и cos, а также правило частного.
Запишите тангенс через синус и косинус
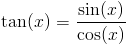
Возьмите производную от обеих сторон
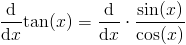
Использовать правило частного
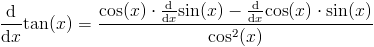
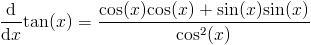
Упростить
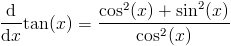
Используйте тождество Пифагора для синуса и косинуса
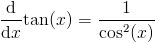
и упростить
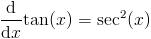

Производные доказательства csc (x), sec (x) и cot (x)
Производная этих триггерных функций может быть легко получена из правило Qoutient, использующее обратные величины sin (x), cos (x) и tan (x).
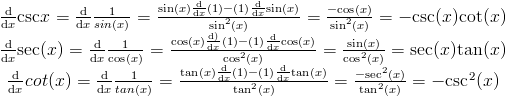

Производные триггерные функции
| Доказательства: Производные Триггерные функции |
| (Математика | Исчисление | Деривативы | Стол Из | Триггерные функции) |
| грех (х) = cos (x) cos (x) = -sin (x) tan (x) = сек ^ 2 (x) csc (x) = -csc (x) детская кроватка (x) сек (х) = сек (х) загар (x) кроватка (x) = -csc ^ 2 (x) |
Доказательства производных триггерных функций
Доказательства sin (x) : алгебраический метод Дано : lim (d-> 0) sin (d) / d = 1.
Решить :
грех (x) = lim (d-> 0) (sin (x + d) — sin (x)) / d
= lim (sin (x) cos (d) + cos (x) sin (d) — sin (x)) / d
= lim (sin (x) cos (d) — sin (x)) / d + lim cos (x) sin (d) / d
= sin (x) lim (cos (d) — 1) / d + cos (x) lim sin (d) / d
= sin (x) lim ((cos (d) -1) (cos (d) +1)) / (d (cos (d) +1)) + Cos (x) lim sin (d) / d
= sin (x) lim (cos ^ 2 (d) -1) / (d (cos (d) +1) + Cos (x) lim sin (d) / d
= sin (x) lim -sin ^ 2 (d) / (d (cos (d) + 1)). + Cos (x) lim sin (d) / d
= sin (x) lim (-sin (d)) * lim sin (d) / d * lim 1 / (cos (d) +1) + Cos (x) lim sin (d) / d
= sin (x) * 0 * 1 * 1/2 + cos (x) * 1 = cos (x) В.E.D.
Подтверждение cos (x) : от производной синуса
Это можно вывести так же, как sin (x) был получен или более легко из результата грех (х)
Дано : грех (х) = соз (х); Правило цепи.
Решить :
cos (x) = sin (x + PI / 2)
cos (x) = грех (x + PI / 2)
= грех (и) * (x + PI / 2) (Установить u = x + PI / 2)
= cos (u) * 1 = cos (x + PI / 2) = -sin (x) В.E.D.
Подтверждение tan (x) : от производных синуса и косинуса
Дано : грех (х) = соз (х); cos (x) = -sin (x); Частное Правило.
Решить :
tan (x) = sin (x) / cos (x)
желто-коричневый (x) = грех (х) / соз (х)
= (cos (x) грех (х) — грех (х) cos (x)) / cos ^ 2 (x)
= (cos (x) cos (x) + sin (x) sin (x)) / cos ^ 2 (x)
= 1 + загар ^ 2 (x) = сек ^ 2 (x) В.E.D.
Взаимные
Подтверждение csc (x), sec (x), детская кроватка (x) : от производные от их взаимных функций
Дано : грех (х) = соз (х); cos (x) = -sin (x); загар (х) = детская кроватка (х); Частное Правило.
Решить :
csc (x) = 1 / sin (x) = ( грех (х) (1) — 1 грех (х)) / грех ^ 2 (х) = -cos (x) / sin ^ 2 (x) = -csc (x) детская кроватка (x)
сек (x) = 1 / cos (x) = ( cos (x) (1) — 1 соз (х)) / соз ^ 2 (х) = sin (x) / cos ^ 2 (x) = sec (x) tan (x)
детская кроватка (x) = 1 / tan (x) = ( загар (х) (1) — 1 tan (x)) / tan ^ 2 (x) = -сек ^ 2 (x) / tan ^ 2 (x) = -csc ^ 2 (x) В.E.D..
Какая производная от tanh (x)?
Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
- Предалгебра
- Precalculus


 α = arctg 9, α = — arctg 11.
α = arctg 9, α = — arctg 11.
 , проведенными в точках с абсциссами 1 и 2.
, проведенными в точках с абсциссами 1 и 2.
 в точке с абсциссой
в точке с абсциссой  .
.
 провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
 .
.
 в точке с абсциссой
в точке с абсциссой .
.
 в точке с абсциссой
в точке с абсциссой

 .
.
 > 0, отсекающей от осей координат треугольник, площадь которого равна
> 0, отсекающей от осей координат треугольник, площадь которого равна .
.


Leave A Comment