Поиск: | ||||||||||||||||||||||||||||||
HOME | § 1 § 2 § 3 § 4 § 5 § 6 § 7 § 8 § 9 § 10 § 11 § 13 § 14 § 15 § 16 § 17 § 18 § 19 § 20 § 21 § 22 § 23 § 24 § 25 § 26 § 27 § 28 § 29 § 30 § 31 § 32 § 33 § 34 § 35 § 36 § 37 § 38 § 39 § 40 § 41 § 105 | ||||||||||||||||||||||||||||||
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | ||||||||||||||||||||||||||||||
| Решения по Физике МИРЭА. sm |
85185. Частицы а и b движутся по оси х. В момент времени t0 = 0 они находились в начале координат и одновременно достигли точки С, координата которой хC = s. Частица а первую половину пути прошла со скоростью vax = 2v, вторую половину пути — со скоростью vax = v/2. Частица b прошла первую половину пути со скоростью vbx = v/2, вторую половину пути — со скоростью vbx = 2v. Найдите интервал времени, в течение которого расстояние между частицами принимает постоянное наибольшее значение sm. Определите sm и среднее значение проекции скорости частиц. Частица а первую половину пути прошла со скоростью vax = 2v, вторую половину пути — со скоростью vax = v/2. Частица b прошла первую половину пути со скоростью vbx = v/2, вторую половину пути — со скоростью vbx = 2v. Найдите интервал времени, в течение которого расстояние между частицами принимает постоянное наибольшее значение sm. Определите sm и среднее значение проекции скорости частиц. |
| 85186. Спортсмены бегут колонной длиной I0 с одинаковыми скоростями v. Навстречу бежит тренер со скоростью u (u < v). Спортсмен, поравнявшийся с тренером, разворачивается и бежит в обратную сторону с той же величиной скорости v. Найдите длину колонны I, когда все спортсмены будут бежать в направлении, противоположном первоначальному. |
85187. Автомобиль начинает двигаться из состояния покоя. Первую половину пути он движется с постоянным ускорением. На втором участке пути он движется с постоянной скоростью v = 18 м/с, которой достиг в конце первого участка. Найдите среднюю скорость автомобиля vср. Найдите среднюю скорость автомобиля vср. |
| 85188. Частица начинает двигаться по прямой линии из состояния покоя с постоянным ускорением. В момент времени t1 = 3 с скорость частицы в точке A равна v1 = 6 м/с. Найдите расстояние s между частицей и точкой A за секунду до пересечения частицей точки A. |
| 85189. Частица движется по оси х. На рис. приведена зависимость проекции ускорения на ось х от времени. В какой момент времени проекция скорости частицы vx(t) достигает наибольшего значения? |
| 85190. Поезд начинает движение по прямой линии, параллельной оси х. На рис. а изображен график зависимости проекции скорости vx(t) от времени. За время 2т поезд прошел путь s = 18 км. Найдите ускорение поезда на отрезке времени [0, т], т = 10 мин. |
85191. Две частицы начинают одновременно двигаться из начала координат по оси х. Зависимость проекции скоростей частиц от времени изображена на рис. В момент времени т = 1 с скорости частиц одинаковы. Найдите значение t = Т, при котором первая частица догонит вторую. В момент времени т = 1 с скорости частиц одинаковы. Найдите значение t = Т, при котором первая частица догонит вторую. |
| 85192. Частица начинает двигаться по оси х из начала координат. На рис. приведена зависимость проекции скорости на ось х от времени (v0 = 10 м/с, т = 1 с). Найдите координату частицы через интервал времени равный 2т. |
| 85193. Частица начинает двигаться по оси х из начала координат. На рис. приведена зависимость проекции скорости на ось х от времени (v0 = 10 м/с, т = 1 с). Найдите значение момента времени Т, в который частица окажется в исходном положении. |
| 85194. Частица начинает двигаться по оси х из начала координат. На рис. приведена зависимость проекции скорости на ось х от времени (v0 = 10 м/с, т = 1 с). Найдите среднее значение проекции скорости частицы в интервале (0,2т). |
85195. Координата частицы, движущейся по прямой линии, x(t) = v0t — at2/2, t > 0. Найдите значение пути s, который частица пройдет за промежуток времени tm = 2v0/a. Найдите значение пути s, который частица пройдет за промежуток времени tm = 2v0/a. |
| 85196. Частица начинает двигаться по оси х из начала координат. На рис. изображен график зависимости проекции скорости vx(t) от времени (v0 = 10 м/с, т = 1 с). Найдите значение х-координаты в момент времени t = 3т. |
| 85197. Частица начинает двигаться по оси х из начала координат. На рис. изображен график зависимости проекции скорости vx(t) от времени (v0 = 10 м/с, т = 1 с). Найдите среднее значение проекции скорости на отрезке времени [0, 2т]. |
| 85198. Частица начинает двигаться по оси х из начала координат. На рис. изображен график зависимости проекции скорости vx(t) от времени. Найдите значение x-координаты в момент времени t = 4т. |
85199. Частица начинает двигаться по оси х из начала координат. На рис. изображен график зависимости проекции скорости vx(t) от времени. Найдите путь, пройденный частицей на отрезке времени [0,4т]. |
| 85200. Частица движется по прямой линии с постоянным ускорением, проходя последовательно два отрезка пути I1 и l2 за интервалы времени t1 и t2. Найдите величину ускорения частицы. |
| 85201. Частица движется по прямой линии. Проекция скорости v(t) = kt (t0 — t), t > 0. Найдите путь s, пройденный частицей за промежуток времени t0. |
| 85202. Частица начинает двигаться по прямой линии с постоянным ускорением, проходит путь I за пятую секунду и останавливается. Найдите путь s, пройденный частицей за третью секунду. |
| 85203. Тормозной путь железнодорожного состава, движущегося со скоростью v = 51 км/ч, равен s = 390 м. Найдите коэффициент трения ц колес о рельсы. |
85204. При торможении автомобиль, движущийся со скоростью v1 = 40 км/ч, прошел до полной остановки путь s1 = 16 м. Определите путь s2, который пройдет автомобиль при уменьшении скорости от значения v3 = 100 км/ч до значения v2 = 60 км/ч. -1. Найдите скорость частицы v = (v1, v2, 0) в начале координат. -1. Найдите скорость частицы v = (v1, v2, 0) в начале координат. |
| 85208. Концы стержня АВ, по которому перемещается частица, скользят по двум взаимно перпендикулярным прямым: точка В движется по оси х, точка А — по оси у. В начальный момент времени t = 0 стержень расположен на оси у, конец стержня В и частица — в начале координат. Величина скорости точки В равна v, частицы относительно стержня — u, длина стержня — I. Найдите максимальное значение у-координаты частицы. |
| 85209. Четыре стержня одинаковой длины а, соединенные шарнирами, образуют ромб ABCD. В момент времени t = 0 вершины А и С начинают смещать в противоположные стороны со скоростями одинаковой величины v(t) = kt(T — t), 0 < t < Т (рис. а). В момент времени t = T ромб переходит в квадрат. Найдите ускорение аb(Т) вершины В в момент времени t = T. |
85210. Конец A тонкой нити длиной l0 закреплен на пересечении кругового цилиндра радиусом R и горизонтальной плоскости. К другому концу Р натянутой нити прикреплена частица, которая движется вокруг цилиндра в той же горизонтальной плоскости. Найдите длину траектории частицы sm через промежуток времени, соответствующий намотке всей нити на цилиндр. К другому концу Р натянутой нити прикреплена частица, которая движется вокруг цилиндра в той же горизонтальной плоскости. Найдите длину траектории частицы sm через промежуток времени, соответствующий намотке всей нити на цилиндр. |
| 85211. На рис. изображены начальные витки двух спиралей Архимеда в координатах х’, у’: отрезок ОР = Аф, 0 < ф < п и отрезок ON = A(2п — ф), п < ф < 2п. Система K’ вращается в направлении движения часовой стрелки вокруг оси z с угловой скоростью w, относительно неподвижной системы отсчета К. Найдите функцию хр = x(t) — координату точки Р пересечения оси х системы К с ветвями спирали, максимальное значение функции x(t) и максимальное значение величины скорости vm точки Р в системе К’. Назовите механические устройства, в которых можно применить эту систему. |
85212. Простое преследование на плоскости. Заяц бежит с постоянной скоростью по прямой линии. За зайцем гонится лиса со скоростью, постоянно направленной в «точку», где находится заяц. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Найдите ускорение лисы в момент времени tm, соответствующий расстоянию sm. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Найдите ускорение лисы в момент времени tm, соответствующий расстоянию sm. |
| 85213. Простое преследование на плоскости. Заяц бежит с постоянной скоростью по прямой линии. За зайцем гонится лиса со скоростью, постоянно направленной в «точку», где находится заяц. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Найдите расстояние между лисой и зайцем s(t) при значениях t >> tm. |
85214. Простое преследование на плоскости. Заяц бежит с постоянной скоростью по прямой линии. За зайцем гонится лиса со скоростью, постоянно направленной в «точку», где находится заяц. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Величина скорости зайца v = 3 м/с, величина скорости лисы u = 5 м/с. Найдите промежуток времени T, через который лиса догонит зайца. Заяц бежит с постоянной скоростью по прямой линии. За зайцем гонится лиса со скоростью, постоянно направленной в «точку», где находится заяц. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Величина скорости зайца v = 3 м/с, величина скорости лисы u = 5 м/с. Найдите промежуток времени T, через который лиса догонит зайца. |
85215. Простое преследование на плоскости. Заяц бежит с постоянной скоростью по прямой линии. За зайцем гонится лиса со скоростью, постоянно направленной в «точку», где находится заяц. В начальный момент времени лиса находится на расстоянии b = 100 м от зайца, скорости зайца и лисы образуют прямой угол. Величина скорости зайца v = 5 м/с, величина скорости лисы u = 4 м/с. Вначале расстояние между ними уменьшается до минимальной величины sm = 10 м, затем возрастает. Найдите минимальное значение расстояния между лисой и зайцем sc, если v = u. Найдите минимальное значение расстояния между лисой и зайцем sc, если v = u. |
| 85216. Прямая линия А1Р образует угол а с отрезком A1A2 длиной а. В момент времени t = 0 две частицы находятся в точках А1 и А2. Двигаясь по прямым линиям А1Р и А2М с постоянными скоростями, частицы встречаются в точке М на прямой А1Р. Первая частица движется со скоростью v1. Найдите наименьшее значение скорости v2 и положение траектории второй частицы. |
| 85217. Автомобиль начинает двигаться из состояния покоя с постоянным ускорением и за десятую секунду проходит путь s = 19 м. Найдите величину ускорения автомобиля. |
| 85218. Частица начинает двигаться по прямой линии из состояния покоя с постоянным ускорением. В момент времени t1 = 3 с частица достигает точки А. Расстояние между частицей и точкой А за секунду до пересечения частицей точки А равно s = 1 м. Найдите скорость частицы v в точке A. |
85219. Пассажир первого вагона прогуливался по перрону. Когда он подошел к концу последнего вагона, поезд начал двигаться с ускорением а = 0,072 м/с2. Пассажир сразу же побежал к своему вагону. Длина поезда I = 250 м. Найдите наименьшую величину скорости пассажира vmin, если он успел сесть в первый вагон. Пассажир первого вагона прогуливался по перрону. Когда он подошел к концу последнего вагона, поезд начал двигаться с ускорением а = 0,072 м/с2. Пассажир сразу же побежал к своему вагону. Длина поезда I = 250 м. Найдите наименьшую величину скорости пассажира vmin, если он успел сесть в первый вагон. |
| 85220. Частица движется по прямой линии с постоянным ускорением. В начале и в конце некоторого участка прямой проекции скорости частицы равны v1 и v2. Найдите величину скорости частицы vm в середине этого участка. |
| 85221. Пассажир, опоздавший на поезд, увидел, что предпоследний вагон прошел мимо него за интервал времени Т1, а последний — за интервал времени T2. Найдите интервал Т между моментами времени отправления поезда и выходом пассажира на перрон. |
85222. Две частицы движутся по оси х. Проекции начальных скоростей частиц u1 = 6 м/с, u2 = -4 м/с. Проекции ускорений частиц a2x = -a1x = а, а = 1 м/с2. Найдите минимальное значение начального расстояния между частицами s, при котором они не столкнутся. Найдите минимальное значение начального расстояния между частицами s, при котором они не столкнутся. |
| 85223. Камень падает с башни с нулевой начальной скоростью. Вторую половину пути он пролетел за интервал времени т = 1 с. Найдите высоту башни h. |
| 85224. Сосулька падает с карниза. Первую половину пути она пролетела за интервал времени Т = 2 с. Найдите интервал времени т, за который она пролетит оставшийся путь. |
| 85225. Сосулька падает с карниза. За последнюю секунду движения она пролетела 3/4 часть всего пути. Найдите интервал времени падения T. |
| 85226. Тело падает с начальной скоростью v(0) = 0. Найдите путь s, пройденный телом за промежуток времени от t1 = 1 с до t2 = 2 с. |
85227. Найдите промежуток времени t0 между моментами времени отрыва дождевых капель от крыши, если через промежуток времени T после начала падения второй капли расстояние между ними равно s. |
| 85228. Камень брошен с поверхности Земли вертикально вверх. На высоте h = 8,6 м он побывал дважды с интервалом времени 2т, т = 1,5 с. Определите начальную скорость камня. |
| 85229. Камень брошен вертикально вверх c начальной скоростью v0 = 9,8 м/с. Найдите максимальную высоту подъема камня hm. |
| 85230. Мяч, брошенный с поверхности земли вертикально вверх, достиг высоты h = 4,9 м. Найдите величину скорости мяча v1 через Т = 0,9 с после бросания. |
| 85231. Камень брошен вертикально вверх. На некоторой высоте камень находился в моменты времени t1 = 1 с и t2 = 3 с. Найдите начальную скорость камня v(0). |
85232. Тело брошено вверх с земли с начальной скоростью v0 = 5 м/с. Когда тело достигло максимальной высоты, с земли бросили вверх второе тело с той же начальной скоростью. Найдите значение высоты h, на которой оба тела окажутся одновременно. |
| 85233. Ракета стартует по вертикали с постоянным ускорением а. В момент времени Т двигатель отключили. Найдите высоту подъема ракеты h. Сопротивлением воздуха пренебречь. |
| 85234. Частица движется по шероховатой горизонтальной плоскости. Если величина начальной скорости v1 = 3 м/с, то частица перемещается на расстояние s1, если величина начальной скорости v2 = 4 м/с, то частица перемещается на расстояние s2. Найдите значение величины начальной скорости частицы v3, при котором частица переместится на расстояние s3 = s1 + s2. |
| 85235. Каркас, представляющий собой стороны параллелограмма ABCD, закреплен над поверхностью земли. Промежутки времени падения капель из точек A, В, С до земли соответственно равны ta = |/5 с, tb = |/2 с, tc = 1 с. Найдите промежуток времени падения капли T из точки D. |
85236. В четырехугольной пирамиде ABCDK две противоположные грани перпендикулярны плоскости основания. Основанием пирамиды является равнобедренная трапеция ABCD, расположенная на поверхности земли. Параметры пирамиды: s0 = s/ |/3 — расстояние между сторонами АВ и CD, s1 = s — расстояние от середины М1 стороны АВ до вершины К, s2 = s/ |/3 — расстояние от середины М2 стороны DC до вершины К. Найдите промежуток времени падения капли T из вершины К до земли. Основанием пирамиды является равнобедренная трапеция ABCD, расположенная на поверхности земли. Параметры пирамиды: s0 = s/ |/3 — расстояние между сторонами АВ и CD, s1 = s — расстояние от середины М1 стороны АВ до вершины К, s2 = s/ |/3 — расстояние от середины М2 стороны DC до вершины К. Найдите промежуток времени падения капли T из вершины К до земли. |
| 85237. Навес в виде прямоугольного треугольника ABD образует двухгранный угол а с горизонтальной поверхностью земли, BD — сторона, навеса расположенная на земле. Сторона AD = L, угол ABD равен п/2, угол ADB равен b. Найдите промежуток времени падения капли Т с вершины А. |
85238. Частица падает на наклонную плоскость, заданную уравнением 3у + 4z = 5d, где z — координата точки плоскости на оси, направленной вертикально вверх, d = 2 м. Начальная скорость частицы v(0), координаты точки столкновения частицы с плоскостью (0, y1, z1). Промежуток времени падения т. Найдите координаты начального положения частицы r0 = (x0, у0, z0) и расстояние s между частицей и плоскостью в момент времени t = 0. |
| 85239. Жонглер бросает с одного уровня два шарика вертикально вверх с начальными скоростями v0 = 5 м/с через промежуток времени t0 = 0,31 с. Определите интервал времени между моментом бросания первого шарика и моментом времени, в который шарики окажутся на одной высоте. |
| 85240. Жонглер бросил шарик вертикально вверх. Когда шарик достиг максимальной высоты hm = 2 м относительно точки бросания, был брошен второй шарик с той же начальной скоростью. Найдите высоту h, на которой шарики окажутся одновременно. |
| 85241. Через равные интервалы времени жонглер бросает три шарика вертикально вверх с одинаковыми начальными скоростями v0 = 4,9 м/с. В некоторый момент времени Т первый и третий шарики находятся на одном уровне. Найдите значение высоты h, на которой находился второй шарик в момент времени T. |
85242. Через равные интервалы времени T жонглер бросает мячи вертикально вверх с одинаковыми начальными скоростями. Каждый мяч находится в полете в течение времени 4T. В момент бросания четвертого мяча расстояние между вторым и третьим мячами b. Найдите интервал времени T и максимальную высоту подъема мячей H. Каждый мяч находится в полете в течение времени 4T. В момент бросания четвертого мяча расстояние между вторым и третьим мячами b. Найдите интервал времени T и максимальную высоту подъема мячей H. |
| 85243. С задней линии корта с высоты H = 2 м теннисист подал мяч, скорость которого направлена по горизонтали. Высота сетки h = 1 м, длина корта s = 20 м. Пренебрегая сопротивлением воздуха, найдите интервал начальных скоростей v0, необходимый для попадания мяча на поле соперника и длину области b, недоступной мячу. |
| 85244. Камень брошен с поверхности Земли с начальной скоростью v0 под углом а к горизонтальной плоскости. Найдите максимальные значения высоты подъема Н и дальности полета D камня. Сопротивлением воздуха пренебрегаем. |
85245. Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема Нm = 3200 м. Найдите максимальную высоту настильной траектории h при той же дальности. |
| 85246. Продолжительность полета мяча, брошенного под углом к горизонту равна т = 2 с. Найдите максимальную высоту подъема мяча Hm. |
| 85247. Спортсмен толкает ядро. Под каким углом а0 к горизонту должна быть направлена скорость, чтобы ядро упало как можно дальше? Начальная скорость ядра v0 = 13,5 м/с, высота точки бросания ядра H = 2 м. |
| 85248. Пикирующий бомбардировщик движется со скоростью v1 по отрезку прямой, образующей угол а с горизонтальной плоскостью. Цель перемещается по земле со скоростью v2 в плоскости движения самолета. На каком расстоянии s по горизонтали от цели должна быть сброшена бомба с высоты H, чтобы поразить цель? |
85249. Из одной точки над поверхностью земли вылетают одновременно две частицы с противоположно направленными по горизонтали скоростями v10 = 4 м/с, и v20 = 9 м/с. Найдите промежуток времени T, через который угол между скоростями частиц станет равным п/2. |
| 85250. В точке А вертикальной плоскости, расположенной на расстоянии s от точки О, находится камень. Из точки О вылетает ядро, которое должно попасть в камень, который начинает падать с высоты h в момент вылета ядра. Начальная скорость камня равна нулю. Найдите угол а между вектором начальной скорости ядра и горизонтальной плоскостью. |
| 85251. На наклонную плоскость, образующую двухгранный угол а с горизонтальной плоскостью, падает шарик с высоты h. После упругого столкновения с плоскостью шарик отскакивает со скоростью величиной v0 = |/2gh. Найдите расстояние от точки падения шарика до точки следующего столкновения с плоскостью. |
85252. На высоте h частице придали горизонтально направленную начальную скорость величиной v0. При отскоке от горизонтальной плоскости отношение величины вертикальной компоненты скорости после отскока к величине вертикальной компоненты скорости до отскока равно k. Найдите расстояние s от плоскости бросания до точки остановки частицы. |
| 85253. Координата первой частицы, движущейся по прямой x1(t) = s — 5vt + 3at2. Вторая частица движется с постоянной скоростью относительно первой частицы, если: A. x2(t) = 2s + 2vt + 3at2, Б. x2(t) = -6s + 5vt — 3at2, B. x2(t) = s — 5vt — 3at2, Г. x2(t) = 6s + 5vt, Д. x2(t) = 2s — 3at2. |
| 85254. По реке плывет щепка. Первый гребец плывет по течению и обгоняет щепку на 20 метров, второй — плывет против течения и отстает от щепки на 20 метров. Гребцы перемещают весла с одинаковой интенсивностью. Какой из гребцов затратил больше времени — первый или второй? |
| 85255. Проплывая под мостом против течения, гребец потерял соломенную шляпу. Обнаружив пропажу через Т = 10 мин, он повернул назад и, гребя по течению с тем же темпом, подобрал шляпу на расстоянии s = 1 км ниже моста. Найдите скорость течения реки u. |
85256. По палубе теплохода ходит пассажир от кормы к носу и обратно без остановок со скоростью v0 относительно теплохода. Скорость теплохода u. Найдите условие, при котором пассажир окажется на уровне любой точки на берегу ровно три раза. Скорость теплохода u. Найдите условие, при котором пассажир окажется на уровне любой точки на берегу ровно три раза. |
| 85257. Приборы, установленные на берегу, показывают, что ветер дует с юго-запада, а величина скорости ветра v = 5 м/с. Что покажут аналогичные приборы, установленные на корабле, идущем на запад cо скоростью u = 36 км/ч? |
| 85258. Поезд движется на север со скоростью v = 30 м/с. Пассажир пролетающего над поездом вертолета, видит, что поезд движется на запад со скоростью v’ = 40 м/с. Найдите скорость вертолета u. |
| 85259. Самолет садится на авианосец, движущийся по океану со скоростью v1 в восточном направлении. Скорость ветра v2 направлена на север, а самолет снижается с вертикальной скоростью v3 относительно авианосца. Найдите величину скорости v самолета по отношению к движущемуся воздуху. |
85260. Скорость бутсы футболиста в момент удара по неподвижному мячу равна u. Определить скорость мяча после удара. Удар абсолютно упругий. Предполагается, что скорость бутсы после удара не изменяется, т.е. масса бутсы значительно больше массы мяча. Определить скорость мяча после удара. Удар абсолютно упругий. Предполагается, что скорость бутсы после удара не изменяется, т.е. масса бутсы значительно больше массы мяча. |
| 85261. Скорость струи пара перед попаданием на лопатки паровой турбины равна v. Найдите значение величины скорости лопатки v, при которой вся кинетическая энергия струи пара может перейти в энергию вращения турбины. |
| 85262. Плита движется вверх с постоянной скоростью u = 4 м/с. На нее падает шарик перпендикулярно плоскости плиты. В момент абсолютно упругого столкновения с плитой скорость шарика v0 = 6 м/с. Найдите величину скорости шарика v после отскока. |
| 85263. Колесо катится по горизонтальной поверхности со скоростью u без проскальзывания (рис. а). Определите величину скоростей точек A, В, С, D. |
85264. Колесо катится без проскальзывания по горизонтальной плоскости. Скорость центра колеса u = (u, 0, 0). Точка K находится на ободе колеса. Найдите значения углов между радиус-вектором точки К и скорости u, при которых величина скорости точки K равна u. Точка K находится на ободе колеса. Найдите значения углов между радиус-вектором точки К и скорости u, при которых величина скорости точки K равна u. |
| 85265. Машина движется со скоростью u по дороге, покрытой гравием. Найдите максимальную высоту Нm, которой достигнет камешек, оторвавшись от покрышки колеса радиусом R? |
| 85266. Кубик массой m лежит на столе. Найдите величину силы реакции плоскости N1, если приложить к кубику силу F, направленную перпендикулярно поверхности верхней грани. |
| 85267. Два соприкасающихся тела массами m1 = 3 кг и m2 = 2 кг движутся по гладкой горизонтальной плоскости, под действием силы F = 10 Н, приложенной к первому телу. Определите горизонтальную компоненту силы, действующей на тело массой m2. |
85268. На рис изображены четыре одинаковых кирпича, которые движутся по гладкой горизонтальной плоскости под действием силы F, приложенной к первому кирпичу. Найдите величину горизонтальной компоненты силы f, действующей на четвертый кирпич. Найдите величину горизонтальной компоненты силы f, действующей на четвертый кирпич. |
| 85269. К двум телам, находящимся на гладком столе, прикреплен шнур, масса которого пренебрежимо мала по сравнению с массами тел m1 = 4 кг и m2 = 6 кг. Шнур разрывается, если к телу массой m1 приложить силу F1 = 200 Н. Найдите минимальное значение силы F2, которую необходимо приложить к телу массой m2, чтобы разорвать шнур. |
| 85270. Пружина прикреплена к обойме динамометра массой М = 3 кг и к крюку массой m = 2 кг. Динамометр находится на гладкой поверхности стола. К крюку приложена сила величиной F1 = 8 Н, к обойме — F2 = 5 Н. Определите показание динамометра. |
85271. На подставке лежит груз, прикрепленный к нерастянутой пружине, ось которой направлена по вертикали. В момент времени t = 0 подставку начинают перемещать вертикально вниз с постоянной величиной ускорения a < g. Найдите промежуток времени t1, через который груз оторвется от подставки? Жесткость пружины k, масса груза m. |
| 85272. Веревка выдерживает неподвижный груз массой не более m1 = 100 кг. На этой веревке поднимают груз массой m2 = 50 кг. Найдите максимальное значение высоты Н, на которую можно поднять груз с постоянным ускорением за интервал времени т = 2 с. |
| 85273. Космический корабль стартует вертикально с Земли или тормозится при спуске, входя по вертикали в плотные слои атмосферы. Величина ускорения равна а. Найдите вес космонавта. |
| 85274. Найдите вес тела Р, лежащего на подставке, ускорение которой равно вектору g. |
| 85275. Коробка массой m1 с гладким дном, в которой находится груз массой m2, скользит по гладкой наклонной плоскости, образующей угол а с горизонтальной плоскостью. Найдите величину силы давления груза Т на переднюю стенку коробки. |
85276. В лифте, движущемся вниз, вес тела массой m = 100 кг равен Р = 1100 Н. Найдите значение величины ускорения лифта а. |
| 85277. В лифте, движущемся вверх, вес тела массой m = 100 кг равен Р = 900 Н. Найдите значение величины ускорения лифта а. |
| 85278. Лифт» движется с ускорением, параллельным вектору g. Величина ускорения лифта а > g. Найдите вес тела Р. |
| 85279. Одна плоская грань клина соприкасается с вертикальной плоскостью стенки. По другой грани — гладкой плоскости, образующей угол а с гладкой горизонтальной плоскостью, скользит тело массой m. Найдите величину силы давления клина G на стенку. |
| 85280. На рис. изображен стержень АВ длиной I, концы которого скользят по двум взаимно перпендикулярным прямым. Скорость точки В равна v. В точке С закреплена частица массой m. Найдите силу реакции N (ф), действующую на частицу. |
85281. На гладкой тонкой оси висит однородный канат длиной I массой m. Найдите величину силы давления N на ось при соскальзывании каната, когда расстояние между его концами равно s. |
| 85282. Два груза масс m1 = М и m2 = М подвешены на нерастяжимой нити, перекинутой через блок. На один из них положили перегрузок массой m3 = m. Определите ускорение перегрузка а, величину силы давления перегрузка на груз N, натяжения нити Т и величину силы, действующей на ось блока Р. |
| 85283. На одном конце нерастяжимой нити, переброшенной через блок, закреплена частица массой m1, а по другой части нити перемещается вниз частица массой m2 с ускорением w относительно нити. Найдите ускорения частиц и величину силы натяжения нити. |
85284. Груз массой m3 прикреплен к невесомой нити, перекинутой через неподвижный блок, конец которой закреплен на оси второго движущегося блока (рис. а). Через этот блок перекинута нить, на одном конце которой прикреплен груз массой m2, а на другом конце нити — груз массой m1. Найдите проекцию ускорения второго блока на вертикаль и величину силы натяжения нити, охватывающей этот блок. |
Камень брошен вертикально вверх с вершины башни высотой 64 метра по закону s=48t−16t2. Наибольшая высота, достигнутая камнем над землей, составляет
Вопрос
Обновлено: 05.02.2021
ГИМАЛАЯ ПУБЛИКАЦИЯ-ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЦИИ-БАНК ВОПРОСОВ
20 видеоРЕКЛАМА 9003 Решение 9003
0 003
100 метр
B
64 метр
C
36 метр
D
32 метра
Ответ
Правильный ответ A
Ответ
Пошаговое решение, разработанное экспертами, чтобы помочь вам в сомнениях и получить отличные оценки на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Камень, брошенный вертикально вверх с начальной скоростью u с вершины башни, упал на землю со скоростью 3u. Высота башни: 9(2))/(g) С какой скоростью камень достигает земли?
52784124
Камень брошен вертикально вверх с вершины башни высотой 64 м по закону движения s=48t−16t2.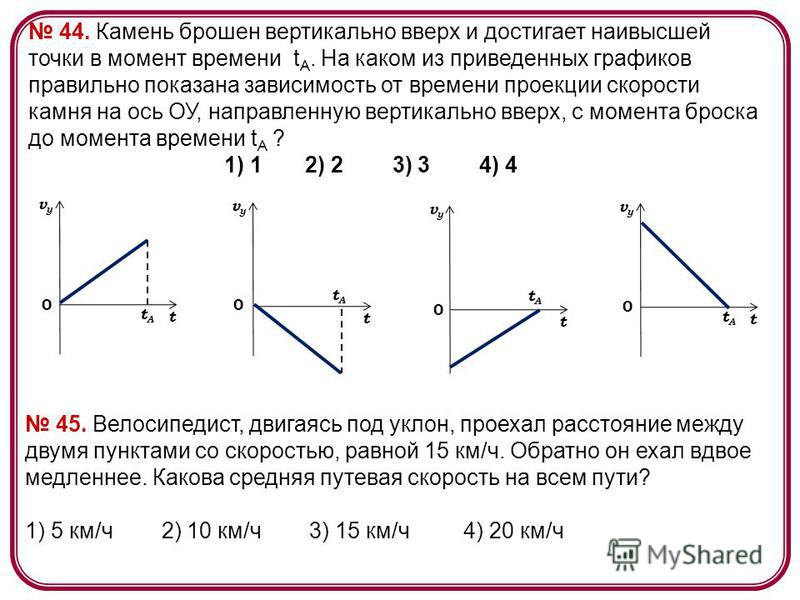 Наибольшая высота, которую достигает камень над землей, равна
Наибольшая высота, которую достигает камень над землей, равна
95420820
. Камень, брошенный вертикально вверх, движется по закону s = 100t−16t2. Максимальная достигнутая высота равна
217277359
Камень, брошенный вертикально вверх, движется по закону s=48t−16t2. Время, за которое камень достигнет точки выброса, равно
217277968
Камень, брошенный вверх со скоростью u с вершины башни, падает на землю со скоростью 4u. Высота башни
304589450
Камень брошен вверх со скоростью y с вершины башни. Он достигает земли со скоростью 3v. Какова высота башни?
427223684
Камень брошен вертикально вверх с вершины башни высотой 64 метра по закону s=48tg−16t∘. Наибольшая высота, которую достигает камень над землей, равна
474045719
Камень брошен вверх с начальной скоростью ‘u’ с вершины башни и достигает земли со скоростью ‘3u’, тогда высота башни ……
621575556
Из С вершины башни высотой 64 м камень брошен вертикально вверх со скоростью 48 м/с.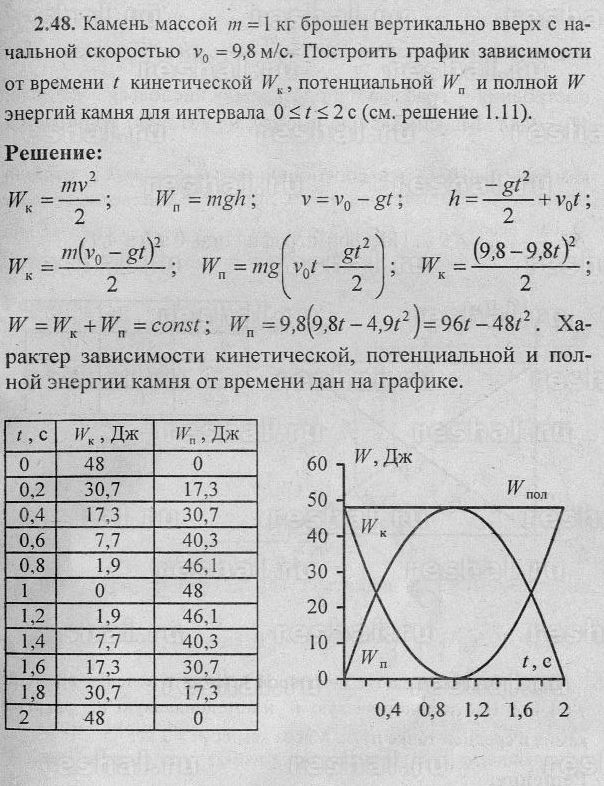 Наибольшая высота (в метрах), достигнутая камнем при значении ускорения свободного падения g−32 м/с2, равна
Наибольшая высота (в метрах), достигнутая камнем при значении ускорения свободного падения g−32 м/с2, равна
621726549
Text Solution
9(2) Выбрасывается по правилам. Максимальная высота, достигнутая камнем от земли, составляет642734567
s=48t−16t2 पत्थर द्वारा धरातल से प्राप्त की गई महत्तम ऊँचा0 ऊँचा0 ऊँचा0 0002 642740437
Камень, брошенный вверх со скоростью u с вершины башни, упал на землю со скоростью 3 u . Высота башни
643049485
Камень, брошенный вертикально вверх с начальной скоростью u с вершины башни, упал на землю со скоростью 3u. Высота башни: 92$)А. 3 мБ. 15 мКл. 1 мД. 10 м
Дата последнего обновления: 20 апреля 2023 г. 5к+ просмотров
Подсказка: Максимальная высота объект на траектории снаряда возникает, когда вертикальный отрезок скорости достигает нуля. Когда снаряд движется вверх, он сталкивается с гравитацией, и таким образом скорость начинает уменьшаться.
9{2}}=20h~~\]
\[100=10h\]
\[h=10m\]
Главной силой сущности, которая следует за объектом, является гравитация, которая действует нисходящим образом, вдоль этих линий, сообщая объект нисходящей скорости вверх. Из-за задержки объекта ожидается, что никакая внешняя плоская сила не будет поддерживать сегмент горизонтальной скорости объекта. С учетом различных сил, например, эрозии от обтекаемого сопротивления или движения внутрь, как в ракете, требуется дополнительная проверка.
Из-за задержки объекта ожидается, что никакая внешняя плоская сила не будет поддерживать сегмент горизонтальной скорости объекта. С учетом различных сил, например, эрозии от обтекаемого сопротивления или движения внутрь, как в ракете, требуется дополнительная проверка.
Баллистическая ракета — это ракета, управляемая в течение умеренно короткого периода полета с пусковым двигателем, последующий курс которой определяется законами механики старого образца.
Баллистика («подбрасывать») — это изучение механики, которая управляет полетом, поведением и попаданием снарядов, особенно выстрелов, неуправляемых бомб, ракет или чего-то подобного; наука или ремесло структурирования и ускорения снарядов для идеальной демонстрации.
Примечание. При движении снаряда горизонтальное и вертикальное движения независимы друг от друга; то есть ни одно из движений не влияет на другое. Это руководство по составному движению, установленное и использованное им для демонстрации объяснительного типа движения снаряда.




 Кинематика
Кинематика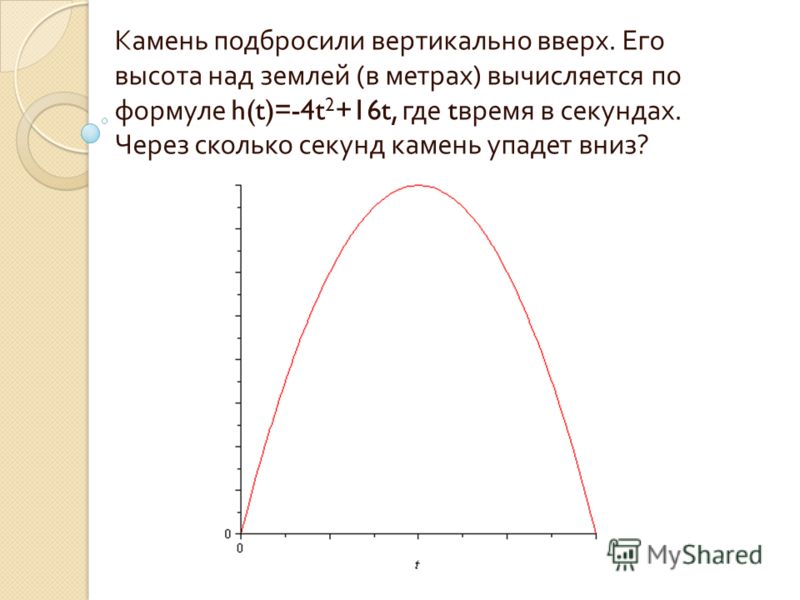 За начало отсчета принять момент, когда направление луча совпадает с ОС.
За начало отсчета принять момент, когда направление луча совпадает с ОС. 1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.
1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.
Leave A Comment