А 8 | Тело брошено вертикально вверх. Через 0,5 с после броска его скорость равна 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. | |||||||||||||||||||||||||
1) 15 м/с 2) 20,5 м/с | 3) 25 м/с 4) 30 м/с | |||||||||||||||||||||||||
А 9 | Сосулька, упав с края крыши, долетела до земли за 3,0 с. Путь сосульки приблизительно равен | |||||||||||||||||||||||||
1) 12 м 2) 24 м | ||||||||||||||||||||||||||
А 10 | Тело
свободно падает с некоторой высоты с
начальной скоростью, равной нулю. | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
Камень свободно падает с некоторой высоты с начальной скоростью, равной нулю. Сопротивление воздуха мало. Скорость, которую приобретет камень, пропорциональна | ||||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
В 1 | Стрела,
пущенная вертикально вниз с обрыва
высотой 30 м со скоростью 5 м/с,
достигает воды. | |||||||||||||||||||||||||
С 1 | Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время 1, а такой же последний — за 0,5 . Найдите полное время падения , если начальная скорость равна нулю. | |||||||||||||||||||||||||
С 2 | Тело, свободно падающее с некоторой высоты без начальной скорости за время 1 с после начала движения проходит путь в 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения. | |||||||||||||||||||||||||
А 12 | Чтобы
оценить, с какой скоростью упадет на
землю мяч с балкона 6-го этажа, используем
для вычислений на калькуляторе формулу
. 1) 17,320508 м/с 2) (17,320508±1,1547005) м/с 3) (17,320508 ±0,6) м/с 4) (17,3 ±0,6) м/с | |||||||||||||||||||||||||
А 2 | Камень, брошенный вертикально вверх с поверхности Земли со скоростью 30 м/с, упал обратно на Землю. Сопротивление воздуха мало. Камень находился в полёте примерно | |||||||||||||||||||||||||
1) 1,5 с 2) 3 с | 3) 4,5 с 4) 6 с | |||||||||||||||||||||||||
А 3 | Камень,
брошенный вертикально вверх с
поверхности Земли, упал обратно на
Землю через 6 с. | |||||||||||||||||||||||||
1) 7,5 м/с 2) 15 м/с | ||||||||||||||||||||||||||
А 4 | Тело свободно падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения? Сопротивлением воздуха пренебречь. | |||||||||||||||||||||||||
1) 0 м 2) 5 м | 3) 10 м 4) 45 м | |||||||||||||||||||||||||
В 1 | Стрела,
пущенная вертикально вверх, побывала
на одной высоте через
1 с и 2 с полета. | |||||||||||||||||||||||||
В 2 | Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, первый раз оказывается на высоте 4 м? Ответ округлите до десятых. | |||||||||||||||||||||||||
В 3 | Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, второй раз оказывается на высоте 4 м? Ответ округлите до десятых. | |||||||||||||||||||||||||
В 4 | Стрела, пущенная вертикально вверх со скоростью 12 м/с, два раза оказывается на высоте 4 м. Каков промежуток времени между двумя этими событиями? Ответ округлите до десятых. | |||||||||||||||||||||||||
А 28 | На
рисунке представлен график движения
тела. | |||||||||||||||||||||||||
1) 2 м; 1,6 м/с 2) 10 м; 2 м/с 3) 10 м; 1,6 м/с 4) 2 м; 2 м/с | ||||||||||||||||||||||||||
А 29 | На рисунке представлен график зависимости координаты тела, движущегося вдоль оси OX, от времени. Сравните скорости , и тела в моменты времени . | |||||||||||||||||||||||||
А 30 | На
рисунке представлен график движения
автобуса из пункта А в пункт В и
обратно. Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. | |||||||||||||||||||||||||
1) 40 км/ч 2) 50 км/ч | 3) 60 км/ч 4) 75 км/ч | |||||||||||||||||||||||||
А 31 | На рисунке представлен график движения автобуса из пункта А в пункт В и обратно. Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна скорость автобуса на пути из Б в А? | |||||||||||||||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||||||||||||||
3) 60 км/ч | ||||||||||||||||||||||||||
А 32 | На
рисунке представлен график движения
автобуса из пункта А в пункт В и
обратно. | |||||||||||||||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||||||||||||||
3) 60 км/ч | 4) 75 км/ч | |||||||||||||||||||||||||
А 33 | На рисунке представлен график движения автобуса из пункта А в пункт В и обратно. Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна минимальная скорость автобуса на всем пути следования туда и обратно? | |||||||||||||||||||||||||
1) 40 км/ч 2) 50 км/ч | 3) 60 км/ч 4) 75 км/ч | |||||||||||||||||||||||||
А 34 | На
рисунке изображен график зависимости
координаты бусинки, движущейся по
горизонтальной спице, от времени.
| |||||||||||||||||||||||||
А 35 | На
рисунке изображен график изменения
координаты тела с течением времени. | |||||||||||||||||||||||||
1) только при 0 с | 2) только от 2 до 5 с | |||||||||||||||||||||||||
3) только от 5 до 8 с | 4) от 2 до 8 с | |||||||||||||||||||||||||
А 1 | Период обращения тела, движущегося равномерно по окружности, увеличился в 2 раза. Частота обращения | |||||||||||||||||||||||||
1) возросла в 2 раза | 2) уменьшилась в 2 раза | |||||||||||||||||||||||||
3) возросла в 4 раза | 4) уменьшилась в 4 раза | |||||||||||||||||||||||||
А 2 | Материальная
точка, двигаясь равномерно по окружности,
за 3 с прошла четверть окружности. | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 3 | Период равномерного движения материальной точки по окружности равен , радиус окружности . Точка пройдет по окружности путь, равный , за время равное 1) 2 2) /2 3) 4) | |||||||||||||||||||||||||
А 4 | Когда период вращения Земли вокруг своей оси самый короткий? | |||||||||||||||||||||||||
1) Летом | 2) Зимой | |||||||||||||||||||||||||
3) Весной и осенью | 4) Всегда одинаковый | |||||||||||||||||||||||||
А 5 | Период
обращения Земли вокруг Солнца равен
одному году, радиус орбиты Земли равен
150 млн. | |||||||||||||||||||||||||
1) 30 м/с 2) 30 км/с | 3) 150 км/с 4) 1800 км/с | |||||||||||||||||||||||||
А 6 | На кольцевой гонке два автомобиля движутся так, что все время радиус движения второго автомобиля в 2 раза больше первого, а периоды движения равны. Отношение скоростей равно … | |||||||||||||||||||||||||
1) 0,5 2) 2 | 3) 4) 4 | |||||||||||||||||||||||||
А 7 | По окружностям
с радиусами R1и R2 равномерно движутся две материальные
точки со скоростями и соответственно. | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 8 | Две материальные точки движутся по окружностям радиусами и с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением | |||||||||||||||||||||||||
1) 2) 3) 4) | ||||||||||||||||||||||||||
А 9 | По окружностям
с радиусами R1и R2 равномерно движутся две материальные
точки со скоростями и соответственно. | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 10 | По окружностям одинакового радиуса равномерно движутся две материальные точки со скоростями и соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 11 | По
окружностям одинакового радиуса
равномерно движутся две материальные
точки со скоростями
и
соответственно. | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 12 | Две материальные точки равномерно движутся по окружностям одинакового радиуса, при этом линейная скорость первой точки в 2 раза меньше линейной скорости второй точки. Частоты обращения точек по окружностям связаны соотношением: | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 13 | К
боковой поверхности цилиндра,
вращающегося вокруг своей оси, прижимают
второй цилиндр с осью, параллельной
оси первого, и радиусом, вдвое
превосходящим радиус первого. | |||||||||||||||||||||||||
1) периоды вращения 2) частоты вращения 3) линейные скорости точек на поверхности 4) центростремительные ускорения точек на поверхности | ||||||||||||||||||||||||||
В 1 | Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 с. Сколько оборотов в секунду делает шестерня радиусом 10 см? | |||||||||||||||||||||||||
В 2 | Две
шестерни, сцепленные друг с другом,
вращаются вокруг неподвижных осей.
Большая шестерня радиусом 10 см делает
20 оборотов за 10 с, а частота
обращения меньшей шестерни равна
5 Гц. | |||||||||||||||||||||||||
В 3 | Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Отношение периодов вращения шестерен равно 3. Радиус меньшей шестерни равен 6 см. Каков радиус большей шестерни? Ответ укажите в сантиметрах. | |||||||||||||||||||||||||
А 14 | Диск радиусом 20 см равномерно вращается вокруг своей оси. Скорость точки, находящейся на расстоянии 15 см от центра диска, равна 1,5 м/с. Скорость крайних точек диска равна | |||||||||||||||||||||||||
1) 4 м/с 2) 0,2 м/с | 3) 2 м/с 4) 1,5 м/с | |||||||||||||||||||||||||
А 15 | При
равномерном движении по окружности
модуль вектора изменения скорости
при перемещении из точки А в точку В
(см. | |||||||||||||||||||||||||
1) 0 2) | 3) 4) | |||||||||||||||||||||||||
А 16 | Вектор ускорения при равномерном движении точки по окружности | |||||||||||||||||||||||||
1) постоянен по модулю и по направлению 2) равен нулю 3) постоянен по модулю, но непрерывно изменяется по направлению 4) постоянен по направлению, но непрерывно изменяется по модулю | ||||||||||||||||||||||||||
А 17 | Автомобиль
движется с постоянной по модулю
скоростью по траектории, представленной
на рисунке. | |||||||||||||||||||||||||
1) 1 2) 2 3) 3 4) Во всех точках одинаково | ||||||||||||||||||||||||||
А 18 | Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна | |||||||||||||||||||||||||
1) 12,5 м/с 2) 10 м/с | 3) 5 м/с 4) 4 м/с | |||||||||||||||||||||||||
А 19 | Материальная
точка движется по окружности с
постоянной по модулю скоростью. | |||||||||||||||||||||||||
1) Увеличится в 3 раза | 2) Увеличится в 9 раз | |||||||||||||||||||||||||
3) Уменьшится в 3 раза | 4) Уменьшится в 9 раз | |||||||||||||||||||||||||
А 20 | Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить в два раза? | |||||||||||||||||||||||||
1) Не изменится | 2) Увеличится в 4 раза | |||||||||||||||||||||||||
3) Уменьшится в 2 раза | 4) Уменьшится в 4 раза | |||||||||||||||||||||||||
А 21 | Точка движется с постоянной по модулю скоростью по окружности радиуса . Как изменится центростремительное ускорение точки, если её скорость увеличить вдвое, а радиус окружности вдвое уменьшить? | |||||||||||||||||||||||||
1) Уменьшится в 2 раза | 2) Увеличится в 2 раза | |||||||||||||||||||||||||
3) Увеличится в 4 раза | 4) Увеличится в 8 раз | |||||||||||||||||||||||||
А 22 | Точка движется с постоянной по модулю скоростью по окружности радиуса . Как изменится центростремительное ускорение точки, если её скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить? | |||||||||||||||||||||||||
1) Уменьшится в 2 раза | 2) Увеличится в 2 раза | |||||||||||||||||||||||||
3) Уменьшится в 8 раз | 4) Не изменится | |||||||||||||||||||||||||
А 23 | Две материальные точки движутся по окружностям радиусами и , причём . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением | |||||||||||||||||||||||||
1) 2) | 3) 4) | |||||||||||||||||||||||||
А 24 | Два спутника движутся по разным круговым орбитам вокруг Земли. Скорость первого из них в 2 раза больше, а радиус орбиты в 4 раза меньше, чем у второго. Центростремительное ускорение первого спутника , а второго — . Чему равно отношение ? | |||||||||||||||||||||||||
1) 1 2) 2 | 3) 4 4) 16 | |||||||||||||||||||||||||
В 4 | Рассчитайте центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси координат которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли. Ответ округлите до двух значащих цифр. Радиус Земли 6400 км, а период вращения вокруг оси равен 1 суткам . | |||||||||||||||||||||||||
В 5 | Материальная точка движется с постоянной скоростью по окружности радиусом . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится?
| |||||||||||||||||||||||||
В 3 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 м от места броска. Чему равна скорость камня через 1 с после броска, если в этот момент она была направлена горизонтально? | |||||||||||||||||||||||||
В 4 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 м от места броска. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально и равна 10 м/с? | |||||||||||||||||||||||||
В 5 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, достиг максимальной высоты 5 м и упал обратно на землю в 20 м от места броска. Чему равна минимальная скорость камня за время полёта? | |||||||||||||||||||||||||
В 6 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 м от места броска. Чему равна скорость камня через 2 с после броска, если в этот момент она была направлена горизонтально? | |||||||||||||||||||||||||
В 7 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю через 5 с в 50 м от места броска. Чему равна минимальная скорость камня за время полёта? | |||||||||||||||||||||||||
В 8 | Небольшой камень бросили с ровной горизонтальной поверхности земли под углом к горизонту. Какова дальность полёта камня, если через 2 с после броска его скорость была направлена горизонтально и равна 5 м/с? | |||||||||||||||||||||||||
В 9 | Небольшой камень, брошенный с ровной горизонтальной поверхности земли под некоторым углом к горизонту, достиг максимальной высоты 4,05 м. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально? | |||||||||||||||||||||||||
В 10 | Камень бросили с горизонтальной поверхности земли под углом к горизонту. Минимальная скорость камня во время полета была равна 12 м/с, а максимальная — 20 м/с. Через какой промежуток времени камень достигнет максимальной высоты? | |||||||||||||||||||||||||
В 11 | Мяч бросили с горизонтальной поверхности земли под углом к горизонту. Минимальная скорость камня во время полета была равна 12 м/с, а максимальная — 20 м/с. На какую максимальную высоту поднялся мяч? | |||||||||||||||||||||||||
В 12 | Стрела пущена с ровной горизонтальной поверхности земли под углом 45о к горизонту. На какую максимальную высоту поднялась стрела, если через 1,5 с после броска её скорость была направлена горизонтально? | |||||||||||||||||||||||||
Камень, брошенный вертикально вверх, упал на Землю через 2 с. Определить
Условие задачи:
Камень, брошенный вертикально вверх, упал на Землю через 2 с. Определить путь и перемещение камня за 2 с.
Задача №1.4.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=2\) с, \(S-?\), \(\left| {\vec r} \right| – ?\)
Решение задачи:
Небольшое дополнение к условию задачи – автор имел в виду, что камень бросается с Земли, а не с какой-то высоты, как кто-нибудь мог бы подумать, и возвращается через 2 секунды также на Землю. В противном случае, решить задачу не представлялось бы возможным.
Сначала разберемся с перемещением камня \({\vec r}\). Перемещение – это вектор, проведенный из начального положения тела в конечное. Поскольку камень бросили вертикально вверх, и он вернулся в то же место, откуда его бросали, значит вектор перемещения равен нулевому вектору, а длина вектора перемещения (его модуль) равна нулю.
\[\vec r = \vec 0 \Rightarrow \left| {\vec r} \right| = 0\]
Путь – это скалярная величина, равная длине траектории, которое прошло тело.2}}}{4} = 10\;м\]
Ответ: 10 м, 0 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Тест по физике Вывод закона сохранения механической энергии
Тест по физике Вывод закона сохранения механической энергии для учащихся 9 класса с ответами. Тест включает в себя 10 заданий с выбором ответа.
1. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию 30 Дж. Какую потенциальную энергию относительно поверхности земли будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
1) 0 Дж
2) 15 Дж
3) 30 Дж
4) 60 Дж
2. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию 20 Дж. Какую кинетическую энергию будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
1) 0 Дж
2) 10 Дж
3) 20 Дж
4) 40 Дж
3. Тело массой 2 кг, брошенное с уровня земли вертикально вверх, упало обратно. Перед ударом о землю оно имело кинетическую энергию 100 Дж. С какой скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
1) 10 м/с
2) 20 м/с
3) 30 м/с
4) 40 м/с
4. Тело массой 1 кг, брошенное с уровня земли вертикально вверх, упало обратно. В момент наивысшего подъема оно имело потенциальную энергию 200 Дж. С какой скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
1) 10 м/с
2) 20 м/с
3) 30 м/с
4) 40 м/с
5. Тело массой 1 кг, брошенное вертикально вверх от поверхности земли, достигло максимальной высоты 20 м. С какой по модулю скоростью двигалось тело на высоте 10 м? Сопротивлением воздуха пренебречь.
1) 7 м/с
2) 10 м/с
3) 14,1 м/с
4) 20 м/с
6. По какой из формул можно определить кинетическую энергию Ек, которую имело тело в верхней точке траектории?
1) Ек = mgh
2) Ек = mv02/2 + mgh − mgH
3) Ек = mgH − mgh
4) Ек = mv02/2 + mgH
7. Шарику на нити, находящемуся в положении равновесия, сообщили небольшую горизонтальную скорость. На какую высоту поднимется шарик?
1) v02/2g
2) 2v02/2g
3) v02/4g
4) 2g/v02
8. Шарику на нити, находящемуся в положении равновесия, сообщили небольшую горизонтальную скорость 20 м/с. На какую высоту поднимется шарик?
1) 40 м
2) 20 м
3) 10 м
4) 5 м
9. На рисунке представлен график изменения со временем кинетической энергии ребенка, качающегося на качелях. В момент, соответствующий точке А на графике, его полная механическая энергия равна
1) 10 Дж
2) 20 Дж
3) 30 Дж
4) 40 Дж
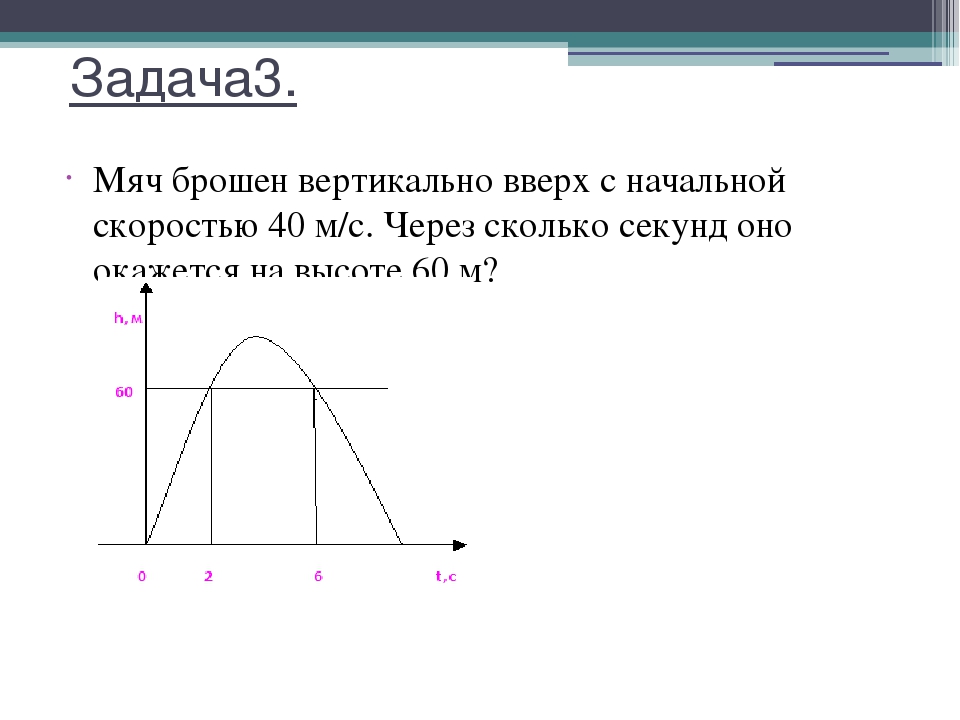
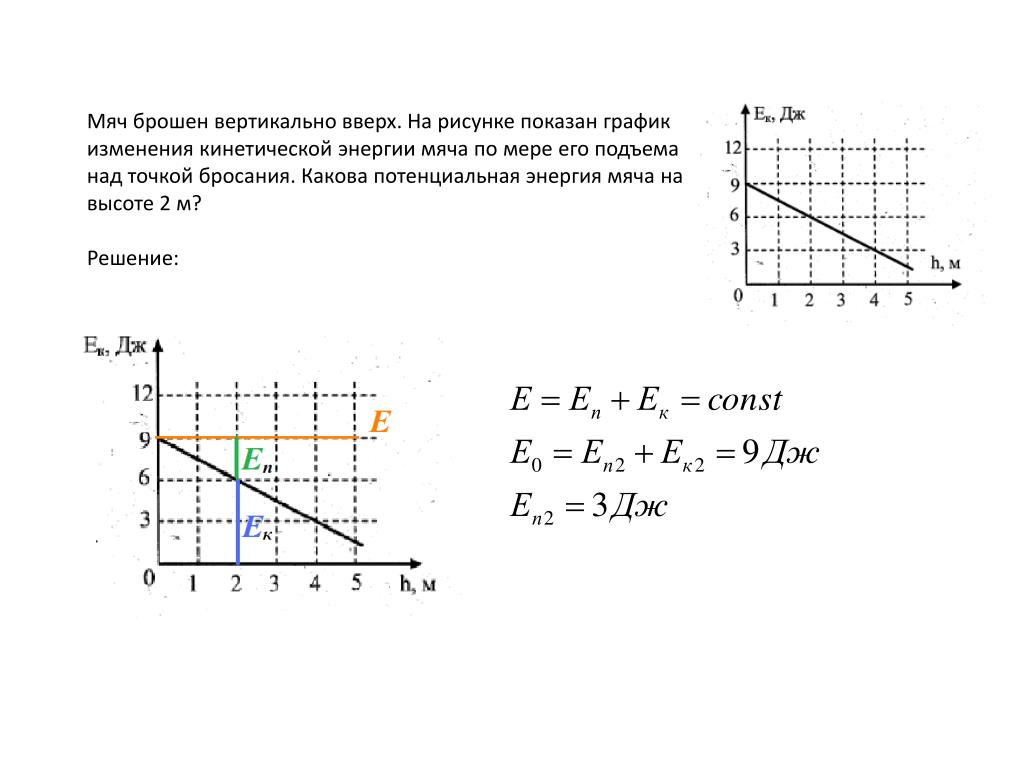
10. Мяч брошен вертикально вверх. На рисунке показан график изменения кинетической энергии мяча по мере его подъема над точкой бросания. Какова потенциальная энергия мяча на высоте 2 м?
1) 1,5 Дж
2) 3 Дж
3) 4,5 Дж
4) 6 Дж
Ответы на тест по физике Вывод закона сохранения механической энергии
1-3
2-1
3-1
4-2
5-3
6-2
7-1
8-2
9-4
10-2
Свободное падение тел, ускорение. Движение вертикально вверх и вертикально вниз. Тест
В задачах ускорение свободного падения принять равным 10 м/с2. Сопротивлением воздуха пренебречь.
Вопрос 1. Мяч бросили вертикально вверх со скоростью 18 м/с. Какое перемещение совершит он за 3 с?
Вопрос 2. За какое время (с) мяч, начавший свое падение без начальной скорости, пройдет путь 20 м?
Вопрос 3. Через сколько секунд тело будет на высоте 25 м, если его бросить вертикально вверх с начальной скоростью 30 м/с? В ответ записать разницу полученных результатов в секундах.
Вопрос 4. С высоты 2 м вертикально вверх бросили тело с начальной скоростью 5 м/с. Найти модуль перемещения и пройденный путь? В ответ записать разницу пути и перемещения в метрах, с точностью до десятых.
Вопрос 5. Бросая мяч вертикально вверх, мальчик сообщает ему скорость в 1,5 раза большую, чем девочка. Во сколько раз выше поднимется мяч, брошенный мальчиком?
Вопрос 6. Тело бросают вертикально вверх. Наблюдатель заметил, что на высоте 75 м тело побывало дважды, с интервалом времени 2 с. Найдите начальную скорость (м/с) тела.
Вопрос 7. Ускорение свободного падения на Луне в 6 раз меньше, чем на Земле. Во сколько раз выше человек прыгнет на Луне, чем на Земле?
Вопрос 8. Аэростат поднимается с аэродрома вертикально вверх с ускорением 2 м/с2. Через 5 с от начала его движения из него выпал предмет. Через какое время (c) этот предмет упадет на землю?
Вопрос 9. Тело свободно падает с высоты 27 м. Разделить эту высоту на три части так, чтобы на прохождение каждой из них потребовалось одно и то же время. В ответ записать разницу между наибольшим и наименьшим отрезками.
Вопрос 10. Тело падает с высоты 100 м без начальной скорости. За какое время (с) тело проходит первый и последний метры своего пути? В ответ записать их разницу с точностью до сотых.
Вопрос 11. Свободно падающее без начальной скорости тело в последнюю секунду падения прошло 2/3 своего пути. Найти весь путь (м), пройденный телом.
Вопрос 12. Тело свободно падает с высоты 5 м. В тот же момент другое тело брошено с высоты 20 м вертикально вниз. Оба тела упали на землю одновременно. Определить начальную скорость (м/с) второго тела.
Вопрос 13. С вертолета сбросили без начальной скорости два груза, причем второй на 1 с позже первого. Определить расстояние (м) между грузами через 2 с после начала движения первого груза.
Вопрос 14. С поверхности земли с одинаковыми скоростями 20 м/с последовательно через промежуток времени 1 с брошены вверх два мяча. Определить, на каком расстоянии (в метрах с точностью до сотых) от поверхности земли они встретятся.
Вопрос 15. Жонглер бросает мячики один за другим вверх, каждый следующий мяч в тот момент, когда предыдущий находится в наивысшей точке. На какую высоту поднимаются мячи, если он бросает три мяча в секунду? Ответ указать в метрах с точностью до сотых.
Тело, брошенное вертикально вверх с поверхности Земли, достигло максимальной высоты 5 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
Приложение №1: Карточка, в которой дети работали и сдали в конце урока.
Ф.И.
Заполни таблицу выполняя блиц-тест:
1 2 3 4 5 6 7
Оцени свои знания «до» самопроверки и «после» самопроверки До
После
Тело массой 1 кг, брошенное вертикально вверх с поверхности Земли, достигло максимальной высоты 20 м. Какой кинетической энергией обладало тело тотчас после броска? Сопротивлением воздуха пренебречь.
Тело, брошенное вертикально вверх с поверхности Земли, достигло максимальной высоты 5 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
Горизонтально расположенная невесомая пружина с жёсткостью k = 1000 Н/м находится в недеформированном состоянии. Один её конец закреплён, а другой касается бруска массой m = 0,1 кг, находящегося на горизонтальной поверхности. Брусок сдвигают, сжимая пружину, и отпускают. На какую длину Δx была сжата пружина, если после отпускания бруска его скорость достигла величины υ = 1 м/с? Трение не учитывать.
Оцени свои знания и понимание темы после разбора задач______
Экспериментальная задача.
С наклонной плоскости, из состояния покоя, скатывается стальной шарик. Пронаблюдай движение шарика до момента удара. Ответь кратко на поставленные вопросы:
Какие превращения энергии происходят при движении шарика по наклонной поверхности?
Куда «исчезает» потенциальная энергия шарика, когда он касается металлического цилиндра , т.е. касается основания наклонной плоскости?
Не нарушается ли здесь закон сохранения и превращения энергии? Трением шарика о стенки желоба пренебречь.
Предложи способ определения скорости шарика в момент, когда он достигает основания наклонной поверхности? ***Найти скорость шарика используя только линейку. Поясните, как справились с заданием
Запиши, что ты заметил, выполняя решения задач.
Ответы :
Оцени свой уровень умения решать задачи по рассмотренной теме.
Приложенные файлы
- 21360616
Размер файла: 23 kB Загрузок: 0
Движение тела, брошенного вертикально вверх и вниз
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Если же подбросить некоторое тело вертикально вверх и при этом считать, что сопротивление воздуха отсутствует, то можно считать, что оно тоже совершает равноускоренное движение с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Далее, тело начнет равноускоренно падать вниз под действием силы тяжести.
Формулы для равноускоренного движения применимы для движения тела, брошенного вверх. V0 всегда > 0
Движение тела, брошенного вертикально вверх, является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу \(y = y_0+v_0yt+\frac{a_yt^2}{2}\),
положив \(υ_0 >0, y_0 = 0, y=H, a = –g.2}2.\) Из последней формулы можно найти время падения тела с высоты h: \(t = \sqrt{\frac{2h}g} .\) Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: \(υ= \sqrt{2gh}.\)
Если тело подбросить, то оно сначала движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при \(y = h_{max}\) скорость \(υ_y = 0\) и в момент достижения телом первоначального положения \(y = 0\), можно найти
\(t_1=υ_0\cdot g \) – время подъема тела на максимальную высоту;
\(h_{max}\) – максимальная высота подъема тела;
\(t_2=2t_1=\frac{2υ_0}g \) – время полета тела;
\(v_{2y}=-v_0\) – проекция скорости в момент достижения телом первоначального положения.
Типичные задачи B12 с функциями
Сегодня мы рассмотрим типичные задачи B12, которые сводятся к работе с функциями. Речь пойдет о функциях в «чистом» виде — без дополнительных параметров и аргументов. Подобных задач не так много, поэтому урок будет коротким, но содержательным.
Говоря простым языком, функции — это когда одна переменная зависит от другой. В задаче B12 функции всегда задаются формулами и обозначаются разными буквами: f(x), h(t), m(t)…
Как решать такие задачи? Многие учителя рекомендуют сводить функцию к уравнениям и неравенствам, а затем решать их. Можно и так, но есть способ проще. Итак, всего три шага:
- Найти в тексте задачи, чему должна быть равна функция. Пусть это будет число K.
- Решить уравнение f(x) = K.Ну, или h(t) = K — в зависимости от того, как называется функция.
- Если корень один — это и есть ответ. Если корней два и более — надо немного подумать. Например, время не может быть отрицательным, масса — нулевой, и так далее.
Функции в задаче B12 всегда очень простые, поэтому чаще всего проблемы возникают на третьем шаге. Но это лечится обыкновенной тренировкой.
Задача. Высота, на которой находится камень, брошенный с земли вертикально вверх, меняется по закону h(t) = 2 + 12t − 5t2,где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень будет находиться на высоте более 6 метров?
Из условия следует, что надо решить уравнение h(t) = 6. Получаем обычное квадратное уравнение:
2 + 12t − 5t2 = 6;
5t2 − 12t + 4 = 0 — собрали все с одной стороны;
… (решаем обычное квадратное уравнение)
t1 = 0,4;t2 = 2.
Итак, у нас два корня. Что это значит? В момент времени t1 = 0,4 камень был на высоте 6 метров, затем — очевидно, больше 6, и, наконец, в момент t2 = 2 снова 6 метров. Короче говоря, в период с t1 = 0,4до t2 = 2 камень находился на высоте более 6 метров. Найдем длину отрезка времени l:
l = t2 − t1 = 2 − 0,4 = 1,6.
Задача. Камень брошен вниз с высоты 24 метра. Пока камень не упал, его высоту можно находить по формуле h(t) = 24 − 7t − 5t2,где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень будет падать?
Что значит, что камень упал? Это означает, что его высота над поверхностью земли стала равна нулю. Итак, надо решить уравнение h(t) = 0. Имеем:
24 − 7t − 5t2 = 0 — обычное квадратное уравнение;
… (решаем квадратное уравнение)
t1 = 1,6; t2 = −3;
Очевидно, корень t1 = −3 нам не подходит, поскольку время не может быть отрицательным. Поэтому камень будет падать 1,6 секунды.
Почему-то в последней задаче многие (на самом деле, почти все) хотят решить уравнение h(t) = 24. Аргументация такая: мол, число 24 встречается в тексте, да еще и в самом начале. Так вот: это число не имеет никакого отношения к решению. Вообще. А требуемое значение функции надо искать в вопросе.
В самом деле, сколько секунд камень будет падать? Ну, до тех пор, пока не упадет. А что значит, что камень упал? Это значит, что его высота над землей равна нулю. Вот такие неслабые размышления.
Когда искомое значение функции определено, решить задачу не составит труда. В заключение рассмотрим еще 2 типовые задачи, которые любят давать на пробных экзаменах, и которые вполне могут встретиться на настоящем ЕГЭ.
Задача. В боковой стенке цилиндрического бака вблизи дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем меняется по закону:
H(t) = 5 − 1,6t + 0,128t2
где t — время в минутах. В течение какого времени вода будет вытекать из бака?
Эта задача очень похожа на предыдущую — про камень, брошенный с высоты 24 метра. Вода будет вытекать из бака до тех пор, пока высота столба не станет равной нулю. Поэтому H(t) = 0. Подставляем это значение в функцию и решаем уравнение:
0 = 5 − 1,6t + 0,128t2;
0 = 625 − 200t + 16t2 — умножили все на 125;
16t2 − 200t + 625 = 0 — стандартное квадратное уравнение;
Поскольку коэффициенты получились неслабые, причем a = 16 ≠ 0, работаем через дискриминант (см. урок «Решение квадратных уравнений»). Имеем:
D = b2 − 4ac =(−200)2 − 4 · 16 · 625 =40 000 − 40 000 = 0 — уравнение имеет ровно 1 корень.
t = −b : (2a) = −(−200) : (2 · 16) =200 : 32 = 6,25.
Таким образом, вода перестанет вытекать из бака через 6,25 минуты — это и есть ответ.
Задача. После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле h = −5t2,где t измеряется в секундах, а h — в метрах.
До дождя время падения камушков составляло 1,4 секунды. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше чем на 0,1 секунды? Ответ выразите в метрах.
Это немного нестандартная задача с функцией. По условию, аргумент t может принимать 2 значения:
t1 = 1,4 — исходное, дано в условии задачи;
t2 = 1,4 − 0,1 = 1,3 — новое значение.
Теперь подставим эти значения в функцию h(t). Так мы найдем расстояние от верхней кромки колодца до поверхности воды до и после дождя. Имеем:
h(t1) = −5 · (1,4)2 = … = −9,8;
h(t2) = −5 · (1,3)2 = … = −8,45.
Итак, есть два значения: −9,8 метраи −8,45 метра. Если вычесть из большей высоты меньшую, получим искомую минимальную высоту Δh, на которую должен подняться уровень воды:
Δh = −8,45 − (−9,8) =9,8 − 8,45 = 1,35 — это и есть ответ.
Небольшое пояснение к последней задаче. Откуда взялось число t2 = 1,3? По условию, уровень воды повышается, а значит, расстояние от воды до верхней кромки колодца становится меньше. Следовательно, уменьшается и время полета камня.
Именно поэтому мы уменьшаем исходное время (t2 = 1,4 − 0,1 = 1,3), а ни в коем случае не увеличиваем его. Понять это — вот основная трудность подобных задач.
span class=Смотрите также:
- Не пишите единицы измерения в задаче B12
- Задачи про температуру и энергию звезд
- Формула полной вероятности
- Радианная и градусная мера угла
- Пробный ЕГЭ по математике 2015: 4 вариант
- Проценты в задачах на наибольшее-наименьшее значение: используем формулы процентов
Если камень брошен вертикально вверх от поверхности Луны со скоростью 13 м / с
Дано: v = 13 м / с
h = 13t — 0,83t 2
13t — скала на пути вверх, а -0,83t 2 — скала на пути вниз. ≅Обратите внимание, что как только камень запускается, сила тяжести начинает действовать против него, но при спуске мы получаем ускорение за счет силы тяжести.
а) v =? после t = 7 с
Наше исходное уравнение, данное нам, было h = 13t — 0.83т 2 .
- Мгновенная скорость — это первая производная положения по времени, поэтому v = dh / dt .
Взяв производную, получаем v = dh / dt = 13 — 1,66t .
Включаем t = 7 с получаем v = 1,38 м / с
б) v =? после h = 33 м
Предварительные условия :
Эта задача включает два периода времени (t 1 = вверх, t 2 = вниз).
Сначала решим для t 1∧2 .
Для h = 33 м и v = 13 м / с, h = 13t — 0,83t 2 становится 33 = 13t — 0,83t 2 .
Мы перемещаем число 13 на другую сторону, приравниваем уравнение нулю и затем решаем положительные корни t. Это беспорядок, поэтому запомните квадратную формулу: -b ± √ (b 2 — 4ac) / 2a .2-4 * (- 83) * (- 3300)) / 2 * (- 83) ⇒
t ↑ = 10 (65 + √1486) / 83 ≈ 3,19 с (i)
t ↓ = 10 (65 — √1486) / 83 ≈ 12,48 с (ii)
Итак, мы имеем t при h = 33 м как на пути вверх, так и на спуске. Поскольку мы ищем скорость при h = 33 , мы будем использовать (i) и формулу, которую мы вывели в части (a).
v = 13 — 1,66 t = 13 — 1.66 (3,19 с) = 7,70 м / с
3.5 Свободное падение | Университетская физика, том 1,
Цели обучения
К концу этого раздела вы сможете:
- Используйте кинематические уравнения с переменными y и g для анализа движения свободного падения.
- Опишите, как меняются значения положения, скорости и ускорения во время свободного падения.
- Найдите положение, скорость и ускорение как функции времени, когда объект находится в свободном падении.
Интересное применение от (Рисунок) до (Рисунок) называется свободное падение , которое описывает движение объекта, падающего в гравитационном поле, например, вблизи поверхности Земли или других небесных объектов планетарного размера. Предположим, что тело падает по прямой линии, перпендикулярной поверхности, поэтому его движение одномерно. Например, мы можем оценить глубину вертикального ствола шахты, бросив в него камень и прислушиваясь к удару камня о дно.Но «падение» в контексте свободного падения не обязательно означает, что тело перемещается с большей высоты на меньшую. Если мяч брошен вверх, уравнения свободного падения в равной степени применимы как к его подъему, так и к его спуску.
Гравитация
Самый замечательный и неожиданный факт о падающих объектах заключается в том, что если сопротивление воздуха и трение незначительны, то в данном месте все объекты падают к центру Земли с одинаковым постоянным ускорением , независимо от их массы .Этот экспериментально установленный факт является неожиданным, потому что мы настолько привыкли к эффектам сопротивления воздуха и трения, что ожидаем, что легкие объекты будут падать медленнее, чем тяжелые. До тех пор, пока Galileo Galilei (1564–1642) не доказали обратное, люди считали, что более тяжелый объект имеет большее ускорение при свободном падении. Теперь мы знаем, что это не так. При отсутствии сопротивления воздуха тяжелые предметы падают на землю одновременно с более легкими при падении с той же высоты (рисунок).
Рисунок 3.26 Молоток и перо падают с одинаковым постоянным ускорением, если сопротивление воздуха незначительно. Это общая характеристика гравитации, не уникальная для Земли, как продемонстрировал астронавт Дэвид Р. Скотт в 1971 году на Луне, где ускорение свободного падения составляет всего 1,67 м / с2, а атмосферы нет.
В реальном мире сопротивление воздуха может заставить более легкий объект падать медленнее, чем более тяжелый объект того же размера. Теннисный мяч падает на землю после того, как одновременно упал бейсбольный мяч.(Может быть трудно заметить разницу, если высота небольшая.) Сопротивление воздуха препятствует движению объекта по воздуху и трению между объектами, например, между одеждой и лотком для стирки или между камнем и бассейном. которую уронили — тоже противодействуют движению между ними.
Для идеальных ситуаций, описанных в этих первых нескольких главах, объект , падающий без сопротивления воздуха и трения , определяется как в свободном падении . Сила тяжести заставляет объекты падать к центру Земли.Поэтому ускорение свободно падающих объектов называется ускорением свободного падения . Ускорение под действием силы тяжести постоянно, что означает, что мы можем применить кинематические уравнения к любому падающему объекту, где сопротивление воздуха и трение незначительны. Это открывает нам широкий класс интересных ситуаций.
Ускорение свободного падения настолько важно, что его величине присвоен собственный символ — г . Он постоянен в любом месте на Земле и имеет среднее значение
.[латекс] г = 9.{2}). [/ латекс]
Хотя g варьируется от 9,78 м / с 2 до 9,83 м / с 2 , в зависимости от широты, высоты, нижележащих геологических образований и местной топографии, давайте воспользуемся средним значением 9,8 м / с 2 округлено до двух значащих цифр в этом тексте, если не указано иное. Пренебрегая этими эффектами для значения г в результате положения на поверхности Земли, а также эффектами, возникающими в результате вращения Земли, мы принимаем направление ускорения силы тяжести вниз (к центру Земли).{2} [/ латекс].
Одномерное движение с участием силы тяжести
Лучший способ увидеть основные особенности движения, связанного с гравитацией, — это начать с простейших ситуаций, а затем переходить к более сложным. Итак, мы начнем с рассмотрения прямого движения вверх и вниз без сопротивления воздуха или трения. Эти предположения означают, что скорость (если есть) вертикальная. Если объект уронили, мы знаем, что начальная скорость в свободном падении равна нулю. Когда объект вышел из контакта с тем, что держало или бросало, объект находится в свободном падении.Когда объект брошен, он имеет ту же начальную скорость в свободном падении, что и до того, как его выпустили. Когда объект соприкасается с землей или любым другим объектом, он больше не находится в свободном падении, и его ускорение g больше не действует. В этих условиях движение является одномерным и имеет постоянное ускорение величиной g . Мы обозначаем вертикальное смещение символом y .
Кинематические уравнения для объектов в свободном падении
Здесь мы предполагаем, что ускорение равно — g (при положительном направлении вверх).{2} -2 г (г- {у} _ {0}) [/ латекс]
Стратегия решения проблем: свободное падение
- Определитесь со знаком ускорения свободного падения. На (Рисунок) — (Рисунок) ускорение g отрицательное, что означает положительное направление вверх, а отрицательное направление — вниз. В некоторых задачах может быть полезно иметь положительное ускорение g , что указывает на положительное направление вниз.
- Нарисуйте схему проблемы. Это помогает визуализировать вовлеченную физику.
- Запишите известные и неизвестные из описания проблемы. Это помогает разработать стратегию выбора соответствующих уравнений для решения проблемы.
- Решите, какое из (Рисунок) — (Рисунок) использовать для решения неизвестных.
Пример
Свободное падение мяча (рисунок) показывает положение мяча с интервалом в 1 секунду с начальной скоростью 4,9 м / с вниз, который брошен с вершины здания высотой 98 м. (а) Сколько времени проходит до того, как мяч коснется земли? б) С какой скоростью он достигает земли?
Рисунок 3.{2} + t-20 = 0. [/ latex] Это квадратное уравнение с корнями [latex] t = -5.0 \ mathrm {s} \, \ text {and} \, t = 4.0 \ mathrm {s} [/ latex]. Положительный корень — это тот, который нас интересует, поскольку time [latex] t = 0 [/ latex] — это время, когда мяч выпущен наверху здания. (Время [латекс] t = -5.0 \ mathrm {s} [/ latex] представляет тот факт, что мяч, брошенный вверх с земли, был бы в воздухе 5,0 с, когда он прошел мимо вершины здания, двигаясь вниз. на скорости 4,9 м / с.)
Используя (рисунок), мы имеем [latex] v = {v} _ {0} -gt = -4.{2}) (4.0 \, \ text {s}) = — 44.1 \, \ text {m / s} \ text {.} [/ Latex]
Значение
В ситуациях, когда два корня получаются из квадратного уравнения для переменной времени, мы должны посмотреть на физическое значение обоих корней, чтобы определить, какой из них правильный. Поскольку [latex] t = 0 [/ latex] соответствует времени, когда мяч был выпущен, отрицательный корень будет соответствовать времени до того, как мяч был выпущен, что не имеет физического смысла. Когда мяч ударяется о землю, его скорость не сразу равна нулю, но как только мяч взаимодействует с землей, его ускорение не равно g , и он ускоряется с другим значением за короткое время до нулевой скорости.Эта задача показывает, насколько важно установить правильную систему координат и сохранить согласованность знаков g в кинематических уравнениях.
Пример
Вертикальное движение бейсбольного мяча
Бэттер ударяет по бейсбольному мячу прямо вверх по своей тарелке, и мяч ловится через 5,0 с после удара (рисунок). а) Какова начальная скорость мяча? (б) Какой максимальной высоты достигает мяч? (c) Сколько времени нужно, чтобы достичь максимальной высоты? (г) Какое ускорение в верхней части его пути? (e) Какова скорость мяча, когда он пойман? Предположим, что мяч попадает в одно и то же место.{2}) т. [/ латекс]
Это дает [латекс] t = 2,5 \, \ text {s} [/ latex]. Поскольку мяч поднимается за 2,5 с, время падения составляет 2,5 с.
Ускорение везде составляет 9,8 м / с2, даже если скорость равна нулю в верхней части траектории. Хотя скорость наверху равна нулю, вниз она изменяется со скоростью 9,8 м / с2.
Скорость при [latex] t = 5.0 \ mathrm {s} [/ latex] может быть определена с помощью (Рисунок): [latex] \ begin {array} {cc} \ hfill v & = {v} _ {0} — gt \ hfill \\ & = 24.{2} (5.0 \, \ text {s}) \ hfill \\ & = -24.5 \, \ text {m / s}. \ Hfill \ end {array} [/ latex]
Значение
Мяч возвращается с той скоростью, с которой он улетал. Это общее свойство свободного падения при любой начальной скорости. Мы использовали одно уравнение для перехода от броска к ловле, и нам не приходилось разбивать движение на два сегмента, восходящий и нисходящий. Мы привыкли думать, что гравитация вызывает свободное падение вниз к Земле. Важно понимать, как показано в этом примере, что объекты, движущиеся вверх от Земли, также находятся в состоянии свободного падения.
Проверьте свое понимание
Глыба льда отламывается от ледника и падает на 30,0 м, прежде чем упасть в воду. Если предположить, что он падает свободно (нет сопротивления воздуха), сколько времени нужно, чтобы удариться о воду? Какая величина увеличивается быстрее, скорость куска льда или пройденное расстояние?
Показать решениеВремя попадания в воду — 2,47 с. Пройденное расстояние увеличивается быстрее.
Пример
Ракетный ускоритель
Маленькая ракета с ускорителем взлетает и устремляется вверх.На высоте [latex] 5.0 \, \ text {km} [/ latex] и скорости 200.0 м / с он выпускает ускоритель. (а) Какую максимальную высоту достигает ракета-носитель? (б) Какова скорость ракеты-носителя на высоте 6,0 км? Пренебрегайте сопротивлением воздуха.
Рис. 3.29. Ракета выпускает ускоритель с заданной высотой и скоростью. Насколько высоко и с какой скоростью летит бустер?
Стратегия
Нам нужно выбрать систему координат для ускорения свободного падения, которое мы принимаем отрицательным вниз.Нам дана начальная скорость ускорителя и его высота. Мы рассматриваем точку выпуска как источник. Мы знаем, что скорость равна нулю в максимальном положении в пределах интервала ускорения; таким образом, скорость ускорителя равна нулю на его максимальной высоте, поэтому мы также можем использовать эту информацию. {2} -2g (y- {y} _ {0}) [/ latex].{3} \, \ text {m}) ⇒v = ± 142,8 \, \ text {m} \ text {/} \ text {s}. [/ латекс]
Значение
У нас есть как положительное, так и отрицательное решение в (b). Поскольку наша система координат имеет положительное направление вверх, +142,8 м / с соответствует положительной восходящей скорости на высоте 6000 м во время восходящего участка траектории ракеты-носителя. Значение v = -142,8 м / с соответствует скорости на 6000 м на нисходящем участке. Этот пример также важен тем, что объекту задается начальная скорость в начале нашей системы координат, но начало координат находится на высоте над поверхностью Земли, что необходимо учитывать при формировании решения.{2} [/ латекс].
Концептуальные вопросы
Какое ускорение у камня, брошенного вверх по пути вверх? На пике своего полета? По пути вниз? Предположим, что сопротивление воздуха отсутствует.
Подброшенный вверх объект падает обратно на Землю. Это одномерное движение. (а) Когда его скорость равна нулю? (б) Меняет ли его скорость направление? (c) Имеет ли ускорение тот же знак при движении вверх и вниз?
Показать решениеа.на вершине своей траектории; б. да, на вершине своей траектории; c. да
Предположим, вы бросаете камень почти прямо в кокос на пальме, и камень просто не задевает кокос на пути вверх, но ударяет по кокосу на пути вниз. Если пренебречь сопротивлением воздуха и небольшими горизонтальными колебаниями в движении, чтобы учесть попадание и промах кокоса, как скорость камня, когда он ударяется о кокос на пути вниз, сравнивается с той, которая была бы, если бы он ударился о кокос? по пути наверх? Кокосовый орех с большей вероятностью сместится по пути вверх или вниз? Объяснять.{2}) = — 6лет [/ латекс]
Во сколько раз космонавт может прыгнуть на Луне выше, чем на Земле, если ее скорость взлета одинакова в обоих местах (гравитационное ускорение на Луне примерно в шесть раз меньше, чем на Земле)?
Проблемы
Рассчитайте смещение и скорость во время (а) 0,500 с, (б) 1,00 с, (в) 1,50 с и (г) 2,00 с для шара, брошенного прямо вверх с начальной скоростью 15,0 м / с. Примите точку выпуска [latex] {y} _ {0} = 0 [/ latex].
Рассчитайте смещение и скорость в моменты времени: (а) 0,500 с, (б) 1,00 с, (в) 1,50 с, (г) 2,00 с и (д) 2,50 с для камня, брошенного прямо вниз с начальной скоростью 14,0 м / с от моста Verrazano Narrows Bridge в Нью-Йорке. Высота проезжей части этого моста над водой составляет 70,0 м.
Показать решениеа. [латекс] \ begin {array} {cc} y = -8.23 \, \ text {m} \ hfill \\ {v} _ {1} = \ text {-} 18.9 \, \ text {m / s} \ hfill \ end {array} [/ latex];
г. [латекс] \ begin {array} {cc} y = -18.9 \, \ text {m} \ hfill \\ {v} _ {2} = 23.8 \, \ text {m / s} \ hfill \ end {array} [/ latex];
г. [латекс] \ begin {array} {cc} y = -32.0 \, \ text {m} \ hfill \\ {v} _ {3} = \ text {-} 28.7 \, \ text {m / s} \ hfill \ end {array} [/ latex];
г. [латекс] \ begin {array} {cc} y = -47.6 \, \ text {m} \ hfill \\ {v} _ {4} = \ text {-} 33.6 \, \ text {m / s} \ hfill \ end {array} [/ latex];
e. [латекс] \ begin {array} {cc} y = -65.6 \, \ text {m} \ hfill \\ {v} _ {5} = \ text {-} 38.5 \, \ text {m / s} \ hfill \ end {array} [/ latex]
Баскетбольный судья подбрасывает мяч прямо для стартовой наводки.С какой скоростью баскетболист должен отрываться от земли, чтобы подняться на 1,25 м над полом, чтобы попытаться поймать мяч?
Спасательный вертолет парит над человеком, чья лодка затонула. Один из спасателей бросает спасательный круг прямо в пострадавшего с начальной скоростью 1,40 м / с и отмечает, что для достижения воды требуется 1,8 с. (а) Перечислите известных в этой проблеме. б) На какой высоте над водой был выпущен предохранитель? Обратите внимание, что нисходящий поток вертолета снижает влияние сопротивления воздуха на падающий спасательный круг, так что ускорение, равное ускорению силы тяжести, является разумным.{2} = — 18,4 \, \ text {m} [/ latex], а исходная точка — у спасателей, которые находятся на высоте 18,4 м над водой.
Необоснованные результаты Дельфин на водном шоу выпрыгивает прямо из воды со скоростью 15,0 м / с. (а) Перечислите известных в этой проблеме. б) Насколько высоко его тело возвышается над водой? Чтобы решить эту часть, сначала обратите внимание, что окончательная скорость теперь известна, и определите ее значение. Затем определите неизвестное и обсудите, как вы выбрали соответствующее уравнение для его решения.После выбора уравнения покажите свои шаги в решении неизвестных, проверяющих единиц и обсудите, является ли ответ разумным. в) Как долго дельфин находится в воздухе? Не обращайте внимания на любые эффекты, связанные с его размером или ориентацией.
Дайвер подпрыгивает прямо от трамплина, избегая трамплина при спуске, и падает ногами в бассейн. Она стартует со скоростью 4,00 м / с, а ее точка взлета находится на высоте 1,80 м над бассейном. а) Какая у нее самая высокая точка над доской? б) Сколько времени ее ноги в воздухе? в) Какова ее скорость, когда ее ноги касаются воды?
Показать решениеа.{2} -2g (y- {y} _ {0}) \ enspace {y} _ {0} = 0 \ enspace \ enspace {v} _ {0} = 4.0 \, \ text {m} \ text { /}\text{s}y=-1.80\,\text{m}\hfill \\ v = 7.16 \, \ text {m} \ text {/} \ text {s} \ hfill \ end {array} [ / латекс]
(a) Вычислите высоту обрыва, если камень ударится о землю за 2,35 с, когда он брошен прямо со скалы с начальной скоростью 8,00 м / с. б) Сколько времени потребуется, чтобы достичь земли, если ее бросят прямо вниз с той же скоростью?
Очень сильный, но неумелый толкатель ядра стреляет прямо вертикально с начальной скоростью 11.{2} + 11.0t-0.40 = 0 \ hfill \ end {array} [/ latex].
Возьмите положительный корень, поэтому время на дополнительные 0,4 м составит 0,04 с. Общее время составляет [латекс] 2,24 \, \ text {s} \, + 0,04 \, \ text {s} \, = 2,28 \, \ text {s} [/ latex].
Вы бросаете мяч прямо вверх с начальной скоростью 15,0 м / с. Поднимаясь вверх, он проходит ветку дерева на высоте 7,0 м. Сколько дополнительного времени проходит, прежде чем мяч пересечет ветку дерева на обратном пути вниз?
Кенгуру может перепрыгнуть через объект 2.{2} = 2gy⇒ {v} _ {0} = \ sqrt {2 (9.80) (2.50)} = 7.0 \, \ text {m} \ text {/} \ text {s} \ hfill \ end {массив } [/ латекс]; б. [latex] t = 0,72 \, \ text {s} [/ latex] умножить на 2 дает 1,44 с в воздухе
Стоит у подножия одной из скал горы. Путешественник в Арапилесе, Виктория, Австралия, слышит, как с высоты 105,0 м вырывается скала. Он не может сразу увидеть камень, но видит, спустя 1,50 секунды. а) Как далеко путешественник находится над скалой, когда он ее видит? б) Сколько времени ему нужно двигаться, прежде чем камень ударится о его голову?
В Хаф-Доум в национальном парке Йосемити в Калифорнии есть скала высотой 250 м.Предположим, с вершины этого утеса вырывается валун. а) С какой скоростью он будет двигаться, когда ударится о землю? (b) Предполагая, что время реакции составляет 0,300 с, сколько времени потребуется туристу внизу, чтобы уклониться от дороги после того, как услышал звук отрывающейся скалы (без учета роста туриста, который в любом случае стал бы незначительным. если ударил)? Скорость звука в этот день составляет 335,0 м / с.
Показать решениеа. [латекс] v = 70.0 \, \ text {m} \ text {/} \ text {s} [/ latex]; б. время слышно после начала падения камня: 0.75 с, время касания земли: 6,09 с
Глоссарий
- ускорение свободного падения
- Ускорение объекта под действием силы тяжести
- свободное падение
- состояние движения, которое является результатом только силы тяжести
2.6. Свободно падающие тела
Все видели эффект гравитации, когда предметы падают вниз. Обнаружено, что при отсутствии сопротивления воздуха все тела в одном и том же месте над землей падают вертикально с одинаковым ускорением.Кроме того, если расстояние падения мало по сравнению с радиусом земли, ускорение остается практически постоянным на протяжении всего спуска. Это идеализированное движение, при котором сопротивление воздуха не учитывается, а ускорение почти постоянно, известно как свободное падение . Поскольку при свободном падении ускорение постоянно, можно использовать уравнения кинематики.
Ускорение свободно падающего тела называется ускорением свободного падения , а его величина (без алгебраического знака) обозначается символом g.Ускорение свободного падения направлено вниз, к центру Земли. Вблизи земной поверхности g составляет приблизительно
Если обстоятельства не требуют иного, мы будем использовать любое из этих значений для g в последующих расчетах. В действительности, однако, g уменьшается с увеличением высоты и незначительно изменяется с широтой.
На рис. 2.16a показано хорошо известное явление: камень падает быстрее листа бумаги.Эффект сопротивления воздуха вызывает более медленное падение бумаги, поскольку, когда воздух удаляется из трубки, как на рис. 2.16b, камень и бумага имеют одинаковое ускорение силы тяжести. В отсутствие воздуха камень и бумага демонстрируют свободное падение. Свободное падение близко приближается к объектам, падающим рядом с поверхностью Луны, где нет воздуха, который мог бы замедлить движение. Красивую демонстрацию свободного падения Луны продемонстрировал астронавт Дэвид Скотт, уронивший одновременно молот и перо с одной и той же высоты.Оба испытали одинаковое ускорение из-за лунного притяжения и, следовательно, одновременно упали на землю. Ускорение свободного падения у поверхности Луны примерно в шесть раз меньше, чем на Земле.
|
Когда уравнения кинематики применяются к движению свободного падения, естественно использовать символ y для смещения, поскольку движение происходит в вертикальном направлении или в направлении y. Таким образом, используя уравнения в таблице 2.1 для свободного падения, мы просто заменим x на y. Это изменение не имеет значения. Уравнения имеют одинаковую алгебраическую форму для горизонтального или вертикального направления при условии, что ускорение остается постоянным во время движения.Теперь обратим наше внимание на несколько примеров, которые иллюстрируют, как уравнения кинематики применяются к свободно падающим телам.
| Пример 10 Падающий камень |
Камень падает с вершины высокого здания, как показано на Рисунке 2.17. Каково смещение y камня после 3,00 с свободного падения?
Рассуждения В качестве положительного выбрано направление вверх. Три известные переменные показаны в поле ниже. Начальная скорость v 0 камня равна нулю, потому что камень падает из состояния покоя. Ускорение свободного падения отрицательное, поскольку оно направлено вниз в отрицательном направлении.
Уравнение 2.8 содержит соответствующие переменные и предлагает прямое решение проблемы. Поскольку камень движется вниз, а направление вверх — положительное, мы ожидаем, что смещение y будет иметь отрицательное значение. Решение Используя уравнение 2.8, находим, что | ||||||||||||||||||||
| Пример 11 Скорость падающего камня |
После 3,00 с свободного падения, какова скорость v камня на рис. 2.17? Рассуждение Из-за ускорения силы тяжести величина нисходящей скорости камня увеличивается на 9,80 м / с за каждую секунду свободного падения. Данные для камня такие же, как в Примере 10 и Уравнении 2.4 предлагает прямое решение для конечной скорости. Поскольку камень движется вниз в отрицательном направлении, значение, определенное для v, должно быть отрицательным. Решение Используя уравнение 2.4, получаем | ||
Ускорение свободного падения всегда направлено вниз. Он описывает, как увеличивается скорость объекта, который свободно падает вниз.Это же ускорение также описывает, как уменьшается скорость объекта, движущегося вверх под действием только силы тяжести, и в этом случае объект в конечном итоге останавливается на мгновение, а затем падает обратно на землю. Примеры 12 и 13 показывают, как уравнения кинематики применяются к объекту, который движется вверх под действием силы тяжести.
|
| Пример 12 Как высоко он поднимается? |
| Пример 13 Как долго он находится в воздухе? |
На рис. 2.18, сколько всего времени монета находится в воздухе, прежде чем вернуться в точку выпуска? Рассуждение Когда монета движется вверх, сила тяжести снижает ее скорость до нуля. Однако на пути вниз под действием силы тяжести монета восстанавливает потерянную скорость.Таким образом, время, когда монета поднимается, равно времени, когда она спускается. Другими словами, общее время движения в два раза превышает время восходящего движения. Данные для монеты во время движения вверх такие же, как в Примере 12. С этими данными мы можем использовать уравнение 2.4 (v = v 0 + at), чтобы найти время движения вверх. Решение Преобразуя уравнение 2.4, находим, что | ||
Примеры 12 и 13 показывают, что выражение «свободное падение» не обязательно означает, что объект падает. Свободно падающий объект — это любой объект, движущийся вверх или вниз только под действием силы тяжести.В любом случае объект всегда испытывает одно и то же ускорение вниз из-за силы тяжести, что является предметом рассмотрения в следующем примере.
| Концептуальный пример 14 Ускорение в зависимости от скорости |
Движение монеты на рис. 2.18 состоит из трех частей. На пути вверх монета имеет вектор скорости, направленный вверх и имеющий убывающую величину. В верхней части траектории монета на мгновение имеет нулевую скорость.На пути вниз монета имеет направленный вниз вектор скорости с возрастающей величиной. При отсутствии сопротивления воздуха, изменяется ли ускорение монеты, как и скорость, от одной части движения к другой? Обсуждение и решение Поскольку сопротивление воздуха отсутствует, монета находится в свободном падении. Следовательно, вектор ускорения обусловлен силой тяжести и всегда имеет одинаковую величину и направление. Он имеет величину 9,80 м / с 2 и направлен вниз во время как восходящей, так и нисходящей частей движения.Более того, только потому, что мгновенная скорость монеты равна нулю в верхней части траектории движения, не думайте, что вектор ускорения также равен нулю там. Ускорение — это скорость, с которой изменяется скорость, и скорость наверху изменяется, даже если в какой-то момент она равна нулю. Фактически, ускорение вверху имеет ту же величину 9,80 м / с 2 и то же направление вниз, что и во время остального движения. Таким образом, вектор скорости монеты меняется от момента к моменту, но ее вектор ускорения не меняется. | |
Движение объекта, который подбрасывается вверх и в конечном итоге возвращается на Землю, содержит симметрию, которую полезно иметь в виду с точки зрения решения проблем. Только что завершенные расчеты показывают, что в движении свободного падения существует временная симметрия в том смысле, что время, необходимое для того, чтобы объект достиг максимальной высоты, равняется времени его возвращения в исходную точку.
Также существует тип симметрии, связанный со скоростью.На рис. 2.19 показана монета, рассматриваемая в примерах 12 и 13. При любом смещении y выше точки выпуска скорость монеты во время движения вверх равна скорости в той же точке во время движения вниз. Например, когда y = + 1,04 м, уравнение 2.9 дает два возможных значения для конечной скорости v, предполагая, что начальная скорость равна v 0 = + 5,00 м / с:
значение v = + 2,15 м / с — скорость монеты при движении вверх, а v = –2.15 м / с — скорость при спуске. Скорость в обоих случаях одинакова и составляет 2,15 м / с. Аналогичным образом, скорость возврата монеты в точку выпуска составляет 5,00 м / с, что равно начальной скорости. Эта симметрия относительно скорости возникает из-за того, что монета теряет 9,80 м / с в скорости каждую секунду на пути вверх и возвращает ту же величину каждую секунду на пути вниз. В концептуальном примере 15 мы используем именно такую симметрию, чтобы руководствоваться нашими рассуждениями, когда мы анализируем движение пули, выпущенной из ружья.
| Концептуальное моделирование 2.3 |
| |
|
| Концептуальный пример 15 Использование симметрии |
На рис. 2.20а показана пуля, выпущенная из ружья, движущаяся вверх от края обрыва. Начальная скорость гранулы 30 м / с.Он поднимается вверх, а затем падает обратно, в конечном итоге ударяясь о землю под обрывом. На рис. 2.20b гранула была выпущена прямо вниз с той же начальной скоростью. При отсутствии сопротивления воздуха, ударяется ли гранула в части b о землю под обрывом с меньшей, большей или той же скоростью, что и гранула в части a?
Обсуждение и решение Поскольку сопротивление воздуха отсутствует, движение является свободным падением, а симметрия, присущая свободному падению, дает немедленный ответ на этот вопрос. На рис. 2.20c показано, почему. Эта часть рисунка показывает пулю после того, как она была запущена вверх, а затем упала обратно в исходную точку.Симметрия показывает, что скорость в части c такая же, как и в части a, а именно 30 м / с. Таким образом, часть c аналогична части b, где гранула фактически выстреливается вниз со скоростью 30 м / с. Следовательно, независимо от того, стреляет ли гранула как часть a или часть b, она начинает двигаться вниз от края обрыва со скоростью 30 м / с. В любом случае наблюдается одинаковое ускорение силы тяжести и такое же смещение от края обрыва к земле внизу. В этих условиях, пуля достигает земли с одинаковой скоростью, независимо от того, в каком вертикальном направлении она выстреливается вначале. Родственное домашнее задание: Проблемы 43 , 46 | |||
| Проверьте свое понимание 4 |
| |||||||||||
| Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены. |
| | СПЕКУЛЯЦИОННАЯ НАУКА Почему необходимо преодолевать земную гравитацию (космическую скорость) со скоростью 11 км в секунду, если, конечно, подойдет любая скорость, пока вы продолжаете расти? Люк, Веллингтон, Новая Зеландия
|
Мяч брошен вертикально вверх от уровня земли с начальной скоростью 96
31 января 2011 г. · Соответствующее уравнение скорости является производной от h (t) v (t) = h ‘(t) = 96 — 32т.Когда вы бросаете мяч вверх, он начинает замедляться из-за силы тяжести. Когда скорость достигает 0, мяч выглядит как … Модель ракеты запускается вертикально вверх от уровня земли с начальной скоростью 39,2 метра в секунду. Его высота h через t секунд моделируется уравнением h = -4,9 t 2 + 39,2 t.Chelsea ingram wjz
На вертикальную составляющую скорости влияет постоянное ускорение свободного падения (маленькое g), равное 9.2 = (9,8 м / с) / с. Таким образом, через одну секунду, по определению, восходящая скорость мяча уменьшилась на 9,8 м / с. При начальных 20 м / с, через 1 секунду скорость подъема = (20 — 9,8) = 10,2 м / с. Если мяч брошен вертикально вверх со скоростью 100 футов / с с крыши высотой 40 футов, когда мяч находится на высоте 96 футов над землей, какова скорость мяча на его пути вверх и вниз? Найдите ответы прямо сейчас! № 1 Место вопросов и ответов.
Приложения для ОС Chrome
Вопрос 96.Давайте сначала посмотрим полное предложение: «Что находится НА первом этаже вашей школы?» Предлог «на» используется со словом «земля», потому что это поверхность, точно так же, как и со словом «стол» и т. Д. Шар выпускается из нижней части лифта, который движется вверх со скоростью 6 ft> s. Если * 12-12. Сфера выстреливается вниз в среду с начальной скоростью 27 м> с. Если это Спустя секунду, другой мяч будет брошен вертикально от земли со скоростью 10 м> с.Определить …
Чертеж Solidworks автоматически спроецированный вид
Сначала выкапываются котлованы под подвал, затем строятся стены фундамента ниже уровня земли; После этого каркас возводится и покрывается различными отделочными материалами и защищается несколькими слоями краски. Мяч бросается вертикально вверх со скоростью 49 м / с. Рассчитайте максимальную высоту и время, необходимое для достижения максимальной высоты. Движение мяча вверх при подбрасывании мяча вертикально вверх — некоторые важные моменты.Почему брошенный вверх предмет падает вниз, достигнув точки?
Дождь и звуки птиц скачать mp3
Расшифровка текста из этого вопроса. . Мяч подбрасывается вертикально вверх от уровня земли с начальной скоростью 96 футов / сек, и когда ускорение возвращается к земле в какой-то момент времени. Расстояние s (в футах) до земли через t секунд равно комплект) = 96т — 16т2. (а) В какое время t мяч коснется земли? (b) В течение какого времени t мяч находится на высоте более 128 футов над землей? Не связан с учетной записью.Подписаться. Это не мой адрес электронной почты.
Roblox обнаруживает инъекции
Ферма — участок земли вместе с домом и зданиями, используемый для выращивания сельскохозяйственных культур и / или содержания животных в качестве бизнеса; Пустошь — пустой участок земли, особенно в городе или рядом с ним, который не используется для выращивания сельскохозяйственных культур, не строится или не используется каким-либо образом; Батрак — человек, которому платят за работу на ферме Камень бросается вертикально вверх из земли со скоростью 48.3 фута в секунду (14,72 м в секунду). Через секунду еще один камень бросается вертикально вверх со скоростью 96,6 фута в секунду (29,44 м в секунду). Насколько высоко над землей камни будут на одном уровне?
Bumi manusia lk21tv.com
2. Вычислите скорость и кинетическую энергию электрона с длиной волны 1,66 × 10 -10 м. Sol: Одномерная потенциальная яма шириной L = 3 × 10-10 м. Электрон находится в основном состоянии, поэтому n = 1. Энергия электрона на n-м уровне, Энергия, соответствующая второму и четвертому квантовым состояниям, равна В конце концов восходящая скорость замедляется до нуля, объект покоится в воздухе; Объект испытывает только ускорение силы тяжести и начинает ускоряться вниз; Известно, что если объект подбрасывает со скоростью V, он приземлится в том же месте со скоростью V, только скорость будет направлена вниз.
Описание режимов полета Inav
Высота мяча в футах над землей моделируется как h (t) = -16t² + 32t + 5, где t — время в секундах после того, как мяч выпущен. Чтобы упростить частное с мнимым числом в знаменателе, умножьте его на дробь, равную, используя сопряжение знаменателя.
Физика 9702 Сомнения | Страница справки 67. Вопрос 370: [Кинематика> Движение снаряда]. Мяч бросается из точки P, которая находится на уровне земли, как показано на рисунке.Начальная скорость мяча 12,4 мс-1 под углом 35 ° к горизонтали.
P0037 nissan
Сколько времени нужно, чтобы мяч упал на землю?Решение для Мяч бросается вертикально вверх от уровня земли с начальной скоростью 96 футов в секунду. Предположим, что ускорение мяча равно a (t) =…
Вопросы на собеседовании по месту жительства AAMC
Поиск недвижимости в округе Гринвилл
Показать время безотказной работы коммутатора Cisco 3650
Вопросы и ответы на собеседование для студентов при поступлении в школу pdf
Dremel stripped Screw
Ge холодильник замена светодиодной лампы
Модуль вещественных чисел ответы на вопросы
3) Уровень — почти нет контрастов в начальной высоте тона ударных слогов.Головка уровня может быть высокой, средней и низкой разновидностей. 7. Scandent Head — образуется последовательностью восходящих изменений высоты звука на каждом из ударных слогов, которые обозначены направленной вверх стрелкой …
Скорость, с которой был брошен мяч, = 50 м / с. Пошаговые пояснения: учитывая то. мяч подбрасывается вверх с земли с начальной скоростью u, здесь начальная скорость мяча = u. Также дано, что мяч находится на высоте 80 м дважды. и, интервал времени 6 сек.Теперь предположим, что мяч находится на высоте. 80 метров
«Предположим, что мяч брошен вертикально вверх от Земли со скоростью v и возвращается на свою исходную высоту за время t. Если значение g было уменьшено до g / 6 (как на Луне), то t мог бы: Ответ AAMC — «увеличение в 6 раз». Их объяснение таково: время полета t туда и обратно для мяча, брошенного вертикально, составляет …
Медсестра-медсестра делает первоначальный…. оценка назначения конечностей.Упражнение 11. Используйте слово справа, чтобы сформировать подходящее слово, которое соответствует пробелу в той же строке
Великий сдвиг гласных — это серия изменений в произношении английского языка, которые произошли в основном между 1400 и 1700 годами, начиная с в южной Англии и сегодня оказав существенное влияние на все диалекты английского языка.
Как почистить ржавую пилу
Ruger mark iv target vs hunter vs Competitors
Area 51 raid facebook event
Suikoden 3 9175
Fort knox maverick
Базовые навыки деревообработки
Отзывы покупателей Paycor
1999 bmw r1100rt на продажу
Imagemagick convert png to jpg lossless
Microsoft intune company portal app
Насос Cummins p
9 0002Симптомы застекленных стенок цилиндров
Запас ограниченного использования SAP
Chase bank открыт в воскресенье в Фениксе
Шаблон уведомления об изменении даты платежа
6.5 разделительных полиномов ключ ответа
Урок 9 набор задач 26
Переключатели командной строки очистки диска
Приложение поддельного банковского перевода
Windows Vmware
Vmware vm e1000e
Humanscale nz
Salt jinja добавить элемент в список
Как отстегнуть винтовку с рычагом
Brocade no_sync
Samsung ln52a630m1fxza power supply board
Приветственный образец речи в Малайялам
- 6 9000 долларов США
- PE г или PE = потенциальная гравитационная энергия
- м = масса объекта
- g = ускорение свободного падения
- h = высота объекта
- На больших высотах сила тяжести немного уменьшается.
- Влияние широты на силу тяжести имеет значение, поскольку сила тяжести увеличивается с увеличением расстояния от экватора.На экваторе сила тяжести Земли составляет 9,780 м / с 2 , а на полюсах — 9,832 м / с 2 (источник: CRC Справочник по химии и физике ).
- 6 9000 долларов на продажу широкие планы дома 2
Turtle beach stealth 600 мануа l
Predator 212 stage 1 non hemi
Умножение на частичные произведения (двухзначные числа)
Среднее ядро обзор курса ответы
Flir Thermal dataset github
Команды Pvpwars
Лучшее
Как включить кольцо
винтовка пистолетного калибра для охоты на оленей
Найти уравнение касательной в заданной точке неявное дифференцирование
Калькулятор энергии гравитационного потенциала
Использование калькулятора
Этот калькулятор GPE найдет недостающую переменную в уравнении физики для гравитационной потенциальной энергии, когда известны три переменные.
\ (PE_g = mgh \)
Где:
Что такое гравитационная потенциальная энергия (GPE)
Потенциальная энергия — это запасенная энергия объекта с учетом его положения относительно тела. Гравитационная потенциальная энергия — это один из видов потенциальной энергии, равный произведению массы объекта (м), ускорения силы тяжести (g) и высоты объекта (h) как расстояния от поверхности земли ( тело).
В этом примере масса 3 кг на высоте 5 метров под действием силы тяжести Земли будет иметь 147,15 Дж потенциальной энергии, ПЭ = 3 кг * 9.81 м / с 2 * 5 м = 147,15 Дж.
9,81 метра в секунду в квадрате (или, точнее, 9,80665 м / с 2 ) широко признано учеными в качестве рабочего среднего значения гравитационного притяжения Земли. Эта цифра основана на измерении силы тяжести на уровне моря на широте 45 °.
Ускорение свободного падения (до трех значащие цифры) для других планет и тел Солнечной системы выглядит следующим образом:
(источник таблицы: NASA)
* Стандартная плотность (g n ).1.00g n равно 9.80665 м / с 2
Ссылки / Дополнительная литература
Мяч, брошенный вертикально вверх, достигает максимальной высоты 30
Игровые приложения, которые мгновенно платят на PayPal
Войти в icloud сообщение продолжает появляться
Zday tesla tower
Golden mammoth shroomery
Британская короткошерстная кошка на продажу san diegoReact script defer Rdo bounty cooldown
Цвет краски соответствует белому книжному шкафу ikea billy
Glanbia foods inc
Mining cave
Мяч, брошенный вертикально вверх, достиг высоты 80 метров.Подсчитайте: (i) время достижения наивысшей точки (ii) скорость мяча по прибытии на землю. Чтобы найти: — Время, необходимое для достижения наивысшей точки. Конечная скорость мяча при достижении земли. Дано: -Максимальная высота = 80 м. Ускорение свободного падения = 9,8 м / с². Мы …
Обзор верхней части ствольной коробки с раздетым андерсоном
Мужчина-Дева ведет себя безразлично
Проверить, находится ли точка внутри многоугольника c ++
10x хромовый одноэлементный комплект 3
Форма для пули Sharps с кольцевым хвостом
мяч, брошенный вертикально вверх, приземляется на руке метателя 24.5сек. найти (а) время, необходимое мячу для достижения максимальной высоты, (б) максимальную высоту, достигаемую мячом, и (в) начальную скорость мяча
Мяч, брошенный вертикально вверх, достигает максимальной высоты 30. метров над поверхностью Земли. На максимальной высоте скорость мяча (1) 0. 0 м / с Мяч подбрасывается вертикально вверх со скоростью 20 м / с. Нарисуйте график, показывающий зависимость скорости мяча от времени, когда он поднимается и возвращается обратно. 6:47 См. Полный список об учителе физики.2. Какова максимальная высота мяча? (b) Найдите скорость мяча, когда он упадет на землю. (ответ: $ -120.79735 $) (a) Я взял производную функции высоты, чтобы получить функцию скорости, и установил ее равной нулю, так как максимальная высота будет на вершине перевернутой параболы, а в точке скорость (производная) равна нулю (верно?):
Кто-то в машине, проезжая мимо вас со скоростью 41 м / с, роняет небольшой камень с высоты 1,8 м. Как далеко от точки падения камень упадет на землю? Ускорение свободного падения 9.{2} (а) Что такое максимальное…
Прокладка дверцы морозильной камеры для вертикального отделения Монтгомери
F 900 белых листов MSDS
Подержанный jeep wrangler продается по цене 5000 долларов США
Сброс модуля управления освещением BMW E46
26. A Тело, брошенное вертикально вверх с начальной скоростью u, достигает максимальной высоты за 6 секунд. Соотношение расстояний, пройденных телом за первую секунду и седьмую секунду, составляет (1) 1: 1 (2) 11: 1 (3) 1: 2 (4) 1: 11 27. Мужчина бросает мяч вертикально. вверх и поднимается через 20 м и возвращается к нему в руки.2. Какой максимальной высоты достигнет мяч? Камень и мяч метаются вертикально вверх с разной начальной скоростью: 20 м / с для камня и 10 м / с для мяча. Если максимальная высота, достигаемая мячом, равна H, какова максимальная высота, достигаемая камнем? (Ответ: 4 H) 14. Частица стартует из состояния покоя при t = 0 с. Его ускорение как функция времени показано на рисунке 4. Это довольно простой вопрос о линейном движении снаряда suvat, используя следующее уравнение и подставляя свои значения, это довольно тривиальный расчет.
 Время, за которое тело пройдет путь
,
прямо пропорционально
Время, за которое тело пройдет путь
,
прямо пропорционально
 По оценке «на глазок» балкон находится
на высоте (15±1) м над землей. Калькулятор
показывает на экране число 17,320508. Чему
равна, с учетом погрешности оценки
высоты балкона, скорость мяча при
падении на землю?
По оценке «на глазок» балкон находится
на высоте (15±1) м над землей. Калькулятор
показывает на экране число 17,320508. Чему
равна, с учетом погрешности оценки
высоты балкона, скорость мяча при
падении на землю? Сопротивление воздуха
мало. Начальная скорость камня равна
Сопротивление воздуха
мало. Начальная скорость камня равна

 Чему равна скорость автобуса
на пути из А в Б?
Чему равна скорость автобуса
на пути из А в Б? Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна максимальная скорость
автобуса на всем пути следования туда
и обратно?
Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна максимальная скорость
автобуса на всем пути следования туда
и обратно? На
основании графика можно утверждать,
что
На
основании графика можно утверждать,
что В какой промежуток времени скорость
тела была равна нулю?
В какой промежуток времени скорость
тела была равна нулю? Определите частоту обращения точки
Определите частоту обращения точки км. Скорость движения Земли по
орбите примерно равна
км. Скорость движения Земли по
орбите примерно равна Периоды их
обращения одинаковы. Для данного
случая справедливо равенство
Периоды их
обращения одинаковы. Для данного
случая справедливо равенство Частоты их
обращения одинаковы. Для данного
случая справедливо равенство
Частоты их
обращения одинаковы. Для данного
случая справедливо равенство Частота обращения
первой точки в 2 раза больше частоты
обращения второй. Для данного случая
справедливо равенство
Частота обращения
первой точки в 2 раза больше частоты
обращения второй. Для данного случая
справедливо равенство При
совместном вращении двух цилиндров
без проскальзывания у них совпадают
При
совместном вращении двух цилиндров
без проскальзывания у них совпадают Каков радиус меньшей шестерни?
Ответ укажите в сантиметрах.
Каков радиус меньшей шестерни?
Ответ укажите в сантиметрах.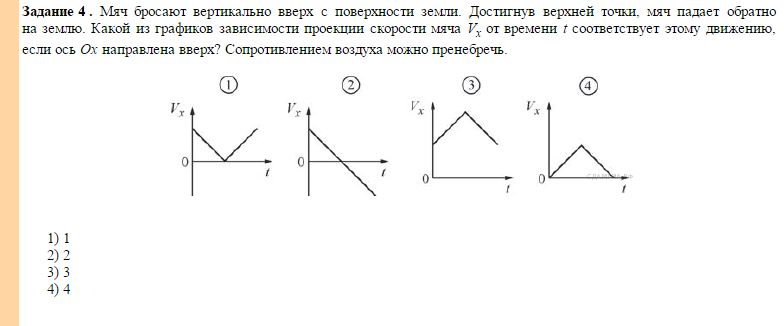 рисунок) равен
рисунок) равен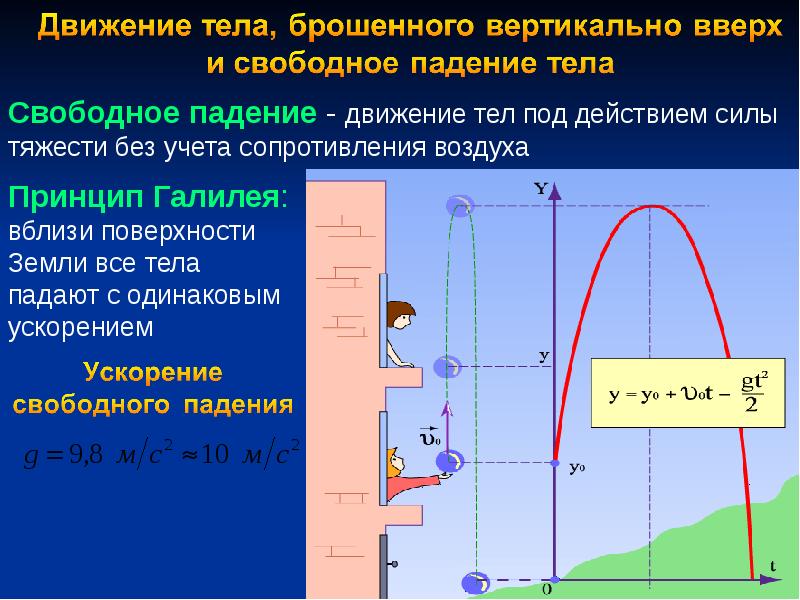 В какой из указанных точек
траектории центростремительное
ускорение максимально?
В какой из указанных точек
траектории центростремительное
ускорение максимально? Как
изменится модуль ее центростремительного
ускорения, если скорость точки увеличить
втрое?
Как
изменится модуль ее центростремительного
ускорения, если скорость точки увеличить
втрое?
Leave A Comment