№ 153 Сборник задач по физике 7-9 класс Лукашик. Какой из графиков соответствует равномерному прямолинейному движению? – Рамблер/класс
№ 153 Сборник задач по физике 7-9 класс Лукашик. Какой из графиков соответствует равномерному прямолинейному движению? – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Какой из графиков на рисунке 32 соответствует
равноускоренному? Можно ли однозначно утверждать,
что точка пересечения графиков 3 и 5 свидетельствует о
том, что в данный момент времени координаты тел сов-
падают?
ответы
Вот, по рисунку:
Равномерному прямолинейному движению соответствует график 4; равноускоренному — графики 1, 2, 5; равнозамедленному график 3. То, что графики 3 и 5 пересекаются, не позволяет однозначно утверждать, что координаты тел совпадают.
То, что графики 3 и 5 пересекаются, не позволяет однозначно утверждать, что координаты тел совпадают.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Мякишев Г.Я.
Психология
Химия
похожие вопросы 5
№ 179 Сборник задач по физике 7-9 класс Лукашик. Почему патрон продолжает вращаться?
У кого есть ответ?
Почему после выключения двигателя сверлильного станка патрон продолжает вращаться?
ГДЗФизика7 класс8 класс9 классЛукашик В.И.
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт.
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?
Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
Тест по теме «Механическое движение.
 Графики зависимости скорости, пути, координаты от времени». Вариант 1
Графики зависимости скорости, пути, координаты от времени». Вариант 1
Не пропустите весеннюю распродажу инструментов учителя! Доступ ко всем комплектам со скидкой до 90%
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Составлен из вопросов ФИПИ Открытый банк заданий ОГЭ по физике
Вопрос 1
Для каждого физического понятия из первого столбца подберите соответствующий пример из второго столбца.
ФИЗИЧЕСКИЕ ПОНЯТИЯ | ПРИМЕРЫ
|
А) физическая величина Б) единица физической величины В) прибор для измерения физической величины | 1) пройденный путь 2) секундомер 3) летит самолет 4) кристалл 5) метр в секунду |
Запишите в таблицу выбранные цифры под соответствующими буквами.
А | Б | В |
|
|
|
Варианты ответов
- 234
- 541
- 152
- 341
Вопрос 2
Сравните пути, пройденные передними колесами движущегося автомобиля, делающего поворот налево.
Варианты ответов
- путь, пройденный правым колесом, больше, чем левым
- путь, пройденный левым колесом, больше, чем правым
- пути, пройденные правым и левым колесами, одинаковы
- пути, пройденные колесами автомобиля, сравнить нельзя
Вопрос 3
Турист, двигаясь равномерно, прошел 1000 м за 15 мин. Турист двигался со скоростью
Варианты ответов
- 0,25 км/ч
- 4 км/ч
- 6,6 км/ч
- 66,6 км/ч
Вопрос 4
На рисунке приведены графики зависимости координаты тела от времени. Какой из графиков соответствует равномерному движению тела в отрицательном направлении оси Ох?
Какой из графиков соответствует равномерному движению тела в отрицательном направлении оси Ох?
1)
2)
3)
4)
Варианты ответов
- 1)
- 2)
- 3)
- 4)
Вопрос 5
На рисунке представлен график зависимости модуля скорости υ от времени
Варианты ответов
- AB
- BC
- CD
- DE
Вопрос 6
На рисунке представлен график зависимости координаты x от времени t для тела, движущегося вдоль оси Ох.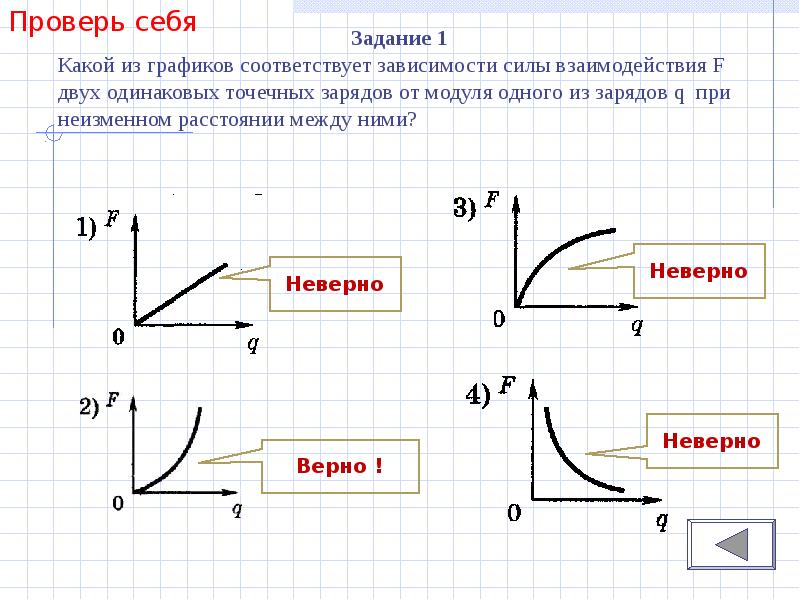
Путь тела за время от 0 до 8 с составил
Варианты ответов
- 3 м
- 6 м
- 10,5 м
- 0
Вопрос 7
На рисунке представлен график зависимости модуля скорости υ тела от времени t. Какой путь прошло тело за первые 40 секунд?
Варианты ответов
- 120 м
- 200 м
- 240 м
Вопрос 8
На рисунке представлен график зависимости координаты x от времени t для тела, движущегося вдоль оси Ох.
Модуль перемещения тела за время от 0 до 8 с равен
Варианты ответов
- 3 м
- 6 м
- 10,5 м
- 0
Вопрос 9
На рисунке точками на линейках показаны положения четырёх равномерно движущихся тел, причём для тел 1 и 2 положения отмечались через каждую секунду, а для тел 3 и 4 – через каждые 2 с.
Наибольшую скорость движения имеет тело
Варианты ответов
- 1
- 2
- 3
- 4
Вопрос 10
На рисунке приведены графики зависимости координаты x двух тел от времени t.
Эти тела имеют
Варианты ответов
- одинаковую начальную координату и одинаковую скорость
- одинаковую начальную координату и разную скорость
- разную начальную координату и одинаковую скорость
- разную начальную координату и разную скорость
Вопрос 11
На рисунке представлен график зависимости координаты x от времени t для четырёх тел (А, Б, В и Г), движущихся вдоль оси Ох.
В положительном направлении оси движется(-утся)
Варианты ответов
- только тело Б
- только тела Б и В
- тела Б, В и Г
- все тела
Вопрос 12
На рисунке представлен график зависимости проекции скорости υx от времени t для четырёх тел, движущихся вдоль оси Ох. Равномерному движению соответствует(-ют) график(-и)
Равномерному движению соответствует(-ют) график(-и)
Варианты ответов
- только 2
- 1 и 2
- только 3
- 3 и 4
Пройти тест
Сохранить у себя:
© 2019, Никифорова Наталья Владиленовна 687
графиков движения — Гиперучебник по физике
[закрыть]
введение
Современные математические обозначения — очень компактный способ кодирования идей. Уравнения могут легко содержать информационный эквивалент нескольких предложений. Описание Галилеем объекта, движущегося с постоянной скоростью (возможно, первое применение математики к движению), потребовало одного определения, четырех аксиом и шести теорем. Теперь все эти отношения можно записать в одном уравнении.
Теперь все эти отношения можно записать в одном уравнении.
| v = | ∆ с |
| ∆ t |
Ну почти ничего. Вспомните предыдущий раздел об уравнениях движения. Вы должны помнить, что три (или четыре) уравнения, представленные в этом разделе, справедливы только для движения с постоянным ускорением вдоль прямой линии. Поскольку, как я правильно заметил, «ни один объект никогда не двигался по прямой линии с постоянным ускорением где-либо во Вселенной в любое время», эти уравнения верны только приблизительно, только время от времени.
Уравнения отлично подходят для описания идеализированных ситуаций, но они не всегда подходят. Иногда вам нужна картинка, чтобы показать, что происходит — математическая картинка, называемая графиком. Графики часто являются лучшим способом передать описание событий реального мира в компактной форме. Графики движения бывают нескольких типов в зависимости от того, какая из кинематических величин (время, положение, скорость, ускорение) назначена какой оси.
позиция-время
Давайте начнем с графического изображения нескольких примеров движения с постоянной скоростью. На графике справа показаны три различные кривые, каждая из которых имеет нулевое начальное положение. Обратите внимание, что все графики прямые. (Любая линия, нарисованная на графике, называется кривой. Даже прямая линия в математике называется кривой.) Этого и следовало ожидать, учитывая линейный характер соответствующего уравнения. (Независимая переменная линейная функция возводится не выше первой степени.)
Сравните уравнение положение-время для постоянной скорости с классическим уравнением пересечения наклона, изучаемым в вводной алгебре.
| с = | с 0 | + | v ∆ т |
| г = | и | + | бх |
Таким образом, скорость соответствует наклону, а начальное положение — точке пересечения на вертикальной оси (обычно называемой осью «у»). Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов имел одинаковое начальное положение. Этот график может представлять собой своего рода гонку, в которой все участники выстраиваются в линию на стартовой линии (хотя при таких скоростях это, должно быть, была гонка между черепахами). Если бы это была гонка, то участники уже двигались, когда гонка началась, поскольку каждая кривая имеет ненулевой наклон в начале. Обратите внимание, что начальное положение, равное нулю, не обязательно означает, что начальная скорость также равна нулю. Высота кривой ничего не говорит о ее наклоне.
Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов имел одинаковое начальное положение. Этот график может представлять собой своего рода гонку, в которой все участники выстраиваются в линию на стартовой линии (хотя при таких скоростях это, должно быть, была гонка между черепахами). Если бы это была гонка, то участники уже двигались, когда гонка началась, поскольку каждая кривая имеет ненулевой наклон в начале. Обратите внимание, что начальное положение, равное нулю, не обязательно означает, что начальная скорость также равна нулю. Высота кривой ничего не говорит о ее наклоне.
- На графике положение-время …
- наклон скорость
- точка пересечения «y» является начальной позицией
- когда две кривые совпадают, два объекта в это время имеют одинаковое положение
В отличие от предыдущих примеров, давайте изобразим положение объекта с постоянным ненулевым ускорением, начиная с состояния покоя в начале координат. Основное различие между этой кривой и кривыми на предыдущем графике заключается в том, что эта кривая на самом деле изгибается. Соотношение между положением и временем является квадратичным, когда ускорение постоянно, и поэтому эта кривая представляет собой 9-кратную кривую.0035 парабола . (Переменная квадратичной функции поднимается не выше, чем вторая мощность.)
Основное различие между этой кривой и кривыми на предыдущем графике заключается в том, что эта кривая на самом деле изгибается. Соотношение между положением и временем является квадратичным, когда ускорение постоянно, и поэтому эта кривая представляет собой 9-кратную кривую.0035 парабола . (Переменная квадратичной функции поднимается не выше, чем вторая мощность.)
| S = S 0 + V 0 ∆ T + | 1 | а ∆ т 2 | |
| 2 | |||
| y = a + bx + cx 2 | |||
В качестве упражнения рассчитаем ускорение этого объекта по его графику. Он пересекает начало координат, поэтому его начальное положение равно нулю, в примере указано, что начальная скорость равна нулю, а на графике видно, что объект прошел 9 м за 10 с. Затем эти числа можно ввести в уравнение.
Затем эти числа можно ввести в уравнение.
| с = |
| ||||
| и = |
| ||||
| и = |
|
Когда график положение-время искривлен, невозможно рассчитать скорость по его наклону. Наклон — это свойство только прямых линий. У такого объекта нет скорости или , потому что у него нет наклона и . Слова «the» и «a» здесь подчеркнуты, чтобы подчеркнуть мысль о том, что при данных обстоятельствах не существует единой скорости. Скорость такого объекта должна меняться. Это ускоряется.
Скорость такого объекта должна меняться. Это ускоряется.
- На графике положение-время …
- прямые сегменты подразумевают постоянную скорость
- сегменты кривой подразумевают ускорение
- объект, испытывающий постоянное ускорение , следует части параболы
Хотя наш гипотетический объект не имеет единой скорости, он все же имеет среднюю скорость и непрерывный набор мгновенных скоростей. Среднюю скорость любого объекта можно найти, разделив общее изменение положения (также известное как смещение) на изменение во времени.
| v = | ∆ с |
| ∆ т |
Это то же самое, что вычисление наклона прямой линии, соединяющей первую и последнюю точки кривой, как показано на диаграмме справа. В этом абстрактном примере средняя скорость объекта была…
| v = | ∆ с | = | 9,5 м | = 0,95 м/с |
| ∆ т | 10,0 с |
Мгновенная скорость — это предел средней скорости при уменьшении временного интервала до нуля.
| v = |
| ∆ с | = | дс | ||
| ∆ т | дт |
Когда конечные точки линии средней скорости сближаются, они становятся лучшим индикатором фактической скорости. Когда две точки совпадают, прямая касается кривой. Этот предельный процесс представлен на анимации справа.
- На графике положение-время …
- средняя скорость наклон прямой линии, соединяющей конечные точки кривой
- мгновенная скорость — наклон линии, касательной к кривой в любой точке .
Семь касательных были добавлены к нашему общему графику положение-время в анимации, показанной выше. Обратите внимание, что наклон равен нулю дважды — один раз в верхней части выступа на 3,0 с и еще раз на дне вмятины на 6,5 с. (Выпуклость — это локальных максимумов , а вмятина — локальных максимумов . В совокупности такие точки известны как локальных экстремумов .) Наклон горизонтальной линии равен нулю, что означает, что объект в это время был неподвижен. . Поскольку график не плоский, объект покоился всего мгновение, прежде чем снова начал двигаться. Хотя его положение в то время не менялось, изменялась его скорость. С этим понятием у многих возникают трудности. Можно ускоряться и все же не двигаться, но только на мгновение.
(Выпуклость — это локальных максимумов , а вмятина — локальных максимумов . В совокупности такие точки известны как локальных экстремумов .) Наклон горизонтальной линии равен нулю, что означает, что объект в это время был неподвижен. . Поскольку график не плоский, объект покоился всего мгновение, прежде чем снова начал двигаться. Хотя его положение в то время не менялось, изменялась его скорость. С этим понятием у многих возникают трудности. Можно ускоряться и все же не двигаться, но только на мгновение.
Обратите также внимание на то, что наклон отрицательный в интервале между ударом в 3,0 с и вмятиной в 6,5 с. Некоторые интерпретируют это как движение в обратном направлении, но так ли это вообще? Ну это абстрактный пример. Он не сопровождается никаким текстом. Графики содержат много информации, но без заголовка или другой формы описания они не имеют смысла. Что представляет этот график? Персона? Автомобиль? Лифт? Носорог? Астероид? Пылинка? Все, что мы можем сказать, это то, что этот объект сначала двигался, замедлился до остановки, изменил направление, снова остановился, а затем возобновил движение в том же направлении, с которого начал (каким бы оно ни было). Отрицательный уклон не означает автоматически движение назад, движение влево или падение. Выбор знаков всегда произволен. В общем, все, что мы можем сказать, это то, что когда наклон отрицательный, объект движется в отрицательном направлении.
Отрицательный уклон не означает автоматически движение назад, движение влево или падение. Выбор знаков всегда произволен. В общем, все, что мы можем сказать, это то, что когда наклон отрицательный, объект движется в отрицательном направлении.
- На графике положение-время …
- положительный наклон подразумевает движение в положительном направлении
- отрицательный наклон подразумевает движение в отрицательном направлении
- нулевой наклон подразумевает состояние покоя
скорость-время
Самое важное, что нужно помнить о графиках скорость-время, это то, что это графики скорость-время, а не графики положение-время. В линейном графике есть что-то, что заставляет людей думать, что они смотрят на путь объекта. Распространенная ошибка новичков состоит в том, что они смотрят на график справа и думают, что v = 9,0 м/с. Линия соответствует объекту, который находится «выше» других объектов. Не думай так. Это не правильно.
Это не правильно.
Не смотрите на эти графики и не думайте о них как о изображении движущегося объекта. Вместо этого думайте о них как о записи скорости объекта. На этих графиках выше означает быстрее не дальше. Линия v = 9,0 м/с выше, потому что этот объект движется быстрее, чем другие.
Все эти графики горизонтальны. Начальная скорость каждого объекта такая же, как и конечная скорость, такая же, как и у всех промежуточных скоростей. Скорость каждого из этих объектов постоянна в течение этого десятисекундного интервала.
Для сравнения, когда кривая на графике скорость-время прямая, но не горизонтальная, скорость меняется. Каждая из трех кривых справа имеет разный наклон. График с самым крутым наклоном испытывает наибольшую скорость изменения скорости. Этот объект имеет наибольшее ускорение. Сравните уравнение скорости-времени для постоянного ускорения с классическим уравнением пересечения наклона, изучаемым в вводной алгебре.
| v = | v 0 | + | а ∆ т |
| г = | и | + | бх |
Вы должны увидеть, что ускорение соответствует наклону, а начальная скорость — точке пересечения на вертикальной оси. Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов изначально находился в состоянии покоя. Однако нулевая начальная скорость не означает, что начальное положение также должно быть нулевым. Этот график ничего не говорит нам о начальном положении этих объектов. Насколько нам известно, они могут быть на разных планетах.
Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов изначально находился в состоянии покоя. Однако нулевая начальная скорость не означает, что начальное положение также должно быть нулевым. Этот график ничего не говорит нам о начальном положении этих объектов. Насколько нам известно, они могут быть на разных планетах.
- На графике скорость-время …
- наклон ускорение
- точка пересечения «y» — это начальная скорость
- когда две кривые совпадают, два объекта в это время имеют одинаковую скорость
Все кривые на предыдущем графике были прямыми. Прямая линия – это кривая с постоянным наклоном. Поскольку наклон представляет собой ускорение на графике скорость-время, каждый из объектов, представленных на этом графике, движется с постоянным ускорением. Если бы графики были кривыми, ускорение не было бы постоянным.
- На графике скорость-время …
- прямые линии означают постоянное ускорение
- изогнутые линии означают непостоянное ускорение
- объект, испытывающий постоянное ускорение , следует по прямой линии
Поскольку кривая линия не имеет единого наклона, мы должны решить, что мы имеем в виду, когда нас спрашивают о ускорении объекта.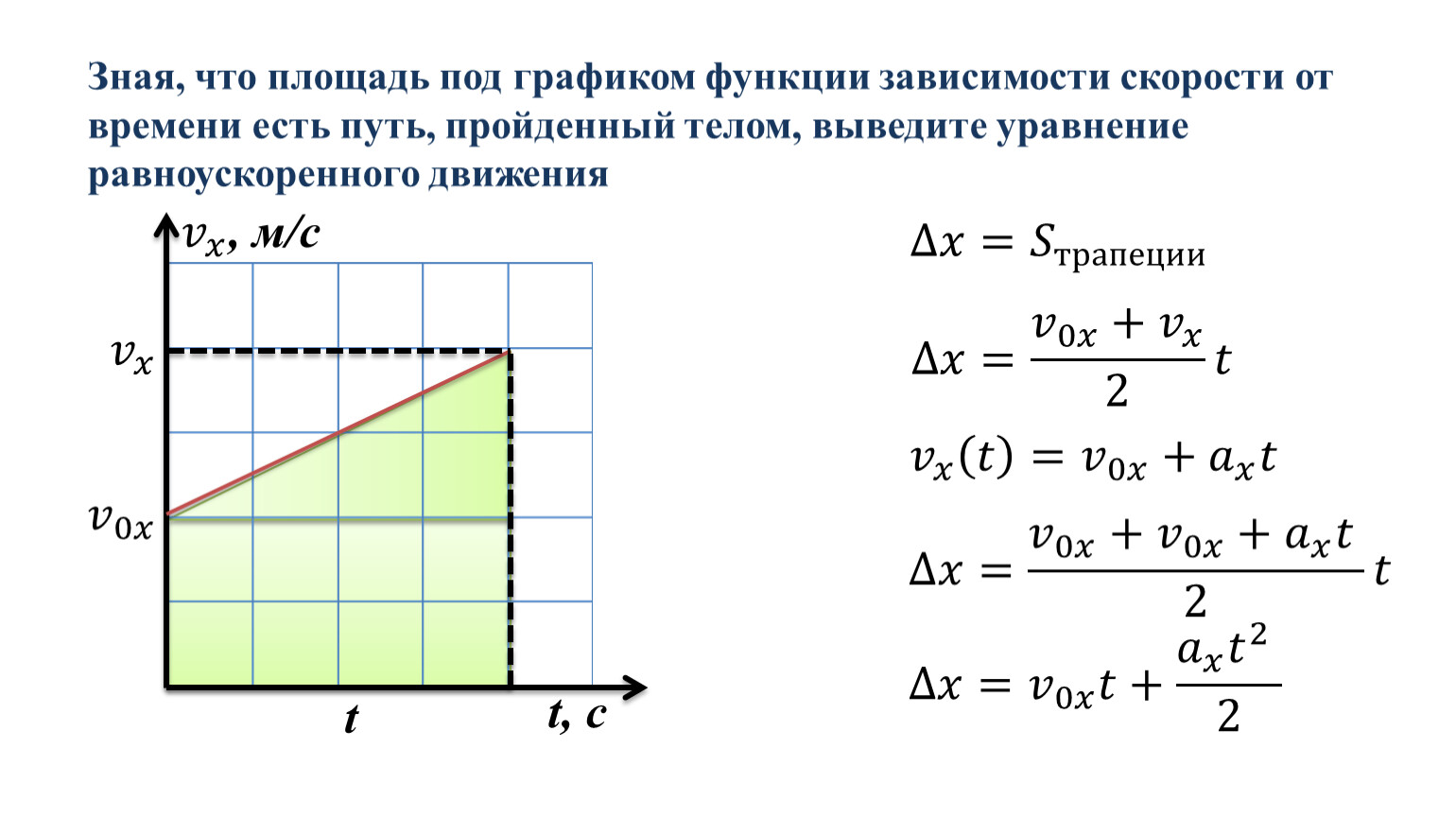 Эти описания следуют непосредственно из определений среднего и мгновенного ускорения. Если требуется среднее ускорение, нарисуйте линию, соединяющую конечные точки кривой, и рассчитайте ее наклон. Если требуется мгновенное ускорение, возьмите предел этого наклона, когда интервал времени сокращается до нуля, то есть возьмите наклон касательной.
Эти описания следуют непосредственно из определений среднего и мгновенного ускорения. Если требуется среднее ускорение, нарисуйте линию, соединяющую конечные точки кривой, и рассчитайте ее наклон. Если требуется мгновенное ускорение, возьмите предел этого наклона, когда интервал времени сокращается до нуля, то есть возьмите наклон касательной.
- На графике скорость-время …
- среднее ускорение наклон прямой линии, соединяющей конечные точки кривой
| и = | ∆ по сравнению с |
| ∆ т | |
- На графике скорость-время …
- мгновенное ускорение — наклон линии, касательной к кривой в любой точке .
| и = |
| ∆ по сравнению с | = | дв | ||
| ∆ т | дт | |||||
Семь касательных были добавлены к нашему общему графику скорость-время в анимации, показанной выше. Обратите внимание, что наклон равен нулю дважды — один раз в верхней части выступа на 3,0 с и еще раз на дне вмятины на 6,5 с. Наклон горизонтальной линии равен нулю, а это означает, что в это время объект мгновенно прекращал ускоряться. В эти два момента ускорение могло быть нулевым, но это не означает, что объект остановился. Для этого кривая должна пересекать горизонтальную ось. Это произошло только один раз — в начале графика. В оба раза, когда ускорение было равно нулю, объект все еще двигался в положительном направлении.
Обратите внимание, что наклон равен нулю дважды — один раз в верхней части выступа на 3,0 с и еще раз на дне вмятины на 6,5 с. Наклон горизонтальной линии равен нулю, а это означает, что в это время объект мгновенно прекращал ускоряться. В эти два момента ускорение могло быть нулевым, но это не означает, что объект остановился. Для этого кривая должна пересекать горизонтальную ось. Это произошло только один раз — в начале графика. В оба раза, когда ускорение было равно нулю, объект все еще двигался в положительном направлении.
Вы также должны заметить, что наклон был отрицательным с 3,0 с до 6,5 с. В это время скорость падала. Однако в целом это неверно. Скорость уменьшается всякий раз, когда кривая возвращается в исходное положение. Выше горизонтальной оси это будет отрицательный наклон, а ниже — положительный наклон. Единственное, что можно сказать об отрицательном наклоне на графике скорость-время, это то, что в течение такого интервала скорость становится более отрицательной (или менее положительной, если хотите).
- На графике скорость-время …
- положительный наклон означает увеличение скорости в положительном направлении
- отрицательный наклон подразумевает увеличение скорости в отрицательном направлении
- нулевой наклон подразумевает движение с постоянной скоростью
В кинематике есть три величины: положение, скорость и ускорение. Имея график любой из этих величин, в принципе всегда можно определить две другие. Ускорение — это скорость изменения скорости во времени, поэтому его можно найти по наклону касательной к кривой на графике зависимости скорости от времени. Но как определить положение? Давайте рассмотрим несколько простых примеров, а затем выведем взаимосвязь.
Начните с простого графика зависимости скорости от времени, показанного справа. (Для простоты предположим, что начальная позиция равна нулю.) На этом графике есть три важных интервала. В течение каждого интервала ускорение постоянно, как показывают отрезки прямой линии. Когда ускорение постоянно, средняя скорость равна среднему значению начального и конечного значений в интервале.
Когда ускорение постоянно, средняя скорость равна среднему значению начального и конечного значений в интервале.
0–4 с: этот сегмент имеет треугольную форму. Площадь треугольника равна половине произведения основания на высоту. По сути, мы только что вычислили площадь треугольного сегмента на этом графике.
| ∆ s = v ∆ t ∆ s = ½( v + v 0 )∆ t ∆ s = ½(8 m/ с)(4 с) ∆ с = 16 м |
Общее расстояние, пройденное в конце этого интервала, составляет…
16 м
4–8 с: Этот отрезок имеет форму трапеции. Площадь трапеции (или трапеции ) равна среднему значению двух оснований, умноженных на высоту. По сути, мы только что вычислили площадь трапециевидного сегмента на этом графике.
| ∆ s = v ∆ t ∆ s = ½( v + v 0 )∆ t ∆ s = ½(10 m/ с + 8 м/с)(4 с) ∆ с = 36 м |
Суммарное расстояние, пройденное в конце этого интервала, равно…
16 м + 36 м = 52 м
8–10 с: этот отрезок имеет прямоугольную форму. Площадь прямоугольника равна произведению его высоты на ширину. По сути, мы только что вычислили площадь прямоугольного сегмента на этом графике.
Площадь прямоугольника равна произведению его высоты на ширину. По сути, мы только что вычислили площадь прямоугольного сегмента на этом графике.
| ∆ S = V ∆ T ∆ S = (10 м/с) (2 с) ∆ S = 20 м |
Суммарное расстояние, пройденное в конце этого интервала, равно…
16 м + 36 м + 20 м = 72 м
Надеюсь, вы уже заметили тенденцию. Площадь под каждым сегментом представляет собой изменение положения объекта в течение этого интервала. Это верно даже тогда, когда ускорение непостоянно.
Любой, кто прошел курс математического анализа, должен был знать это, прежде чем читать это здесь (или, по крайней мере, когда они читали это, они должны были сказать: «О да, я это помню»). Первая производная положения по времени есть скорость. Производная функции — это наклон прямой, касательной к ее кривой в данной точке. Обратная операция производной называется интегралом. Интеграл функции — это совокупная площадь между кривой и горизонтальной осью за некоторый интервал. Эта обратная связь между действиями производной (наклон) и интеграла (площадь) настолько важна, что ее называют основная теорема исчисления . Это означает, что это важные отношения. Узнать его! Это «фундаментально». Вы не видели последний из этого.
Эта обратная связь между действиями производной (наклон) и интеграла (площадь) настолько важна, что ее называют основная теорема исчисления . Это означает, что это важные отношения. Узнать его! Это «фундаментально». Вы не видели последний из этого.
- На графике скорость-время …
- площадь под кривой изменение позиции
ускорение-время
График зависимости ускорения от времени любого объекта, движущегося с постоянной скоростью, одинаков. Это верно независимо от скорости объекта. Самолет, летящий с постоянной скоростью 270 м/с (600 миль/ч), ленивец, идущий с постоянной скоростью 0,4 м/с (1 миль/ч), и лежащий неподвижно перед телевизором в течение нескольких часов диванчик будут иметь одинаковое ускорение: временные графики — горизонтальная линия, коллинеарная горизонтальной оси. Это потому, что скорость каждого из этих объектов постоянна. Они не ускоряются. Их ускорения равны нулю. Как и в случае с графиками скорость-время, важно помнить, что высота над горизонтальной осью не соответствует положению или скорости, она соответствует ускорение .
Если вы споткнетесь и упадете по дороге в школу, ваше ускорение по отношению к земле будет больше, чем вы испытали бы во всех, кроме нескольких высокопроизводительных автомобилях с «педалью до упора». Ускорение и скорость — разные величины. Быстро ехать не означает быстро ускоряться. Эти две величины независимы друг от друга. Большое ускорение соответствует быстрому изменению скорости, но ничего не говорит вам о значениях самой скорости.
При постоянном ускорении кривая зависимости ускорения от времени представляет собой горизонтальную линию. Скорость изменения ускорения во времени обсуждается нечасто, поэтому наклон кривой на этом графике пока не будем учитывать. Если вам нравится знать названия вещей, эта величина называется придурок . На первый взгляд, единственная информация, которую можно получить из графика зависимости ускорения от времени, — это ускорение в любой заданный момент времени.
- На графике ускорение-время …
- уклон рывок
- точка пересечения «y» равна начальному ускорению
- когда две кривые совпадают, два объекта имеют одинаковое ускорение в это время
- объект, испытывающий постоянное ускорение , следует горизонтальной линии
- нулевой наклон подразумевает движение с постоянным ускорением
Ускорение — скорость изменения скорости во времени. Преобразование графика скорости-времени в график ускорения-времени означает вычисление наклона линии, касательной к кривой в любой точке. (В исчислении это называется нахождением производной.) Обратный процесс влечет за собой вычисление совокупной площади под кривой. (В математическом анализе это называется нахождением интеграла.) Затем это число представляет собой изменение значения на графике скорость-время.
Преобразование графика скорости-времени в график ускорения-времени означает вычисление наклона линии, касательной к кривой в любой точке. (В исчислении это называется нахождением производной.) Обратный процесс влечет за собой вычисление совокупной площади под кривой. (В математическом анализе это называется нахождением интеграла.) Затем это число представляет собой изменение значения на графике скорость-время.
При нулевой начальной скорости (и предположении, что значение вниз положительное), конечная скорость человека, падающего на графике вправо, равна…
| ∆ v = | а ∆t |
| ∆ v = | (9,8 м/с 2 )(1,0 с) |
| ∆ v = | 9,8 м/с = 22 миль в час |
и конечная скорость разгоняющегося автомобиля равна…
| ∆ v = | а ∆t |
| ∆ v = | (5,0 м/с 2 )(6,0 с) |
| ∆ v = | 30 м/с = 67 миль/час |
- На графике ускорение-время …
- площадь под кривой равна изменению скорости
Есть еще много вещей, которые можно сказать о графиках ускорение-время, но по большей части они тривиальны.
фазовое пространство
Существует четвертый график движения, который связывает скорость с положением. Он так же важен, как и три других типа, но ему редко уделяется внимание ниже продвинутого уровня бакалавриата. Когда-нибудь я напишу что-нибудь об этих графиках, называемых диаграммами фазового пространства , но не сегодня.
Графики скорости-времени: значение формы
Наше исследование одномерной кинематики было связано с многочисленными средствами, с помощью которых может быть представлено движение объектов. К таким средствам относятся использование слов, использование диаграмм, использование чисел, использование уравнений и использование графиков. Урок 4 посвящен использованию графиков зависимости скорости от времени для описания движения. Как мы узнаем, особенности движения объектов демонстрируются формой и наклоном линий на графике зависимости скорости от времени. Первая часть этого урока включает в себя изучение взаимосвязи между формой v-t графика и движением объекта.
Постоянная скорость в сравнении с изменяющейся скоростью
Рассмотрим автомобиль, движущийся с постоянной скоростью вправо (+), скажем, +10 м/с. Как вы узнали из предыдущего урока, автомобиль, движущийся с постоянной скоростью, — это автомобиль с нулевым ускорением.
Если построить график зависимости скорости от времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как постоянная положительная скорость, приводит к линии с нулевым наклоном (горизонтальная линия имеет нулевой наклон) при построении графика зависимости скорости от времени. Кроме того, на график наносятся только положительные значения скорости, соответствующие движению с положительной скоростью.
Теперь рассмотрим автомобиль, движущийся вправо (+) с изменяющейся скоростью, то есть автомобиль, который движется вправо, но ускоряется или ускоряется . Поскольку автомобиль движется в положительном направлении и ускоряется, говорят, что автомобиль имеет положительное ускорение .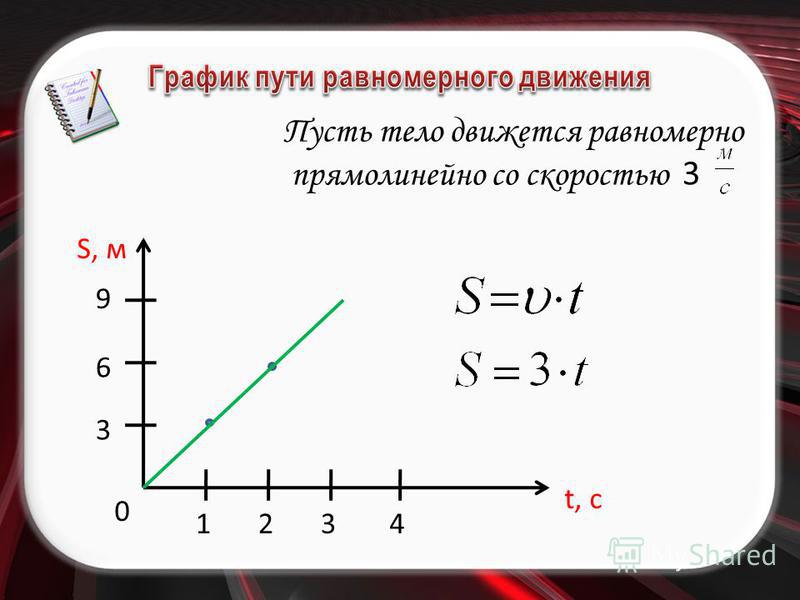
Если построить график зависимости скорости от времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как изменение положительной скорости, приводит к наклонной линии при построении графика зависимости скорости от времени. Наклон линии положительный, что соответствует положительному ускорению. Кроме того, на график наносятся только положительные значения скорости, соответствующие движению с положительной скоростью.
Графики зависимости скорости от времени для двух типов движения — с постоянной скоростью и изменяющейся скоростью (ускорение) — можно обобщить следующим образом.
| Положительная скорость Нулевое ускорение | Положительная скорость Положительное ускорение |
|---|---|
Значение уклона
Формы графиков зависимости скорости от времени для этих двух основных типов движения — движения с постоянной скоростью и движения с ускорением (т. е. с изменением скорости) — раскрывают важный принцип. Принцип заключается в том, что наклон линии на графике скорость-время дает полезную информацию об ускорении объекта. Если ускорение равно нулю, то наклон равен нулю (т. Е. Горизонтальная линия). Если ускорение положительное, то и наклон положительный (т. е. линия с наклоном вверх). Если ускорение отрицательное, то и наклон отрицательный (т. е. линия с наклоном вниз). Этот самый принцип может быть распространен на любое мыслимое движение.
е. с изменением скорости) — раскрывают важный принцип. Принцип заключается в том, что наклон линии на графике скорость-время дает полезную информацию об ускорении объекта. Если ускорение равно нулю, то наклон равен нулю (т. Е. Горизонтальная линия). Если ускорение положительное, то и наклон положительный (т. е. линия с наклоном вверх). Если ускорение отрицательное, то и наклон отрицательный (т. е. линия с наклоном вниз). Этот самый принцип может быть распространен на любое мыслимое движение.
Наклон графика зависимости скорости от времени дает информацию об ускорении объекта. Но как определить, движется ли объект в положительном направлении (т. е. с положительной скоростью) или в отрицательном направлении (т. е. с отрицательной скоростью)? И как определить, ускоряется объект или замедляется?
Ответы на эти вопросы зависят от способности человека читать график. Поскольку график представляет собой график зависимости скорости от времени, скорость будет положительной всякий раз, когда линия лежит в положительной области (над осью x) графика. Точно так же скорость будет отрицательной всякий раз, когда линия лежит в отрицательной области (ниже оси x) графика. Как вы узнали из Урока 1, положительная скорость означает, что объект движется в положительном направлении; а отрицательная скорость означает, что объект движется в отрицательном направлении. Таким образом, известно, что объект движется в положительном направлении, если линия расположена в положительной области графика (независимо от того, имеет ли она наклон вверх или вниз). А известно, что объект движется в отрицательном направлении, если линия расположена в отрицательной области графика (независимо от того, идет ли она с наклоном вверх или вниз). И, наконец, если линия пересекает ось абсцисс из положительной области графика в отрицательную (или наоборот), то объект изменил направление.
Точно так же скорость будет отрицательной всякий раз, когда линия лежит в отрицательной области (ниже оси x) графика. Как вы узнали из Урока 1, положительная скорость означает, что объект движется в положительном направлении; а отрицательная скорость означает, что объект движется в отрицательном направлении. Таким образом, известно, что объект движется в положительном направлении, если линия расположена в положительной области графика (независимо от того, имеет ли она наклон вверх или вниз). А известно, что объект движется в отрицательном направлении, если линия расположена в отрицательной области графика (независимо от того, идет ли она с наклоном вверх или вниз). И, наконец, если линия пересекает ось абсцисс из положительной области графика в отрицательную (или наоборот), то объект изменил направление.
Как теперь определить, ускоряется объект или замедляется? Ускорение означает, что величина (или числовое значение) скорости становится большой. Например, ускоряется объект, скорость которого изменяется от +3 м/с до +9 м/с. Точно так же ускоряется и объект, скорость которого изменяется от -3 м/с до -9 м/с. В каждом случае величина скорости (само число, а не знак или направление) увеличивается; скорость становится больше. Учитывая этот факт, можно было бы предположить, что объект ускоряется, если линия на графике скорость-время изменяется от точки, близкой к точке с нулевой скоростью, к точке, расположенной дальше от точки с нулевой скоростью. То есть, если линия удаляется дальше от оси x (точка нулевой скорости), то объект ускоряется. И наоборот, если линия приближается к оси x, то объект замедляется.
Например, ускоряется объект, скорость которого изменяется от +3 м/с до +9 м/с. Точно так же ускоряется и объект, скорость которого изменяется от -3 м/с до -9 м/с. В каждом случае величина скорости (само число, а не знак или направление) увеличивается; скорость становится больше. Учитывая этот факт, можно было бы предположить, что объект ускоряется, если линия на графике скорость-время изменяется от точки, близкой к точке с нулевой скоростью, к точке, расположенной дальше от точки с нулевой скоростью. То есть, если линия удаляется дальше от оси x (точка нулевой скорости), то объект ускоряется. И наоборот, если линия приближается к оси x, то объект замедляется.
См. анимацию различных движений с сопровождающими графиками
Проверьте свое понимание
1. Рассмотрите график справа. Объект, движение которого представлено на этом графике, это .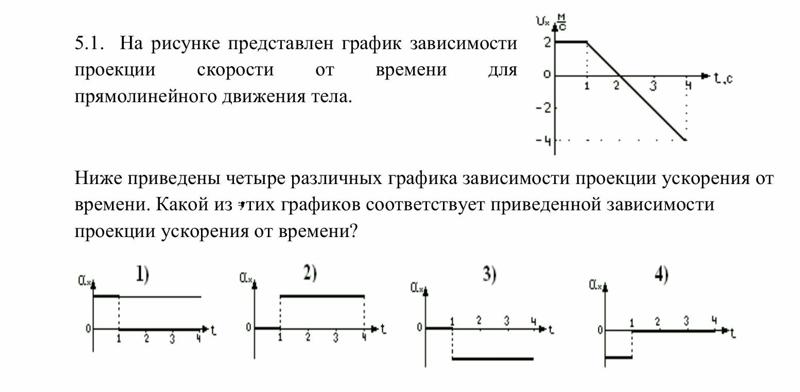 .. (включая все верные):
.. (включая все верные):
- , движущийся в положительном направлении.
- движется с постоянной скоростью.
- движется с отрицательной скоростью.
- замедляется.
- изменение направления.
- ускоряется.
- движется с положительным ускорением.
- движется с постоянным ускорением.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Graph That Motion или наших Graphs and Ramps Interactives. Каждый из них находится в разделе Physics Interactives на нашем веб-сайте и позволяет учащимся применять концепции кинематических графиков (как положение-время, так и скорость-время) для описания движения объектов.

Leave A Comment