Уравнение прямой
Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
A x + B y + C = 0
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
y = k x + b
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
k = tg φ
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M(x1, y1) и N(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2, то уравнение прямой можно найти, используя следующую формулу
| x — x1 | = | y — y1 |
| x2 — x1 | y2 — y1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x0y = m t + y0
где N(x0, y0) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N(x0, y0) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 12 — 1 = y — 73 — 7
Упростив это уравнение получим каноническое уравнение прямой
x — 11 = y — 7-4
Выразим y через x и получим уравнение прямой с угловым коэффициентом
y — 7 = -4(x — 1)
y = -4x + 11
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.
MN = {2 — 1; 3 — 7} = {1; -4}
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем
x = t + 1y = -4t + 7
Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).Решение. Так как My — Ny = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.
MN = {2 — 1; 3 — 3} = {1; 0}
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1y = 3
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M(x1, y1, z1) и N(x
| x — x1 | = | y — y1 | = | z — z1 |
| x2 — x1 | y2 — y1 | z2 — z1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
| x = l t + x0 | |
| y = m t + y0 | |
| z = n t + z0 |
где (x0, y0, z0) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x0 | = | y — y0 | z — z0 | |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
| A1x + B1y + C1z + D1 = 0 | |
| A2x + B2y + C2z + D2 = 0 |
при условии, что не имеет место равенство
| A1 | B1 | = | C1 | . | |
| A2 | B2 | C2 |
ru.onlinemschool.com
Уравнение прямой проходящей через две точки
Уравнение прямой проходящей через две точки. В статье «Геометрический смысл производной. Часть 1» я обещал вам разобрать второй способ решения представленных задач на нахождение производной, при данном графике функции и касательной к этому графику. Этот способ мы разберём в следующей статье, не пропустите! Почему в следующей?
Дело в том, что там будет использоваться формула уравнения прямой. Конечно, можно было бы просто показать данную формулу и посоветовать вам её выучить. Но лучше объяснить – от куда она исходит (как выводится). Это необходимо! Если вы её забудете, то быстро восстановить её не представит труда. Ниже подробно всё изложено. Итак, у нас на координатной плоскости имеется две точки А(х1;у1) и В(х2;у2), через указанные точки проведена прямая: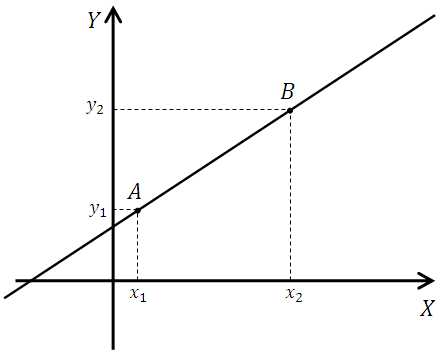
Вот сама формула прямой:
*То есть при подстановке конкретных координат точек мы получим уравнение вида y=kx+b.
**Если данную формулу просто «зазубрить», то имеется большая вероятность запутаться с индексами при х. Кроме того, индексы могут обозначаться по разному, например:
Поэтому-то и важно понимать смысл.
Теперь вывод этой формулы. Всё очень просто!
Отметим на прямой точку С(x;у), далее построим прямую проходящую через точку А параллельную оси оХ:
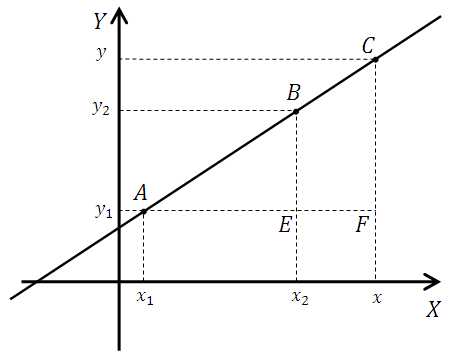
Треугольники АВЕ и ACF подобны по острому углу (первый признак подобия прямоугольных треугольников). Из этого следует, что отношения соответственных элементов равны, то есть:
Теперь просто выражаем данные отрезки через разность координат точек:
Конечно, не будет никакой ошибки если вы запишите отношения элементов в другом порядке (главное соблюдать соответствие):
В результате получится одно и тоже уравнение прямой. Это всё!
То есть, как бы не были обозначены сами точки (и их координаты), понимая данную формулу вы всегда найдёте уравнение прямой.
Формулу можно вывести используя свойства векторов, но принцип вывода будет тот же, так как речь будет идти о пропорциональности их координат. В этом случае работает всё то же подобие прямоугольных треугольников. На мой взгляд описанный выше вывод более понятнее )).
Посмотреть вывод через координаты векторов >>>
Пусть на координатной плоскости построена прямая, проходящая через две заданные точки А(х1;у1) и В(х2;у2). Отметим на прямой произвольную точку С с координатами (x;y). Также обозначим два вектора:
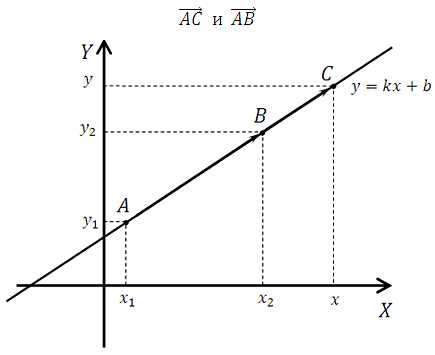
Известно, что у векторов лежащих на параллельных прямых (либо на одной прямой), их соответствующие координаты пропорциональны, то есть:
— имеем координаты векторов
— записываем равенство отношений соответствующих координат:
Рассмотрим пример:
Найти уравнение прямой, проходящей через две точки с координатами (2;5) и (7:3).
Можно даже не строить саму прямую. Применяем формулу:
Важно, чтобы вы уловили соответствие, при составлении соотношения. Вы не ошибётесь, если запишите:
Решаем:
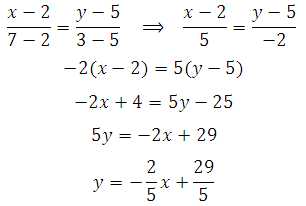
Ответ: у=-2/5x+29/5 иди у=-0,4x+5,8
Для того, чтобы убедится, что полученное уравнение найдено верно, обязательно делайте проверку — подставьте в него координаты данных в условии точек. Должны получится верные равенства.
На этом всё. Надеюсь, материал был вам полезен.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки М1 (х1; у1
где k — пока неизвестный коэффициент.
Так как прямая проходит через точку М2(х2 у2), то координаты этой точки должны удовлетворять уравнению (10.6): у2—у1 = k (х2—х1).
Отсюда
находим 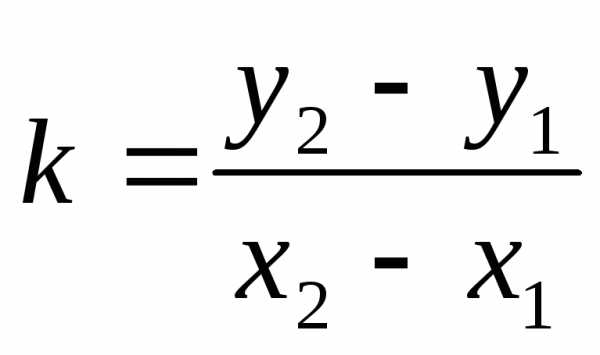 Подставляя найденное значениеk в уравнение (10.6), получим уравнение
прямой, проходящей через точки М
Подставляя найденное значениеk в уравнение (10.6), получим уравнение
прямой, проходящей через точки М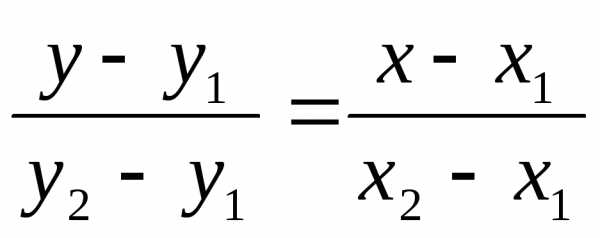
Предполагается, что в этом уравнении х1 ≠ х2, у1 ≠ у2
Если х1 = х2, то прямая, проходящая через точки М1 (х1 ,уI) и М2 (х2,у2) параллельна оси ординат. Ее уравнение имеет вид х = х1.
Если у2 = уI, то уравнение прямой может быть записано в виде у = у1
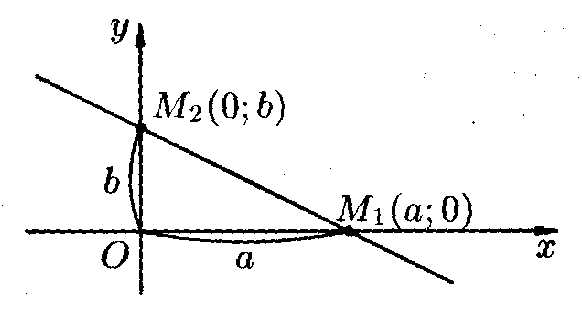
Уравнение прямой в отрезках
Пусть
прямая пересекает ось Ох в точке М1(а;0),
а ось Оу – в точке М2(0;b).
Уравнение примет вид: 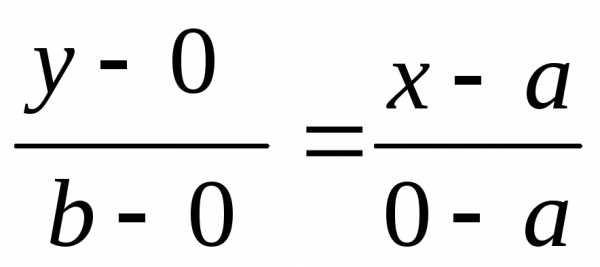 т.е.
т.е.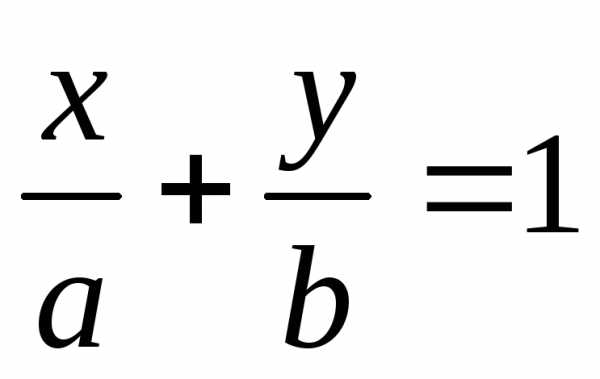 .
Это уравнение называетсяуравнением
прямой в отрезках, т.к. числа а и b
указывают, какие отрезки отсекает прямая
на осях координат.
.
Это уравнение называетсяуравнением
прямой в отрезках, т.к. числа а и b
указывают, какие отрезки отсекает прямая
на осях координат.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем
уравнение прямой, проходящей через
заданную точку Мо (х
Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М0М (х — х0; у — уо) (см. рис.1). Поскольку векторы n и МоМ перпендикулярны, то их скалярное произведение равно нулю: то есть
А(х — хо) + В(у — уо) = 0. (10.8)
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой.
где А и В координаты нормального вектора, С = —Ахо — Вуо — свободный член. Уравнение (10.9) есть общее уравнение прямой (см. рис.2).
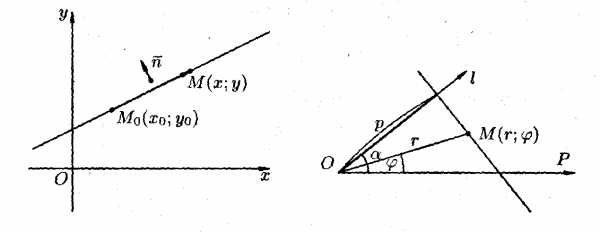
Рис.1 Рис.2
Канонические уравнения прямой
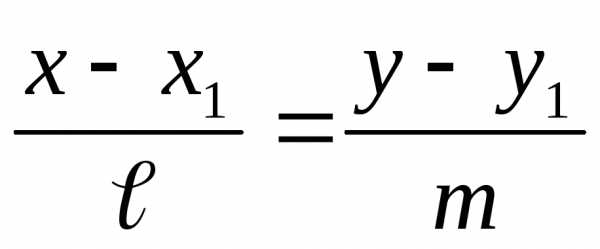 ,
,
Где 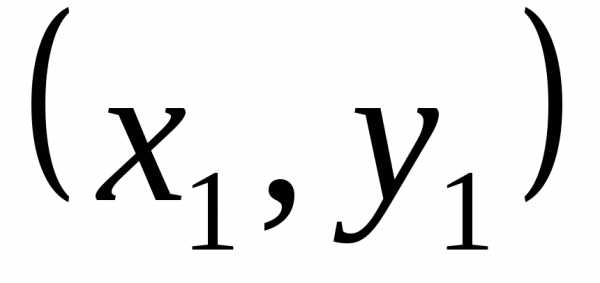
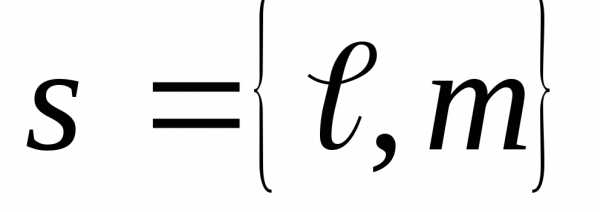 — направляющий вектор.
— направляющий вектор.Кривые второго порядка Окружность
Окружностью называется множество всех точек плоскости, равноотстоящих от данной точки, которая называется центром.
Каноническое
уравнение круга радиуса R с
центром в точке 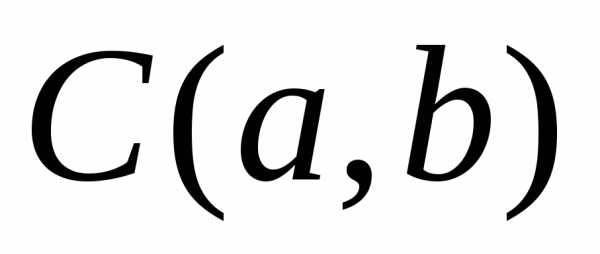 :
:
В частности, если центр кола совпадает с началом координат, то уравнение будет иметь вид:
Эллипс
Эллипсом
называется множество точек плоскости,
сумма расстояний от каждой из которых
до двух заданных точек  и
и ,
которые называются фокусами, есть
величина постоянная
,
которые называются фокусами, есть
величина постоянная ,
большая чем расстояние между фокусами
,
большая чем расстояние между фокусами .
.
x
Каноническое уравнение эллипса, фокусы которого лежат на оси Ох, а начало координат посредине между фокусами имеет видгдеa длина большой полуоси; b– длина малой полуоси (рис. 2). Зависимость
между параметрами эллипса 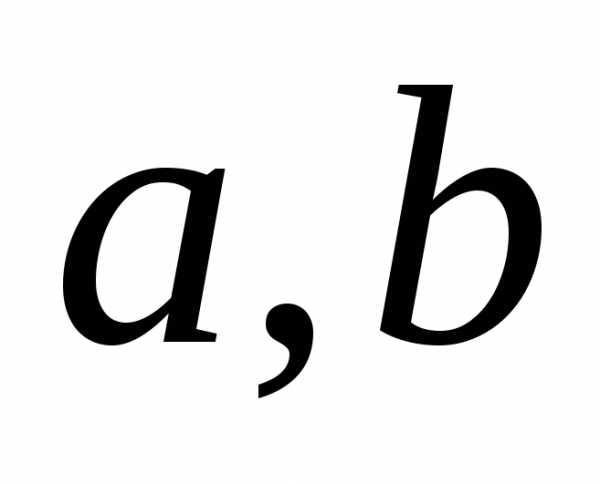 и
и выражается соотношением:
выражается соотношением:
(4)
Эксцентриситетом
эллипса называется отношение
межфокусного расстояния 2с к
большой оси 2а: 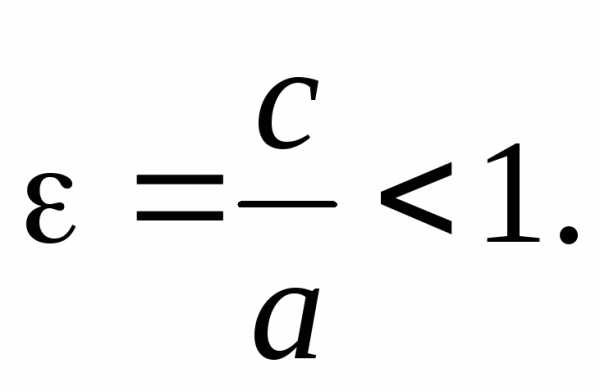
Директрисами эллипса называются прямые, параллельные
оси Оу, которые находятся от этой оси
на расстоянии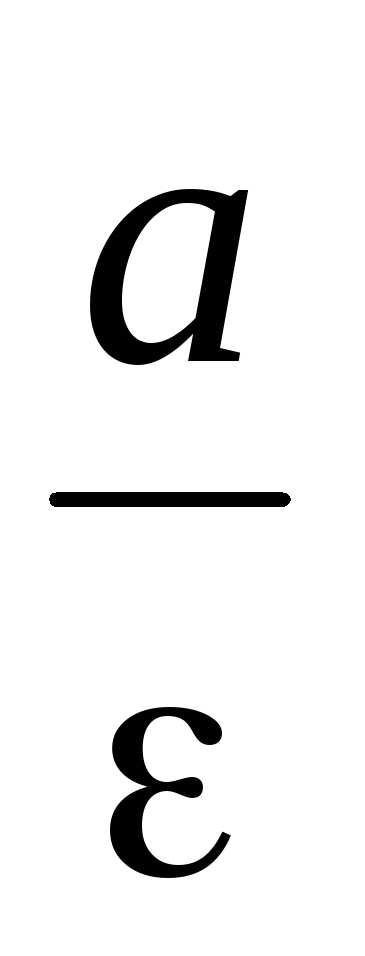 .
Уравнения директрис:
.
Уравнения директрис: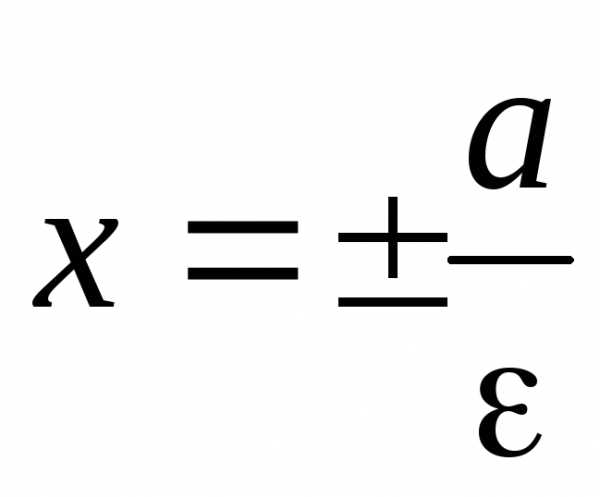 .
.
Если в уравнении
эллипса 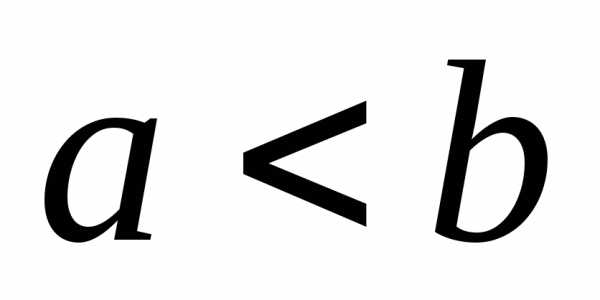 ,
тогда фокусы эллипса находятся на оси
Оу.
,
тогда фокусы эллипса находятся на оси
Оу.
Итак,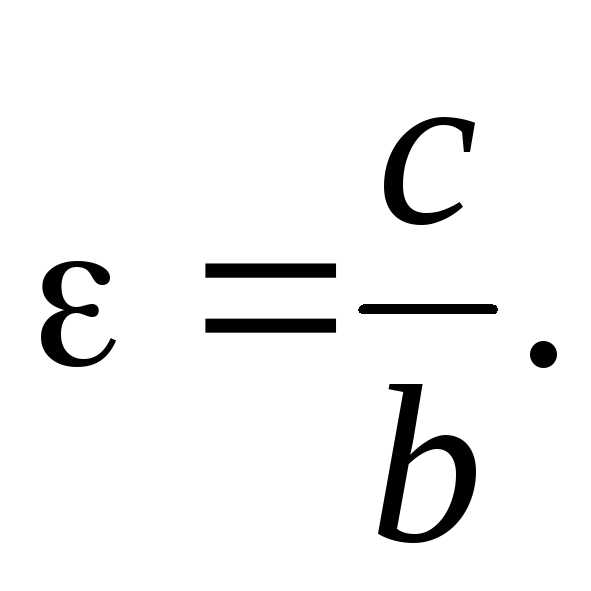
studfiles.net
Уравнение прямой, проходящей через две точки.
Пусть прямая проходит через две точки и. Уравнение этой прямой можно построить, сведя задачу к предыдущей. То есть надо найти направляющий вектор, а в качестве точкивзять любую из заданных точек, например,.
Упражнение 2
1. Прямая L1 задана двумя точкамии.
Определиться с входными данными.
Выразить из канонического уравнения y, как функцию отx.
Используя функцию plot(), построить прямуюL1.
Отметить и подписать на прямой точки и
Провести с помощью функции line( ) оси координат черного цвета.
Построить направляющий вектор , берущим начало
а) из начала координат
б) из точки, в которой прямая L1 пересекает ось абсцисс.
2. Используя готовую программу, сделать все тоже самое для прямой L2, проходящую через точкии.
Параметрическое задание прямой
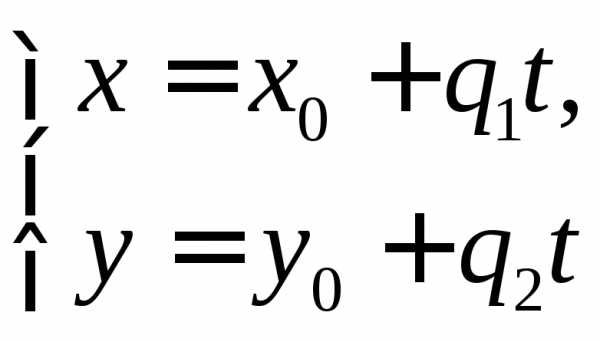 (4)
(4)
Число 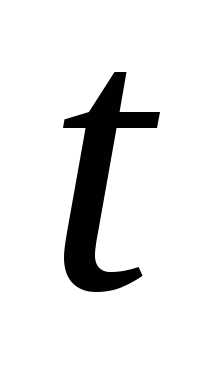 называетсяпараметром. Система
уравнений (4) равносильна векторному
уравнению
называетсяпараметром. Система
уравнений (4) равносильна векторному
уравнению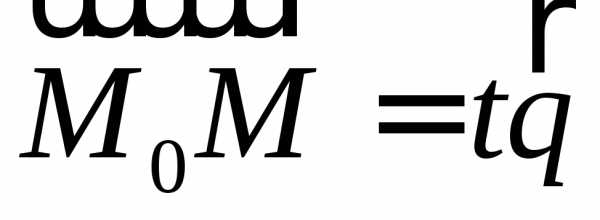 (см. рис. 5).
(см. рис. 5).
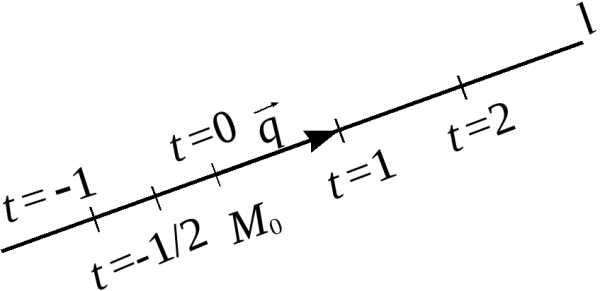
Рис.5.
Параметр  имеет прозрачныйгеометрический
смысл: модуль числа
имеет прозрачныйгеометрический
смысл: модуль числа означает, сколько векторов
означает, сколько векторов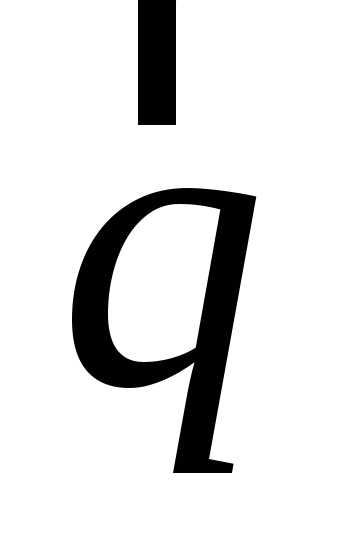 “укладывается” на векторе
“укладывается” на векторе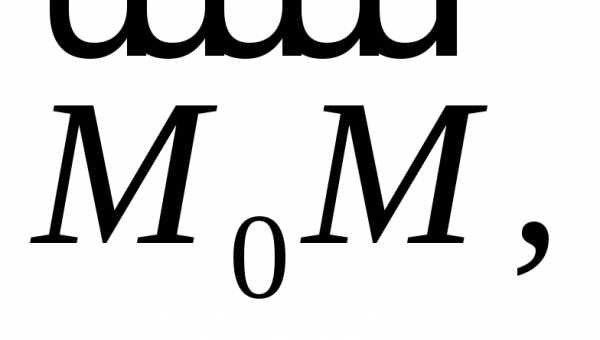 а знак обозначает расположение точки
а знак обозначает расположение точки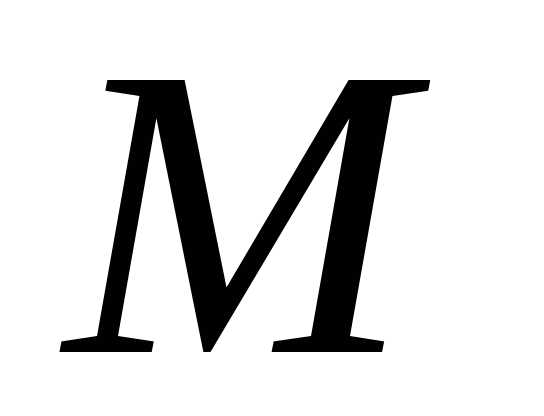 на прямой
на прямой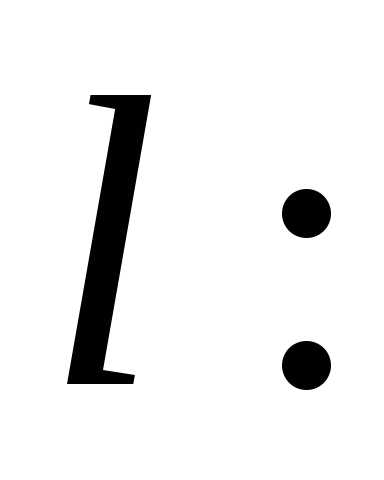 при
при точка
точка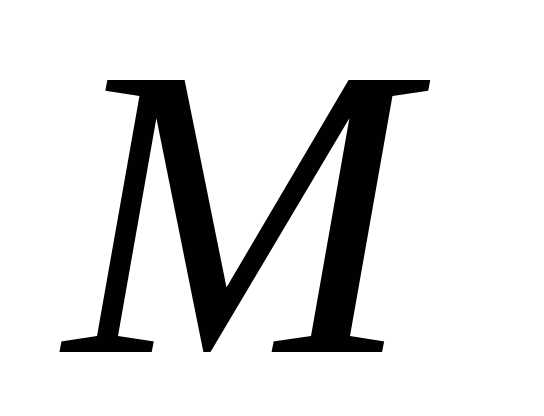 находится с той стороны, куда направлен
вектор
находится с той стороны, куда направлен
вектор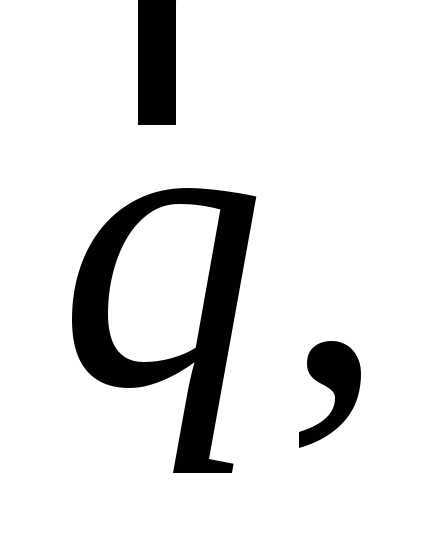 а при
а при – в противоположной стороне.
– в противоположной стороне.
Упражнение 3
Построить прямую, заданную параметрическим уравнением . Найти ее направляющий вектор, найти нормальный вектор. Изобразить данные векторы исходящими из начала координат и из какой-нибудь точки, лежащей на прямой.
Уравнение прямой с угловым коэффициентом
(см. рис. 6)
(5)
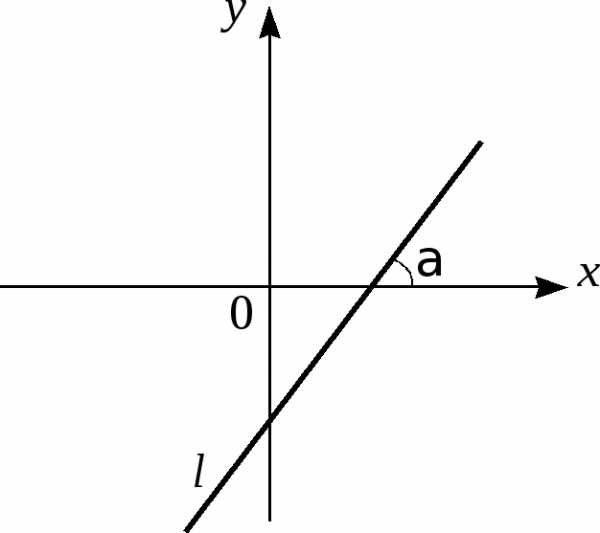
Рис.6.
Здесь 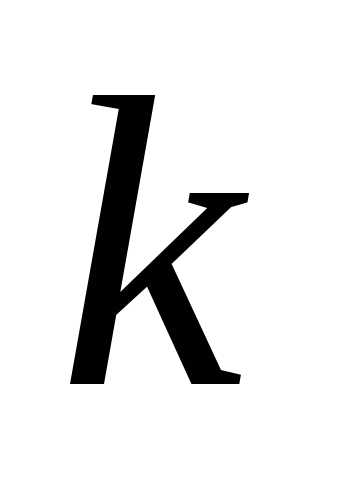 – угловой коэффициент, т.е.,
где– угол наклона прямой
– угловой коэффициент, т.е.,
где– угол наклона прямой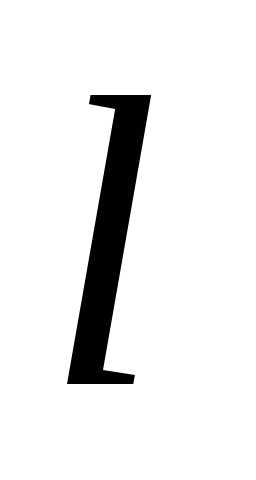 к оси
к оси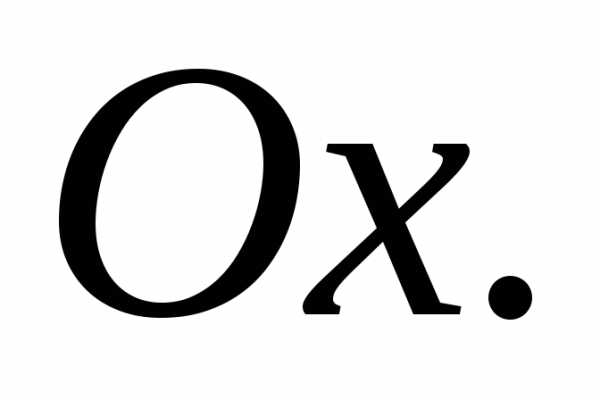 Уравнением (6) может быть задана любая
прямая, не коллинеарная оси
Уравнением (6) может быть задана любая
прямая, не коллинеарная оси
Уравнение прямой“в отрезках”
(см. рис. 7):
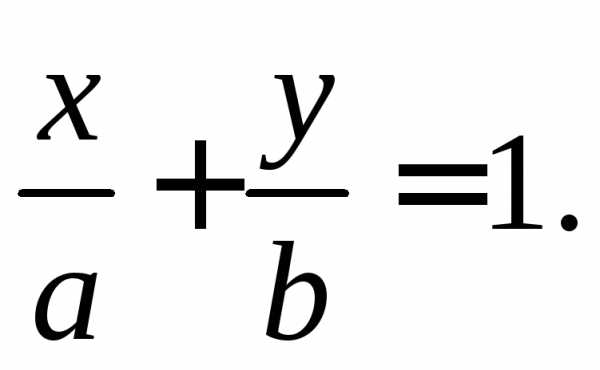 (7)
(7)
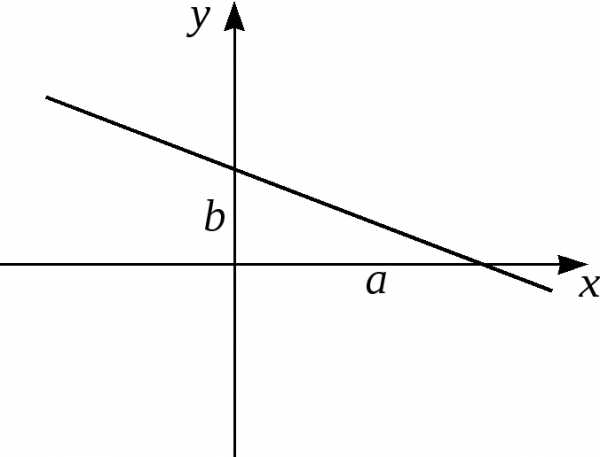
Рис.7.
Здесь 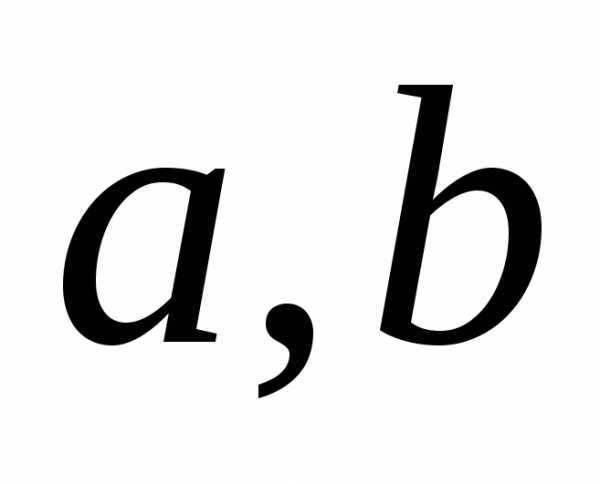 – отрезки, отсекаемые прямой
– отрезки, отсекаемые прямой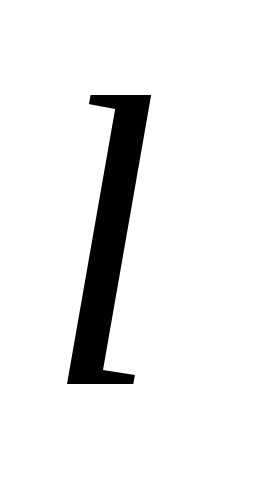 от осей координат. При этом допускается,
что
от осей координат. При этом допускается,
что или
или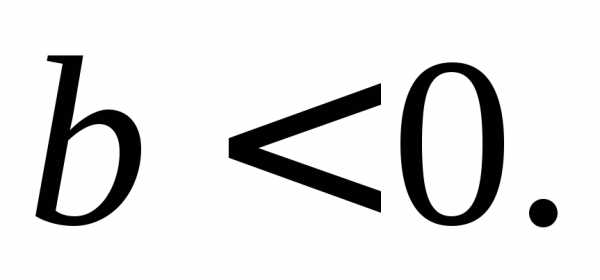 Уравнением (7) может быть задана любая
прямая, за исключением прямых, коллинеарных
какой-либо из осей координат, а также
прямых, проходящих через начало координат.
Уравнением (7) может быть задана любая
прямая, за исключением прямых, коллинеарных
какой-либо из осей координат, а также
прямых, проходящих через начало координат.
Задание на «5»
Задача 1
Найти уравнения сторон-катетов прямоугольного равнобедренного треугольника, если дана вершина прямого угла и уравнение гипотенузы. Изобразить все три прямые. При изображении прямых (катетов) использовать угловой коэффициент прямой как входящий параметр. При построении уравнения гипотенузы использоватьпример 1(набрав заново соответствующую программу). К прямым найти и построить направляющие векторы и нормальные векторы. Каждую группу (прямая, нормаль, направляющий вектор) выделить отдельным цветом. Точку С также выделить и подписать.
Задача 2.
Через точку 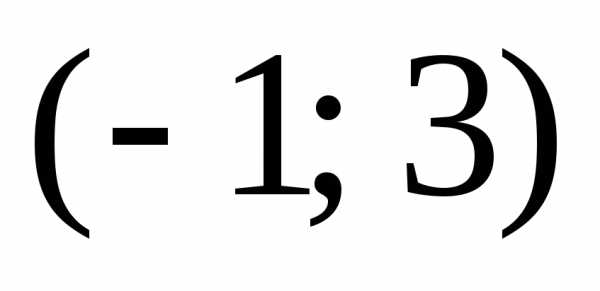 построить прямую, отсекающую от осей
координат треугольник площадью 2.
построить прямую, отсекающую от осей
координат треугольник площадью 2.
При построении прямой, полученной при ответе, использовать отрезки ииз формулы (6) как входящие параметры. Найти и построить направляющий и нормальный векторы.
10
studfiles.net
Уравнение прямой, проходящей через две точки.
Пусть прямая проходит через две точки и. Уравнение этой прямой можно построить, сведя задачу к предыдущей. То есть надо найти направляющий вектор, а в качестве точкивзять любую из заданных точек, например,.
Упражнение 2
1. Прямая L1 задана двумя точкамии.
Определиться с входными данными.
Выразить из канонического уравнения y, как функцию отx.
Используя функцию plot(), построить прямуюL1.
Отметить и подписать на прямой точки и
Провести с помощью функции line( ) оси координат черного цвета.
Построить направляющий вектор , берущим начало
а) из начала координат
б) из точки, в которой прямая L1 пересекает ось абсцисс.
2. Используя готовую программу, сделать все тоже самое для прямой L2, проходящую через точкии.
Параметрическое задание прямой
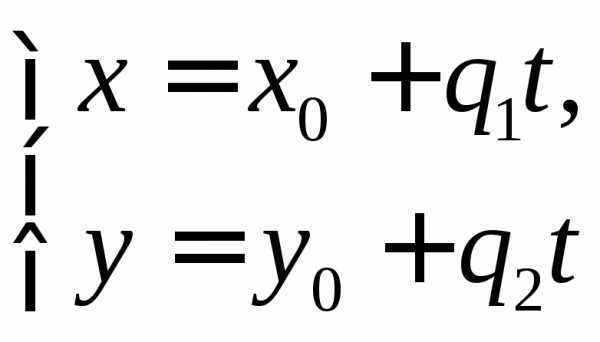 (4)
(4)
Число 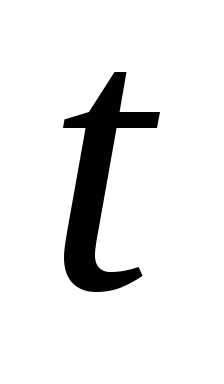 называетсяпараметром. Система
уравнений (4) равносильна векторному
уравнению
называетсяпараметром. Система
уравнений (4) равносильна векторному
уравнению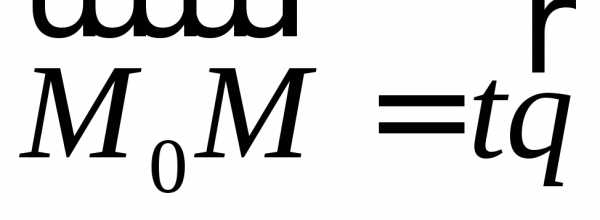 (см. рис. 5).
(см. рис. 5).
Рис.5.
Параметр  имеет прозрачныйгеометрический
смысл: модуль числа
имеет прозрачныйгеометрический
смысл: модуль числа означает, сколько векторов
означает, сколько векторов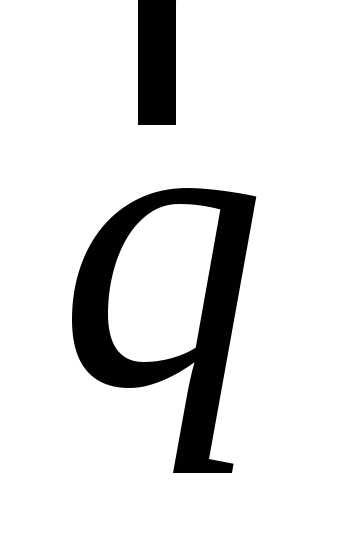 “укладывается” на векторе
“укладывается” на векторе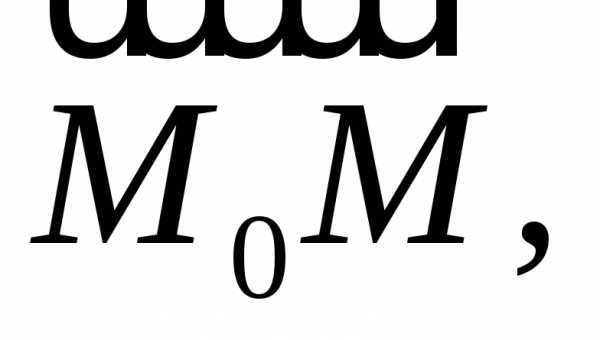 а знак обозначает расположение точки
а знак обозначает расположение точки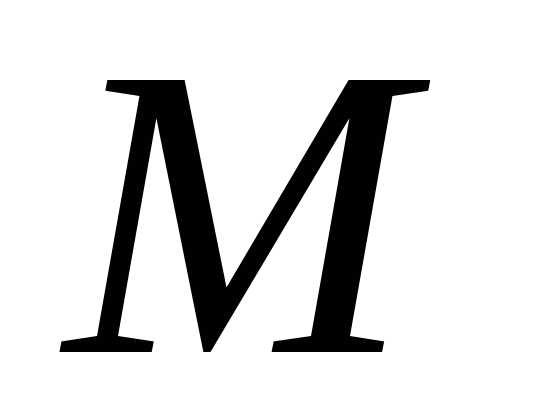 на прямой
на прямой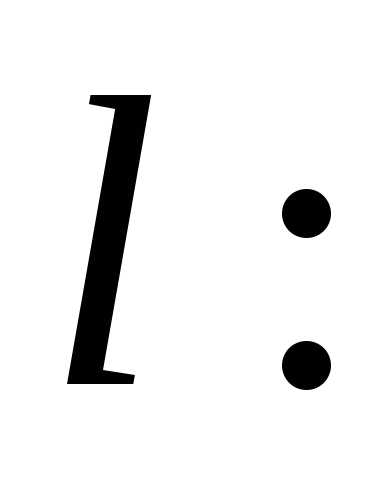 при
при точка
точка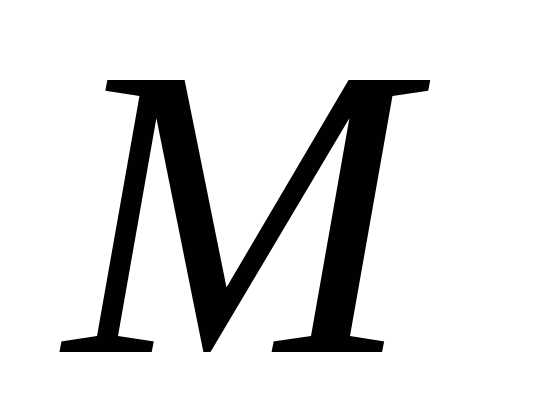 находится с той стороны, куда направлен
вектор
находится с той стороны, куда направлен
вектор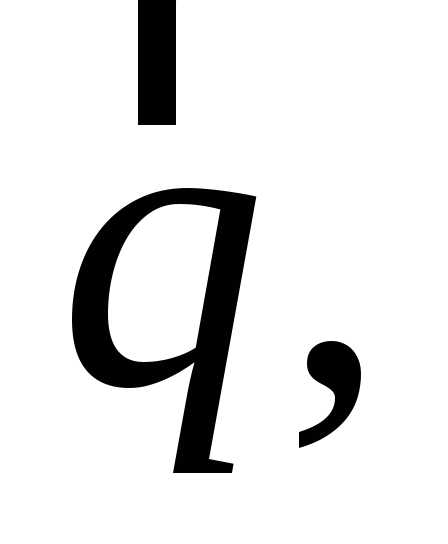 а при
а при – в противоположной стороне.
– в противоположной стороне.
Упражнение 3
Построить прямую, заданную параметрическим уравнением . Найти ее направляющий вектор, найти нормальный вектор. Изобразить данные векторы исходящими из начала координат и из какой-нибудь точки, лежащей на прямой.
Уравнение прямой с угловым коэффициентом
(см. рис. 6)
(5)
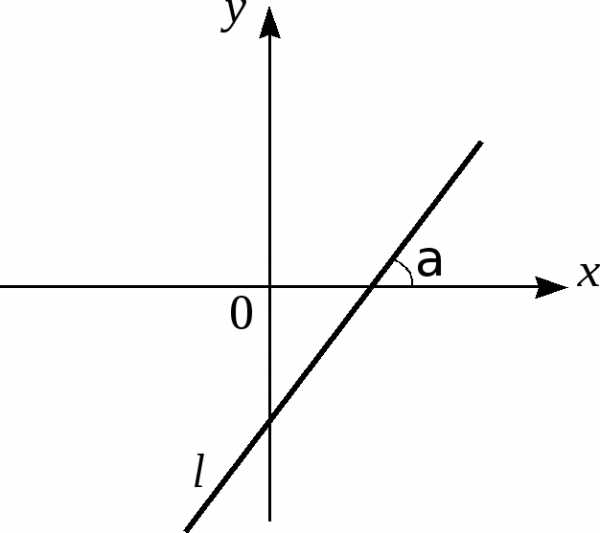
Рис.6.
Здесь 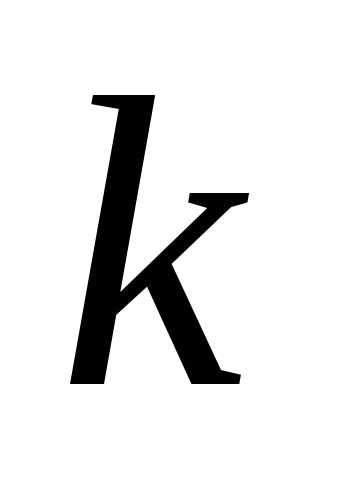 – угловой коэффициент, т.е.,
где– угол наклона прямой
– угловой коэффициент, т.е.,
где– угол наклона прямой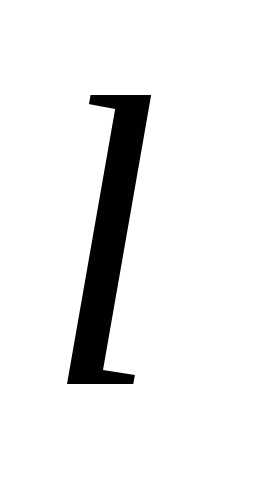 к оси
к оси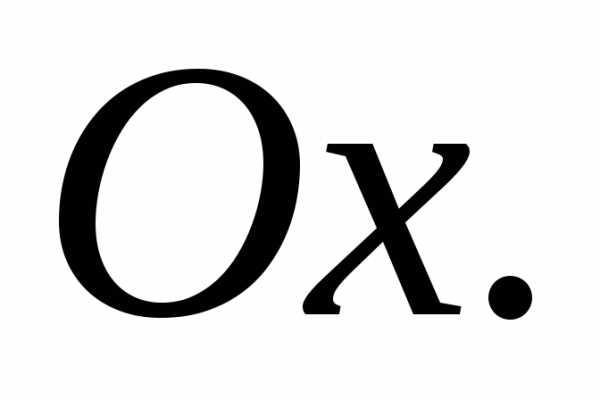 Уравнением (6) может быть задана любая
прямая, не коллинеарная оси
Уравнением (6) может быть задана любая
прямая, не коллинеарная оси
Уравнение прямой“в отрезках”
(см. рис. 7):
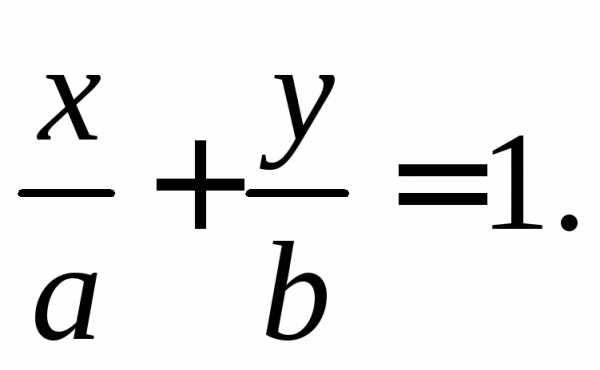 (7)
(7)
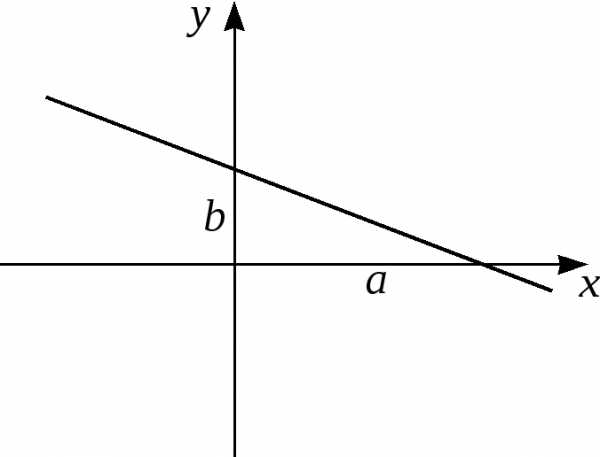
Рис.7.
Здесь 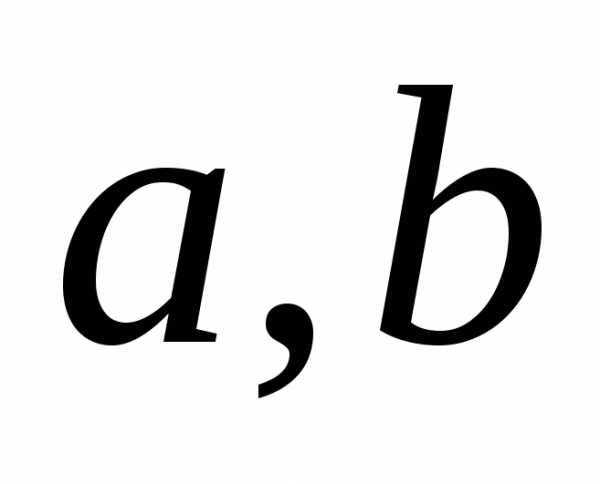 – отрезки, отсекаемые прямой
– отрезки, отсекаемые прямой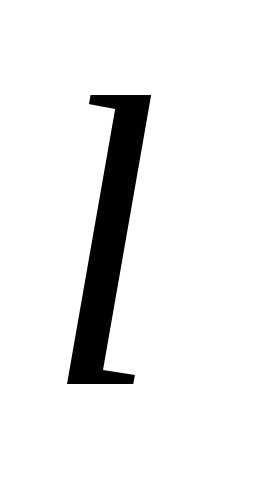 от осей координат. При этом допускается,
что
от осей координат. При этом допускается,
что или
или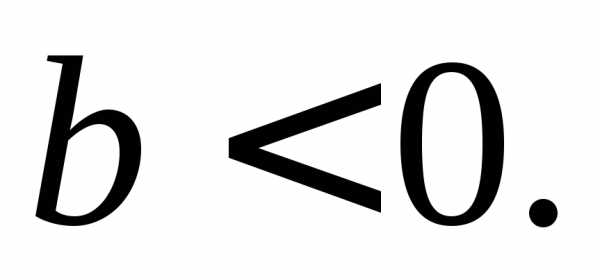 Уравнением (7) может быть задана любая
прямая, за исключением прямых, коллинеарных
какой-либо из осей координат, а также
прямых, проходящих через начало координат.
Уравнением (7) может быть задана любая
прямая, за исключением прямых, коллинеарных
какой-либо из осей координат, а также
прямых, проходящих через начало координат.
Задание на «5»
Задача 1
Найти уравнения сторон-катетов прямоугольного равнобедренного треугольника, если дана вершина прямого угла и уравнение гипотенузы. Изобразить все три прямые. При изображении прямых (катетов) использовать угловой коэффициент прямой как входящий параметр. При построении уравнения гипотенузы использоватьпример 1(набрав заново соответствующую программу). К прямым найти и построить направляющие векторы и нормальные векторы. Каждую группу (прямая, нормаль, направляющий вектор) выделить отдельным цветом. Точку С также выделить и подписать.
Задача 2.
Через точку 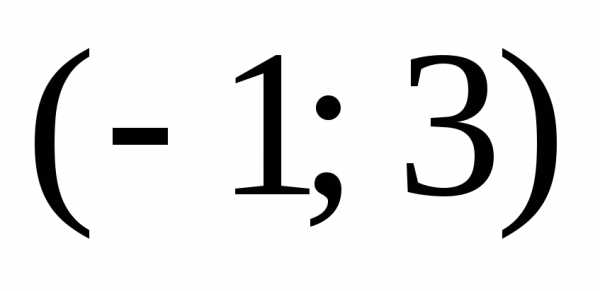 построить прямую, отсекающую от осей
координат треугольник площадью 2.
построить прямую, отсекающую от осей
координат треугольник площадью 2.
При построении прямой, полученной при ответе, использовать отрезки ииз формулы (6) как входящие параметры. Найти и построить направляющий и нормальный векторы.
10
studfiles.net

Leave A Comment