Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2 / Хабр
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2).
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу.
 Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.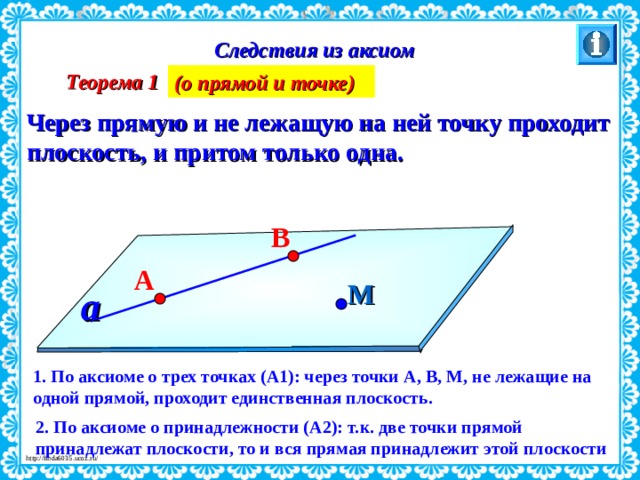
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.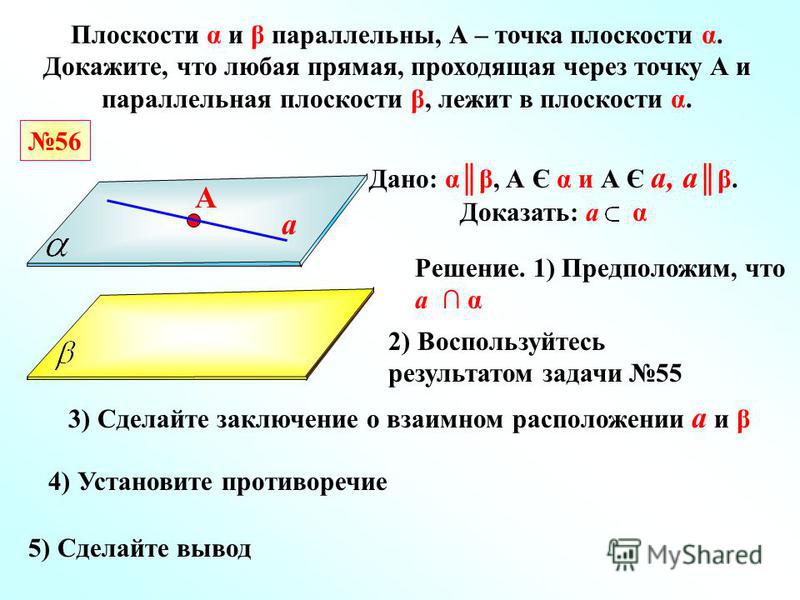
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] < 0 – точки лежат по разные стороны.
2. [P1P2, P1M1] * [P
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также.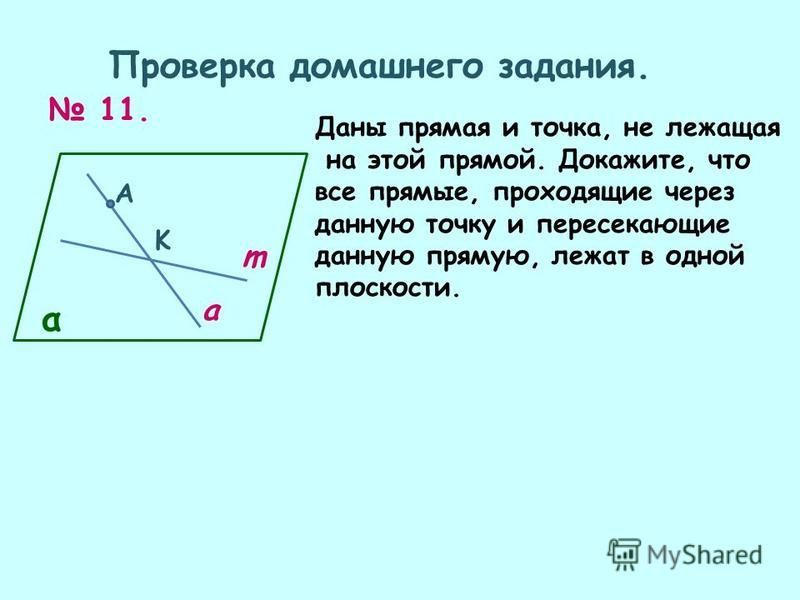 Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P
Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] < 0 => [P1P2, P1M2] * [P1P2, P1M1] < 0. Аналогично
[M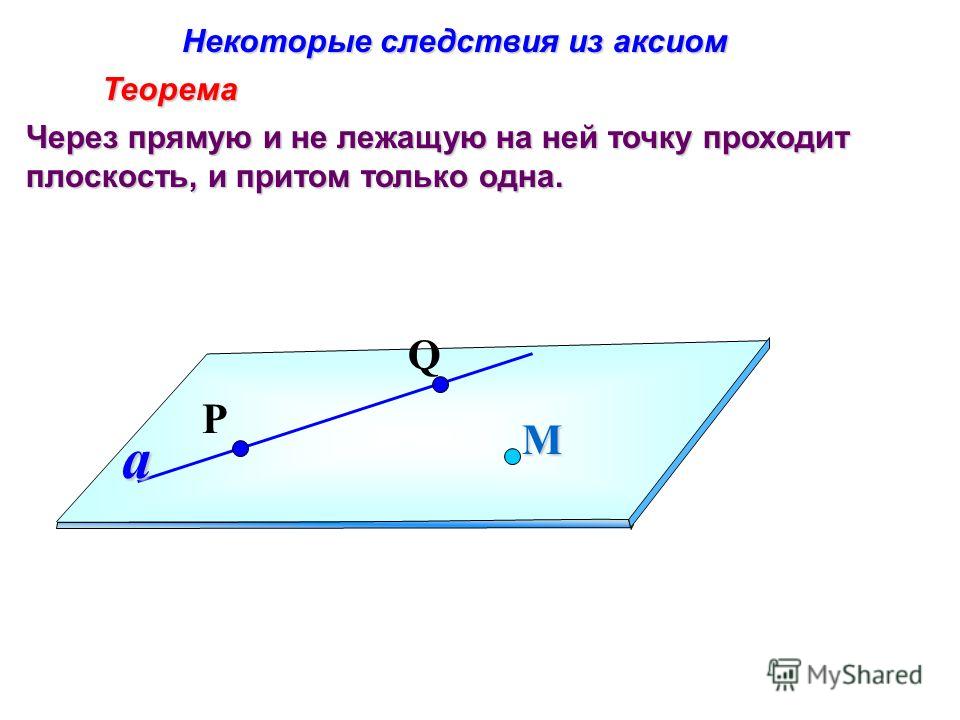 Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:
Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:
Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.
Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:
1. Концы отрезков лежат по разные стороны относительно другого отрезка.
2. Хотя бы один из концов одного отрезка принадлежит другому отрезку.
Задача №7
Расстояние от точки до прямой.
Решение
Пусть прямая задана двумя точками P1(x1, y1) и P2(x2, y2).
В предыдущей статье мы говорили о том, что геометрически косое произведение — это ориентированная площадь параллелограмма, поэтому SP1P2M = 0,5*[P1P2, P1M]. С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.
С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.
Приравнивая эти площади, находим
По модулю взяли потому, что первая площадь ориентированная.
Если же прямая задана уравнением ax + by + c = 0, то уравнение прямой проходящей через точку M перпендикулярной заданной прямой есть: a(y — y0) – b(x — x0) = 0. Теперь спокойно можно решить систему из полученных уравнений, найти их точку пересечения и вычислить расстояние от исходной точки до найденной: оно будет ровно ρ = (ax0 + by0 + c)/√(a2 + b2).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) < 0 перпендикуляр не попадает на луч
2. (P1M, P1P2) ≥ 0 перпендикуляр попадает на луч
Задача №9
Расстояние от точки до отрезка.
Решение
Рассуждаем аналогично предыдущей задаче. Если перпендикуляр не падает на отрезок, то ответом будет минимальное из расстояний от данной точки до концов отрезка.
Чтобы определить попадает ли перпендикуляр на отрезок нужно по аналогии с предыдущей задачей использовать скалярное произведение векторов. Если перпендикуляр не падает на отрезок, то либо угол MP1P2 либо угол MP2P1 будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:
Если перпендикуляр не падает на отрезок, то либо угол MP1P2 либо угол MP2P1 будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:
Если (P1M, P1P2) < 0 или (P2M, P2P1) < 0 то перпендикуляр не падает на отрезок.
Задача №10
Определить количество точек прямой и окружности.
Решение
Прямая и окружность может иметь нуль, одну или две точки пересечения. Давайте посмотрим на рисунки:
Здесь из рисунков и так все понятно. Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.
Задача №11
Взаимное расположение двух окружностей.
Решение
Возможные случаи расположения окружностей: пересекаются, касаются, не пересекаются.
Рассмотрим случай, когда окружности пересекаются, и найдем площадь их пересечения. Эту задачу я очень люблю, так как потратил на ее решение изрядное количество времени (было это давно — на первом курсе).
Вспомним теперь, что такое сектор и сегмент.
Пересечение кругов состоит из двух сегментов O1AB и O2AB.
Казалось бы необходимо сложить площади этих сегментов и все. Однако, все не так просто. Необходимо еще определить всегда ли эти формулы верны. Оказывается, нет!
Рассмотрим случай, когда центр второго круга O2 совпадает с точкой C. В этом случае d2 = 0 и за значение α примем α = π. В этом случае имеем полукруг с площадью 1/2 πR22.
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C.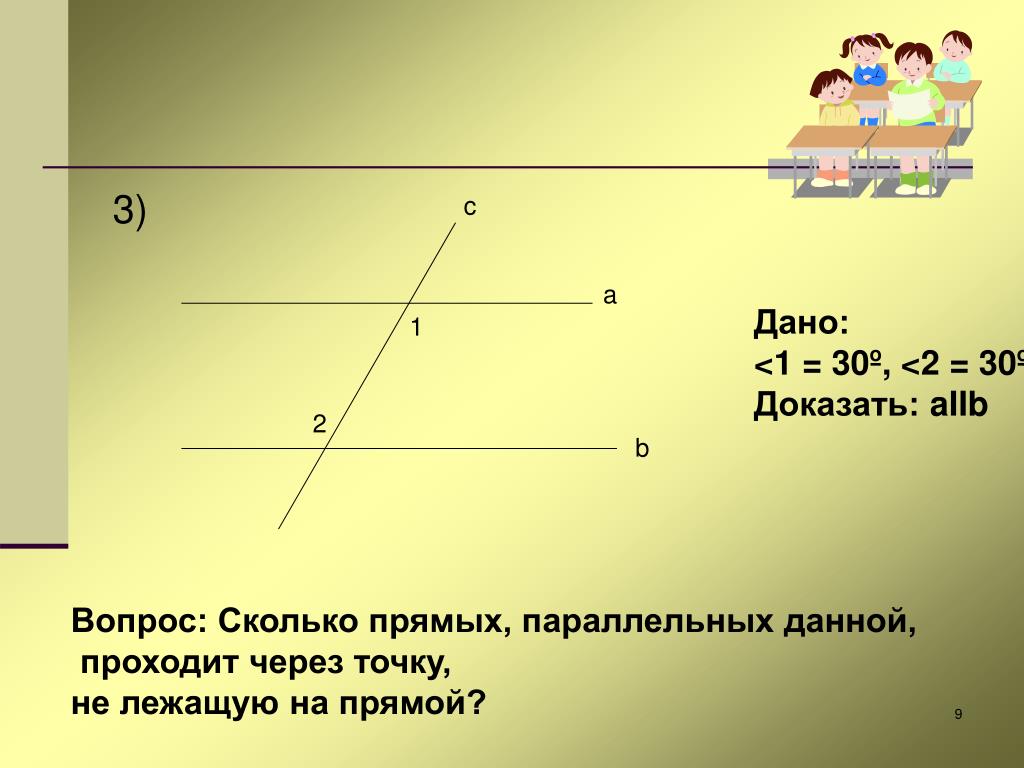 В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
Надеюсь, Вам понравилось.
Уравнение прямой 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 5: Метод координат
- Видео
- Тренажер
- Теория
Заметили ошибку?
Тема 29.
Уравнение прямой.
Выведем уравнение данной прямой l в заданной прямоугольной системе координат. Отметим две точки Ax1;y1 и Bx2;y2 так, чтобы прямая l была серединным перпендикуляром к отрезку AB.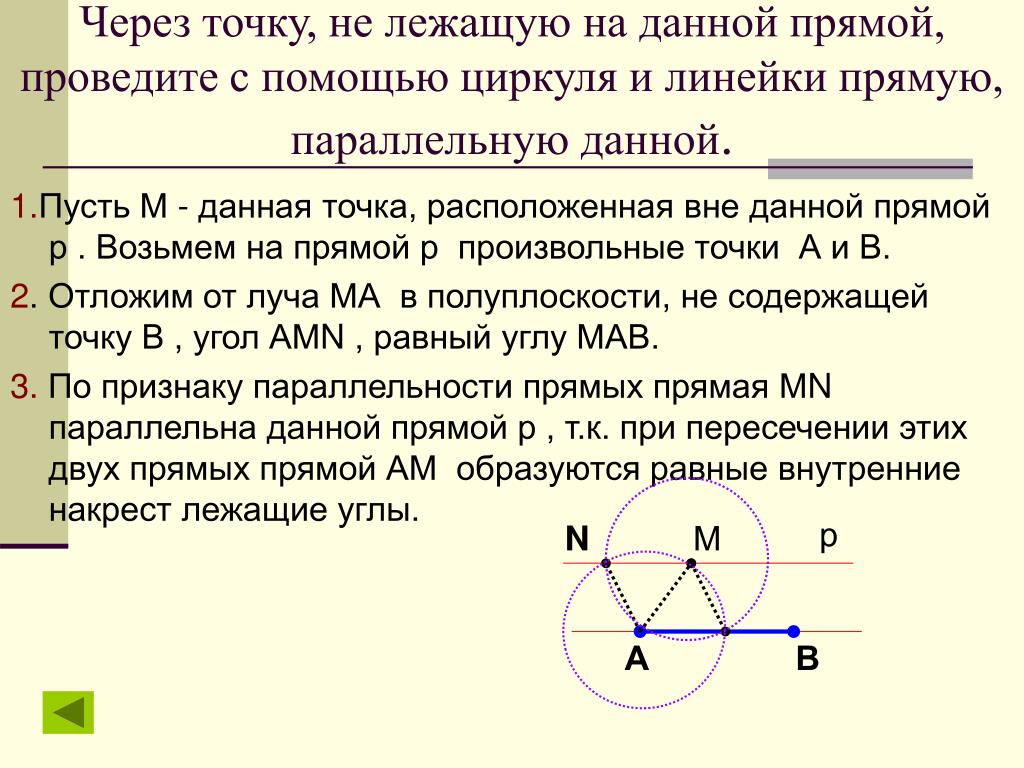
Если точка M(x; y) лежит на прямой l, то AM = BM или AM 2 = BM 2, то есть координаты точки M удовлетворяют уравнению
x-x12+y-y12=x-x22+y-y22
Если же точка M(x; y) не лежит на прямой l, то AM 2 ≠ BM 2, и, значит, координаты точки M не удовлетворяют уравнению этому уравнению. Следовательно, данное уравнение является уравнением прямой l в заданной системе координат. После возведения выражений в скобках в квадрат и приведения подобных членов уравнение принимает вид ax + by + c = 0, где
a=2×1-x2,
b=2y1-y2,
c=x22+y22-x12-y12.
Так как A(x1; y1) и B(x2; y2) — различные точки, то хотя бы одна из разностей (x1 — x2) и (y1 — y2) не равна нулю, т. е. хотя бы один из коэффициентов a и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.
е. хотя бы один из коэффициентов a и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.
Выведем уравнение прямой l, проходящей через точку M0(x0; y0) и параллельной оси Ox.
Ордината любой точки M(x; y) прямой l равна y0, т.е. координаты любой точки M(x; y)прямой l удовлетворяют уравнению y = y0. В то же время координаты любой точки, не лежащей на прямой l, этому уравнению не удовлетворяют.
Следовательно, уравнение y = y0 является уравнением прямой l. Аналогично уравнение прямой, проходящей через точку M0(x0; y0) параллельно оси Oy, имеет вид x = x0.
Ясно, что ось Ox имеет уравнение y = 0, а ось Oy — уравнение x = 0.
Рассмотрим несколько примеров:
-
Напишем уравнение прямой, проходящей через точки A(1; -1) и B(-3; 2).
Уравнение прямой AB: ax + by + c = 0.
Так как точки A и B лежат на прямой AB, то их координаты удовлетворяют этому уравнению, значит, можно подставить координаты этих точек в данное уравнение, получим:
a∙1+b∙(-1)+c=0,a∙-3+b∙2+c=0,
a-b+c=0,-3a+2b+c=0, a=b-c,-3b-c+2b+c=0, a=b-c,-3b+3c+2b+c=0,
a=b-c,-b+4c=0, a=4c-c,b=4c, a=3c,b=4c.
3cx + 4cx + c = 0, c ≠ 0
3x + 4x + 1 = 0
Ответ: 3x + 4x + 1 = 0.

-
Написать уравнение прямой, содержащей медиану CM треугольника ABC, если точка A(4; 6), B(-4; 0), C(-1; -4).
CM – медиана треугольника, следовательно, M – середина стороны AB.
Пусть точка M(x; y), тогда найдем координаты середины AB, получим:
x=4-42=0 y=6+02=3
Напишем уравнение прямой, проходящей через точки M(0; 3) и C(-1; -4). Любая прямая имеет вид: ax + by + c = 0.
a∙0+b∙3+c=0,a∙-1+b∙-4+c=0, 3b+c=0,-a-4b+c=0,
b=-c3,a=c-4b, b=-c3,a=c+43c, b=-c3,a=73c,
73cx-13cy+c=0, c≠0
73x-13y+1=0,
Умножим обе части данного уравнения на 3, получим:
7x — y + 3 = 0 – это и есть уравнение медианы CM.

Ответ: 7x — y + 3 = 0
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Как узнать, находится ли точка на прямой с помощью уравнения
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Алгебра 1 Помощь » Функции и линии » Уравнения прямых » Формула точек и расстояний » Как узнать, находится ли точка на прямой с уравнением
Какая из следующих точек не лежит на прямой y = 7x + 2?
Возможные ответы:
(–1, –5)
(–2, –12)
(0, 2)
(1, 10)
15 904 (2, 16) 9000 ответ:(1, 10)
Объяснение:
Чтобы узнать, находится ли точка (x, y) на графике линии, мы подставляем значения и смотрим, получается ли верное утверждение, например, 10 = 10. Если мы получаем что-то другое, например 6 = 4, мы знаем, что точка не лежит на прямой, потому что она не удовлетворяет уравнению. В данных вариантах, когда мы подставляем (1, 10), мы получаем 10 = 7 + 2, что неверно, что делает этот ответ искомым.
Если мы получаем что-то другое, например 6 = 4, мы знаем, что точка не лежит на прямой, потому что она не удовлетворяет уравнению. В данных вариантах, когда мы подставляем (1, 10), мы получаем 10 = 7 + 2, что неверно, что делает этот ответ искомым.
y = 7x + 2
(2, 16) дает 16 = 7(2) + 2 = 14 + 2 = 16
(–1, –5) дает –5 = 7(–1) + 2 = –7 + 2 = –5
(0, 2) дает 2 = 7(0) + 2 = 0 + 2 = 2
(–2, –12) дает –12 = 7(–2) + 2 = –14 + 2 = –12
Все это правда.
(1, 10) дает 10 = 7(1) + 2 = 7 + 2 = 9
10 = 9 — ложное утверждение.
Сообщить об ошибке
Какая точка находится на линии ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить, находится ли точка на прямой, просто подставьте точки обратно в уравнение. Когда мы подставляем (2,7) в уравнение as и соответственно, уравнение получается, что указывает на то, что точка расположена на прямой.
Сообщить об ошибке
Какое из следующих утверждений неверно?
Возможные ответы:
Прямые и параллельны.
перпендикулярно .
Точки и лежат на прямой .
и оба выпадают на строчку .
Правильный ответ:
и оба падают на строку .
Объяснение:
Линии с одинаковым наклоном параллельны (если только две линии не идентичны), а линии с противоположно обратными наклонами перпендикулярны. Таким образом, осталось оценить только те два оператора, которые содержат набор точек.
Рассмотрим и .
Таким образом, наклон или равен 2.
Подстановка точки в наполовину законченное уравнение дает нам значение . Таким образом, это утверждение верно, и единственным ответом может быть утверждение, содержащее и .
На всякий случай проверим.
дает нам значение наклона 6, поэтому мы уже можем сказать, что уравнение для линии не будет . Мы нашли свой ответ.
Сообщить об ошибке
Какие из этих прямых проходят через точку (6,5) на координатной плоскости xy?
Возможные ответы:
Другие ответы отсутствуют Объяснение:
Чтобы узнать, находится ли точка на прямой, вы можете снова подставить точки в уравнение. Если значения равны друг другу, то точка должна быть на прямой. В этом случае единственное уравнение, где (6,5) правильно подходит в качестве значения, — это .
Сообщить об ошибке
Какие из следующих точек находятся на линии, описываемой уравнением?
Возможные ответы:
Два из этих вариантов ответа верны.
Правильный ответ:
Два из этих вариантов ответа верны.
Объяснение:
Самый простой способ узнать, попадает ли точка на определенную линию, — это подставить первое значение точки для и второе значение для .
Если мы сделаем это для , мы обнаружим, что
, что верно.
Уравнение также верно для , но неверно для других значений. Итак, два варианта ответа верны.
Сообщить об ошибке
Какая из следующих упорядоченных пар лежит на линии, заданной уравнением?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить, какая упорядоченная пара удовлетворяет уравнению, было бы полезно преобразовать уравнение в форму пересечения наклона.
Затем подставьте каждую заказанную пару и посмотрите, удовлетворяет ли она уравнению. Мы ищем значение, которое дает желаемый ответ.
Мы ищем значение, которое дает желаемый ответ.
удовлетворяет уравнению. Все остальные пункты нет.
(Примечание: вы также можете использовать исходное уравнение в стандартной форме).
Сообщить об ошибке
На какой из этих прямых расположена точка (3,2)?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить, находится ли точка на линии, вы можете включить ее в уравнение, чтобы увидеть, остается ли уравнение действительным/равным точке.
Подстановка точки (3,2) в уравнение дает вам
, что работает. Ни одно из других уравнений не останется равным после включения в (3,2).
Сообщить об ошибке
На какой из этих прямых лежит точка (2,7)?
Возможные ответы:
Ни один из этих ответов
Правильный ответ:9 5 5
Объяснение: Чтобы определить, находится ли точка на заданной линии, просто вставьте координаты точки в линию. Сообщить об ошибке Какие из этих точек попадают на график прямой Возможные ответы: Две из этих точек попадают на график этого уравнения. Все три эти точки попадают на график этого уравнения. Правильный ответ: Все три эти точки попадают на график этого уравнения. Объяснение: Чтобы узнать, находится ли точка на линии с уравнением, нам просто нужно подставить значения точки и и посмотреть, верно ли уравнение. Например, давайте посмотрим на точку . Подстановка в уравнение дает нам или , что верно. Итак, эта точка попадает на прямую. Сообщить об ошибке Какая точка находится на прямой Возможные ответы: Правильный ответ: Объяснение: Чтобы определить, находится ли точка на прямой, вы можете просто подставить координаты x и y в уравнение. Другой способ решить эту проблему — построить график линии и посмотреть, попадает ли она на линию. Подключение даст верное утверждение, так что оно на линии. Сообщить об ошибке ← Предыдущий 1 2 3 Далее → Уведомление об авторских правах 10 Диагностические тесты
557 практических тестов
Вопрос дня
Карточки
Learn by Concept В этом объяснении мы узнаем, как найти наклон линии, проходящей через две заданные точки. Наклон прямой линии в координатной плоскости — это число, которое позволяет нам точно
опишите крутизну линии. Одной из возможностей было бы описать крутизну
линия с углом между прямой линией и, например, положительной 𝑥-осью. Однако,
поскольку прямые описываются уравнением, дающим связь между 𝑥- и
𝑦-координаты точек, лежащих на прямой, определение наклона, которое мы будем использовать, будет
по координатам точек прямой. Давайте посмотрим, как. Рассмотрим две точки на прямой, отстоящие на одну единицу друг от друга по горизонтали. Наклон
линия 𝑚 задается изменением 𝑦-координаты между точкой слева и
что справа. Из этого определения мы сначала видим, что наклон равен
положительный, когда прямая линия идет
вверх слева направо и
отрицательный, когда он идет
вниз слева направо. Во-вторых, мы видим, что чем больше абсолютное значение 𝑚, тем круче линия (тем больше
наклонена по отношению к горизонтали). Два крайних случая: Для первого случая заметим, что все точки, лежащие на горизонтальной прямой, имеют одинаковые
𝑦-координата. Следовательно, нет изменения 𝑦-координаты от одной точки к другой, когда
они находятся на расстоянии одной единицы друг от друга по горизонтали; наклон горизонтальной линии равен нулю. Для второго случая вертикальная линия, все точки лежащие на прямой имеют одинаковые
𝑥-координата. Поэтому невозможно применить определение наклона, поскольку существуют
никакие две точки не отстоят друг от друга на одну единицу по горизонтали (то есть с разницей между их
𝑥-координаты равны 1). Таким образом, наклон вертикальной линии не определен. Давайте проверим наше понимание наклона линии на первых двух примерах. Заполните пропуск: На этом рисунке наклон ⃖⃗𝐴𝐵 равен . Дан треугольник 𝐴𝐵𝐶, но вопрос касается только прямой У нас есть только
отрезок здесь, но достаточно увидеть, что линия идет вниз слева направо. Напомним, что наклон прямой линии положителен, когда линия идет вверх слева направо
вправо и отрицательный, когда он идет вниз слева направо. Следовательно, наклон здесь
отрицательный, что является ответом A. Теперь попробуем найти наклон прямой, параллельной оси. ⃖⃗𝐴𝐵 параллелен оси 𝑦. Если координаты точек 𝐴 и 𝐵 равны (𝑚,2)
и (8,6) соответственно, найти значение 𝑚. Если ⃖⃗𝐴𝐵 параллельна оси 𝑦, то это вертикальная линия. Все точки, лежащие на
вертикальная линия имеет одинаковую 𝑥-координату. Вернемся к определению наклона. Предположим, что две заданные точки на прямой
1 единица друг от друга по горизонтали. Затем мы можем нарисовать прямоугольный треугольник, где его гипотенуза является частью
линии между точками, а две другие стороны параллельны 𝑥- и 𝑦-осям
соответственно. Сторона, параллельная оси 𝑥, будет иметь длину 1 единицу, а сторона, параллельная
𝑦-ось будет |𝑚| единицы длины, как показано. Рассмотрим теперь несколько точек, равномерно отстоящих друг от друга по горизонтали на 1 единицу так, чтобы наш прямоугольный треугольник
можно провести между каждой парой соседних точек. (Обратите внимание, что угол между горизонталью
линия и линия одинаковы в любой точке линии; подумайте об отношениях углов
между парой параллельных прямых и секущей.) Таким образом, мы можем понять, что две точки 2
единицы, разделенные по горизонтали, находятся на расстоянии 2𝑚 единиц по вертикали, а две точки — на расстоянии 3 единиц друг от друга. Мы можем обобщить это наблюдение: если две точки 𝐴 и 𝐵 лежат на невертикальной прямой с
наклон 𝑚, то изменение в 𝑦 при переходе от 𝐴 к 𝐵, определяемое как 𝑦−𝑦, в 𝑚 раз больше изменение 𝑥 при переходе от 𝐴 к 𝐵, заданное 𝑥−𝑥. Следовательно, у нас есть
𝑦−𝑦=𝑚(𝑥−𝑥). Разделив обе части уравнения на 𝑥−𝑥 (мы имеем 𝑥−𝑥≠0, поскольку прямая не
по вертикали), находим
𝑚=𝑦−𝑦𝑥−𝑥. Заметим это выражение для наклона прямой через изменение 𝑦 и
изменение 𝑥 при переходе из одной точки прямой в другую. Наклон прямой, проходящей через 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦), определяется выражением
𝑚=𝑦𝑥=𝑦−𝑦𝑥−𝑥.changeinchangein Стоит отметить, что не имеет значения, осталось ли 𝐴 от 𝐵 или нет; если бы мы поменялись местами 𝐴
и 𝐵 в приведенном выше уравнении, мы бы изменили знаки как 𝑦−𝑦, так и 𝑥−𝑥, что
поэтому не изменится 𝑚:
𝑚=𝑦−𝑦𝑥−𝑥=𝑦−𝑦𝑥−𝑥. Теперь мы установили зависимость между наклоном прямой линии 𝑚 и
координаты любых двух точек, лежащих на прямой. В нашем следующем примере мы будем использовать это
отношение, чтобы найти наклон прямой, проходящей через две заданные точки. Определите наклон прямой, проходящей через точки 𝐴(2,−5) и 𝐵(4,5). Напомним, что наклон прямой, проходящей через точки 𝐴 и 𝐵, определяется выражением
𝑚=𝑦𝑥=𝑦−𝑦𝑥−𝑥.changeinchangein Подставляя значения 𝑥=2, 𝑦=−5, 𝑥=4 и 𝑦=5, находим
𝑚=5−(−5)4−2=102=5. Следовательно, наклон линии равен 5. Мы также можем проверить это графически. Мы видим, что при переходе от 𝐴 к 𝐵 мы двигаемся по горизонтали +2 и по вертикали +10, что
соответствует двум перемещениям +1 по горизонтали и +5 по вертикали, т. е. наклону 5. Связь между наклоном и координатами двух точек на прямой действительна для
любые две точки на прямой. Используем это свойство для решения нашего следующего примера. Каково значение 𝑦, чтобы 𝐴(−9,6), 𝐵(3,−3) и 𝐶(−1,𝑦) лежали на одной прямой? Нам даны координаты двух точек, 𝐴 и 𝐵, и только 𝑥-координата точки
𝐶. Нам нужно найти 𝑦-координату 𝐶 так, чтобы три точки лежали на одной прямой, что
означает, что все они лежат на одной прямой. Напомним, что отношение изменения 𝑦 к изменению 𝑥 между любыми двумя точками на
линия равна наклону линии. Поскольку у нас есть координаты 𝐴 и 𝐵, мы можем найти
наклон линии, проходящей через 𝐴 и 𝐵. Тогда можно написать, что отношение
изменение 𝑦 на изменение 𝑥 между 𝐵 (или 𝐴) и 𝐶 должно равняться наклону линии, если
𝐶 лежит на нем, что позволит найти соответствующее значение 𝑦. Сначала вычислим наклон линии, проходящей через 𝐴 и 𝐵. У нас есть
𝑚=𝑦𝑥=𝑦−𝑦𝑥−𝑥.changeinchangein Подставляя значения 𝑥=−9, 𝑦=6, 𝑥=3 и 𝑦=−3, находим
𝑚=-3-63-(-9)=-912. Деление числителя и знаменателя на 3 дает
𝑚=−34. Если точка 𝐶 лежит на прямой, проходящей через 𝐴 и 𝐵, то имеем
𝑚=𝑦𝑥=𝑦−𝑦𝑥−𝑥.changeinchangein находить
−34=𝑦−(−3)−1−3−34=𝑦+3−4−34=−𝑦+34. Умножение обеих сторон на −4 дает 3=𝑦+3,
что означает, что 𝑦=0. Таким образом, 𝑦-координата точки 𝐶 должна быть равна 0, чтобы 𝐴, 𝐵 и 𝐶 были коллинеарны. До сих пор мы использовали понятие наклона в чисто математических примерах. Однако
переменные 𝑥 и 𝑦 могут представлять реальные величины. Например, 𝑦 может представлять объем
воды в ванне, пока она опорожняется, и 𝑥 время, как показано на следующем
диаграмма. Диаграмма показывает нам, что ванна превратилась из 100 литров воды в пустую
в течение 5 минут. Значение наклона -20 означает, что объем воды в ванне каждую минуту уменьшается на 20 литров. В нашем последнем примере нам нужно будет найти наклоны различных отрезков прямой в
реальной жизненной ситуации и понять их значение. На следующем графике показано путешествие на автомобиле. Он состоит из 3-х частей. Часть 1
представлено 𝐴𝐵, часть 2 представлена 𝐵𝐶, а часть 3 представлена
𝐶𝐷. Часть 1 Нам нужно найти наклон 𝐴𝐵. На графике читаем, что 𝐴=(1,50) и 𝐵=(2,100). Напомним, что наклон определяется выражением
𝑚=𝑦𝑥=𝑦−𝑦𝑥−𝑥=100−502−1=50.changeinchangein Это также показано на графике ниже. Следовательно, наклон 𝐴𝐵 равен 50. Часть 2 Действуем так же, как и в вопросе 1, чтобы найти наклон 𝐶𝐷. Графически это можно представить следующим образом. Таким образом, наклон 𝐶𝐷 равен 100. Часть 3 Давайте посмотрим на каждое из данных утверждений, чтобы выяснить, какое из них неверно. Следовательно, ложным утверждением является ответ D. Часть 4 Нам нужно найти истинное утверждение относительно наклона отрезка 𝐵𝐶. Поскольку 𝐵𝐶
горизонтальна, ее наклон равен нулю. Это означает, что расстояние не меняется в течение части 2
путешествие. Автомобиль неподвижен, то есть не движется. Следовательно, ответ C является верным
заявление. В этом случае вставка координат в единственную строку, где вы можете вставить координаты и получить правильное уравнение, это . Подстановка (2,7) даст вам уравнение , которое соответствует .
В этом случае вставка координат в единственную строку, где вы можете вставить координаты и получить правильное уравнение, это . Подстановка (2,7) даст вам уравнение , которое соответствует . Проделав то же самое с двумя другими точками, мы увидим, что да, все три точки попадают на линию, выраженную этим уравнением.
Проделав то же самое с двумя другими точками, мы увидим, что да, все три точки попадают на линию, выраженную этим уравнением. Все ресурсы по алгебре 1
Объяснение урока: Наклон линии, проходящей через две точки
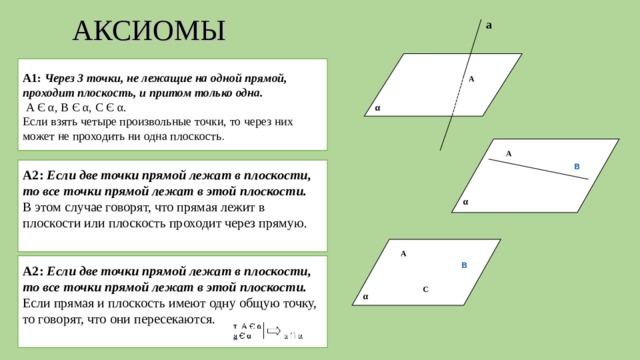
Определение: Наклон прямой
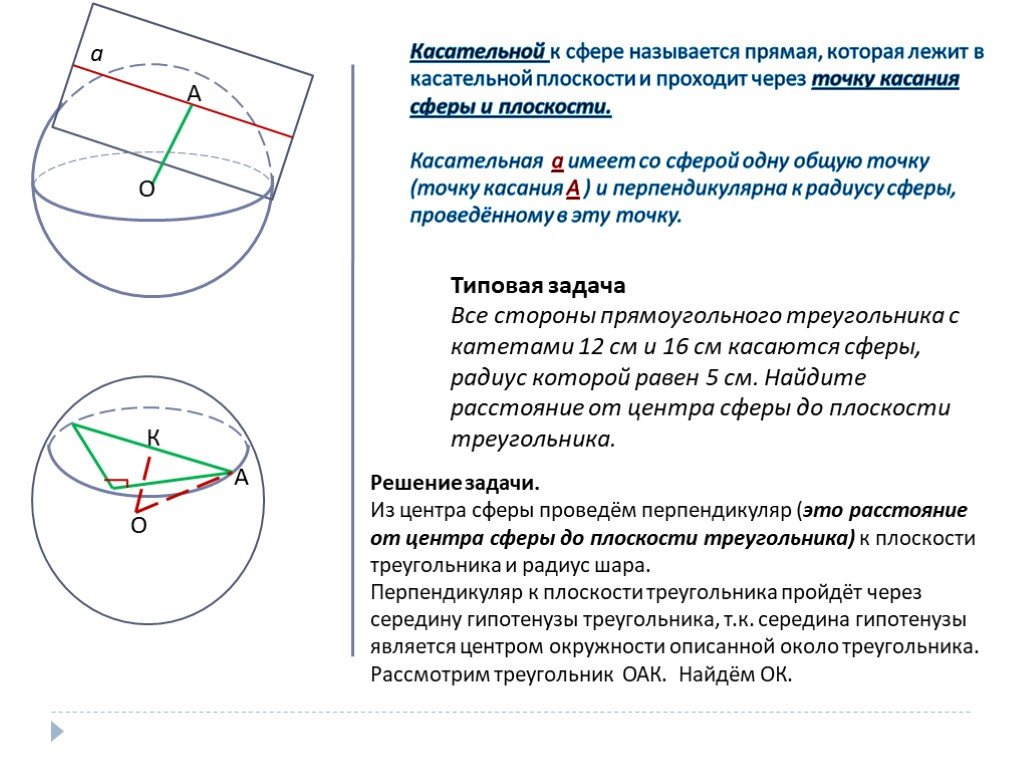
Пример 1: Нахождение знака наклона прямой линии

Ответ
Пример 2. Использование известных свойств горизонтальных и вертикальных линий для поиска неизвестных
Координаты
Ответ
 Итак, если 𝑥-координата 𝐵 равна 8, то
𝑥-координата 𝐴, 𝑚 тоже должна быть равна 8. Следовательно, значение 𝑚 равно 8.
Итак, если 𝑥-координата 𝐵 равна 8, то
𝑥-координата 𝐴, 𝑚 тоже должна быть равна 8. Следовательно, значение 𝑚 равно 8. по горизонтали отстоят друг от друга на 3𝑚 единицы по вертикали и так далее.
по горизонтали отстоят друг от друга на 3𝑚 единицы по вертикали и так далее. Связь: наклон прямой линии и координаты двух точек на
Линия
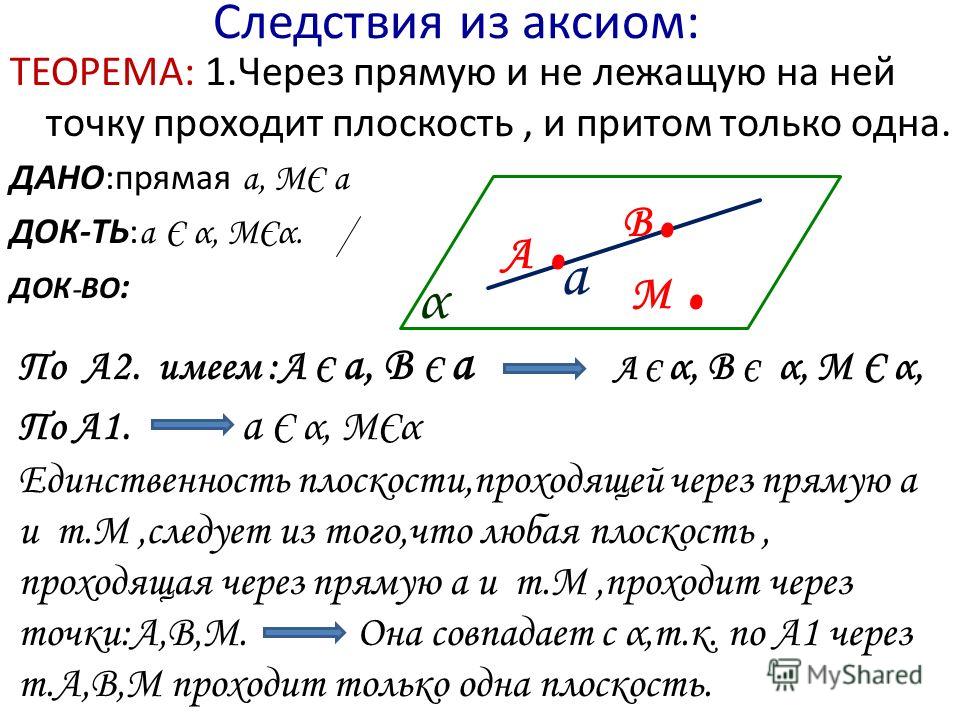
Пример 3. Нахождение наклона прямой по двум точкам
Ответ
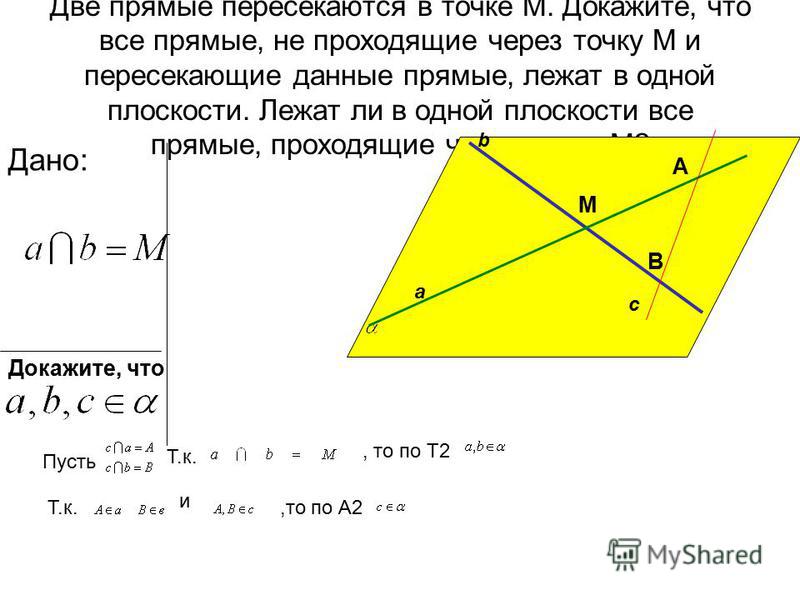 Другими словами, все точки, лежащие на прямой, связаны этой
отношения: отношение их изменения в 𝑦 к их изменению в 𝑥 является константой, называемой
наклон линии. Говорят, что точки коллинеарны, если они лежат на одной прямой
линия.
Другими словами, все точки, лежащие на прямой, связаны этой
отношения: отношение их изменения в 𝑦 к их изменению в 𝑥 является константой, называемой
наклон линии. Говорят, что точки коллинеарны, если они лежат на одной прямой
линия. Пример 4. Нахождение 𝑦-координаты точки при условии, что она коллинеарна двум другим данным
Points
Ответ
 Это соответствует изменению 𝑦 на -100 л и изменению 𝑥 на 5 мин,
дающий наклон
𝑚=𝑦𝑥=−1005=−20.changeinchangein
Это соответствует изменению 𝑦 на -100 л и изменению 𝑥 на 5 мин,
дающий наклон
𝑚=𝑦𝑥=−1005=−20.changeinchangein Пример 5. Определение уклона между двумя точками в реальной ситуации
Ответ
 Мы читаем на
изобразите координаты 𝐶(3100) и 𝐷(3,5150). Наклон
𝑚′=𝑦𝑥=𝑦−𝑦𝑥−𝑥=150−1003,5−3=500,5=100.changeinchangein
Мы читаем на
изобразите координаты 𝐶(3100) и 𝐷(3,5150). Наклон
𝑚′=𝑦𝑥=𝑦−𝑦𝑥−𝑥=150−1003,5−3=500,5=100.changeinchangein
Расстояние, пройденное в части 1, равно
100−50=50 км, а то, что описано в части 3, равно
150−100=50 км, поэтому первая часть этого
утверждение верно.
Время, затраченное на часть 1, равно 2−1=1 часу, а время, затраченное на
часть 3 составляет 3,5−3=0,5 часа. Итак, это правда, что время, затраченное на часть 3, вдвое меньше, чем
время, затраченное на часть 1.
Наклон – это изменение
расстояние, когда изменение часов составляет 1 час. Следовательно, это расстояние, пройденное за
один час.
Мы обнаружили, что наклон в части 1 равен 50
а в части 3 это 100, поэтому наклон в части 1 вдвое меньше, чем в части 3. Второй
часть утверждения относится к скорости; напомню, что скорость измеряется расстоянием
в единицу времени (например, километры в час или метры в секунду). Так как наклон
дает нам расстояние, пройденное за один час, поэтому оно эквивалентно скорости
машина. Значит, скорость в первой части 50 км/ч, а в третьей 100 км/ч. Так что, это
верно, что скорость в части 1 вдвое меньше, чем в части 3.
Мы видели, что изменение времени в части 1 (т. е. длительность части
1) составляет 2−1=1 час, а изменение времени в части 3 составляет 3,5−3=0,5 часа. У нас есть
также найдено выше, что пройденное расстояние одинаково. Однако это означает, что
скорость была выше в части 3, так как 50 км были пройдены всего за полчаса, а
они были пройдены за один час в части 1. При ее скорости в части 3 машина
проехал 100 км за один час, что в два раза больше расстояния, пройденного в части 1 за один час
час.

Leave A Comment