Перемещение и описание движения | Частная школа. 8 класс
Конспект по физике для 8 класса «Перемещение и описание движения». Как определить координаты тела, движущегося равномерно и прямолинейно. Что такое уравнение движения.
Конспекты по физике Учебник физики Тесты по физике
Система отсчёта используется для того, чтобы определить положение тела в пространстве в некоторый момент времени. В случае когда тело движется, возникает задача вычисления его координат в некоторые моменты времени.
ПРОЕКЦИИ ПЕРЕМЕЩЕНИЯ НА КООРДИНАТНЫЕ ОСИ
Если известен вектор перемещения тела, то при расчетах, как правило, используют не координаты вектора, как такового, а его проекции на оси координат. Если опустить перпендикуляры из начала и конца вектора перемещения s на координатную ось X, то получится отрезок sx, который называют проекцией перемещения. При этом проекция вектора на ось считается положительной, если координата конца вектора перемещения оказывается больше координаты его начала. В противном случае проекция считается отрицательной.
В противном случае проекция считается отрицательной.
Если вектор и ось параллельны, то длина вектора равна его проекции на эту ось.
При решении многих задач необходимо уметь находить проекции вектора перемещения на координатные оси. Если (х0; у0) и (х; у) — координаты начала и конца вектора, то его проекции на оси абсцисс и ординат будут равны соответственно
sx = x – x0, (1)
sy = y – y0
Зная проекции вектора перемещения, можно найти его длину (модуль) по теореме Пифагора:
ОПРЕДЕЛЕНИЕ КООРДИНАТ ДВИЖУЩЕГОСЯ ТЕЛА И ЕГО ПЕРЕМЕЩЕНИЯ
Если тело движется прямолинейно, то траектория его движения совпадает с перемещением. При этом пройденный телом путь равен значению модуля вектора перемещения.
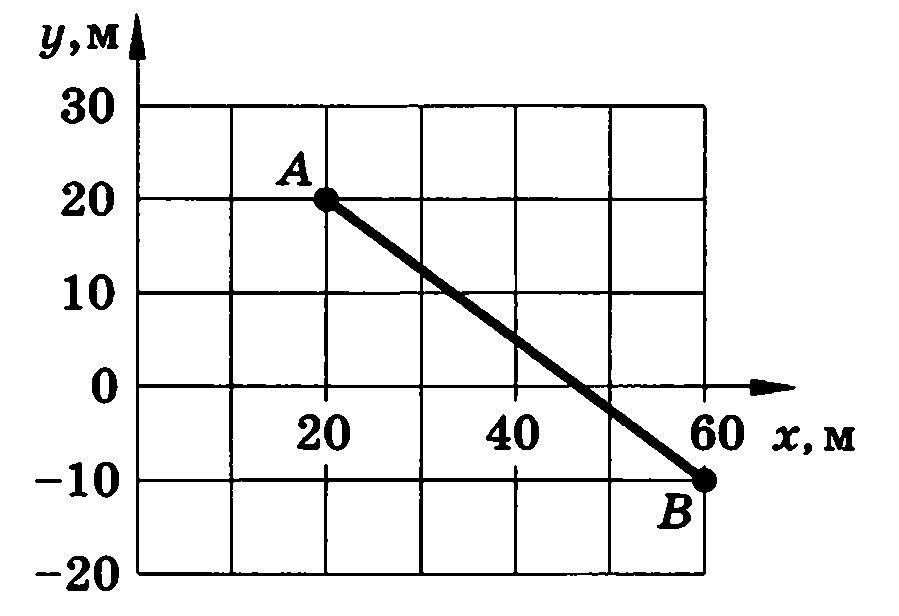
А как описать движение тела в более сложном случае? На рисунке представлен график движения самолёта. Сначала он набирал высоту, двигаясь из точки А в точку В, затем двигался на одной и той же высоте (до точки С) и, наконец, приземлился в точке D. На какой высоте проходил полёт? Высоте полёта соответствуют координаты по оси OY, значит, в точке В самолёт набрал высоту 3 км.
Сначала он набирал высоту, двигаясь из точки А в точку В, затем двигался на одной и той же высоте (до точки С) и, наконец, приземлился в точке D. На какой высоте проходил полёт? Высоте полёта соответствуют координаты по оси OY, значит, в точке В самолёт набрал высоту 3 км.
Теперь ответим на вопрос: какой путь проделал самолёт на этой высоте? Проекция перемещения s2x = 80 — 20 = 60 км.
Так как всё это время самолёт двигался параллельно оси ОХ, длина вектора перемещения равна его проекции на эту ось. Следовательно, модуль перемещения самолёта из точки В в точку С равен 60 км. Этому же значению равен и путь самолёта из точки В в точку С.
И наконец, определим дальность полёта самолёта. Для этого нам надо найти модуль перемещения самолёта из точки А в точку D: |s| = sx = 100 — 0 = 100 км.
Таким образом, при помощи перемещения и его проекций мы описали сложное движение самолёта.
youtube.com/embed/-JKMvLw6LlA?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ
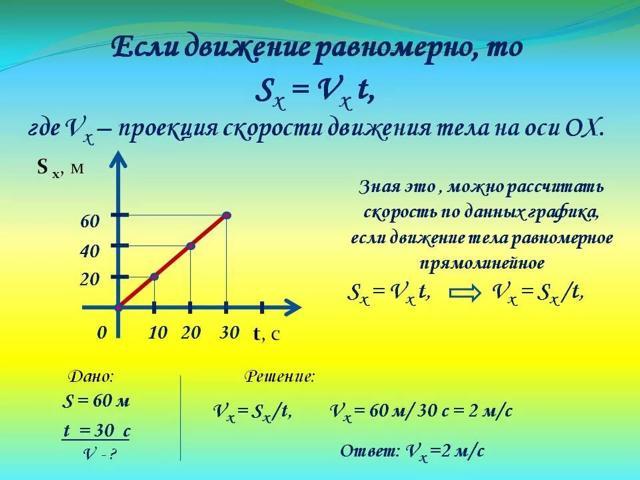
Так как при прямолинейном движении пройденный телом путь равен значению модуля вектора перемещения, мы можем сказать, что скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела ко времени, за которое это перемещение произошло. При равномерном прямолинейном движении векторы скорости и перемещения направлены в одну сторону. Зная скорость равномерного движения, можно найти перемещение тела за любой промежуток времени:
Поскольку скорость υ является векторной величиной, её тоже можно изобразить графически. Обозначим её проекцию на координатную ось υx. Если направление координатной оси совпадает с направлением движения тела, то для расчёта перемещения тела можно использовать формулу
УРАВНЕНИЕ ДВИЖЕНИЯ
Уравнение зависимости координаты тела от времени называют уравнением движения.
Пусть тело совершило перемещение s. Направим координатную ось X по направлению перемещения тела. Обозначим начальную координату тела х0, а конечную координату тела х. Тогда по формуле (1) sx = х – х0.
Но по формуле (3) sx = υxt. Следовательно,
Таким образом, координату тела при равномерном прямолинейном движении в любой момент времени можно определить, если известны его начальная координата и проекция скорости движения на ось X.
Ранее при решении задач мы использовали формулу s = υt без стрелочек. Почему? Символом s здесь обозначался путь, пройденный телом, а символом и — модуль скорости. Теперь нам известно, что при равномерном прямолинейном движении путь равен модулю перемещения. Поэтому если нас не интересует направление движения тела, а необходимо только найти его путь, то эта формула поможет нам найти решение.
Вы смотрели Конспект по физике для 8 класса «Перемещение и описание движения».
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров: 12 337
§ 5. ПРОЕКЦИИ ВЕКТОРА НА КООРДИНАТНЫЕ ОСИ. ДЕЙСТВИЯ НАД ПРОЕКЦИЯМИ. Вопросы
1. Что называют проекцией вектора на координатную ось?
1. Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.
2. Как связан вектор перемещения тела с его координатами?
2. Проекции вектора перемещения s на оси координат равны изменению соответствующих координат тела.
3. Если координата точки с течением времени увеличивается, то какой знак имеет проекция вектора перемещения на координатную ось? А если она уменьшается?
3. Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени будет уменьшаться, то проекция вектора перемещения на координатную ось будет отрицательной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора против направляющей самой оси.
4. Если вектор перемещения параллелен оси X, то чему равен модуль проекции вектора на эту ось? А модуль проекции этого же вектора на ось У?
4. Если вектор перемещения параллелен оси Х, то модуль проекции вектора на эту ось равен модулю самого вектора, а его проекция на ось Y равна нулю.
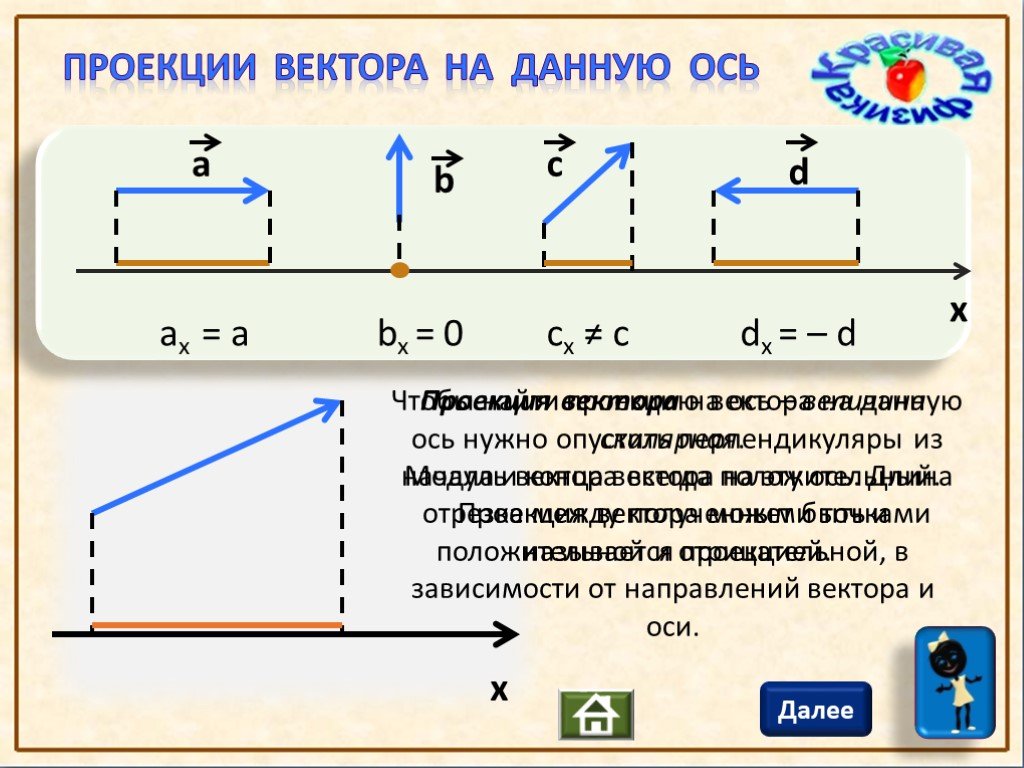
5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 22. Как при этих перемещениях изменяются координаты тела?
5. Во всех нижеследующих случаях координата Y тела не изменяется, а координата Х тела будет изменяться следующим образом:
a) s1;
проекция вектора s1, на ось Х отрицательна и по модулю равна длине вектора s1 . При таком перемещении координата Х тела уменьшится на длину вектора s1.
При таком перемещении координата Х тела уменьшится на длину вектора s1.
b) s2;
проекция вектора s2 на ось X положительна и равна по модулю длине вектора s1 . При таком перемещении координата Х тела увеличится на длину вектора s2 .
c) s3;
проекция вектора s3 на ось Х отрицательна и равна по модулю длине вектора s3. При таком перемещении координата Х тела уменьшится на длину вектора s3.
d) s4;
проекция вектора s4 на ось X положительна и равна по модулю длине вектора s4 . При таком перемещении координата Х тела увеличится на длину вектора s4.
e) s5;
проекция вектора s5 на ось Х отрицательна и равна по модулю длине вектора s5. При таком перемещении координата Х тела уменьшится на длину вектора s5 .
6. Если значение пройденного пути велико, то может ли модуль перемещения быть малым?
6. Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
7. Почему в механике более важен вектор перемещения тела, чем пройденный им путь?
7. Основной задачей механики является определение положения тела в любой момент времени. Зная вектор перемещения тела мы можем определить координаты тела, т.е. положение тела в любой момент времени, а зная только пройденный путь мы не можем определить координаты тела, т.к. мы не имеем сведений о направлении движения, а можем только судить о длине пройденного пути на данный момент времени.
Источник:
Решебник
по
физике
за 9 класс (И. К.Кикоин, А.К.Кикоин, 1999 год),
К.Кикоин, А.К.Кикоин, 1999 год),
задача №5
к главе «ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О ДВИЖЕНИИ».
Все задачи
§ 5. ПРОЕКЦИИ ВЕКТОРА НА КООРДИНАТНЫЕ ОСИ. ДЕЙСТВИЯ НАД ПРОЕКЦИЯМИ. Задание →
Положение и смещение
Положение и смещениеМногие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей. которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением этих объектов универсальны, т.е. все объекты движутся по одним и тем же правилам, и одна из целей этого класса состоит в том, чтобы понять эти правила.
Когда объект движется, его позиция изменяется как функция времени.
 Мы также должны указать направление . Расстояние скаляр количество, это число, данное в каких-то единицах . Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает. Единичный вектор
Мы также должны указать направление . Расстояние скаляр количество, это число, данное в каких-то единицах . Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает. Единичный вектор Ссылки:
Скаляры и векторы
(Пожалуйста, изучите!)
Направление вектора
Позиция
Удобный способ указать позицию
объекта
с помощью системы координат . Мы выбираем фиксированную точку, называемую
Мы выбираем фиксированную точку, называемую
Координаты точки P являются компонентами вектора положения. Единичный вектор указание в направлении x имеет x-компоненту 1 и y- и z-компоненты нуль. Обозначается цифрой

Компоненты любого вектора в сумме образуют
сам вектор.
Вектор положения точки P с координатами (a, b, c)
может быть записано с точки зрения его компонентов как
р = а и + б к
Величина вектора положения равна его длине r. Это зависит от выбора начала системы координат. Это — прямолинейное расстояние P от начала координат.
Ниже приведено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на изображении!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
Чтобы получить наилучший вид, измените окно просмотра, перетащив мышь и
увеличить или уменьшить масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления векторов компонентов.
Пример:
Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат.
Рабочий объем
Изменение положения называется смещением . На приведенной ниже диаграмме показано позиции P 1 и P 2 игрока в два разных момента времени.
Стрелка, указывающая от P 1 к P 2 , является вектор смещения .
Его величина — прямая линия
Компоненты смещения
вектор из P 1 по
P 2 (x 2 — x 1 ) вдоль оси x, (y 2 —
y 1 ) по оси Y.
Вектор смещения d от P 1 до P 2 может
можно записать как d = (x 2 — x 1 ) i + (y 2 -у 1 ) у .
Водоизмещение d составляет (x 2 — x 1 ) единиц в
направление x плюс (y 2
Величина смещения d = ((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 ) ½ . Этот следует из пифагорейский теорема.
Расстояние между двумя точками P 1 с координатами (х 1 ,
у 1 ,
z 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) равно
d =
((х 2 — х 1 ) 2 + (у 2 — у 1 ) 2 + (z 2 — z1)
- Расстояние d является величиной вектора смещения д .
- Направление вектора смещения d – направленный отрезок прямой от P 1 к Р 2 .

- Мы называем этот направленный отрезок геометрической или графической представление вектора d .
- Мы рисуем стрелку на P 2 , чтобы указать что сегмент линии начинается с P 1 и заканчивается на P 2 .
Тройка действительных чисел d x = (x 2 — x 1 ), d y = (y 2 — y 1 ), d z = (z 2 — z 1 ) называются декартовыми компонентами d .
Ссылка: Расстояние и смещение (Пожалуйста, изучите!)
Проблема:
Футбольный защитник пробегает 15,0 м.
прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.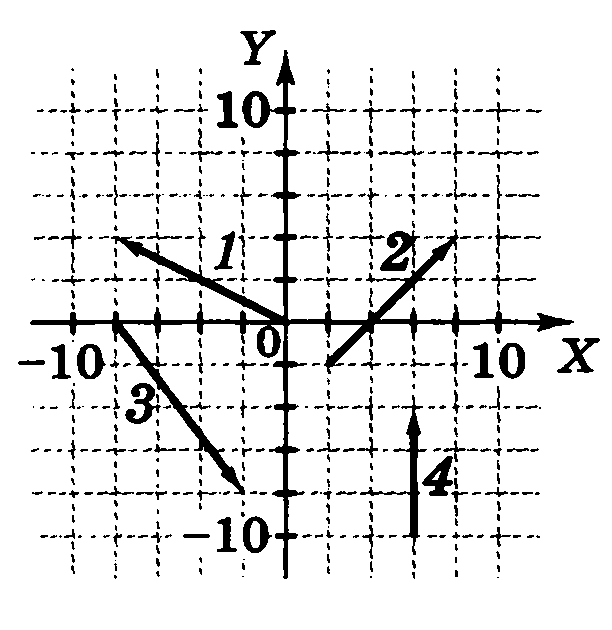 Вычислите его вектор смещения и
общее пройденное расстояние.
Вычислите его вектор смещения и
общее пройденное расстояние.
Решение:
Проблема:
Во время движения по прямому межгосударственному шоссе вы обратите внимание, что на отметке 260 миль. отметку, а затем вернитесь к отметке 175 миль. Что величина вашего результирующего смещения от 260-мильной отметки?
Решение:
- Обоснование:
Результирующее смещение представляет собой вектор d , сумму двух векторов д 1 и d 2 , которые указывают в противоположных направлениях. - Детали расчета:
Сумма двух векторов смещения равна d = d 1 + д 1 = (-110 м) + 25 м = -85 м.
Также можно рассуждать следующим образом.
Для полного водоизмещения важно только то, где вы начинаете и где вы останавливаться.
d = позиция 2 — позиция 1 = 175 м — 260 м = -85 м.
Проблема:
Кончик лопасти вертолета 5,00 м от центра вращения. За один оборот лезвия вычислить вектор смещения и общее расстояние, пройденное наконечником лезвия.
Решение:
- Обоснование:
После одного оборота наконечник возвращается в исходное положение. Вектор его смещения d = 0. - Детали расчета:
Общее пройденное расстояние кончик равен окружности окружности радиусом r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное вершина 31,42 м.
Вектор смещения имеет одинаковую величину и направление независимо от выбор начала координат системы координат. Величина и направление
вектор смещения, однако, зависит от системы отсчета , в которой
система координат закреплена и находится в состоянии покоя.
Пример:
Автомобиль двинулся вперед расстояние 6 м, пока ребенок переместился с заднего сиденья на переднее сидеть на расстоянии 1 м.
- Использование автомобиля в качестве системы отсчета и привязка системы координат в машине водоизмещение ребенка d (автомобиль) = (1 м) i .
- Использование дороги в качестве системы отсчета и привязка системы координат на дороге перемещение ребенка d (дорога) = (6 м) i + (1 м) i = (7 м) i .
3.4: Системы координат и компоненты вектора (Часть 1)
Цели обучения
- Описывать вектора в двух и трех измерениях с точки зрения их компонентов, используя единичные векторы вдоль осей.
- Различать векторные компоненты вектора и скалярные компоненты вектора.
- Объясните, как величина вектора определяется через компоненты вектора.

- Определите угол направления вектора на плоскости.
- Объясните связь между полярными координатами и декартовыми координатами на плоскости.
Векторы обычно описываются с точки зрения их компонентов в системе координат. Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь направление к определенному месту, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37° к северу от востока.
В прямоугольной (декартовой) системе координат xy на плоскости точка на плоскости описывается парой координат (x, y). Аналогичным образом вектор \(\vec{A}\) на плоскости описывается парой своих векторных координат. Координата x вектора \(\vec{A}\) называется его x-компонентой, а y-координата вектора \(\vec{A}\) называется его y-компонентой. Компонента x вектора — это вектор, обозначаемый \(\vec{A}_{x}\). Компонента вектора y — это вектор, обозначаемый \(\vec{A}_{y}\).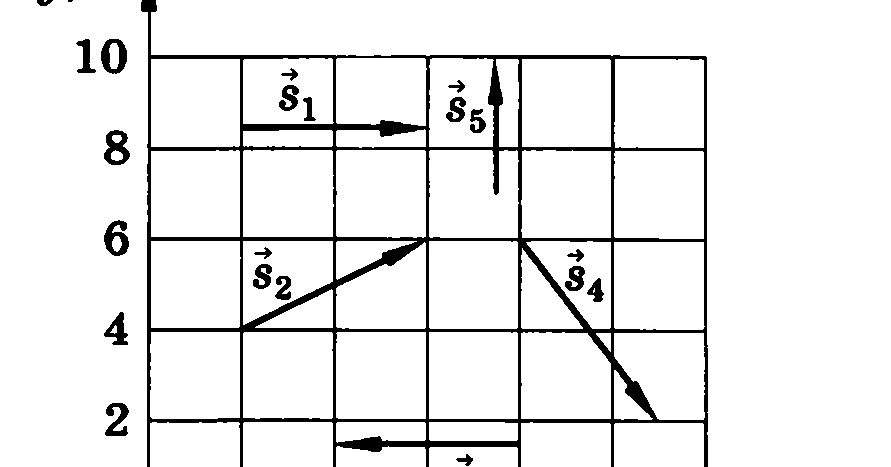 В декартовой системе x и y компоненты вектора вектора являются ортогональными проекциями этого вектора на оси \(х\) и \(у\) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонент:
В декартовой системе x и y компоненты вектора вектора являются ортогональными проекциями этого вектора на оси \(х\) и \(у\) соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонент:
\[ \vec{A} = \vec{A}_{x} + \vec{A}_{y} \ldotp \label{2.10}\]
Как показано на рисунке \(\PageIndex{1}\), вектор \(\vec{A}\) является диагональю прямоугольника где x-компонента \(\vec{A}_{x}\) — это сторона, параллельная оси x, а y-компонента \(\vec{A}_{y}\) — это сторона, параллельная ось Y. Компонента вектора \(\vec{A}_{x}\) ортогональна компоненте вектора \(\vec{A}_{y}\).
Рисунок \(\PageIndex{1}\): Вектор \(\vec{A}\) на плоскости в декартовой системе координат представляет собой векторную сумму своих векторных x- и y-компонент. Компонента x-вектора \(\vec{A}_{x}\) является ортогональной проекцией вектора \(\vec{A}\) на ось x. Компонента вектора y \(\vec{A}_{y}\) является ортогональной проекцией вектора \(\vec{A}\) на ось y. Числа A x и A y , на которые умножаются единичные векторы, являются скалярными компонентами вектора.
Числа A x и A y , на которые умножаются единичные векторы, являются скалярными компонентами вектора.Обычно принято обозначать положительное направление по оси x единичным вектором \(\hat{i}\), а положительное направление по оси y — единичным вектором \(\hat{j}\). Единичные векторы осей \(\hat{i}\) и \(\hat{j}\) определяют два ортогональных направления на плоскости. Как показано на рисунке \(\PageIndex{1}\), компоненты вектора x и y теперь могут быть записаны в терминах единичных векторов осей:
\[ \begin{case} \vec{A}_{x} = A_{x} \hat{i} \\ \vec{A}_{y} = A_{y} \hat{j} \ end{cases} \label{2.11}\]
Векторы \(\vec{A}_{x}\) и \(\vec{A}_{y}\), определяемые уравнением 2.11, являются компонентами вектора вектора \(\vec{A}\). Числа A x и A y , которые определяют компоненты вектора в уравнении \ref{2.11}, являются скалярными компонентами вектора \(\vec{A}\). Комбинируя уравнение \ref{2.10} с уравнением \ref{2. 11}, мы получаем компонентную форму вектора :
11}, мы получаем компонентную форму вектора :
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} \ldotp \label{2.12}\]
Если мы знаем координаты \(b (x_b, y_b)\) исходной точки вектора (где b означает «начало») и координаты e(x e , y e ) конечной точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:
\[ \begin{cases} A_{x} = x_{e} — x_{b} \\ A_{y} = y_{e} — y_{b} \ldotp \end{cases} \label{2.13}\]
Пример \(\PageIndex{1}\): смещение указателя мыши
Указатель мыши на мониторе компьютера в исходном положении находится в точке (6,0 см, 1,6 см) относительно левого нижнего -боковой угол. Если вы переместите указатель на значок, расположенный в точке (2,0 см, 4,5 см), каков будет вектор смещения указателя?
Стратегия
Начало системы координат xy — нижний левый угол монитора компьютера.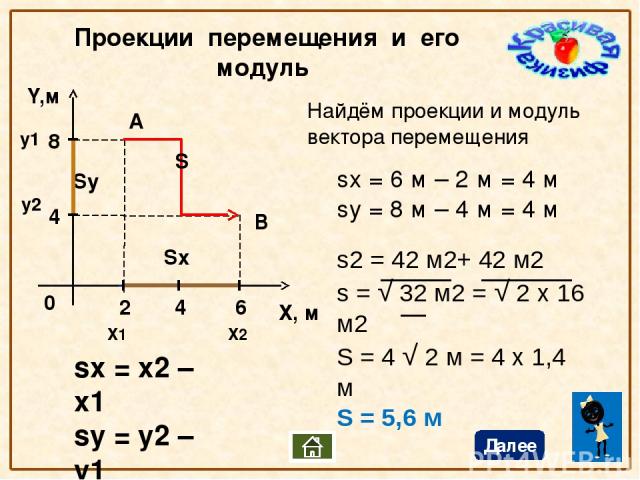 Таким образом, единичный вектор \(\hat{i}\) на оси x указывает горизонтально вправо, а единичный вектор \(\hat{j}\) на оси y указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2.0, 4.5). Подставьте координаты этих точек в уравнение \ref{2.13}, чтобы найти скалярные компоненты D x и D y вектора смещения \(\vec{D}\). Наконец, подставьте координаты в уравнение \ref{2.12}, чтобы записать вектор смещения в форме компонента вектора.
Таким образом, единичный вектор \(\hat{i}\) на оси x указывает горизонтально вправо, а единичный вектор \(\hat{j}\) на оси y указывает вертикально вверх. Начало вектора смещения расположено в точке b(6.0, 1.6), а конец вектора смещения расположен в точке e(2.0, 4.5). Подставьте координаты этих точек в уравнение \ref{2.13}, чтобы найти скалярные компоненты D x и D y вектора смещения \(\vec{D}\). Наконец, подставьте координаты в уравнение \ref{2.12}, чтобы записать вектор смещения в форме компонента вектора.
Решение
Отождествляем x b = 6,0, x e = 2,0, y b = 1,6 и y e = 4,5, где физическая единица равна 1 см. Скалярные x- и y-компоненты вектора смещения равны
\[D_{x} = x_{e} — x_{b} = (2,0 — 6,0)\; см = -4,0\; см,\]
\[D_{y} = y_{e} — y_{b} = (4,5 — 1,6)\; см = + 2,9\; см \ldotp\]
Форма векторной компоненты вектора смещения:
\[\vec{D} = D_{x}\; \шляпа{я} + D_{у}\; \шляпа{j} = (-4,0\; см)\; \шляпа{i} + (2,9\; см)\; \шляпа{j} = (-4.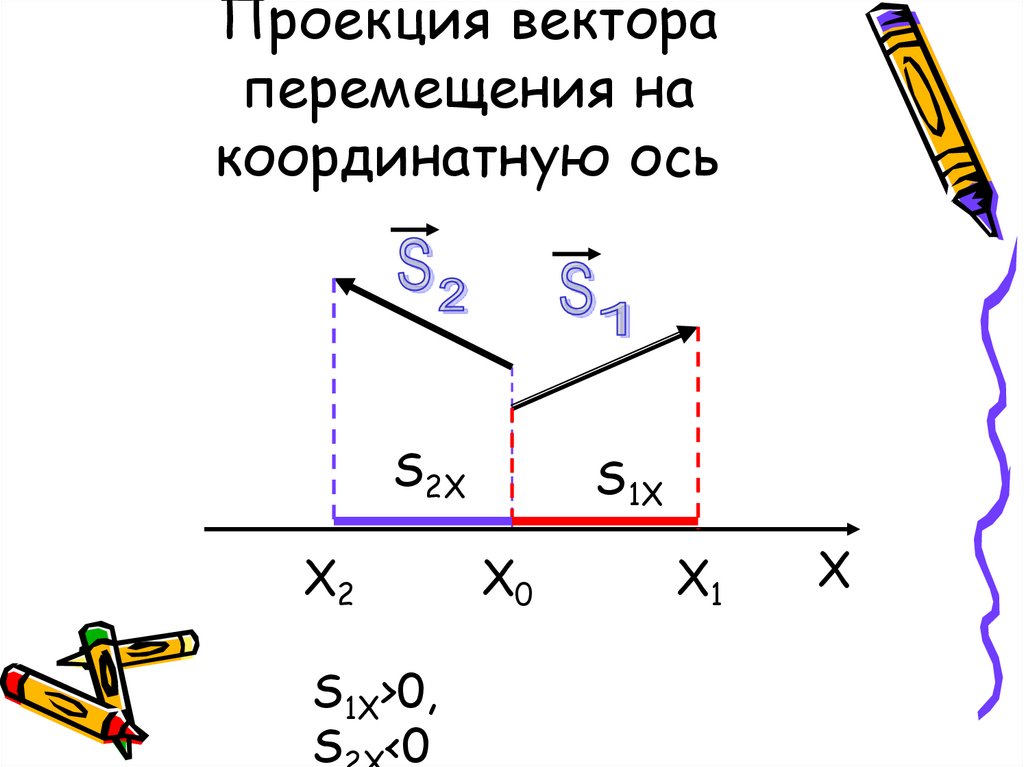 0\; \шляпа{i} + 2.9\; \шляпа{j})\; cm \ldotp \label{2.14}\]
0\; \шляпа{i} + 2.9\; \шляпа{j})\; cm \ldotp \label{2.14}\]
Это решение показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): График вектора смещения. Вектор указывает от начальной точки \(b\) до конечной точки \(e\).Значение
Обратите внимание, что физическая единица — здесь 1 см — может быть помещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении \ref{2.14}. Часто последний способ удобнее, потому что он проще.
Компонента вектора x \(\vec{D}_{x}\) = −4,0 \(\hat{i}\) = 4,0(\(- \hat{i}\)) вектора смещения имеет величину |\(\vec{D}_{x}\)| = |− 4,0||\(\шляпа{i}\)| = 4,0, потому что модуль единичного вектора равен |\(\hat{i}\)| = 1. Обратите внимание также, что направление x-компоненты равно \(− \hat{i}\), что антипараллельно направлению +x-оси; следовательно, вектор x-компоненты \(\vec{D}_{x}\) указывает налево, как показано на рисунке \(\PageIndex{2}\). Скалярная x-компонента вектора \(\vec{D}\) равна D х = -4,0. Аналогично, векторная y-компонента \(\vec{D}_{y}\) = \(+ 2,9 \hat{j}\) вектора смещения имеет величину |\(\vec{D}_{y} \)| = |2.9||\(\шляпа{j}\)| = 2,9, потому что модуль единичного вектора равен |\(\hat{j}\)| = 1. Направление компонента y равно \(+ \hat{j}\), которое параллельно направлению оси +y. Следовательно, вектор y-компоненты \(\vec{D}_{y}\) направлен вверх, как показано на рисунке \(\PageIndex{2}\). Скалярная y-компонента вектора \(\vec{D}\) равна D y = + 2,9. Вектор смещения \(\vec{D}\) является равнодействующей двух его компонент вектора.
Скалярная x-компонента вектора \(\vec{D}\) равна D х = -4,0. Аналогично, векторная y-компонента \(\vec{D}_{y}\) = \(+ 2,9 \hat{j}\) вектора смещения имеет величину |\(\vec{D}_{y} \)| = |2.9||\(\шляпа{j}\)| = 2,9, потому что модуль единичного вектора равен |\(\hat{j}\)| = 1. Направление компонента y равно \(+ \hat{j}\), которое параллельно направлению оси +y. Следовательно, вектор y-компоненты \(\vec{D}_{y}\) направлен вверх, как показано на рисунке \(\PageIndex{2}\). Скалярная y-компонента вектора \(\vec{D}\) равна D y = + 2,9. Вектор смещения \(\vec{D}\) является равнодействующей двух его компонент вектора.
Форма векторной составляющей вектора смещения Уравнение \ref{2.14} говорит нам, что указатель мыши переместился на мониторе на 4,0 см влево и на 2,9 см вверх от своего начального положения.
Упражнение 2.4
Синяя муха садится на лист миллиметровой бумаги в точку, расположенную на 10,0 см правее его левого края и на 8,0 см выше его нижнего края, и медленно движется к точке, расположенной на расстоянии 5,0 см от левого края и 5,0 см от нижнего края.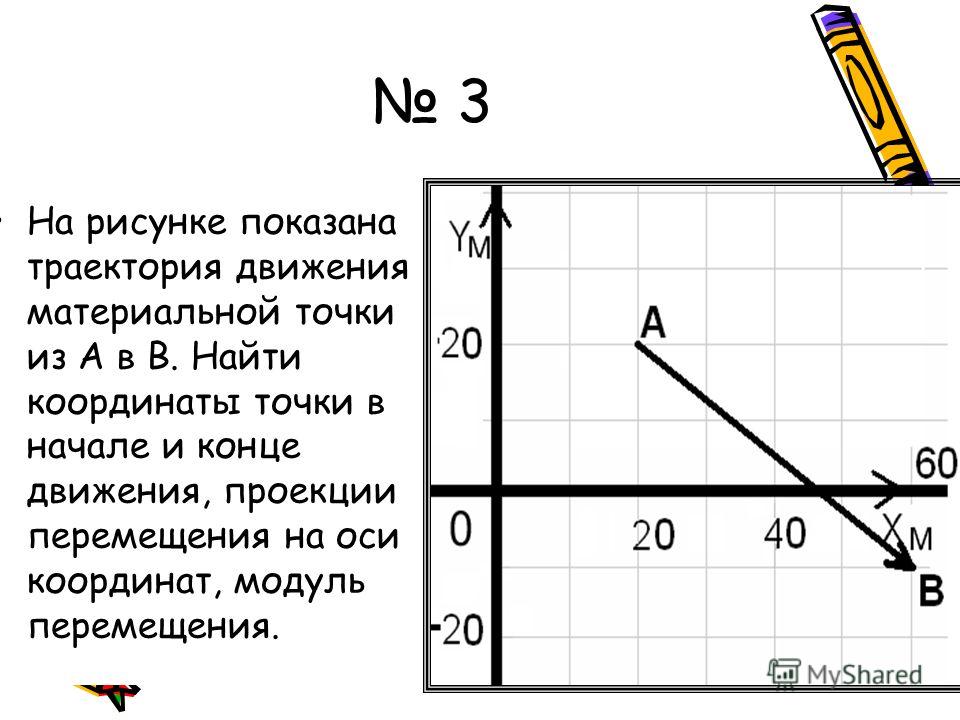 Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Зная скалярные компоненты A x и A y вектора \(\vec{A}\), мы можем найти его величину A и направляющий угол \(\theta_{A}\). Угол направления — или, для краткости, направление — это угол, который образует вектор с положительным направлением на оси x. Угол \(\theta_{A}\) измеряется против часовой стрелки от оси +x к вектору (рисунок \(\PageIndex{3}\)). Поскольку длины A, A x и A y образуют прямоугольный треугольник, они связаны по теореме Пифагора: 9{-1} \left(\dfrac{A_{y}}{A_{x}}\right) \ldotp \label{2.16}\]
Рисунок \(\PageIndex{3}\): Для вектора \(\ vec{A}\), его величина A и его направляющий угол \(\theta_{A}\) связаны с величинами его скалярных компонентов, потому что A, A x и A y образуют прямоугольный треугольник. Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент A x положителен (рисунок \(\PageIndex{4}\)), угол \(\theta\) в уравнении \ref{ 2.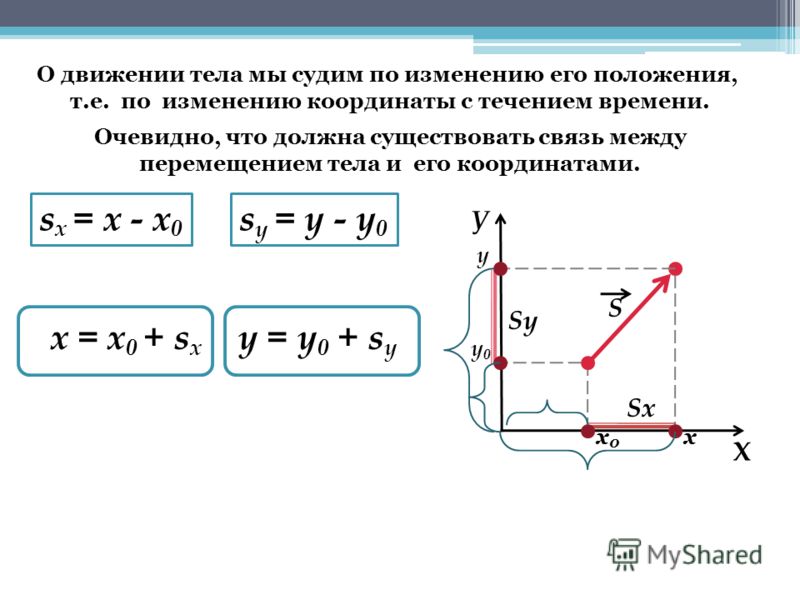 16}) идентичен дирекционному углу \(\theta_{A}\). Для векторов в четвертом квадранте угол \(\theta\) отрицателен, что означает, что для этих векторов направляющий угол \(\theta_{A}\) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \(\theta\) отрицателен. Когда вектор лежит либо во втором, либо в третьем квадранте, где компонент A x — отрицательное значение, угол направления равен \(\theta_{A}\) = \(\theta\) + 180° (рис. \(\PageIndex{4}\)).
16}) идентичен дирекционному углу \(\theta_{A}\). Для векторов в четвертом квадранте угол \(\theta\) отрицателен, что означает, что для этих векторов направляющий угол \(\theta_{A}\) измеряется по часовой стрелке от положительной оси x. Точно так же для векторов во втором квадранте угол \(\theta\) отрицателен. Когда вектор лежит либо во втором, либо в третьем квадранте, где компонент A x — отрицательное значение, угол направления равен \(\theta_{A}\) = \(\theta\) + 180° (рис. \(\PageIndex{4}\)).
Пример \(\PageIndex{2}\): Величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см). Каковы величина и направление вектора смещения указателя?
Каковы величина и направление вектора смещения указателя?
Стратегия
В примере \(\PageIndex{1}\) мы нашли вектор смещения \(\vec{D}\) указателя мыши (см. уравнение \ref{2.14}). Мы идентифицируем его скалярные компоненты D x = -4,0 см и D y = + 2,9 см и подставляем в уравнение \ref{2.15} и уравнение \ref{2.16}, чтобы найти величину D и направление \(\theta_{ Д}\) соответственно. 9{o} \ldotp\]
Упражнение 2.5
Если вектор смещения синей мухи, идущей по листу миллиметровой бумаги, равен \(\vec{D} = (−5,00\; \hat{i} − 3,00\ ; \hat{j})\) см, найти его величину и направление.
Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте, что 400 автомобилей движутся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина дает мосту разные толчки в разных направлениях, и мы хотели бы знать, насколько большим может быть результирующий толчок. У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения равнодействующей путем рисования векторов и измерения их длин и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам. Подобного беспокойства не возникает, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе состоит в том, чтобы найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к прямоугольному треугольнику на рисунке \(\PageIndex{3}\). Отношение смежной стороны A x к гипотенузе A есть функция косинуса направляющего угла \(\theta_{A}\), A x /A = cos \(\theta_{A}\), и отношение противоположной стороны A y к гипотенузе A является синусоидальной функцией \(\theta_{A}\), A y /A = sin \(\theta_{A}\). Когда величина A и направление \(\theta_{A}\) известны, мы можем решить эти соотношения для скалярных компонент:
\[\begin{cases} A_{x} = A \cos \theta_{A} \\ A_{y} = A \sin \theta_{A} \ldotp \end{cases} \label{2. 17}\ ]
17}\ ]
При расчете компонентов вектора по уравнению \ref{2.17} необходимо соблюдать осторожность при выборе угла. Направленный угол \(\theta\) A вектора представляет собой угол, измеренный против часовой стрелки от положительного направления по оси x к вектору. Измерение по часовой стрелке дает отрицательный угол.
Пример \(\PageIndex{3}\): Компоненты векторов смещения
Группа спасения пропавшего ребенка следует за поисковой собакой по кличке Солдат. Десантник много бродит и делает много пробных обнюхиваний по разным тропам. Солдат в конце концов находит ребенка, и у истории счастливый конец, но его перемещения на разных ногах кажутся действительно запутанными. На одной из ног он проходит 200,0 м на юго-восток, затем бежит на север около 300,0 м. На третьем этапе он внимательно исследует запахи на протяжении 50,0 м в направлении 30° к западу от севера. На четвертом этапе Trooper идет прямо на юг на 80,0 м, улавливает свежий запах и поворачивает на 23° к западу от юга на 150,0 м. Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
Найдите скалярные компоненты векторов смещения Десантника и его векторов смещения в форме векторных компонент для каждой ноги.
Стратегия
Давайте примем прямоугольную систему координат с положительной осью x в направлении географического востока с положительным направлением y, указывающим на географический север. В явном виде единичный вектор \(\hat{i}\) оси x указывает на восток, а единичный вектор \(\hat{j}\) оси y указывает на север. Десантник делает пять ног, поэтому есть пять векторов смещения. Начнем с определения их величин и углов направления, затем воспользуемся уравнением \ref{2.17}, чтобы найти скалярные компоненты перемещений, и уравнением \ref{2.12} для векторов смещения.
Решение
На первом участке величина смещения L 1 = 200,0 м, направление юго-восточное. В качестве дирекционного угла \(\theta_{1}\) мы можем взять либо 45°, измеренные по часовой стрелке с востока, либо 45° + 270°, измеренные против часовой стрелки с востока.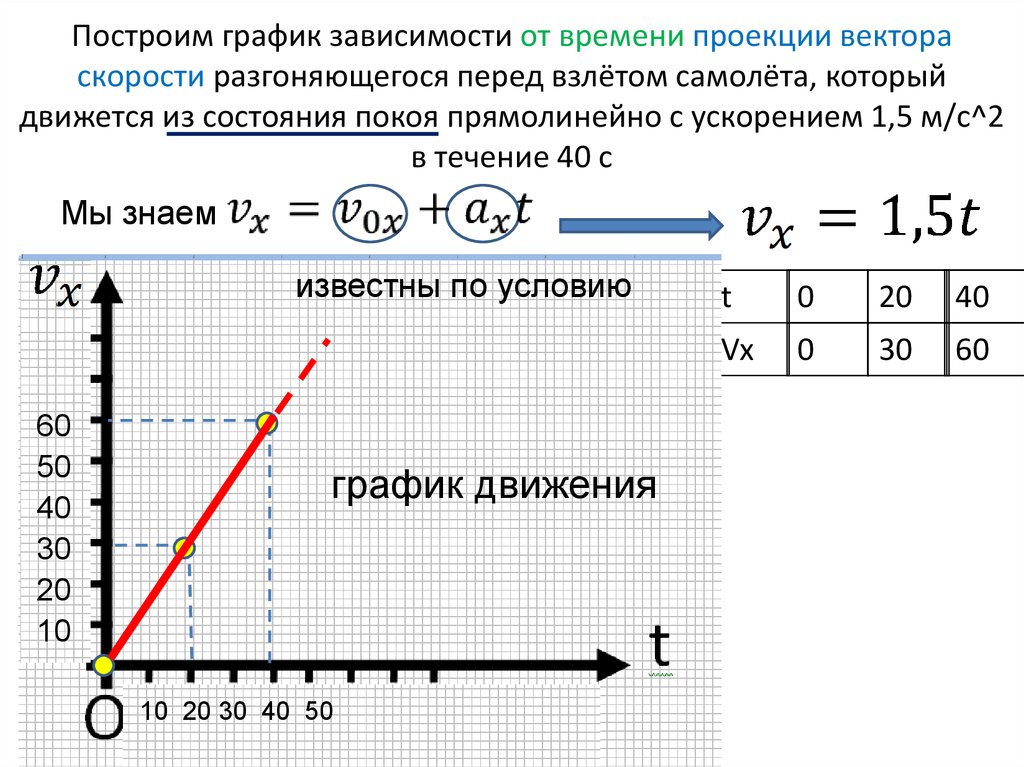

Leave A Comment