Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
| Формулы для радиуса окружности, вписанной в треугольник |
| Вывод формул для радиуса окружности, вписанной в треугольник |
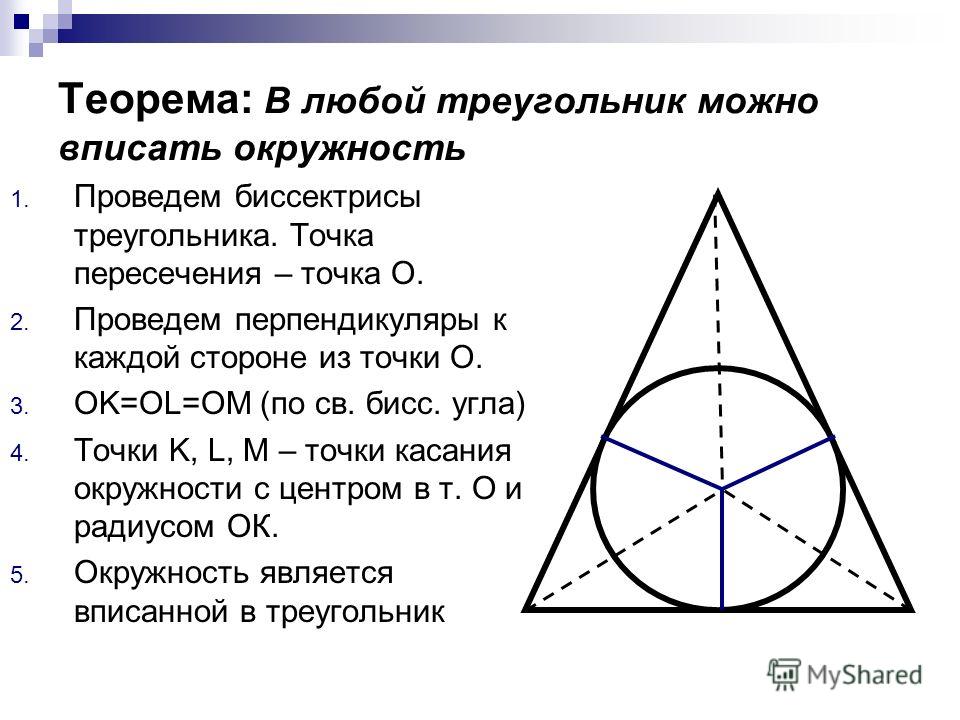
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис. 1).
1).
Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.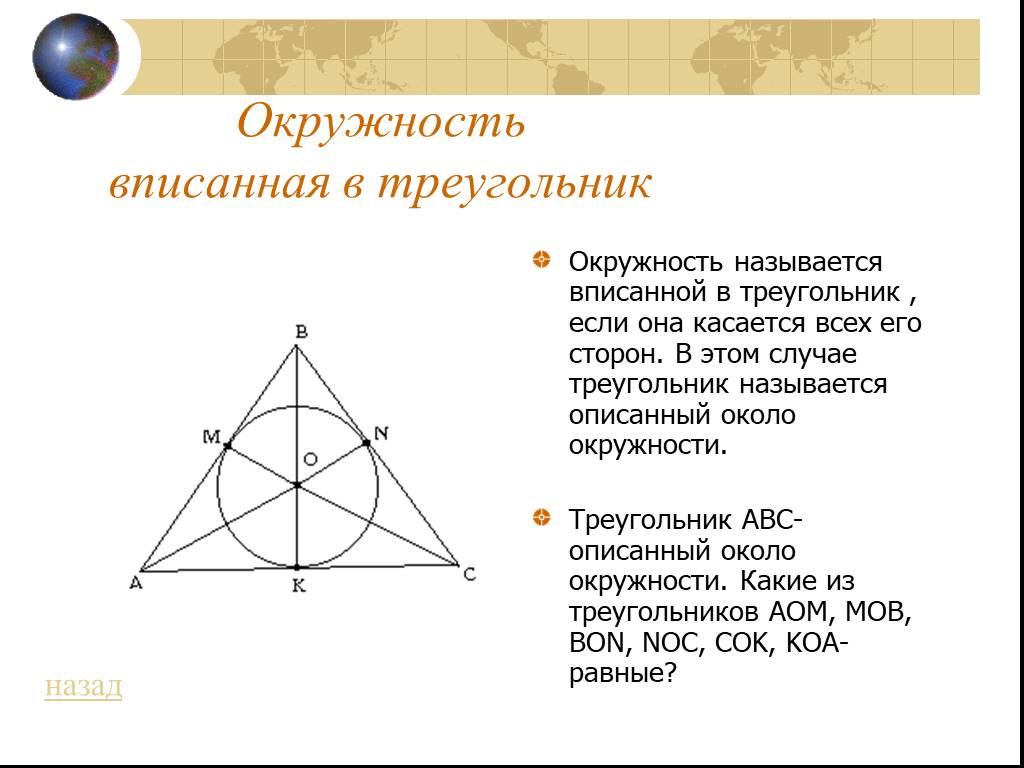
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).
Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.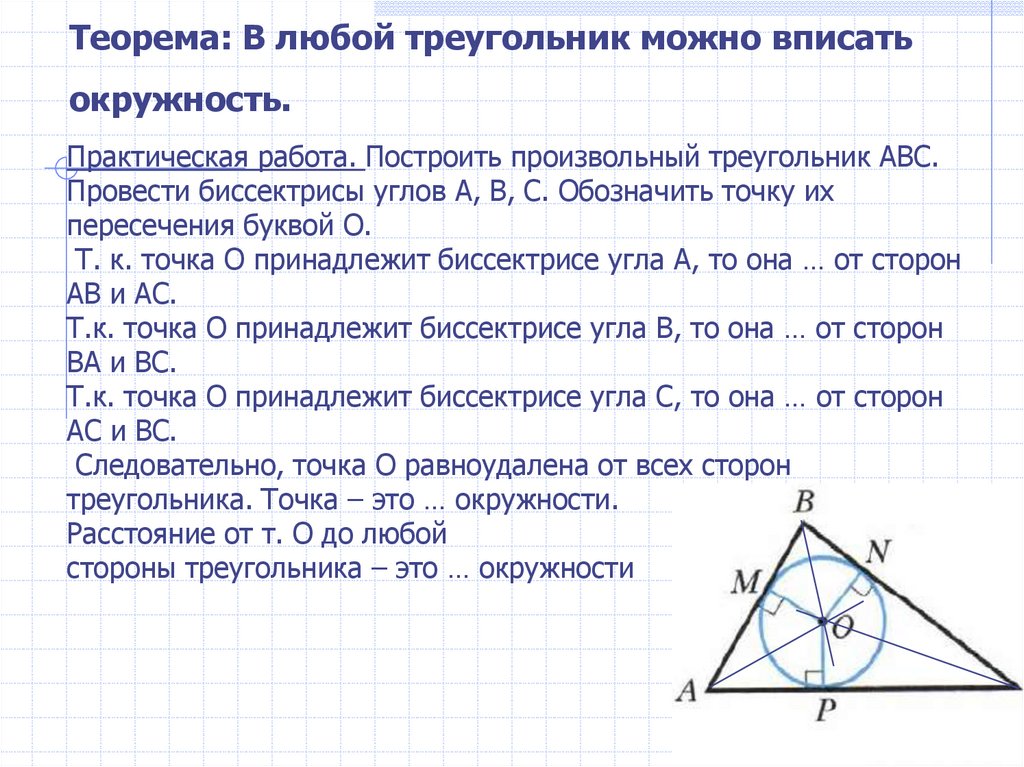
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).
Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
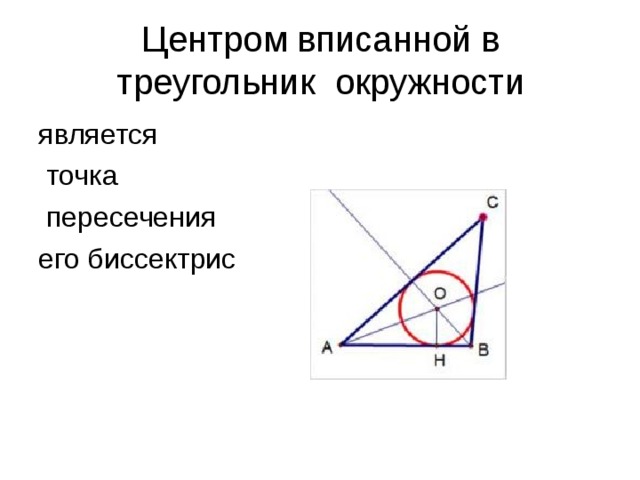
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.
Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник | Посмотреть вывод формулы | a, b, c – стороны треугольника, . | |
Посмотреть вывод формулы | |||
| Равнобедренный треугольник | Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, | |
| Равносторонний треугольник | Посмотреть вывод формулы | a – сторона равностороннего треугольника, | |
| Прямоугольный треугольник | Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
где Посмотреть вывод формулы | |
| Равносторонний треугольник | |
где Посмотреть вывод формулы | |
| Прямоугольный треугольник | |
где Посмотреть вывод формул | |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Равнобедренный треугольник |
где Посмотреть вывод формулы |
| Равносторонний треугольник |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
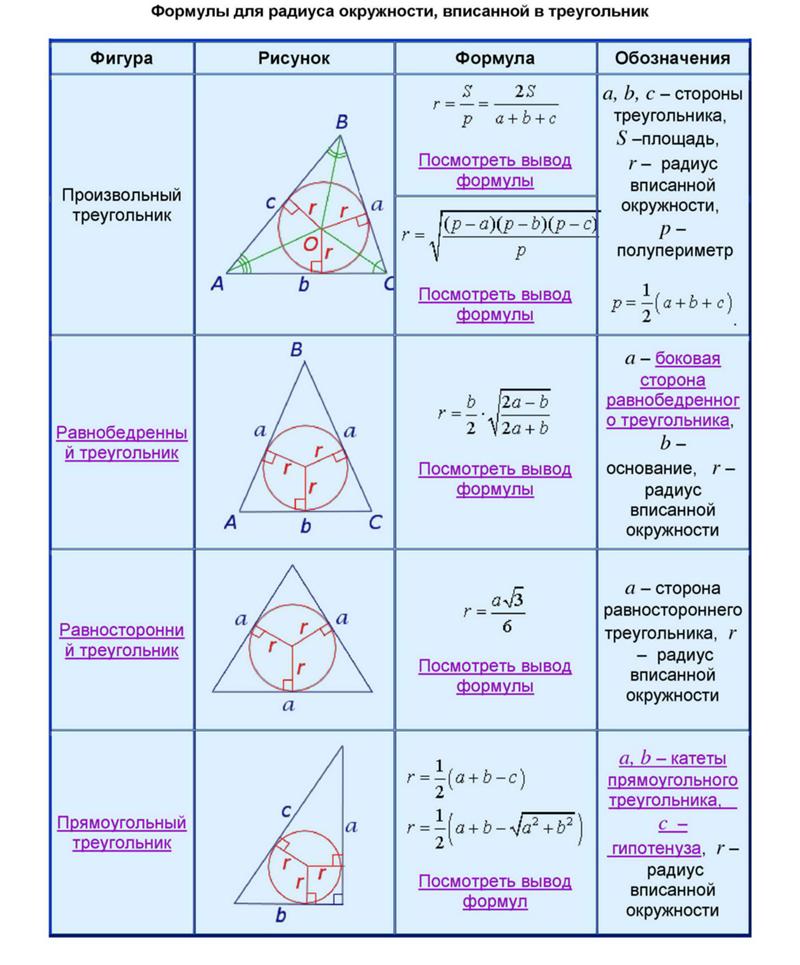
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).
Рис. 6
Доказательство. Из формулы
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
где
то, в случае равнобедренного треугольника, когда
получаем
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
то, в случае равностороннего треугольника, когда
b = a,
получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.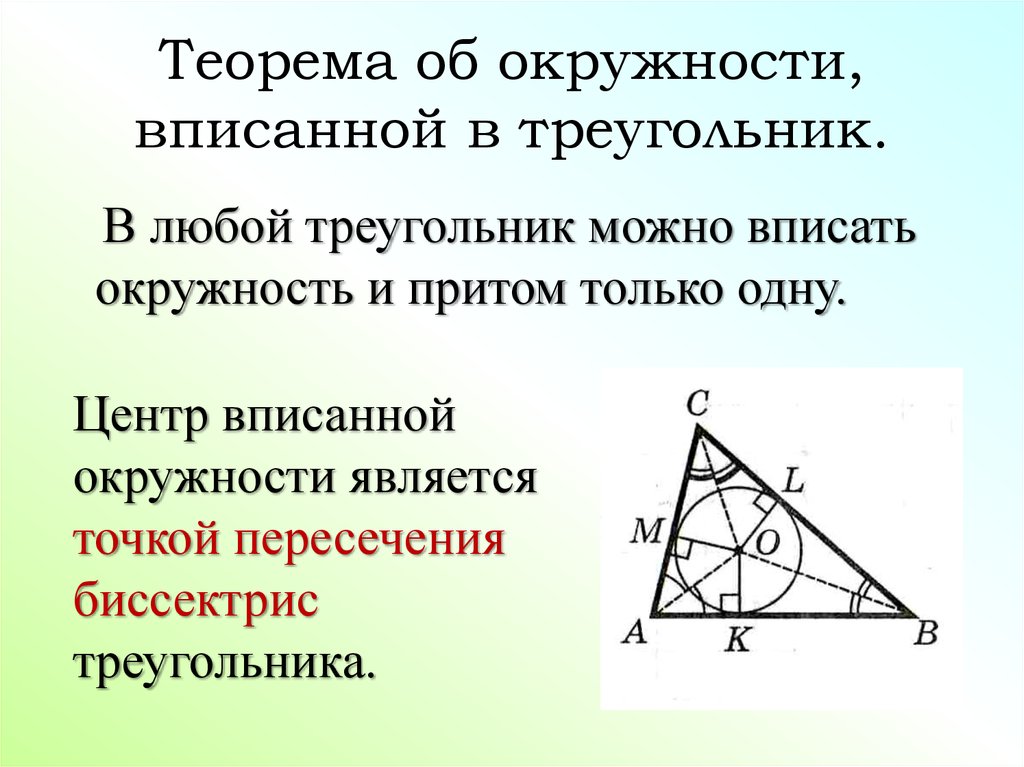
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Окружность, вписанная в правильный многоугольник 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Длина окружности и площадь круга
Урок: Окружность, вписанная в правильный многоугольник
1.
 Введение
Введение
Напомним определение: правильным многоугольником называется такой выпуклый многоугольник, у которого все стороны равны и все углы равны.
На Рис. 1 приведен фрагмент правильного многоугольника А1 … Аn.
Рис. 1.
Все стороны многоугольника равны между собой:
an = A1A2 = A2A3 = … = An-1An = AnA1.
Все углы фигуры также равны между собой, причем .
Вписанная окружность касается каждой стороны многоугольника, поэтому целесообразно напомнить, что называется касанием прямой и окружности.
Определение: прямая, имеющая только одну общую точку с окружностью, называется касательной к этой окружности, а их общая точка называется точкой касания прямой и окружности.
Рис. 2.
На Рис.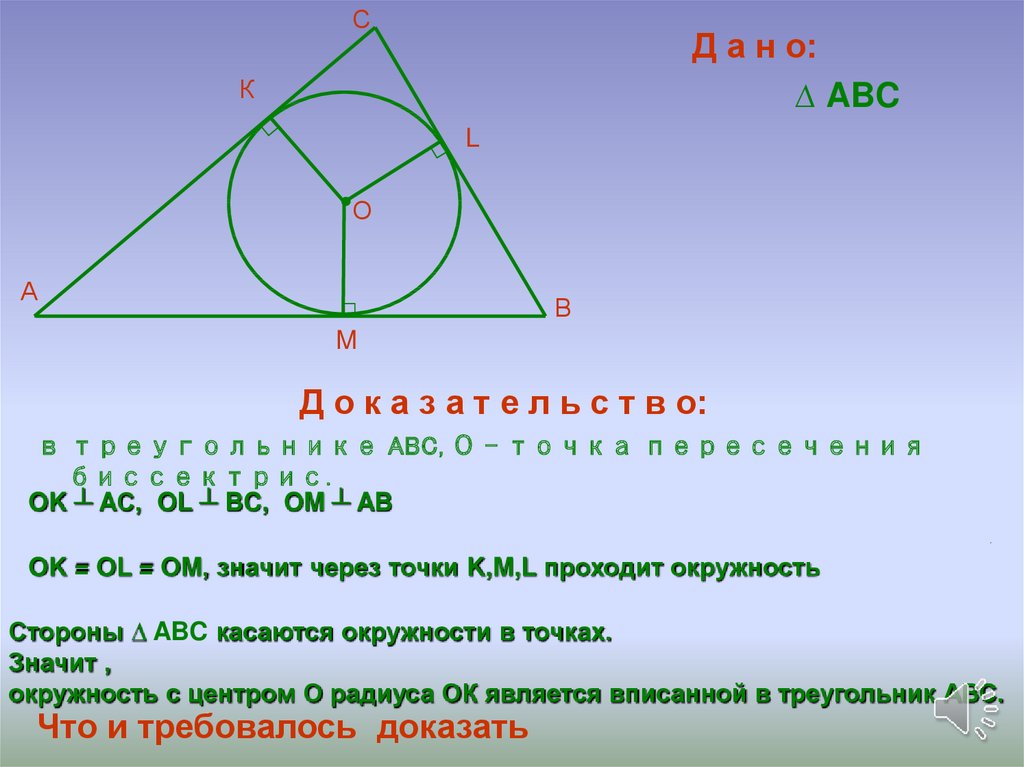 2 прямая m – касательная к окружности с центром в точке О. Точка А – точка касания.
2 прямая m – касательная к окружности с центром в точке О. Точка А – точка касания.
Единственность точки касания доказывается теоремой, утверждающей, что m – касательная к заданной окружности тогда и только тогда, когда радиус, проведенный в точку А, перпендикулярен этой прямой.
Теория вписанных окружностей базируется на фундаментальном свойстве биссектрисы угла.
Биссектриса угла есть геометрическое место точек, равноудаленных от сторон угла.
На Рис. 3 приведен ÐА и его биссектриса – луч АО (обозначена на Рис. 3 как l). Если точка О принадлежит биссектрисе, то она равноудалена от сторон угла, т. е. ОВ = ОС (перпендикуляры, опущенные из точки О на стороны угла есть расстояния от точки до сторон угла).
Обратное утверждение: если точка О равноудалена от сторон угла, то она лежит на биссектрисе. Доказывается это утверждение очень просто, если принять во внимание равенство прямоугольных треугольников АОВ и АОС: биссектриса у них общая и меньшие катеты равны.
Рис. 3.
Еще одно следствие равенства указанных треугольников: отрезки касательных, проведенных из одной точки к окружности, равны между собой (АВ = АС).
Теперь дадим определение вписанной в многоугольник окружности и приведем примеры.
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности.
Проиллюстрируем это определение на примере правильного треугольника АВС (Рис. 4).
Рис. 4.
Особенностью данного случая является тот факт, что серединные перпендикуляры, медианы, биссектрисы и высоты треугольника лежат на одних и тех же прямых, которые пересекаются в одной точке О. Эта точка является центром вписанной окружности. Точка О равноудалена от сторон любого из углов треугольника, т. к. одновременно принадлежит любой из указанных биссектрис, т.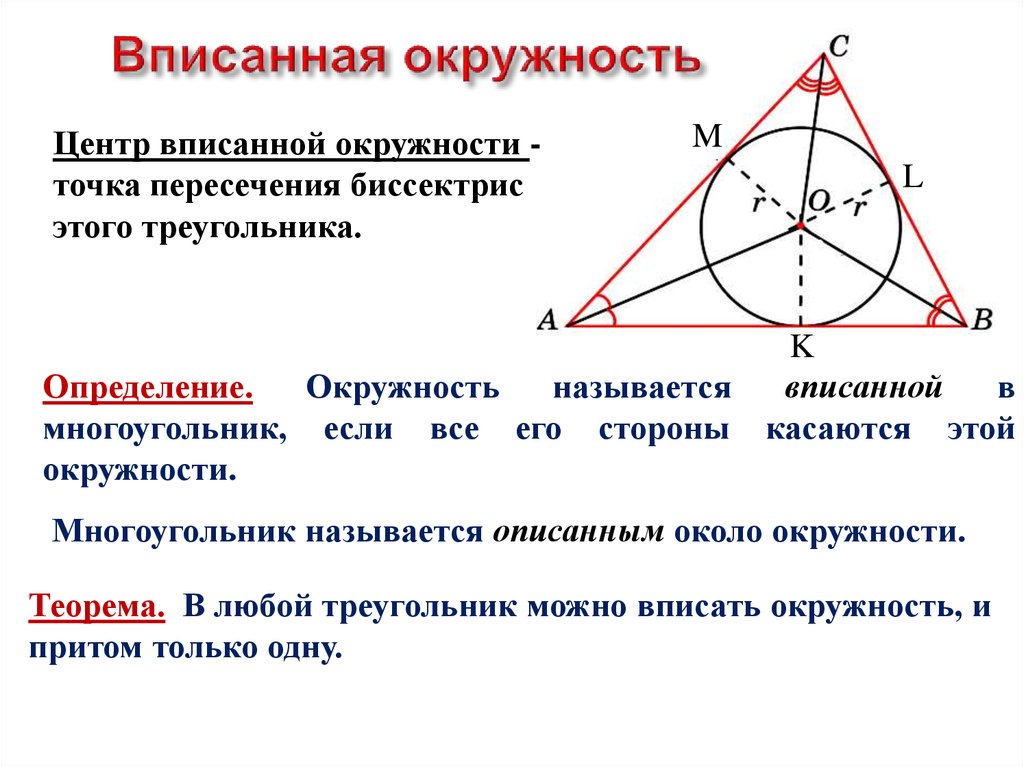 A4A5.
A4A5.
Рис. 7.
Перейдем к рассмотрению правильных многоугольников.
Следующее утверждение касается свойств биссектрис углов правильного многоугольника.
Биссектрисы соседних углов правильного многоугольника пересекаются.
Это утверждение уже было доказано нами ранее, но здесь мы кратко восстановим цепочку рассуждений, используемую при этом доказательстве.
Рассмотрим фрагмент правильного многоугольника, изображенный на Рис. 7.
Предположим, что биссектрисы l1 и l2 параллельны. Тогда по свойствам параллельных прямых, сумма внутренних односторонних улов равна 180°, то есть Þ α = 180° (все обозначения показаны на рисунках). Последнее равенство говорит о том, что смежные стороны многоугольника должны лежать на одной прямой, что противоречит условию. Значит, . Отсюда следует, что если соединить точку О с остальными вершинами многоугольника, то полученные отрезки также будут биссектрисами соответствующих углов (доказать это утверждение для следующей ближайшей вершины многоугольника можно, опираясь на равенство треугольников, например ∆ОA2A1 и ∆ОA2A3, по двум сторонам и углу между ними).
Рис. 7а.
Еще раз вернемся к свойствам точки О – точки пересечения биссектрис соседних углов правильного многоугольника.
Так как в точке О биссектрисы соседних углов пересекаются попарно, то можно утверждать, что все биссектрисы многоугольника пересекаются в этой точке, т. е. .
Основная теорема урока:
В любой правильный многоугольник можно вписать окружность, и притом только одну. На Рис. 8 дан фрагмент правильного многоугольника.
Рис. 8.
Доказательство.
1. Как было показано выше, существует точка О – точка пересечения всех биссектрис данного многоугольника.
2. Эта точка равноудалена от всех сторон многоугольника. Как мы помним, расстояние от точки до стороны – это длина перпендикуляра, опущенного из данной точки на данную сторону (перпендикуляры на Рис. 8 обозначены ОН1, ОН2, … ОНn). Если построить окружность радиуса ОН1 = ОН2 = … = ОНn = r с центром в точке О, то все стороны многоугольника будут касаться этой окружности (по свойствам касательной к окружности). Следовательно, в данный многоугольник можно вписать окружность.
Если построить окружность радиуса ОН1 = ОН2 = … = ОНn = r с центром в точке О, то все стороны многоугольника будут касаться этой окружности (по свойствам касательной к окружности). Следовательно, в данный многоугольник можно вписать окружность.
3. Поскольку точка О – единственная точка пересечения биссектрис, расстояние от этой точки до любой из сторон также единственно, то и вписанная в данный многоугольник окружность может быть только одна.
4. Можно привести и более подробное доказательство пункта 3, а именно: пусть существует и другая окружность, вписанная в данный многоугольник, центр ее будет располагаться в некоторой точке О1. Тогда этот центр будет равноудален от всех сторон окружности, то есть лежать на пересечении биссектрис, т. е. будет совпадать с точкой О. Раз центры окружностей (а вместе с ними и радиусы) совпадают, то и сами окружности совпадут.
Рассмотрим несколько следствий из доказанной теоремы.
Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.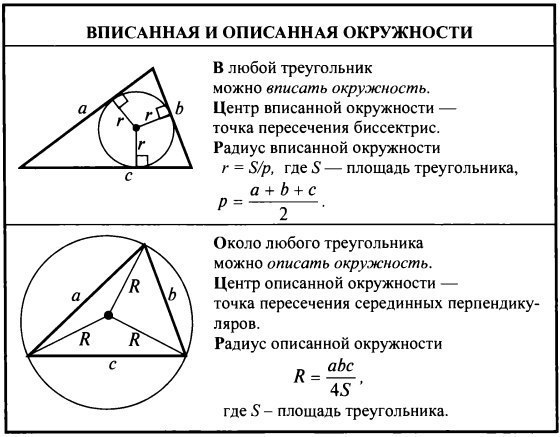 А1 А2, т. е. является высотой данного треугольника, а по свойствам равнобедренного треугольника – и его медианой, опущенной на основание. Следовательно, Н1 – середина стороны А1 А2.
А1 А2, т. е. является высотой данного треугольника, а по свойствам равнобедренного треугольника – и его медианой, опущенной на основание. Следовательно, Н1 – середина стороны А1 А2.
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в него. Эта точка называется центром правильного многоугольника.
Итак, в данном уроке мы рассмотрели окружность, вписанную в правильный многоугольник, доказали ее существование и единственность и вывели следствия из этого доказательства.
Список рекомендованной литературы
1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Рекомендованные ссылки на интернет-ресурсы
1. Uztest.ru (Источник).
Uztest.ru (Источник).
2. Средняя математическая интернет-школа (Источник).
Рекомендованное домашнее задание
1. Учебник Погорелова (см. список литературы), стр. 211, вопросы 9–11.
Вписанный треугольник | Brilliant Math & Science Wiki
Махиндра Джейн, Адитья Вирани, Кэлвин Лин, и
способствовал
Содержимое
- Краткое содержание
- Примеры проблем
Окружность вписана в треугольник, если все три стороны треугольника касаются окружности. В этой ситуации окружность называется вписанной окружностью , а ее центр называется внутренним центром или в центре .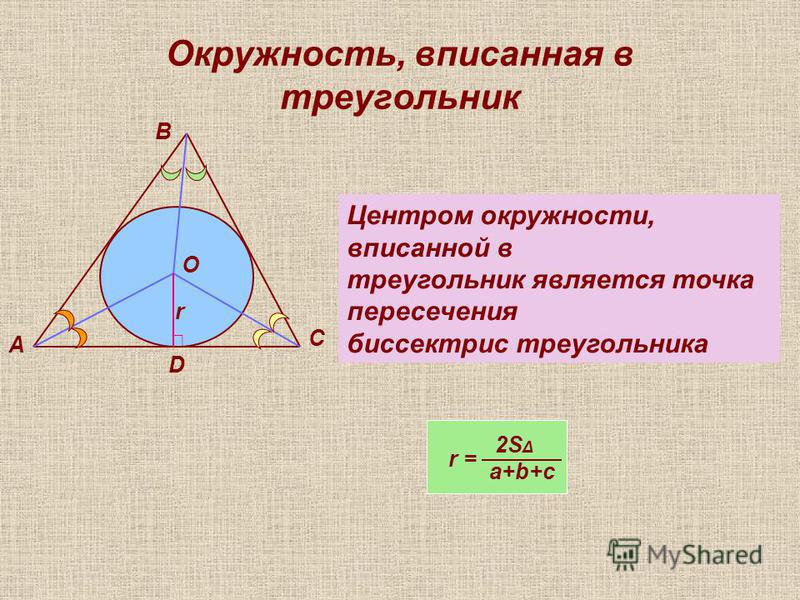
Imgur
Поскольку все три стороны треугольника касаются вписанной окружности, расстояния от центра окружности до трех сторон равны радиусу окружности. Таким образом, на диаграмме выше 9\circ,\) и \(\lvert\overline{OD}\rvert=\lvert\overline{OE}\rvert=r,\) находятся в RHS-конгруэнтности. Поэтому \(\угол OAD=\угол OAE.\) Используя тот же метод, мы также можем вывести \(\угол OBD=\угол OBF,\) и \(\угол OCE=\угол OCF.\)
Другой Важным свойством описанных треугольников является то, что мы можем представить площадь \(\треугольника ABC\) как сумму площадей треугольников \(\треугольник AOB,\) \(\треугольник BOC,\) и \(\треугольник COA.\) Поскольку каждый из трех треугольников имеет одну сторону \(\треугольник ABC\) в качестве основания и \(r\) в качестве высоты, площадь \(\треугольник ABC\) может быть выражена как
\[(\text{площадь }\треугольника ABC)=\frac{1}{2} \times r \times (\text{периметр треугольника}). \]
\]
В заключение, три основных свойства описанного треугольника следующие:
- Отрезки от центра вписанной стороны до каждой вершины делят каждый угол пополам.
- Расстояния от центра до каждой стороны равны радиусу вписанной окружности.
- Площадь треугольника равна \(\frac{1}{2}\times r\times(\text{периметр треугольника}),\), где \(r\) — радиус вписанной окружности.
На приведенной выше диаграмме окружность \(O\) радиуса 3 вписана в \(\треугольник ABC.\) Если периметр \(\треугольника ABC\) равен 30, какова площадь \(\треугольника ABC ?\)
Площадь описанного треугольника находится по формуле
\[\frac{1}{2} \times r \times (\text{периметр треугольника}),\]
, где \(r\) — радиус вписанной окружности. Поэтому ответ
\[\frac{1}{2} \times 3 \times 30 = 45. \ _\square \]
На приведенной выше диаграмме окружность \(O\) вписана в \(\треугольник ABC,\), где точками касания являются \(D, E\) и \(F.
\) Если \(\lvert\overline {AD}\rvert=2, \lvert\overline{CF}\rvert=4\) и \(\lvert\overline{BE}\rvert=3,\) каков периметр \(\треугольника ABC?\ ) Поскольку окружность вписана в \(\треугольник ABC,\), мы имеем
\[\lvert \overline{AD} \rvert = \lvert \overline{AF} \rvert,\quad \lvert \overline{BD} \rvert = \lvert \overline{BE} \rvert,\quad \lvert \ overline{CE} \rvert = \lvert \overline{CF} \rvert.\]
Следовательно, периметр \(\треугольника ABC\) равен
\[\begin{выравнивание} \left(\lvert \overline{AD} \rvert + \lvert \overline{AF} \rvert\right) + \left(\lvert \overline{BD} \rvert + \lvert \overline{BE} \rvert\right ) + \left(\lvert \overline{CE} \rvert + \lvert \overline{CF} \rvert\right) &= 2 \× 2 +2 \× 4 +2 \× 3 \\ &= 18. \ _\квадрат \конец{выравнивание}\]
На приведенной выше диаграмме точка \(O\) находится в центре \(\треугольника ABC.\), если \(\angle{BAO} = 35^{\circ}\) и \(\angle{CBO} = 25^{\circ},\) что такое \(\angle{ACO}?\) 9{\ circ}.
\ _ \ квадрат \]
На приведенной выше диаграмме точка \(O\) находится в центре \(\треугольника ABC.\). Отрезок \(\overline {DE}\) проходит через \(O,\) и параллелен \( \overline {BC}.\) Если \(\lvert \overline{BD} \rvert=3\) и \(\lvert \overline{CE} \rvert=4,\), что такое \(\lvert\overline { DE}\rvert?\)
Поскольку \(O\) находится в центре \(\треугольника ABC\), а \(\overline {DE}\) параллелен \(\overline {BC},\) \(\треугольник BOD\) и \ (\треугольник COE\) равнобедренные треугольники. Таким образом, \(\lvert \overline {BD} \rvert = \lvert \overline {DO} \rvert\) и \(\lvert \overline {CE} \rvert = \lvert \overline {EO} \rvert.\)
Тогда у нас есть
\[\lvert \overline {DE} \rvert = \lvert \overline {BD} \rvert + \lvert \overline {CE} \rvert.\]
Таким образом, ответ равен \(3 + 4 = 7.\) \(_\квадрат\)
Процитировать как: Вписанная окружность треугольника. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/inscribed-triangles/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/inscribed-triangles/
Вписанные и описанные окружности – определение, диаграмма
Иногда окружность может быть как вписанной, так и описанной относительно многоугольника. Их тогда называют вписанными или описанными кругами. Ниже показаны вписанная и описанная окружность относительно треугольника.
Вписанные и описанные окружностиОбсудим их подробно.
Что такое вписанный круг
«Вписать» означает рисовать внутри любой фигуры, просто касаясь ее, но не пересекая фигуру. Таким образом, это противоположность описанному кругу.
В геометрии вписанная окружность, также известная как вписанная окружность многоугольника, представляет собой максимально возможную окружность, которую можно нарисовать внутри правильного циклического многоугольника. Вписанный круг будет касаться каждой из трех сторон треугольника ровно в одной точке. Центр такой окружности называется вписанным центром. Это точка, где сходятся биссектрисы треугольника. Радиус такой окружности называется внутренним радиусом.
Это точка, где сходятся биссектрисы треугольника. Радиус такой окружности называется внутренним радиусом.
Окружность, вписанная в треугольник
Когда окружность вписана в треугольник, треугольник находится вне круга, и окружность касается сторон треугольника в одной точке с каждой стороны. Стороны треугольника касаются окружности. Таким образом, для многоугольника окружность не вписана, если только каждая сторона многоугольника не касается окружности.
Таким образом, во все треугольники и правильные многоугольники вписаны окружности.
Ниже приведена окружность, вписанная в треугольник
Вписанная окружностьОбратите внимание, что каждая сторона треугольника касается окружности, поэтому, если мы проведем радиус от центра окружности до точки, где окружность касается края треугольник, радиус будет образовывать прямой угол с краем треугольника.
Как вписать окружность в треугольник
Ниже приведена ссылка, показывающая, как вписать окружность в треугольник.
Что такое описанная окружность
Описанная окружность многоугольника — это окружность, которая касается всех трех вершин многоугольника. Центр такой окружности называется центром описанной окружности, точкой, где пересекаются серединные перпендикуляры сторон. Радиус такой окружности называется радиусом описанной окружности.
Не каждый полигон имеет описанную окружность. Многоугольник, имеющий описанную окружность, называется вписанным многоугольником. Его также называют конциклическим многоугольником, поскольку его вершины концикличны. Все треугольники и все правильные многоугольники, такие как квадрат, прямоугольник, трапеция и воздушный змей, концикличны.
Описанная окружность треугольника
Поскольку все треугольники циклические, у них всегда есть описанная окружность.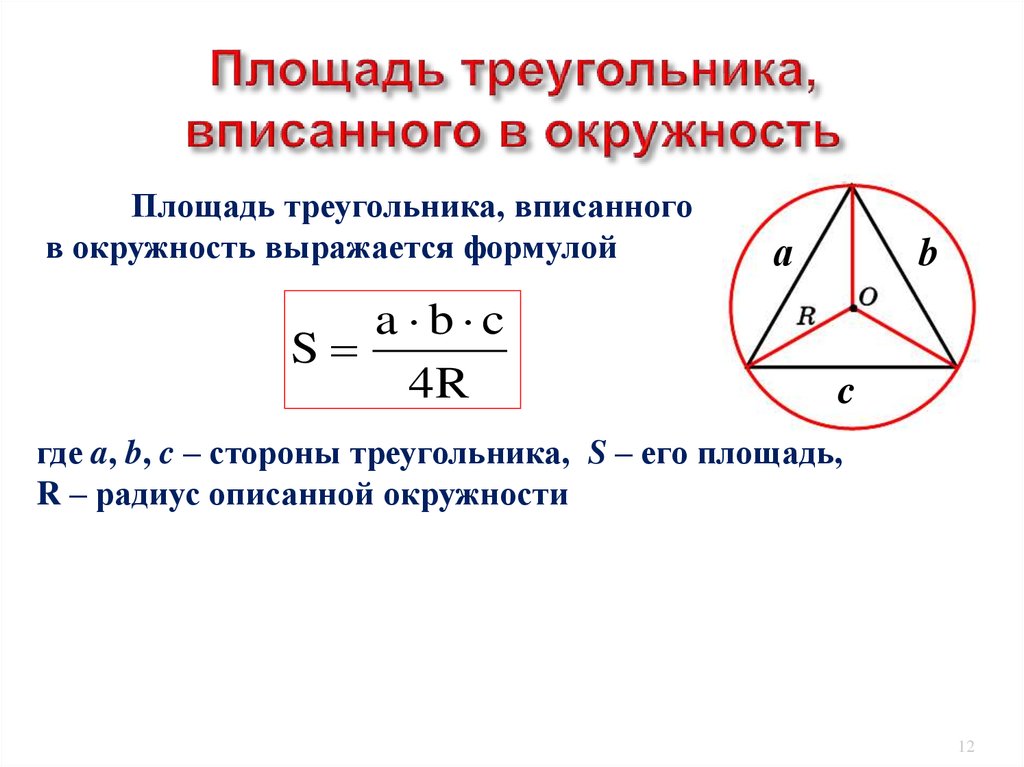



 \ _ \ квадрат \]
\ _ \ квадрат \]
Leave A Comment