период и амплитуда колебани1, формула, жесткость
Работа большинства механизмов основана на простейших законах физики и математики. Довольно большое распространение получило понятие пружинного маятника. Подобный механизм получил весьма широкое распространение, так как пружина обеспечивает требуемую функциональность, может быть элементом автоматических устройств. Рассмотрим подробнее подобное устройство, принцип действия и многие другие моменты подробнее.


Определения пружинного маятника
Как ранее было отмечено, пружинный маятник получил весьма широкое распространение. Среди особенностей можно отметить следующее:
- Устройство представлено сочетанием груза и пружины, масса которой может не учитываться. В качестве груза может выступать самый различный объект. При этом на него может оказываться воздействие со стороны внешней силы. Распространенным примером можно назвать создание предохранительного клапана, который устанавливается в системе трубопровода. Крепление груза к пружине проводится самым различным образом. При этом используется исключительно классический винтовой вариант исполнения, который получил наиболее широкое распространение. Основные свойства во многом зависят от типа применяемого материала при изготовлении, диаметра витка, правильности центровки и многих других моментов. Крайние витки часто изготавливаются таким образом, чтобы могли воспринимать большую нагрузку при эксплуатации.
- До начала деформации полная механическая энергия отсутствует. При этом на тело не влияет сила упругости. Каждая пружина имеет исходное положение, которое она сохраняет на протяжении длительного периода. Однако, за счет определенной жесткости происходит фиксация тела в начальном положении. Имеет значение то, каким образом прикладывается усилие. Примером назовем то, что она должна быть направлена вдоль оси пружины, так как в противном случае есть вероятность появления деформации и многих других проблем. У каждой пружины есть свои определенный придел сжатия и растяжения. При этом максимальное сжатие представлено отсутствием зазора между отдельными витками, при растяжении есть момент, когда происходит невозвратная деформация изделия. При слишком сильном удлинении проволоки происходит изменение основных свойств, после чего изделие не возвращается в свое первоначальное положение.
- В рассматриваемом случае колебания совершаются за счет действия силы упругости. Она характеризуется довольно большим количество особенностей, которые должны учитываться. Воздействие упругости достигается за счет определенного расположения витков и типа применяемого материала при изготовлении. При этом сила упругости может действовать в обе стороны. Чаще всего происходит сжатие, но также может проводится растяжение – все зависит от особенностей конкретного случая.
- Скорость перемещения тела может варьировать в достаточно большом диапазоне, все зависит от того, какое оказывается воздействие. К примеру, пружинный маятник может перемещать подвешенный груз в горизонтальной и вертикальной плоскости. Действие направленного усилия во многом зависит от вертикальной или горизонтальной установки.


В целом можно сказать, что пружинный маятник определение довольно обобщенное. При этом скорость перемещения объекта зависит от различных параметров, к примеру, величины приложенного усилия и других моментов. Перед непосредственным проведением расчетов проводится создание схемы:
- Указывается опора, к которой крепится пружина. Зачастую для ее отображения рисуется линия с обратной штриховкой.
- Схематически отображается пружина. Она часта представлена волнистой линией. При схематическом отображении не имеет значение длина и диаметральный показатель.
- Также изображается тело. Оно не должно соответствовать размерам, однако имеет значение место непосредственного крепления.
Схема требуется для схематического отображения всех сил, которые оказывают влияние на устройство. Только в этом случае можно учесть все, что влияет на скорость перемещения, инерцию и многие другие моменты.
Пружинные маятники применяются не только при расчетах ил решении различных задач, но также и на практике. Однако, не все свойства подобного механизма применимы.
Примером можно назвать случай, когда колебательные движения не требуются:
- Создание запорных элементов.
- Пружинные механизмы, связанные с транспортировкой различных материалов и объектов.
Проводимые расчеты пружинного маятника позволяют подобрать наиболее подходящий вес тела, а также тип пружины. Она характеризуется следующими особенностями:
- Диаметр витков. Он может быть самым различным. От показателя диаметра во многом зависит то, сколько требуется материала для производства. Диаметр витков также определяет то, какое усилие должно прикладываться для полного сжатия или частичного растяжения. Однако, увеличение размеров может создать существенные трудности с установкой изделия.
- Диаметр проволоки. Еще одним важным параметром можно назвать диаметральный размер проволоки. Он может варьировать в широком диапазоне, зависит прочность и степень упругости.
- Длина изделия. Этот показатель определяет то, какое усилие требуется для полного сжатия, а также какой упругостью может обладать изделие.
- Тип применяемого материала также определяет основные свойства. Чаще всего пружина изготавливается при применении специального сплава, который обладает соответствующие свойствами.
При математических расчетах многие моменты не учитываются. Усилие упругости и многие другие показатели выявляются путем расчета.
Виды пружинного маятника
Выделяют несколько различных видов пружинного маятника. Стоит учитывать, что классификация может проводится по типу устанавливаемой пружины. Среди особенностей отметим:
- Довольно большое распространение получили вертикальные колебания, так как в этом случае на груз не оказывается сила трения и другое воздействие. При вертикальном расположении груза существенно увеличивается степень воздействия силы тяжести. Распространен этот вариант исполнения при проведении самых различных расчетов. За счет силы тяжести есть вероятность того, что тело в исходной точке будет совершать большое количество инерционных движений. Этому также способствует упругость и инерция движения тела в конце хода.
- Также применяется горизонтальный пружинный маятник. В этом случае груз находится на опорной поверхности и на момент перемещения также возникает трение. При горизонтальном расположении сила тяжести работает несколько иначе. Горизонтальное расположение тела получило широкое распространение в различных задачах.
Рассчитывается движение пружинного маятника можно при использовании достаточно большого количества различных формул, который должны учитывать воздействие всех сил. В большинстве случаев устанавливается классическая пружина. Среди особенностей отметим следующее:
- Классическая витая пружина сжатия сегодня получила весьма широкое распространение. В этом случае между витками есть пространство, которое называется шагом. Пружина сжатия может и растягиваться, но зачастую она для этого не устанавливается. Отличительной особенностью можно назвать то, что последние витки выполнены в виде плоскости, за счет чего обеспечивается равномерное распределения усилия.
- Может устанавливаться вариант исполнения для растяжения. Он рассчитан на установку в случае, когда приложенное усилие становится причиной увеличения длины. Для крепления проводится размещение крючков.
Распространены оба варианта исполнения. При этом важно уделить внимание тому, чтобы сила прикладывалась параллельно оси. В противном случае есть вероятность смещения витков, что становится причиной возникновения серьезных проблем, к примеру, деформации.
Сила упругости в пружинном маятнике
Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.
Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:
- Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
- При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
- На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
- После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
- Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.
Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.
Уравнения колебаний пружинного маятника
Колебания пружинного маятника совершаются по гармоническому закону. Формула, по которой проводится расчет, выглядит следующим образом: F(t)=ma(t)=-mw2x(t).
В приведенной выше формуле указывается (w) радиальная частота гармонического колебания. Она свойственна силе, которая распространяется в границах применимости закона Гука. Уравнение движения может существенно отличаться, все зависит от конкретного случая.
Если рассматривать колебательное движение, то следует уделить внимание следующим моментам:
- Колебательные движения наблюдаются только в конце перемещения тела. Изначально оно прямолинейное до полного освобождения усилия. При этом сила упругости сохраняется на протяжении всего времени, пока тело находится в максимально отдаленном положении от нуля координат.
- После растяжения тело возвращается в исходное положение. Возникающая инерция становится причиной, по которой может оказываться воздействие на пружину. Инерция во многом зависит от массы тела, развитой скорости и многих других моментов.


В результате этого возникает колебание, которое может длиться в течение длительного периода. Приведенная выше формула позволяет провести расчет с учетом всех моментов.
Формулы периода и частоты колебаний пружинного маятника
При проектировании и вычислении основных показателей также уделяется довольно много внимания частоте и периоду колебания. Косинус – периодическая функция, в которой применяется значение, неизменяемое через определенный промежуток времени. Именно этот показатель называют период колебаний пружинного маятника. Для обозначения этого показателя применяется буква Т, также часто используется понятие, характеризующее значение, обратное периоду колебания (v). В большинстве случаев при расчетах применяется формула T=1/v.
Период колебаний вычисляется по несколько усложненной формуле. Она следующая: T=2п√m/k. Для определения частоты колебания используется формула: v=1/2п√k/m.
Рассматриваемая циклическая частота колебаний пружинного маятника зависит от следующих моментов:
- Масса груза, который прикреплен к пружине. Этот показатель считается наиболее важным, так как оказывает влияние на самые различные параметры. От массы зависит сила инерции, скорость и многие другие показатели. Кроме этого, масса груза – величина, с измерением которой не возникает проблем из-за наличия специального измерительного оборудования.
- Коэффициент упругости. Для каждой пружины этот показатель существенно отличается. Коэффициент упругости указывается для определения основных параметров пружины. Зависит этот параметр от количества витков, длины изделия, расстояние между витками, их диаметра и многого другого. Определяется он самым различным образом, зачастую при применении специального оборудования.
Не стоит забывать о том, что при сильном растяжении пружины закон Гука прекращает действовать. При этом период пружинного колебания начинает зависеть от амплитуды.
Для измерения периода применяется всемирная единица времени, в большинстве случаев секунды. В большинстве случаев амплитуда колебаний вычисляется при решении самых различных задач. Для упрощения процесса проводится построение упрощенной схемы, на которой отображаются основные силы.


Формулы амплитуды и начальной фазы пружинного маятника
Определившись с особенностями проходимых процессов и зная уравнение колебаний пружинного маятника, а также начальные значения можно провести расчет амплитуды и начальной фазы пружинного маятника. Для определения начальной фазы применяется значение f, амплитуда обозначается символом A.
Для определения амплитуды может использоваться формула: А=√x2+v2/w2. Начальная фаза высчитывается по формуле: tgf=-v/xw.
Применяя эти формулы можно провести определение основных параметров, которые применяются при расчетах.
Энергия колебаний пружинного маятника
Рассматривая колебание груза на пружине нужно учитывать тот момент, что при движение маятника может описываться двумя точками, то есть оно носит прямолинейный характер. Этот момент определяет выполнение условий, касающихся рассматриваемой силы. Можно сказать, что полная энергия потенциальная.
Провести расчет энергии колебаний пружинного маятника можно при учете всех особенностей. Основными моментами назовем следующее:
- Колебания могут проходить в горизонтальной и вертикальной плоскости.
- Ноль потенциальной энергии выбирается в качестве положения равновесия. Именно в этом месте устанавливается начало координат. Как правило, в этом положении пружина сохраняет свою форму при условии отсутствия деформирующей силы.
- В рассматриваемом случае рассчитываемая энергия пружинного маятника не учитывает силу трения. При вертикальном расположении груза сила трения несущественна, при горизонтальном тело находится на поверхности и при движении может возникнуть трение.
- Для расчета энергии колебания применяется следующая формула: E=-dF/dx.
Приведенная выше информация указывают на то, что закон сохранения энергии выглядит следующим образом: mx2/2+mw2x2/2=const. Применяемая формула говорит о следующем:
- Максимальная кинетическая энергия установленного маятника прямо пропорциональна максимальному значению потенциальной.
- На момент осциллятора среднее значение обоих сил равны.


Провести определение энергии колебания пружинного маятника можно при решении самых различных задач.
Свободные колебания пружинного маятника
Рассматривая то, чем вызваны свободные колебания пружинного маятника следует уделить внимание действию внутренних сил. Они начинают формироваться практически сразу после того, как телу было передано движение. Особенности гармонических колебаний заключаются в нижеприведенных моментах:
- Могут также возникать и другие типы сил воздействующего характера, который удовлетворяют все нормы закона, называются квазиупругими.
- Основными причинами действия закона могут быть внутренние силы, которые формируются непосредственно на момент изменения положения тела в пространстве. При этом груз обладает определенной массой, усилие создается за счет фиксации одного конца за неподвижный объект с достаточной прочностью, второго за сам груз. При условии отсутствия трения тело может совершать колебательные движения. В этом случае закрепленный груз называется линейным.


Не стоит забывать о том, что существует просто огромное количество различных видов систем, в которых осуществляется движение колебательного характера. В них также возникает упругая деформация, которая становится причиной применения для выполнения какой-либо работы.
Пружинный маятник, формулы и примеры
Определения и формулы пружинного маятника
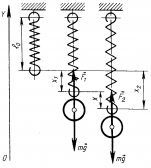
Рис.1. Пружинный маятник: а) в положении равновесия; б) в состоянии колебаний
Когда пружина не деформирована, тело находится в положении равновесия (рис.1,а). Если растянув или сжав пружину, вывести тело из положения равновесия, на него будет действовать сила упругости со стороны деформированной пружины. Эта сила направлена к положению равновесия и в данном случае является возвращающей силой.
Сила упругости в пружинном маятнике
Сила упругости пропорциональна смещению тела (удлинению пружины):
здесь — коэффициент жесткости пружины.
В положении, соответствующем максимальному отклонению тела от положения равновесия (смещение тела равно амплитуде колебаний) сила упругости максимальна, поэтому максимально и ускорение тела. По мере приближения тела к положению равновесия удлинение пружины уменьшается, и, следовательно, уменьшается ускорение тела, которое обусловлено силой упругости. Достигнув положения равновесия, тело не остановится, хотя в этот момент сила упругости равна нулю. Скорость тела в момент прохождения им положения равновесия имеет максимальное значение, и тело по инерции будет двигаться дальше, растягивая пружину. Возникающая при этом сила упругости будет тормозить тело, так как теперь она направлена в сторону, противоположную движению тела. Дойдя до крайнего положения, тело остановится и начнет движение в противоположном направлении. Движение тела будет повторяться в описанной последовательности.
Таким образом, причинами свободных колебаний пружинного маятника является сила упругости деформированной пружины (возвращающая сила) и инертность тела.
Период свободных колебаний пружинного маятника
Период свободных колебаний пружинного маятника определяется по формуле:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Частота колебаний пружинного маятника
Свойства пружинного маятника
Определение 1
Идеальный пружинный маятник представляет собой пружину, массой которой можно пренебречь, с закрепленным на ней телом с точечной массой. При этом один или оба конца пружины закреплены, а силой трения можно пренебречь.
Такую конструкцию можно рассматривать лишь как математическую модель. Примерами реальных пружинных маятников (навитых из упругой проволоки цилиндрических спиралей) могут служить всевозможные устройства, гасящие колебания: амортизаторы, подвески, рессоры и т.п. Пружинные маятники, хотя и несколько иной конструкции (в виде плоских спиралей) используются в механических часах.
Свойства пружин зависят от вещества, из которого они изготовлены (как правило, это особая пружинная сталь), диаметра проволоки, формы ее сечения, диаметра цилиндра пружины, его длины. Эти показатели в совокупности обуславливают ключевую характеристику пружины — ее жесткость.
Пружина запасает энергию при продольном растяжении или сжатии за счет упругих деформаций в кристаллической решетке своего вещества.
Готовые работы на аналогичную тему
Замечание 1
При слишком сильном растяжении или сжатии материал пружины теряет упругие свойства. Такая деформация называется пластической или остаточной.
Формула для расчета частоты колебаний
Если пружину с закрепленной на ней грузом, подвергнуть продольной упругой деформации, а затем отпустить, она начнет совершать возвратно-поступательные гармонические колебания, в ходе которых перемещение закрепленного на ней груза описывается формулой:
$x = A \cdot \cos(\omega_0 \cdot t + \phi)$
Здесь $A$ — амплитуда колебаний, $\phi$ — начальная фаза, $\omega_0$ — собственная циклическая частота колебаний пружинного маятника, рассчитываемая как
$\omega_0 = \sqrt{\frac{k}{m}}$ > $0$,
где:
- $k$ — жесткость пружины,
- $m$ — масса закрепленного на ней тела.
Циклическая частота отличается тем, что характеризует не количество полных циклов за единицу времени, а количество «пройденных» колеблющейся по гармоническому закону точкой радиан.
Период колебаний пружинного маятника вычисляется как
$T = 2 \cdot \pi \cdot \sqrt{\frac{m}{k}}$.
Пример 1
Найти частоту и циклическую частоту пружинного маятника, период колебаний которого составляет 0,1 с.
Частоту можно найти как величину обратную к периоду:
$f = \frac{1}{T}$
$f = \frac{1}{0,1} = 10 Гц$
Циклическую частоту можно выразить как
$\omega_0 = 2 \cdot \pi \cdot f$
$\omega_0 = 2 \cdot 3,1415927 \cdot 10 \approx 62,831854 \frac{рад}{с}$
Ответ: 10 герц и $\approx$ 62,831854 радиан в секунду.
Пружинный маятник ☑️ формулы определения периода и частоты свободных колебаний, полной, кинетической и потенциальной энергий, виды, уравнения свободных и гармонических колебаний маятника
Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.
Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.
В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.
Что такое пружинный маятник
Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.
Приняты следующие обозначения:
Общий вид маятника:
Особенностями пружинных маятников являются:
-
Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
-
У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
-
Полная механическая энергия появляется с началом процесса обратимого деформирования.
-
Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
-
От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.
Виды пружинных маятников
Существует два типа данной системы:
-
Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.
-
Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.
Сила упругости в пружинном маятнике
До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.
Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.
Расчёт силы упругости может быть проведен таким образом:
Fупр = — k*x
где k — коэффициент жесткости пружины (Н\м),
x – смещение (м).
Уравнения колебаний пружинного маятника
Свободные колебания пружинного маятника описываются с помощью гармонического закона.
Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:
F(t) = ma(t) = — mw2x(t),
где w — радиальная частота гармонического колебания.
Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:
Период и частота свободных колебаний пружинного маятника
При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.
Изменение циклической частоты покажет формула, приведенная на рисунке:
Факторы, от которых зависит частота:
-
Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.
-
Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.
Амплитуда и начальная фаза пружинного маятника
Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.
В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).
Энергия пружинного маятника
При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.
Потенциальная энергия:
Кинетическая энергия:
Полная энергия:
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:
-
Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
-
В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
-
Влияние силы трения при расчете не учитывают.
Дифференциальное уравнение гармонических колебаний пружинного маятника
Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.
Формулы пружинного маятника в физике
Определение и формулы пружинного маятника
ОпределениеПружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
\[\ddot{x}+{\omega }^2_0x=0\left(1\right),\]где ${щu}^2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
\[Re\ \tilde{x}=Re\left(A\cdot exp\ \left(i\left({\omega }_0t+\varphi \right)\right)\right)\left(3\right).\]Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
\[T=2\pi \sqrt{\frac{m}{k}}\left(4\right).\]Так как частота колебаний ($\nu $) — величина обратная к периоду, то:
\[\nu =\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\left(5\right).\]Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и н
Период пружинного маятника | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Период пружинного маятника зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается
![Rendered by QuickLaTeX.com \[\Large T=2\pi \sqrt{\frac{m}{k}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-0ab669923ec1de86565eee9a2504e069_l3.png)
Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.
Давайте выведем формулу периода пружинного маятника.
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :
![Rendered by QuickLaTeX.com \[\Large m \vec a = \vec F_{упр}+m\vec g+ \vec N\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c779b3ec4314d7ae5f24e7adcccb6167_l3.png)
Все проецируем на ось ОХ:
![Rendered by QuickLaTeX.com \[\Large OX: ma_x= -F_{упр}=-kx\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bfafa29d3b38b06a454555a05417e2b0_l3.png)
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:
![Rendered by QuickLaTeX.com \[\Large a_x+\frac{k}{m}x=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f9d0c805ca6f6f948c72a11e33771950_l3.png)
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
![Rendered by QuickLaTeX.com \[\Large a_x(t)+\omega ^2 x(t)=0\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-744f3174c7aaacf6ebc4c66c5ad95689_l3.png)
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
![Rendered by QuickLaTeX.com \[\Large \omega=\sqrt{\frac{k}{m} }\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-52a31ee5b2f6bc52bb879c8c54cb2573_l3.png)
Тогда период колебаний пружинного маятника будет равен:
![Rendered by QuickLaTeX.com \[\Large T=\frac{2\pi }{\omega } =2\pi \sqrt{\frac{m}{k}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-868c4373fae25c0a700af658f849f754_l3.png)
Так же есть:
Период математического маятника
![Rendered by QuickLaTeX.com \[T=2\pi \sqrt{\frac{L}{g}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-22fd3e655b9d9b9a6bc536617fac4135_l3.png)
Период физического маятника
![Rendered by QuickLaTeX.com \[T=2\pi \sqrt{\frac{J}{mgl}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-51cb472f4dbeb16880139f4016585e15_l3.png)
Период крутильного маятника
![Rendered by QuickLaTeX.com \[T=2\pi \sqrt{\frac{I}{K}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-ba35318992c2e27481c49d10a7a71a93_l3.png)
В Формуле мы использовали :
T — Период пружинного маятника маятника
m — Масса груза
x — Изменение длины пружины
k — Коэффициент упругости пружины
g=9.8 — Ускорение свободного падения
![Rendered by QuickLaTeX.com \[\omega\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-231d76a1dcdb84e30834c95bc7591fce_l3.png)
— Циклическая частота пружинного маятника
N — Сила реакции опоры
![Rendered by QuickLaTeX.com \[ F_{упр}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8e7c356a13709ef158ecf122869a8109_l3.png)
— Сила упругости
Пружинный маятник | Объединение учителей Санкт-Петербурга
Колебания пружинного маятника. | |
В вертикальном положении на груз на пружине действуют сила тяжести и сила упругости пружины. Под действием силы тяжести пружина растягивается на х1, а затем мы отклоняем его от этого положения на х. |
|
Тогда согласно второму закону Ньютона, учитывая знаки проекций, получим: тогда: Или | |
Выразим ускорение: |
|
Сравним полученное уравнение с уравнением колебательного движения Видно, что |
|
Период колебаний | Формула Гюйгенса: |
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия упруго деформированного тела равна |
|
Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: Т.к. производная от постоянной величины равна нулю, то Производная суммы равна сумме производных: Следовательно: |
|
В данном случае этот способ более трудоемкий, но он более общий. |
|
Колебание простого маятника
Уравнение движения
Простой маятник состоит из шарика (острия) м , подвешенного на (безмассовой) струне длиной L и закрепленной в точке поворота P. При смещении на начальный угол и отпускании маятник качнется назад и вперед с периодическим движением. Применяя второй закон Ньютона для вращательных систем, можно получить уравнение движения маятника $$ \ tau = I \ alpha \ qquad \ Rightarrow \ qquad -mg \ sin \ theta \; L = мл ^ 2 \; \ frac {d ^ 2 \ theta} {dt ^ 2} $$ и переставил как $$ \ frac {d ^ 2 \ theta} {dt ^ 2} + \ frac {g} {L} \ sin \ theta = 0 $$ Если амплитуда углового смещения достаточно мала, так что приближение малых углов ($ \ sin \ theta \ приблизительно \ theta $) выполняется, то уравнение движения сводится к уравнению простого гармонического движения $$ \ frac {d ^ 2 \ theta} {dt ^ 2} + \ frac {g} {L} \ theta = 0 $$ Простое гармоническое решение $$ \ theta (t) = \ theta_o \ cos (\ omega t) \, $$ где \ (\ theta_o \) — начальное угловое смещение, а \ (\ omega = \ sqrt {g / L} \) — собственная частота движения.Период этой системы (время одного колебания) равен $$ T = \ frac {2 \ pi} {\ omega} = 2 \ pi \ sqrt {\ frac {L} {g}}. $$Период маятника не зависит от массы шара, а только от длины струны. Два маятника с разной массой, но одинаковой длины будут иметь одинаковый период. Два маятника разной длины будут иметь разные периоды; у маятника с более длинной струной будет более длительный период.
Сколько полных колебаний совершают синий и коричневый маятник за время за одно полное колебание более длинного (черного) маятника?
На основании этой информации и определения периода простого маятника, каково соотношение длин трех маятников?
При условии малых углов частота и период маятника не зависят от начальной амплитуды углового смещения.Маятник будет иметь одинаковый период независимо от его начального угла. Это простое приближение показано на анимации слева. Все три маятника совершают одно полное колебание за один и тот же промежуток времени, независимо от начального угла.Реальный (нелинейный) простой маятник
Когда амплитуда углового смещения маятника настолько велика, что приближение малого угла больше не выполняется, тогда уравнение движения должно оставаться в своей нелинейной форме. $$ \ frac {d ^ 2 \ theta} {dt ^ 2} + \ frac {g} {L} \ sin \ theta = 0 $$ Это дифференциальное уравнение не имеет решения в замкнутой форме, вместо этого его необходимо решать численно с помощью компьютера. Mathematica очень легко численно решает это дифференциальное уравнение с помощью встроенной функции NDSolve [] .
Приближение малых углов справедливо для начальных угловых смещений около 20 ° или меньше. Если начальный угол меньше этой величины, то достаточно простого гармонического приближения. Но, если угол больше, то разница между приближением малого угла и точным решением быстро становится очевидной.
На анимации внизу слева начальный угол небольшой.Темно-синий маятник — это приближение малого угла, а голубой маятник (изначально скрытый позади) — точное решение. Для небольшого начального угла требуется довольно большое количество колебаний, прежде чем разница между приближением малого угла (темно-синий) и точным решением (светло-синий) начнет заметно расходиться.
На анимации внизу справа начальный угол большой. Черный маятник — это приближение малого угла, а более светлый серый маятник (изначально скрытый позади) — точное решение.Для большого начального угла разница между приближением малого угла (черный) и точным решением (светло-серый) становится очевидной почти сразу.
,Колебания: от Physclips
Простой маятник
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Колебаний: Масса на пружине и маятники
Простые гармонические колебания
 Простое гармоническое движение 1 Объект Для определения периода движения объектов, выполняющих простое гармоническое движение, и для проверки теоретического предсказания таких периодов.2 Гиря различного назначения
Простое гармоническое движение 1 Объект Для определения периода движения объектов, выполняющих простое гармоническое движение, и для проверки теоретического предсказания таких периодов.2 Гиря различного назначения
ЗАКОН КРЮКА И КОЛЕБАНИЯ
 9 ЗАКОН КРЮКА И КОЛЕБАНИЯ ЦЕЛЬ Измерить влияние амплитуды, массы и жесткости пружины на период осциллятора пружинной массы.ВВЕДЕНИЕ Сила, возвращающая пружину в состояние равновесия
9 ЗАКОН КРЮКА И КОЛЕБАНИЯ ЦЕЛЬ Измерить влияние амплитуды, массы и жесткости пружины на период осциллятора пружинной массы.ВВЕДЕНИЕ Сила, возвращающая пружину в состояние равновесия
Эксперимент 9. Маятник.
 Эксперимент 9 Маятник 9.1 Цели Изучить функциональную зависимость периода (τ) 1 маятника от его длины (L), массы его опоры (м) и начального угла (θ 0). Используйте маятник
Эксперимент 9 Маятник 9.1 Цели Изучить функциональную зависимость периода (τ) 1 маятника от его длины (L), массы его опоры (м) и начального угла (θ 0). Используйте маятник
Практический тест SHM с ответами
 Практический тест SHM с ответами MPC 1) Если мы удвоим частоту системы, претерпевающей простое гармоническое движение, какие из следующих утверждений об этой системе верны? (Может быть более одного
Практический тест SHM с ответами MPC 1) Если мы удвоим частоту системы, претерпевающей простое гармоническое движение, какие из следующих утверждений об этой системе верны? (Может быть более одного
УПРУГИЕ СИЛЫ и ЗАКОН КРЮКА
 PHYS-101 LAB-03 УПРУГИЕ СИЛЫ и ЗАКОН 1.Цель. Цель данной лабораторной работы — показать, что реакцию пружины, когда внешний агент изменяет ее равновесную длину на x, можно описать
PHYS-101 LAB-03 УПРУГИЕ СИЛЫ и ЗАКОН 1.Цель. Цель данной лабораторной работы — показать, что реакцию пружины, когда внешний агент изменяет ее равновесную длину на x, можно описать
Лаборатория 8: Баллистический маятник
 Лабораторная работа 8: Баллистический маятник Оборудование: баллистический маятник, 2-метровая линейка, 30-сантиметровая линейка, чистый лист бумаги, копировальная бумага, малярная лента, шкала. Внимание! В этом эксперименте стальной шар проецируется горизонтально
Лабораторная работа 8: Баллистический маятник Оборудование: баллистический маятник, 2-метровая линейка, 30-сантиметровая линейка, чистый лист бумаги, копировальная бумага, малярная лента, шкала. Внимание! В этом эксперименте стальной шар проецируется горизонтально
Физика 41 HW Set 1 Глава 15
 Physics 4 HW Set Chapter 5 Serway 8 th OC :, 4, 7 CQ: 4, 8 P: 4, 5, 8, 8, 0, 9 ,, 4, 9, 4, 5, 5 Обсуждение задач :, 57, 59, 67, 74 OC CQ P: 4, 5, 8, 8, 0, 9 ,, 4, 9, 4, 5, 5 Проблемы с обсуждением :, 57, 59,
Physics 4 HW Set Chapter 5 Serway 8 th OC :, 4, 7 CQ: 4, 8 P: 4, 5, 8, 8, 0, 9 ,, 4, 9, 4, 5, 5 Обсуждение задач :, 57, 59, 67, 74 OC CQ P: 4, 5, 8, 8, 0, 9 ,, 4, 9, 4, 5, 5 Проблемы с обсуждением :, 57, 59,
Физика 231 Лекция 15
 Физика 31 лекция 15 Основные темы сегодняшней лекции: Простое гармоническое движение Масса и пружинный маятник Круговое движение T 1 / f; f 1 / T; ω πf для массы и пружины ω x Acos (ωt) v ωasin (ωt) x ax ω Acos (ωt)
Физика 31 лекция 15 Основные темы сегодняшней лекции: Простое гармоническое движение Масса и пружинный маятник Круговое движение T 1 / f; f 1 / T; ω πf для массы и пружины ω x Acos (ωt) v ωasin (ωt) x ax ω Acos (ωt)
Крутящий момент и вращение.физика
 Физика крутящего момента и вращения Сила крутящего момента — это действие, которое вызывает изменения в линейном движении. Для вращательного движения одна и та же сила может привести к очень разным результатам. Крутящий момент — это действие, которое вызывает объекты
Физика крутящего момента и вращения Сила крутящего момента — это действие, которое вызывает изменения в линейном движении. Для вращательного движения одна и та же сила может привести к очень разным результатам. Крутящий момент — это действие, которое вызывает объекты
Э Х П Е Р И М Е Н Т 8
 E X P E R I M E N T 8 Крутящий момент, равновесие и центр тяжести, произведенные физическим составом Коллинского колледжа Авторские права Коллинский факультет физики.Все права защищены. Университетская физика, Опыт 8:
E X P E R I M E N T 8 Крутящий момент, равновесие и центр тяжести, произведенные физическим составом Коллинского колледжа Авторские права Коллинский факультет физики.Все права защищены. Университетская физика, Опыт 8:
Крутящий момент и вращательное движение
 Крутящий момент и вращательное движение Имя Партнер Введение Движение по окружности является прямым продолжением линейного движения. По учебнику все, что вам нужно сделать, это заменить смещение, скорость,
Крутящий момент и вращательное движение Имя Партнер Введение Движение по окружности является прямым продолжением линейного движения. По учебнику все, что вам нужно сделать, это заменить смещение, скорость,
226 Глава 15: КОЛЕБАНИЯ
 Глава 15: КОЛЕБАНИЯ 1.В простом гармоническом движении восстанавливающая сила должна быть пропорциональна: A. амплитуде B. частоте C. скорости D. смещению E. смещению в квадрате 2. Колебательному движению
Глава 15: КОЛЕБАНИЯ 1.В простом гармоническом движении восстанавливающая сила должна быть пропорциональна: A. амплитуде B. частоте C. скорости D. смещению E. смещению в квадрате 2. Колебательному движению
Финальный веб-обзор AP Physics C Fall
 Имя: Класс: _ Дата: _ AP Physics C Fall Final Web Review Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. 1. На графике зависимости позиции от времени наклон
Имя: Класс: _ Дата: _ AP Physics C Fall Final Web Review Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. 1. На графике зависимости позиции от времени наклон
Государственный университет Теннесси
 Департамент государственного университета Теннессифизико-математических наук PHYS 2010 CF SU 2009 Имя 30% Время 2 часа. Мошенничество даст вам оценку F. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР.
Департамент государственного университета Теннессифизико-математических наук PHYS 2010 CF SU 2009 Имя 30% Время 2 часа. Мошенничество даст вам оценку F. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР.
Определение g с помощью пружины
 ВВЕДЕНИЕ УНИВЕРСИТЕТ СЮРРЕИ ОТДЕЛЕНИЕ ФИЗИКИ Лаборатория уровня 1: Введение Эксперимент Определение g с помощью пружины Этот эксперимент разработан, чтобы вы были уверены в использовании количественного метода
ВВЕДЕНИЕ УНИВЕРСИТЕТ СЮРРЕИ ОТДЕЛЕНИЕ ФИЗИКИ Лаборатория уровня 1: Введение Эксперимент Определение g с помощью пружины Этот эксперимент разработан, чтобы вы были уверены в использовании количественного метода
Стоячие волны на струне
 1 из 6 Стоячие волны на струне Лето 2004 г. Стоячие волны на струне Если струна привязана между двумя фиксированными опорами, туго натянута и резко выщипана за один конец, импульс будет проходить от одного конца
1 из 6 Стоячие волны на струне Лето 2004 г. Стоячие волны на струне Если струна привязана между двумя фиксированными опорами, туго натянута и резко выщипана за один конец, импульс будет проходить от одного конца
УСКОРЕНИЕ СИЛЫ ТЯЖЕСТИ
 ЭКСПЕРИМЕНТ 1 ФИЗИКА 107 УСКОРЕНИЕ ОТ ГРАВИТАЦИИ Навыки, которые вы изучите или на практике: Вычислите скорость и ускорение на основе экспериментальных измерений x vs t (положения искр) Найдите средние скорости
ЭКСПЕРИМЕНТ 1 ФИЗИКА 107 УСКОРЕНИЕ ОТ ГРАВИТАЦИИ Навыки, которые вы изучите или на практике: Вычислите скорость и ускорение на основе экспериментальных измерений x vs t (положения искр) Найдите средние скорости
Свободно падающие предметы
 Физика свободно падающих объектов 1425 Лекция 3 Майкл Фаулер, UVa.Сегодняшние темы В предыдущей лекции мы проанализировали одномерное движение, определив смещение, скорость и ускорение, и нашли
Физика свободно падающих объектов 1425 Лекция 3 Майкл Фаулер, UVa.Сегодняшние темы В предыдущей лекции мы проанализировали одномерное движение, определив смещение, скорость и ускорение, и нашли
Лабораторная работа 2: Векторный анализ.
 Лабораторная работа 2: Векторный анализ Цели: отработать использование графических и аналитических методов для добавления векторов в двух измерениях Оборудование: измерительная ручка Линейка Транспортир Таблица силы Кольцевые шкивы с насадками
Лабораторная работа 2: Векторный анализ Цели: отработать использование графических и аналитических методов для добавления векторов в двух измерениях Оборудование: измерительная ручка Линейка Транспортир Таблица силы Кольцевые шкивы с насадками
РАБОТА, ВЫПОЛНЯЕМАЯ ПОСТОЯННОЙ СИЛОЙ
 РАБОТА, ВЫПОЛНЯЕМАЯ ПОСТОЯННОЙ СИЛОЙ Определение работы W, когда постоянная сила (F) направлена в направлении перемещения (d): W = Fd Единица СИ — Ньютон-метр (Нм) = Джоуль, Дж. сила
РАБОТА, ВЫПОЛНЯЕМАЯ ПОСТОЯННОЙ СИЛОЙ Определение работы W, когда постоянная сила (F) направлена в направлении перемещения (d): W = Fd Единица СИ — Ньютон-метр (Нм) = Джоуль, Дж. сила
Ускорение силы тяжести
 Ускорение свободного падения 1 Объект Определить ускорение свободного падения различными методами.2 Весы для приборов, шарикоподшипник, зажимы, электрические таймеры, счетчик, бумажные полоски, точность
Ускорение свободного падения 1 Объект Определить ускорение свободного падения различными методами.2 Весы для приборов, шарикоподшипник, зажимы, электрические таймеры, счетчик, бумажные полоски, точность
PHY121 # 8 Среднесрочный период I 3.06.2013
 PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Exam Multiple Choice Questions # 1 # 4 1. Когда показанная выше система без трения ускоряется приложенной силой величиной F, натяжение
PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Exam Multiple Choice Questions # 1 # 4 1. Когда показанная выше система без трения ускоряется приложенной силой величиной F, натяжение
Глава 6 Работа и энергия
 Глава 6 ПРЕДВАРИТЕЛЬНЫЙ ОБЗОР РАБОТЫ И ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, посредством которого он действует.Когда работа выполняется в системе или с ее помощью, энергия этой системы
Глава 6 ПРЕДВАРИТЕЛЬНЫЙ ОБЗОР РАБОТЫ И ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, посредством которого он действует.Когда работа выполняется в системе или с ее помощью, энергия этой системы
4 Гравитация: сила притяжения
 ГЛАВА 1 РАЗДЕЛ Материя в движении 4 Гравитация: сила притяжения ПРЕЖДЕ ЧЕМ ВЫ ПРОЧИТАЕТЕ Прочитав этот раздел, вы сможете ответить на следующие вопросы: Что такое гравитация? Чем отличаются вес и масса?
ГЛАВА 1 РАЗДЕЛ Материя в движении 4 Гравитация: сила притяжения ПРЕЖДЕ ЧЕМ ВЫ ПРОЧИТАЕТЕ Прочитав этот раздел, вы сможете ответить на следующие вопросы: Что такое гравитация? Чем отличаются вес и масса?
PHYS 211, ФИНАЛЬНАЯ ОСЕНЬ 2004, Форма A
 1.Два мальчика массой 40 и 60 кг держатся за любой конец безмассового шеста длиной 10 м, который изначально находится в состоянии покоя и плавает в стоячей воде. Они тянутся вдоль шеста к каждому
1.Два мальчика массой 40 и 60 кг держатся за любой конец безмассового шеста длиной 10 м, который изначально находится в состоянии покоя и плавает в стоячей воде. Они тянутся вдоль шеста к каждому
ЗАДАНИЕ 6: Падающие предметы
 UNIT FM Разработка идей ЗАДАНИЕ 6: Падающие объекты Цель и ключевой вопрос Вы разработали свои идеи о том, как движение объекта связано с силами, действующими на него с помощью объектов, движущихся горизонтально.
UNIT FM Разработка идей ЗАДАНИЕ 6: Падающие объекты Цель и ключевой вопрос Вы разработали свои идеи о том, как движение объекта связано с силами, действующими на него с помощью объектов, движущихся горизонтально.
Упражнения на колебаниях и волнах
 Упражнения на колебания и волны. Упражнение 1.1. В лаборатории вы нашли пружину. Когда вы вешаете 100 грамм на конец пружины, она растягивается на 10 см. Вы вытягиваете 100-граммовый груз на 6 см из равновесия
Упражнения на колебания и волны. Упражнение 1.1. В лаборатории вы нашли пружину. Когда вы вешаете 100 грамм на конец пружины, она растягивается на 10 см. Вы вытягиваете 100-граммовый груз на 6 см из равновесия
Физика 201 Домашнее задание 8
 Физика 201 Домашнее задание 8 27 февраля 2013 г. 1.Включают потолочный вентилятор и к лопастям прикладывают крутящий момент 1,8 Н · м. 8,2 рад / с 2 Лопасти имеют общий момент инерции 0,22 кг-м 2. Что такое
Физика 201 Домашнее задание 8 27 февраля 2013 г. 1.Включают потолочный вентилятор и к лопастям прикладывают крутящий момент 1,8 Н · м. 8,2 рад / с 2 Лопасти имеют общий момент инерции 0,22 кг-м 2. Что такое
Глава 3.8 и 6 Решения
 Глава 3.8 и 6. Решения P3.37. Подготовьтесь: нас просят определить период, скорость и ускорение. Период и частота инвертированы согласно уравнению 3.26. Чтобы определить скорость, нам нужно знать пройденное расстояние
Глава 3.8 и 6. Решения P3.37. Подготовьтесь: нас просят определить период, скорость и ускорение. Период и частота инвертированы согласно уравнению 3.26. Чтобы определить скорость, нам нужно знать пройденное расстояние
Раскачивание на веревке — Урок
Качание на веревке — Урок — TeachEngineeringБыстрый просмотр
Уровень оценки: 8 (7-9)
Требуемое время: 45 минут
Зависимость урока:
Тематические области: Алгебра, Физические науки, Физика
Подпишитесь на нашу рассылку новостей


Резюме
Студенты изучают, как работают маятники и почему они полезны в повседневных применениях.В практической деятельности они экспериментируют с длиной струны, весом маятника и углом выпуска. В рамках сопутствующей деятельности по обучению грамоте учащиеся изучают механическую концепцию ритма, основанную на принципе колебаний, в более широком биологическом и культурном контексте — в танцах и спорте, поэзии и других литературных формах, а также в общении в целом.Инженерное соединение
Инженеры знают, что понимание физики поведения маятников — важный шаг к пониманию всех видов движения.Многие другие объекты регулярно движутся вперед и назад, как маятники, например, вес, подпрыгивающий вверх и вниз на пружине, и движение радиоволн вперед и назад. Помимо использования маятников в часах, инженеры используют их для обнаружения землетрясений, измерения скорости полета пули, помощи зданиям в сопротивлении сотрясениям землетрясений и помощи роботам в равновесии. В столице Тайваня небоскребе Taipei 101 висит гигантский 726-тонный маятник, подвешенный над 88-м этажом, чтобы противодействовать ветрам, уменьшая раскачивание здания и сдерживая укачивание.
Цели обучения
После этого урока учащиеся должны уметь:
- Объясните, как вес, длина и угол поворота влияют на период маятника.
- Свяжите изучение физики и эксперименты Галилея с созданием часов.
- Опишите, как сохранение импульса связано с маятниками.
- Приведите примеры того, как инженеры используют маятники.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты имеют иерархическую структуру: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ
Предложите выравнивание, не указанное вышеКакое альтернативное выравнивание вы предлагаете для этого контента?
Больше подобной программы
Наука о качеляхСтуденты узнают, что такое маятник и как он работает во время аттракционов.Изучая физику маятников, они также знакомятся с первым законом движения Ньютона — о непрерывном движении и инерции.
 В ходу дела
В ходу дела После просмотра видеоклипа 1940 года об обрушении моста «Галопирующая Герти» и демонстрации учителя с простым маятником группы студентов обсуждают, а затем исследуют идею повторяющегося движения — в частности, концепции периодического и гармонического движения.Они изучают основные свойства этого типа …
 Качающийся со стилем
Качающийся со стилем Студенты на собственном опыте узнают о характеристиках простого физического явления — маятника — катаясь на качелях на игровой площадке. Они используют маятниковые термины и таймер, чтобы экспериментировать с колебательными переменными.Они расширяют свои знания, следуя этапам процесса инженерного проектирования до …
 Качели во времени
Качели во времени Учащиеся изучают движение маятников и приходят к пониманию того, что чем длиннее струна маятника, тем меньше количество колебаний в заданный интервал времени.Студенческие группы проводят эксперимент, собирая и отображая данные на листе.

Предварительные знания
Базовое понимание сил, таких как подъемная сила, вес, тяга и сопротивление, а также вращательное движение и угловой момент.
Введение / Мотивация
Вы когда-нибудь играли на качелях? Когда вы качаетесь, вы плавно едете от вершины одной дуги через основание к вершине на другой стороне качелей и обратно. Когда вы качаетесь, вы двигаетесь как маятник. Маятник — это веревка, свисающая с фиксированной точки с грузом (называемым бобом) на одном конце, который может качаться вперед и назад.
Однажды в конце XVI века человек по имени Галилео Галилей сидел в церкви и заметил, что лампы, свисающие с потолка, раскачиваются взад и вперед. Некоторые из ламп сильно раскачивались, а другие лишь слегка раскачивались взад и вперед, но все они довольно регулярно ходили взад и вперед. Галилей был любопытным человеком, и поэтому он решил использовать свое сердцебиение, чтобы измерить, сколько времени требуется маятникам, чтобы качаться туда-сюда. Он был очень удивлен тем, что узнал.Сегодня вы повторите эксперимент Галилея, чтобы узнать о маятниках.
Многие считают Галилея «отцом экспериментальной науки». До Галилея большинство людей пытались понять окружающий мир, просто думая о том, что они видели. Галилей, конечно, много думал, но он сделал то, что сделали немногие другие: он провел эксперименты, чтобы проверить свои идеи. Вот как сегодня люди занимаются наукой и техникой!
Благодаря своим экспериментам Галилей смог описать движение маятника с помощью математического уравнения, включенного в этот урок.В конце концов, ему пришла в голову идея использовать маятник как способ отслеживать время. Он использовал свои открытия как инструмент для других экспериментов, в которых он сделал много других открытий.
Инженеры также используют изобретения и открытия для создания новых вещей. Сегодня инженеры используют маятники в часах, но они также используют их для обнаружения землетрясений и защиты зданий от сотрясений. Инженеры используют маятники, чтобы измерить скорость полета пули и помочь роботам балансировать. Может быть, вы тоже придумаете новые способы использования маятника!
Оказывается, понимание движения маятника действительно полезно.Многие другие объекты регулярно движутся вперед и назад, как маятники, например, вес, подпрыгивающий на пружине, вращающееся колесо — даже радиоволны идут вперед и назад! Физика понимания того, как ведут себя маятники, — важный шаг к пониманию всех видов движения. Обратитесь к соответствующему упражнению «Качели во времени» для учащихся, чтобы узнать, как работают маятники, используя простые, сделанные вручную маятники, для экспериментов с веревками различной длины и веса.
За свою жизнь Галилей сделал множество научных открытий, включая описания гравитации и движения падающих объектов, спутников Юпитера, новых видов термометров и многих других вещей.Он был пионером научного метода исследования окружающего мира. Сегодня мы пойдем по стопам Галилея, чтобы узнать, как ведут себя маятники.
Предпосылки и концепции урока для учителей
Считается, что интерес Галилея к маятникам возник, когда он сидел в соборе в Пизе, Италия. После того, как он заметил, что лампы регулярно качаются вперед и назад, он начал экспериментировать с маятниками, чтобы узнать об их движении.Маятники — довольно простые устройства, и факторы, которые могут повлиять на их движение, — это длина струны, вес боба и размер качания. Галилей экспериментировал, чтобы определить, какая из этих переменных определяет частоту качаний маятника.
На этом уроке ученики наблюдают, что размер качелей не влияет на время, необходимое маятнику, чтобы качаться взад и вперед. Как и Галилей, ученики обнаруживают, что даже когда маятник качается на небольшой угол, время каждого качания (период) остается таким же, как если бы он качался на большой угол! Как и Галилей, студенты также обнаруживают, что не имеет значения, какой массы объект на конце струны — время каждого колебания (период) остается тем же.Поскольку Галилей учился в медицинской школе, когда проводил свои эксперименты, он решил, что маятник будет полезен для измерения пульса пациентов. Возможно, студенты тоже подумают о новых применениях! Обратитесь к соответствующему заданию «Космический ритм» для учащихся, чтобы изучить механическую концепцию ритма, основанную на принципе колебания, в более широком биологическом и культурном контексте
Благодаря Галилею мы теперь знаем, что период маятника можно математически описать уравнением:

Где:
P = период; я.е., время одного качания маятника [сек]
l = длина от фиксированной точки наверху маятника до центра масс боба [м]
г = гравитационная постоянная (9,8 м / сек 2 )
π ≈ 3,14 (безразмерная постоянная)
Обратите внимание, что это уравнение не включает членов для массы маятника или угла, на который он качается. Единственный фактор, который существенно влияет на раскачивание маятника на Земле, — это длина его струны.
Студенты могут задаться вопросом, почему длина веревки — единственное, что влияет на период маятника. Это можно объяснить, исследуя возможные эффекты каждой из трех переменных: длины струны, массы боба и смещенного угла. Длина струны влияет на период маятника, так что чем больше длина струны, тем длиннее период маятника. Это также влияет на частоту маятника, то есть скорость, с которой маятник раскачивается вперед и назад.Маятник с более длинной струной имеет более низкую частоту, что означает, что он качается назад и вперед меньше раз за заданный промежуток времени, чем маятник с более короткой длиной струны. Это приводит к тому, что маятник с более длинной струной совершает меньше циклов вперед и назад за заданный промежуток времени, потому что каждый цикл занимает больше времени.
Масса боба не влияет на период маятника, потому что (как обнаружил Галилей и объяснил Ньютон) масса боба ускоряется к земле с постоянной скоростью — гравитационной постоянной, г .Подобно тому, как предметы разной массы, но одинаковой формы падают с одинаковой скоростью (например, мяч для пинг-понга и мяч для гольфа или виноград и большой шарикоподшипник), маятник тянется вниз с одинаковой скоростью, независимо от того, насколько сколько весит боб.
Наконец, угол, под которым маятник качается (большое или маленькое качание), не влияет на период маятника, потому что маятники, качающиеся на больший угол, ускоряются больше, чем маятники, качающиеся на небольшой угол.Это происходит из-за того, как падают предметы; когда что-то падает, оно продолжает ускоряться. Пока объект движется не так быстро, как может, он ускоряется. Следовательно, то, что падало дольше, будет двигаться быстрее, чем то, что только что было выпущено. Маятник, раскачивающийся под большим углом, притягивается вниз под действием силы тяжести на протяжении большей части своего поворота, чем маятник, раскачивающийся под небольшим углом, поэтому он ускоряется больше, преодолевая большее расстояние своего большого колебания за то же время, что и маятник, качающийся на небольшой угол, преодолевает меньшее пройденное расстояние.
Сопутствующие мероприятия
- Качели во времени — в этом практическом упражнении учащийся узнает, как работают маятники, используя простые, сделанные вручную маятники, для экспериментов с струнами различной длины и веса.
- Космический ритм — учащиеся изучают механическую концепцию ритма, основанную на принципе колебаний, в более широком биологическом и культурном контексте — в танцах и спорте, поэзии и других литературных формах, а также в общении в целом.В рамках задания ученики пишут стихи, используя рифму и размер.
Закрытие урока
Попросите учащихся объяснить, какие факторы могут повлиять на период маятника. (Ответ: длина маятника, вес боба, угол качания маятника.) Какие факторы действительно влияют на период маятника? (Ответ: длина маятника.) Почему вес не имеет значения? (Ответ: потому что маятник, как и падающие предметы, не зависит от веса.) Как длина струны маятника влияет на его период? (Ответ: маятник с более длинной струной имеет более длительный период, что означает, что для завершения одного цикла вперед и назад требуется больше времени по сравнению с маятником с более короткой струной. Кроме того, маятник с более длинной струной имеет более низкую частоту, Это означает, что он совершает меньше циклов вперед и назад за заданный промежуток времени по сравнению с маятником с более короткой струной.) Почему угол начала маятника не влияет на период? (Ответ: потому что маятники, которые начинаются под большим углом, быстрее ускоряются, поэтому они движутся быстрее, чем маятники, начинающиеся под небольшим углом.)
Словарь / Определение
bob: качающийся груз на конце маятника.
гравитация: сила, притягивающая тела к центру Земли.
колебание: колебательное движение качения маятника вперед и назад. Одно колебание завершается, когда боб возвращается в исходное положение.
маятник: струна с грузом на одном конце, подвешенная к неподвижной опоре, так что она свободно качается вперед и назад под действием силы тяжести.
период: время, необходимое качению маятника, чтобы вернуться в исходное положение.
оценка
Оценка перед уроком
Вопросы для обсуждения: Задайте ученикам и обсудите их всем классом.
- Вы когда-нибудь качались на качелях? Вы двигаетесь быстрее, когда делаете большие или маленькие качели? (Ответ: Большие колебания.) Вы когда-нибудь наблюдали маятник? Что быстрее: маятник на длинной струне или маятник на короткой струне? (Ответ: длинная нить.) Можете ли вы представить себе вещи, которые движутся как маятники? (Возможные ответы: качели на качелях, качели из веревки, качели из шин, напольные часы, механизмы балансировки на роботах, цирковая трапеция и т. Д.) Скажите учащимся, что они узнают больше о маятниках на сегодняшнем уроке.
Оценка после введения
Голосование: Задайте вопрос «правда / ложь» и попросите учащихся проголосовать, подняв палец вверх за истину и вниз за ложь. Подсчитайте голоса и запишите итоги на доске. Дай правильный ответ.
- Верно или неверно: Галилей считается основателем современной науки, поскольку он проводил эксперименты. (Ответ: Верно)
- Верно или неверно: движение маятника можно описать математически. (Ответ: Верно)
- Верно или неверно: маятники используются только в часах.(Ответ: неверно)
- Верно или неверно: маятники помогают нам понять многие вещи, которые движутся вперед и назад. (Ответ: Верно)
- Верно или неверно: инженеры используют маятники для конструирования разных вещей, например роботов. (Ответ: Верно)
Итоги урока Оценка
Human Matching: На десяти листах бумаги напишите термин или определение пяти словарных слов. Попросите десять добровольцев из класса выйти в переднюю часть комнаты и раздайте каждому по одному из листов бумаги.Попросите каждого добровольца по очереди прочитать, что написано на его / ее бумаге. Остаток термина класса должен соответствовать определению путем голосования. Попросите студенческие «термины» стоять рядом с их «определениями». В конце дайте краткое объяснение понятий.
Мероприятия по продлению урока
В качестве исследовательского проекта библиотеки предложите студентам изучить Галилео Галил
.
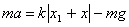 . Но
. Но 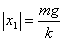 ,
,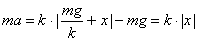 .
.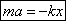 — ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к изменению положения равновесия.
— ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к изменению положения равновесия.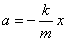 .
.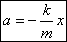
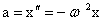 .
.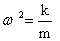 или
или 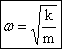 — циклическая частота при колебаниях пружинного маятника.
— циклическая частота при колебаниях пружинного маятника.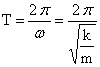 или
или 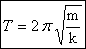 (формула Гюйгенса).
(формула Гюйгенса).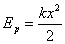 , а полная механическая энергия равна максимальной потенциальной или кинетической.
, а полная механическая энергия равна максимальной потенциальной или кинетической.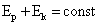 .
.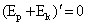 .
.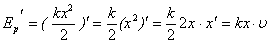 и
и 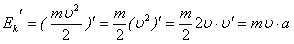 .
.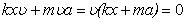 , а значит
, а значит 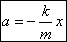 .
.

Leave A Comment