Формула частоты колебаний пружинного маятника в физике

Формула частоты колебаний пружинного маятника в физике

Частота колебаний

Определение

Частота колебаний ($\nu$) является одним из параметров, которые характеризуют колебания Это величина обратная периоду колебаний ($T$):

\[\nu =\frac{1}{T}\left(1\right).\]

Таким образом, частотой колебаний называют физическую величину, равную числу повторений колебаний за единицу времени.

\[\nu =\frac{N}{\Delta t}\left(2\right),\]

где $N$ — число полных колебательных движений; $\Delta t$ — время, за которые произошли данные колебания.

Циклическая частота колебаний (${\omega }_0$) связана с частотой $\nu $ формулой:

\[\nu =\frac{{\omega }_0}{2\pi }\left(3\right).\]

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:

\[\left[\nu \right]=с^{-1}=Гц. 2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решение уравнения (4) это функция синуса или косинуса вида:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(5\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний пружинного маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.

Частота колебаний пружинного маятника

Из формулы (3) и ${\omega }_0=\sqrt{\frac{k}{m}}$, следует, что частота колебаний пружинного маятника равна:

\[\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(6\right).\]

Формула (6) справедлива в случае, если:

  • пружина в маятнике считается невесомой;
  • груз, прикрепленный к пружине, является абсолютно твердым телом;
  • крутильные колебания отсутствуют.

Выражение (6) показывает, что частота колебаний пружинного маятника увеличивается с уменьшением массы груза и увеличением коэффициента упругости пружины. {-3}}=200\ \left(Гц\right).\]

Циклическая частота связана с частотой $\nu $ как:

\[{\omega }_0=2\pi \nu \ \left(1.2\right).\]

Вычислим циклическую частоту:

\[{\omega }_0=2\pi \cdot 200\approx 1256\ \left(\frac{рад}{с}\right).\]

Ответ. $1)\ \nu =200$ Гц. 2) ${\omega }_0=1256\ \frac{рад}{с}$

Пример 2

Задание. Массу груза, висящего на упругой пружине (рис.2), увеличивают на величину $\Delta m$, при этом частота уменьшается в $n$ раз. Какова масса первого груза?

Решение. Будем считать, что грузы на пружине совершают свободные гармонические колебания, тогда за основу решения задачи примем формулу:

\[\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(2.1\right).\]

Для первого груза частота будет равна:

\[{\nu }_1=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(2. 2-1}$

Читать дальше: формула частоты.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Глава 11. Механические колебания и волны

Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где — некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний.

Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде

(11.1)

где , и — некоторые числа.

Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний — это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус — периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем

(11.2)

Частотой колебаний тела называется число колебаний, совершаемых в единицу времени.

Очевидно, что частота колебаний связана с периодом колебаний по формуле

(11.3)

Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).

Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.

В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную

математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника

(11.4)

где — коэффициент жесткости пружины, — масса груза. Период колебаний математического маятника определяется следующим соотношением

(11. 5)

где — длина нити, — ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.

Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c

-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с-1 (ответ 1).

Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая.

За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4).

Величина перемещения тела — расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3).

По определению фаза колебаний — это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в

задаче 11.1.5 — 3.

Период — это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад.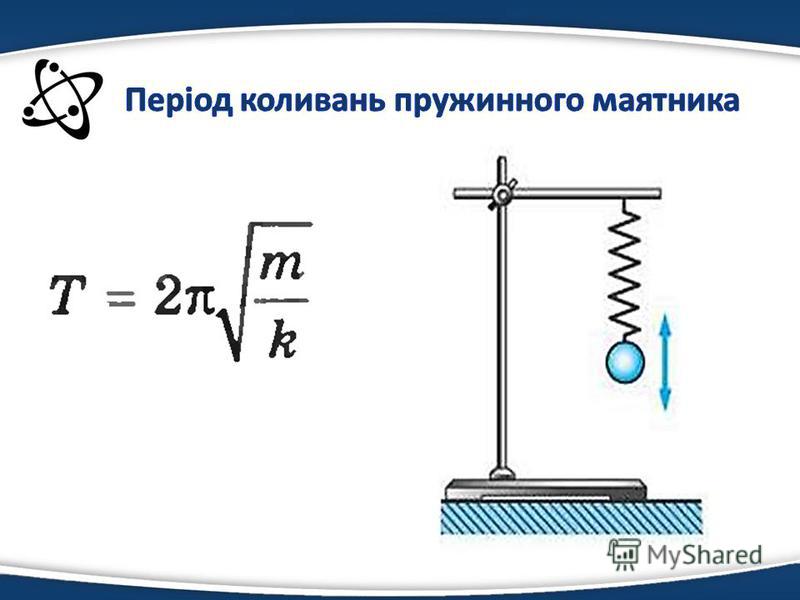 Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (

задача 11.1.6) тело затрачивает четвертую часть периода (ответ 3).

Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2. Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).

При гармонических колебаниях скорость тела изменяется по закону , где — амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени (задача 11. 1.8). Используя далее известную тригонометрическую формулу, получаем

Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2).

За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2).

Амплитуду колебаний скорости (задача 11.1.10) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где — коэффициент жесткости пружины, — амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где — масса тела, — скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим

(ответ 1), где использовано выражение для круговой частоты колебаний груза на пружине:

По формуле (11.4) получаем в задаче 11.2.1

(ответ 4).

Из формулы (11.5) заключаем (задача 11.2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).

Часы — это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3).

Чтобы найти амплитуду колебаний в задаче 11.2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим

где — такой угол, что . Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).

В задаче 11.2.5 имеем при см. Откуда см (ответ 2).

Задачи 11.2.6 и 11.2.7 посвящены механическим волнам. Волна – некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом (или связанной с ним частотой ), скоростью и длиной волны , которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны

(11.6)

которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Например, в задаче 11.2.6 по формуле (11.6) находим длину волны м (ответ 2).

Как следует из рисунка в задаче 11.2.7 длина волны, распространяющейся по шнуру, равна м. Поэтому по формуле (11. 6) имеем Гц (ответ 4).

Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то

где — амплитуда колебаний, — жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в раз (задача 11.2.8 – ответ 1).

Используя известную тригонометрическую формулу, получим в задаче 11.2.9

Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки . Амплитудой этих колебаний является множитель перед косинусом — (так как сам косинус меняется в интервале от -1 до 1). Циклической частотой — величина (ответ 4).

Вертикальный пружинный маятник отличается от горизонтального (задача 11.2.10) наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника от положения равновесия по закону (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине — одинаков (конечно, при условии, что и сам груз и пружины одинаковы). Правильный ответ в задаче — 3.

Физика — простое гармоническое движение

Колебания происходят повсюду вокруг нас, от биения человеческого сердца до вибрирующих атомов, из которых состоит все. Простое гармоническое движение является очень важным типом периодических колебаний, где ускорение ( α ) пропорционально смещению ( x ) от положения равновесия в направлении положения равновесия.

Перейти к:

Введение

Видео

В фокусе

Подкаст

Заключение

Следующие шаги

Что такое частота и период?

Поскольку простое гармоническое движение представляет собой периодическое колебание, мы можем измерить его период (время, необходимое для одного колебания) и, следовательно, определить его частоту (количество колебаний в единицу времени или обратную величину периода).

Два наиболее распространенных эксперимента, демонстрирующих это:

1. Маятник. Масса m , прикрепленная к концу маятника длиной l , будет колебаться с периодом ( T ). Описывается формулой: T = 2π√(l/g) , где g — ускорение свободного падения.

2. Масса на пружине. Если масса m , прикрепленная к пружине с жесткостью пружины k , будет колебаться с периодом ( T ). Описывается: T = 2π√(m/k) .

Измерив продолжительность одного полного колебания, мы можем определить период и, следовательно, частоту. Обратите внимание, что в случае маятника период не зависит от массы, а в случае массы на пружине период не зависит от длины пружины. Период простого гармонического осциллятора также не зависит от его амплитуды.

По определению, ускорение a объекта в простом гармоническом движении пропорционально его смещению, х :

, где ω — угловая частота, которую можно определить, зная период ( ω = 2π/T ) или частоту ( ω = 2πf ). Вспоминая, что скорость ( v ) является производной расстояния по времени, а ускорение является производной скорости по времени, можно показать, что, начиная с амплитуды ( A ), решение следует синусоидальной функции формы x = А cos(ωt)

Смещение во времени будет выглядеть примерно так: 

С графиками скорости и ускорения, заданными производными по времени. Эти осцилляторы также демонстрируют передачу кинетической и потенциальной энергии. При максимальном смещении вся энергия в системе находится в форме потенциальной энергии, а скорость равна нулю, но вся эта энергия преобразуется в кинетическую энергию, как только масса достигает положения равновесия, при котором она имеет максимальную скорость.

 Как мы измеряем колебания?

 

Простые гармонические колебания

 Насколько точны наши измерения?

Описанные здесь эксперименты демонстрируют использование комбинации аналоговых и цифровых приборов для измерения величин, включая массу, длину и время. В этом эксперименте одним из основных источников ошибки является время реакции человека при измерении периода. Чтобы повысить точность периода, синхронизация может быть получена по нескольким колебаниям и путем усреднения по нескольким измерениям периода. Чтобы получить более точные измерения жесткости пружины и ускорения свободного падения, следует проводить повторные измерения с использованием маятника различной длины и массы.

Кроме того, измерение периода на более длительном временном интервале (и, следовательно, на нескольких колебаниях) повысит точность, поскольку человеческая ошибка будет составлять меньшую часть записанного времени. Также может быть полезно использовать булавку или бирку в качестве фидуциарного маркера, показывающего положение равновесия. Предполагая простое гармоническое движение, периодическая природа этих систем означает, что не должно быть никаких оправданий, когда дело доходит до проведения нескольких измерений!

Labor Confessions

В подкасте Labor Confessions исследователи рассказывают о своем лабораторном опыте в контексте практических оценок уровня A. В этом выпуске мы рассмотрим генерацию и измерение волн и использование соответствующих цифровых инструментов.


Что означают ваши измерения?

Вибрации и колебания, окружающие нас в повседневной жизни, как правило, намного сложнее, чем те, с которыми мы сталкиваемся в простом гармоническом движении. Это означает, что такие эффекты, как демпфирование, уменьшающее амплитуду за счет удаления энергии из системы, являются хорошим примером того, как простое гармоническое движение способствует улучшению нашей повседневной жизни. Хотя простое гармоническое движение является упрощением, оно все же является очень хорошим приближением.

Простое гармоническое движение играет важную роль в исследованиях по моделированию колебаний, например, в ветряных турбинах и вибраций в автомобильных подвесках. В Университете Бирмингема один из исследовательских проектов, в котором мы участвовали, — обнаружение гравитационных волн в обсерватории лазерных интерферометров гравитационных волн (LIGO). Там детекторы настолько чувствительны, что решающее значение имеет тщательное моделирование и минимизация окружающих вибраций и шума. Еще одним заметным исследовательским проектом является работа Бирмингемской сети солнечных колебаний (BiSON), которая занимается измерением колебаний Солнца (гелиосейсмология) и близлежащих звезд (астросейсмология), чтобы узнать об их внутреннем строении.

Следующие шаги

 

Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания. 2} + \frac{g}{L}\theta = 0 $$ Простое гармоническое решение $$\theta(t) = \theta_o \cos(\omega t) \ , $$ где \(\theta_o\) — начальное угловое смещение, а \(\omega = \sqrt{g/L}\) собственная частота движения. Период этой системы (время одного колебания) равен $$ T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{L}{g}} . $$

Небольшие угловые смещения создают простое гармоническое движение

Период маятника зависит не от массы шара, а только от длины нити. Два маятника с разными массами, но одинаковой длины будут иметь одинаковый период. Два маятника разной длины будут иметь разные периоды; маятник с более длинной нитью будет иметь больший период.

Сколько полных колебаний совершают синий и коричневый маятники за время одного полного колебания более длинного (черного) маятника?

Исходя из этой информации и определения периода простого маятника, каково отношение длин трех маятников?

В предположении малых углов частота и период маятника не зависят от начальной амплитуды углового смещения. Маятник будет иметь один и тот же период независимо от его начального угла. Это простое приближение показано на анимации слева. Все три маятника совершают одно полное колебание за одинаковое время, независимо от начального угла. 92} + \frac{g}{L}\sin\theta = 0 $$ Это дифференциальное уравнение не имеет решения в закрытой форме, а вместо этого должно решаться численно с помощью компьютера. Mathematica очень легко численно решает это дифференциальное уравнение с помощью встроенной функции NDSolve[ ] .

Приближение малого угла справедливо для начальных угловых смещений около 20° или меньше. Если начальный угол меньше этой величины, то достаточно простого гармонического приближения. Но если угол больше, то различия между малоугловым приближением и точным решением быстро становятся очевидными.

На анимации внизу слева начальный угол мал. Темно-синий маятник — приближение малого угла, а светло-голубой маятник (изначально спрятанный сзади) — точное решение. Для малого начального угла требуется довольно большое количество колебаний, прежде чем разница между малоугловым приближением (темно-синий) и точным решением (светло-синий) начнет заметно расходиться.