Дробные выражения 6 класс онлайн-подготовка на Ростелеком Лицей

Дробное выражение

 

Что же такое дробь? Например, дробь  – это деление числа 7 на число 12, записанное с помощью дробной черты.

 

 

 

 

Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Примеры дробных выражений:

                                        

Дробь  также является дробным выражением.

 

Упрощение дробных выражений

 

 

У дробного выражения существуют эквивалентные, равные ему, выражения. Выбрать из всех эквивалентных выражений самое простое – значит упростить дробное выражение.

 

 

Пример

Упростить дробное выражение:

 

 

 

Решение

 

Выполним вычитание в числители и сложение в знаменателе:

 

 

 

Разделим числитель и знаменатель на 17:

 

 

 

Ответ: .

 

Задача 1

 

 

Упростите дробное выражение:

 

 

 

 

Решение

В числителе и знаменателе – смешанные дроби. Чтобы разделить одну смешанную дробь на другую, нужно обе записать как неправильные.

 

 

Получившееся дробное выражение эквивалентно произведению дробных выражений:

 

 

Сократим знаменатель первой дроби и числитель второй дроби на 3:

 

 

Ответ: .

 

Задача 2

 

 

Сложите дробные выражения:

 

 

 

Решение

1 способ

Приведем эти дробные выражения к одному знаменателю, для этого умножим числитель и знаменатель первой дроби на 2:

 

 

Чтобы избавиться от десятичной дроби в знаменателе, умножим числитель и знаменатель на 10:

 

 

Сократим числитель и знаменатель на 7:

 

 

2 способ

Можно сразу избавиться от десятичных дробей в знаменателях, для этого умножим числитель и знаменатель каждой дроби на 10:

 

 

Далее приводим два дробных выражения к общему знаменателю:

 

 

Сократим числитель и знаменатель на 7:

 

 

Ответ: .

 

Задача 3

 

 

Упростите дробное выражение:

 

 

 

Решение

Преобразуем числитель и знаменатель в обыкновенные дроби:

 

 

Запишем получившееся выражение с помощью знака деления:

 

 

Чтобы разделить на дробь, нужно умножить на перевернутую дробь:

 

 

Числитель первой дроби и знаменатель второй можно сократить на 5 и на 4:

 

 

Ответ: .

 

Задача 4

 

 

Упростите дробное выражение:

 

 

1.

 

Решение

Преобразуем числитель и знаменатель в обыкновенные дроби:

 

 

Запишем это дробное выражение с помощью знака деления, а далее заменим знак деления на знак умножения и перевернем вторую дробь:

 

 

Сократим числитель первой дроби и знаменатель второй на 3 и 7, а числитель второй дроби и знаменатель первой – на 5:

 

 

Сократим числитель и знаменатель на 2:

 

 

2)

 

Решение

Преобразуем числитель первого дробного выражения и знаменатель второго:

 

 

Распишем данные дробные выражения с помощью знака деления:

 

 

Заменим знаки деления на знаки умножения и перевернем соответствующие дроби:

 

 

Первое дробное выражение сократим на 9:

 

 

Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:

 

 

Вычислим числители обеих дробей и сложим эти дроби:

 

 

Сократим полученную дробь на 2:

 

 

Ответ: 1. ; 2. .

Преобразование «многоэтажных» дробей

Существует очень простой алгоритм, который позволяет за одно действие разобрать «многоэтажную» дробь и получить обычную «двухэтажную».

Необходимо после знака равно начертить дробную черту и для каждого элемента из «многоэтажной» дроби найти его место в новой дроби. Для этого нужно рассмотреть каждое число в исходной дроби.

 

Если число находилось в исходной дроби нечетное число раз в знаменателе, то в новой дроби оно окажется в знаменателе; если число находилось в исходной дроби четное число раз в знаменателе или не находилось в знаменателе вообще, то в новой дроби оно окажется в числителе.

 

Рассмотрим примеры.

Упростите дробные выражения.

 

1.

 

Рассмотрим каждое число данного дробного выражения:

Число 5 (в данном выражении две пятерки, их рассматриваем отдельно) находится в числителе дроби  и в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе дроби  и в числителе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;

число 16 находится в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 4 находится в числителе дроби  и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;

число 3 находится в знаменателе дроби  и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе четное число раз, следовательно, в новой дроби это число окажется в числителе;

число 5 находится в знаменателе всего дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе.

 

Запишем полученное дробное выражение:

 

 

 

Сократим числитель и знаменатель на 5 и на 4:

 

 

 

2.

 

Рассмотрим каждое число данного дробного выражения:

Число 3 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 5 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 7 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 6 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 8 находится в знаменателе дроби  и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 5 находится в знаменателе всего дробного выражения и в знаменателе выражения , то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 9 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

 

Запишем полученное дробное выражение:

 

 

 

Сократим числитель и знаменатель на 5, 7, 2 и 3:

 

 

 

3.

 

Рассмотрим числа в каждом дробном выражении:

 

а) выражение

 

Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 9 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 18 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

 

б) выражение

Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 2 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 7 находится в знаменателе дроби  и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 3 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

 

Запишем полученные дробные выражения:

 

 

 

Сократим числитель и знаменатель первого выражения на 9:

 

 

 

Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:

 

 

 

Вычислим числители обеих дробей и сложим эти дроби:

 

 

 

Сократим полученную дробь на 2:

 

 

 

Ответ: 1. ;  2. ;  3. .

 

 

Задача 5 (дробные выражения с переменными)

 

 

Чтобы найти значение выражения с переменными, необходимо подставить в это выражение значения этих переменных. Но предварительно имеет смысл упростить выражение, если это возможно.

 

 

Найти значение выражения.

 

1. , при ;

 

Решение

Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:

 

 

Подставим в полученное выражение значение переменных:

 

 

2. , при ;

 

Решение

Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:

 

 

Так как , то:

 

Мы получили ответ, даже не подставив значения переменных.

 

Ответ: . 1; 2. 0.

 

Список литературы

            1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

            2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

            3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

4. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «School-assistant.ru» (Источник)

2. Интернет портал «School.xvatit.com» (Источник)

3. Видеохостинг «YouTube» (Источник)

 

Домашнее задание

1. Задания 695 (ж, и), 698, 703 (в) (стр. 111–113) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6

2. Найдите значение выражения:

 

 

 

3. Найдите значение выражения

 

, при

 

Сложение и вычитание дробей

Репетиторы ❯ Математика ❯ Сложение и вычитание дробей

Автор: Валентин В., онлайн репетитор по математике

●

05.10.2011

●

Раздел: Математика

Сложение и вычитание дробей с одинаковым знаменателем отличается от сложения и вычитания дробей с разным знаменателем.

Если мы складываем / вычитаем дроби с одинаковым знаменателем, то:

1. производим требуемую вычислительную операцию с числителем;

2. знаменатель оставляем тем же.

Решим пример 5/6 – 2/6 = ?

1. Выполняем вычитание в чилителе: 5 – 2 = 3.

2. Знаменатель оставляем прежним, т.е. 6, следовательно, мы получаем дробь 3/6. Это и есть наш ответ.

НО! Нашу дробь можно сократить на 3: делим и числитель, и знаменатель на 3 и получаем 3/6 = 1/2.

Запишем полное решение нашего примера: 5/6 – 2/6 = (5 – 2)/6 = 3/6 = 1/2.

Чтобы сложить или вычесть дроби с разными знаменателями, нужно:

1. привести дроби к общему знаменателю;

2. сложить / вычесть получившиеся дроби с одинаковым знаменателем.

Как видим, сложение и вычитание дробей с разными знаменателями сводится к операциям с дробями с одинаковыми знаменателями. 

Рассмотрим пример: 3/10 + 4/15.

1. Наши дроби имеют разные знаменатели, поэтому приведем их к общему знаменателю.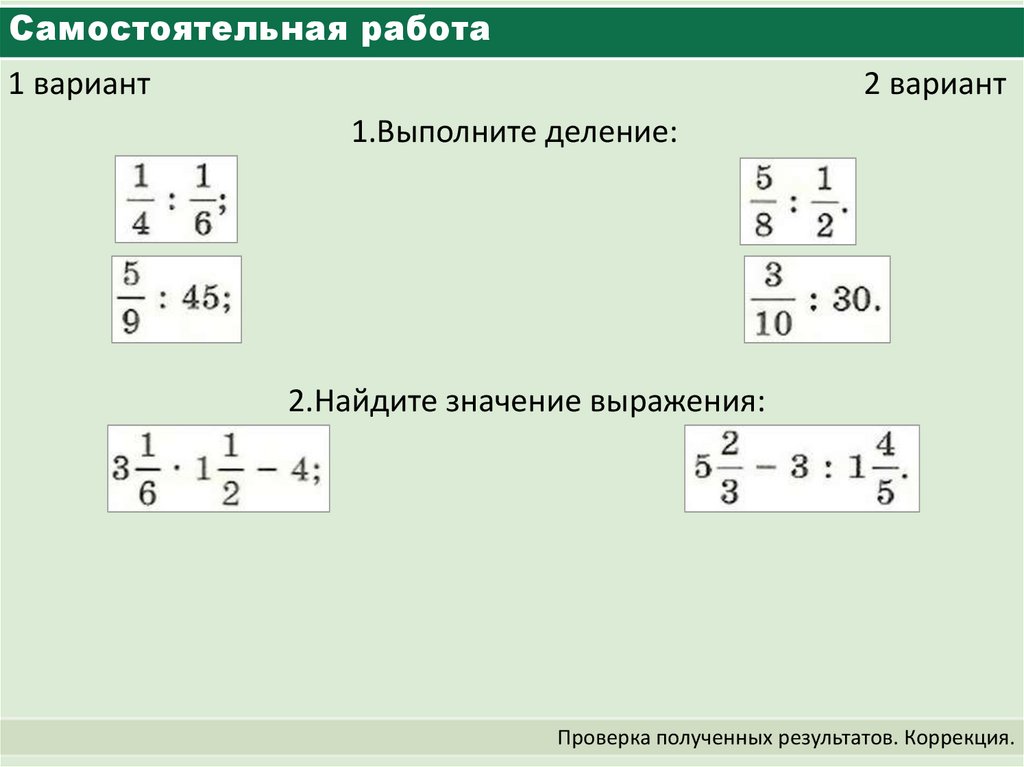 И 10, и 15 являются делителями числа 30, которое и будет нашим общим знаменателем. Чтобы привести наши дроби к общему знаменателю 30, первую дробь (и числитель, и знаменатель) нам нужно домножить на 3, а вторую (и числитель, и знаменатель) – на 2. Получаем: 3 ∙ 3/10 ∙ 3 + 4 ∙ 2/15 ∙ 2 = 9/30 + 8/30.

2. Складываем дроби с одинаковыми знаменателями: 9/30 + 8/30 = (9 + 8)/30 = 17/30. Итак, наш ответ 17/30.

Запишем решение примера:

3/10 + 4/15 = 3 ∙ 3/10 ∙ 3 + 4 ∙ 2/15 ∙ 2 = (9 + 8)/30

(9 + 8)/30 = 17/30.

Решим пример 3/8 + 1/4 = ?

1. Наши дроби имеют разные знаменатели, поэтому приведем их к общему знаменателю. И 8, и 4 являются делителями числа 8, которое и будет нашим общим знаменателем. Чтобы привести наши дроби к общему знаменателю 8, первую дробь (и числитель, и знаменатель) нам нужно домножить на 1 (она остается в первоначальном виде), а вторую (и числитель, и знаменатель) – на 2. Получаем: 3/8 + 1 ∙ 2/4 ∙ 2 = 3/8 + 2/8.

2. Складываем дроби с одинаковыми знаменателями: 3/8 + 2/8 = (3 + 2)/8 = 5/8.

Итак, наш ответ 5/8.

Запишем решение примера: 3/8 + 1/4 = 3/8 + 1 ∙ 2/4 ∙ 2 = 3/8 + 2/8 = (3 + 2)/8 = 5/8.

Основные законы сложения – переместительный, сочетательный и распределительный – также актуальны и при сложении и вычитании дробей.

Пример 1.

Найдем значение выражения 5 – 4/9.

Решение.

1. Чтобы облегчить вычисления представим 5 как сумму 4 + 1. Наше выражение примет вид: 4 + 1 – 4/9.

2. Для удобства вычисления и используя наши законы, вычтем 4/9 из 1 (представим ее как 9/9) и прибавим к 4, т.е. выражение примет вид: 4 + (9/9 – 4/9).

3. Находим значение: 4 + (9/9 – 4/9) = 4 + 5/9 = 4 5/9.

Ответ: 4 5/9.

Пример 2.

Найдем значение выражения 3 – 1 3/7.

Решение.

1. Чтобы облегчить вычисления представим 1 3/7 как сумму 1 + 3/7. Наше выражение примет вид: 3 – (1 + 3/7).

2. Раскроем скобки нашего выражения: 3 – (1 + 3/7) = 3 – 1 – 3/7.

3. Для удобства вычисления и используя наши законы, вычтем 3 – 1, а затем от результата вычтем 3/7, т. е. выражение примет вид: (3 – 1) – 3/7.

4. Находим значение: (3 – 1) – 3/7 = 2 – 3/7 = 1 4/7.

Ответ: 1 4/7.

Пример 3.

Найдем значение выражения 2 3/5 + 1 1/4.

Решение.

1. Для удобства вычисления сложим целые части и дроби по отдельности, сгруппировав их.

Выражение примет вид: 2 + 1 + 3/5 + 1/4 = 3 + 3/5 + 1/4.

2. Чтобы сложить наши дроби, нам нужно привести их к общему знаменателю. Общий знаменатель для наших дробей – 20. Значит, первую дробь мы домножим на 4, а вторую на 5 и получим: 3 ∙ 4/5 ∙ 4 + 1 ∙ 5/4 ∙ 5 = 12/20 + 5/20 = 17/20.

3. Таким образом, наше выражение примет вид: 3 + 17/20 = 3 17/20.

Ответ: 3 17/20.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Алгебраические дроби — GCSE Maths

Здесь мы узнаем о алгебраических дробях , включая операции с дробями и решение линейных и квадратных уравнений, записанных в виде алгебраических дробей.

Существуют также рабочие листы с алгебраическими дробями, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое алгебраические дроби?

Алгебраические дроби — это дроби, содержащие хотя бы одну переменную.

Следующие алгебраические выражения являются примерами алгебраических дробей:

x — числитель:
 
 
 
\quad \quad \quad \frac{x}{12}
 
И числитель, и знаменатель содержат член x :
 
 
 
\quad \quad \quad \frac{x+1}{2x}

   Выражение в    членах x является    знаменателем:
 
    \quad \quad \frac{3}{x+1}\

   И числитель    и    знаменатель    содержат    выражение с x : 9{2}-9}

Основная цель этого урока — понять, как решать уравнения, включающие алгебраические дроби.

Все приведенные выше примеры являются выражениями, тогда как приведенные ниже примеры являются уравнениями, поскольку мы можем найти конкретные значения для x для каждого примера, чтобы решить уравнение.

Одношаговое уравнение:
 
 
\quad \quad \frac{x}{12}=4
 
Отдельный постоянный член:
 
\quad \frac{x+1}{2x}+4=x

Квадратное    уравнение: 9{2}-9}=2x-1

Важно уметь приводить алгебраические дроби к их простейшей форме. Если вам нужно попрактиковаться в этом или быстро освежить в памяти, см. урок , упрощающий алгебраические дроби , для получения дополнительной информации.

Пошаговое руководство: Упрощение алгебраических дробей

Что такое алгебраические дроби?

Как решать уравнения с алгебраическими дробями

Нам нужно уметь решать уравнения с алгебраическими дробями.

Давайте рассмотрим простой пример, когда \frac{8}{x}=2 .

Здесь знаменатель дроби содержит переменную, поэтому сначала нам нужно получить переменную из знаменателя.

Преобразовав уравнение, умножив обе части на x и затем разделив на 2, мы получим значение x=4.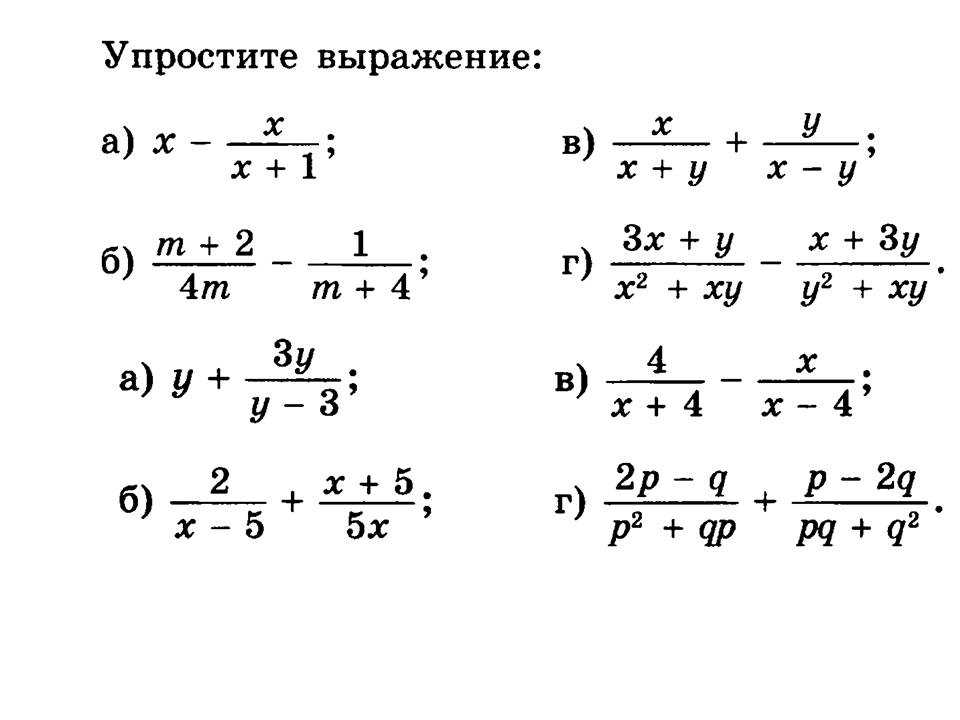

Мы можем подставить это в исходное уравнение, чтобы доказать, что ответ правильный.

Здесь \frac{8}{4}=2, поэтому у нас есть правильный ответ.

Рассмотрим теперь более сложные случаи, когда в уравнения входят алгебраические дроби.

Для решения уравнений, включающих алгебраические дроби.

  1. Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.
  2. Умножьте уравнение на общий знаменатель.
  3. Решите уравнение (линейное или квадратное).

Объясните, как решать уравнения, включая алгебраические дроби

Рабочий лист алгебраических дробей

Получите бесплатный рабочий лист алгебраических дробей, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист по алгебраическим дробям

Получите бесплатный рабочий лист по алгебраическим дробям, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры алгебраических дробей

Пример 1: Уравнение с одной дробью

Решить уравнение

\фракция{2x-1}{3}+x=3

  1. Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь у нас есть только одна дробь, поэтому нам не нужно преобразовывать какой-либо другой член в дробь.

2 Умножьте уравнение на общий знаменатель .

Умножая уравнение на 3 (знаменатель дробного члена), мы получаем

Убедитесь, что вы умножаете через каждые члена уравнения на 3 .

3 Решите уравнение (линейное или квадратное) .

Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.

Здесь

Пример 2: Уравнение с двумя дробями

Решить уравнение

\ гидроразрыва {х + 1} {2} + \ гидроразрыва {х + 3} {5} = 6

Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь у нас есть две дроби со знаменателями 2 и 5 . Наименьшее общее кратное 2 и 5 равно 10, поэтому мы можем преобразовать две дроби так, чтобы они имели одинаковый знаменатель.


Не забудьте использовать скобки, чтобы убедиться, что вы умножаете весь числитель на 5.


Не забудьте использовать скобки, чтобы убедиться, что вы умножаете весь числитель на 2.


Теперь у нас есть уравнение

Умножьте уравнение на общий знаменатель .

Умножая уравнение на 10 (знаменатель дробных членов), получаем

Решить уравнение (линейное или квадратное) .


Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.


Здесь

Пример 3: Уравнение с x в знаменателе

Решите уравнение

3-\фракция{5}{х+1}=6

Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь у нас одна дробь, поэтому нам не нужно находить общий знаменатель.

Умножьте уравнение на общий знаменатель .

Умножая уравнение на x + 1 (знаменатель дробных членов), мы получаем

Решите уравнение (линейное или квадратное) .


Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.


Здесь

Пример 4: Уравнение с тремя дробями

Решить уравнение

\frac{1}{x}+\frac{1}{2x}+\frac{1}{3x}=11

Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь нам нужно найти наименьшее общее кратное x, 2x и 3x. Поскольку х является наибольшим общим множителем, х \ умножить на 1 \ умножить на 2 \ умножить на 3 является наименьшим общим кратным, равным 6х. .


Итак, умножая числитель и знаменатель каждой дроби на константу, мы можем преобразовать каждую дробь, чтобы иметь общий знаменатель 6x:.


Теперь у нас есть уравнение, которое мы можем немедленно упростить.

Умножьте уравнение на общий знаменатель .

Умножая уравнение на 6x (знаменатель дробей), получаем

Решить уравнение (линейное или квадратное) .


Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.


Здесь

Пример 5: Знаменатели выражены через x

Решить уравнение

\ гидроразрыва {х + 1} {х + 2} + \ гидроразрыва {3} {х-4} = 1

Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь нам нужно найти общий знаменатель для (x + 2) и (x − 4) .


Самый простой способ сделать это — перемножить два выражения вместе.


Полезный совет: не раскрывайте скобки слишком рано, так как вы можете упростить дробь перед решением уравнения.


Умножая каждую дробь на знаменатель другой дроби, мы получаем


Теперь у нас есть уравнение, которое мы можем немедленно упростить.

Умножьте уравнение на общий знаменатель .

Умножив уравнение на (x+2)(x-4) (знаменатель дробной части), мы получим

Решите уравнение (линейное или квадратное) .


Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.


Здесь

Пример 6: Уравнение, включающее квадратное число

Решить уравнение

\фракция{9x+4}{x}=-2x

Преобразуйте каждую дробь так, чтобы все они имели общий знаменатель.

Здесь у нас одна дробь, поэтому нам не нужно находить общий знаменатель.

Умножьте уравнение на общий знаменатель .

Умножая уравнение на x (знаменатель дробных членов), получаем

Решить уравнение (линейное или квадратное) .


Вы можете проверить свое решение, подставив значение x в исходное уравнение и оценив его.


Здесь у нас есть два возможных решения для x, поэтому мы можем проверить оба:

Распространенные заблуждения

  • Умножение числителя на знаменатель

Рассмотрим пример 2 . При умножении на 10 для удаления знаменателя из каждой дроби числитель также умножается на 10.

Это означает, что дроби были умножены на 100 , а не на 10 , что делает следующую строку работы неверной.

  • Без учета знаменателей

При задании уравнения, включающего алгебраическую дробь, игнорирование знаменателей приведет к неправильному ответу на вопрос.

  • Без умножения всех членов на знаменатель

При перестановке уравнения знаменатель переносится на другую сторону знака равенства, а не умножается на него каждый член. Вы должны не забывать умножать на любое значение, а не только на противоположную сторону от знака равенства.

  • Неправильное упрощение дробей (1)

При сложении двух дробей знаменатель должен совпадать. Распространенным заблуждением для сложения двух дробей является сложение числителей и знаменателей вместе, потому что этот метод подчеркивается при рассмотрении умножения дробей.

  • Неправильное упрощение дробей (2)

Один и тот же член в числителе и знаменателе позволяет ошибочно предположить, что их можно отменить.

Практические вопросы с алгебраическими дробями

x=22,5

x=-\frac{39}{46}

x=\sqrt{11}

90 005

х=\фракция{14}{3 }

x=-5\pm\sqrt{31}

 

x=\frac{23}{3}

x=-1\pm2\sqrt{23}

x=-\frac{23}{3}

 

Алгебраические дроби Вопросы GCSE

1. Аррон зарабатывает 40 фунтов стерлингов в час. Однажды он получает бонус в размере 5 фунтов стерлингов. Заработок за этот день он делит поровну со своими братом и сестрой. Если он отдаст 190 фунтов стерлингов, сколько часов Аррон проработал в тот день?

 

(2 балла)

Показать ответ

2(\frac{40x+5}{3})=19{2}-4\times1\times{-24}}}{2\times{3}}

(1)

 

x=\frac{1\pm{17}}{6}

(1)

 

x=3 или x=-\frac{8}{3}

(1)

3. Две приведенные ниже фигуры имеют одинаковую площадь. Вычислите значение для x .

 

 

(7 баллов)

Показать ответ

Площадь треугольника = \frac{2(x+8)}{2}=x+8

92+8x-9=0

(1)

 

(х+9)(х-1)=0

(1)

 

x=1 или x=-9

(1)

 

Вывод: только x=1

(1)

Контрольный список для обучения

Вы теперь научились:

  • использовать алгебраические методы для решения линейных уравнений с 1 переменной (включая все формы, требующие перестановки)
  • упростить алгебраические дроби и управлять ими

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Дроби в выражениях и уравнениях: правила

Алгебраические выражения в математике состоят из констант и переменных связанных алгебраическими операциями (сложение, вычитание, умножение и деление). Дробь — это деление двух выражений: например, 12,x+13,xyx+y — дроби выражений, содержащих константы и/или переменные.

Уравнение — это математическое выражение, состоящее из символа равенства между двумя алгебраическими выражениями . Например, 12+x=2x+1 — это уравнение.

Решить уравнение означает найти значение переменной, которая составляет выражения в левой и правой частях равно ; это значение называется решением уравнения. Например, решение уравнения 12+x=2x+1 равно x=-12: если вы подставите это значение в обе части уравнения, вы получите 0=0.

В этой статье рассматривается наличие дробей в выражениях и уравнениях ; такие уравнения называются (что неудивительно) дробными уравнениями.

Первый шаг в работе с дробными уравнениями — исключить из них дроби . Давайте погрузимся и посмотрим, как этого добиться!

Что такое термины, коэффициенты, переменные и константы?

  • Термины являются строительными блоками алгебраических выражений: в выражении каждый термин отделяется знаком плюс (+) или минус (-). В уравнении 3x+4=10, 3x и 4 — члены выражения в левой части; а 10 — член выражения в правой части.
  • Коэффициенты — это значения, которые умножают переменные в выражении или уравнении. Учитывая выражение 34x+4, коэффициент — это число, которое умножает x, что равно 34.
  • Переменные — это буквы в выражениях и уравнениях, которые используются для представления неизвестных величин. Когда у вас есть выражение, заданное как 32x+12y, x и y идентифицируются как переменные.
  • Константы — это числа в выражениях и уравнениях, которые не изменяются. Например, в уравнении 2x-4y+4=0 константой является 4.

Рисунок 1. Термины по алгебре, siyavula.com

Как решать выражения с дробями: пошаговые примеры

Если вы имеете дело с дробями в выражениях, их проще всего складывать и вычитать, когда есть общих знаменателя . Это означает, что мы найдем эквивалентную долю участвующих дробей, найдя наименьший общий делитель (LCD) для знаменателей терминов.

Упростить 3×5+x4

Решение:

Здесь мы найдем общий знаменатель для двух членов, чтобы их можно было сложить. Во-первых, нам нужно будет найти LCD для знаменателей двух дробей, 5 и 4. Наименьший общий делитель для обоих чисел будет 20. Теперь мы найдем эквивалентную дробь для обоих.

Если знаменатель первой дроби теперь должен быть равен 20, это означает, что мы, вероятно, умножили первоначальный знаменатель, 5, на 4. Это означает, что нам придется умножить числитель также на 4, чтобы получить эквивалентную дробь.

443×5=12×20

Проделаем то же самое для второй дроби. 20 в знаменателе также означает, что мы должны были умножить 4 (в знаменателе) на 5, чтобы получить 20 в качестве нового знаменателя эквивалентной дроби. Это означает, что нам придется умножать числитель также на 5.

55×4=5×20

Теперь у нас есть новое выражение:

12×20+5×20

Это становится намного проще решить, поскольку все, что нам нужно сделать, это добавить числители и сохранить знаменатели.

12×20+5×20=17×20

Поскольку дальнейшее упрощение невозможно, остановимся на этом.

Решите выражения с дробями с помощью F

актуализация и G группировка

Могут быть более сложные задачи, где нам, возможно, придется использовать несколько методов, таких как факторизация и группировка . В этих ситуациях нужно быть очень осторожным в отношении того, что конкретно представляет собой термин и когда разделяются его компоненты. Давайте посмотрим на следующий пример:

Упростить ax-b+x-abax2-abx

Решение:

ситуация. Сначала мы сгруппируем одинаковые члены в числителе, переставив так, чтобы члены, содержащие x будут близки друг к другу, и термины, содержащие b , также будут близки.

ax-b+ x-abax2-abx

ax+x-b-abax2-abx

Теперь разложим на множители. Общий множитель первых двух членов числителя равен х. Это можно исключить. Общий множитель в последних двух членах числителя равен -b , и его также можно вынести за скобки.

x(a+1)-b(1+a)ax2-abx

Вся идея разложения на множители здесь заключается в построении общей скобки, чтобы можно было убрать одну из них. Здесь мы имеем (а+1) и (1+а). Учитывая коммутативность сложения, обе скобки совпадают.

Это оставит нас с:

(x-b)(a+1)ax2-abx

Теперь мы немедленно разложим знаменатель на множители. Поскольку x кажется общим в обоих терминах, это то, что будет исключено.

(x-b)(a+1)ax(x-b)

Теперь у нас осталась ситуация, когда мы можем свободно отменить. (x-b) в знаменателе отменяет (x-b) в числителе. Это верно, если x отличается от b.

(a+1)ax

Это самая простая форма, которую мы можем получить из этого выражения.

Как решать уравнения с дробями: пошаговые примеры

Как упоминалось ранее, при работе с уравнениями, содержащими дроби, нужно следить за тем, чтобы сначала исключить дробь . Вы должны умножить все члены в обеих частях уравнения на знаменатель дроби.

Если бы нам дали уравнение 5x+12=12, мы бы сначала умножили это уравнение (технически это также каждый член уравнения) на 2.

Решение:

2(5x+ 12=12)

2(5x)+2(12)=2(12)

После умножения на 2 дробь сократится.

10x+1=24

Теперь мы изменим уравнение, чтобы поместить одинаковые члены в разные стороны уравнения.

10x=24-1

10x=23

Разделить обе части на 10

10×10=2310

x= 2,3

в решение уравнения нужно подставить значение х обратно в исходное уравнение:

5(2. 3)+12=12

11.5+12=12

12=12

Solve32x+12(x-4)=6

Решение: 900 05

Уравнение с двумя дробями с одинаковыми члены знаменателя будут умножены на знаменатель, как упоминалось ранее.

2(32x)+2(12(x-4))=2(6)

3x+x-4=12

4x-4=12

Аналогичные термины теперь будут сгруппированы с этой точки.

4x=12+4

4x=16

Разделить обе части на 4

4×4=164

x=4

Чтобы оценить это, вам нужно подставить значение x обратно в исходное уравнение.

32(4)+12(4-4)=6

(3×2)+12(0)=6

6+0=6

6=6

Решить14x+32(2x-1 )=2

Решение:

Наш пример сильно отличается от обычного. Поскольку у нас есть две дроби с разными знаменателями, мы найдем НОК для обеих и умножим их на уравнение. LCM равно 4, поэтому

4(14x)+4(32(2x-1))=4(2)

1x+2(3(2x-1))=4(2)

Теперь расширим то, что в скобках :

1x+2(6x-3)=8

1x+12x-6=8

Групповые термины:

12x+1x=8+6

13x=14

Разделить e обе стороны на 13:

13×13=1413

x=1413

Чтобы оценить это, вам нужно подставить значение x обратно в исходное уравнение.