Построение графиков с модулями методом интервалов — ЗФТШ, МФТИ

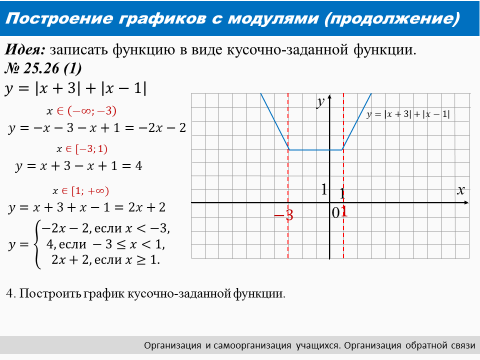
Если нужно построить график функции вида y=f(|x−a1|,y = f(|x − a_1|,|x−a2|,…,|x−an|)|x − a_2|,…,|x − a_n|), где a1,a_1,a2,…,ana_2,…,a_n – некоторые фиксированные числа, то в общем случае нет иного подхода, помимо раскрытия всех модулей. Ясно, что для всякого k=1,2,3,…,nk = 1, 2, 3,…, n

|x-ak|=|x — a_k| =x-ak=x-ak, если x ≥ak;ak-x, если x<ak.\left|x-a_k\right|=\left\{\begin{array}{l}x-a_k,\;\mathrm{если}\;x\;\geq a_k;\\a_k-x,\;\mathrm{если}\;x<a_k.\end{array}\right.

Однако, например, в случае a1<a2a_1 < a_2 невозможно выполнение одновременно двух условий: x<a1x < a_1 и x>a2x > a_2. Поэтому простое раскрытие модулей приведет к лишним действиям. Чтобы этого избежать, применяют так называемый метод интервалов. Суть его состоит в следующем. Числа a1a_1, a2,…,ana_2,…, a_n упорядочивают по неубыванию и наносят на числовую ось (рис. 35). Если для определённости положить a1<a2<⋯<ana_1 < a_2 < ⋯ < a_n, то это будет выглядеть так:

Получаем, что числовая ось разбивается на n+1n + 1 интервалов. Если xx лежит в любом из них, то мы однозначно можем определить знаки всех выражений под модулями и раскрыть модули. В каждом из получившихся интервалов график функции выстраивается отдельно. Граничную точку (a1,a2,…,an)(a_1, a_2,…, a_n) можно включать в любой из промежутков, концом которого она является. Проиллюстрируем этот алгоритм на примере.

Перед тем как перейти к нахождению наименьшего значения, сделаем небольшое теоретическое отступление.

С помощью графиков удобно исследовать функции на возрастание и убывание. Функцию y=f(x)y = f(x) называют строго возрастающей, если f(x1)<f(x2)f(x_1) < f(x_2) при x1<x2x_1 < x_2. Строго убывающие функции определяются неравенством f(x1)>f(x2)f(x_1) > f(x_2) при x1<x2x_1 < x_2. Если при x1<x2x_1 < x_2 верно f(x1)≤f(x2)f(x_1) ≤ f(x_2), то функцию y=f(x)y = f(x) называют возрастающей, а если f(x2)≤f(x1)f(x_2) ≤ f(x_1), то – убывающей. Для линейных функций признаком возрастания и убывания является знак коэффициента при хх. Если этот коэффициент отрицателен, то такая функция строго убывает на данном интервале. В случае положительности коэффициента функция строго возрастает. Таким образом, можно сделать такой вывод.

Характер возрастания (возрастание или убывание) функции вида

f(x)=c1|x−a1|+c2|x−a2|+ …+cn|x−an|f(x) = c_1|x − a_1| + c_2|x − a_2| +  … + c_n|x − a_n|,

может меняться только в точках x=a1,a2,…,anx = a_1, a_2,…, a_n (здесь a1≤a2≤…≤ana_1 ≤ a_2 ≤ … ≤ a_n, а c1c_1, c2,…,cnc_2,…, c_n – некоторые числа). Поэтому для нахождения наибольшего или наименьшего значения функции такого вида стoит обратить внимание на то, возрастает или убывает такая функция при x<a1x < a_1 и x>anx > a_n, а также сравнить значения функции ff в точках x=a1,a2,…,anx = a_1, a_2,…, a_n.

Возвращаемся к нашей задаче.

Похожую схему рассуждений можно применить и в задачах следующего типа.

Графики функций с модулями.

10 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Графики функций с модулями.

Проект:
Угарина Сергея, ученика
10п класса.

2. Цель работы:

Научится
строить графики функций
с модулями.
Хорошая подготовка к ЕГЭ.

3. 1 ФУНКЦИЯ С МОДУЛЕМ

Y=lXl
Строим график функции у = x
Из-за модуля положительная
часть графика отразится
вдоль оси У.
x 1 2
y 1 2

4.

2 функция с модулем.У=l10х+4l
Строим график функции
у=10х+4
Подставляем модуль и
функция станет
положительной во всей
области определения.
Положительная часть
первой функции
отразится от х=-0,4
х
у
0
4
-1
-6

5. 3 функция с модулем

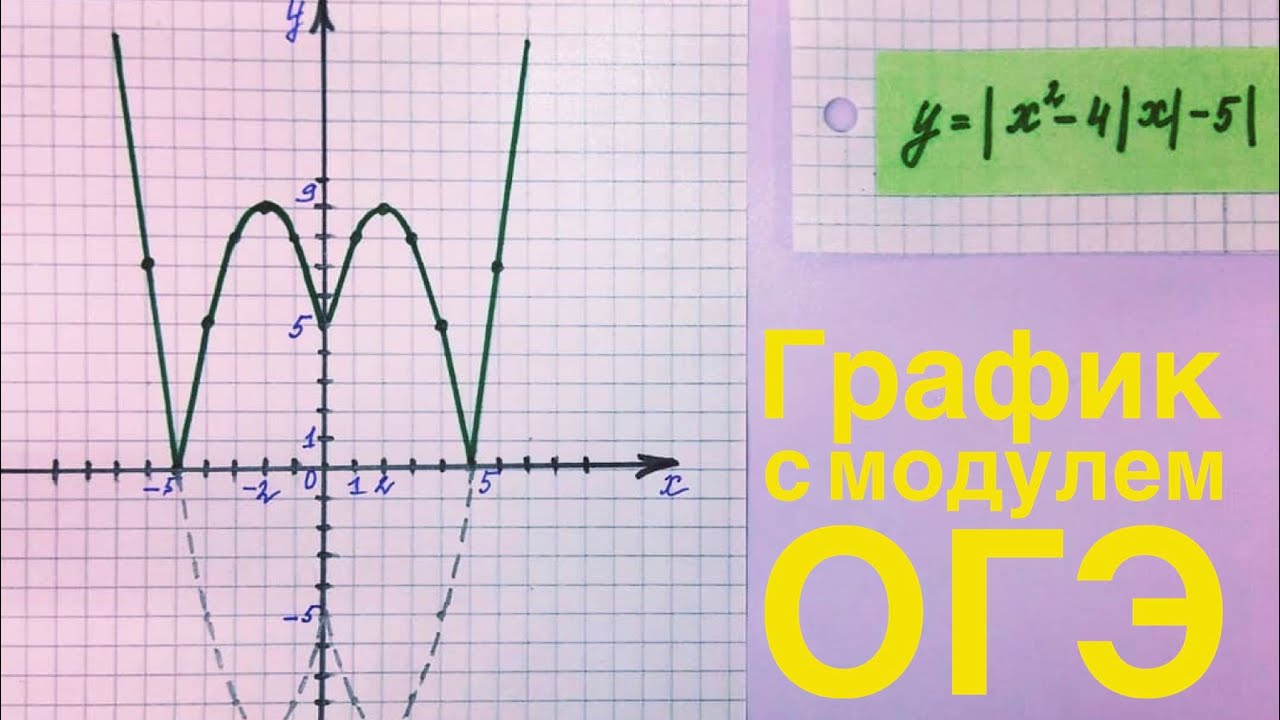
У=lx²-4l
Строим график функции у= х²-4
Это квадратичная функция,
графиком является парабола.
Чтобы построить параболу надо
найти как можно больше точек.
Сейчас строим график функции
у=lх²-4l, тогда отрицательная
сторона графика функции
у=х²-4 отразится по оси Х.
Областью определения будут все
числа, функция будет равняться
нулю в точках х = ±2.
х 1 2 -1 -2
у -4 0 -3 0

6. 4 функция с модулем

У=2х²-5lхl-7
Строим гр.функции
у=2х²-5х-7, приравняем
нулю и получим два
корня х=3,5 и х’=-1
Найдём вершину
функции. В точке х=1,5
у=-10
Строим график функции
у=2х²-5lхl-7.

7. 5 функция с модулем

У=l2х²-5х-7l
Строим график функции
у=2х²-5х-7
Всё также ,как и в
предыдущем слайде.
Потом строим график
функции у=l2х²-5х-7l
Функция станет только
положительным.
Отрицательная сторона
первой функции
отразится по оси Х

8. 6 функция с модулем

У=l2х²-5lхl-7l – сложная
функция. Строим сперва
график функции у=2х²5lхl-7 как в 4-ом слайде.
Потом всю эту функцию
берём под модуль.
Функция у=l2х²-5lхl-7l
будет положительным на
всей области
определения. Функция
будет равняться нулю в
точках х=±3,5

9. 7 функция с модулем

У=lх²+хl
Строим гр.ф у=х²+х
Эта квадратичная функция,
графиком является
парабола. Чтобы построить
параболу надо как можно
больше точек.
Строим гр.ф у=lх²+хl
Отрицательная сторона
отразится в положительную
сторону по оси Х.
х 1 -1 0 -2
у 2 0 0 2

10. 8 функция с модулем

У=lх³+х²-lхl+1l – сложная
функция.
Строи график функции
у=х³+х²-х+1. Это кубическая
функция, графиком является
гипербола. Чтобы построить
гиперболу надо найти как
можно больше точек. Потом
строим гр.ф. у=х³+х²-lхl+1 Изза модуль х, первая функция от
х=0 понижется резко. Потом
строим гр.ф. у=lх³+х²-lхl+1l
х
у
0
1
1
2
-1 2 -2
2 11 -1
Графики
функций с модулями
очень много встречаются на Е.Г.Э.
В средней школе графики функций
с модулями обучают в 10, 11
классах.
Вывод:Графики
функций надо
обязательно уметь строить, чтобы
не было проблем с такими
функциями на экзамене.

English     Русский Правила

Модуль скорости и графиков.

Модуль скорости и графиков.

ВВЕДЕНИЕ:

Понятие скорости важно во многих областях математики и наука. Эта концепция также дает возможность изучить и использовать некоторые из основных навыков и идей алгебры. Во многих случаях учащиеся сталкиваются с задачами «скорость-время». которые, как правило, решаются механическими процедурами, а не изучением реальные ситуации, в которых процедуры, необходимые для решения задача должна разрабатываться заново для каждой ситуации.

это только в упражнения устанавливаются в конце урока в учебнике, где все из проблем имеют одинаковую настройку.

Этот модуль посвящен скорости. Студенты будут исследовать скорость объекта, а также думать о скорости во многих ситуациях. Цель – получить хороший качественное понимание взаимосвязи между положение объекта в данный момент времени и его скорость. учащиеся также узнают, как измерять среднюю скорость и они исследуют, как получить более точные измерения скорость объекта. Акцент будет сделан на построении графиков для показать скорость в зависимости от времени, с формой графика больше интереса, чем фактические цифры на данный момент. Этот урок был первоначально разработан для класса алгебры восьмого класса. у учеников в классе был очень сильный курс предварительной алгебры, который включал многие из основных навыков манипулирования символами и написание выражений. Они не потратили много времени графические функции.

ПРЕДПОСЫЛКИ:

Минимальные предпосылки — это базовое понимание система координат (оси, зависимые и независимые переменные, нахождение и построение точек) и хорошие арифметические навыки — особенно дробь и десятичная арифметика.

Знакомство с графические калькуляторы или графические утилиты были бы полезны для расширения этих видов деятельности, но этот модуль не предполагает доступ к этим инструментам. Этот модуль развивает некоторые идеи о единиц измерения и интерпретации графиков довольно быстро.

Мотивацией для остальной части этого урока будет видео показывающее движение цилиндра, протаскиваемого через резервуар с вода. Это видео было записано в инженерной лаборатории в г. Университет штата Вашингтон. Лазерный световой лист используется для освещают один слой воды, а отражающие частицы равномерно распределяется по воде. Отражение лазера световой лист позволяет изучать движение жидкости за цилиндром. Мы будем использовать это видео для расследования скорость цилиндра.

Основное движение состоит из постоянного ускорения в течение короткого время, за которым следует период с постоянной скоростью (т. е. нулевой ускорение), и, наконец, происходит торможение до нуля. скорость. Фаза замедления прямо противоположна фаза разгона.

Основная проблема, которую мы будем исследовать, состоит в том, как получить график скорость против времени.

ПРОЦЕДУРА:

  1. Спросите класс, что означает слово «скорость». Попросите дать столько ответов, сколько сможет собрать класс — примите предложения без замечаний, или внесите позитив, прием комментариев по каждому предложению.

    Вебстерс Словарь New World Dictionary определяет скорость следующим образом: 1. быстрота или быстрота движения или действия; скорость 2. скорость изменения положения по отношению ко времени; курс движение в определенном направлении во времени.

    Так как это будет первое исследование скорости для многих студентов формальные или строгие определения не являются необходимый. В этот момент вам не нужно беспокоиться о представления о том, как измерять скорость или в каких единицах она должны быть измерены.

    В частности, понятие скорости как вектор с величиной и направлением не нужный. В начале нас интересует просто скорость. Хорошее определение в обсуждении с классом может быть «скорость есть мера того, насколько быстро что-то движется.»

    После того, как класс достигает приемлемого определения или скорость, спросите, сделает ли «отрицательная скорость» любое чувство. Даже при наивном определении скорости учащиеся должны уметь воспринимать отрицательную скорость как «скорость движения назад».

  2. Скажите классу, что вы что-то измерили и обнаружили, что это отмерил «сорок два». Пауза. Спросите класс, если что-то кажется неправильным в том, что вы только что сказали. Класс следует указать, что вы не сказали, какие единицы измерения, т.е. «сорок два что такое ?» Возможно, у вас есть измерил вес вашей собаки как 42 фунта, или ваш рост ребенка должен быть 42 дюйма.
    Спросите класс, сколько вещи, которые могли бы быть, и какое измерение, и какие единицы.

    Если класс не происходит по скорости в качестве измерения предположите, что вы, возможно, имели в виду скорость в какой-то момент по дороге в школу составляла 42 мили в секунду. час. Спросите, кажется ли это разумным: эта скорость могла бы измеряться в милях в час. Спросите, могут ли они придумать другие единицы измерения скорости, например: дюймы в секунду, футы в минуту, мили в сутки, сантиметры в секунду. Предложите классу придумать как можно больше.

    Изобретение единиц скорости должно привести к открытие, что все единицы включают единицу длины в единицу времени. При необходимости сделайте это явным для студенты. Это может быть добавлено к определению класса скорость.

  3. Имея под рукой определение скорости класса, спросите класс, чтобы предположить, кто может быть заинтересован в скорости. В каких профессиях люди будут заинтересованы в скорости, и скорость когда-либо играет роль в их повседневной жизни. Ответы и комментарии могут сильно различаться. Не беспокойся с нахождением какого-либо конкретного набора ответов; осознание цель с этим вопросом.
  4. Покажите видео, время от времени останавливаясь, чтобы описать ситуации, включая проводимые исследования. В этом исследования, необходимо знать скорость цилиндр. Спросите учащихся, как они могут определить скорость цилиндра за один из его ходов. Давать подсказки по мере необходимости, чтобы помочь им придумать некоторые идеи или идеи. В этот момент средняя скорость равна иметь самый интуитивный смысл. Общее расстояние поездки деленное на время дает среднюю скорость. Проверьте, чтобы посмотреть, есть ли у студентов какие-либо мысли относительно того, почему это можно назвать «средней скоростью».
    Быть уверенным они правильно рассчитали среднюю скорость для одного путешествие.
  5. Спросить, полностью ли вычислена средняя скорость описывает скорость цилиндра для этой поездки. В другими словами, двигался ли цилиндр с такой скоростью за всю поездку? Это очевидно в большинстве ситуаций что цилиндр ускоряется и замедляется. Таким образом средняя скорость не говорит всего о скорости. Обсудите это в контексте вождения автомобиля: если поездка от, скажем, Стивенсона до реки Худ, на расстоянии примерно 30 миль, занимает 32 минуты, это значит скорость во все времена была 56,25 миль в час? Нет. Как с цилиндром, скорость изменяется во времени.
  6. Сообщите учащимся, что для целей исследования с участием цилиндра, инженеры должны знать точную скорость цилиндра в любой момент времени. средней скорости просто не хватает для их работы. Просить если у кого-нибудь есть идеи, как дать лучшее представление о скорость цилиндра.

    Это намеренно открытый вопрос — не только для студентов, но и также для учителя. Одна из возможностей для улучшения картина скорости будет определять среднюю скорости за меньшие промежутки времени, например, средняя скорость за одну половину пути или один четвертая часть пути. Все это можно определить из видео. Когда учащиеся сравнивают их со своим первым средняя скорость, они могут продолжать делать это с меньшими интервалами времени, чтобы дать достаточно точную описание скорости. Если это не выходит из свою работу, предлагайте ее, но не форсируйте ее.

    Пока ученики бьются над вопросом, как дают очень хорошее представление о том, как изменяется скорость во время движение цилиндра, постановка основных задач для этого расследования может появиться. Когда студенты готово, может быть сформулировано утверждение: «Как может скорость цилиндра можно описать так, чтобы мы знали точную скорость в любой момент во время его путешествия?»

  7. Оставьте на время вопрос о цилиндре. Следующим действием является интерпретация графиков скорости. Подарок следующую картинку ученикам и скажите им, что это график, показывающий скорость во времени. Попросите их «расскажи историю», описывающую ситуацию.

    Повторите для следующих графиков.

  8. Обратный процесс от действия 7. Прочтите следующее «рассказ» детям и попросить их нарисовать график, представляющий скорость во времени.

    «Я прыгнул в моем Subaru и взлетел так быстро, как я мог. Я сделал от нуля до шестидесяти миль в час за 10 секунд. Затем я увидел государство Патрульная машина и быстро сбросила скорость до 55. Я добрался до Стивенсон и поехал прямо через город со скоростью 25 миль в час. я остановился в магазине на окраине города, чтобы возьми немного Fritos и Mountain Dew. »

    «Я гулял с собакой. Мы шли не слишком быстро. Затем моя собака увидела кролика и начала тянуть изо всех сил. он мог, так что мы шли быстрее в течение нескольких минут. Затем Джордж (моя собака) должен был остановиться и «напоить куста». Это заняло много времени. Потом мы пошли дальше исходной скорости, пока мы не приблизились к дому. Мы провели в последний раз перед тем, как остановиться дома.»

    «В крупных городах почтальоны доставляют почту от двери к двери, останавливаясь для доставки почты, затем переходя к следующий дом»

    «Йо-йо».

    При обмене картинками для этих историй слова «ускорение» и «торможение» должны быть введены надлежащим образом. Поощряйте использование этих условия там, где это уместно.

  9. Теперь учащиеся готовы нарисовать график скорость цилиндра в зависимости от времени. Как и выше, количественная оценка графики (прикрепление цифр и масштаба) не важны в этот момент. Попросите их нарисовать график, который будет работать для «истории» цилиндра. В других словами, вы просите их нарисовать зависимость скорости от времени график для цилиндра. Делитесь и обсуждайте эти фотографии для достижения общего понимания между студенты.
  10. Теперь, когда учащиеся имеют общую форму графика, они могут начать добавлять числа. На данный момент это полезно знать, сколько времени цилиндр тратит ускорение. Сообщите эту информацию учащимся и спросите их, как они могут использовать эту информацию.

    С момента ускорение и торможение равномерны и симметричны, теперь график можно построить достаточно точно. Поскольку скорость, конечно, постоянна между ускорением и замедление, любая средняя скорость, вычисленная в этом временной интервал будет представлять точную скорость цилиндр для этого интервала.

  11. К этому моменту класс будет готов рассмотреть другие ситуации. Настройка устройства для определения времени приличия мяч или другой предмет, катящий модель автомобиля или мяч вниз склоне или любой другой ситуации, в которой скорость изменения со временем послужили бы отличными расширениями. Позвольте учащимся рассмотреть основную форму график перед нанесением чисел. Это будет способствовать росту интуитивное понимание скорости.

    Другие расширения может включать рассмотрение положения в зависимости от времени. Идти через процесс, указанный выше, рисование общих графиков позиции в зависимости от времени для подгонки «истории» или Подгонка рассказа к графику. Нарисуйте и сравните положение графики и графики скоростей. Добавление графиков, показывающих ускорение во времени покажет учащимся все аспекты движения. Взаимосвязь этих трех величин есть важный аспект изучения исчисления и физики. Некоторый качественное понимание этих вопросов будет доступны для студентов из такого рода исследований.

Конечная математика | | Course Sidekick

Авторское право: Следующее программное обеспечение курса включает ресурсы, защищенные авторским правом и открыто лицензированные третьими сторонами в соответствии с лицензией Creative Commons. Нажмите «Лицензии и ссылки» внизу каждой страницы, чтобы просмотреть информацию об авторских правах и лицензии, относящиеся к материалам на этой странице. Если вы считаете, что этот учебный курс нарушает ваши авторские права, свяжитесь с нами.

Содержание курса

Краткий обзор содержания курса

Модуль 1: Функции и графики

Почему это важно

Чтение: функции и обозначения функций (часть I )

Чтение: функции и обозначения функций ( Часть II.0005

Чтение: Средняя скорость изменений

Собираем вместе

Модуль 2: Линейные функции в бизнесе

Почему это важно
9 0005

Чтение: линейные функции

Чтение: графики Линейные функции (часть I)

Интерактивное моделирование: графические линии

Чтение: Подгонка линейных моделей к данным

Видео: Линейная регрессия в Excel

Интерактивное моделирование: концепции регрессии методом наименьших квадратов

Литература: спрос, предложение и равновесие на рынках товаров и услуг ация)

Видео : Входы и выходы функции функции затрат (линейной)

Видео: Функции выручки, затрат и прибыли с использованием неравенств

Видео: Определение линейной функции спроса

Для чтения: Графики линейных функций (часть II)

Для чтения: Равновесие — где пересекаются спрос и предложение

Видео: Как рассчитать равновесную цену и количество 90 098

Чтение: Доход, Стоимость, и функции прибыли

Чтение: Анализ безубыточности

Видео: Анализ безубыточности

Видео: Применение линейной функции

Чтение: Решение одношаговых неравенств

Чтение: Многошаговые неравенства

Собираем вместе

Модуль 3: Функции в бизнесе

90 005

Почему это важно

Чтение: Факторинг

Чтение: Квадратичная формула

Чтение: Квадратичные графики

Чтение: Кратковременное поведение: Вершина Нахождение вершины квадратного числа

Видео: Нахождение квадратичной функции по пересечениям с графиком

Примеры работы : Приложения квадратичных функций

Видео: Спрос и выручка

Видео: Приложение квадратичных моделей

Видео: Квадратичный анализ спроса и предложения

Чтение: Графики полиномиальных функций (часть I)

Чтение: Графики полиномиальных функций (часть II)

Видео.