Определить допускаемую абсолютную и относительную погрешность
Задача 1. Вольтметр класса точности 0,5 имеет диапазон измерений от 0 до 100 В. Определить допускаемую абсолютную и относительную погрешность, если стрелка вольтметра остановилась на делении шкалы против цифры 30 В.
Решение:
Абсолютная погрешность:
γ=∆x∙100 %; ∆=γ∙x100%,
где γ – класс точности вольтметра; x – верхний предел вольтметра.
∆=0,5∙100100%=0,5 В.
Относительная погрешность:
δ=∆Y∙100%,
где ∆ – абсолютная погрешность вольтметра; Y – значение вольтметра.
δ=0,530∙100%=1,67%.
Ответ: Допустимая абсолютная погрешность вольтметра ∆=0,5 В. Допустимая относительная погрешность вольтметра δ=1,67 %.
Задача 2. Двумя амперметрами на 20 А был измерен ток на выходе трансформатора. Первый имеет погрешность 1% от верхнего предела и показал 4 А, а второй имеет погрешность 2% от верхнего предела и показал 3,98 А. Найти относительную погрешность второго амперметра.
Решение:
Абсолютная погрешность измерения этого амперметра составляет:
∆=3,98-4А=-0,02 А
Относительная погрешность второго амперметра:
δ=∆xд∙100%=-0,024∙100%=-0,5%
Ответ: Относительная погрешность второго амперметра равна –0,5%.
Задача 3. Пользуясь правилом округления, как следует записать результаты 148935 и 575,3455, если первая из заменяемых цифр является пятой по счету (слева направо)?
Ответ: Если первая (слева направо) из заменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются, т. е.
Задача 4. 1 аршин равен 2/3 м с погрешностью 6,7%. В обиходе пользуются еще соотношением 1 м = 1,5 аршина. Зная, что 1 аршин 0,7112 м, определите погрешность последнего допущения.
Решение:
∆=δ∙x100%=23∙6,7%100=0,04467 (ед)
Погрешность измерения при первом допущении составляет 0,04467 единиц. При этом допущение можно написать следующим образом – 1 аршин = (2/3±0,045) м. Однако величина второго допущения может быть расписана следующим образом: 1 аршин = 0,7112 м = (2/3+0,045). Из этого делаем вывод, что погрешность последнего допущения составляет также 6,7%.
Ответ: Погрешность последнего допущения составляет 6,7%.
Задача 1. Определить вероятность внезапного отказа измерительного преобразователя за 1000 ч работы, если он состоит из 5 резисторов с интенсивностью отказов λp=10-6 и 2 конденсаторов с λk=0,25∙10-4.
Решение:
Интенсивность отказов измерительного преобразователя:
λΣ=5∙λp+2∙λk=5∙10-6+2∙0,25∙10-4;
λΣ=5∙10-6+5∙10-510-5 ч-1 .
Вероятность безотказной работы за 1000 ч:
Р1000 ч=e-0tλΣtdt=e-010005,5∙10-5dt=e-0,055≈0,95
Вероятность отказа за 1000 ч:
Ротк1000 ч=1-Р1000 ч=1-0,95=0,05
Ответ: Вероятность внезапного отказа измерительного преобразования равна 0,05.
Задача 2. Определить пригодность вольтметра класса точности 1,0 с диапазоном измерений от 0 до 200 В, если при непосредственном сличении его показаний с показаниями образцового вольтметра были получены следующие данные:
Рабочий, В
25
50
75
100
150
175
200
Образцовый, В
24,9
51,5
77,9
101,5
149,9
199,9
Образцовый вольтметр имеет систематическую погрешность 0,5 В.
Решение:
По условию приведенная погрешность γ=1,0%.
∆max=77,9-75=2,9 В
γ=∆∙100%xN=2,9∙100200=1,45
Ответ: Вольтметр непригоден для использования, так как погрешность измерения превышает класс точности (погрешность измерения не может превышать допустимую, которая равна 2 В).
Задача 3. Для измерения тока от 20 А до 60 А с относительной погрешностью, не превышающей 2%, был заказан амперметр с верхним пределом измерения 100 А и классом точности 0,5. Удовлетворяет ли он поставленным условиям?
Решение:
δ=∆x∙100 % ⇒ ∆=δ∙x100%=2%∙20А100%=0,4 А
(измеренное значение тока x берем в начале шкалы, так как в начале шкалы относительная погрешность измерения больше).
γ=∆∙100%xN=0,4А∙100100=0,4%
что соответствует классу точности 0,5.
Ответ: Амперметр с верхним пределом измерения 100 А и классом точности 0,5 удовлетворяет поставленным условиям.
Задача 4. Электроизмерительный преобразователь состоит из 2 транзисторов с интенсивностью отказов λT=2∙10-7, 3 керамических сопротивлений с λс=6∙10-6 и 8 резисторов с λp=10-5. Определить вероятность безотказной работы этого средства измерений за 1000 ч работы.
Решение:
Интенсивность отказов электроизмерительного преобразователя:
λΣ=2∙λT+3∙λс+8∙λp=2∙2∙10-7+3∙6∙10-6+8∙10-5;
λΣ=4∙10-7+18∙10-6+8∙10-5=9,84∙10-5≈10-4 ч-1 .
Вероятность безотказной работы за 1000 ч:
Р1000 ч=e-λΣ∙t=e-10-4∙103=e-0,1≈0,9
Ответ: Вероятность безотказной работы электроизмерительного преобразователя равна 0,9.
megadocs.ru
1.1. Погрешности в метрологии
Ни одно измерение не свободно от погрешностей, или, точнее, вероятность измерения без погрешностей приближается к нулю. Род и причины погрешностей весьма разнообразны и на них влияют многие факторы (рис.1.2).
Общая характеристика влияющих факторов может быть систематизирована с различных точек зрения, например, по влиянию перечисленных факторов (рис.1.2).
По результатам измерения погрешности можно разделить на три вида: систематические, случайные и промахи.
Систематические погрешности, в свою очередь, делят на группы по причине их возникновения и характеру проявления. Они могут быть устранены различными способами, например, введением поправок.
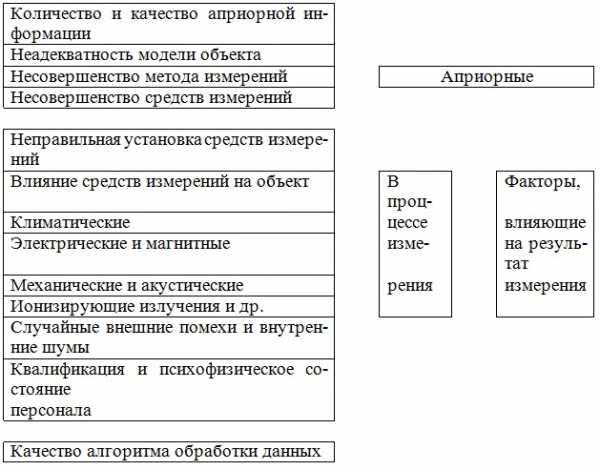
Случайные погрешности вызываются сложной совокупностью изменяющихся факторов, обычно неизвестных и трудно поддающихся анализу. Их влияние на результат измерения можно уменьшить, например, путем многократных измерений с дальнейшей статистической обработкой полученных результатов методом теории вероятностей.
К промахам относятся грубые погрешности, которые возникают при внезапных изменениях условия эксперимента. Эти погрешности по своей природе тоже случайны, и после выявления должны быть исключены.
Точность измерений оценивается погрешностями измерений, которые подразделяются по природе возникновения на инструментальную и методическую и по методу вычислений на абсолютную, относительную и приведенную.
Инструментальная погрешность характеризуется классом точности измерительного прибора, который приведен в его паспорте в виде нормируемых основной и дополнительных погрешностей.
Методическая погрешность обусловлена несовершенством методов и средств измерений.
Абсолютная погрешность есть разность между измеренным Guи истинным G значениями величины, определяемая по формуле:
Δ=ΔG=Gu-G
Заметим, что величина имеет размерность измеряемой величины.
Относительную
δ=±ΔG/Gu·100%
Приведенную погрешность рассчитывают по формуле (класс точности измерительного прибора)
δ=±ΔG/Gнорм·100%
где Gнорм – нормирующее значение измеряемой величины. Ее принимают равной:
а) конечному значению шкалы прибора, если нулевая отметка находится на краю или вне шкалы;
б) сумме конечных значений шкалы без учета знаков, если нулевая отметка расположена внутри шкалы;
в) длине шкалы, если шкала неравномерная.
Класс точности прибора устанавливается при его проверке и является нормируемой погрешностью, вычисляемой по формулам
γ=±ΔG/Gнорм·100%, если ΔG
где ΔGm – наибольшая возможная абсолютная погрешность прибора;
Gk – конечное значение предела измерения прибора; с и d – коэффициенты, учитывающие конструктивные параметры и свойства измерительного механизма прибора.
Например, для вольтметра с постоянной относительной погрешностью имеет место равенство
δm=±c
Относительная и приведенная погрешности связаны следующими зависимостями:
а) для любого значения приведенной погрешности
δ=±γ·Gнорм/Gu
б) для наибольшей приведенной погрешности
δ=±γm·Gнорм
Из этих соотношений следует, что при измерениях, например вольтметром, в цепи при одном и том же значении напряжения относительная погрешность тем больше, чем меньше измеряемое напряжение. И если этот вольтметр выбран неправильно, то относительная погрешность может быть соизмерима со значением Gн, что является недопустимым. Заметим, что в соответствии с терминологией решаемых задач, например, при измерении напряжения G = U, при измерении тока C = I, буквенные обозначения в формулах для вычисления погрешностей необходимо заменять на соответствующие символы.
Пример 1.1. Вольтметром, имеющим значения γm= 1,0 %, Uн = Gнорм, Gk = 450 В, измеряют напряжение Uu, равное 10 В. Оценим погрешности измерений.
Решение.
Ответ. Погрешность измерений составляет 45 %. При такой погрешности измеренное напряжение нельзя считать достоверным.
При ограниченных возможностях выбора прибора (вольтметра), методическая погрешность может быть учтена поправкой, вычисленной по формуле
Пример 1.2. Вычислить абсолютную погрешность вольтметра В7-26 при измерениях напряжения в цепи постоянного тока. Класс точности вольтметра задан максимально приведенной погрешностью γm=±2,5 %. Используемый в работе предел шкалы вольтметра Uнорм=30 В.
Решение. Абсолютная погрешность вычисляется по известным формулам:
(так как приведенная погрешность, по определению, выражается формулой , то отсюда можно найти и абсолютную погрешность:
Ответ. ΔU = ±0,75 В.
Важными этапами в процессе измерений являются обработка результатов и правила округления. Теория приближенных вычислений позволяет, зная степень точности данных, оценить степень точности результатов еще до выполнения действий: отобрать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата, но не слишком большую, чтобы избавить вычислителя от бесполезных расчетов; рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результаты.
При обработке результатов применяют правила округления.
- Правило 1. Если первая из отбрасываемых цифр больше пяти, то последняя из сохраняемых цифр увеличивается на единицу.
- Правило 2. Если первая из отбрасываемых цифр меньше пяти, то увеличение не делается.
- Правило 3. Если отбрасываемая цифра равняется пяти, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается, если она не четная.
Если за цифрой пять есть значащие цифры, то округление производится по правилу 2.
Применяя правило 3 к округлению одного числа, мы не увеличиваем точность округления. Но при многочисленных округлениях избыточные числа будут встречаться примерно столь же часто, как недостаточно. Взаимная компенсация погрешности обеспечит наибольшую точность результата.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью.
Величина предельной погрешности не является вполне определенной. Для каждого приближенного числа должна быть известна его предельная погрешность (абсолютная или относительная).
Когда она прямо не указана, то подразумевается, что предельная абсолютная погрешность составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого соглашения всегда можно обойтись без указания предельной погрешности числа, округленного по правилам 1-3, т.е., если приближенное число обозначить буквой α, то
, где Δn – предельная абсолютная погрешность; а δn – предельная относительная погрешность.
Кроме того, при обработке результатов используются правила нахождения погрешности суммы, разности, произведения и частного.
- Правило 1. Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей отдельных слагаемых, но при значительном числе погрешностей слагаемых обычно происходит взаимная компенсация погрешностей, поэтому истинная погрешность суммы лишь в исключительных случаях совпадает с предельной погрешностью или близка к ней.
- Правило 2. Предельная абсолютная погрешность разности равна сумме предельных абсолютных погрешностей уменьшаемого или вычитаемого.
Предельную относительную погрешность легко найти, вычислив предельную абсолютную погрешность.
- Правило 3. Предельная относительная погрешность суммы (но не разности) лежит между наименьшей и наибольшей из относительных погрешностей слагаемых.
Если все слагаемые имеют одну и ту же предельную относительную погрешность, то и сумма имеет ту же предельную относительную погрешность. Иными словами, в этом случае точность суммы (в процентном выражении) не уступает точности слагаемых.
В противоположность сумме разность приближенных чисел может быть менее точной, чем уменьшаемое и вычитаемое. Потеря точности особенно велика в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.
- Правило 4. Предельная относительная погрешность произведения приближенно равна сумме предельных относительных погрешностей сомножителей: δ=δ1+δ2, или, точнее, δ=δ1+δ2+δ1δ2 где δ – относительная погрешность произведения, δ1δ2 — относительные погрешности сомножителей.
Примечания:
1. Если перемножаются приближенные числа с одним и тем же количеством значащих цифр, то в произведении следует сохранить столько же значащих цифр. Последняя из сохраняемых цифр будет не вполне надежна.
2. Если некоторые сомножители имеют больше значащих цифр, чем другие, то до умножения следует первые округлить, сохранив в них столько цифр, сколько имеет наименее точный сомножитель или еще одну (в качестве запасной), дальнейшие цифры сохранять бесполезно.
3. Если требуется, чтобы произведение двух чисел имело заранее данное число вполне надежное, то в каждом из сомножителей число точных цифр (полученное измерением или вычислением) должно быть на единицу больше. Если количество сомножителей больше двух и меньше десяти, то в каждом из сомножителей число точных цифр для полной гарантии должно быть на две единицы больше, чем требуемое число точных цифр. Практически же вполне достаточно взять лишь одну лишнюю цифру.
- Правило 5. Предельная относительная погрешность частного приближенно равна сумме предельных относительных погрешностей делимого и делителя. Точная величина предельной относительной погрешности всегда превышает приближенную. Процент превышения примерно равен предельно относительной погрешности делителя.
Пример 1.3. Найти предельную абсолютную погрешность частного 2,81 : 0,571.
Решение. Предельная относительная погрешность делимого есть 0,005:2,81=0,2%; делителя – 0,005:0,571=0,1%; частного – 0,2% + 0,1%=0,3%. Предельная абсолютная погрешность частного приближенно составит 2,81:0,571·0,0030=0,015
Значит, в частном 2,81:0,571=4,92 уже третья значащая цифра не надежна.
Ответ. 0,015.
Пример 1.4. Вычислить относительную погрешность показаний вольтметра, включенного по схеме (рис. 1.3), которая получается, если предположить, что вольтметр имеет бесконечно большое сопротивление и не вносит искажений в измеряемую цепь. Классифицировать погрешность измерения для этой задачи.
рис. 1.3
Решение. Обозначим показания реального вольтметра через И, а вольтметра с бесконечно большим сопротивлением через И∞. Искомая относительная погрешность
Заметим, что
,
тогда получим
Так как RИ >>R и R > r, то дробь в знаменателе последнего равенства много меньше единицы. Поэтому можно воспользоваться приближенной формулой , справедливой при λ≤1 для любого α. Предположив, что в этой формуле α = -1 и λ= rR (r+R)-1 RИ-1, получим δ ≈ rR/(r+R) RИ.
Чем больше сопротивление вольтметра по сравнению с внешним сопротивлением цепи, тем меньше погрешность. Но условие R<<RИ – достаточное, но не необходимое условие малости δ. Погрешность будет мала также и в том случае, когда выполняется условие r≤RИ, т.е. сопротивление вольтметра много больше внутреннего сопротивления источника тока. При этом внешнее сопротивление может быть как угодно велико.
Ответ. Погрешность систематическая методическая.
Пример 1.5. В цепь постоянного тока (рис.1.4) включены приборы: А – амперметр типа М 330 класса точности КА = 1,5 с пределом измерения Ik = 20 А; А1 – амперметр типа М 366 класса точности КА1 = 1,0 с пределом измерения Iк1 = 7,5 А. Найти наибольшую возможную относительную погрешность измерения тока I2 и возможные пределы его действительного значения, если приборы показали, что I=8,0А. и I1 = 6,0А. Классифицировать измерение.
рис. 1.4
Решение. Определяем ток I2 по показаниям прибора (без учета их погрешностей): I2=I-I1=8,0-6,0=2,0 А.
Найдем модули абсолютных погрешностей амперметров А и А1
Для А имеем равенство для амперметра
Найдем сумму модулей абсолютных погрешностей:
Следовательно, наибольшая возможная и той же величины, выраженная в долях этой величины, равна 1 . 103 – для одного прибора; 2·103 – для другого прибора. Какой из этих приборов будет наиболее точным?
Решение. Точность прибора характеризуется значением, обратным погрешности (чем точнее прибор, тем меньше погрешность), т.е. для первого прибора это составит 1/(1 . 103) = 1000, для второго – 1/(2 . 103) = 500. Заметим, что 1000 > 500. Следовательно, первый прибор точнее второго в два раза.
К аналогичному выводу можно прийти, проверив соответствие погрешностей: 2 . 103 / 1 . 103 = 2.
Ответ. Первый прибор в два раза точнее второго.
Пример 1.6. Найти сумму приближенных замеров прибора. Найти количество верных знаков: 0,0909 + 0,0833 + 0,0769 + 0.0714 + 0,0667 + 0.0625 + 0,0588+ 0,0556 + 0,0526.
Решение. Сложив все результаты замеров, получим 0,6187. Предельная наибольшая погрешность суммы 0,00005·9=0,00045. Значит, в последнем четвертом знаке суммы возможна ошибка до 5 единиц. Поэтому округляем сумму до третьего знака, т.е. тысячных, получаем 0,619 – результат, в котором все знаки верные.
Ответ. 0,619. Количество верных знаков – три знака после запятой.
| 1. Метрология< Предыдущая | Следующая >1.2. Вероятный подход к оценке измерений |
|---|
xn—-8sbnaarbiedfksmiphlmncm1d9b0i.xn--p1ai
Расчет погрешностей средств измерений
Погрешность результата измерений в значительной мере зависит от погрешности средств измерений, являющейся важнейшей составляющей, от которой зависит качество измерений.
Технические характеристики, оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками средств измерений. В зависимости от специфики и назначения средств измерений, нормируются различные наборы или комплекты метрологических характеристик. В соответствии со стандартом метрологические характеристики средств измерений используются для определения результата измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений, расчета метрологических характеристик каналов измерительных систем и оптимального выбора средств измерений.
Инструментальная погрешность измерения – погрешность из-за несовершенства средств измерений. Эта погрешность в свою очередь обычно подразделяется на основную погрешность средств измерения и дополнительную.
Основная погрешность средства измерений – это погрешность в условиях, принятых за нормальные, т.е. при нормальных значениях всех величин, влияющих на результат измерения (температуры, влажности, напряжения питания и др.):
Δ=а или Δ=(а+bх), (1.1)
где Δ и хвыражаются в единицах измеряемой величины.
Абсолютной погрешностью прибора называется разность между показанием прибора и действительным значением измеряемой величины:
(1.2)
Поправкой прибора называется разность между действительным значением измеряемой величины и показанием прибора. Численно поправка равна абсолютной погрешности, взятой с обратным знаком:
=-Δх. (1.3)
Дополнительная погрешность возникает при отличии значений влияющих величин от нормальных. Обычно различают отдельные составляющие дополнительной погрешности, например, температурную погрешность, погрешность из-за изменения напряжения питания и т.п.
Относительная погрешностьсредств измерений — погрешность средств измерений, выраженная отношением абсолютной погрешности к действительному значению физической величины, в пределах диапазона измерений.
. (1.4)
где Δx — абсолютная погрешность;
xп — показания прибора.
Приведенная погрешностьсредств измерений — относительная погрешность, определяемая отношением абсолютной погрешности измерительного прибора к нормирующему значению. Нормирующее значение — это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы и т. д. Например, для милливольтметра термоэлектрического термометра с пределами измерений 200 и 600°С нормирующее значение
xN = 4000С. Приведенную погрешность можно определить по формуле
. (1.5)
где xn — нормирующее значение.
Например, значения абсолютной, относительной, приведенной погрешности потенциометра с верхним пределом измерений 150°С при хп=120°C, действительным значением измеряемой температуры Х=120,6°С и нормирующим значением верхнего предела измерений xn=150°С будут, соответственно, составлять Δxп = — 0,6°С, δ= — 0,5 %, γ= — 0,4 %.
Предел допускаемой погрешности средств измерений — наибольшая погрешность средств измерений, при которой оно может быть признано годным и допущено к применению. В случае превышения установленного предела средство измерений остается непригодным к применению.
Пределы допускаемой приведенной основной погрешности, определяемой по формуле (1.5),
, (1.6)
где p — отвлеченное положительное число, выбираемое из ряда: 1,0·10n; 1,5·10n; 1,6·10n; 2·10n ; 2,5·10n ; 3·10n; 4·10n; 5·10n; 6·10n (где п=1; 0; -1; -2 и т. д.).
Для средств измерений, используемых в повседневной практике, принято деление по точности на классы.
Класс точности средств измерений — обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполненных с помощью этих средств.
Классы точности устанавливаются стандартами, содержащими технические требования к средствам измерений, подразделяемым по точности. Средства измерений должны удовлетворять требованиям, предъявляемым к метрологическим характеристикам, установленным для присвоенного им класса точности как при выпуске их из производства, так и в процессе эксплуатации.
Пределы допускаемых дополнительных погрешностей устанавливают в виде дольного значения предела допускаемой основной погрешности для всей рабочей области влияющей величины или ее интервала, отношения предела допускаемой дополнительной погрешности, соответствующей интервалу величины, к этому интервалу, либо в виде зависимости предела, допускаемой относительной погрешности от номинальной или предельной функции влияния. Пределы всех основных и дополнительных допускаемых погрешностей выражаются не более чем двумя значащими цифрами, причем погрешность округления при вычислении пределов не должна превышать 5 %.
Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений, приводятся в нормативно-технических документах.
Пример
Десять одинаковых осветительных ламп соединены параллельно. Ток каждой лампы Iл = 0,3 А. Определить абсолютную и относительную погрешности амперметра, включенного в неразветвленную часть цепи, если его показания I1 = 3,3 А.
Решение
1. Ток в неразветвленной части цепи
.
2. Абсолютная погрешность
.
3. Относительная погрешность
.
Задачи
1. Температура в термостате измерялась техническим термометром со шкалой 0…500°С, имеющим пределы допускаемой основной погрешности ±4°С. Показания термометра составили 346 °С. Одновременно с техническим термометром в термостат был погружен лабораторный термометр, имеющий свидетельство о поверке. Показания лабораторного термометра составили 352°С, поправка по свидетельству составляет — 1°С. Определите, выходит ли за пределы допускаемой основной погрешности действительное значение погрешности показаний технического термометра.
2. Было проведено однократное измерение термо-ЭДС автоматическим потенциометром класса 0,5 градуировки ХК со шкалой 200…600°С. Указатель стоит на отметке 550°С. Оцените максимальную относительную погрешность измерения термо-ЭДС потенциометром на отметке 550°С. Условия работы нормальные.
3. Определить относительную погрешность измерения напряжения 100 В вольтметром класса точности 2,5 на номинальное напряжение 250 В.
4. Амперметр с верхним пределом измерения 10А показал ток 5,3 А при его действительном значении, равном 5,23 А. Определить абсолютную, относительную и относительную приведенную погрешности амперметра, а также абсолютную поправку.
5. При поверке амперметра с пределом измерения 5А в точках шкалы: 1; 2; 3; 4 и 5А получены следующие показания образцового прибора: 0,95; 2,06; 3,05; 4,07 и 4,95 А. Определить абсолютные, относительные и относительные приведенные погрешности в каждой точке шкалы и класс точности амперметра.
6. При поверке технического амперметра получены следующие показания приборов: поверяемый амперметр 1—2—3—4—5—4—3—2—1А,
образцовый ход вверх l,2—2,2—2,9—3,8—4,8 А
амперметр ход вниз 4,8—3,9—2,9—2,3—1,1 А.
Найти абсолютную и относительную приведенную погрешности, а также вариации показаний прибора. Определить, к какому классу точности его можно отнести.
7. Поверка вольтметра методом сравнения с показаниями образцового прибора дала следующие результаты:
Образцовый Поверяемый
прибор, V прибор, V
при увеличении при уменьшении
1 1,020 1,025
2 1,990 2,010
3 2,980 2,990
4 3,975 3,980
5 4,950 4,975
Определить наибольшую относительную приведенную погрешность и класс точности.
8. Определить относительную погрешность измерения напряжения, если показание вольтметра класса 1,0 с пределом измерения 300 В составило 75 В.
9. Определить абсолютную и относительную погрешности измерений, если вольтметр с пределом измерений 300 В класса 2,5 показывает 100 В.
10. Для измерения напряжения используются два вольтметра: V1(Uном=30 B; Кv= 2,5) и V2(Uном=150 В;Kv=1,0). Определить, какой вольтметр измеряет напряжение точнее, если первый показал 29,5 В, а другой — 30 В.
11. В цепь током 15 А включены три амперметра со следующими параметрами: класса точности 1,0 со шкалой на 50 А, класса 1,5 на 30 A и класса 2,5 на 20 А. Определить, какой из амперметров обеспечит большую точность измерения тока в цепи.
12. Имеются три вольтметра: класса 1,0 номинальным напряжением 300 В класса 1,5 на 250 В и класса 2,5 на 150 В. Определить, какой из вольтметров обеспечит большую точность измерениянапряжения 130 В.
13. Показания амперметра I1= 20 А, его верхний предел Iн = 50 А; показания образцового прибора, включенного последовательно, I = 20,5 А. Определить относительную и приведенную относительную погрешности амперметра.
14. Определить относительную погрешность измерения тока 10 А амперметром с Iн = 30 А класса точности 1,5.
15. При измерении мощности ваттметром класса точности 0,5, рассчитанным на номинальную мощность Рн = 500 Вт записано показание Р1=150 Вт. Найти пределы, между которыми заключено действительное значение измеряемой мощности.
16. Сопротивления включены по схеме, изображенной на рис.1.1. Ток в неразветвленной части цепи I=12 А, в сопротивлениях I1=3 А; I2=5А. Чему равны абсолютная и относительная погрешности амперметра, указанного на схеме, если его показания I3=3,8 А?
R1
R2
R3
Рис.1.1. Схема измерения тока
infopedia.su
Метрология
Тема 1. Единицы физических величин. Система СИ.
Задача 1.
Скорость автомобиля на прямолинейном участке трассы составила 169 км/ч. Перевести в единицы измерения системы СИ.
Решение:
169 км/ч=169000м/ч=169000м/3600с=46,94 м/с,
Ответ: скорость автомобиля составила 46,94 м/с.
Задача 2.
Во многих странах Европы температура измеряется по шкале Фаренгейта. Если в Париже 68ºF, а в Запорожье 21,5ºС то где теплее?
Решение:
tºF=9/5tºC+32 21,5·9/5+32=21,5·1,8+32=70,7ºF,
21,5·9/5+32=21,5·1,8+32=70,7ºF,
Ответ: по шкале Фаренгейта температура в Запорожье равна 70,7ºF что на 2,7ºF выше чем в Париже, следовательно в Запорожье теплее.
Задача 3.
Определить в единицах СИ среднюю скорость (v) объекта, если за время t=310м/с им пройдено расстояние S=15см.
Решение:
t=310м/с = 0,31с; S=15см=0,15м; v =S/t=0,15/0,31=0,4838м/с
Ответ: Средняя скорость объекта v=0,4838м/с.
Тема 2.Расчет погрешностей и округление результатов измерений. Оценка величины систематической погрешности ( введение поправок )
Задача 1.
Определить относительную и приведённую погрешности вольтметра, если его диапазон измерений от -12В до +12В. Значение поверяемой отметки шкалы х=7В. Действительное значение измеряемой величины У=7,978
Решение:
Относительная погрешность вольтметра
Приведённая погрешность вольтметра
где xN –нормирующее значение ( Верхний предел измерений )
Ответ:δ=13,86% ; γ=8,08%;
δ=14%; γ=8%;
Задача 2.
Определить погрешность при измерении тока амперметром класса точности z=1,5 если номинальный ток амперметра 30А , а показания амперметра х=11А
Решение:
Погрешность амперметра 30/100·1,5=±0,45А
30·0,015=±0,45А
Поэтому при показаниях амперметра х=11А
Погрешность Δх=±0,45А точнее как и в любой точке измерений.
Ответ: Δх=±0,45А
Задача 3.
Показания вольтметра с диапазоном измерений от 0В до 200В равных=154В. Образцовый вольтметр , включенный паралельно , показывает у= 147В. Определить относительную и приведенню погрешность рабочего вольтметра.
Решение:
Относительная погрешность рабочего вольтметра
Приведення погрешность рабочего вольтметра
Отивет: δ=4,76%; γ=3,5%.
Задача 4.
Найти относительную погрешность вольтметра класса точности Z=2
с диапазоном измерений от 0 до 120В. В точке шкалы х=47В.
Решение:
Абсолютная погрешность вольтметра
Δх= 120·0,02%=2,4В
Относительная погрешность
Ответ:δ=5,1%.
Тема 3. Методі и методики измерений. Расчёт надёжности приборов.
Задача 1.
Определить пригодность к дальнейшему применению рабочего вольтметра класса точности 1,75 с диапазоном измерений от 0 до 300В , если при непосредственном изменении его показаний с показаниями образцового вольтметра были получены следующие данные
Рабочий В | 60 | 120 | 180 | 240 | 300 |
Образцовый В | 61 | 119,3 | 180,8 | 239,4 | 299,06 |
Решение:
По условию приведённая погрешность γ=1,75%
Δmax= 61 — 60 = 1B
Ответ: Рабочий вольтметр пригоден к дальнейшему использованию.
Задача 2.
При поверке вольтметра класса точности с пределом точности 100В
Были получены следующие показания образцового и поверяемого вольтметров
Поверяемый В | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Образцовый В | 11,5 | 21,36 | 31,25 | 41,15 | 51,07 | 61 | 70,94 | 80,9 | 90,83 | 100,79 |
Оценить годность прибора. В случае брака указать точку, из-за которой принято данное решение.
Решение:
По условию приведённая погрешность γ=1% , что составляет 1В от придела измерений 100В. Следовательно вольтметр непригоден так как в точках 10; 20; 30; 40; 50- погрешность допускает допустимую.
Задача 3.
Определить относительную погрешность в начале шкалы на У=75 делениях для прибора класса 0,5 имеющего шкалу х=800 делений. На сколько эта погрешность больше погрешности на сотом делении шкалы прибора?
Решение:
По условию приведённая погрешность γ=0,5%
деления

Ответ: Погрешность в точке75 на 1,33% больше чем в точке 100.
Задача 4.
При контроле метрологических параметров деформационных (пружинных) манометров со шкалой на 450 делений , смещение стрелки от постукивания по корпусу должно оцениватся с погрешностьюне превышающей 0,1 цены деления шкалы. Составте эту погрешность отчёта с допустимой погрешностью для манометра класса 0,01.
Решение:
По условию приведённая погрешность γ=0,01%
Допустимая погрешность Δ=0,045 деления
Ответ:
Погрешность 0,1 цены деления превышает погрешность Δ=0,045 деления.
Задача 5.
Класс точности весов 0,01 определить допускаемую погрешность этих весов в начале ( 1деление ) в середине шкалы, если весы рассчитаны на 450 делений
Решение:
По условию приведённая погрешность γ=0,01%
Ответ:
Допускаемая погрешность Δ=0,045 делениям. Действует по всей длинне шкалы как в начале шкалы как и в середине так и в концешкалы.
Задача 6.
При измерении напряжения вольтметром класса точности 0,5 с верхним диапазоном измерений х=300В его показания были У= 155В. Определить относительную погрешность вольтметра.
Решение:
По условию приведенная погрешность γ=0,5%
Ответ:
Относительная погрешность вольтметра δ=0,97%
Задача 7.
Амперметр класса точности 1,5 имеет диапазон измерений от 0 до 300А. Определить допускаемую а бсолютную и относительные погрешности, если стрелка амперметра остановилась на делении шкалы против цифры У=155А.
Решение:
По условию  γ=1,5%
γ=1,5%
абсолютная погрешность
относительная погрешность
Ответ:
Абсолютная погрешность амперметра Δ=4,5А
Относительная погрешность амперметра δ=2,9%
Задача 8.
При определении класса точности ваттметра рассчитанного на 750Вт получили следующие данные:
50Вт – при мощности 50 Вт;
96Вт – при мощности 100Вт;
204Вт – при мощности 200Вт;
398Вт – при мощности 400Вт;
746Вт – при мощности 750Вт;
Какой класс точности прибора ?
Решение:
Класс точности показывает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, следовательно приведённой погрешности
Произведём погрешность прибора
Абсолютная погрешность при классе 0,53 составляет:
Так как приведённая погрешность действует по всей длинне шкалы то в любой точке шкалы погрешность не должна превышать Δ=4Вт
На шкале таких точек три:
750Вт — 746Вт = 4Вт
100Вт – 96Вт = 4Вт
200Вт – 204Вт = -4Вт
Также не существует класса точности 0,53
Поэтому ваттметру можно присвоить класс точности 1,0.
На шкале измерительного прибора маркеруют значение класса точности в виде числа , указывающего нормированное значение погрешности.
Выраженное в процентах , оно может иметь значения:
6;5;4;2,5;1,5;1,0;0,5;0,2;0,1;0,05;0,02;0,01;0,005 и т.д.
7
studfiles.net
Пример 1
Пример 1. Определить класс точности амперметра с конечным значением шкалы Iк=1,0 мА для измерения тока в диапазоне от 0,2 до 1,0 мА так, чтобы относительная погрешность δ1 не превышала 1%.
Решение:
Из относительной погрешности δ выразим абсолютную погрешность
===0,002 мА.
Измеренное значение тока –x, берём в начале шкалы, т.к. в начале шкалы относительная погрешность измерения больше.
γ===0,2% .
Нормированное значение — xN, берём в конце шкалы.
Ответ: класс точности амперметра 0,2%.
Пример 3. Определить класс точности вольтметра с конечным значением диапазона измерения Uк=300 В, если предел абсолютной погрешности измерения напряжения этим прибором равен =±0,5 В.
Решение:
Т.к. нам известна абсолютная погрешность, мы можем найти приведённую погрешность, приняв за нормированное значение xN конечное значение диапазона измерения Uк.
γ===0,2 %.
Ответ: класс точности вольтметра 0,2%.
Пример 4. Класс точности СИ 0,5/0,1. Записать выражение для относительной погрешности СИ и определить относительную погрешность для середины и края диапазона измерения.
Решение:
δ=[c+d·(-1)] =[0,5+0,1·(-1)]
δсеред.=[0,5+0,1·(-1)]= [0,5+0,1·(-1)]=0,6
δкрая.=[0,5+0,1·(-1)]= [0,5+0,1·(-1)]=0,5
Ответ: относительную погрешность для середины δсеред.=0,6 и относительную погрешность края диапазона измерения δкрая.=0,5.
Пример 8. Указатель относительного устройства амперметра класса точности 0,02/0,01 показывает минус 26 А. Шкала амперметра имеет конечные значения ±50 А с нулём в центре шкалы. Цена деления шкалы 1 А. Оценить результат измерения.
Решение:
По условию c/d=0,02/0,01, x=-26 А, xк=±50 А.
Из относительной погрешности δ выразим абсолютную погрешность
=.
δ=[c+d·(-1)]
== ±0,002 А.
Ответ: погрешность измерения амперметра составила ((-26) ±0,002) А.
studfiles.net
Погрешности измерения сопротивлений.
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
При измерениях возникают погрешности, имеющие различную природу. Погрешность метода (или методическая погрешность) связана с несовершенством метода, с упрощениями, принятыми в уравнениях для измерений. Погрешность метода проявляется, прежде всего, как систематическая, для компенсации которой возможно введение поправок. При измерении сопротивления методом «амперметра-вольтметра» возникает погрешность, определяемая способом подключения амперметра и вольтметра к исследуемому участку цепи.
Для измерения сопротивления R вольтметр и амперметр могут быть включены в цепь по одной из схем, изображенных на рис.1.
Технический метод с точным измерением тока. В схеме 1а вольтметр измеряет разность потенциалов U =j1 -j2 на последовательно соединенных проводнике сопротивлением R и амперметре PA сопротивлением RA. Поэтому разность потенциалов, измеренная вольтметром между точками 1 и 2, будет равна сумме падений напряжения на сопротивлении R проводника и сопротивлении RA амперметра:
(5)
а б
Рис.1
Расчет по формуле (4) будет содержать систематическую погрешность, обусловленную особенностями метода, т.е. по формуле (4), исходя из показаний вольтметра и амперметра, будет рассчитываться «экспериментальное» сопротивление RЭ, которое представляет собой сопротивление участка между точками 1и 2, содержащего последовательное соединение амперметра и исследуемого проводника.
Из (5) следует, что величина истинного сопротивления R проводника будет равна
(6)
где через U обозначена разность потенциалов на участке 1-2, измеряемая вольтметром.
Следовательно, разница DR между результатами измерения сопротивления RЭ по формуле (4) и истинным R и является той методической ошибкой, которая возникает при данном способе включения измерительных приборов:
(7)
Для расчета относительной погрешности этого метода примем допущение R≈RЭ (в силу малости сопротивления амперметра по сравнению с измеряемым сопротивлением R), тогда относительная погрешность этого метода равна:
(8)
Т.е. точность измерения сопротивления будет тем больше, чем меньше сопротивление RA амперметра по сравнению с сопротивлением R проводника. (Идеальным будет амперметр с бесконечно малым собственным сопротивлением).
Технический метод с точным измерением напряжения.В схеме 1б амперметром измеряется суммарный ток I , текущий через сопротивление R и вольтметр PV, имеющий собственное сопротивление RV. Разность потенциалов в этом случае одинакова как для проводника, так и для вольтметра.
Тогда по закону Ома:
, (9)
где IR и IV — токи, текущие соответственно через проводник и вольтметр PV , U — разность потенциалов, измеренная вольтметром.
Так как измеряемый ток равен I=IR + IV то, учитывая (9), получим:
IR=I – IV=(10)
Если не учитывать тока IV, текущего через сопротивление RV вольтметра, то величину сопротивления RЭ проводника также можно найти из результатов эксперимента по формуле (4).
Величина истинного сопротивления R проводника будет, согласно (9) и (10) равна
(11)
Разделив это выражение на I, с учетом RЭ=U/I, приходим к равенству:
(11′)
Следовательно, в этом способе измерения также возникает методическая погрешность:
(12)
Произведя незначительные преобразования, приходим к более лаконичному выражению:
(13)
Для расчета относительной погрешности этого метода примем следующие допущения:
1) R≈RЭ;
2) Так как сопротивление вольтметра, как правило, велико по сравнению с RЭ (т.е. RV>>RЭ ), томожно принять RV–RЭ ≈ RV.
Вычисляем относительную погрешность метода с точным измерением напряжения:
. (14)
Из равенства (14) видно, что точность измерения сопротивления будет тем больше, чем больше сопротивление вольтметра по сравнению с сопротивлением R проводника. Идеальным будет вольтметр с бесконечно большим собственным сопротивлением. Высокоомными являются электронные аналоговые и цифровые вольтметры, вносящие малую погрешность.
Погрешности метода возникают при использовании формулы (4). Они могут быть скорректированы, если известны сопротивления амперметра RA или вольтметра RV . Формулы (6) и (10) дают уже исправленный результат измерений, свободный от погрешности этого типа.
Другим источником систематической погрешности являются инструментальные погрешности, обусловленные конструкцией прибора и определяемые его классом точности. Однако в рамках данной лабораторной работы они не исследуются.
ОПИСАНИЕ УСТАНОВКИ
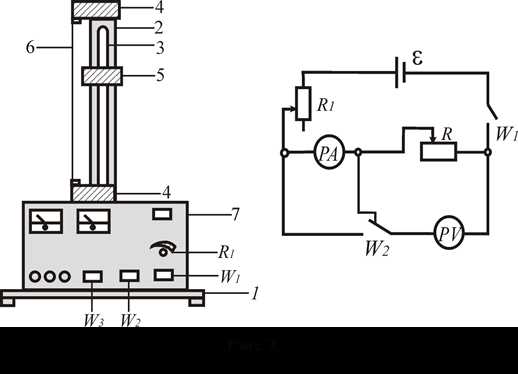 |
Прибор FRM-01 представлен на рис.2. К основанию 1 прикреплена колонна 2 с нанесенной миллиметровой шкалой 3. На колонне укреплены два неподвижных кронштейна 4 и один подвижный кронштейн 5, который может передвигаться вдоль колонны и фиксироваться в любом положении. Между верхним и нижним кронштейном натянут нихромовый провод 6.
Через контактный зажим на подвижном кронштейне обеспечивается хорошее гальваническое соединение с проводом. На подвижном кронштейне нанесена черта, которая облегчает определение по шкале длины отрезка измеряемого нихромового провода. Нижний, верхний и центральный подвижный контакты нихромового провода подведены при помощи проводов низкого сопротивления к измерительной части прибора 7, которая помещена в центральном корпусе.
На лицевой панели корпуса расположены амперметр PA, вольтметр PV , клавиша W1 для включения установки в сеть напряжением 220 В, переключатели W2 и W3, ручка реостата R1 регулировки тока. Отжатая клавиша переключателя W3 позволяет использовать нихромовый провод в мостовых схемах измерения сопротивления. Нажатая клавиша W3 позволяет произвести измерение активного сопротивления провода с использованием амперметра и вольтметра.
Если клавиша W2 отжата, то измерение происходит по схеме рис.1а — технический метод с точным измерением тока, если нажата- по схеме рис.1б — технический метод с точным измерением напряжения.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Заготовьте таблицу результатов измерений.
Таблица 2
| № | I i ,мА | U i, B | RЭ i,Ом | R i ,Ом |
2. Ручку регулятора тока установите в положение минимального тока (поверните против часовой стрелки до упора). Передвигая подвижный кронштейн (5), установите произвольную длину l проводника. Определите длину проводника, его диаметр (микрометром), а также сопротивление приборов (из паспортных данных), и запишите результаты в табл. 3.
Таблица 3
| l, мм | d, мм | R A ,Ом | R V,Ом |
3. Включите установку и произведите пять измерений сопротивления при разных токах методом точного измерения тока.
4. Заготовьте таблицу, аналогичную табл. 2. Произведите аналогичную серию измерений методом с точным измерением напряжения.
5. Выключите установку.
ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Вычислите неисправленное RЭi и исправленное значения Ri сопротивления проводника по формулам (4), (6) и (11), а также их средние значения <RЭ> и <R> в каждом методе измерения.
2. Определите погрешности метода em1 и em2 по формулам (8) и (14) для каждого метода измерения. Сделайте выводы о том, какая схема включения предпочтительней.
3. Определите удельное сопротивление r нихромового провода по формуле (3). Для этого используйте значение <R> для той схемы, для которой методическая погрешность оказалась наименьшей.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение разности потенциалов и падения напряжения на участке цепи. В каком случае они равны?
2. Каков физический смысл сопротивления проводника? От чего оно зависит?
3. В чем состоит метод измерения сопротивления с точным измерением тока? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить?
4. В чем состоит метод измерения сопротивления с точным измерением напряжения? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить?
ЛИТЕРАТУРА
1. Трофимова, Т.И. Курс физики: учеб. пособие: рек. Мин. обр. РФ/ Т.И. Трофимова.-8-15-е изд., стер.- М.: Высш. шк., 2004,2005, 2007, 2008, 2010. Глава 12.
2. СавельевИ. В. Курс общей физики : В 5 кн.: учеб. пособие/ И. В. Савельев. -М. : Астрель : АСТ.
Кн. 2 : Электричество и магнетизм. –2004.
megapredmet.ru
1. Как определить приборную погрешность X?
Величина приборной погрешности может быть найдена одним из следующих способов:
Приборная погрешность может быть указана или на самом приборе, или в его паспорте (в описании лабораторной работы).
Приборная погрешность электроизмерительных приборов определяется по классу точности прибора. Класс точности указывается в нижней части шкалы прибора, как правило, в виде числа, обведенного в кружочек.
Например:2.0 или 0.5 . Класс точности прибора равен
приборной погрешности, выраженной в процентах от максимального значения, измеряемого на данной шкале. Обозначим класс точности прибора буквой N. Тогда:
% . (3)
Таким образом, зная класс точности прибора Nможно рассчитать приборную погрешностьxпо формуле:
. (4)
Пример.Пусть необходимо измерить силу тока амперметром класса
точности 0,05 и с диапазоном измерения (0 — 10) А. Абсолютную погрешность определим по формуле (4):
А.
Так как относительная погрешность зависит от значения измеряемой величины, то она оказывается тем меньше, чем ближе значение измеряемой величины к предельному значению шкалы. Так, в рассматриваемом примере, если измеренное значение тока оказалось бы равным 10А, то %, а если 1А, тоI= 0,5 %.
Следовательно, при работе с многопредельными приборами, в целях получения наименьшей погрешности измерения, следует выбирать такой предел измерения, при котором стрелка прибора имела бы максимальное отклонение.
3. В остальных случаях, когда отсутствует паспорт прибора и не указан класс точности, приборную погрешность следует считать равной половине наименьшего деления шкалы прибора (половине цены деления шкалы).
Пример.При измерении длины обычной линейкой, у которой наименьшее деление шкалы равно 1 мм, следует считать приборную погрешность равной 0,5 мм.
2. Как определить случайную погрешность X?
Если после проведения нескольких
измерений одной и той же физической
величины обнаруживается, что она
принимает различные значения после
каждого измерения, то это свидетельствует
о наличии случайной погрешности 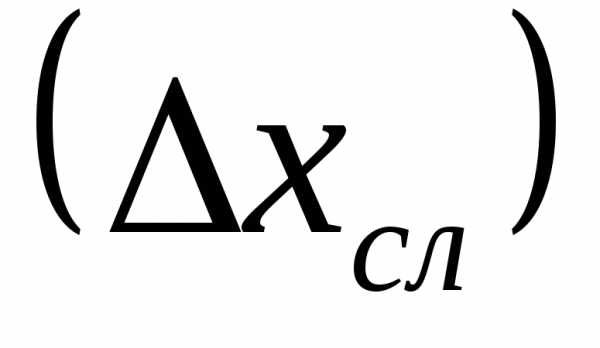 .
.
Допустим, что проделано nизмерений физической величиныx, и полученыnеё различных значений.
Оценку истинного значения измеряемой величины x принято находить как среднее арифметическое значение результатов измерений:
. (5)
Для того, чтобы вычислить абсолютную погрешность xследует найти разности между каждым из результатов отдельных измерений и среднеарифметическим значением:
(6)
Величины являютсяслучайными отклоненияминаблюдаемой величины от среднеарифметического значения и могут оказаться как положительными (еслиxx), так и отрицательными (еслиxx).
За величину погрешности принимается средняя абсолютная ошибка измерения, равная среднему арифметическому значению модулей случайных отклонений:
(7)
или
. (8)
studfiles.net

Leave A Comment