Цилиндр. Формулы и свойства
Определение.
Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра).Цилиндрическая поверхность — поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.
Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.
Круговой цилиндр
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.
Прямой круговой цилиндр можно описать, как объёмного фигуру, образующуюся вращением прямоугольника вокруг своей стороны на 360°.
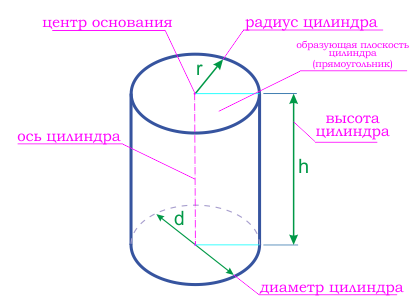
Определение. Радиус цилиндра r — это радиус основания цилиндра.
Определение. Диаметр цилиндра d — это диаметр основания цилиндра.
Определение. Высота цилиндра h — это расстояние между основаниями цилиндра.
Определение. Ось цилиндра — это прямая O1O2, которая проходит через центры оснований цилиндра.
Определение. Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.
Определение. Осевое сечение цилиндра — это сечение цилиндра плоскостью, проходящей через ось цилиндра.
Определение. Касательная плоскость к цилиндру — это плоскость, которая проходит через образующую цилиндра и перпендикулярно к осевому сечении цилиндра.
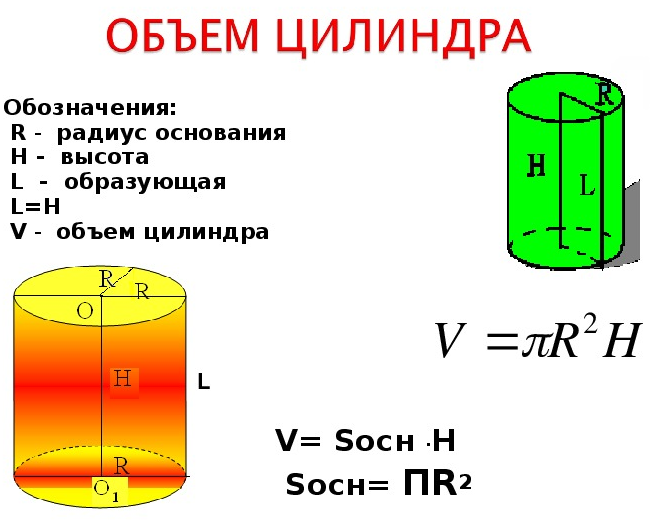
Формула. Объём цилиндра:| V = πr2h = π | d2 | h , |
| 4 |
Sb = 2πrh = πdh
Формула. Полная площадь поверхности цилиндра:S = 2πr(h + r)
Косой цилиндр — цилиндр, основы которого не параллельны (Рис.2)
Наклонный цилиндр — цилиндр, у которого образующие не перпендикулярно основам цилиндра (Рис.3 — наклонный круговой цилиндр).
формула через диаметр и высоту
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
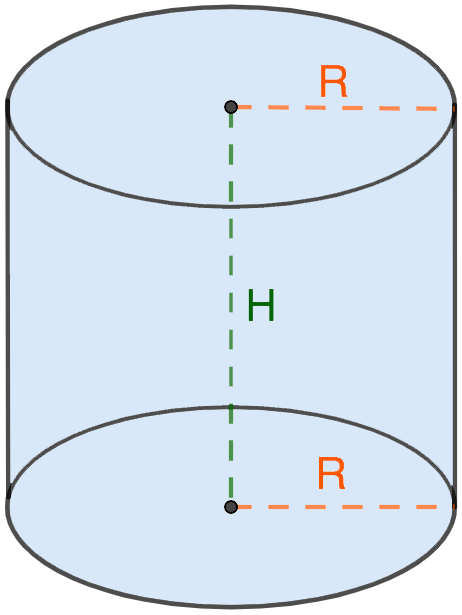
2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2)2 ⋅ H
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.
Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
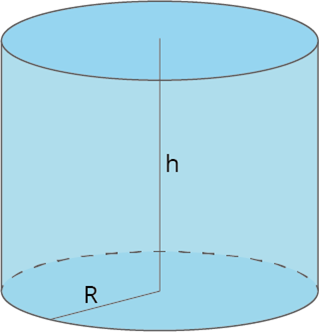
r — радиус основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра… вычисление …
Площадь боковой поверхности… вычисление …
Общая площадь… вычисление …
Упрощение формулы:
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

S — площадь основания цилиндра
h — высота цилиндра
… вычисление …
Площадь боковой поверхности… вычисление …
Общая площадь… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d — диаметр основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра… вычисление …
Площадь боковой поверхности… вычисление …
Общая площадь… вычисление …
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на
Теория
Цилиндр может быть правильным или наклонным .
.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Поверхности цилиндра
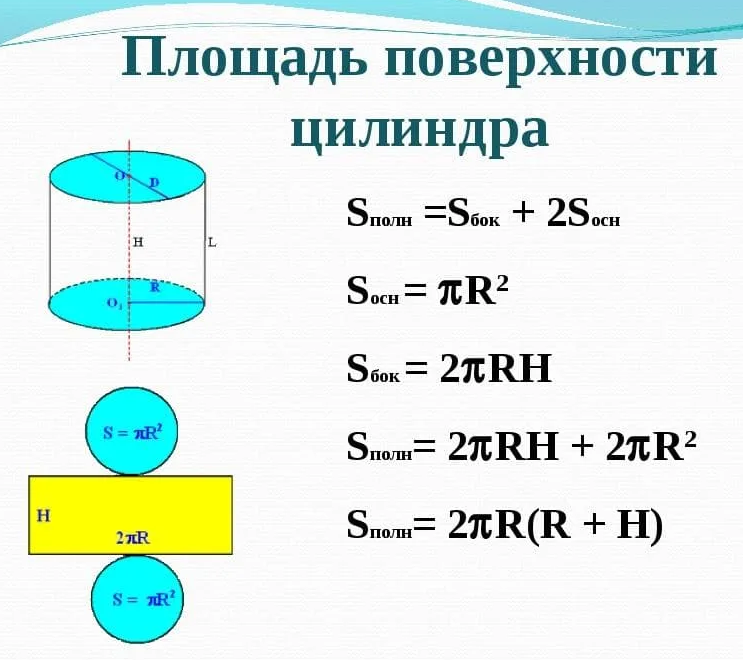
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
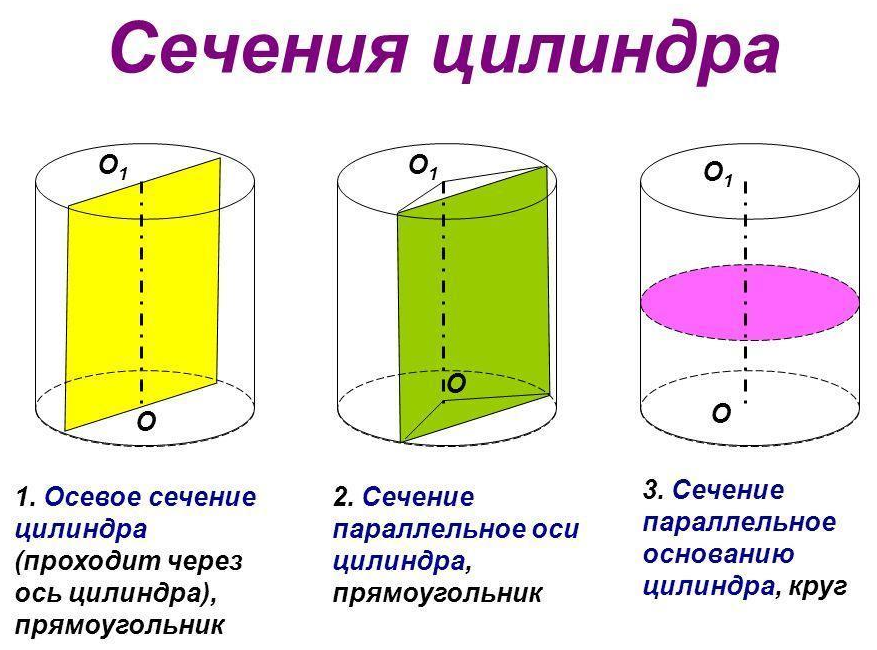
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса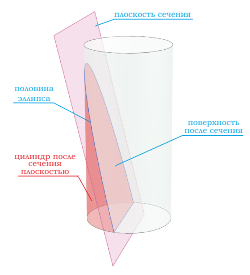 .
.
Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Как посчитать объем цилиндра — онлайн калькулятор
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания So и высоту h
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
V = So⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см3
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
V = Sb2/4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3.14⋅ 5 = 900/62.8 = 14.33 см3
См. также
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.
Объем прямого цилиндра
Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через радиус основания и высоту цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
\[ \LARGE V = \pi \cdot R^{2} \cdot H \]
где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
\[ \LARGE V = S \cdot H \]
где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра
Объем цилиндра через диаметр основания и высоту цилиндра
Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра
\[ \LARGE V = \frac {\pi \cdot D^{2} }{4 \cdot H} \]
где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра
Калькулятор объёма цилиндра
Входные данные
Радиус цилиндра r:
Высота цилиндра h:
Количество знаков после запятой в результате вычислений
1 2 3 4 5 6 7
Результат
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Объём стенки цилиндра — онлайн калькулятор
Чтобы посчитать объём стенки цилиндра, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объём полого цилиндра (Vст) можно зная (либо-либо):
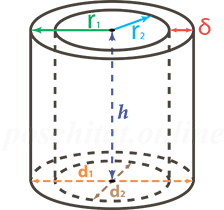
- Высоту цилиндра h, внешний радиус r1 и внутренний радиус r2
- Высоту цилиндра h, внешний диаметр d1 и внутренний диаметр d2
- Высоту цилиндра h, внешний радиус r1 и толщину стенки δ
- Высоту цилиндра h, внутренний радиус r2 и толщину стенки δ
- Высоту цилиндра h, внешний диаметр d1 и толщину стенки δ
- Высоту цилиндра h, внутренний диаметр d2 и толщину стенки δ
Зная оба радиуса (диаметра)
Зная толщину стенки
Теория
Чему равен объём полого цилиндра Vст если:
Формулы
Через радиусы или диаметры цилиндра
Vст = π ⋅ (r1² — r2²) ⋅ h , где r1 — внешний радиус, r2 — внутренний радиус , а h — высота
Vст = π ⋅ ((d1/2)² — (d2/2)²) ⋅ h , где d1 — внешний диаметр, d2 — внутренний диаметр, а h — высота
Через толщину стенки цилиндра
Vст = π ⋅ (d2 ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d2 — внутренний диаметр, а h — высота
Vст = π ⋅ ((d1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d1 — внешний диаметр, а h — высота
Vст = π ⋅ (2 ⋅ r2 ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r2 — внутренний радиус, а h — высота
Vст = π ⋅ ((2 ⋅ r1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r1 — внешний радиус, а h — высота
Пример №1
К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d1=5 см, а внутренний d2=4.5 см?
Vст = 3.14 ⋅ ((5/2)² — (4.5/2)²) ⋅ 300 = 3.14 ⋅ (6.25 — 5.0625) ⋅ 300 ≈ 1119 см³
Пример №2
Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r2 = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):
Vст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³
См. также
Объем цилиндра с калькулятором
Объем цилиндра с калькулятором — Math Open ReferenceОпределение: Количество кубических единиц, которые точно заполнят цилиндр
Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра. Объем рассчитывается при перетаскивании.
Как найти объем цилиндра
Хотя цилиндр технически не является призмой, он обладает многими свойствами призмы.Как призмы, объем определяется путем умножения площади одного конца цилиндра (основания) на его высоту.
Поскольку конец (основание) цилиндра представляет собой круг, площадь этого круга определяется по формуле:
Умножая на высоту ч получим где:
π — это пи, примерно 3,142
, р — радиус круглого конца цилиндра
ч, высота цилиндра
Калькулятор
Используйте калькулятор выше, чтобы рассчитать высоту, радиус или объем цилиндра.
Введите любые два значения, и недостающее будет вычислено. Например: введите радиус и высоту и нажмите «Рассчитать». Объем будет рассчитан.
Точно так же, если вы введете высоту и объем, будет рассчитан радиус, необходимый для получения этого объема.
Объем частично заполненного цилиндра

Одним из практических применений является горизонтальный цилиндрический резервуар, частично заполненный жидкостью. Используя формулу выше, вы можете найти объем цилиндра, который дает максимальную вместимость, но вам часто нужно знать объем жидкости в резервуаре, учитывая глубину жидкости.
Это можно сделать с помощью методов, описанных в Объем горизонтального цилиндрического сегмента.
Наклонные цилиндры
Напомним, что наклонный цилиндр это тот, который «наклоняется» — где верхний центр не находится над базовой центральной точкой. На рисунке выше отметьте «Разрешить наклон» и перетащите верхнюю оранжевую точку в сторону, чтобы увидеть наклонный цилиндр.
Оказывается, что формула объема работает точно так же для них. Однако вы должны использовать перпендикулярную высоту в формуле.Это вертикальная линия слева на рисунке выше. Чтобы проиллюстрировать это, отметьте «Высота замораживания». При перетаскивании верхней части цилиндра влево и вправо следите за расчетом объема и обратите внимание, что объем никогда не меняется.
Смотрите косые цилиндры для более глубокого обсуждения, почему это так.
единиц
Помните, что радиус и высота должны быть в одинаковых единицах — конвертировать их при необходимости. Результирующий объем будет в этих кубических единицах. Так, например, если высота и радиус указаны в сантиметрах, то объем будет в кубических сантиметрах.Что попробовать
- На рисунке выше нажмите «Сброс» и «Скрыть детали»
- Перетащите две точки, чтобы изменить размер и форму цилиндра
- Рассчитайте объем этого цилиндра
- Нажмите «показать подробности», чтобы проверить свой ответ.
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Площадь поверхности цилиндра с калькулятором
Площадь поверхности цилиндра с калькулятором — Math Open ReferenceОпределение: Количество квадратных единиц, необходимое для точного покрытия поверхности цилиндра. Дается по формуле:
где:π — это пи, примерно 3,142
р — радиус цилиндра
ч высота цилиндра
Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра, обратите внимание, как рассчитывается площадь.
Площадь поверхности цилиндра можно найти, разбив его на три части:
- Два круга, которые составляют концы цилиндра.
- Сторона цилиндра, которая при «развёртывании» представляет собой прямоугольник
π — это пи, примерно 3,142
r — — радиус цилиндра
ч высота цилиндра
Для детального взгляда на то, как эта формула получена, см. Вывод площади поверхности цилиндра.
единиц
Помните, что радиус и высота должны быть в одинаковых единицах — конвертировать их при необходимости. Полученная площадь будет в этих квадратных единицах. Так, например, если высота и радиус указаны в сантиметрах, то площадь будет в квадратных сантиметрах.Калькулятор
Используйте калькулятор выше, чтобы вычислить высоту, радиус или площадь поверхности цилиндра.
Введите любые два значения, и недостающее будет вычислено.Например: введите радиус и высоту и нажмите «Рассчитать». Площадь поверхности будет рассчитана.
Точно так же, если вы введете высоту и площадь, будет рассчитан радиус, необходимый для получения этой области.
Что попробовать
- На рисунке выше отрегулируйте высоту и диаметр цилиндра и обратите внимание, как рассчитывается площадь поверхности.
- Нажмите «Сброс» и «Скрыть детали». Отрегулируйте цилиндр до нового размера и рассчитайте площадь поверхности.Нажмите «показать детали», чтобы подтвердить свой ответ.
- Нажмите «Сброс». Рассчитайте, что произойдет, если вы удвоите высоту — удваивается ли площадь поверхности?
- Нажмите «Сброс». Рассчитайте, что произойдет, если вы удвоите диаметр — удвоится ли площадь поверхности?
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
. Основы и примеры
00: 00: 03.060
На этом уроке мы узнаем об объеме цилиндра.
00: 00: 07.090
Давайте начнем, рассмотрим этот круг с радиусом r.
00: 00: 12.040
К настоящему времени мы уже должны знать, что область A этого круга является пи квадратной.
00: 00: 18.080
Далее, давайте превратим этот круг в цилиндр.
00: 00: 22.140
После этого этот цилиндр имеет радиус r и высоту h.
00: 00: 29.000
Теперь, чтобы найти объем этого цилиндра V, мы просто умножим площадь A на высоту h.
00: 00: 38.100
Следовательно, мы умножаем квадрат pi r на h.
00: 00: 43.070
Это дает формулу для объема цилиндра, V, равного pi r квадрат h.
00: 00: 51.080
Теперь важно включить единицу измерения объема.
00: 00: 55.170
Поскольку единица не задана, мы можем записать единицу измерения в кубической единице.
00:01:01.210
Хорошо, давайте посмотрим несколько примеров по определению объема цилиндра. Для этих примеров мы берем пи как 3,14.
00: 01: 11.200
Найдите объем этого цилиндра с радиусом 3 см и высотой 5 см.
00: 01: 18.140
Начнем с формулы: V равно pi r квадрат h.
00: 01: 24.040
Теперь, поскольку радиус задан как 3 см, мы можем заменить ‘r’ на 3.
00: 01: 31.140
Далее, давайте упростим 3 квадрата. Здесь мы видим, что 3 квадрат равен 3 умножить на 3.Это дает 9. Давайте запишем это здесь.
00: 01: 46.180
Давайте продолжим. Высота h дана как 5 см. Следовательно, мы можем заменить h на 5.
00: 01: 54.240
Теперь мы можем упростить это уравнение, умножив 9 на 5. Это дает 45.
00: 02: 02.220
Далее, пи дается как 3.14. Итак, давайте заменим пи на 3.14.
00: 02: 12.140
Наконец, мы можем найти объем, умножив 3,14 на 45. Это дает 141,30.
00: 02: 23.110
Обратите внимание, что это число не имеет значения, если мы не включим в него единицу измерения.
00: 02: 28.190
Поскольку радиус и высота указаны в сантиметрах, объем будет в кубических сантиметрах.
00: 02: 34.200
Следовательно, объем этого цилиндра составляет 141,30 кубического сантиметра.
00: 02: 42.130
Следующий пример, объем этого цилиндра составляет 50 кубических футов, а его радиус равен 2 футам. Найдите его высоту, ч.
00: 02: 51.180
Теперь давайте начнем с формулы: V = pi r квадрат h.
00: 02: 57.130
Поскольку объем цилиндра задан как 50, мы можем заменить V на 50.
00: 03: 03.230
Далее, поскольку радиус задан как 2, мы можем заменить r на 2.
00: 03: 10.050
Теперь давайте упростим 2 квадрата. 2 квадрат на самом деле, 2 умножить на 2, что равно 4. Давайте запишем это здесь.
00: 03: 22.120
Далее мы можем заменить пи на 3.14.
00: 03: 27.120
Здесь мы можем упростить это уравнение, умножив 3.14 на 4.
00: 03: 33.120
Это дает 12.56.
00: 03: 36.240
Теперь у нас есть 12.56 ч равно 50. Давайте перепишем это уравнение, чтобы было легче увидеть.
00: 03: 46.230
Далее, чтобы решить для «H», мы разделим обе части уравнения с 12,56.
00: 03: 54.140
Это дает, h равно 50, деленное на 12,56.
00: 04: 01.180
Теперь мы можем найти h, разделив 50 на 12,56. Это дает 3,98.
00: 04: 10.180
Опять же, это число не имеет смысла, если только мы не включим для него единицу измерения.
00: 04: 15.180
Поскольку радиус указан в футах, высота цилиндра также будет в футах.
00: 04: 21.060
Следовательно, высота цилиндра составляет 3.98 фута.
00: 04: 27.090
Это все для этого урока. Попробуйте практический вопрос, чтобы проверить свое понимание.
Math Made Easy! Как найти площадь поверхности цилиндра
Учебное пособие по геометрии
Общая площадь поверхности цилиндра
Для старшеклассников, изучающих геометрию, которые на самом деле не являются «поклонниками» предмета по геометрии, такие проблемы, как поиск площади цилиндра, часто заставляют детей закрывать учебники и сдаваться или находить учителя по геометрии.
Но пока не паникуйте. Геометрия, как и многие другие виды математики, часто намного легче понять, если разбить ее на кусочки размером с укус.Этот урок геометрии сделает именно это — разбить уравнение для определения площади поверхности цилиндра на легкие для понимания части.
Обязательно ознакомьтесь с проблемами и решениями по площади поверхности цилиндра в разделе Geometry Help Online ниже, а также попробуйте Math Made Easy! викторина .
Уравнение для общей площади поверхности цилиндра
S.A. = 2 π r 2 + 2 π rh
Где: r — радиус цилиндра, а h — высота цилиндра.
Прежде чем начать, убедитесь, что вы понимаете следующие уроки геометрии:
Math Made Easy! Совет
Правда, формула для площади поверхности цилиндра не слишком красивая. Итак, давайте попробуем разбить формулу на понятные части. Хороший математический совет — попытаться визуализировать геометрическую форму с помощью объекта, с которым вы уже знакомы.
Какие предметы в вашем доме являются цилиндрами? Я знаю, что в моей кладовой у меня много цилиндров — более известных как консервы.
Давайте рассмотрим банку. Банка состоит из верхней и нижней частей, а также изогнутой стороны. Если бы вы могли развернуть сторону банки, это был бы прямоугольник. Хотя я не собираюсь раскрывать банку, я могу легко развернуть этикетку вокруг нее и увидеть, что это прямоугольник.
Теперь вы можете визуализировать общую площадь поверхности цилиндра (банки):
- банка может иметь 2 круга, а
- банка может иметь 1 прямоугольник
Другими словами, вы можете думать об уравнении общей площади цилиндра как:
с.A. = (2) (площадь круга) + (площадь прямоугольника)
Следовательно, для расчета площади поверхности цилиндра необходимо рассчитать площадь круга (дважды) и площадь прямоугольника (один раз).
Давайте снова посмотрим на общую площадь поверхности уравнения цилиндра и разберем его на легкие для понимания части.
Площадь цилиндра = 2 № r 2 (часть 1) + 2 № rh (часть 2)
- Часть 1: Первая часть уравнения цилиндра связана с площадью двух окружностей (верх и низ банки).Поскольку мы знаем, что площадь одного круга равна πr 2 , то площадь двух кругов составляет 2πr 2 . Итак, первая часть уравнения цилиндра дает нам площадь двух окружностей.
- Часть 2: Вторая часть уравнения дает нам площадь прямоугольника, который изгибается вокруг банки (развернутая метка в нашем хорошем готовом примере). Мы знаем, что площадь прямоугольника — это просто его ширина (w) раз его высота (ч). Так почему же ширина во второй части уравнения ( 2 π r) (h ) записывается как (2 π r)? Опять изобразите этикетку.Обратите внимание, что ширина прямоугольника при откате вокруг банки точно такая же, как и длина банки. И уравнение для окружности 2πr. Умножьте (2πr) раз (h), и вы получите площадь прямоугольной части цилиндра.
Справка по геометрии онлайн: площадь поверхности цилиндра
Ознакомьтесь с тремя распространенными типами геометрических задач для определения площади поверхности цилиндра при различных измерениях.
# 1 Найти площадь поверхности цилиндра с учетом радиуса и высоты
Задача: Найти общую площадь поверхности цилиндра с радиусом 5 см.и высотой 12 см.
Решение: Поскольку мы знаем, что r = 5 и h = 12, замените 5 в для r и 12 в для h в уравнении площади поверхности цилиндра и решите.
- S.A. = (2) π (5) 2 + (2) π (5) (12)
- S.A. = (2) (3,14) (25) + (2) (3,14) (5) (12)
- S.A. = 157 + 376,8
- S.A. = 533,8
Ответ: Площадь поверхности цилиндра с радиусом 5 см. и высотой 12 см. 5338 см в квадрате.
# 2 Найти площадь поверхности цилиндра с учетом диаметра и высоты
Задача: Какова общая площадь поверхности цилиндра диаметром 4 дюйма и высотой 10 дюймов?
Решение: Поскольку диаметр 4 дюйма, мы знаем, что радиус равен 2 дюйма, поскольку радиус всегда равен 1/2 диаметра. Вставьте 2 для r и 10 для h в уравнение для площади поверхности цилиндра и решите:
- с.A. = 2π (2) 2 + 2π (2) (10)
- S.A. = (2) (3,14) (4) + (2) (3,14) (2) (10)
- S.A. = 25,12 + 125,6
- S.A. = 150,72
Ответ: Площадь поверхности цилиндра диаметром 4 дюйма и высотой 10 дюймов составляет 150,72 дюйма в квадрате.
# 3 Найти площадь поверхности цилиндра с учетом площади одного конца и высоты
Задача: Площадь одного конца цилиндра составляет 28,26 кв. Фута, а его высота — 10 футов.Какова общая площадь поверхности цилиндра?
Решение: Мы знаем, что площадь круга равна πr 2 , и мы знаем, что в нашем примере площадь одного конца цилиндра (который является кругом) составляет 28,26 кв. Футов. Следовательно, вместо 28,26 № 2 в формуле для площади цилиндра. Вы также можете заменить 10 на h, так как это дано.
S.A. = (2) (28,26) + 2πr (10)
Эта проблема все еще не может быть решена, так как мы не знаем радиус, r.Чтобы решить для r мы можем использовать площадь уравнения окружности. Мы знаем, что площадь круга в этой задаче составляет 28,26 фута, поэтому мы можем заменить его на A в области формулы круга, а затем решить для r:
.- Площадь круга (решите для r):
- 28,26 = № 2
- 9 = r 2 (разделите обе части уравнения на 3,14)
- r = 3 (возьмите квадратный корень с обеих сторон уравнения)
Теперь, когда мы знаем r = 3, мы можем подставить его в область формулы цилиндра вместе с другими заменами следующим образом:
- с.A. = (2) (28,26) + 2π (3) (10)
- S.A. = (2) (28,26) + (2) (3,14) (3) (10)
- S.A. = 56,52 + 188,4
- S.A. = 244,92
Ответ: Общая площадь поверхности цилиндра, конец которого имеет площадь 28,26 кв. Футов и высоту 10, составляет 244,92 кв. Футов .
Вам нужна дополнительная помощь по геометрии?
Если у вас есть другая конкретная проблема, вам нужна помощь, связанная с общей площадью поверхности цилиндра , пожалуйста, спросите в разделе комментариев ниже.Я буду рад помочь и даже включить вашу проблему в раздел «проблема / решение» выше.
,
Leave A Comment