Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Вписанные четырехугольники и их свойства |
| Теорема Птолемея |
Вписанные четырёхугольники и их свойства
Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
Рис.1
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Доказательство. Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A, B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D. Приведём это предположение к противоречию.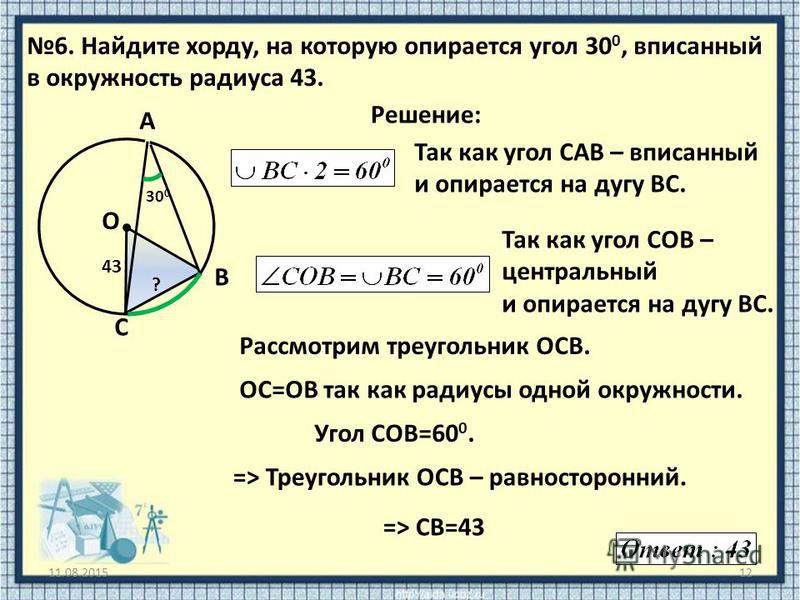 Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Рис.2
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E, и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180°. При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC. Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC, не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.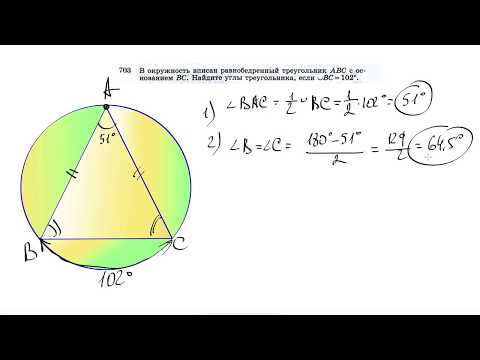 | |
| Окружность, описанная около ромба | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
|
| Окружность, описанная около параллелограмма | |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.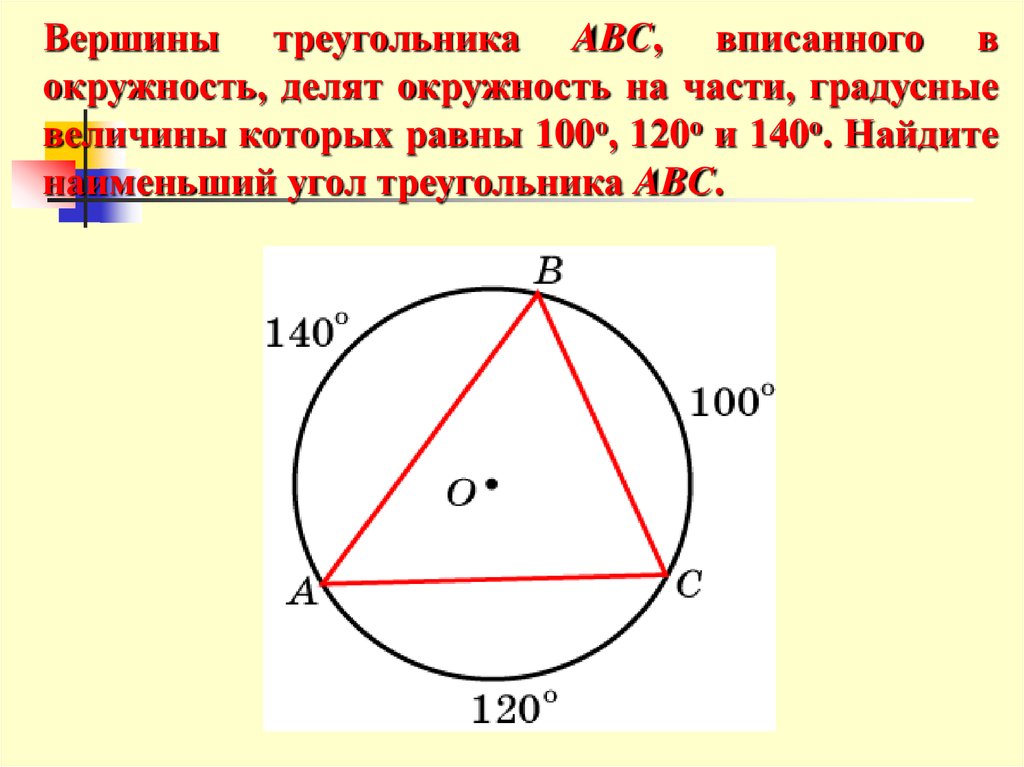 | |
| Окружность, описанная около ромба | |
| Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | |
| Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | |
| Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
| |
| Окружность, описанная около параллелограмма |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
Теорема Птолемея
Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.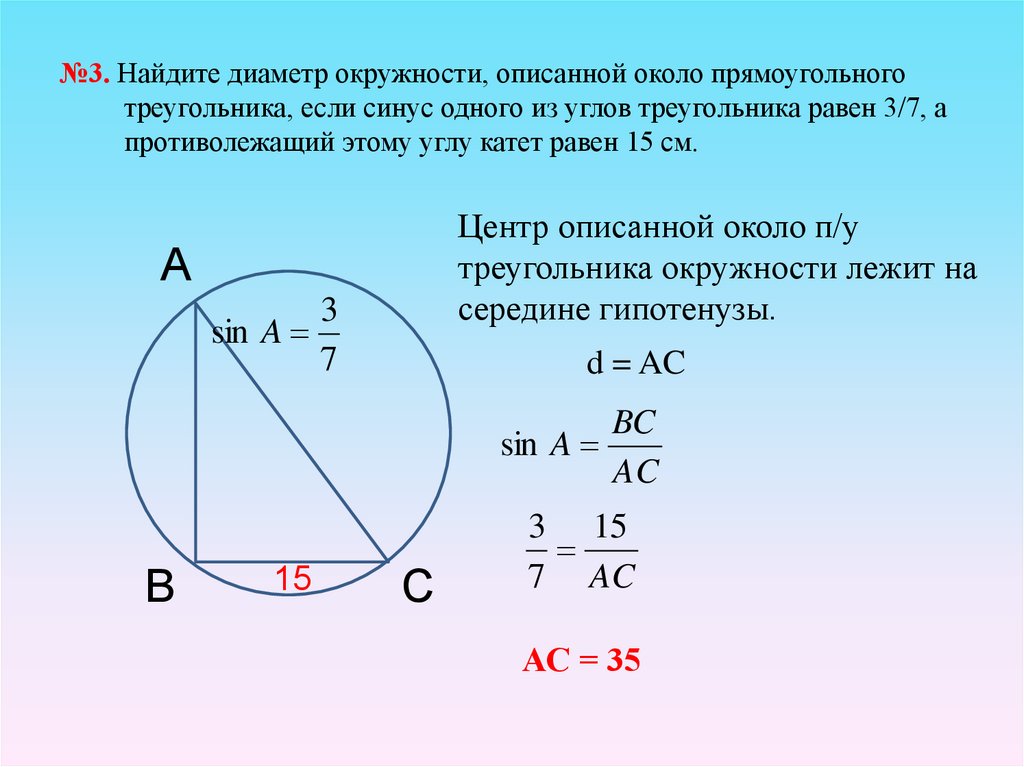
Доказательство. Рассмотрим произвольный четырёхугольник ABCD, вписанный в окружность (рис.3).
Рис.3
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Рис.4
Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (1) |
Заметим, что треугольник ABE подобен треугольнику BCD. Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (2) |
Складывая равенства (1) и (2), получаем:
Теорема Птолемея доказана.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Свойства вписанной в треугольник окружности
В этой статье Вы сможете найти свойства вписанной в треугольник окружности, а также их доказательства.
Вписанная в треугольник окружность — это такая окружность, которая находится внутри треугольника и при этом касается всех его сторон (то есть все стороны треугольника являются касательными к окружности). Стоит отметить, что в этом случае сам треугольник является описанным вокруг данной окружности.
Рисунок 1
Свойства вписанной в треугольник окружности
- Центр вписанной в треугольник окружности (на рис.
 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО). - В любой треугольник вписывается окружность и притом только одна.
-
Радиус вписанной в треугольник окружности равен:
p — полупериметр треугольника,
a, b, c — стороны треугольника.
Доказательства свойств
Первое свойство
Доказать, что центр вписанной в треугольник окружности находится на пересечении биссектрис.
Доказательство.
- Опустим из центра окружности перпендикуляры (OL, OK и OM) к каждой из сторон треугольника ABC (рис. 2). Также из каждого угла проведем прямую к центру окружности (OA, OC и OB).
Рисунок 2
- Рассмотрим 2 треугольника AOM и AOK. Они являются прямоугольными, т.

- Поскольку касательная к окружности перпендикулярна радиусу, проведенному в точку касания (свойство касательной к окружности), то катеты OМ и OК являются радиусами окружности и, следовательно, равны.
- Из вышесказанного следует, что прямоугольные треугольники AOМ и AOК равны по гипотенузе и катету. Т.к. треугольники равны, то углы OAМ и OAК тоже равны, отсюда следует, что OA – биссектриса угла BAC.
- Аналогичным образом доказывается, что OC – биссектриса угла ACB, а OB – биссектриса угла ABC.
- То есть биссектрисы треугольника пересекаются в одной точке и этой точкой является центр вписанной окружности.
Что и требовалось доказать.
Второе свойство
Доказать, что в любой треугольник можно вписать окружность и притом только одну.
Доказательство
- В треугольник можно вписать окружность только в том случае, если найдется точка равноудаленная от его сторон.

- Проведем 2 биссектрисы OA и OC. Опустим из точки их пресечения перпендикуляры (OK, OL и OM) ко всем трем сторонам треугольника ABC (рис. 3).
Рисунок 3
- Рассмотрим треугольники AOK и AOM.
- У них общая гипотенуза AO. Углы OAK и OAM равны (т.к. OA – биссектриса угла KAM). Углы OKA и OMA прямые (т.е. тоже равны), т.к. OK и OM – перпендикуляры к сторонам AB и AC соответственно.
- Поскольку 2 пары углов равны, то и 3-я пара (AOM и AOK) также является равной.
- Из вышенаписанного следует, что треугольники AOK и AOM равны по стороне (AO) и 2-м прилежащим к ней углам (рис. 4).
Рисунок 4
- Отсюда следует, что стороны OM и OK равны, т.е. равноудалены от сторон треугольника AC и AB соответственно.
- Аналогичным образом доказывается, что OM и OL равны, т.е. они равноудалены от сторон треугольника AC и BC соответственно.
- Из вышенаписанного следует, что точка O равноудалена от сторон треугольника, т.
 е. является центром вписанной окружности.
е. является центром вписанной окружности. - Аналогичным образом можно найти точку внутри любого треугольника, которая будет равноудалена от его сторон, то есть будет центром вписанной в этот треугольник окружности.
- Из вышенаписанного следует, что в любой треугольник можно вписать окружность.
- Следует отметить, что центр данной окружности лежит на пересечении биссектрис треугольника.
- Допустим, что в треугольник можно вписать две (или более) окружности.
- Проведя 3 отрезка из вершин треугольника к центру этой окружности и, опустив перпендикуляры из этого центра к каждой из сторон треугольника, мы сможем доказать, что эта окружность лежит на пересечении биссектрис треугольника (см. доказательство первого свойства).
- То есть центр этой окружности совпадает с центром первой окружности, уже вписанной в треугольник, а ее радиус равен перпендикуляру, опущенному на сторону треугольника (как и в первом случае).
 Это говорит о том, что данные окружности совпадают.
Это говорит о том, что данные окружности совпадают. - Аналогичным образом можно доказать, что любая новая вписанная окружность совпадает с первой, которую мы впишем.
- То есть вписать в треугольник можно только одну окружность.
Что и требовалось доказать.
Третье свойство
Доказать, что радиус вписанной окружности r равен отношению площади треугольника S к полупериметру p.
А также равенство:
Доказательство.
Рисунок 5
-
Рассмотрим произвольный треугольник ABC со сторонами a, b и c (рис 5). Полупериметр данного треугольника p рассчитывается по формуле:
-
Центр нашей окружности (точка O на рис. 5) находиться на пересечении биссектрис треугольника. Отрезки OA, OB и OC, соединяющие O с вершинами треугольника АВС, делят треугольник на три: AOC, COB, BOA.
 Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.
Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.
-
Поскольку площадь любого треугольника равна половине произведения его основания на высоту, а высота треугольников AOC, COB, BOA равна радиусу окружности r, то площади треугольников AOC, COB и BOA можно найти как:
- Выразим площадь S треугольника ABC через сумму площадей этих трех треугольников:
-
Заметив, что второй множитель – это полупериметр треугольника ABC, можно представить наше равенство в виде:
Или -
Итак, мы доказали, что радиус вписанной окружности равен отношению площади треугольника к полупериметру.

- Вспомним формулу Герона, которая в нашем случае будет иметь вид:
-
Теперь радиус можно выразить как:
Что и требовалось доказать.
Скорее всего, Вам будет интересно:
- Свойства медианы в прямоугольном треугольнике с доказательствами
- Первый признак равенства треугольников: формулировка и доказательство (7 класс)
- Третий признак равенства треугольников формулировка и доказательство
- Средняя линия трапеции: чему равна, свойства, доказательство теоремы
- Свойства прямоугольной трапеции
- Таблица прямых и обратных тригонометрических функций, онлайн калькулятор
- Как найти область определения функции онлайн
- Основные положения молекулярно-кинетической теории (МКТ), формулы МКТ
- Состав служебного программного обеспечения
- Уравнение состояния идеального газа Менделеева-Клапейрона с выводом
геометрия — угол вписанного треугольника
Задавать вопрос
спросил
Изменено 8 лет, 6 месяцев назад
Просмотрено 2к раз
$\begingroup$
У меня есть вписанный в окружность разносторонний треугольник, одна из сторон которого $a$ равна $2\sqrt3$, а длина $r$ от этой стороны до центра равна $1$.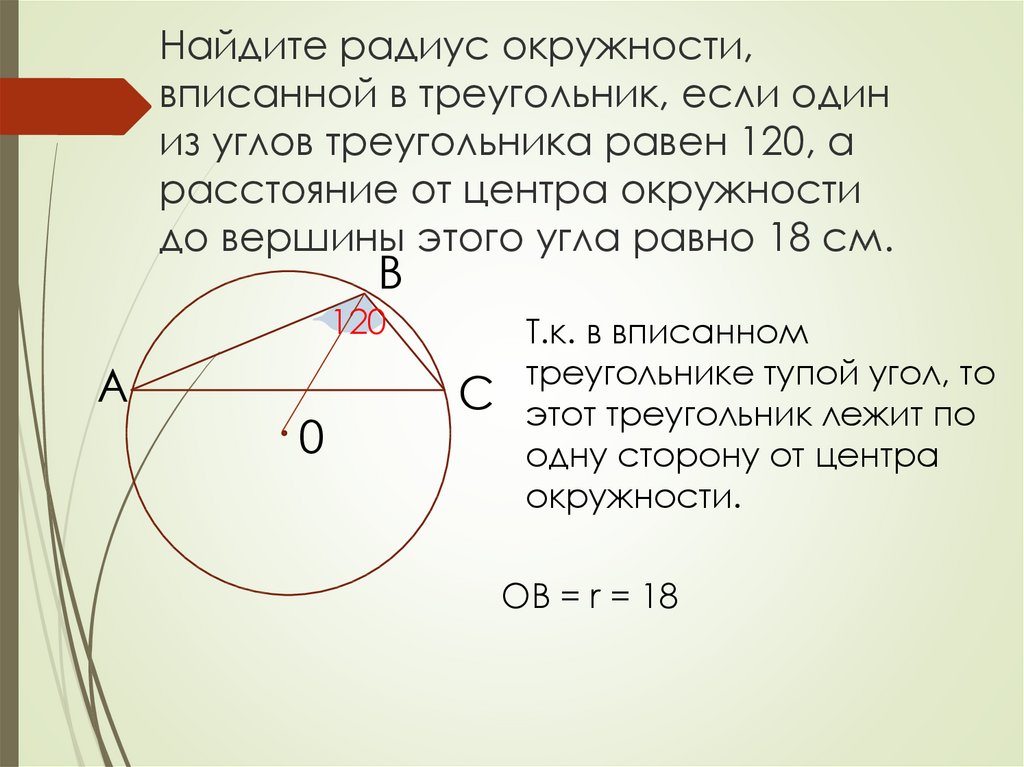 Мне нужно найти угол $x$, противоположный данной стороне. Вот как это выглядит:
Мне нужно найти угол $x$, противоположный данной стороне. Вот как это выглядит:
Как найти $x$?
- геометрия
- круги
- треугольники
$\endgroup$
3
$\begingroup$
Начертите радиусы от центра к концам $a$, чтобы сформировать два конгруэнтных прямоугольных треугольника, имеющих общую сторону длины $r=1$ и каждый из которых имеет другую сторону длины $\sqrt{3}$. Из тригонометрии прямоугольного треугольника углы в этих прямоугольных треугольниках в центре окружности имеют меру $\arctan(\sqrt{3})=\frac{\pi}{3},$, поэтому мера всего центрального угла ( угол в центре окружности), опирающийся на ту же дугу, что и хорда $a$, равна $2\arctan(\sqrt{3})=\frac{2\pi}{3},$, а мера вписанного угла $x$ составляет половину этого, $$\arctan(\sqrt{3})=\frac{\pi}{3}.$$
$\endgroup$
3
$\begingroup$
http://www11.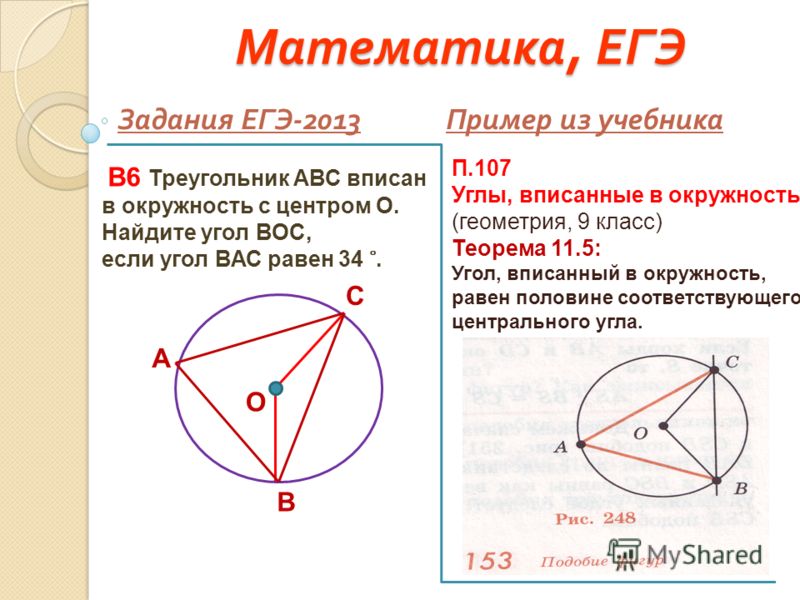 0zz0.com/2012/05/02/15/202577206.jpg
0zz0.com/2012/05/02/15/202577206.jpg
построением во вписанном треугольнике
центра $M$
нарисуйте $ML$ & $MN$
, так как $r$ перпендикулярно $a$ поскольку $LM = NM$ >> радиус & $r$ — общая сторона поэтому треугольник $\triangle LMO$ согласуется с треугольником $\Delta NMO$ 92 = 3$ поэтому $LM=2$
, так как сторона, противоположная $30°$, составляет половину гипотоны поэтому угол $\угол MNO = 30°$ и угол $\угол MLO = 30°$ тоже!
IN треугольник $\треугольник LMO$ угол $\угол M = 180° — ( 30°+30° ) = 120°$
так как угол $X$ равен половине центрального угла поэтому угол $X = 60°$
$\endgroup$
$\begingroup$
Это задание для теоремы о вписанном угле 🙂
Применим ее к треугольнику, образованному соединением концов $A$ с центром, и треугольнику, образованному концами $A$ с вершиной в $X $.
$\endgroup$
Теоремы о кругах
Несколько интересных фактов об углах и окружностях
Вписанный угол
Прежде всего, определение:
Вписанный угол : угол, образованный точками, лежащими на окружности окружности.
A и C — «конечные точки»
B — «вершина»
Поиграй с этим здесь:
изображений/circle-prop.js?mode=inscribe
Когда вы перемещаете точку «B», что происходит с углом?
Теоремы о вписанном угле
Фиксация конечных точек …
… угол a° равен всегда один и тот же ,
независимо от того, где он находится на той же дуге между конечными точками:
(называется углов, опирающихся на одну и ту же дугу, теорема )
А вписанный угол а° составляет половину центрального угла 2а°
(называется Угол в центре Теорема )
Попробуйте здесь (не всегда точно из-за округления):
изображений/circle-prop.js?mode=inscribe2
Пример: Каков размер Angle POQ? (О — центр окружности)
Угол POQ = 2 × Угол PRQ = 2 × 62° = 124°
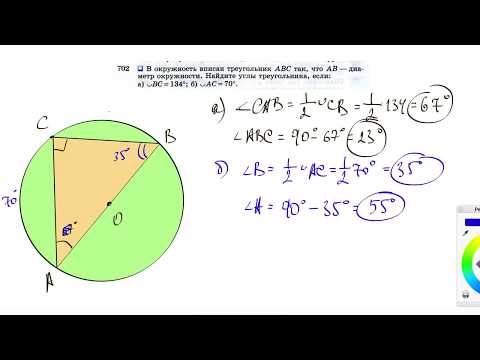
Пример: Каков размер Angle CBX?
Угол ADB = 32° также равен углу ACB.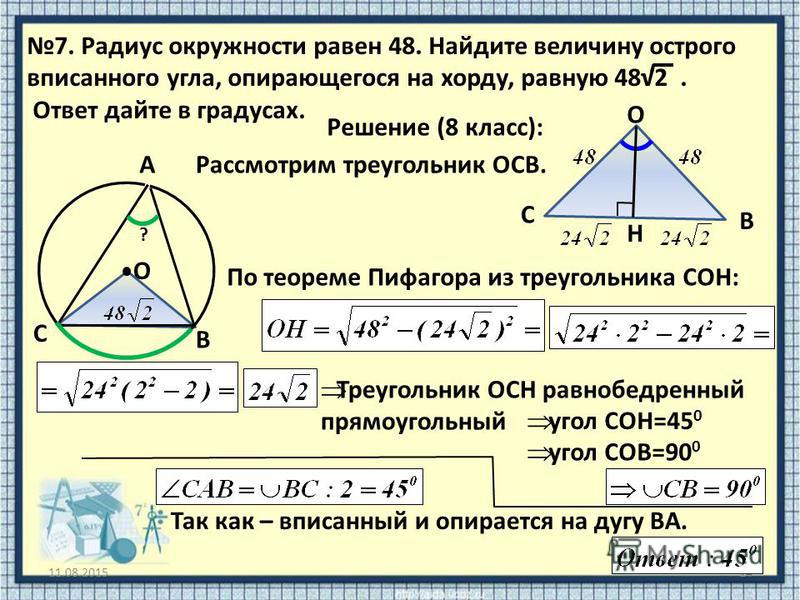
И угол ACB также равен углу XCB.
Итак, в треугольнике BXC мы знаем, что угол BXC = 85°, а угол XCB = 32°
Теперь используйте углы треугольника, прибавив к 180° :
Угол CBX + Угол BXC + Угол XCB = 180°
Угол CBX + 85° + 32° = 180°
Угол CBX = 63°
Угол полуокружности (теорема Фалеса)
Угол , вписанный в окружность с диаметром , всегда прямой:
(Конечными точками являются концы диаметра окружности,
точка вершины может находиться в любом месте окружности.)
Поиграй с этим здесь:
изображений/circle-prop.js?mode=thales
Почему? Потому что: Вписанный угол 90° составляет половину центрального угла 180° (с использованием приведенной выше теоремы об угле в центре) |
Еще одна веская причина, почему это работает
Мы также можем повернуть фигуру на 180°, чтобы получился прямоугольник!
Это это прямоугольник, потому что все стороны параллельны, а обе диагонали равны.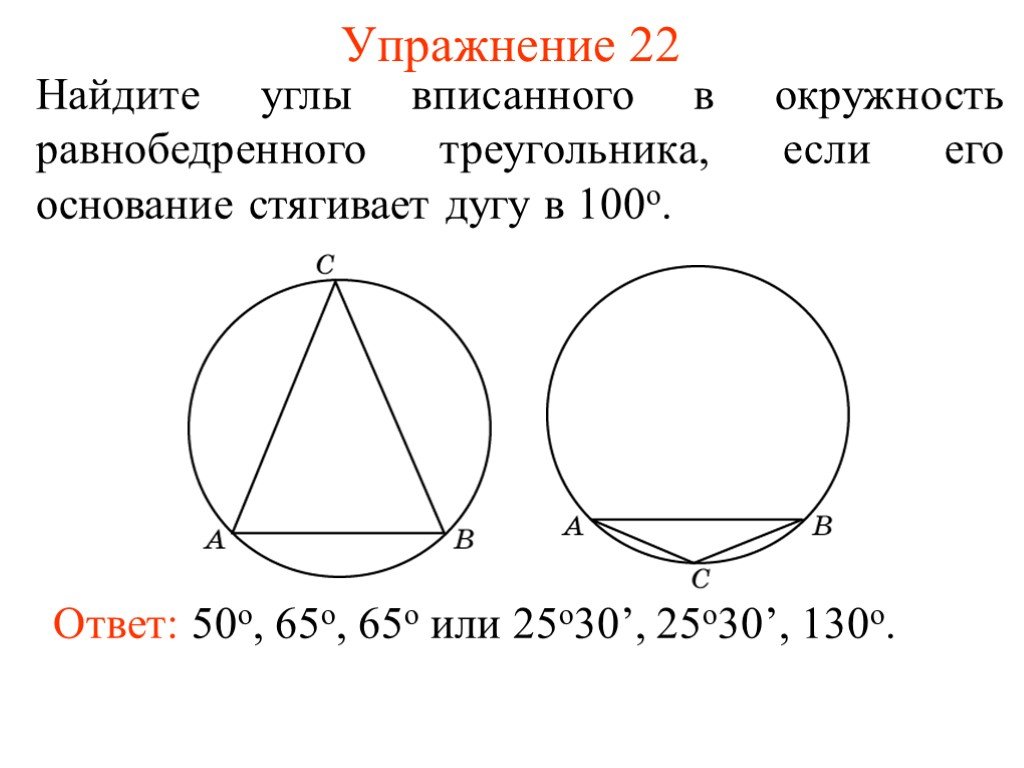
Итак, все его внутренние углы прямые (90°).
Пример: Каков размер угла BAC?
Теорема об угле в полуокружности говорит нам, что угол ACB = 90°
Теперь используйте углы треугольника, добавленные к 180°, чтобы найти угол BAC:
Угол BAC + 55° + 90° = 180°
Угол ВАС = 35°
Итак, поехали! Независимо от того, , где , этот угол равен
по окружности, всегда равен 90°
Нахождение центра круга
Мы можем использовать эту идею, чтобы найти центр круга:
- начертите прямой угол из любой точки окружности круга, затем нарисуйте диаметр в том месте, где две ножки касаются круга
- сделайте это снова, но с другим диаметром
Где пересекаются диаметры, там центр!
Рисование окружности из двух противоположных точек
Когда мы знаем две противоположные точки на окружности, мы можем нарисовать эту окружность.

 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
 е. является центром вписанной окружности.
е. является центром вписанной окружности. Это говорит о том, что данные окружности совпадают.
Это говорит о том, что данные окружности совпадают. Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.
Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.

Leave A Comment