Через точку о лежащую на радиусе оа окружности с центром о проведена хорда: ГДЗ по геометрии для 10 класса Атанасян Л.С.

Докажите, что луч В А — биссектриса угла СВЕ. ГДЗ, задача 816, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Докажите, что луч В А — биссектриса угла СВЕ. ГДЗ, задача 816, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Через точку D, лежащую на радиусе ОА окружности с центром О, проведена хорда ВС, перпендикулярная к ОА, а через точку В проведена касательная к окружности, пересекающая прямую ОА в точке Е.

Докажите, что луч В А — биссектриса угла СВЕ.

Лучший ответ

Привет!

Т. к. ∟ЕВА — угол между касательной и хордой, (т.к. OD — биссектриса в ∆ВОС — равнобедренный) => ∟ЕВА — ∟AВС .

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.

 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.

произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Конспект урока по геометрии.

8 класс.Касательная к окружности, ее свойства

Урок по геометрии, 8 класс

“Касательная к окружности”

 

Тема урока: Касательная к окружности, ее свойства.

Урок объяснения нового материала.

Цели урока:

Ввести понятия касательной, точки касания, отрезков касательных, проведённых из одной точки.

Рассмотреть свойство касательной и её признак и показать их применение при решении задач.

Рассмотреть свойство отрезков касательных, проведённых из одной точки и показать его применение в процессе решения задач, направленных на выявление понимания содержания теоремы на уровне узнавания и формально-логическом уровне.

Способствовать формированию приёмов критического мышления, анализа и синтеза.

Воспитание коммуникативной культуры, приобретение опыта самостоятельной работы.

Оборудование: компьютер, презентация, проектор с экраном, доска, тесты.

План урока:

Орг. момент.

Актуализация опорных знаний.

Мотивация введения данного понятия.

Введение теоремы о касательной к окружности.

Анализ предложенных утверждений (выявление понимания содержания теоремы).

Доказательство теоремы.

Разбор задач.

Подведение итогов и задание ДЗ.

Ход урока:

I. Организационный момент.

“Ни 30 лет, ни 30 столетий не оказывают никакого влияния на ясность или на красоту геометрических истин”. Кэрролл Л.

Сообщить тему урока, сформулировать цели урока.

II. Актуализация знаний учащихся

1. Устный опрос. (Цель: вызвать интерес к изучению темы)

1. Верите ли вы, что самая простая из кривых линий – окружность?

2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?

3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?

4. Верите ли вы, что в переводе с латинского радиус означает “луч”?

5. Верите ли вы, что при заданном периметре именно окружность ограничивает наибольшую площадь?

6. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

7. Верите ли вы, что выражение “ходить по кругу” когда-то означало “прогресс”?

8. Верите ли вы, что хорда в переводе с греческого означает “струна”?

9. Верите ли вы, что определение “касательной” уже есть в первом учебнике геометрии — “Начала” Евклида?

В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая. Одно из интереснейших свойств круга состоит в том, что он при заданном периметре ограничивает максимальную площадь.

В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.

Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего “погоняли по кругу”. Фраза “ходить по кругу” обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение “ходить по кругу” очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.

Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.

Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.

Термин “хорда” (от греческого “струна”) был введён в современном смысле европейскими учёными в XII-XIII веках.

Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике “Элементы геометрии” французского математика Лежандра (1752-1833 гг.). В “Началах” Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его.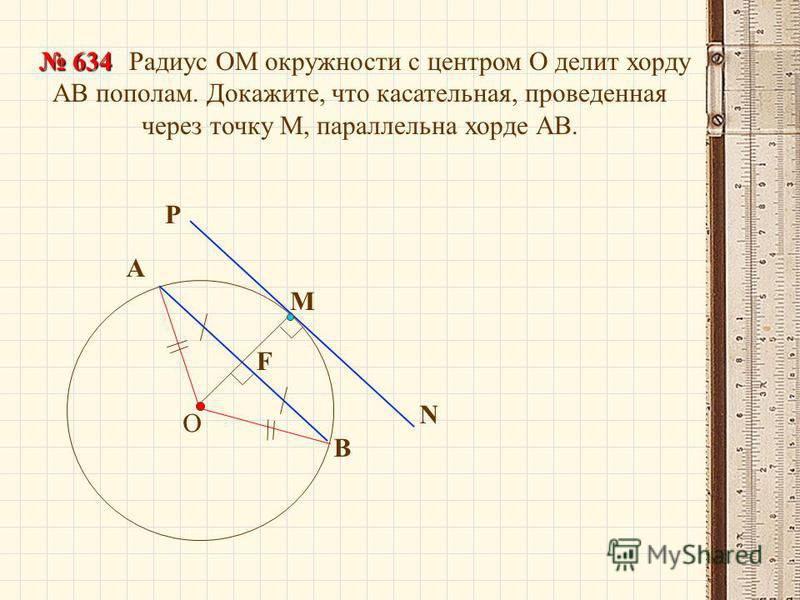

2. Сформулируйте геометрические определения понятий, используя ключевые слова.

№	рисунок	Определяемое понятие	Используемые ключевые понятия
1		Окружность	Точки плоскости, одинаковое расстояние, точка — центр.
2		радиус	Точки окружности, центр окружности, отрезок.
3		Хорда	Отрезок, точки окружности.
4		Диаметр	Хорда окружности, центр окружности.

1. Что такое окружность?

Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности)

2. Назовите элементы окружности.                (радиус, хорда, диаметр, дуга)

3. Что такое радиус?

Радиус – отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

4. Хорда.

Хорда – отрезок, соединяющий две точки окружности.

5. Диаметр.

Диаметр – отрезок, соединяющий две точки на окружности и проходящий через центр окружности.

6. Как связаны между собой диаметр и радиус окружности?        (d = 2r)

3. Заполните таблицу

Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой

Радиус окружности меньше расстояния от центра окружности до прямой	Радиус окружности больше расстояния от центра окружности до прямой	Радиус окружности равен расстоянию от центра окружности до прямой
Прямая и окружность ……….	Прямая и окружность ……….	Прямая и окружность ……….

Определение:  Прямая, имеющая с окружностью две общие точки, называется секущей.

4. Задача. Устно.

Каково взаимное расположение прямой p и окружности.

1) r = 12см, d = 9см:   r > d – прямая пересекает окружность в двух точках, является секущей;

2) r = 5,2см, d = 4,6см:   r > d – прямая p пересекает окружность в двух точках, является секущей;

3) r = 3,2дм, d = 3,7дм:   r < d – прямая p не пересекает окружность;

4) r = 80мм, d = 14cм = 140мм:   r < d – прямая p не пересекает окружность;

5) r = 6см, d = 0,6дм = 6см:   r = d – прямая p – касательная.

III. Изучение нового материала. Касательная к окружности. Свойства касательной.

Мы показали, что прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки.

Прямая, имеющая с окружностью только одну общую точку. Называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Ребята, постройте, пожалуйста, радиус к точке касания.  Вы заметили какую-нибудь особенность взаимного расположения этого радиуса и касательной? (если нет, то попросить воспользоваться угольником).

Формулируем теорему о свойстве касательной

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Докажем теорему о свойстве касательной и окружности.

Доказательства теоремы о свойстве касательной к окружности (см. п. 69, с. 166) лучше провести в ходе беседы учителя с учащимися по рис. 212, приготовленному на доске.

Наводящие вопросы:

— Предположим, что прямая р не перпендикулярна радиусу ОА.

Сравните расстояние от центра окружности до прямой р с радиусом окружности.

(Расстояние от точки О – центра окружности – до прямой р меньше радиуса, так как радиус ОА в данном случае является наклонной по отношению к прямой р, а как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой

что и наклонная. )

— Каково взаимное расположение прямой р и окружности? Почему?

— Может ли прямая р быть касательной к окружности? Объясни.

(Прямая р не может быть касательной к окружности, так как она имеет с ней две общие точки.)

— Верно ли предположение, что прямая р не перпендикулярна радиусу ОА? О чём говорит? (Предположение о том, что прямая р не перпендикулярна радиусу неверное, следовательно прямая р перпендикулярна радиусу.)

Теперь запишем это доказательство в тетради.

Дано: окр. (О;r=ОА), р-касательная A к окружности, А-точка касания. Доказать: рОА. Доказательство:

Предположим, что р не ОА, тогда ОА наклонная к прямой р, а ОВр, т. к. ОВ<ОА, то расстояние от центра окружности О до прямой р меньше радиуса, следовательно прямая р и окружность имеют две общие точки, что противоречит условию: прямая р – касательная, т.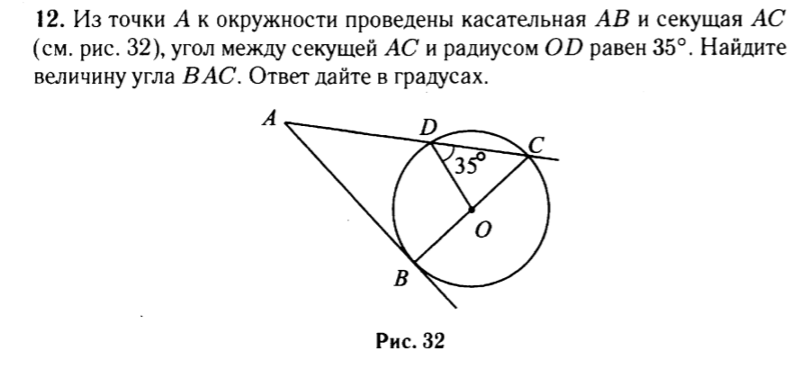 о. р ОА.

IV. Закрепление нового материала

1. Решите задач

         

 

Задания выполняются на доске учащимися, учитель по необходимости помогает им.

V. Продолжение объяснения нового материала

Ребята, а теперь постройте окружность и точку  Р  лежащую вне этой окружности.

Проведите через точку  Р  две касательные к окружности. Соедините центр окружности и точки касания отрезками.

                                        Р

Что вы можете сказать о отрезках РВ и РА ? Как луч РО делит АРВ ?

А вот как раз и это свойство

Откуда взять равенство этих элементов? Кто готов доказать нам этот факт.

Ученики сами доказывают данную теорему на доске и в тетради.

VII. Закрепление изученного. Решение задач

№ 635 

Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.

Решение. ОА=ОВ=R, АВ=R (по условию), следует ∆АВС – равносторонний.

<ОАВ=<АВО=<ВОА=60⁰, ∠ВАN = 90⁰ – 60⁰ = 30⁰.

№ 637 

Угол между диаметром АВ и хордой АС равен 30⁰. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD – равнобедренный.

Решение: ∆АОС – равнобедренный, т.к. ОС=ОА=R, значит <А=<АСО=30⁰.

<АСD=<АСO+< span=»»>⁰+90⁰=120⁰ .<>

По свойству касательной ОС=R┴CD (касательная),

∆СDO – прямоугольный. <ОСD=90⁰.

<ОDС=180⁰ – (<a+< span=»»>⁰ – (30⁰+120⁰)=30⁰.</a+<>

<ОDС=<А=30⁰, следовательно ∆АСD – равнобедренный.

№ 638 

Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если ОА = 2 см, а r = 1,5 см.

Решение. По свойству касательной АВ┴ОВ, следовательно ∆ОВА – прямоугольный.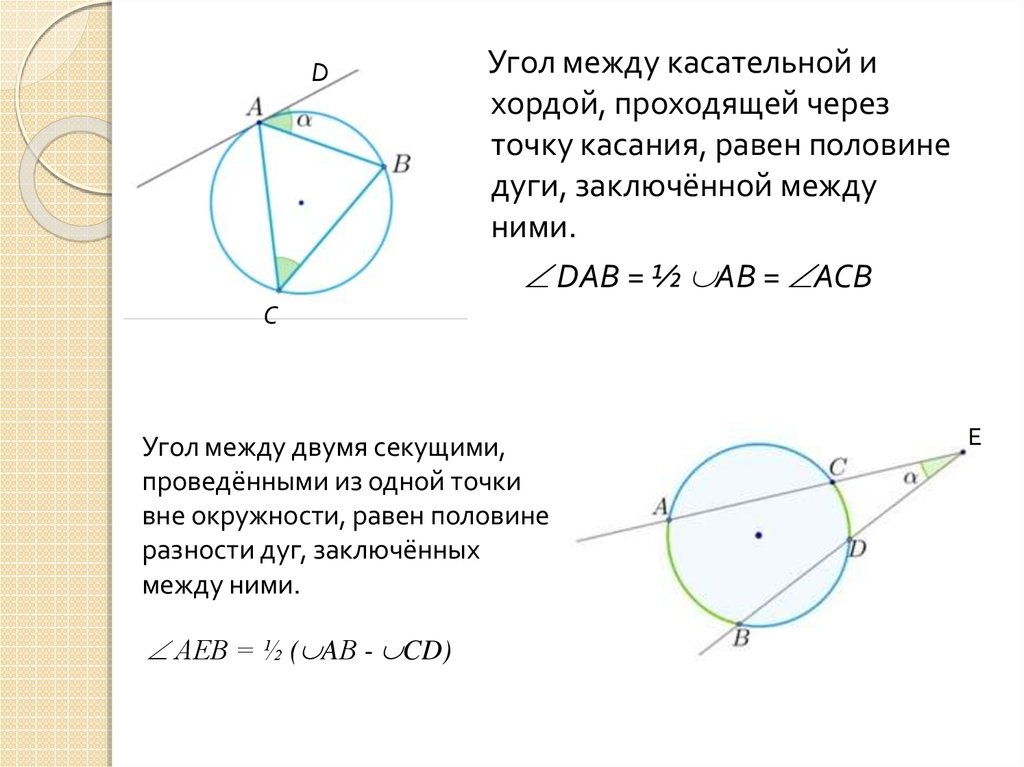

По теореме Пифагора: АВ² = ОА² – ОВ²,  .

№ 639

Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если угол АОВ равен 60⁰, а r = 12 см.

Решение. 

По свойству касательной АВ┴ОВ, следовательно, ∆ОВА – прямоугольный.

∠ОАВ = 90⁰ – 60⁰ = 30⁰. Отсюда АО = ОВ * 2 = 12 * 2 = 24 (см)

По теореме Пифагора:   АВ² = ОА² – ОВ²,

 (см)

VII. Рефлексия

Каким свойством обладает касательная к окружности?

Сформулируйте теорему о двух касательных к окружности, проведенных из одной точки, лежащей вне этой окружности.

Возникали ли у вас трудности с усвоением сегодняшнего материала? И по какой причине?

VIII. Подведение итогов

На дом:   п. 69,  № 633,   № 636.

 

глав-кругов| 9 класс математика

Совокупность всех точек плоскости, находящихся на фиксированном расстоянии от фиксированной точки плоскости, называется окружностью.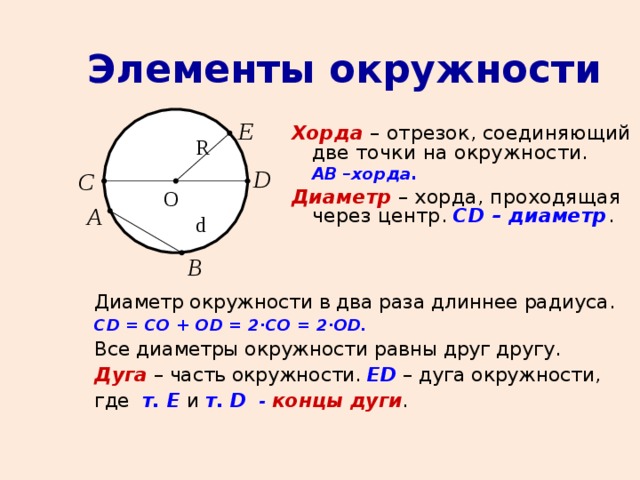

Фиксированная точка называется центром окружности, а фиксированное расстояние называется радиусом окружности.

Окружность — это геометрическая фигура на плоскости, все точки которой равноудалены от фиксированной точки плоскости. Фиксированная точка — это центр окружности, а постоянное расстояние от центра — это радиус окружности.

Окружность имеет центр O, а радиус r обычно обозначается C (O, r). Поэтому в системе обозначений мы пишем
. С(0, г) = {Х; ОХ = г}.

На рисунке O — центр, а длина OX — радиус окружности. Таким образом, отрезок, соединяющий центр и любую точку окружности, называется радиусом окружности.

ОКРУЖНОСТЬ КРУГА:

Окружность круга — это длина полной круговой кривой, образующей круг.

ХОРДА КРУГА:

На рисунке отрезок AB или CD, соединяющий две точки A, C и D окружности, называется хордой окружности. Отрезок, соединяющий любые две точки окружности, называется хордой окружности. Хорда, проходящая через центр С окружности, называется диаметром окружности. Диаметр окружности — это самая длинная хорда окружности, а ее длина в два раза больше радиуса окружности. У нас Диаметр круга = 2 × радиус круга т. е. D = 2 r Здесь D — длина диаметра, а r — радиус окружности.

ДУГА КРУГА:

Любые две точки А и В окружности делят окружность на две части, как показано на рисунке (i). Меньшая часть называется малой дугой окружности, как показано на рисунке (ii), и обозначается . Большая часть называется большой дугой, как показано на рисунке (iii). Обозначается где P — точка на этой части дуги.

В случае, если две части равны, тогда мы находим LM диаметр круга и две части круга равны. Каждая часть круга, как показано на рисунке (iv), является полукругом.

Длина дуги

Длина дуги — это длина тонкой нити, которая полностью покрывает дугу. Если это большая дуга и это второстепенная дуга, то мы получаем, что

Окружность делит плоскость на три части: внутреннюю, внешнюю и саму окружность. Внутренняя область называется круговой областью. Хорда делит круговую область на две части, называемые сегментами круговой области или сегментами окружности. Меньший сегмент называется малым сегментом, а большой — большим сегментом. В случае, если два сегмента равны, каждый из них называется полукруглой областью.

ИНТЕРЬЕР КРУГА:

Плоская область, лежащая в окружности, как показано на рисунке, называется внутренней частью окружности.

Круг и его внутренняя часть в целом составляют круговую область.

СЕГМЕНТ КРУГЛОЙ ОБЛАСТИ:

Хорда LM делит круговую область на две части, как показано на рисунке. Меньшая часть называется малым сегментом, а большая часть называется большим сегментом круглой области. Если хорда LM является диаметром окружности, то два отрезка равны и каждый называется полукруглой областью.

ВНЕШНИЙ ВИД КРУГА: Если на плоскости X начертить круг (бесконечные размеры), то часть плоской области за пределами круговой области называется внешней стороной круга, как показано на рисунке.

СООТВЕТСТВУЮЩИЕ КРУГИ:

Две окружности конгруэнтны друг другу тогда и только тогда, когда они имеют равные радиусы.

На рисунке две окружности имеют равные радиусы. Следовательно, две окружности конгруэнтны друг другу.

ДИАМЕТР (d):

Хорда, проходящая через центр окружности, называется диаметром окружности.

Диаметр — это самая длинная хорда, и все диаметры имеют одинаковую длину, которая в два раза больше радиуса. На рисунке АОВ — это диаметр окружности.

СЕКТОР (ч):

Область между дугой и двумя радиусами, соединяющими центр с конечными точками дуги, называется сектором. Как и в случае сегментов, мы обнаруживаем, что малая дуга соответствует малому сектору, а большая дуга соответствует большому сектору. На рисунке область OPQ в малом секторе и оставшаяся часть круглой области является основным сектором. Когда две дуги равны, то оба сегмента и оба сектора становятся одинаковыми, и каждый называется полукруглой областью.

Теорема 1:

Равные хорды окружности опираются на равные углы в центре.

Даны: AB и CD — две равные хорды окружности с центром O.

Чтобы доказать: ∠AOB = ∠COD.

Доказательство: В ΔAOB и ΔCOD,

OA = OC [Радиусы окружности]

OB = OD [Радиусы окружности]

AB = CD [Дано]

ΔAOB ≅ΔCOD [по SSS]

∠AO B = ∠COD. [По cpctc]

Теорема, обратная приведенной выше:

В углах, образуемых окружностью, хорды окружности в центре равны, тогда хорды равны.

Даны: ∠AOB и ∠POQ — два равных угла, опирающиеся на хорды AB и PQ окружности в ее центре O.

Чтобы доказать: AB = PQ

Доказательство: в ΔAOB и ΔPOQ,

OA = OP [Радиусы окружности]

OB = OQ [Радиус окружности]

∠AOB = ∠POQ [Дано]

ΔAOB≅ΔPOQ [по SAS]

AB = PQ [По cpctc] Отсюда доказано.

вопрос 1 AB — хорда окружности с центром в точке O. Если ∠AOB = 60º, докажите, что длина хорды AB равна радиусу.

Решение: На рисунке O — это центр, а r — радиус окружности. Хорда AB тянется ∠AOB = 60º в центре окружности. Здесь OA = OB = r ⇒ ∠OAB = ∠OBA [∠s opp. на равные стороны] т. е. ∠A = ∠B… (i) В ΔOAB, ∠O + ∠A + ∠B = 180º [свойство суммы углов] ⇒ 60º + ∠A + ∠B = 180º ⇒ ∠A + ∠B = 120º … (ii)

Из (i) и (ii) ∠A = ∠B = 60º

Таким образом, ∠O = ∠A = ∠B = 60º

⇒ ΔOAB — равносторонний треугольник.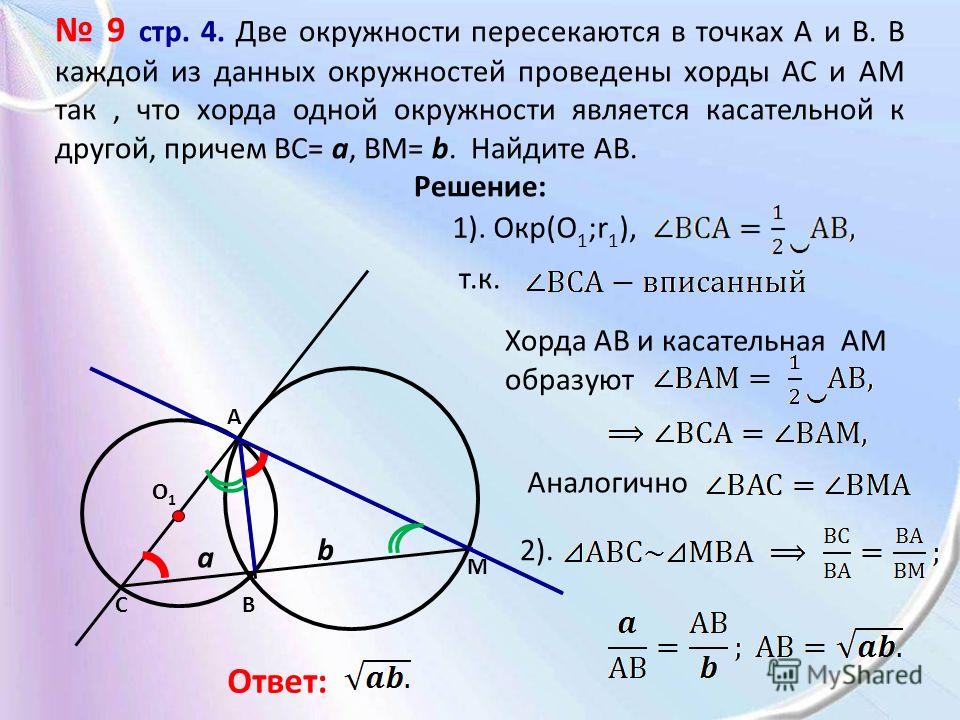

⇒ АВ = ОА = ОВ = r.

т. е. АВ = r

Теорема 2:

Перпендикуляр из центра окружности к хорде делит хорду пополам.

Дано: Окружность с центром О. AB — хорда этой окружности. ОМ АБ.

Доказать: MA = MB.

Конструкция: Соединить OA и OB.

Доказательство: в прямоугольных треугольниках OMA и OMB,

OA = OB [Радиусы окружности]

ОМ = ОМ [Общий]

∠OMA = ∠OMB [по 90° каждый]

ΔOMA≅ΔOMB [По правой стороне]

MA = MB [По cpctc] Следовательно Доказано.

Теорема, обратная приведенной выше:

Линия, проведенная через центр окружности и делящая хорду пополам перпендикулярно хорде.

Дано: Окружность с центром O. AB — хорда этой окружности, середина которой — M.

Доказать: ОМ АВ.

Строительство: соедините OA и OB.

Доказательство: в ΔOMA и ΔOMB.

МА = МБ [Дано]

ОМ = ОМ [Общий]

OA = OB [Радиусы окружности]

ΔOMA≅ΔOMB [по SSS]

∠AMO = ∠BMO [от cpctc]

Но ∠AMO + ∠BMO = 180o [аксиома линейной пары]

∠АМО = ∠ВМО = 90°

⇒ ОМ АБ.

Теорема 3:

Через три заданные неколлинеарные точки проходит одна и только одна окружность.

Доказательство: Возьмем три точки A, B и C, которые не лежат на одной прямой, или, другими словами, они не лежат на одной прямой [как на рисунке]. Проведите серединные перпендикуляры к AB и BC, скажем, PQ и RS соответственно. Пусть эти перпендикулярные бистро пересекаются в одной точке O. (Обратите внимание, что PQ и RS пересекутся, потому что они не параллельны) [как на рисунке].

O лежит на серединном перпендикуляре PQ к AB.

ОА = ОБ

[Каждая точка на биссектрисе отрезка равноудалена от его конечных точек]

Аналогично,

O лежит на серединном перпендикуляре RS к BC.

ОБ = ОС

[Каждая точка на биссектрисе отрезка равноудалена от его конечных точек]

Итак, ОА = ОВ = ОС

т. е. точки A, B и C находятся на равном расстоянии от точки O.

Итак, если мы нарисуем окружность с центром O и радиусом OA, она также пройдет через B и C.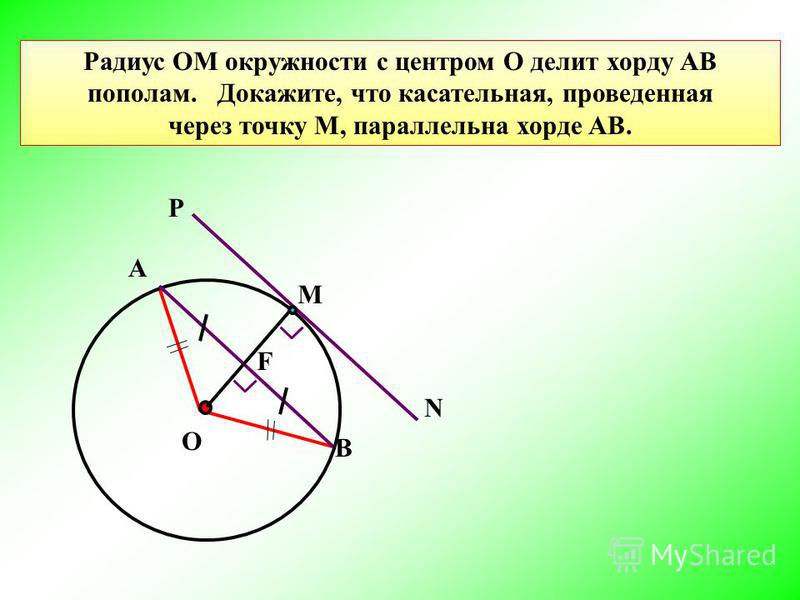 Это показывает, что существует окружность, проходящая через три точки A, B и C. Мы знаем, что две прямые (перпендикулярные биссектрисы) могут пересекаются только в одной точке, поэтому мы можем нарисовать только одну окружность радиусом OA. Другими словами, существует единственная окружность, проходящая через A, B и C.

Отсюда доказано.

Что нужно помнить:

Если ABC — треугольник, то по приведенной выше теореме существует единственная окружность, проходящая через три вершины A, B и C треугольника. Этот круг описывает описанную окружность ΔABC. Его центр и радиус называются соответственно центром описанной окружности и радиусом описанной окружности треугольника.

вопрос 2 На данном рисунке АВ — диаметр окружности. Если C точка на окружности такая, что ADC = 700, то BAC равно

(а) 200 (б) 600 (в) 700 (г) 300

Решение: Дан диаметр AB, ADC = 700

Поскольку AB — диаметр окружности, ADB = 900 (угол в полуокружности = 900)

БДК = АБР – АЦП = 900 – 700 = 200

и BAC = BDC (так как углы на одном отрезке равны)

БАК = 200

вопрос 3 На рисунке AB = CB, а O — центр окружности. Докажите, что BO делит ABC пополам.

Решение: Дано: На рисунке AB = CB, а O — центр окружности.

Доказать: BO делит ABC пополам.

Строительство: соедините OA и OC.

Доказательство: в ΔOAB и ΔOCB,

OA = OC [Радиусы одной окружности]

AB = CB [Дано]

OB = OB [Общий]

ΔOAB≅ΔOCB [по SSS]

∠ABO = ∠CBO [По cpctc]

⇒ BO делит пополам ∠ABC. Отсюда доказано.

вопрос 4 A, B и C — три точки окружности, центр которой не указан. Как вы будете располагать центр.

Решение: A, B и C — три точки. Присоединяйтесь к AB, BC и AC. Нарисуйте их биссектрисы, эти перпендикулярные биссектрисы пройдут через центр и встретятся в точке O, которая будет центром.

 

вопрос 5 Две окружности с центрами A и B пересекаются в точках C и D. Докажите, что ∠ACB = ∠ADB.

Решение: Дано: две окружности с центрами A и B пересекаются в точках C и D.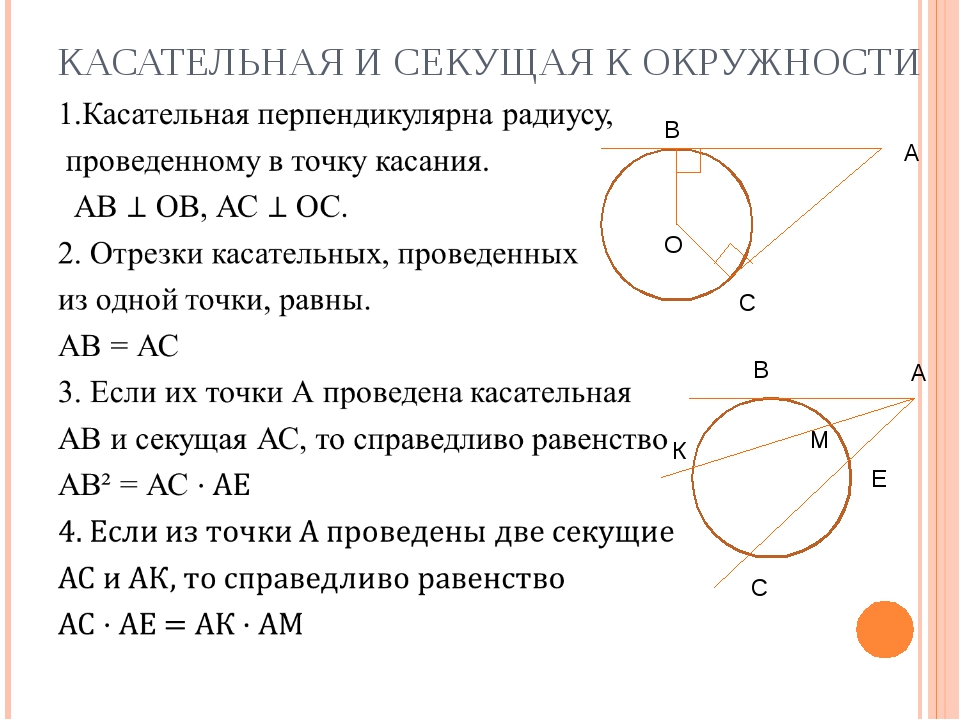

Чтобы доказать: ∠ACB = ∠ADB.

Строительство: присоединяйтесь к AC, AD, BC, BD и AB.

Доказательство: в ΔACB и ΔADB,

AC = AD [Радиусы одного круга]

BC = BD [Радиусы одной окружности]

AB = AB [Общий]

ΔACB≅ΔADB [по SSS]

∠ACB = ∠ADB. [По cpctc] Следовательно доказано.

вопрос 6 На рисунке AB≅AC и O является центром круга. Докажите, что OA является серединным перпендикуляром к BC.

Решение: Дано: На рисунке AB≅AC, а O — центр круга.

Доказать: ОА — серединный перпендикуляр к ВС.

Строительство: Присоединяйтесь к OB и OC.

Доказательство:

AB≅AC [Дано]

хорда АВ = хорда АС.

[Если две дуги окружности конгруэнтны, то их соответствующие хорды равны.]

∠AOB = ∠AOC ….(i)

[Равные хорды окружности образуют равные углы в центре]

В ΔOBC и ΔOCD,

∠DOB = ∠DOC [Из (1)]

OB = OC [Радиусы одной окружности]

OD = OD [Общий]

ΔOBD≅ΔOCD [по SAS]

∠ODB = ∠ODC . …(ii) [По cpctc]

AndBD = CD … (ii) [По cpctc]

Но ∠BDC = 180 ^o

∠ODB + ∠ODC = 180 ^или

⇒ ∠ODB + ∠ODB = 180 ^o [Из уравнения (ii)]

⇒ 2∠ОДБ = 180 ^или

⇒ ∠ОДБ = 90 ^или

∠ODB = ∠ODC = 90 ^o ….(iv) [Из (ii)]

Итак, согласно (iii) и (iv), OA является серединным перпендикуляром к BC. Отсюда доказано.

вопрос 7 Две окружности с центрами A и B пересекаются друг с другом в точках P и Q, а M является серединой точки PQ. Обоснуйте следующие утверждения:

(и) AM PQ

(ii) BM PQ

(iii) A, M, B коллинеарны

Решение: (i) M — середина хорды PQ. А это центр

(ii) аналогично (i)

(iii) A, M, B коллинеарны по части (i) и (ii)

АМБ — прямая.

вопрос 8 На следующем рисунке биссектрисы углов BAD и BCD пересекают окружность в точках E и F соответственно. Если EFA = 400, то AEF равно 9.0003

(а) 600 (б) 500 (в) 400 (г) 300

Решение: На рисунке, если DAE = x и BCF = y.

BAE = x0 и BCD = y0 ( A и C — биссектрисы)

2DAE + 2DCF = 1800

⇒DAE + DCF =

т. е. х + у = 900

Поскольку углы в отрезке равны FAD = DCF = y

Отсюда EAF = EAD + DAF = 900

AEF = 1800 – (EAF + EFA) = 1800 – (900 + 400) = 500

Теорема 4:

Равные хорды окружности (или конгруэнтных окружностей) равноудалены от центра (или центров).

Дано: Окружность имеет две равные хорды AB и CD. .э. AB = CD и OM AB, ON CD

Доказать: ОМ = ВКЛ

Конструкция: соединение OB и OD

Доказательство: AB = CD (Дано)

[Перпендикуляр, проведенный из центра окружности и делящий хорду пополам.]

⇒ ВМ = DN

В ΔOMB &ΔOND

∠OMB = ∠OND = 90 ^o [Дано]

OB = OD [Радиусы одной окружности]

Сторона BM = сторона DN [доказано выше]

ΔOMB≅ΔOND [по R.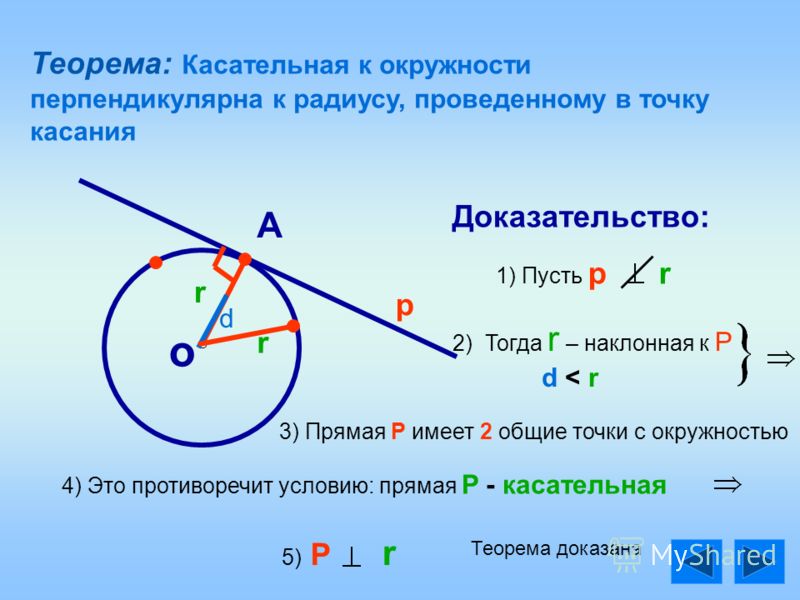 H.S.]

OM = ON [По cpctc] Следовательно Доказано.

Что нужно помнить:

Хорды, равноудаленные от центра окружности, равны по длине.

вопрос 9 В круге радиусом 13 см найдите расстояние от центра по хорде длиной 24 см.

Если ОМ || до н.э., найти до н.э.

Решение: Пусть PQ — хорда окружности с центром O, такая что OP = 13 см, PQ = 24 см.

Пусть ,OM PQ тогда PM = MB = 12 см.

Из прямоугольного треугольника OPM

Расстояние по хорде = 5 см

С

ПК диаметром

БК = 10 см

вопрос 10 AB и CD — равные хорды окружности с центром в точке O. При построении эти хорды пересекаются в точке E. Докажите, что EB = ED.

Решение: Даны: AB и CD — равные хорды окружности с центром в точке O. При построении эти хорды пересекаются в точке E.

Доказать: EB = ED.

Конструкция: От O нарисуйте OP AB и OQ CD.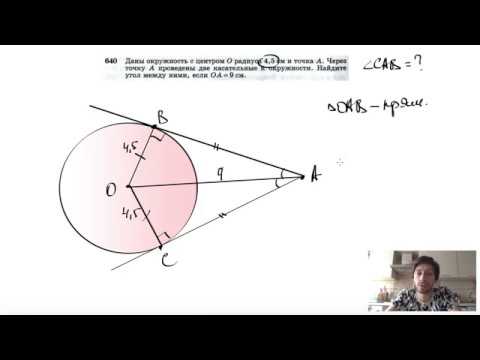 Присоединяйтесь к ОЕ.

Доказательство: AB = CD [Дано]

OP = OQ [Равные хорды окружности равноудалены от центра]

Теперь в правой покалывает OPE и OQE,

OE = OE [Общий]

Сторона OP = сторона OQ [доказано выше]

ΔOPEΔOQE [По правой стороне]

OE = QE [по cpctc]

⇒ PE –1/2AB = QE –1/2CD [ AB = CD (Дано)]

⇒ PE – PB = QE – QD

⇒ ЭБ = ЭД. Отсюда доказано.

вопрос 11 Биссектриса AD ∠BAC дуги ΔABC проходит через центр O описанной окружности ΔABC. Докажите, что АВ = АС.

Решение: Дано: Биссектриса AD ∠BAC ΔABC прошла через центр O описанной окружности ΔABC,

Доказать: АВ = АС.

Построение: Нарисуйте OP AB и OQ AC.

Доказательство:

В ΔAPO и ΔAQO,

∠OPA = ∠OQA [Каждый = 90° (по построению)]

∠OAP = ∠OAQ [Дано]

ОА = ОА [Общий]

∴ ΔAPO≅ΔAQO [По ASS cong. прог.]

∴ OP = OQ [По cpctc]

∴ АВ = АС. [Аккорды, равноудаленные от центра, равны] Отсюда Доказано.

Теорема 5:

Угол, образуемый дугой в центре, вдвое больше угла, образуемого дугой в любой точке оставшейся части окружности.

Дано: дуга PQ окружности, опирающаяся на углы POQ в центре O и PAQ в точке A на оставшейся части окружности.

Чтобы доказать: ∠POQ = 2∠PAQ.

Строительство: присоединитесь к AO и продлите его до точки B.

(а) (б) (в)

Доказательство: возникает три случая:

(a) PQ незначителен

(b)дуга PQ представляет собой полукруг

(c) дуга PQ является главной.

Во всех случаях

∠BOQ = ∠OAQ + ∠AQO ….(i)

[Внешний угол треугольника равен сумме двух внутренних противоположных углов]

В OAQ,

OA = OQ [Радиусы окружности]

∴ ∠OAQ = ∠OQA …(ii) [Углы, противоположные равным треугольнику, равны]

(i) и (ii), дать,

∠BOQ = 2∠OAQ ….(iii)

Аналогично,

∠BOP = 2∠OAP . …(iv)

Складывая (iii) и (iv), получаем

∠BOP + ∠BOQ = 2(∠OAP + ∠OAQ)

⇒ ∠POQ = 2∠PA. ….(в)

ПРИМЕЧАНИЕ. Для случая (c), где PQ является большой дугой, (v) заменяется углами рефлекса.

Таким образом, ∠POQ = 2∠PAQ.

Теорема 6:

Углы одного и того же сегмента окружности равны.

Доказательство: пусть P и Q — любые две точки на окружности, образующие хорду PQ, A и C — любые другие точки на оставшейся части окружности, а O — центр окружности. Затем

∠POQ = 2∠PAQ … (i)

And∠POQ = 2∠PCQ …(ii)

Из приведенных выше уравнений мы получаем

2∠PAQ = 2∠PCQ

⇒ ∠PAQ = ∠PCQ Следовательно, доказано

вопрос 12 На данном рисунке, если ∠ACB = 400, ∠DPB = 1200, то y будет

(а) 400 (б) 200 (в) 00 (г) 600

Решение: ADB = ACB = 400 (Углы в одном сегменте)

⇒ PDB = 400  ⇒ DPB = 1200

В ∆ DPB, PBD + DPB + PDB = 1800

ПБД + 1200 + 400 = 1800

ПБД + 1600 = 1800

ПБД = 1800 – 1600 = 200

у = 200

Теорема 7:

Угол в полуокружности прямой.

Доказательство: ∠PAQ — это угол в отрезке, являющемся полуокружностью.

∴ ∠PAQ = 1/2 ∠PAO = 1/2 × 180 ^o = 90 ^o

[∴∠PQR — прямой угол или ∠PQR = 180 ^o ]

Если мы возьмем любую другую точку С на полуокружности, то снова получим

∠PCQ = 1/2 ∠POQ = 1/2 × 180 ^o = 90 ^o Отсюда доказано.

Теорема 8:

Если отрезок, соединяющий две точки, образует равные углы в двух других точках, лежащих по одну сторону от селезенки, содержащей отрезок, четыре точки лежат на окружности (т. Е. Они концикличны).

Дан отрезок AB, который образует равные углы в двух точках C и D, т. е. ∠ACB = ∠ADB.

Доказать: Точки А, В, С и D лежат на окружности.

Доказательство. Проведем окружность через точки A, C и B.

Предположим, что он не проходит через точку D.

Затем он пересечет AD (или расширенный AD) в точке, скажем, E (или E’).

Если точки A, C, E и B лежат на окружности,

∠ACD = ∠AEB [∴ Углы в одном сегменте окружности равны]

Но дано, что ∠ACB = ∠ADB

Следовательно, ∠AEB = ∠ADB

. Это возможно только тогда, когда E совпадает с D. [В противном случае ∠AEB >∠ADB]

Точно так же E’ также должен совпадать с D. Таким образом, A, B, C и D концикличны. Отсюда доказано.

вопрос 13. На данном рисунке PR — это диаметр окружности с центром O. ∠QPS = 400 и ∠PQT = 300. Тогда ∠TUR равно

(а) 400 (б) 500 (в) 600 (г) 700

Решение: QTS = QPS + PQT = 400 + 300 = 700

(Поскольку внешний угол QTS для треугольника QPT равен сумме внутренних противоположных углов)

QTS = PTO = 700 (оба угла вертикально противоположны)

Поскольку PR — это диаметр круга, PTR = 900, 

RTO = PTR – PTO = 900 – 700 = 200

ТУР = 1/2 ТОР = 1/2 (1800 – ОТР – ОРТ) = 1/2 (1800 – 2ОТР) (как ОТ = ИЛИ)

= 1/2 (1800 – 400) = 700

вопрос 14. На данном рисунке CAB = 800, ABC = 400. Сумма DAB + ABD равна

(а) 800 (б) 1000 (в) 1200 (г) 1400

Решение: Учитывая CAB = 800, ABC = 400

из треугольника ABC, ACB = 600

ADB = 600 (Углы в одном сегменте равны)

В ∆ ABD, ADB + DAB + DBA = 1800

ДАБ + ДБА = (1800 – 600) = 1200

ЦИКЛИЧЕСКИЙ ЧЕТЫРЕХСТОРОННИЙ

Четырехугольник ABCD называется вписанным, если все его четыре вершины лежат на окружности.

Аккорды по кругу | bartleby

Что понимают под аккордами в круге?

Хорда окружности — это отрезок, концы которого лежат на окружности. Хорда, проходящая через центр окружности, является диаметром окружности. Следует отметить, что это самая длинная хорда окружности. Слово «аккорд» произошло от латинского слова «9».0870 хорда ’, что означает тетива. Существует несколько отрезков, но хорда является единственным отрезком, концы которого лежат на периферии окружности.

СС0 | Кредиты изображений: https://en.wikipedia.org | Qef

Свойства хорд

• Все хорды имеют одинаковую длину (равноудаленные) от центра окружности при условии, что все они имеют одинаковую длину.
• Биссектриса хорды всегда проходит через центр окружности.
• Перпендикулярная линия, проходящая из центра окружности, делит хорду пополам.
• Отрезок, делящий хорду пополам и проходящий через ее центр, перпендикулярен хорде.
• Если центральный угол и вписанный угол опираются на одну и ту же хорду и на одну и ту же часть хорды окружности, то центральный угол в два раза больше вписанного угла.
• Если пара углов вписана в одну и ту же хорду и по одну сторону хорды, то они называются равными.
• Если два угла вписаны в одну и ту же хорду и с противоположных сторон хорды, то они являются дополнительными.
• В случае вписанного четырехугольника внешний угол равен внутреннему противолежащему углу.
• Согласно теореме Фалеса вписанный угол, продолженный на диаметр, является прямым углом
• Известно, что наибольшей хордой окружности является диаметр, который в два раза превышает длину радиуса окружности.
• Если пересечение любых двух хорд делит одну хорду на длины «a» и «b», а другую хорду на длины «c» и «d», то «ab» равно «cd».
• Если схождение любых двух перпендикулярных хорд делит одну хорду на длины «а» и «b», а другую хорду на длины «с» и «d», то сумма a2, b2, c2 и d2 равна квадрат диаметра круга.
• Сложение квадратов длин любых двух хорд, пересекающихся под прямым углом в определенной точке, такое же, как и сложение любых двух других перпендикулярных хорд, пересекающихся в той же точке. Уравнение имеет вид 8r ² − 4p ² , где «r» — радиус окружности, а «p» — расстояние от центральной точки до точки пересечения окружности.

• Длина от данной точки окружности до данной хорды, умноженная на диаметр окружности, равна произведению расстояний от данной точки до концов хорды окружности.
• Существует только одна окружность, проходящая через все три коллинеарные точки
• Когда создается хорда, она разделяет окружность на две части, также известные как сегменты окружности, одна из которых является большим сегментом, а другая — малый сегмент.
• Для двух неравных хорд окружности большая хорда всегда будет ближе к центру, чем меньшая хорда. (Теорема о неравных хордах)
• В одинаковых или конгруэнтных окружностях меньшие дуги конгруэнтны при условии, что их соответствующие хорды также конгруэнтны.

Теоремы о хордах

Теорема 1: Одинаковые хорды стягивают равные углы в центре окружности.

Рис. 1

Дано: Окружность с центром «О», AB и CD — равные хорды окружности; Итак, АВ = CD.

Докажите, что: ∠ AOB = ∠ DOC

Решение:

В △ AOB и △ DOC

AO = OD (радиусы конгруэнтных окружностей)

AB = CD (дано) 900 03

OB = OC (радиусы конгруэнтных окружностей)

Таким образом,

△ AOB ≅ △ COD (все три соответствующие стороны имеют одинаковые свойства.)

Следовательно, ∠ AOB = ∠ DOC. (Соответствующие части конгруэнтных треугольников)

Теорема 2: Перпендикуляр, проведенный из центра окружности, делит хорду пополам, и это означает, что обе половины хорды равны по длине.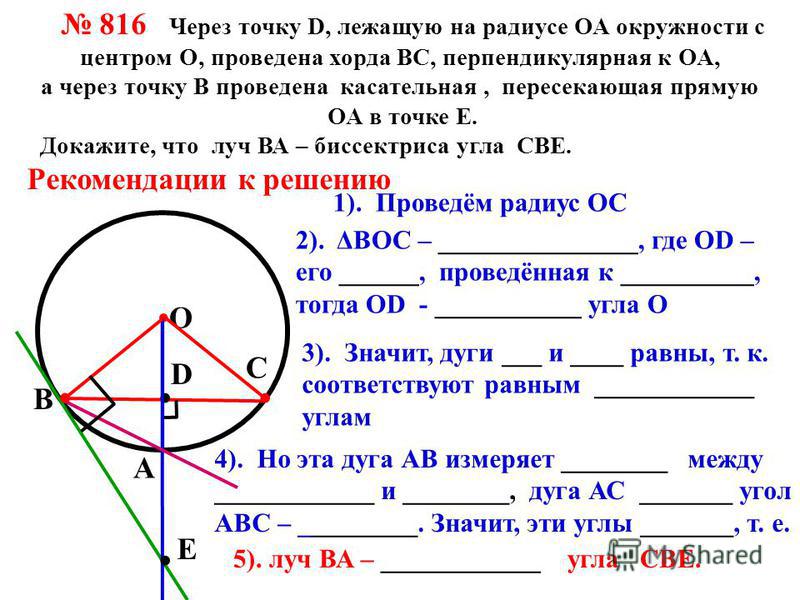

Рисунок 2

Дано: Окружность с центром ‘O’ и AB является хордой, т. е. OX перпендикулярна AB

Докажите: что OX делит хорду AB пополам или AX = BX

Решение:

In △ OAX и △ OBX,

∠ OXA = ∠ OXB (при условии, что оба угла прямые)

OA = OB (оба радиуса)

OX = OX (общая линия)

△ OAX ≅ △ OBX

Теорема 3: Линия, проведенная через центр окружности к середине хорд, перпендикулярна ей. Другими словами, любая линия из центра, которая делит хорду пополам, перпендикулярна хорде.

Рисунок 3

Дано: Окружность с центром ‘O’, хорда AB и OX делит AB или AX пополам AB или AX = BX

Докажите: что OX перпендикулярна AB

Решение:

В △ OAX и △ BOX,

OA = OB (оба радиуса)

OX = OX (общая линия)

AX = BX (дано)

△ OAX ≅ △ BOX (все три соответствующие стороны имеют одинаковые свойства.)

∠ AXO = ∠ БХО (соответствующие части равных треугольников) ……………. (1)

В линии AB,

∠ AXO и ∠ BXO образуют линейную пару,

∠ AXO + ∠ BXO = 180°

∠ AXO = ∠ AXO = 180° (из (1))

2 ∠ AXO = 18 0°

∠ АХО = 180°2

Таким образом, ∠ AXO = 90°

Следовательно, ∠ AXO = ∠ BXO = 90° и, следовательно, OX перпендикулярен AB.

Теорема 4: Если есть три не лежащих на одной прямой точки, то только одна окружность может пройти через них все.

Рисунок 4

Дано: PQR – три коллинеарных точки

Докажите: через точки PQR проходит только одна окружность

Построение: сделайте AB серединным перпендикуляром к PQ в точке ‘M’ и CD серединным перпендикуляром к QR в точке ‘N’.

Решение:

PQ не параллелен QR, поскольку они не лежат на одной прямой

Таким образом, AB и CD также не параллельны и, следовательно, они должны пересекаться в определенной точке, примем здесь за ‘O’

Подключить OP, OQ и OR

In △ OPM и △ OQM,

OM = OM (общая линия)

тий omp = ↑ OMQ (оба являются прямыми угнами, а AB перпендикулярно PQ)

PM = QM (поскольку AB BISECTS PQ)

Следовательно, △ OPM △ OQM (Правило стороной стороной стороны)

Таким OP = OQ (соответствующие части конгруэнтных треугольников) …………. (1)

и аналогично, OQ = OR …………. (2)

из (1) и (2) получаем

OP = OQ = OR

Теперь пусть OP = OQ = OR = r

Возьмем ‘O’ как центр, а ‘r’ как радиус и нарисуйте окружность. Заметим, что окружность проходит через точки P, Q и R. Таким образом, они концикличны.

Рисунок 5

Рассмотрим другую окружность с центром «O!» и радиусом «r1», проходящую через точки P, Q и R. Опустите перпендикуляр так, чтобы OM был перпендикулярен PQ.

Итак, PM’ = QM’ (перпендикуляр, опущенный из центра, делит его пополам), и, таким образом, M’ является серединой PQ. Поскольку прямая может иметь только одну биссектрису, O1M’ совпадает с OM, а O1 совпадает с O.

Таким образом, может существовать только одна такая окружность, проходящая через точки P, Q и R.

Теорема 5: Равные хорды окружности находятся на одинаковом расстоянии от центра окружности. Обратное также верно.

Рисунок 6

Дано: Окружность с центром «О», AB и CD являются двумя хордами окружности равной длины (AB = CD), а OX и OY перпендикулярны AB и CD соответственно.

Докажите: что OX = OY

Решение:

OX перпендикулярен AB (так как перпендикуляр из центра к хорде делит его пополам)

Итак, AX = BX = AB2 …………… (1)

Аналогично, OY перпендикулярна CD (поскольку перпендикуляр из центра к хорде делит ее пополам)

Итак, CY = DY = CD2 …………… (2)

Теперь AB = CD (дано)

Тогда AB2+CD2

AX = CY (из (1) и (2)) …………… (3)

In △ AOX и △ COY,

∠ OXA = ∠ OYC (Учитывая, что оба верны углов)

OA = OC (радиус)

AX = CY (из (3))

△ AOX ≅△ COY (по правилу правой руки)

Следовательно, OX = OY (соответствующие части конгруэнтных треугольников)

Теорема 6: Угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого дугой в любой другой заданной точке окружности.

Дано: Окружность с центром «O», дугой окружности является PQ, она стягивает ∠ POQ в точке «O» и ∠ PAQ в точке «A» окружности.

Построение: соедините АО и продлите до точки «В»

Докажите: Два случая:

Рисунок 70003

OP = OA (Радиус)

∠ OPA = ∠ OAP (противолежащие равным сторонам углы равны по длине) ………. (1)

Используя внешнее свойство углов, которое гласит, что внешний угол есть сложение внутренних противоположных углов, мы получаем ∠ BOP = 2 ∠ OAP ………… (3)

In △ AQO,

OQ = OA (Радиус)

∠ OQA = ∠ OAQ (углы, противоположные равным сторонам, равны по длине) ………. (2)

Используя внешнее свойство углов, которое гласит, что внешний угол есть сложение внутренних противоположных углов, мы получаем ОП = 2 ∠ OAQ ………… (4)

Суммируя уравнения (3) и (4), получаем,

∠ BOP + ∠ BOQ = 2 ∠ OAP + 2 ∠ OAQ

∠ POQ = 2 (∠ OAP + ∠ OAQ)

Следовательно, ∠ POQ = 2 ∠ PAQ

Решение (вариант 2):

In △ APO,

OP = OA (радиус)

∠ OPA = ∠ OAP (противолежащие равным сторонам углы равны по длине) ………. (1)

Используя внешнее свойство углов, которое гласит, что внешний угол есть сложение внутренних противоположных углов, мы получаем ∠ BOP = 2 ∠ OAP ………… (3)

In △ AQO,

OQ = OA (Радиус)

∠ OQA = ∠ OAQ (углы, противоположные равным сторонам, равны по длине) ……….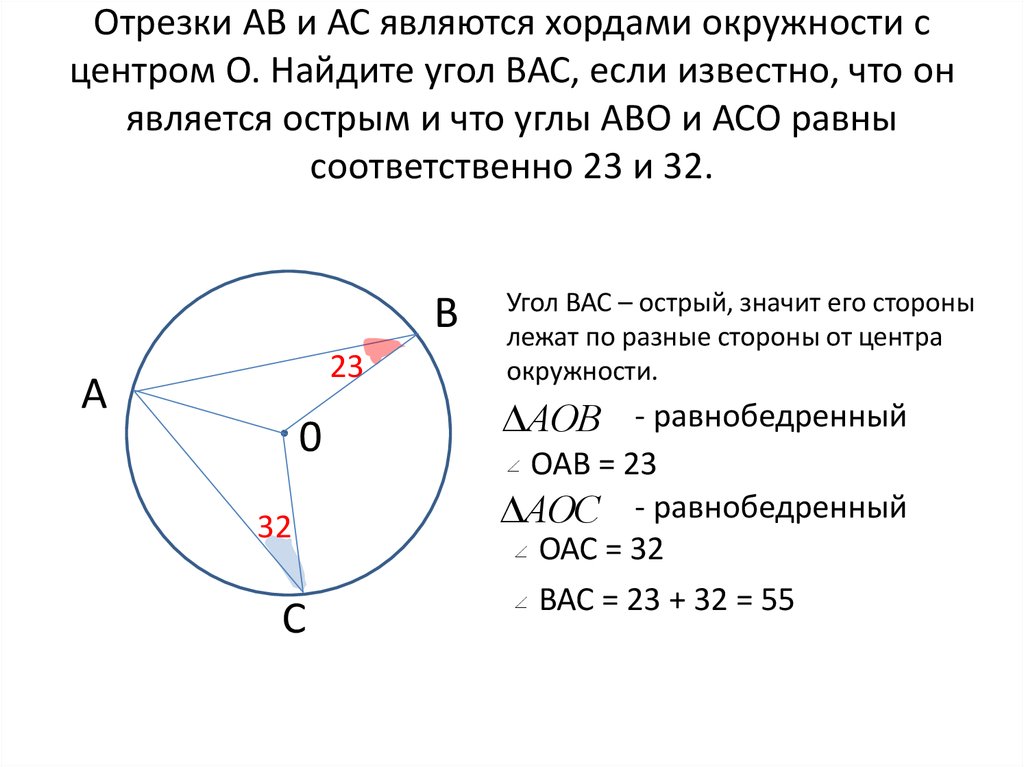 (2)

Используя внешнее свойство углов, которое гласит, что внешний угол есть сложение внутренних противоположных углов, мы получаем,

∠ BOQ = ∠ OQA + ∠ OAQ

∠ BOP = ∠ OAQ + ∠ OAQ

∠ BOP = 2 ∠ OAQ …………. ) и (4), мы get,

∠ BOP + ∠ BOQ = 2 ∠ OAP + 2 ∠ OAQ

Угол рефлекса ∠ POQ = 2 (∠ OAP + ∠ OAQ)

Угол рефлекса ∠ POQ = 2 ∠ PAQ 90 003

Следовательно, 360° — ∠ POQ = 2 ∠ PAQ

Теорема 7: Угол, опирающийся на диаметр или полуокружность в любой точке окружности, является прямым углом.

Рисунок 8

Дано: Окружность с центром «О», диаметр окружности PQ, и она стягивает ∠ PAQ в точке «А» на окружности.

Докажите: что ∠ PAQ = 90°

Решение:

POQ — прямая, проходящая через центр окружности «О».

Итак, угол, образуемый дугой PQ в точке «О», равен ∠ PAQ = 180° …………. (1)

Согласно теореме о хорде окружности угол, образуемый дугой в центре, в два раза больше угла, образуемого ею в любой точке оставшейся части окружности.

Таким образом, ∠ POQ = 2 ∠ PAQ

∠ POQ /2 = ∠ PAQ

180° / 2 = ∠ PAQ

Следовательно, ∠ PAQ = 90°

Формулы, используемые в хордах

Две формулы для определения длины хорды окружности:

1. Длина хорды с использованием перпендикулярного расстояния от центр круга равен 2(r2-d2), где «r» — радиус круга, а «d» — перпендикулярное расстояние прямоугольного треугольника.

2. Длина хорды с помощью тригонометрии равна 2r sinθ2, где «r» — радиус окружности, а «θ» — угол, образуемый в центральной части хорды.

Контекст и применение

Тема аккордов применима во многих областях, таких как архитектура и дизайн. Везде, где мы используем круги, нам также необходимо знать понятия аккордов. Эту тему изучают студенты, изучающие такие курсы, как бакалавр технологии (инженерное дело), ​​магистр естественных наук (алгебра, геометрия и криптография) и магистр естественных наук (математика и приложения).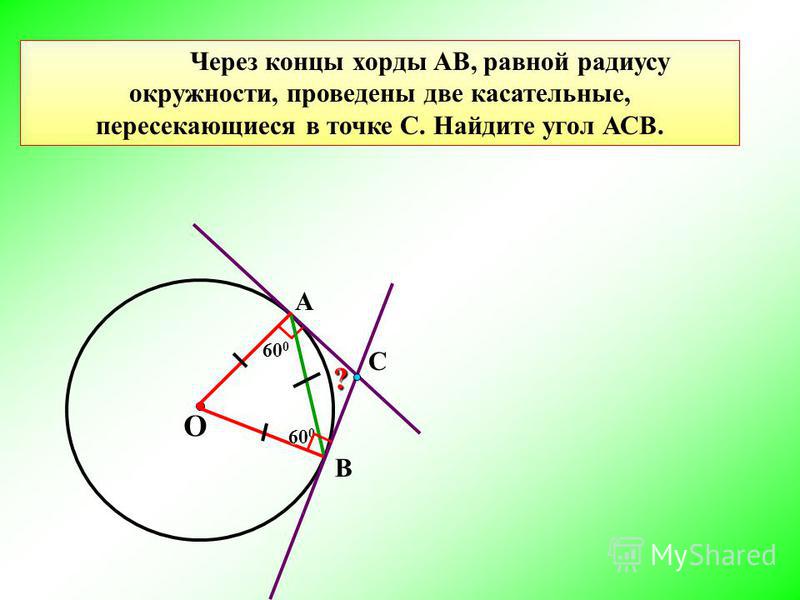

• Синтетическая геометрия
• Обратная теорема Пифагора

Практические задачи

Q1. Что означает слово «аккорд» на латыни?

1. хорда
2. хорда
3. перезвон
4. цепь

Правильный вариант: 1.

Пояснение: Слово «аккорд» на латыни означает хорда. Существует несколько отрезков, но хорда является единственным отрезком, концы которого лежат на периферии окружности.

Q2. Как называются части, которые образуются при проведении хорды в окружности?

1. Малая часть и большая часть

2. Малая часть и большая часть
3. Малая часть и большая часть
4. Малая часть и большая часть

Правильный вариант: 2.

Объяснение: Когда хорда рисуется круг, части называются меньший сегмент и большой сегмент.

Q3. Какая самая длинная хорда окружности?

1. Радиус
2. Касательная
3. Диаметр
4. Дуга

Правильный вариант: 3.

Пояснение: Самая длинная хорда окружности — это диаметр. Хорда, проходящая через центр окружности, является диаметром окружности.

Q4. Что утверждает теорема Фалеса?

1. Вписанная дуга, продолженная на радиус, является прямым углом
2. Вписанный сектор, продолженный на хорду, является прямым углом
3. Вписанная дуга, продолженная по касательной, является прямым углом прямой угол

Правильный вариант: 4.

Пояснение: Теорема Фалеса утверждает, что вписанный угол, продолженный на диаметр, является прямым углом.

Q5. Какие из следующих утверждений неверны?

1. Равные хорды образуют равные углы в центре окружности.
2. Существует множество окружностей, проходящих через все три коллинеарные точки
3. Равные хорды окружности находятся на одинаковом расстоянии от центра окружности.
4. В случае вписанного четырехугольника внешний угол равен внутреннему противолежащему углу.