Закон Кулона | Электрикам
Опытами Кулона установлено, что электрическое поле точечного заряда q1 действует на помещенный в точке А (рис. 1) второй точечный пробный заряд q2 с силой F12 прямо пропорциональной численным значениям обоих зарядов, обратно пропорциональной квадрату расстояния R между ними и зависящей от среды, в которой находятся заряды.
Электрическое поле точечного заряда
Таким образом, по закону Кулона сила
Коэффициент εa, называемый абсолютной диэлектрической проницаемостью среды, учитывает влияние на силу заряженных частиц среды, в которой находятся заряды q1 и q2; его численное значение зависит от системы единиц.
Величинапредставляет собой напряженность электрического поля заряда q1 в точке A. Так как поле симметричное, то во всех точках, удаленных от заряда q1 на равные расстояния R, напряженность поля численно одинакова. Направление вектора напряженности поля E1 в точке А совпадает с направлением прямой, проходящей через точечные заряды q1 и q2, и определяется по направлению силы F
Таким образом, силу, действующую на заряд q2 можно представить произведением напряженности поля заряда q1 и значения заряда q2:C другой стороны, заряд q1 расположен в поле заряда q2 и на заряд q1 действует силат. е. численно равная силе, с которой поле заряда q1 действует не заряд q2.
Силы взаимодействия (кулоновские силы) вызывают притяжение разноименных зарядов и отталкивание одноименных (рис. 2).
Рис.2 Силы взаимодействия между электрическими зарядами (кулоновские силы)
Если электрическое поле создается несколькими зарядами, то для определения силы и напряженности поля
в среде, в которой εa не зависит от напряженности поля (линейная среда), применяют принцип наложения. Например, сила, с которой заряды q1 и q2 действуют на пробный
точечный заряд q находящийся в точке С (рис. 3), равна геометрической сумме двух сил. во-первых, силе F1, с которой q1 действует на заряд q в отсутствие q2, во-вторых, силе F2 с которой q2 действует на заряд q в отсутствие q1.
Силы F1 и F2 определяются по выражению, аналогичному (1). Поэтому и напряженность поля зарядов q1 и q2 в точке C или любой другой точке поля определяется как геометрическая сумма или сумма векторовгде E1 и E2 —
Из (2) определяется единица измерения абсолютной проницаемости среды в системе СИ:Единица Кл/В называется фарад (Ф) — единица емкости, единица абсолютной диэлектрической проницаемости называется фарад на метр (Ф/м).
Различные среды имеют разные значения абсолютной диэлектрической проницаемости. Абсолютная диэлектрическая проницаемость вакуума, называемая электрической постоянной, в системе СИДиэлектрические проницаемости других сред обычно измеряют в относительных единицах (по отношению к электрической постоянной). Отношение абсолютной диэлектрической проницаемости среды к электрической постоянной ε
Для вакуума εr= 1, для воздуха практически εr = 1, для дистиллированной воды εr= 80, для большинства веществ и материалов ε
Пример. Два точечных заряда q1 = q2 = 6*10-11 Кл находятся на расстоянии 12 см друг от друга в воздухе Определить напряженность поля этих зарядов в точке С (рис. 3), если она находится на перпендикуляре CD к прямой AB и если отрезки АD = DВ = CD, и силу F, действующую не точечный заряд q=2*10-11 H*Кл, находящийся в точке С.
Определим расстояние R1, между точками А и C:
По (2) напряженность E1
Так как R2=R1 и q1 и q2, то E2 = E1 = 76 В/м.
Векторы E1 и E2 расположены под углом 90 градусов друг к другу (рис.
3), и так как результирующий вектор равен геометрической сумме слагающих, то
По (3)
07.12.2015
ТОЭ,Задачи с решением
Электрическое поле
Закон Кулона. Калькулятор онлайн.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор Закона Кулона с решением позволит вычислить силу взаимодействия двух зарядов, электрический заряд, а так же расстояние между зарядами, единицы измерения которых, могут включать любые приставки Си.
-24]| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Калькулятор закона Кулона | Как найти q1 и q2, используя уравнение закона Кулона?
Создатель: Нааз Фатима
Отзыв: Раджашекхар Валипишетти
Последнее обновление: 10 апр.
2023 г.
Калькулятор закона Кулона — удобный инструмент для оценки силы притяжения или отталкивания между двумя статически заряженными частицами. Все, что вам нужно сделать, это указать соответствующие заряды q1, q2, расстояние между ними и нажать кнопку расчета, чтобы быстро получить электрическую силу.
Сборы…
равно не равно
Калькулятор закона Кулона: Если вы ищете исчерпывающий источник, который предоставляет бесплатный инструмент для упрощения расчетов закона Кулона, то вы попали в нужное место. Вы можете быстро найти заряды, расстояние между ними или фокус с помощью нашего калькулятора закона Кулона. Он делает все за вас и дает четкое объяснение, облегчая вам понимание концепции. Читайте дальше, чтобы узнать, что подразумевается под законом Кулона, формулой, единицами электрического заряда, расчетом электростатической силы, расстоянием между объектами, зарядом объекта и т.
д.
Сила притяжения или отталкивания между двумя заряженными телами прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними. Закон Кулона, также известный как закон обратных квадратов Кулона, представляет собой закон физики, который количественно определяет силу между двумя стационарными электрически заряженными телами или частицами. Единицей электрического заряда является кулон, который обозначается символом C.
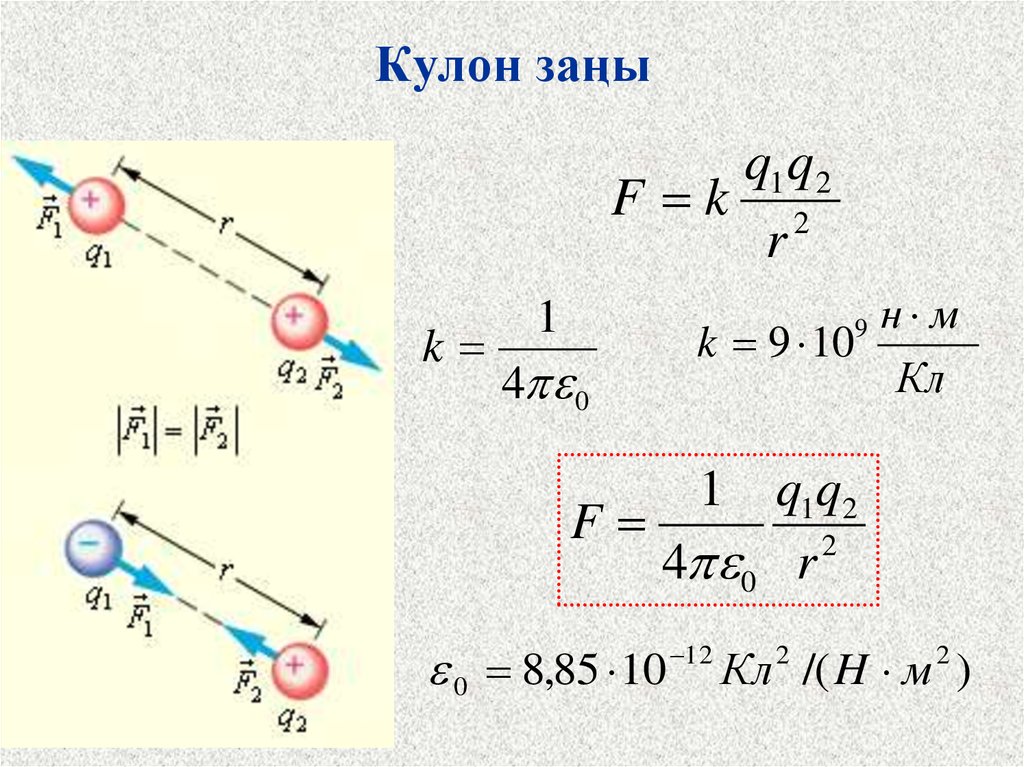
Закон Кулона, также известный как закон обратных квадратов Кулона, используется для определения электростатической силы между двумя заряженными телами. Сила действует вдоль кратчайшей линии, соединяющей заряды. Он отталкивающий, если оба заряда имеют один и тот же знак, и притягательный, если они имеют противоположные знаки. Формула закона Кулона задается уравнением F = k e qΓéüqΓéé/r┬▓
- Где F — электростатическая сила между зарядами, выраженная в единицах Netwons
- qΓéü – величина первого заряда, выраженная в кулонах единиц.
- qΓéé – величина второго заряда, выраженная в единицах кулонов
- r — кратчайшее расстояние между объектами с единицами м
- ke — постоянная Кулона, равная 8,98755 ├ù 10Γ╣ N┬╖m┬▓/C┬▓
Physicscalc.Com содержит такие понятия, как трение, ускорение под действием силы тяжести, давление воды, гравитация и многое другое. вместе с их соответствующими калькуляторами все под одной крышей.
Мы можем легко определить электростатическую силу между двумя объектами, если знаем расстояние между ними. Сила F определяется как произведение постоянной Кулона qΓéü, умноженное на другой заряд qΓéé, деленное на квадрат расстояния между ними. т.е. F = K E Qγéüqγéé / r┬▓
Переставление закона Кулона. Мы можем рассчитать расстояние между объектами, то есть R = γêü (K E ├ Qγ ├ Qγ Qγ • F)0019
Если известны электростатический заряд одного объекта, сила, расстояние между ними, то можно вычислить другой заряд по формуле qΓéé = (F*r┬▓)/(k e ├ù qΓéü)
У закона Кулона есть несколько ограничений, и мы подробно объяснили их все для вашей идеи.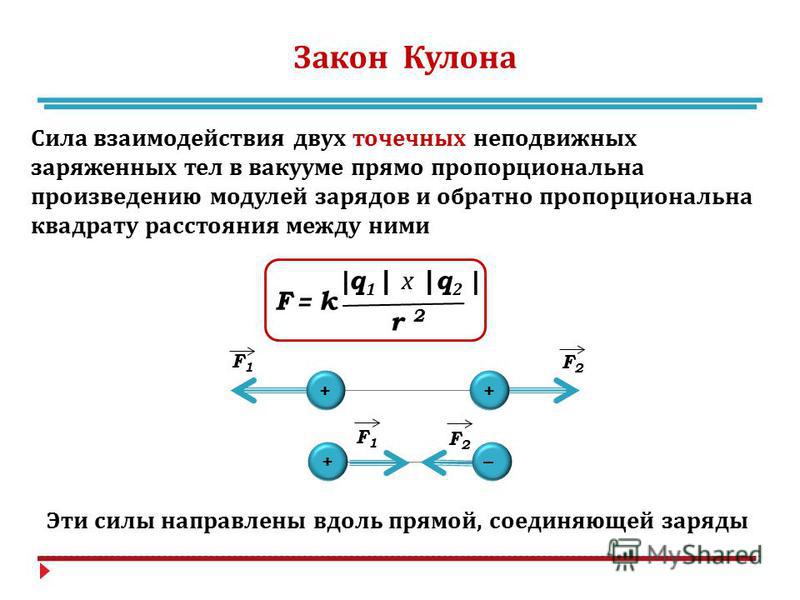
Они расположены по линиям
- Закон Кулона применим только к зарядам в состоянии покоя.
- Может применяться в случаях, когда соблюдается закон обратных квадратов.
- Трудно применить закон кулона для зарядов произвольной формы, так как мы не можем вычислить расстояние между ними.
- Мы не можем напрямую использовать этот закон для определения зарядов на больших планетах.
1. Что такое закон Кулона?
Закон Кулона гласит, что сила притяжения или отталкивания между двумя заряженными телами прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними.
2. Что такое единица электрического заряда?
Единицей электрического заряда является кулон.
3. Каковы ограничения закона Кулона?
Ограниченность закона Кулона заключается в том, что он применим только к точечным покоящимся зарядам, зарядам произвольной формы.
Мы не можем вычислить заряд на больших планетах.
4.Что такое формула закона Кулона?
Формула закона Кулона: F = keqΓéüqΓéé/r┬▓
Калькулятор закона Кулона
Создано Bogna Szyk
Отзыв Стивена Вудинга
Последнее обновление: 04 февраля 2023 г.
Содержание:- Как использовать закон Кулона 0039
- Интерпретация результатов
- FAQ
Этот калькулятор электрической силы позволит вам определить силу отталкивания или притяжения между двумя статически заряженными частицами. Продолжайте читать, чтобы лучше понять закон Кулона, условия его справедливости и физическую интерпретацию полученного результата. 92}}8,98755⋅109 C2N⋅м2. Это значение уже заложено в калькуляторе — запоминать не надо 🙂
Просто введите любые три значения в наш калькулятор электрической силы, чтобы в результате получить четвертое.
Чтобы вычислить электрический потенциал в точке, обусловленный либо единичным точечным зарядом, либо системой точечных зарядов, воспользуйтесь нашим калькулятором электрического потенциала.
У нас также есть калькулятор электрического поля для точечных зарядов.
Электрические зарядные устройства
Единицей электрического заряда является кулон (обозначение: C). Он определяется как заряд, переносимый постоянным током в 1 ампер в течение 1 секунды. Следовательно, 1 C=1 A⋅1 s\mathrm{1 \ C = 1 \ A \cdot 1 \ s}1 C=1 A⋅1 s, выраженное в единицах СИ.
Если вы не помните, что такое ампер, воспользуйтесь нашим калькулятором закона Ома.
Условия достоверности
Чтобы калькулятор электростатической силы выдавал действительные значения, должны быть выполнены три основных условия:
- Заряды должны быть неподвижны — они не могут двигаться друг относительно друга.
- Предусмотрены начисления баллов. Это предположение справедливо и для любых сферических и симметричных зарядов. Например, заряженный металлический шар удовлетворяет этому условию, а заряженный металлический ящик — нет.
- Заряды не могут перекрываться — они должны быть различны и иметь хотя бы минимальное расстояние между собой.
Интерпретация результатов
Сила, полученная с помощью нашего калькулятора закона Кулона, может быть как положительной, так и отрицательной. Положительная сила подразумевает отталкивающее взаимодействие между зарядами. Отрицательная сила означает, что взаимодействие является привлекательным. 9{-9} \ C}10−9 C.
Часто задаваемые вопросы
Как рассчитать силу между двумя заряженными частицами?
Для расчета силы между двумя заряженными частицами мы используем закон Кулона . Выполните следующие простые шаги, чтобы найти результат:
- Найдите заряды
q1иq2частиц в кулонах и умножьте их. - Умножьте результат шага 1 на константу
ke = 8,988E9 (N ⋅ м²)/C². - Разделить результат на квадрат расстояния между частицами .
Результатом является сила (притягивающая, если знак отрицательный, и отталкивающая, если положительный), действующая между заряженными частицами.
Является ли закон Кулона законом обратных квадратов?
Наличие квадрата расстояния между двумя частицами в знаменателе формулы закона Кулона делает ее законом обратных квадратов . Это свойство связано с точечным характером электрического заряда, учитываемого в формуле: так как электрическое поле излучает радиально , поле распространяется по поверхности сферы, что равно 4 · π · r² . В случае закона Кулона экспериментальные результаты подтверждают это открытие, утверждая, что показатель степени равен 2 , за которым следуют 15 нулей!
Какая сила взаимодействует между протоном и электроном в атоме водорода?
Сила притяжения между электроном и протоном в атоме водорода равна 1,60E-8 Н . Чтобы найти этот результат, начните с размещения известных данных:
- Заряд электрона и протона одинаковый, с противоположным знаком, и равен
qe = -qp = -1,602176634E-19 C.
Leave A Comment