Как найти производную функции по графику и касательной: Производная функции. Геометрический смысл производной.

Производная функции. Геометрический смысл производной.

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть

производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Определение.

Производная – это скорость изменения функции.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку А с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции.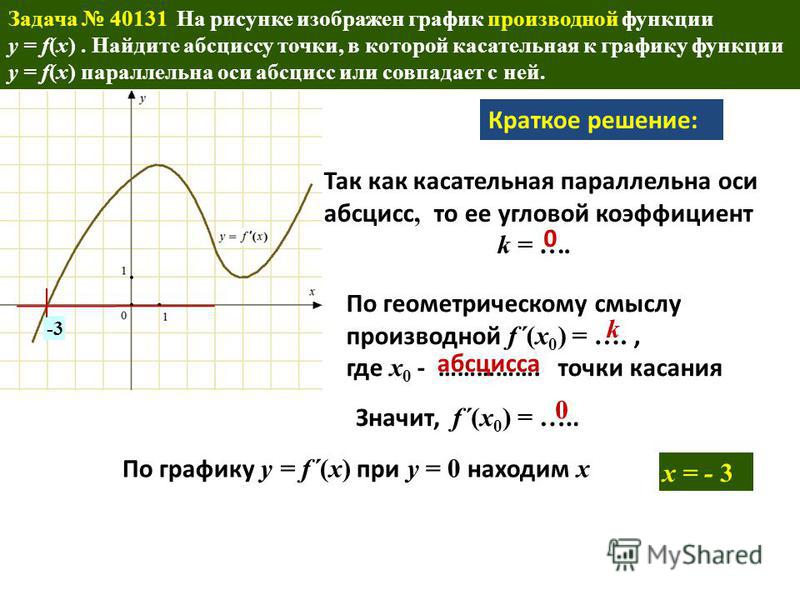 Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси ОХ.

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина k в этом уравнении называется угловым коэффициентом прямой.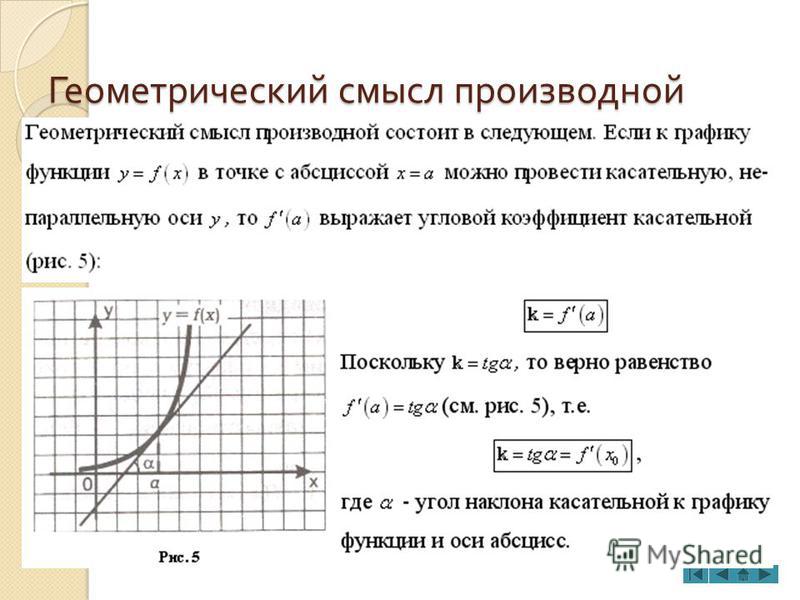

Она равна тангенсу угла наклона прямой к оси X.

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке A функция возрастает. Касательная к графику, проведенная в точке A, образует острый угол  с положительным направлением оси X. Значит, в точке A производная положительна.

В точке B наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси X.  Поскольку тангенс тупого угла отрицателен, в точке B производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках C (точка максимума) и D (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка С — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке С с «плюса» на «минус».

В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».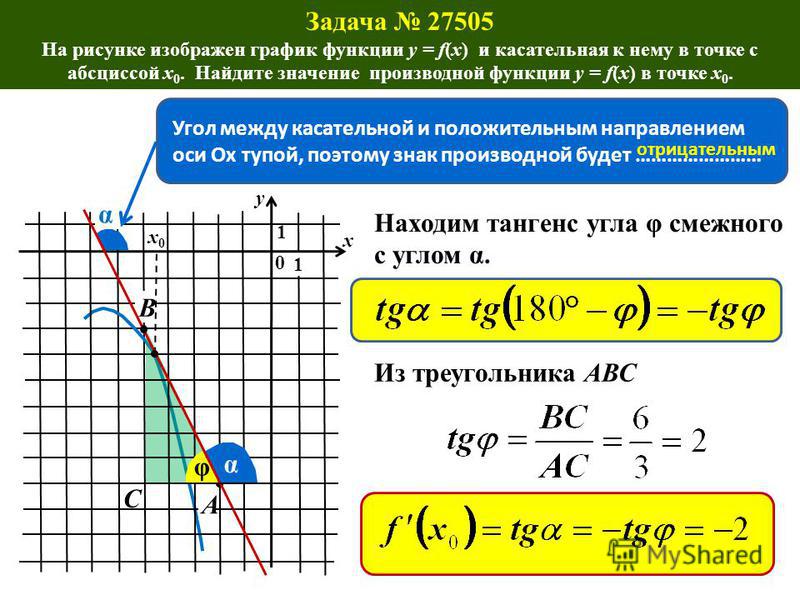

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

1. Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке E касательная к графику горизонтальна, и производная равна нулю. Однако до точки E функция возрастала — и после точки E продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

2. Бывает и так, что в точке максимума или минимума производная не существует.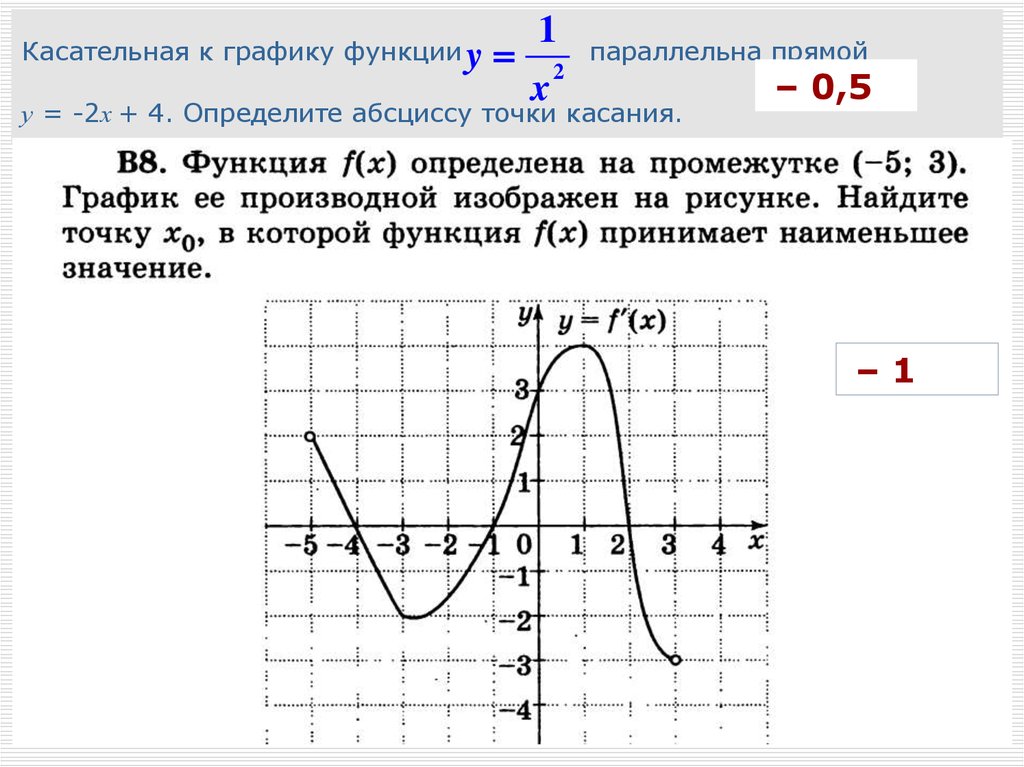 На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.

Геометрический смысл производной, задачи

Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.

Задача 1. На рисунке изображен график функции ). Найдите количество решений уравнения )=0 на отрезке [-2,5; 9,5].

Решение:

Производная функции равна нулю в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

Задача 2. На рисунке изображен график функции y= ) — производной функции ). Сколько точек максимума имеет функция ) на отрезке ? В ответе запишите это число.

Решение:

Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.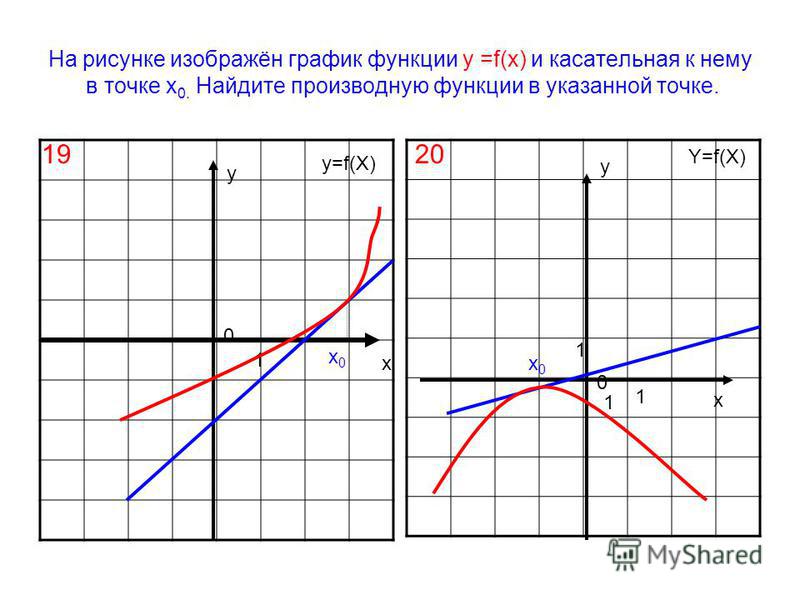

В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.

В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке на графике одна.

Ответ: 1.

Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Вспомним определение.

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).

Это геометрический смысл производной.

В точке функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол с положительным направлением оси Х. Найдем тангенс острого угла смежного с углом

Ответ: -0,5.

Задача 4. На рисунке изображен график производной функции определенной на отрезке В какой точке отрезка принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 1,5.

Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает.

Значит, — точка минимума функции

Поэтому и свое наименьшее значение функция принимает в точке 1,5.

Ответ: 1,5.

Задача 5. На рисунке изображен график — производной функции В какой точке отрезка функция принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 3.

Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает.

Значит, — точка минимума функции

Кстати, вид графика функции определить нетрудно. Это квадратичная парабола с ветвями вверх.

Ответ: 3.

Задача 6. На рисунке изображен график производной непрерывной функции В какой точке отрезка функция принимает наибольшее значение?

Решение:

На отрезке расположена точка в которой производная равна нулю и меняет знак с «+» на «-».

Это значит, что — точка максимума функции на отрезке и наибольшее значение функция принимает именно в этой точке.

Ответ: — 2,5.

Задача 7. На рисунке изображен график производной функции определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция принимает наименьшее значение?

Решение:

Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс».

Слева от точки 0 производная отрицательна, функция убывает.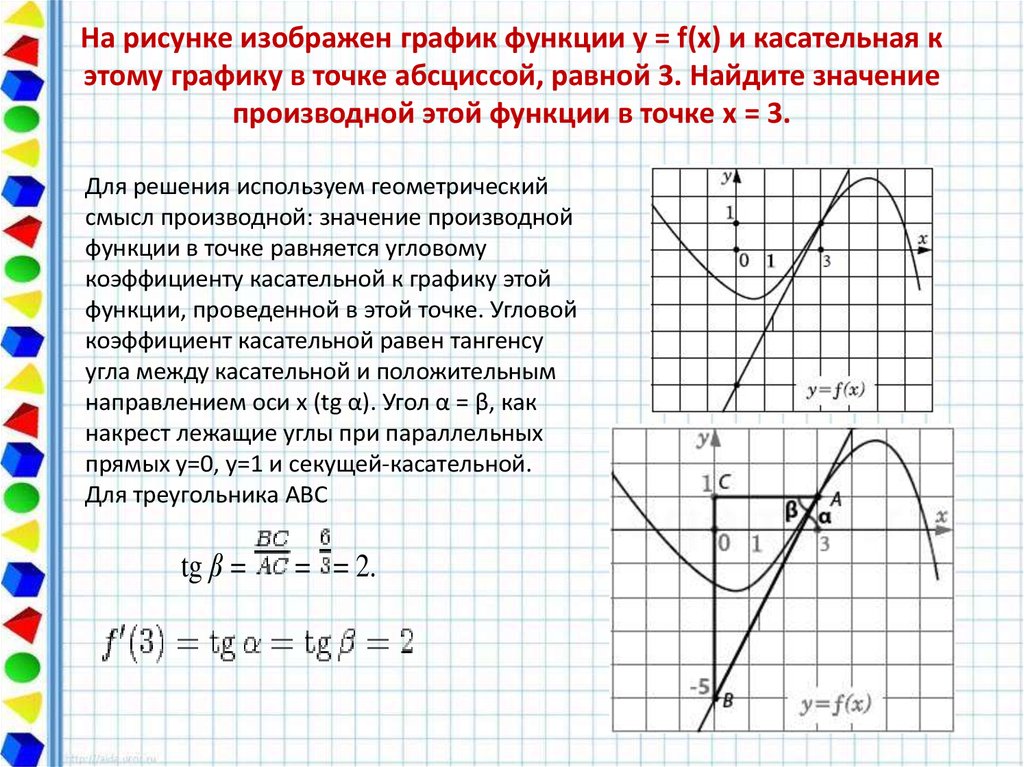 Справа от этой точки производная положительна, функция возрастает.

Наименьшее значение на отрезке достигается при x = 0.

Ответ: 0.

Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.

— касательная к

В точке производная отрицательная, т.к. функция — убывает в этой точке.

— угол, который образует касательная с положительным направлением оси Х.

Угол — тупой, а смежный с ним угол — острый.

Ответ: -0,375.

Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:

Найдём значения производных в точках А и В с помощью графика.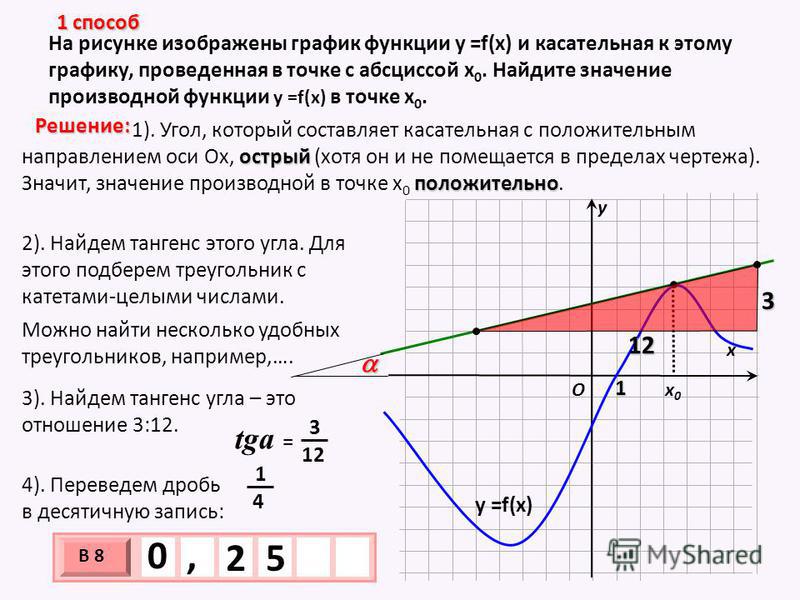

где — угол наклона касательной к графику функции в точке с абсциссой

Для точки А:

Для точки В:

Отношение производных:

Ответ: 0,15.

Условия касания

Пусть прямая касается графика функции в точке Тогда для точки выполняются условия касания:

Первое уравнение показывает, что значения функций и в точке равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.

Второе условие показывает, что производная функции в точке равна угловому коэффициенту касательной, то есть k.

Задача 10. Прямая касается графика функции причем абсцисса точки касания положительна. Найдите b.

Решение:

Запишем условие касания:

Начнем со второго уравнения:

Т.к. то

Найдем подставив в первое уравнение:

отсюда

Ответ: -7.

Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.

Физический смысл производной

Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.

И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».

Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.

Вспомним формулу для равномерного прямолинейного движения: где x — координата.

Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно едет. Для второго автомобиля = 40 км/ч, для третьего = 75 км/ч.

Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.

Скорость тела — это производная от его координаты по времени.

А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени и проведем в этой точке касательную к графику функции.

Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент

Мы получили, что мгновенная скорость — это производная от координаты по времени.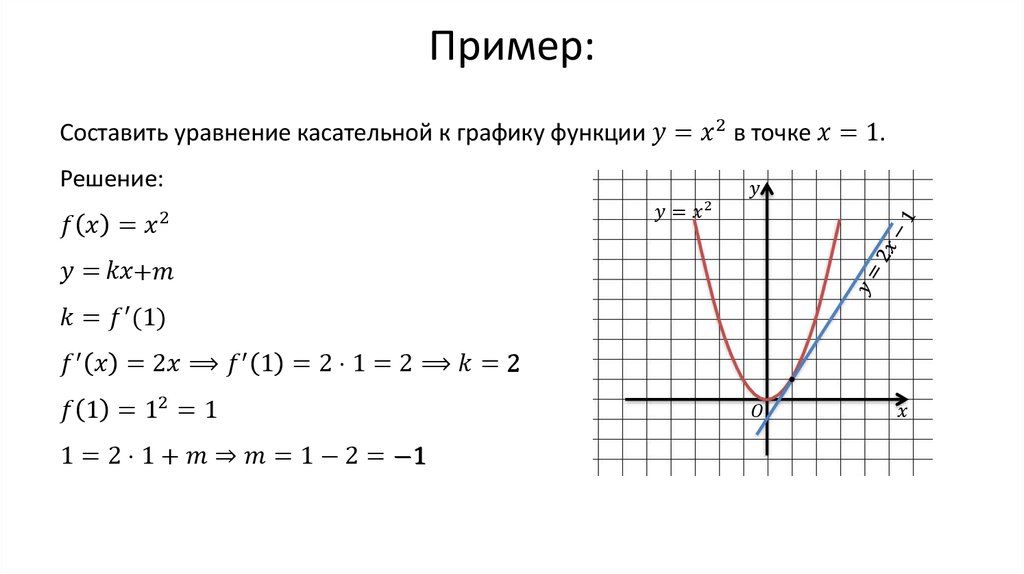

Это физический смысл производной.

Но не только скорость в физике является производной от другой физической величины, координаты.

Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.

Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются

дифференциальными. А само действие взятия производной называется дифференцированием.

Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.

Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).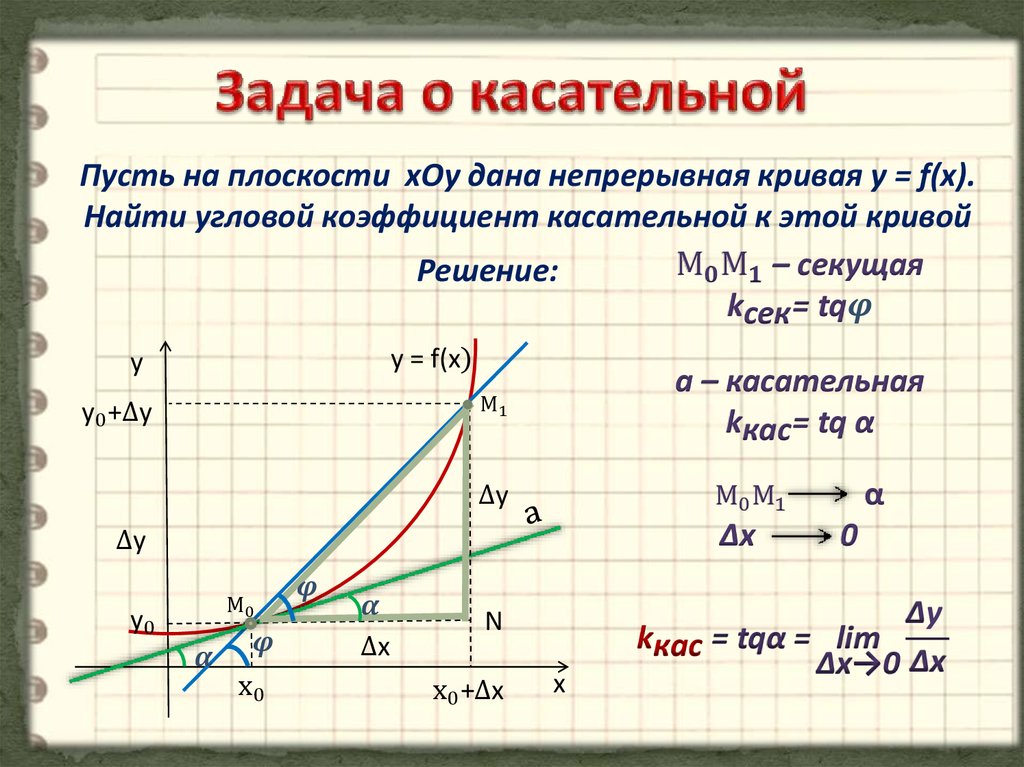

Решение:

Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.

Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).

Ответ: 6.

Изучая высшую математику в вузе, вы узнаете еще одно определение производной.

Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.

Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.

Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Производная функции. Геометрический смысл производной» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 09.03.2023

Уравнение касательной к графику функции. Как его найти?

Поможем понять и полюбить математику

Начать учиться

В чем заключается геометрический смысл производной

Одну из главных ролей в записи касательной к графику играет производная, поэтому определим ее геометрический смысл.

Пусть задана произвольная функция y = f(x).

На графике этой функции возьмем точку А с координатами .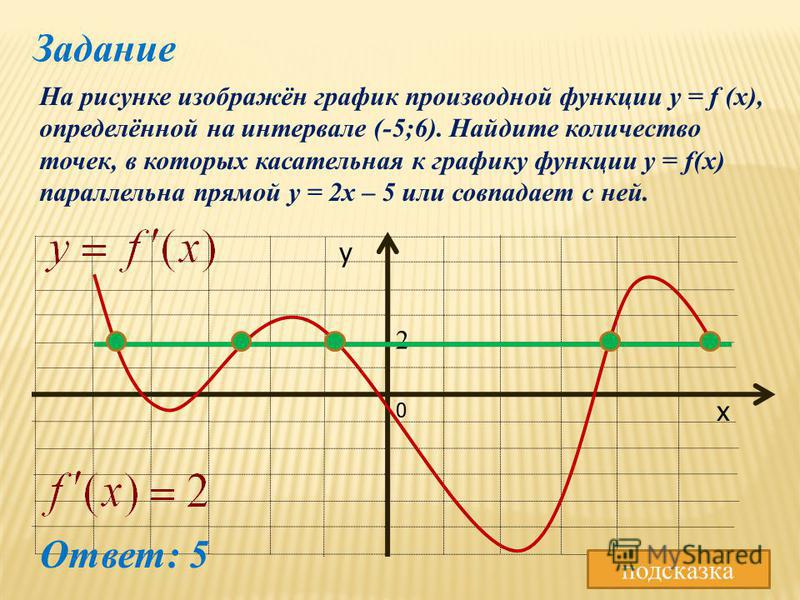 А теперь выберем точку B с координатами недалеко от точки А.

Проведем через точки A и B прямую.

Угол наклона прямой к оси абсцисс обозначим буквой .

Проведем через точку А прямую, параллельную оси абсцисс, а через точку B — прямую, параллельную оси ординат. Пусть эти две прямые пересекутся в точке C.

Тогда катет , а катет .

Если взять отношения этих значений , то получим отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике ABC, что равно .

Если уменьшать расстояние между точками A и B, то будут уменьшаться длины отрезков и и в какой-то момент точка В совпадет с точкой A, а отношение станет равно производной функции y = f(x) в точке .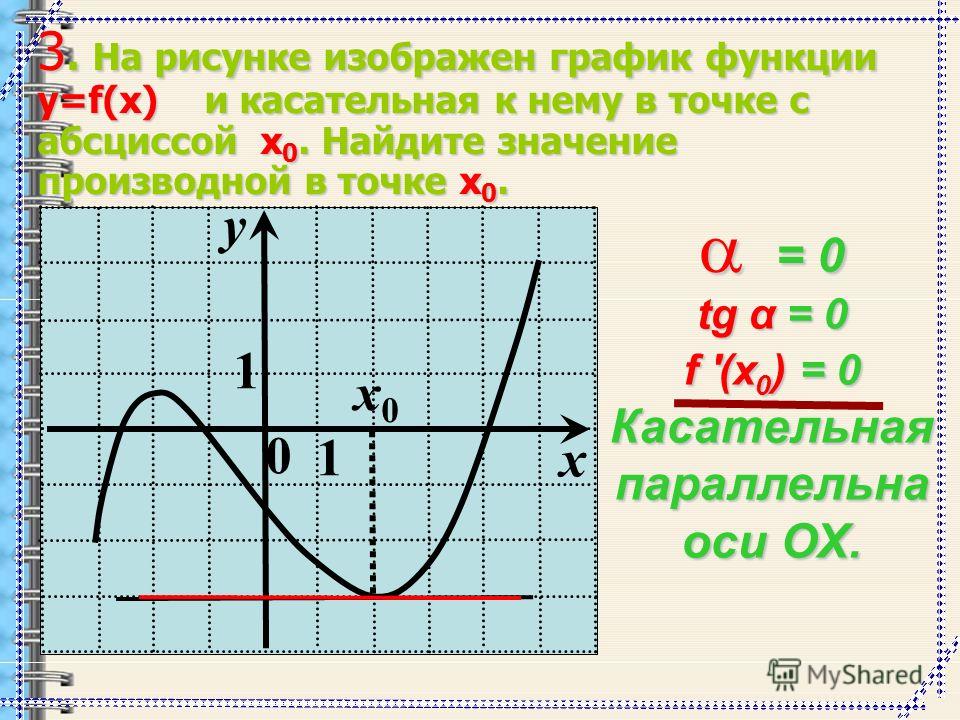

Тут может возникнуть вопрос: при чем здесь геометрический смысл производной, если мы начали с касательной?

Касательная — это прямая. Вспомним уравнение прямой: y = kx + b, где k — это коэффициент наклона прямой, и он равен тангенсу угла между прямой и осью абсцисс. А теперь совмещаем все данные и делаем вывод, что .

Это очень важный для нас вывод, попробуем применить его на практике, а именно на задачах формата профильного ЕГЭ по математике.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Решение задач

Задача 1

К графику функции y = f(x) проведена касательная в точке с абсциссой . Нужно найти угловой коэффициент касательной к графику данной функции.

Из теории выше мы узнали, как найти угловой коэффициент касательной — он равен тангенсу угла наклона касательной к графику функции в точке. Значит, через целочисленные точки на прямой построим прямоугольный треугольник и найдем отношение противолежащего катета к прилежащему — получится .

Ответ: 3.

Задача 2

К графику функции y = f(x) проведена касательная в точке с абсциссой . Определите угловой коэффициент касательной в точке .

Действуйте по уже известным правилам. Получился ответ 0,25? А вот и нет! В данном случае нужно обратить внимание на убывание графика касательной. Видите, она слева направо идет вниз? Значит, к ответу нужно добавить минус и записать его — получится −0,25.

Ответ: −0,25.

Будьте внимательны

Не позвольте маленькому минусу лишить вас дополнительных баллов на экзамене или контрольной. 😩

Задача 3

На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 36.

Надеюсь, вы не подумали, что мы будем изображать прямую y = 36 и искать касательные, параллельные ей. 🤯 Достаточно будет рассуждений. Прямая y = 36 — горизонтальная прямая с k = 0, а значит, и у касательных к графику k = 0 или тангенс угла наклона касательной к графику функции также будет равен нулю, что может быть только в точках экстремума функции или, проще говоря, в «бугорках» функции.

В ответе просили указать количество таких точек, значит, ответ — 5.

Ответ: 5.

Задача 4

Прямая y = 4x + 13 параллельна касательной к графику функции . Найдите абсциссу точки касания.

Если прямая параллельна касательной к графику функции, то у них будут равные угловые коэффициенты. Угловой коэффициент прямой y = 4x + 13 равен 4, а угловой коэффициент касательной к графику функции равен производной от этой функции, то есть 2x − 3. Приравняем полученные значения и найдем x:

2x − 3 = 4;

x = 3,5.

Ответ: 3,5 — абсцисса точки касания.

Как составить уравнение касательной к графику функции

Но как поступать, если нужно составить уравнение касательной к графику функции?

Уравнение касательной к графику функции y = f(x) в точке находится по формуле .

Для упрощения понимания этой формулы запишем алгоритм составления уравнения касательной к кривой y = f(x) в точке :

1. Вычислим значение функции в точке касания, для этого подставим в y = f(x) и посчитаем.

2. Продифференцируем функцию y = f(x).

3. Вычислим значение функции в точке касания, для этого подставим в и посчитаем.

4. Составим уравнение касательной и приведем его к виду y = kx + b.

Задача 5

Запишите уравнение касательной к параболе в точке .

Воспользуемся алгоритмом выше:

1. Вычислим значение функции в точке касания, для этого подставим в и посчитаем: .

2. Продифференцируем функцию: .

3. Вычислим значение функции в точке касания: .

4. Все найденные значения подставим в уравнение касательной: .

5. Приведем полученное выражение к виду y = kx + b: y = −2x + 24.

Ответ: уравнение касательной y = −2x + 24.

По условию задачи нас не просили, но мы можем изобразить график квадратичной функции и касательную к параболе для проверки. Если получилась лишь одна точка касания с правильными координатами, значит, наши расчеты были верны!

Некоторые темы математики, как клубок ниток, содержат в себе понятия и правила из других тем. Не понимая прошлые темы, не удастся разобраться и в новой. На каждом уроке курсов обучения математике в онлайн-школе Skysmart мы актуализируем уже имеющиеся знания, поэтому не разобраться не получится. Приходите на бесплатный вводный урок за подробным разбором сильных и слабых сторон и конкретными рекомендациями, как улучшить оценки и подготовиться к экзаменам!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Кристина Тоскина

К предыдущей статье

Коллинеарность векторов

К следующей статье

Все формулы приведения

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Как оценить производную по графику

Обновлено 08 декабря 2020 г.

Ли Джонсон

Скорость изменения проявляется повсюду в науке, и особенно в физике, через такие величины, как скорость и ускорение. Производные математически описывают скорость изменения одной величины по отношению к другой, но иногда их вычисление может быть сложным, и вам может быть представлен график, а не функция в форме уравнения. Если вам представлен график кривой и вам нужно найти производную от него, вы, возможно, не сможете быть столь же точными, как с уравнением, но вы можете легко сделать надежную оценку.

TL;DR (слишком длинный; не читал)

Выберите точку на графике, чтобы найти значение производной.

Проведите прямую, касательную к кривой графика в этой точке.

Возьмите наклон этой линии, чтобы найти значение производной в выбранной вами точке на графике.

Помимо абстрактной настройки дифференцирования уравнения, вы можете немного запутаться в том, что такое производная на самом деле. В алгебре производная функции — это уравнение, которое сообщает вам значение «наклона» функции в любой точке. Другими словами, он говорит вам, насколько изменится одна величина при небольшом изменении другой. На графике градиент или наклон линии говорит вам, насколько зависимая переменная (помещенная на y ​-оси) изменяется с независимой переменной (по ​ x ​-оси).

Для прямолинейных графиков вы определяете (постоянную) скорость изменения, вычисляя наклон графика. С отношениями, описываемыми кривыми, не так просто иметь дело, но принцип, что производная просто означает наклон (в этой конкретной точке), остается верным.

Для отношений, описываемых кривыми, производная принимает разные значения в каждой точке кривой. Чтобы оценить производную графика, вам нужно выбрать точку, в которой будет браться производная. Например, если у вас есть график, показывающий пройденное расстояние в зависимости от времени, на прямолинейном графике наклон покажет вам постоянную скорость. Для скоростей, которые меняются со временем, график будет представлять собой кривую, но прямая линия, которая касается кривой только в одной точке (линия, касательная к кривой), представляет скорость изменения в этой конкретной точке.

Выберите точку, в которой вам нужно знать производную. Используя пример зависимости пройденного расстояния от времени, выберите время, в которое вы хотите узнать скорость движения. Если вам нужно узнать скорость в нескольких разных точках, вы можете запустить этот процесс для каждой отдельной точки. Если вы хотите узнать скорость через 15 секунд после начала движения, выберите точку на кривой через 15 секунд по оси ​ x ​.

Нарисуйте линию, касательную к кривой в интересующей вас точке. Не торопитесь, потому что это самая важная и самая сложная часть процесса. Ваша оценка будет лучше, если вы проведете более точную касательную. Держите линейку до точки на кривой и отрегулируйте ее ориентацию, чтобы линия, которую вы рисуете, была только ​ коснитесь кривой в интересующей вас точке.

Нарисуйте линию, насколько позволяет график. Убедитесь, что вы можете легко прочитать два значения для координат x и y , одно рядом с началом вашей строки, а другое ближе к концу. Вам не обязательно рисовать длинную линию (технически подходит любая прямая линия), но наклон более длинных линий, как правило, легче измерить.

Найдите два места на вашей линии и запишите цифру x ​ и ​ y ​ координаты для них. Например, представьте свою касательную в виде двух примечательных точек x = 1, y = 3 и x = 10, y = 30, которые вы можете назвать точкой 1. и Точка 2. Использование символов x ₁ и y ₁ для обозначения координат первой точки и x ₂ и 90 5 7 9 90 90 для представления координат второй точки, наклон ​ м ​ определяется как:

м = \frac{y_2 — y_1}{x_2 — x_1}

Это говорит вам о производной кривой в точке, где линия касается кривой. В примере x ₁ = 1, x ₂ = 10, y ₁ = 3 и y ₂ = 30, SO:

\begin{align} m &= \frac{30 — 3}{10 — 1} \\ \,\\ &= \frac{27}{9} \\ \,\\ &=9 \end{ выровнено}

В примере этим результатом будет скорость в выбранной точке. Итак, если 9Ось 0017 x ​ измерялась в секундах, а ось ​ y ​ измерялась в метрах, результат будет означать, что рассматриваемое транспортное средство двигалось со скоростью 3 метра в секунду. Независимо от конкретной величины, которую вы вычисляете, процесс оценки производной одинаков.

2.4 Производная функция

Мы видели, как создать или вывести новую функцию $f'(x)$ из функция $f(x)$, резюмированная в абзаце, содержащем уравнение 2.1.1. Теперь, когда у нас есть концепция пределов, мы можем сделать это более точным.

Определение 2.4.1 Производная функции $f$, обозначаемой $f’$, есть $$f'(x)=\lim_{\Delta x\to 0} {f(x+\Delta x)-f(x)\over \Delta x}.$$ $\квадрат$

Мы знаем, что $f’$ несет важную информацию об исходном функция $f$. В одном примере мы видели, что $f'(x)$ говорит нам, насколько крутой график $f(x)$ есть; в другом мы видели, что $f'(x)$ сообщает нам скорость объекта, если $f(x)$ сообщает нам положение объекта в время $х$. Как мы уже говорили ранее, эта же математическая идея полезна всякий раз, когда $f(x)$ представляет некоторую изменяющуюся величину, и мы хотим знать что-то о том, как оно меняется, или, грубо говоря, о «скорости», с которой оно изменения. Большинство функций, встречающихся на практике, строятся из небольшой набор «примитивных» функций несколькими простыми способами, для например, добавляя или перемножая функции вместе, чтобы получить новые, более сложные функции. Чтобы эффективно использовать информацию, предоставленную $f'(x)$ нам нужно уметь вычислять его для множества таких функции. 92} — 24\над\Дельта х}. $$ Знаменатель здесь измеряет расстояние в направлении $x$, иногда называемый «бегом», а числитель измеряет расстояние в направление $y$, иногда называемое «подъем» и «подъем над run» — это наклон линии. Напомним, что иногда такой числитель сокращенно $\Delta y$, заменив краткость более подробным выражение. Таким образом, в общем случае производная определяется выражением $$ y’=\lim_{\Delta x\to0} {\Delta y\over \Delta x}. 2}\cr } $$

$\квадрат$

Примечание. Если вы знаете некоторые «производные формулы» из более ранний курс, на данный момент вы должны делать вид, что вы делаете не знать их. В примерах, подобных приведенным выше и приведенным ниже упражнениям, от вас требуется знать, как найти производную формулу, исходя из основных принципов. Позже мы разработаем некоторые формулы, чтобы нам не всегда нужно было делать такие вычисления, но нам по-прежнему нужно знать, как делать более сложные вычисления.

Иногда встречается точка в области определения функции $y=f(x)$, где нет производной , потому что нет касательной. Чтобы чтобы понятие касательной в точке имело смысл, кривая должна быть «гладкой» в этой точке. Это означает, что если вы представляете себе частицу движущейся с некоторой постоянной скоростью вдоль кривой, то частица не испытать резкое изменение направления. Есть два типа ситуации, о которых вы должны знать — углы и выступы — где есть внезапная смена направления и, следовательно, отсутствие производной.

Пример 2.4.4 Обсудите производную функции абсолютного значения $y=f(x)=|x|$.

Если $x$ положительна, то это функция $y=x$, производная которой равна константа 1. (Напомним, что когда $y=f(x)=mx+b$, производная есть наклон $m$.) Если $x$ отрицательно, то мы имеем дело с функцией $y=-x$, производная которой есть константа $-1$. Если $x=0$, то функция имеет угол, т. е. касательной нет. Касательная линия должны указывать в направлении кривой, но есть 93$. (отвечать)

Пример 2.4.6 Показан график функции $f(x)$. Нарисуйте график $f'(x)$ оценивая производную в ряде точек интервала: оценивайте производную через равные промежутки времени с одного конца интервале от другого, а также в «особых» точках, например, когда производная равна нулю. Убедитесь, что вы указали все места, где производной не существует.

Пример 2.4.7 Показан график функции $f(x)$. Нарисуйте график $f'(x)$ оценивая производную в ряде точек интервала: оценивайте производную через равные промежутки времени с одного конца интервале от другого, а также в «особых» точках, например, когда производная равна нулю.