Найдите площадь поверхности прямой призмы
Заключительная статья про параллелепипеды. По крайней мере, на данный момент рассмотрены все задания, которые имеются в открытом банке заданий ЕГЭ. Здесь представлены две задачи, связанные с площадью поверхности прямого параллелепипеда.
Это взаимообратные задачи: в одной даны диагонали ромба лежащего в основании и боковое ребро, требуется найти площадь поверхности параллелепипеда; в другой задаче дана площадь поверхности, диагонали ромба лежащего в основании и требуется найти боковое ребро. Напомню формулы. Площадь поверхности прямой призмы:
Так же для нахождения площади ромба будет использована формула площади четырёхугольника:
Понятно, что диагонали ромба пересекаются под углом 900. Известно, что синус этого угла равен единице, поэтому формула примет вид:

Рассмотрим задачи:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.
Площадь поверхности данной призмы равна сумме площадей оснований и четырёх боковых граней:
Основание призмы – ромб, его площадь мы найдём по формуле:

Значит:

Так как призма прямая, то её высота равна боковому ребру:

Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:
Тогда площадь поверхности призмы равна:

Ответ: 4870
В основании прямой призмы лежит ромб с диагоналями, равными 15 и 36. Площадь ее поверхности равна 2100. Найдите боковое ребро этой призмы.

Данная задача является обратной предыдущей. Здесь известна площадь поверхности и требуется найти боковое ребро. У прямой призмы боковое ребро равно её высоте.
Запишем формулу площади поверхности призмы:

Площадь поверхности известна, значит нам необходимо найти площадь ромба лежащего в основании и его сторону.
Площадь ромба:

Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:

Таким образом:
Ответ: 20
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

Посмотреть решение
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

Посмотреть решение
В будущем вас ожидают задачи с пирамидами, не пропустите! На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Площадь полной поверхности призмы — сумма площадей всех граней призмы.
Она состоит из площади боковой поверхности и площади оснований
Sполн.=Sбок.+2⋅Sосн.
Все грани куба — квадраты, поэтому рациональнее использовать формулу
Sполн. пов. куба=6⋅a2.
Объём прямой призмы находится по формуле:
V=Sосн.⋅H.
Для прямоугольного параллелепипеда можно использовать формулу \(V = abc\) , где \(a\), \(b\), \(c\) — измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где \(a\) — ребро куба.
Основанием призмы может быть любой \(n\)-угольник, поэтому важно знать формулы вычисления их площадей.
Важные формулы нахождения площади \(n\)-угольников
| Квадрат | a2 | ||
| Прямоугольник | a⋅b | ||
| a⋅b⋅sinα | a⋅h | d1⋅d22 | |
| Параллелограмм | a⋅b⋅sinα | a⋅h | |
| Равносторонний треугольник | a234 | ||
| Прямоугольный треугольник | a⋅b2 | a⋅h3 | |
| Произвольный треугольник | a⋅b⋅sinα2 | a⋅h3 | p⋅p−ap−bp−c |
| Трапеция | a+b2⋅h |
Формула нахождения площади правильного шестиугольника
Правильный шестиугольник состоит из \(6\) правильных треугольников.
Sправ. ш.=6⋅a234, где \(a\) — сторона шестиугольника |
Объем и площадь поверхности — это две важные характеристики любого тела, имеющего конечные размеры в трехмерном пространстве. В данной статье рассмотрим известный класс многогранников — призмы. В частности, будет раскрыт вопрос, как найти площадь поверхности прямой призмы.
Что собой представляет призма?
Призмой называется любой многогранник, который ограничен несколькими параллелограммами и двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. Эти многоугольники считают основаниями фигуры, а ее параллелограммы — это боковые стороны. Количество сторон (углов) основания определяет название фигуры. Например, на рисунке ниже изображена пятиугольная призма.
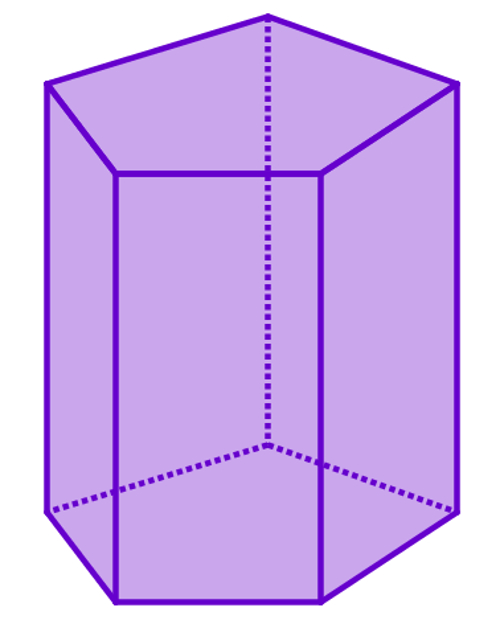
Расстояние между основаниями называется высотой фигуры. Если высота равна длине любого бокового ребра, то такая призма будет прямой. Вторым достаточным признаком для прямой призмы является то, что у нее все боковые стороны представляют собой прямоугольники или квадраты. Если же хотя бы одна боковая сторона является параллелограммом общего вида, то фигура будет наклонной. Ниже можно посмотреть, как визуально отличаются прямая и наклонная призмы на примере четырехугольных фигур.
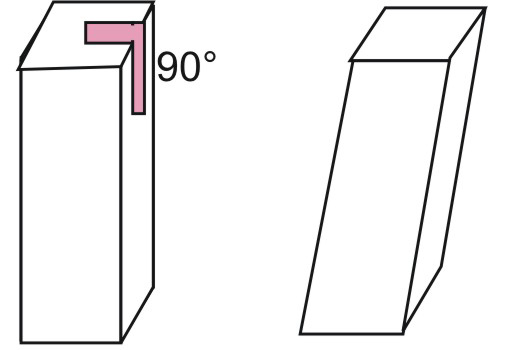
Площадь поверхности прямой призмы
Если геометрическая фигура имеет n-угольное основание, тогда она состоит из n+2 граней, n из которых являются прямоугольниками. Обозначим длины сторон основания символом ai, где i = 1,2,…,n, а высоту фигуры, которая равна длине бокового ребра, обозначим h. Чтобы определить площадь (S) поверхности всех граней, необходимо сложить площадь So каждого из оснований и все площади боковых сторон (прямоугольников). Таким образом, формулу для S в общем виде можно записать так:
S = 2*So + Sb
Где Sb — площадь боковой поверхности.
Поскольку основанием прямой призмы может быть совершенно любой плоский многоугольник, то единой формулы для вычисления So привести нельзя, и для определения этой величины в общем случае следует проводить геометрический анализ. Например, если основание представляет собой правильный n-угольник со стороной a, тогда его площадь вычисляется по формуле:
So = n/4*ctg(pi/n)*a2
Что касается величины Sb, то выражение для ее вычисления привести можно. Площадь боковой поверхности прямой призмы равна:
Sb = h*∑i=1n(ai)
То есть величина Sb вычисляется как произведение высоты фигуры на периметр ее основания.
Пример решения задачи
Применим полученные знания для решения следующей геометрической задачи. Дана призма, основание которой представляет собой прямоугольный треугольник со сторонами при прямом угле 5 см и 7 см. Высота фигуры составляет 10 см. Необходимо найти площадь поверхности прямой призмы треугольной.
Для начала вычислим гипотенузу треугольника. Она будет равна:
c = √(52 + 72) = 8,6 см
Теперь сделаем еще одну подготовительную математическую операцию — рассчитаем периметр основания. Он составит:
P = 5 + 7 + 8,6 = 20,6 см
Площадь боковой поверхности фигуры вычисляется как произведение величины P на высоту h=10 см, то есть Sb = 206 см2.
Чтобы найти площадь всей поверхности, к найденной величине следует добавить две площади основания. Поскольку площадь прямоугольного треугольника определяется половиной произведения катетов, то получаем:
2*So = 2*5*7/2 = 35 см2
Тогда получаем, что площадь поверхности прямой призмы треугольной составляет 35 + 206 = 241 см2.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы

Основание: квадрат.
| Площадь | Формула |
| основание | |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
1. Площадь поверхности и объём призмы
Площадь полной поверхности призмы — сумма площадей всех граней призмы.
Она состоит из площади боковой поверхности и площади оснований:
Sполн.=Sбок.+2⋅Sосн.
Все грани куба — квадраты, поэтому рациональнее использовать формулу
Sполн. пов. куба=6⋅a2.
Объём прямой призмы находится по формуле:
V=Sосн.⋅H.
Для прямоугольного параллелепипеда можно использовать формулу \(V = abc\) , где \(a\), \(b\), \(c\) — измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где \(a\) — ребро куба.
Основанием призмы может быть любой \(n\)-угольник, поэтому важно знать формулы вычисления их площадей.
Важные формулы нахождения площади \(n\)-угольников
| Квадрат | a2 | ||
| Прямоугольник | a⋅b | ||
| Ромб | a⋅b⋅sinα | a⋅h | d1⋅d22 |
| Параллелограмм | a⋅b⋅sinα | a⋅h | |
| Равносторонний треугольник | a234 | ||
| Прямоугольный треугольник | a⋅b2 | a⋅h3 | |
| Произвольный треугольник | a⋅b⋅sinα2 | a⋅h3 | p⋅p−ap−bp−c |
| Трапеция | a+b2⋅h |
Формула нахождения площади правильного шестиугольника
Правильный шестиугольник состоит из \(6\) правильных треугольников.
Sправ. ш.=6⋅a234, где \(a\) — сторона шестиугольника |
Призма — Формулы | Свойства
Для расчёта всех основных параметров призма воспользуйтесь калькулятором.
Виды призм
Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра. Наклонная призма — это призма, в которой боковые грани не перпендикулярны к основанию. Правильная призма — это призма, в которой основания являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной. Усечённая призма — это призма, в которой основания не параллельны друг другу. Усечённая призма может быть, как прямой, так наклонной.
Основные свойства призмы
- Основание призмы — равные многоугольники
- Высота прямой призмы равна длине бокового ребра.
- Боковые ребра призмы параллельны и равны между собой.
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
- Боковые грани призмы — параллелограммы
- Высота наклонной призмы всегда меньше длины ребра.
- В прямой призме грани могут быть прямоугольниками или квадратами.
Площадь основания правильной призмы
$$ S_{осн} = {N * a^2 \over 4 * tan(180/N)} $$| Где: | N – количество сторон у основания пирамиды |
Формулы объёма призмы
Объём призмы через площадь основания (SОСН) и высоту (h):
$$ V = S_{ОСН} * h $$Объём наклонной призмы через площадь перпендикулярного сечения (SП) и длину бокового ребра (b):
$$ V = S_П * b $$Объём правильной прямой призмы через высоту, длину стороны и количество сторон:
$$ V = {N \over 4} * h * a * ctg({\pi \over N}) $$| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Формулы площади поверхности правильной призмы
Площадь боковой поверхности призмы через периметр (P) основания и высоту (h)
$$ S_Б = P * h $$Площадь поверхности призмы через площадь основания (SОСН), периметр основания (P) и высоту (h):
$$ S = 2 * S_{ОСН} + P * h $$Площадь поверхности правильной призмы через высоту, длину стороны и количество сторон:
$$ S = {N \over 2} * a^2 * ctg({\pi \over N}) + N * a * h $$| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Треугольная призма все формулы и примеры задач
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
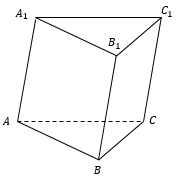
Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
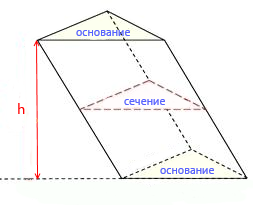
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
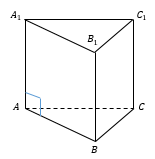
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
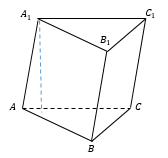
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
Sбок=Pосн.h
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
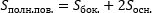
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
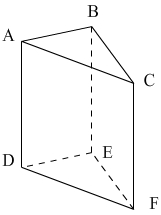
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
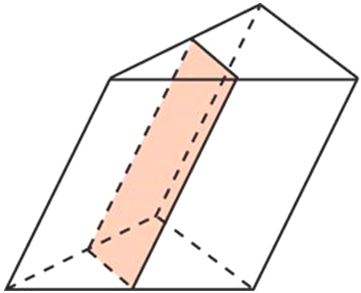
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Что такое призма?
Призма — это трехмерный объект, две торцевые поверхности которого идентичны, а боковые стороны параллелограммы (четырехсторонняя форма с двумя парами параллельных сторон). Тип призмы определяется формой ее концов. Следовательно, призма с треугольником на каждом конце называется треугольной призмой. Не имеет значения, является ли эта призма прямоугольной или равнобедренной, способ, которым мы находим площадь поверхности, одинаков для обоих типов.
Как мы находим площадь поверхности?
Площадь поверхности любой призмы — это общая площадь всех ее сторон и граней. Треугольная призма имеет три прямоугольные стороны и две треугольные грани. Чтобы найти площадь прямоугольных сторон, используйте формулу A = lw , где A = площадь, l = длина и h = высота. Чтобы найти площадь треугольных граней, используйте формулу A = 1 / 2bh , где A = площадь, b = основание и h = высота. Когда у вас есть области всех сторон и граней, вы просто складываете их вместе, чтобы получить площадь поверхности.
Пример 1. Найти площадь поверхности прямоугольной треугольной призмы выше
Давайте начнем с треугольных граней. Оба лица имеют одинаковую площадь, потому что они совпадают! Просто умножьте основание и высоту и разделите ответ на 2:
Площадь треугольных граней
= 1/2 (основание × высота)
= 1/2 (3 × 4) = 6 см²
Далее отрабатываем площадь прямоугольных граней. Каждая сторона имеет разный размер и может быть рассчитана путем умножения длины на ширину:
Площадь наклонной прямоугольной стороны
= длина х ширина
= 11 х 5
= 55 см²
Площадь задней стороны
= 11 x 3
= 33 см²
Площадь нижней стороны
= 11 x 4
= 44 см²
Все, что вам нужно сделать, это все эти области:
6 + 6 + 55 + 33 + 44 = 144 см²
Таким образом, общая площадь поверхности этой треугольной призмы составляет 144 см².
Использование формулы для определения площади поверхности
Теперь, когда мы рассмотрели основы, пришло время представить менее утомительный метод.Существует одна формула, которую можно использовать для расчета площади поверхности треугольной призмы:
SA = bh + (s1 + s2 + s3) H
В приведенной выше формуле b = основание и h = высота треугольника, s1, s2 и s3 = длина каждой стороны треугольника, а H = высота призмы (которая равна прямоугольникам ‘ длина).
Вам может быть интересно, как мы придумали эту формулу. Ну, это довольно просто. Если вы помните, площадь поверхности определяется сложением площади каждой стороны и лица.Давайте начнем с двух треугольников на концах. Площадь каждого треугольника составляет 1 / 2bh. Поскольку оба они идентичны, мы можем удвоить эту формулу, чтобы найти обе их области одновременно.
Площадь обоих треугольников
= 2 (1 / 2bh)
= 2 / 2bh
= bh
Обычно для определения площади трех прямоугольных сторон вы должны умножить длину каждой из них на соответствующую ширину. Однако в этом нет необходимости, поскольку стороны треугольников равны ширине трех прямоугольников.Точно так же высота призмы, H , равна длине каждого прямоугольника. Следовательно, умножив высоту H призмы (длину прямоугольников) на периметр (три ширины прямоугольника) ее основания, мы получим площадь каждого прямоугольника.
Площадь прямоугольных граней
= (s1 + s2 + s3) H
Следовательно, площадь треугольной призмы
= площадь треугольных граней + площадь прямоугольных граней
= bh + (s1 + s2 + s3) H
Пример 1.1
Давайте используем нашу новую формулу, чтобы повторить приведенный выше пример!
Площадь поверхности
= bh + (s1 + s2 + s3) H
= 4 (3) + (3 + 5 + 4) (11)
= 12 + 12 (11)
= 12 + 132
= 144 см 2
Как видите, наш ответ соответствует приведенному выше. Теперь, когда мы знаем, что наша формула работает, давайте применим ее в следующем примере.
Пример 2. Найти площадь поверхности равнобедренной треугольной призмы выше
Сначала включите известные значения в уравнение.
SA = bh + (s1 + s2 + s3) H
SA = 4 (6) + (4 + 7 + 7) (12)
Затем вычислите периметр треугольников (сложите вместе три стороны), а затем их площадь (базовая временная высота).
SA = 24 + 18 (12)
Затем умножьте периметр на высоту призмы.
SA = 24 + 216
Наконец, сложите оставшиеся значения вместе, чтобы получить ответ.
,SA = 240 см 2
Площадь поверхности призмы
Площадь поверхности призмы — Math Open Reference где:b = площадь основания
p = периметр основания
h = высота призмы
Попробуй это Измените высоту и размеры треугольной призмы, перетаскивая оранжевые точки. Обратите внимание, как рассчитывается площадь поверхности.
Правая призма состоит из набора плоских поверхностей.
Общая площадь поверхности является суммой этих.Основы
каждый База является многоугольником. На рисунке выше это правильный пятиугольник, но это может быть любой правильный или неправильный многоугольник. Найти Площадь базовых полигонов, см. Площадь правильного многоугольника и Площадь неправильного многоугольника. Поскольку существует два основания, это удваивается и учитывает член «2b» в уравнении выше.
Боковые грани
Каждая боковая грань (сторона) правой призмы представляет собой прямоугольник. Одна сторона — высота призмы, другая — длина этой стороны основания. Следовательно, передняя левая грань призмы выше является ее высотой, умноженной на ширину или Таким образом, общая площадь лица Если мы вычтем из выражения выражение «h», то получим Обратите внимание, что выражение в скобках — это периметр (p) основания, поэтому мы можем записать окончательную формулу площади как
Следовательно, передняя левая грань призмы выше является ее высотой, умноженной на ширину или Таким образом, общая площадь лица Если мы вычтем из выражения выражение «h», то получим Обратите внимание, что выражение в скобках — это периметр (p) основания, поэтому мы можем записать окончательную формулу площади как 
Регулярные призмы
Если призма регулярна, основания
правильные многоугольники.
и поэтому периметр ‘ns’, где s — длина стороны
а n — количество сторон.В этом случае формула площади поверхности упрощается до где:
b = площадь основания
n = количество сторон основания
s = длина сторон основания
h = высота призмы
Наклонные призмы
Нет простого способа вычислить площадь поверхности наклонной призмы в целом. Лучший способ — это работать на основе того факта, что он состоит из двух баз, чьи площади можно рассчитать, как указано выше. Но чтобы найти области лица, вам нужно будет рассмотреть их отдельно и найти область каждого из них на основе того, что вам дают.
Что попробовать
- На рисунке выше, нажмите «скрыть детали».
(чтобы сделать его немного сложнее, спрячьте и базовую область.) - Перетащите оранжевые точки, чтобы задать форму новой призмы.
- Рассчитайте площадь поверхности призмы.
- Нажмите «показать подробности», чтобы проверить свой ответ.
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Площадь поверхности прямоугольной призмы
Чтобы получить формулу площади поверхности прямоугольной призмы, внимательно следуйте инструкциям ниже. Начните с правой прямоугольной призмы, как показано ниже, и назовите длину l, ширину w и высоту h.  |
Чтобы сделать прямоугольную призму, подобную показанной выше, вы в основном используете следующий шаблон прямоугольной призмы:
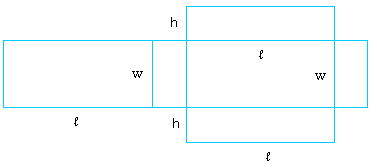 |
Глядя на шаблон прямоугольной призмы, легко увидеть, что тело имеет шесть сторон, и каждая сторона представляет собой прямоугольник.
Нижняя сторона и верхняя сторона равны и имеют размеры l и w в качестве размеров.
Площадь верхней и нижней сторон равна l × w + l × w = 2 × l × w.
Лицевая сторона (показана синим цветом) и задняя сторона (не показана) равны и имеют h и l. как размеры.
Площадь для передней и задней сторон составляет l × h + l × h = 2 × l × h
Тогда размеры левой и правой сторон имеют h и w. Одна сторона показана фиолетовым цветом.
Площадь для левой и правой сторон равна w × h + w × h = 2 × w × h
Общая площадь поверхности, называемая SA:
SA = 2 × l × w + 2 × l × h + 2 × w × h
Примеры, показывающие, как найти площадь поверхности прямоугольной призмы
Пример № 1:
Найдите площадь поверхности прямоугольной призмы длиной 6 см, шириной 4 см и высотой 2 см.
SA = 2 × 1 × w + 2 × l × h + 2 × w × h
SA = 2 × 6 × 4 + 2 × 6 × 2 + 2 × 4 × 2
SA = 48 + 24 + 16
SA = 88 см 2
Пример № 2:
Найдите площадь поверхности прямоугольной призмы длиной 4 см, шириной 5 см и высотой 10 см.
SA = 2 × 1 × w + 2 × l × h + 2 × w × h
SA = 2 × 4 × 5 + 2 × 4 × 10 + 2 × 5 × 10
SA = 40 + 80 + 100
SA = 220 см 2
Пример № 3:
Найдите площадь поверхности длиной 1/2 см, шириной 8 см и высотой 1/4 см.
SA = 2 × l × w + 2 × l × h + 2 × w × h
SA = 2 × 1/2 × 8 + 2 × 1/2 × 1/4 + 2 × 8 × 1/4
SA = 1 × 8 + 1 × 1/4 + 16 × 1/4
SA = 8 + 1/4 + 4
SA = 12 + 1/4
SA = 48/4 + 1/4
SA = 49/4 см 2
SA = 12,25 см 2
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела. Когда мы определяем площади поверхности геометрического тела, мы берем сумму площади для каждой геометрической формы в теле.
Объем является мерой того, сколько может вместить фигура, и измеряется в кубических единицах. Объем говорит нам кое-что о способности фигуры.
Призма — это сплошная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, которые являются параллелограммами. Существуют как прямоугольные, так и треугольные призмы.
Чтобы найти площадь поверхности призмы (или любого другого геометрического тела), мы открываем тело, как картонную коробку, и выравниваем его, чтобы найти все включенные геометрические формы.
Чтобы найти объем призмы (не имеет значения, прямоугольная она или треугольная), мы умножаем площадь основания, называемого основанием B, на высоту h.{2} \ cdot h $$
Пирамида состоит из трех или четырех треугольных боковых поверхностей и трех или четырех сторонних поверхностей, соответственно, в ее основании. Когда мы рассчитываем площадь поверхности пирамиды ниже, мы берем сумму площадей 4 треугольников и базового квадрата. Высота треугольника внутри пирамиды называется наклонной высотой.
Объем пирамиды составляет одну треть от объема призмы.
$$ V = \ frac {1} {3} \ cdot B \ cdot h $$
Основание конуса — это круг, и это легко увидеть.{3} $$
Видеоурок
Найти площадь поверхности цилиндра с радиусом 4 и высотой 8
Найдите объем конуса с высотой 5 и радиусом 3
,

Leave A Comment