Вычисление длины (модуля) вектора в EXCEL. Примеры и описание
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL
4. Нахождение длины вектора через координаты точек треугольника
Пусть заданы 3 точки треугольника, образованного векторами.
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .
Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).
5. Нахождение координат вектора через координаты точек
Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.
Модуль вектора примеры. Вычисление длины (модуля) вектора в MS EXCEL. Понятие вектора. Свободный вектор
модуль вектора — величина вектора — [Л. Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …
Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
— (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
Абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
Характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости) .
Является одним из основополагающих понятий линейной алгебры . При использовании наиболее общего определения векторами оказываются практически все изучаемые в линейной алгебре объекты, в том числе матрицы , тензоры , однако, при наличии в окружающем контексте этих объектов, под вектором понимаются соответственно вектор-строка или вектор-столбец , тензор первого ранга. Свойства операций над векторами изучаются в векторном исчислении .
Обозначения [ | ]
Вектор, представленный набором n {\displaystyle n} элементов (компонент) a 1 , a 2 , … , a n {\displaystyle a_{1},a_{2},\ldots ,a_{n}} обозначают следующими способами:
⟨ a 1 , a 2 , … , a n ⟩ , (a 1 , a 2 , … , a n) , { a 1 , a 2 , … , a n } {\displaystyle \langle a_{1},a_{2},\ldots ,a_{n}\,\rangle ,\ \left(a_{1},a_{2},\ldots ,a_{n}\,\right),\{a_{1},a_{2},\ldots ,a_{n}\,\}} .Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
a ¯ , a → , a , A , a . {\displaystyle {\bar {a}},\ {\vec {a}},\mathbf {a} ,{\mathfrak {A}},\ {\mathfrak {a}}.}Сложение векторов почти всегда обозначается знаком плюс:
a → + b → {\displaystyle {\vec {a}}+{\vec {b}}} .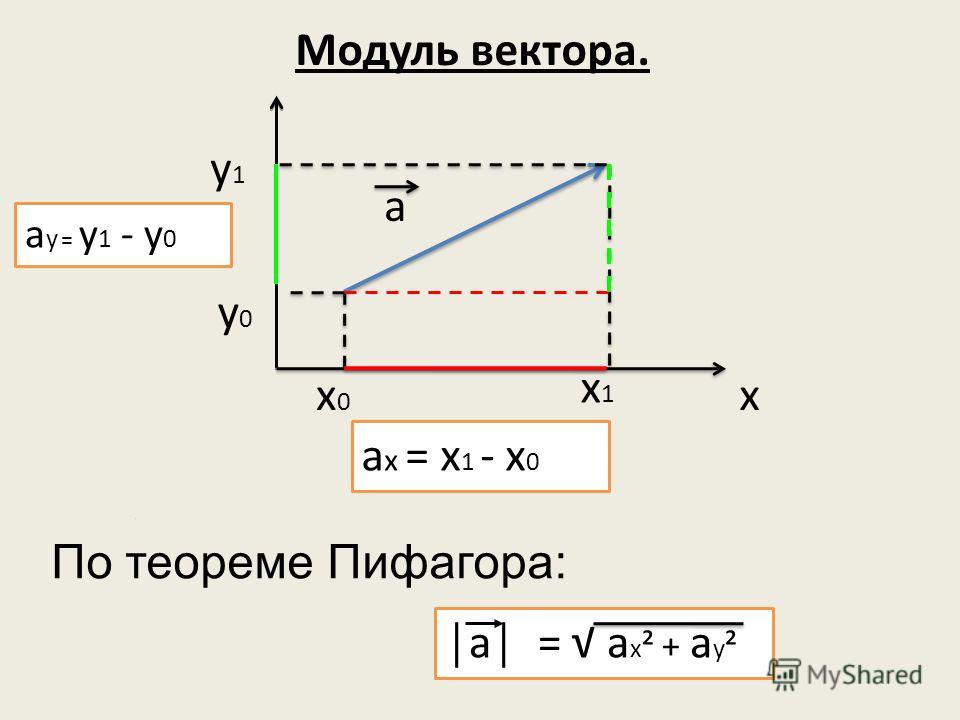
Умножение на число — просто написанием рядом, без специального знака, например:
k b → {\displaystyle k{\vec {b}}} ,причём число при этом обычно пишут слева.
Общепринятых обозначений вектора не существует, используются жирный шрифт, черта или стрелка над буквой, готический алфавит и др.
В геометрии [ | ]
В геометрии под векторами понимают направленные отрезки. Эту интерпретацию часто используют в компьютерной графике , строя карты освещения , с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов , а также объёмы тел: тетраэдра и параллелепипеда .
Иногда с вектором отождествляют направление.
Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector , несущий ). Действительно, любой направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства, и обратно, параллельный перенос однозначно определяет собой единственный направленный отрезок (однозначно — если считать равными все направленные отрезки одинакового направления и длины — то есть рассматривать их как свободные векторы).
Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.
В линейной алгебре [ | ]
Общее определение [ | ]
Наиболее общее определение вектора даётся средствами общей алгебры :
- Обозначим
F
{\displaystyle {\mathfrak {F}}}
(готическая F) некоторое поле с множеством элементов
F
{\displaystyle F} , аддитивной операцией
+
{\displaystyle +} , мультипликативной операцией
∗
{\displaystyle *} , и соответствующими нейтральными элементами : аддитивной единицей и мультипликативной единицей
1
{\displaystyle 1} .

- Обозначим V {\displaystyle {\mathfrak {V}}} (готическая V) некоторую абелеву группу с множеством элементов V {\displaystyle V} , аддитивной операцией + {\displaystyle +} и, соответственно, с аддитивной единицей 0 {\displaystyle \mathbf {0} } .
Иначе говоря, пусть F = ⟨ F ; + , ∗ ⟩ {\displaystyle {\mathfrak {F}}=\langle F;+,*\rangle } и V = ⟨ V ; + ⟩ {\displaystyle {\mathfrak {V}}=\langle V;+\rangle } .
Если существует операция F × V → V {\displaystyle F\times V\to V} , такая что для любых a , b ∈ F {\displaystyle a,b\in F} и для любых x , y ∈ V {\displaystyle \mathbf {x} ,\mathbf {y} \in V} выполняются соотношения:
Вектор как последовательность [ | ]
Вектор — (последовательность , кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства . Именно в таком виде вектор понимается в программировании , где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object ). Перечень свойств моделирует принятое в
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Пример 1
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
Ответ: a → = 49 + e .
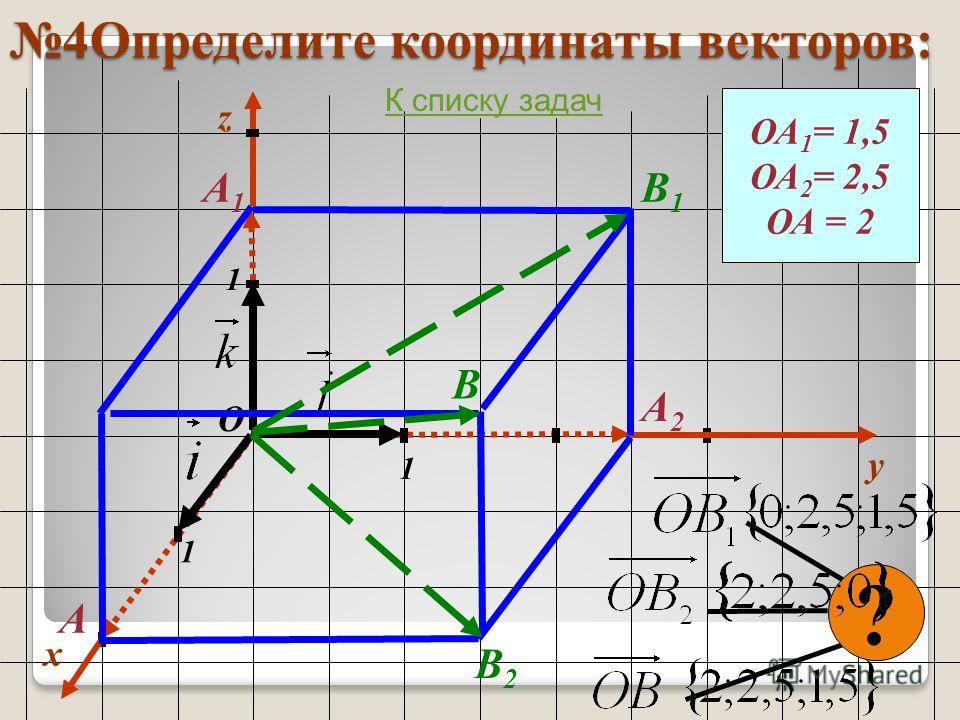
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Пример 2
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.
Решение
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .
Ответ: a → = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам.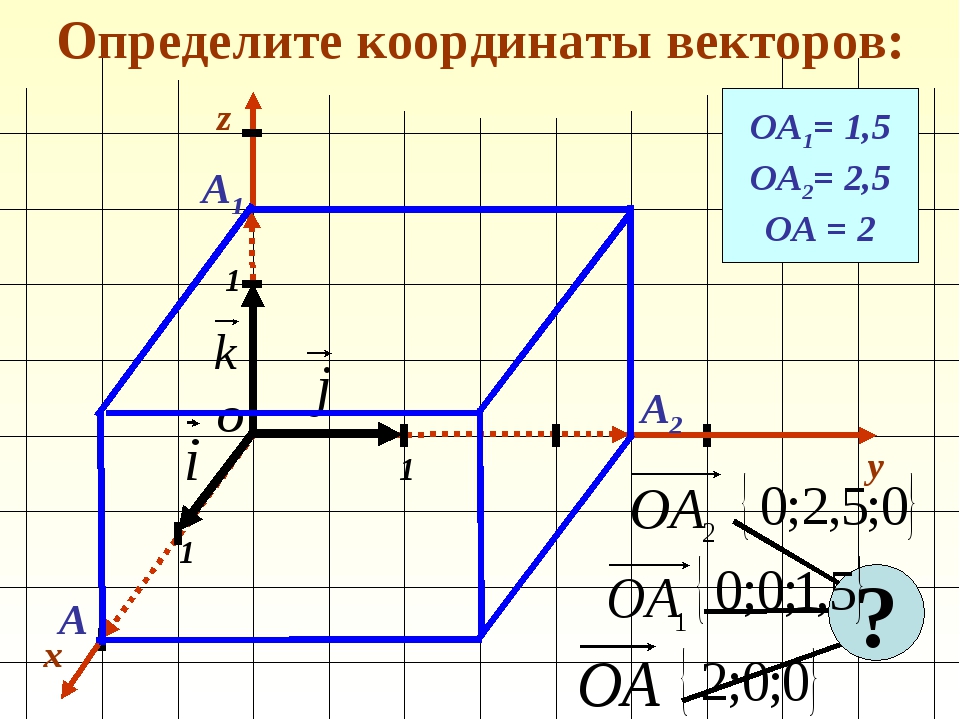 Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A (a x ; a y) и B (b x ; b y) , отсюда вектор A B → имеет координаты (b x — a x ; b y — a y) значит, его длина может быть определена по формуле: A B → = (b x — a x) 2 + (b y — a y) 2
А если даны точки с заданными координатами A (a x ; a y ; a z) и B (b x ; b y ; b z) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2
Пример 3
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = (b x — a x) 2 + (b y — a y) 2: A B → = (- 3 — 1) 2 + (1 — 3) 2 = 20 — 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = (- 3 — 1 ; 1 — 3) = (- 4 ; 1 — 3) ; A B → = (- 4) 2 + (1 — 3) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Пример 4
Определить, при каких значениях длина вектора A B → равна 30 , если A (0 , 1 , 2) ; B (5 , 2 , λ 2) .
Решение
Для начала распишем длину вектора A B → по формуле: A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 = (5 — 0) 2 + (2 — 1) 2 + (λ 2 — 2) 2 = 26 + (λ 2 — 2) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ:
26 + (λ 2 — 2) 2 = 30 26 + (λ 2 — 2) 2 = 30 (λ 2 — 2) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Пример 5
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Решение
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ (A B , → A C →) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Ответ: B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = (b x — a x) 2 + (b y — a y) 2 или A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 , в некоторых случаях следует использовать теорему косинусов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
7.3. Разложение вектора по базису. Координаты вектора Модуль вектора. Направляющие косинусы
Пусть — единичные векторы осей координат, т.е. и каждый из них одинаково направлен с координатными осями. Тройка векторов называется координатным базисом.
Теорема. Любой вектор пространства можно разложить по базису , т.е. представить в виде , где — некоторые числа (буквы: — «мю», — «ню»).
Это разложение единственное.
Доказательство. Приложим вектор к началу координат, обозначим его конец . Проведем
через точку плоскости,
перпендикулярные осям координат. Пусть ,
, — точки
пересечения этих плоскостей с осями
координат.
Приложим вектор к началу координат, обозначим его конец . Проведем
через точку плоскости,
перпендикулярные осям координат. Пусть ,
, — точки
пересечения этих плоскостей с осями
координат.
Существует единственная тройка чисел , , таких, что
.
Формула называется разложением вектора по координатному базису.
Числа , , — называются координатами вектора , т.е. координаты вектора есть его проекции на соответствующие координатные оси. В символическом виде записывают .
Например, если, то его координаты .
Зная координаты вектора , длину его можно найти по формуле
Если известны координаты точек и , то координаты вектора равны: .
Пусть углы вектора с осями , , соответственно равны , , . Числа , , называются направляющими косинусами вектора .
; ; ;
— основное свойство направляющих косинусов вектора.
7.4. Действия над векторами, заданными координатами
Пусть векторы и заданы своими координатами.
При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), т.е.
При умножении вектора на число координаты его умножаются на это число, т.е. .
Если вектор коллинеарен вектору , то можно записать , где — некоторое число, т.е. , , . Отсюда, , , или — условие коллинеарности векторов.
7.5. Деление отрезка в данном отношении
,
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, Пусть даны координаты
точек и ;
и отношение . Требуется найти координаты точки .
Требуется найти координаты точки .
Из равенства векторов следует равенство соответствующих координат:
.
Аналогично, ; .
В частном случае: — середина отрезка, т.е. .
Пример. Дан треугольник , где , , .
Найти координаты точки — пересечения биссектрисы угла со стороной .
, ,
, .
.
Ответ: .
§ 8. Скалярное произведение векторов
8.1. Определение скалярного произведения
Определение. Скалярным произведением вектора на вектор
называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.
Обозначается: или .
Найдем проекцию вектора на вектор .
Из геометрии известно .
Умножим и разделим левую часть на :
, аналогично находим .
8.2. Свойства скалярного произведения
1.
Доказательство. .
2. .
3. .
4. .
Определение: Число, равное , называется скалярным квадратом вектора .
5. Скалярный квадрат вектора равен квадрату его длины .
Доказательство. .
6. Скалярное произведение базисных векторов:
,
.
8.3. Вычисление скалярного произведения векторов через координаты
Теорема. Если , , то .
Доказательство. Запишем векторы и в виде разложения по базису, т.е. и .
Тогда
По свойству скалярного произведения базисных векторов :
Таким образом, .
8.4. Приложения скалярного произведения векторов
Установление перпендикулярности ненулевых векторов:
.
Если , то | — условие перпендикулярности векторов. |
2. Вычисление проекции вектора на вектор:
и .
3. Определение угла между векторами: |
, т.е. .
4. Работа постоянной силы.
Если точка перемещается прямолинейно из положения в положение под действием силы , то работа по перемещению равна:
.
Пример 1. К точке приложены три силы .
Вычислить работу по перемещению точки в точку .
— равнодействующая трех сил.
.
.
Пример 2. Дано: , , , .
Найти угол между векторами и .
Так как или .
,
,
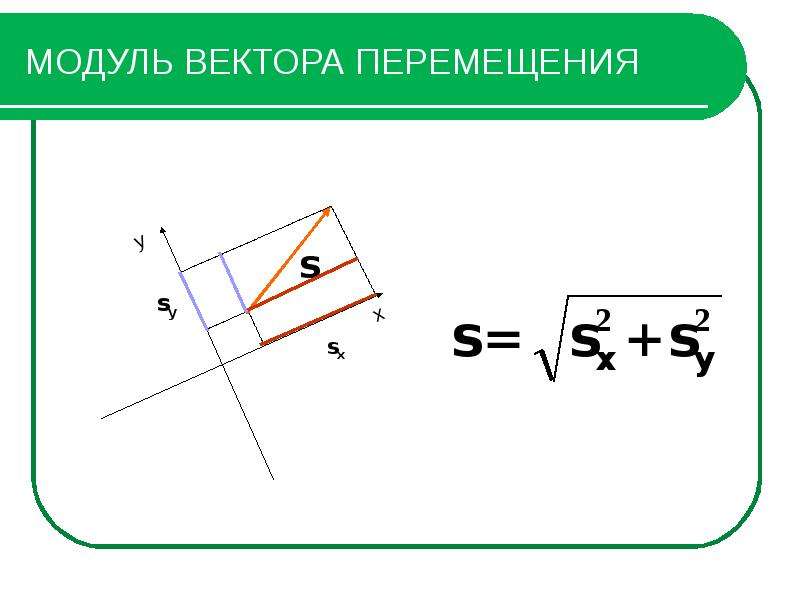
Таким образом,
.
Пример 3. Найти длину вектора , если , ,.
вектор с является суммой векторов а и б найдите модуль вектора с
Вы искали вектор с является суммой векторов а и б найдите модуль вектора с? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисления производят только с модулями векторов, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор с является суммой векторов а и б найдите модуль вектора с».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор с является суммой векторов а и б найдите модуль вектора с,вычисления производят только с модулями векторов,вычислить модуль вектора,как вычислить модуль вектора,как зная проекции вектора найти модуль вектора и сам вектор,как найти модули векторов,как найти модуль вектора,как найти модуль вектора по координатам,как найти модуль суммы векторов,как найти модуль суммы двух векторов,как определить модуль вектора,модули векторов,модули векторов как найти,модуль вектора,модуль вектора как найти по координатам,модуль вектора может быть любым числом,модуль вектора равен,модуль вектора формула,модуль вектора это,модуль векторов,модуль суммы векторов,модуль суммы векторов формула,найти модуль вектора,формула модуль вектора,формула модуль суммы векторов,чему равен модуль вектора. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор с является суммой векторов а и б найдите модуль вектора с. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить модуль вектора).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор с является суммой векторов а и б найдите модуль вектора с. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить модуль вектора).
Где можно решить любую задачу по математике, а так же вектор с является суммой векторов а и б найдите модуль вектора с Онлайн?
Решить задачу вектор с является суммой векторов а и б найдите модуль вектора с вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Задачи по физике и математике с решениями и ответами
Задача по физике — 7343
Две безграничные плоскости, отстоящие друг от друга на расстояние $l$, заряжены равномерно с поверхностной плотностью $\sigma$ и $- \sigma$а (рис.). Плоскости имеют коаксиальные отверстия радиуса $R$, причем $l \ll R$. Взяв координатную ось $x$ с началом отсчета О, как показано на рисунке, найти потенциал и проекцию вектора напряженности электрического поля $E_{x}$ на оси системы как функции координаты $x$. Изобразить примерный график $\phi(x)$.Подробнее
Задача по физике — 7344
Имеется плоский конденсатор с круглыми тонкими пластинами радиуса $R$, отстоящими друг от друга на расстояние $l (l \ll R)$ и заряженными равномерно с поверхностной плотностью $\sigma$ и $- \sigma$. {2} + b$, где $a$ и $b$ — постоянные. Найти распределение объемного заряда $\rho(r)$ внутри шара. Подробнее
{2} + b$, где $a$ и $b$ — постоянные. Найти распределение объемного заряда $\rho(r)$ внутри шара. Подробнее Задача по физике — 7353
Небольшой шарик висит над горизонтальной безграничной проводящей плоскостью на изолирующей упругой нити жесткости $k$. После того как шарик зарядили, он опустился на $x$ см, и его расстояние до проводящей плоскости стало равным $l$. Найти заряд шарика. ПодробнееЗадача по физике — 7354
Точечный заряд $q$ находится на расстоянии $l$ от безграничной проводящей плоскости. Какую работу необходимо совершить, чтобы медленно удалить этот заряд на очень большое расстояние от плоскости? ПодробнееЗадача по физике — 7355
Два точечных заряда, $q$ и $-q$, расположены на расстоянии $l$ друг от друга и на одинаковом расстоянии $l/2$ от безграничной проводящей плоскости. Найти:а) модуль вектора электрической силы, действующей на каждый заряд;
б) модуль вектора напряженности электрического поля в точке, расположенной на середине между этими зарядами. Подробнее
Задача по физике — 7356
Точечный заряд $q$ находится между двумя проводящими взаимно перпендикулярными полуплоскостями. Расстояние заряда до каждой полуплоскости равно $l$. Найти модуль вектора силы, действующей на заряд. ПодробнееЗадача по физике — 7357
Точечный диполь с электрическим моментом $\vec{p}$ находится на расстоянии $l$ от бесконечной проводящей плоскости. Найти модуль вектора силы, действующей на диполь, если вектор $\vec{p}$ перпендикулярен плоскости. Подробнее
Найти модуль вектора силы, действующей на диполь, если вектор $\vec{p}$ перпендикулярен плоскости. Подробнее 3D векторов | Суперпроф
Мы живем в трехмерном мире, что означает, что у нас есть 3 оси в качестве ориентира. Эти оси — ось x, ось y и ось z. Векторное знание применимо в реальной жизни, что в конечном итоге означает, что применяются все векторные законы, но в предыдущих источниках мы были привязаны к 2-мерному, изменяет ли 3-мерный мир все законы? Абсолютно! но неужели это изменение слишком велико? Нет, все, что вам нужно сделать, это добавить третье измерение (ось z) ко всем этим законам.Трехмерный вектор — это отрезок прямой в трехмерном пространстве, проходящий от точки A (хвост) до точки B (голова).
Каждый вектор имеет величину (или длину) и направление. Помните, что основы не изменятся, потому что мы просто добавляем здесь еще одно измерение. Это не означает, что то, что вы изучали раньше, будет полностью изменено, всего несколько изменений в формуле, но концепция останется прежней. Если у вас есть хорошее понимание предыдущих законов, то понимание законов в трехмерном пространстве не будет для вас проблемой.
Компоненты трехмерного вектора
Когда мы работаем в трехмерном пространстве, мы всегда рассматриваем все три базы координат, которые являются осью x, осью y и осью z. Например, у нас есть две точки в трехмерном пространстве, и это точка A и точка B. Координаты точек A и B будут записаны (в трехмерном пространстве) следующим образом:
и. Ваш учитель также попросил вас найти вектор, но как вы это будете делать в трехмерном пространстве? Та же голова без хвоста? Да точно так же! Вам нужно вычесть координату головы из координаты хвоста.Вычислите компоненты векторов, которые можно нарисовать в треугольнике с вершинами
и. Не забывайте, что вектор состоит из двух вещей: одна — это направление, а другая — величина. Если вы измените направление, это означает, что все координаты вектора также будут перевернуты:
Если вы измените направление, это означает, что все координаты вектора также будут перевернуты:
Лучшие доступные репетиторы по математике
Первый урок бесплатноВеличина или длина вектора
Величина — ключ элемент вектора и вектор без величины — это просто направление без мощности.Величина вектора — это длина отрезка линии, который его определяет. Величина вектора всегда представлена положительным числом, и только нулевой вектор имеет величину ноль .
Расчет величины для определения ее компонентов
Возможно, вы знакомы с формулой величин, которая равна
, но с третьим новым измерением все будет немного иначе. Чтобы найти величину трехмерного вектора, вам нужно просуммировать все возведенные в квадрат компоненты различных осей, а затем извлечь квадратный корень из ответа.Ниже приведен решенный вопрос для уточнения.
Учитывая векторы
и, найдите величины и ·Расчет модуля, зная координаты точек
Чтобы вычислить величину, мы воспользуемся формулой расстояния, но с небольшим изменением. Возможно, вы раньше сталкивались с проблемами двух измерений, поэтому в то время вы использовали только компоненты x и y, но теперь все изменилось.На этот раз вы будете использовать три компонента, но не волнуйтесь, если вы хорошо понимаете формулу расстояния, это будет для вас кусок пирога. Например, у вас есть две точки A и B. Координаты точки A равны
, а координаты точки B равны. Первый шаг — вычесть компонент хвоста из компонента головы, как вы делали это раньше. Найдите разницу для всех компонентов, а затем возьмите квадрат всех этих ответов. Сложите все эти квадраты ответов, а затем извлеките квадратный корень из полученного ответа, и это будет ваша величина из двух разных векторов, или вы можете использовать приведенную ниже формулу и просто подставить значения и найти ответ всего за один шаг.
Расстояние между двумя точками
Формула для расстояния между двумя точками аналогична найденной величине двух векторов.
ПРИМЕР
Найдите расстояние между точками
и.Единичный вектор
Векторы бывают самых разных форм и размеров, но как мы описываем эти векторы? С помощью единичного вектора. Определение единичного вектора довольно просто, это вектор с величиной
.Это означает, что любой вектор, величина которого равна единице, независимо от направления, называется единичным вектором. Один из наиболее распространенных терминов, которые мы используем в главе, посвященной векторам, называется нормализация. Нормализация означает получение другого единичного вектора в том же направлении. Чтобы нормализовать вектор, вам нужно разделить компоненты этого вектора на величину вектора.Вектор положения — объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам расположение одного объекта относительно другого.В частности, вектор положения:
«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».
В этом разделе мы обсудим следующие аспекты векторов положения:
- Что такое вектор положения?
- Как найти вектор положения
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения.Они используются для определения положения точки относительно начала координат.
Направление вектора положения указывает от начала координат к данной точке. В c \ декартовой системе координат, если точка O — начало координат, а Q — некоторая точка (x1, y1), тогда вектор положения, направленный из точки O в точку Q, представлен как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представлен следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора, A и B, с векторами положения a = (2,4) и b = (3, 5) соответственно. Затем мы можем записать координаты векторов A и B как:
Затем мы можем записать координаты векторов A и B как:
A = (2,4), B = (3, 5)
Как найти вектор положения
Перед определяя вектор положения точки, нам сначала нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Затем мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :
MN = (x2-x1, y2-y1)
Формула вектора положения
Используя информацию выше, мы можем обобщить формула, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.
Например, рассмотрим точку P, которая имеет координаты (xk, yk) в плоскости xy, и другую точку Q, которая имеет координаты (xk + 1, yk + 1). Формула для определения вектора положения от P до Q:
PQ = ((xk + 1) -xk, (yk + 1) -yk)
Помните, что вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Аналогично, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk — (xk + 1), yk — (yk + 1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения.Это поможет глубже понять векторы позиций.
Пример 1
Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения AB. Затем , вычисляют величину вектора AB .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения AB :
AB = (x2-x1, y2-y1)
Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.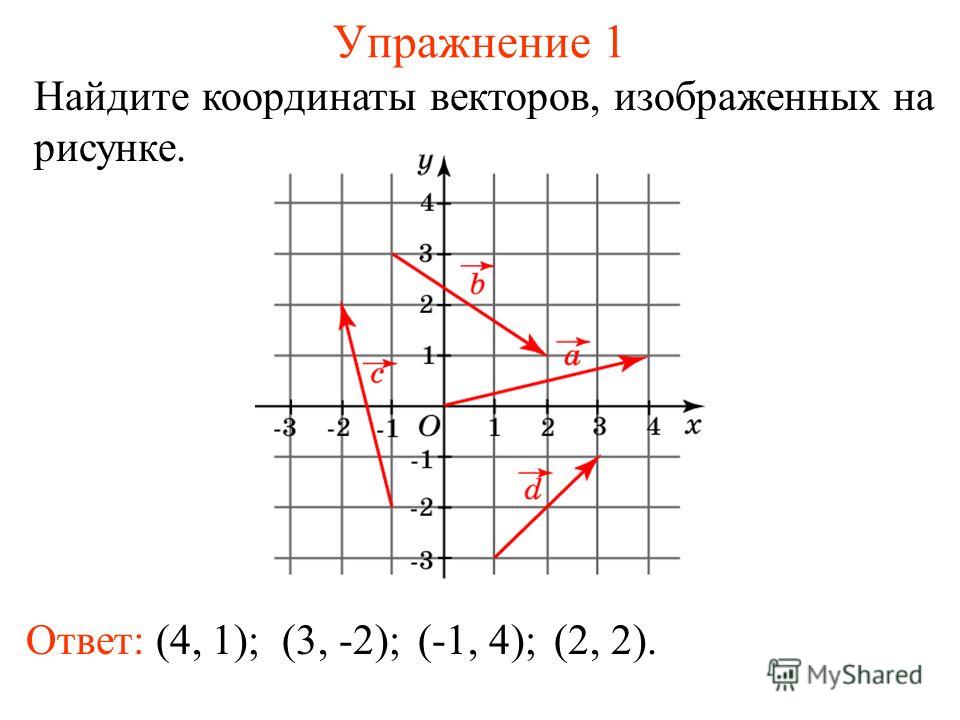 2
2
| AB | = √81 + 36
| AB | = √117
| AB | = 3√13
Пример 2
Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто помещая значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y.2
| BA | = √81 + 36
| BA | = √117
| BA | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношения между ними следующие:
BA = -1 * (9, 6)
BA = -1 * AB
BA = — AB
Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.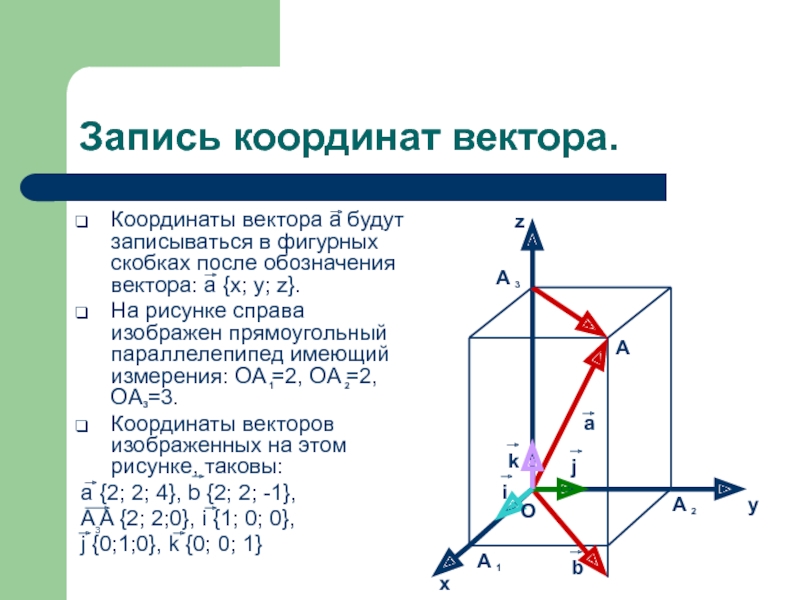 То есть они отрицания друг друга.
То есть они отрицания друг друга.
Пример 3
Учитывая, что вектор положения точки, S1, равен OS1 = (2, 3), и что вектор S1S2 = (-3, 6), определить вектор положения точки точка S2, OS2 .
Решение
Сначала мы строим вектор OS1 с его начальной точкой в начале координат (0,0) и конечной точкой в точке (2,3). Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает связь между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:
S1S2 = OS1 + OS2
OS2 = S1S2 — OS1
Подставляя данные значения в это уравнение, мы получаем:
OS2 = (-3, 6) — (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 = (- 5, 3) является вектор положения для точки S2.
Пример 4
Учитывая две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .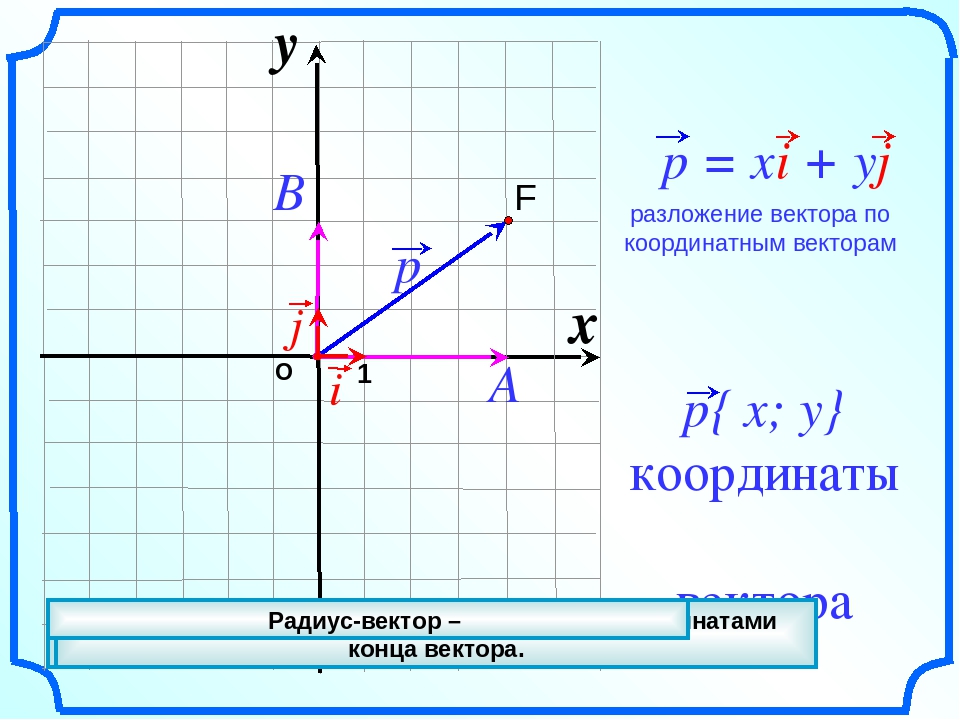
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| R | = √100 + 25 + 9
| R | = √100 + 25 + 9
| R | = √134
Пример 6
Учитывая точки c = 5i + 6j + 3k и d = 2i + 5j — 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы- Пусть u = (-1, 4) и v = (2 , 5).Определите вектор положения, представленный UV .
- Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- Учитывая b = (3,2,5), определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается с a = (1, 2) и заканчивается на Ь = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается с o = (0,0) и заканчивается на b = (-2, 6). Определите его вектор положения.
Ответы
- UV = (3,1). Направление UV на 3 единицы вправо по оси x и на 1 единицу вверх.
- VU = (-3, -1). Направление VU составляет 3 единицы влево по оси x и 1 единицу вниз. Два вектора UV и VU, противоположны по направлению.
- Вектор положения точки m может быть задан OM = (-9, -2)
- R = 3i + 2j + 5k — вектор положения, и его длина | R | = √38
- Вектор положения равен AB = (1,1), а его длина равна | AB | = √2
- Вектор положения — OB = (-2,6), а его длина — | OB | = √40
Прямоугольная система координат
Следующее обсуждение ограничено векторами в двумерной координатной плоскости, хотя концепции могут быть расширены на более высокие измерения.
Если вектор сдвинут так, что его начальная точка находится в начале прямоугольной координатной плоскости, говорят, что он находится в стандартной позиции . Если вектор равен вектору и имеет начальную точку в начале координат, он называется стандартным вектором для. Другие названия стандартного вектора включают радиус-вектор и вектор положения (рисунок 1).
Рис. 1
Векторы, нарисованные на плоскости.
Вектор — это стандартный вектор для всех векторов в плоскости с тем же направлением и величиной, что и.Чтобы найти стандартный вектор для геометрического вектора в координатной плоскости, необходимо найти только координаты точки P , потому что точка 0 находится в начале координат. Если координаты точки A равны ( x a , y a ) , а координаты точки B равны ( x b , y b ), то координаты точки P равны ( x b — x a , y ab — y a ).
Пример 1: Если конечные точки вектора имеют координаты A (−2, −7) и B (3, 2), то каковы координаты точки P , которая является стандартным вектором и = (см. рисунок 2)?
Рисунок 2
Рисунок для примера 1.
Если координаты точки P равны ( x , y ),
Алгебраический вектор — это упорядоченная пара действительных чисел.Алгебраический вектор, соответствующий стандартному геометрическому вектору, обозначается как ⟨ a, b ⟩, если конечная точка P имеет координаты (a, b) . Числа a и b называются компонентами вектора ⟨a, b⟩ (см. Рисунок 3).
Рисунок 3
Компоненты вектора.
Если a, b, c и d — все действительные числа, такие что a = c и b = d , то вектор v = ⟨a, b⟩ и вектор u = ⟨c, d⟩ считаются равными.То есть алгебраические векторы с равными соответствующими компонентами равны. Если оба компонента вектора равны нулю, вектор называется нулевым вектором . звездная величина вектора v = ⟨a, b⟩ равна.
Пример 2: Какова величина вектора u = ⟨3, −5⟩?
Сложение векторов определяется как добавление соответствующих компонентов векторов, то есть, если v = a, b⟩ и u = ⟨c, d⟩ , то v + u = ⟨a + c, b + d⟩ (рисунок 4).
Рисунок 4
Сложение вектора.
Скалярное умножение определяется как умножение каждого компонента на константу, то есть, если v = ⟨a, b⟩ и q является константой, то q v = q⟨a , b⟩ = ⟨qa, qb⟩ .
Пример 3: Если v = ⟨8, −2⟩ и w = ⟨3, 7⟩, то найдите 5 v −2 w .
Единичный вектор — это вектор, величина которого равна 1. Единичный вектор v с тем же направлением, что и ненулевой вектор u , может быть найден следующим образом:
Пример 4 : Найдите единичный вектор v с тем же направлением, что и вектор u , учитывая, что u = ⟨7, — 1⟩.
Два специальных единичных вектора, i = 1, 0⟩ и j = ⟨0, 1⟩, могут использоваться для выражения любого вектора v = ⟨a, b⟩ .
Пример 5: Запишите u = ⟨5, 3⟩ в терминах единичных векторов i и j (рисунок 5).
Рисунок 5
Чертеж для примера 5.
Векторы обладают алгебраическими свойствами, аналогичными свойствам действительных чисел (таблица 1).
Пример 6: Найдите 4 u + 5 v , если u = 7 i -3 j и v = −2 i + 5 j .
Для двух векторов u = ⟨a, b⟩ = a i + b j и v = ⟨c, d⟩ = c i + d j , скалярное произведение , записанное как u · v , является скалярной величиной u ˙ v = ac + bd . Если u, v и w — векторы, а q — действительное число, то скалярные произведения демонстрируют следующие свойства:
Последнее свойство, u ˙ v = | u | | v | cos α, можно использовать для определения угла между двумя ненулевыми векторами u и v .Если два вектора перпендикулярны друг другу и образуют угол 90 °, они называются ортогональными . Поскольку cos 90 ° = 0, скалярное произведение любых двух ортогональных векторов равно 0.
Пример 7: Учитывая, что u = ⟨ 5 , −3⟩ и v = ⟨6, 10⟩, покажите, что u и v ортогональны, продемонстрировав, что скалярное произведение u и v равно нулю.
Пример 8: Какой угол между u = ⟨5, −2⟩ и v = ⟨6, 11⟩?
Считается, что объект находится в состоянии статического равновесия , если все векторы силы, действующие на объект, в сумме равны нулю.
Пример 9: Канатоходец весом 150 фунтов стоит ближе к одному концу каната, чем к другому. Более короткая веревка отклоняется от горизонтали на 5 °. Более длинная веревка отклоняется на 3 °. Каково натяжение каждой части веревки?
Нарисуйте силовую диаграмму со всеми тремя векторами сил в стандартном положении (Рисунок 6).
Рисунок 6
Чертеж для примера 9.
Сумма векторов силы должна быть равна нулю для каждого компонента.
Для компонента i : — | u | cos 5 ° + | v | cos 3 ° = 0
Для компонента j : | u | sin5 ° + | v | cos 3 ° — 150 =
Решите эти два уравнения относительно | u | и | v |:
Подставляем значения синусов и косинусов:
Умножьте первое уравнение на 0,0872, а второе — на 0,9962:
.Сложите два уравнения и решите относительно | v |:
Заменить и решить для | u |:
Нахождение координат точек с помощью векторов? (См. Рисунок)
Чтобы найти координаты A B C , нам нужно найти пересечение векторных линий.Это можно сделать, приравняв каждую пару векторных линий.
Для поиска точки A воспользуемся векторными линиями AB и AC . См. Диаграмму.
#AB = AC #
# ((0), (2)) + r ((2), (1)) = ((0), (5)) + t ((1), (- 1)) #
# цвет (белый) (->) 2r = t #
# 2 + r = 5-t #
Решение для # r # и # t #:
# г = 3-т #
# 2 (3-t) = t => t = 2 #
# 2r = 2 => r = 1 #
Использование их в #AB = AC #
# ((0), (2)) + 1 ((2), (1)) = ((0), (5)) + 2 ((1), (- 1)) #
# ((2), (3)) = ((2), (3)) #
Координата A : # цвет (белый) (8) (2 цвета (белый) (1), 3) #
Для поиска точки B воспользуемся векторными линиями AB и BC .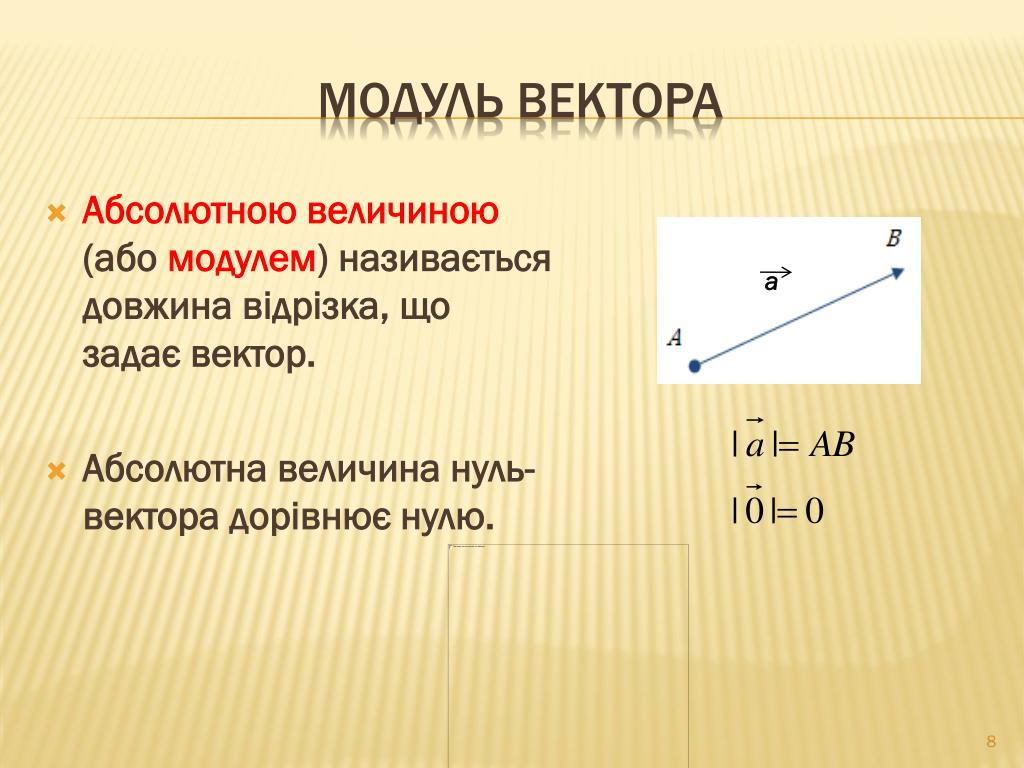
#AB = BC #
# ((0), (2)) + r ((2), (1)) = ((8), (6)) + s ((- 1), (- 2)) #
# цвет (белый) (888) 2r = 8-s #
# 2 + r = 6-2s #
# r = 4-2s #
# 2 (4-2s) = 8-s => s = 0 #
# 2 + r = 6-2 (0) => r = 4 #
Используя их в #AB = BC #
# ((0), (2)) + 4 ((2), (1)) = ((8), (6)) + 0 ((- 1), (- 2)) #
# ((8), (6)) = ((8), (6)) #
Координата B : # цвет (белый) (8) (8 цвет (белый) (1), 6) #
Для поиска точки C воспользуемся векторными линиями AC и BC .
# AC = BC #
# ((0), (5)) + t ((1), (- 1)) = ((8), (6)) + s ((- 1), (- 2)) #
# цвет (белый) (8888) t = 8-s #
# 5-t = 6-2s #
# 5- (8-с) = 6-2с => s = 3 #
# t = 8-3 => t = 5 #
Использование их в #AC = BC #
# ((0), (5)) + 5 ((1), (- 1)) = ((8), (6)) + 3 ((- 1), (- 2)) #
# ((5), (0)) = ((5), (0)) #
Координата C : # цвет (белый) (8) (5 цвет (белый) (1), 0) #
Чтобы вычислить длины сторон, мы могли бы использовать формулу расстояния или найти векторы #vec (AB), vec (AC) и vec (CB) # и найти их величину.2)) = sqrt (45) = 3sqrt (5) #
Стороны AB и BC имеют одинаковую длину.
Координаты:
# A = (2, 3) #
# B = (8, 6) #
# C = (5, 0) #
Длина сторон:
# AB = 3sqrt (5) #
# BC = 3sqrt (5) #
# AC = 3sqrt (2) #
— обзор
1 Предварительные сведения
Сначала напомним несколько ключевых свойств L p и ℓ p , которые обсуждаются на протяжении всей главы, посвященной основным концепциям.
Базис единичного вектора для ℓ p является 1-симметричным базисом [49, раздел 3]. Базис Хаара ( h i ) 0 ∞ является безусловным базисом L p для 1 < p <∞ [49, раздел 3], [24]. Это также монотонная основа для L p для 1 ≤ p <∞. Функции Радемахера
(rn) n = 1∞, [49, раздел 4], эквивалентны базису единичного вектора 2 для p <∞, (и базису единичного вектора 1 для p = ∞).
Это также монотонная основа для L p для 1 ≤ p <∞. Функции Радемахера
(rn) n = 1∞, [49, раздел 4], эквивалентны базису единичного вектора 2 для p <∞, (и базису единичного вектора 1 для p = ∞).
Таким образом, для 0 < p <∞ существуют константы A p , B p с
(1.1) Ap (∑ | an | 2) 1 / 2≤ (∫01 | ∑anrn (t) | pdt) 1 / p≤Bp (∑ | an | 2) 1/2
для всех скаляров ( a n ). A p = 1, если 2 ≤ p <∞ и B p = 1, если p ≤ 2.
Если (xi) 1∞ — это нормализованная последовательность функций с дизъюнктным носителем на [0, 1] в L p с (1 ≤ p <∞), тогда ( x i ) эквивалентно 1 базис единичного вектора ℓ p и [( x i )] дополняется 1 через проекцию
P (x) = ∑i = 1∞ (∫01sign xi (t) | xi (t) | p − 1x (t) dt) xi.
Для 1 < p <∞, L p равномерно выпуклый и равномерно гладкий с модулем выпуклости (соответственно гладкости) степенного типа p (соответственно степенного типа q с 1p + 1q = 1), [49, Раздел 6], L p относится к типу min (2, p ) и котиру max (2, p ) для 1 ≤ p <∞ [ 49, Раздел 8].
Для (xi) 1n⊆Lp
(1.2) Ap (∑1n || xi || p2) 1 / 2≤ (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || pp) 1 / p
, если 1 ≤ p <2, и
(1.3) (∑1n || xi || pp) 1 / p≤ (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤Bp (∑1n || xi || p2) 1/2
, если 2 < p <∞.
Например, чтобы увидеть (1.2), воспользуемся теоремой Фубини, || ⋅ || Lp≤ || ⋅ || L2, (1.1) при p = 2 и || ⋅ || ℓp≥ || ⋅ || ℓ2, чтобы получить
(1.4) 01 || ∑1nri (t) xi || ppdt = ∫01∫01 | ∑1nri (t) xi (s) | pdt ds≤∫01 [∫01 | ∑1nri (t) xi ( s) | 2dt] p / 2ds = ∫01 (∑1n | xi (s) | 2) p / 2ds≤∫01∑1n | xi (s) | pds
, что дает правое неравенство (1. 2). Также согласно (1.1)
2). Также согласно (1.1)
∫01∫01 | ∑1nri (t) xi (s) | pdt ds ≥ App∫01 (∑1n | xi (s) | 2) p / 2ds.
Сейчас
(∑1n || xi || p2) p / 2 = || (|| xi || pp) 1n || ℓ2 / p = ∑1n || xi || ppai | для некоторого (ai) 1n∈ℓ2 / (2 − p) нормы 1≤∫01 (∑1n | xi (s) | 2) p / 2 (∑1n | ai | 2 / (2 − p)) (2 − p) / 2ds по неравенству Хёдера = ∫01 (∑1n | xi (s) | 2) p / 2ds,
, что завершает доказательство (1.2).
(1.2) и (1.3) можно рассматривать как обобщения неравенств Кларксона [29]. С || ⋅ || Lp≤ || ⋅ || L2 для p ≤ 2 мы также имеем, используя (1.2) для p = 2, что
(1.5) (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || 22) 1/2 для 1 ≤ p <2,
и аналогично
(1.6) (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || 22) 1/2 для 2 Техника интегрирования против Радемахера дает некоторые полезные неравенства для безусловных базовых последовательностей в L p . Если ( x n ) является λ-безусловной базовой последовательностью в L p , то (1,7) λ − 1 [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds] 1 / 2≤ || ∑anxn || p ≤λBp [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds], если 2≤p <∞, (1.8) (λ, Ap) −1 [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds] 1 / p≤ || ∑anxn || p ≤λ [∫01 (∑ | an | 2 | xn (s) | 2) p / 2] 1 / p, если 1≤p≤2, откуда следует, что ( x n ) и
(| xn |) эквивалентны. Если ( x n ) также нормализовано, (1.9) λ − 1 (∑ | an | p) 1 / p≤ || ∑anxn || p≤λBp (∑ | an | 2) 1/2, если 2≤p <∞. (1,10) (λAp) −1 (∑ | an | 2) 1 / 2≤ || ∑anxn || p≤λ (∑ | an | p) 1 / p, если 2 ≤ p ≤2. Последние два неравенства являются непосредственными следствиями (1.2) и (1.3). Любая разностная последовательность мартингалов в L p является безусловной [25], что обобщает тот факт, что базис Хаара безусловен. В частности, любая последовательность независимых случайных величин со средним нулевым значением в L p является безусловной. (1.11) 12max {(∑i = 1n || xi || pp) 1 / p, (∑i = 1n || xi || 22)} ≤ || ∑i = 1nxi || p≤Kpmax {( ∑i = 1n || xi || pp) 1 / p, (∑i = 1n || xi || 22) 1/2}. В [55] показано, что K p ~ p / ln p . Банахово пространство X — это
L p , λ -пространство, если для всех конечномерных пространств F ⊆ X существует конечномерное E с
F⊆E⊆X так что
d (E, ℓpdim E) ≤λ. В конечном итоге оказывается (см. Раздел 5), что разделимое X является
L p , λ для некоторого λ и 1 < p <∞ тогда и только тогда, когда X изоморфно дополненному подпространству L p , которое не изоморфно гильбертову пространству [66,68]. Ситуация для L 1 более сложная. Предполагается, что каждое бесконечномерное дополняемое подпространство X из L 1 изоморфно L 1 или ℓ 1 . Известно, что если X содержит изоморф L 1 , то X изоморфен L 1 [36], и если X встраивается в ℓ 1 , то X является изоморфна ℓ 1 [65].Различные характеристики
L 1 — (и
L ∞ ) приведены в [68]. Была проделана большая работа по изучению и попыткам классификации
L p -пространство с точностью до изоморфизма, и это обсуждается в разделе 5 ниже. Мы начнем с некоторых результатов по глобальной структуре L p и, в частности, с теми, которые связаны с базисом Хаара. Обновлено 8 декабря 2020 г. Ли Джонсон Расчет величин сил — важная часть физики.Когда вы работаете в одном измерении, вам не нужно учитывать величину силы. Расчет величины является более сложной задачей в двух или более измерениях, потому что сила будет иметь «компоненты» по осям x- и y и, возможно, по оси z, если это трехмерная сила. Научиться делать это с помощью одной силы и результирующей силы двух или более отдельных сил — важный навык для любого начинающего физика или любого, кто работает над проблемами классической физики в школе. Найдите результирующую силу из двух векторов, сначала сложив -компоненты x и y -компоненты, чтобы найти результирующий вектор, а затем использовать та же формула для его величины. Первый шаг к пониманию того, что значит вычислить величину силы в физике, — это узнать, что такое вектор. «Скаляр» — это простая величина, которая просто имеет значение, например температуру или скорость.Когда вы читаете температуру 50 градусов по Фаренгейту, он сообщает вам все, что вам нужно знать о температуре объекта. Если вы читаете, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро оно движется. Вектор отличается, потому что он имеет направление, а также величину. Если вы посмотрите прогноз погоды, вы узнаете, с какой скоростью дует ветер и в каком направлении. Это вектор, потому что он дает вам дополнительную информацию.Скорость — это векторный эквивалент скорости, в котором вы узнаете направление движения, а также его скорость. Итак, если что-то движется со скоростью 10 миль в час на северо-восток, скорость (10 миль в час) — это величина, северо-восток — направление, и обе части вместе составляют вектор скорости. На словах результирующая сила — это квадратный корень из x 2 плюс y 2 .2} Направление силы не является предметом внимания в этом вопросе, но его легко вычислить на основе треугольника компонентов и результирующей силы из последнего раздела. Определить направление можно с помощью тригонометрии. Идентификатор, наиболее подходящий для решения большинства задач: \ tan {\ theta} = \ frac {y} {x} Здесь θ обозначает угол между вектором и ось x .{-1} (3/4) = 36,9 \ text {градусы} Итак, вектор составляет около 37 градусов с осью x. Если у вас есть две или более сил, вычислите величину результирующей силы, сначала найдя результирующий вектор, а затем применив тот же подход, что и выше. Единственный дополнительный навык, который вам понадобится, — это найти результирующий вектор, и это довольно просто. Хитрость заключается в том, что вы складываете вместе соответствующие компоненты x и y .Использование примера должно прояснить это. Представьте себе парусник на воде, движущийся вместе с силой ветра и течением воды. Вода передает силу 4 Н в направлении x и 1 Н в направлении y, а ветер добавляет силу 5 Н в направлении x и 3 Н в направлении y. Результирующий вектор представляет собой сложенные вместе компоненты x (4 + 5 = 9 N) и компоненты y , сложенные вместе (3 + 1 = 4 N). Таким образом, вы получите 9 N в направлении x и 4 N в направлении y.2} \\ & = \ sqrt {81 + 16} \\ & = \ sqrt {97} \\ & = 9.85 \ text {N} \ end {align} К концу этого раздела вы сможете: Векторы обычно описываются в терминах их компонентов в системе координат. Даже в повседневной жизни мы естественно обращаемся к концепции ортогональных проекций в прямоугольной системе координат. Например, если вы спросите кого-нибудь, как добраться до определенного места, вам, скорее всего, предложат пойти на 40 км на восток и 30 км на север, чем на 50 км в направлении 37 ° 37 ° к северу от востока. В прямоугольной (декартовой) системе координат xy на плоскости точка на плоскости описывается парой координат ( x , y ). Аналогичным образом вектор A → A → на плоскости описывается парой его координат вектора . Координата x вектора A → A → называется его составляющей x , а координата y вектора A → A → называется его составляющей y . Компонент вектора x — это вектор, обозначаемый A → xA → x.Вектор y -компонент — это вектор, обозначенный A → yA → y. В декартовой системе компоненты вектора x и y являются ортогональными проекциями этого вектора на оси x и y соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов: 2,10 Как показано на Рисунке 2.16 вектор A → A → является диагональю прямоугольника, где x -компонента A → xA → x является стороной, параллельной оси x , а y -компонента A → yA → y является стороной, параллельной оси x . сторона параллельна оси y . Компонента вектора A → xA → x ортогональна компоненту вектора A → yA → y. 2,12 Если нам известны координаты b (xb, yb) b (xb, yb) начальной точки вектора (где b означает «начало») и координаты e (xe, ye) e (xe, ye ) конечной точки вектора (где e означает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты начальной точки из координат конечной точки: 2,13 2,14 Это решение показано на Рисунке 2. Рисунок 2.17 График вектора смещения. Вектор указывает от начальной точки на b до конечной точки на e .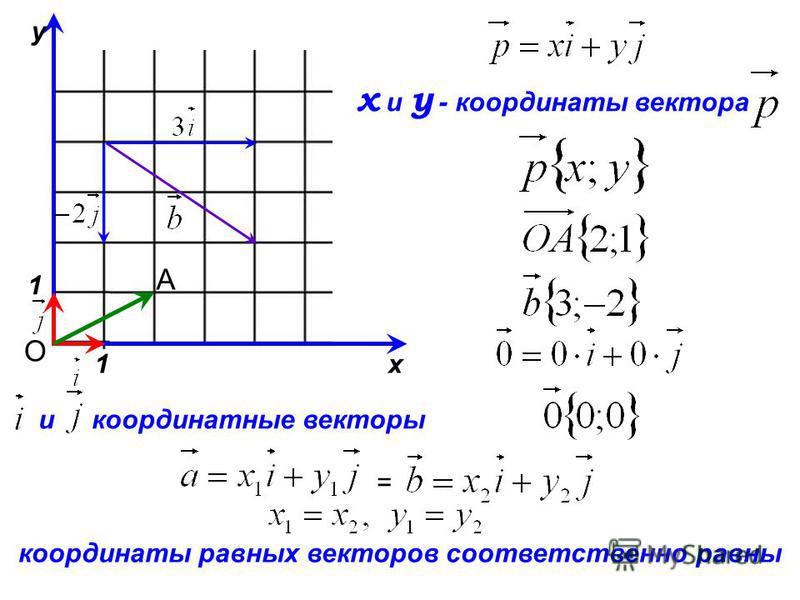 Неравенство Розенталя [91] дает нам некоторую информацию о таких последовательностях. Пусть 2 < p <∞. Существует K p <∞, так что если ( x i ) n 1 являются независимыми средними нулевыми случайными величинами в L p , то
Неравенство Розенталя [91] дает нам некоторую информацию о таких последовательностях. Пусть 2 < p <∞. Существует K p <∞, так что если ( x i ) n 1 являются независимыми средними нулевыми случайными величинами в L p , то Все банаховы пространства считаются сепарабельными, если не указано иное.
Все банаховы пространства считаются сепарабельными, если не указано иное. Как рассчитать величину силы в физике
TL; DR (слишком долго; не читал)
Основы: что такое вектор?
 2}
2} Направление вектора одиночной силы
Результирующая сила и величина двух или более векторов
2.2 Системы координат и компоненты вектора — Университетская физика Том 1
Цели обучения

Пример 2.3
Смещение указателя мыши
Указатель мыши на мониторе компьютера в исходном положении находится в точке (6.на y — ось направлена вертикально вверх. Начало вектора смещения находится в точке b (6.0, 1.6), а конец вектора смещения расположен в точке e (2.0, 4.5). Подставьте координаты этих точек в уравнение 2.13, чтобы найти скалярные компоненты DxDx и DyDy вектора смещения D → D →. Наконец, подставьте координаты в уравнение 2.12, чтобы записать вектор смещения в форме компонента вектора. Решение
Отождествляем xb = 6.0xb = 6.0, xe = 2.)см. 17.
17. Значение
Обратите внимание, что физическая единица — здесь 1 см — может быть размещена либо с каждым компонентом непосредственно перед единичным вектором, либо глобально для обоих компонентов, как в уравнении 2.14. Часто второй способ удобнее, потому что он проще., которая параллельна направлению оси + y . Следовательно, вектор D → yD → y, составляющий y , направлен вверх, как показано на рис. 2.17. Скалярная y -компонента вектора D → D → равна Dy = + 2.9Dy = + 2.9. Вектор смещения D → D → является равнодействующим его двух компонентов вектора .
Форма векторной составляющей вектора смещения Уравнение 2.14 говорит нам, что указатель мыши был перемещен на мониторе на 4,0 см влево и 2,9 см вверх от своего исходного положения.
Проверьте свое понимание 2.4
Синяя муха приземляется на миллиметровую бумагу в точке, расположенной на 10,0 см справа от ее левого края и на 8,0 см выше ее нижнего края, и медленно идет к точке, расположенной на расстоянии 5,0 см от левого края и 5,0 см от низа. край. Выберите прямоугольную систему координат с началом в левом нижнем углу листа и найдите вектор смещения мухи. Проиллюстрируйте свое решение графиком.
Зная скалярные компоненты AxAx и AyAy вектора A → A →, мы можем найти его величину A и угол направления θAθA.Угол направления — или, для краткости, направление — это угол, который вектор образует с положительным направлением на оси x . Угол θAθA измеряется в направлении против часовой стрелки от оси + x к вектору (рисунок 2. 18). Поскольку длины A , AxAx и AyAy образуют прямоугольный треугольник, они связаны теоремой Пифагора:
18). Поскольку длины A , AxAx и AyAy образуют прямоугольный треугольник, они связаны теоремой Пифагора:
2,15
Это уравнение работает, даже если скалярные компоненты вектора отрицательны.Направляющий угол θAθA вектора определяется через касательную функцию угла θAθA в треугольнике, показанном на рисунке 2.18:
Рисунок 2.18 Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент AxAx положительный (рисунок 2.19), угол направления θAθA в уравнении 2.16) идентичен углу θθ.Когда вектор лежит либо в первом квадранте, либо в четвертом квадранте, где компонент AxAx положительный (рисунок 2.19), угол θθ в уравнении 2.16 совпадает с направлением угла θAθA. Для векторов в четвертом квадранте угол θθ отрицателен, что означает, что для этих векторов угол направления θAθA измеряется на по часовой стрелке от положительной оси x . Точно так же для векторов во втором квадранте угол θθ отрицателен. Когда вектор лежит во втором или третьем квадранте, где компонент AxAx отрицательный, угол направления равен θA = θ + 180 ° θA = θ + 180 ° (рисунок 2.19).
Рис. 2.19. Скалярные компоненты вектора могут быть положительными или отрицательными.Векторы в первом квадранте (I) имеют обе скалярные компоненты положительные, а векторы в третьем квадранте имеют обе скалярные компоненты отрицательные. Для векторов в квадрантах II и III угол направления вектора равен θA = θ + 180 ° θA = θ + 180 °.Пример 2.4
Величина и направление вектора смещения
Вы перемещаете указатель мыши на мониторе из его исходного положения в точке (6,0 см, 1,6 см) к значку, расположенному в точке (2,0 см, 4,5 см). Каковы величина и направление вектора смещения указателя?Стратегия
В примере 2.3, мы нашли вектор смещения D → D → указателя мыши (см. Уравнение 2.14). Мы идентифицируем его скалярные компоненты Dx = −4.0cmDx = −4.0cm и Dy = + 2.9cmDy = + 2.9cm и подставляем в Уравнение 2.15 и Уравнение 2.16, чтобы найти звездную величину D и направление θDθD соответственно.
Уравнение 2.14). Мы идентифицируем его скалярные компоненты Dx = −4.0cmDx = −4.0cm и Dy = + 2.9cmDy = + 2.9cm и подставляем в Уравнение 2.15 и Уравнение 2.16, чтобы найти звездную величину D и направление θDθD соответственно.Решение
Величина вектора D → D → равна D = Dx2 + Dy2 = (- 4,0 см) 2+ (2,9 см) 2 = (4,0) 2+ (2,9) 2 см = 4,9 см D = Dx2 + Dy2 = (- 4,0 см) 2+ (2,9 см) 2 = (4,0) 2+ (2,9) 2 см = 4,9 см.Угол направления
tanθ = DyDx = + 2,9 см − 4,0 см = −0.) см, найдите его величину и направление.Во многих приложениях величины и направления векторных величин известны, и нам нужно найти равнодействующую многих векторов. Например, представьте 400 автомобилей, движущихся по мосту Золотые Ворота в Сан-Франциско при сильном ветре. Каждая машина толкает мост в разных направлениях, и мы хотели бы знать, насколько сильным может быть результирующий толчок. У нас уже есть некоторый опыт геометрического построения векторных сумм, поэтому мы знаем, что задача нахождения результирующей путем рисования векторов и измерения их длины и углов может довольно быстро стать неразрешимой, что приведет к огромным ошибкам.Подобные опасения не возникают, когда мы используем аналитические методы. Самый первый шаг в аналитическом подходе — найти компоненты вектора, когда известны направление и величина вектора.
Вернемся к прямоугольному треугольнику на рис. 2.18. Отношение соседней стороны AxAx к гипотенузе A является функцией косинуса угла направления θAθA, Ax / A = cosθAAx / A = cosθA, а отношение противоположной стороны AyAy к гипотенузе A является функцией синуса. из θAθA, Ay / A = sinθAAy / A = sinθA.Когда звездная величина A и направление θAθA известны, мы можем решить эти соотношения для скалярных компонентов:
{Ax = AcosθAAy = AsinθA. {Ax = AcosθAAy = AsinθA.2,17
При вычислении компонентов вектора с помощью уравнения 2. .direction указывает, как угол φφ изменяется в направлении против часовой стрелки. Таким образом, точка P , имеющая координаты ( x , y ) в прямоугольной системе, может быть эквивалентно описана в полярной системе координат двумя полярными координатами (r, φ) (r, φ). Уравнение 2.17 справедливо для любого вектора, поэтому мы можем использовать его для выражения x и y -координат вектора r → r →. Таким образом, мы получаем связь между полярными координатами и прямоугольными координатами точки P :
.direction указывает, как угол φφ изменяется в направлении против часовой стрелки. Таким образом, точка P , имеющая координаты ( x , y ) в прямоугольной системе, может быть эквивалентно описана в полярной системе координат двумя полярными координатами (r, φ) (r, φ). Уравнение 2.17 справедливо для любого вектора, поэтому мы можем использовать его для выражения x и y -координат вектора r → r →. Таким образом, мы получаем связь между полярными координатами и прямоугольными координатами точки P :
Пример 2.6
Полярные координаты
Охотник за сокровищами находит одну серебряную монету на расстоянии 20,0 м от сухого колодца в направлении 20 ° 20 ° к северу от востока и находит одну золотую монету на расстоянии 10,0 м от колодца в направлении 20 ° 20 ° к северу от него. Запад. Каковы полярные и прямоугольные координаты этих находок относительно скважины?Стратегия
Колодец отмечает начало системы координат, а восток — направление + x .Мы определяем радиальные расстояния от местоположений до начала координат, которые составляют rS = 20.0mrS = 20.0 м (для серебряной монеты) и rG = 10.0mrG = 10.0 м (для золотой монеты). Чтобы найти угловые координаты, преобразуем 20 ° 20 ° в радианы: 20 ° = π20 / 180 = π / 920 ° = π20 / 180 = π / 9. Мы используем уравнение 2.18, чтобы найти координаты x и y монет.Решение
Угловая координата серебряной монеты φS = π / 9φS = π / 9, тогда как угловая координата золотой монеты φG = π − π / 9 = 8π / 9φG = π − π / 9 = 8π / 9.Следовательно, полярные координаты серебряной монеты равны (rS, φS) = (20,0 м, π / 9) (rS, φS) = (20,0 м, π / 9), а координаты золотой монеты — (rG, φG) = (10,0 м, 8π / 9) (rG, φG) = (10,0 м, 8π / 9). Мы подставляем эти координаты в уравнение 2.18, чтобы получить прямоугольные координаты. Для золотой монеты координаты
{xG = rGcosφG = (10,0 м) cos8π / 9 = −9,4myG = rGsinφG = (10,0 м) sin8π / 9 = 3,4 м⇒ (xG, yG) = (- 9,4 м, 3,4 м). {xG = rGcosφG = (10,0 м) cos8π / 9 = −9,4myG = rGsinφG = (10,0 м) sin8π / 9 = 3,4 м⇒ (xG, yG) = (- 9,4 м, 3,4 м).
Мы подставляем эти координаты в уравнение 2.18, чтобы получить прямоугольные координаты. Для золотой монеты координаты
{xG = rGcosφG = (10,0 м) cos8π / 9 = −9,4myG = rGsinφG = (10,0 м) sin8π / 9 = 3,4 м⇒ (xG, yG) = (- 9,4 м, 3,4 м). {xG = rGcosφG = (10,0 м) cos8π / 9 = −9,4myG = rGsinφG = (10,0 м) sin8π / 9 = 3,4 м⇒ (xG, yG) = (- 9,4 м, 3,4 м).Для серебряной монеты координаты
. {xS = rScosφS = (20.0 м) cosπ / 9 = 18,9myS = rSsinφS = (20,0 м) sinπ / 9 = 6,8 м⇒ (xS, yS) = (18,9 м, 6,8 м). {XS = rScosφS = (20,0 м) cosπ / 9 = 18,9 myS = rSsinφS = (20,0 м) sinπ / 9 = 6,8 м⇒ (xS, yS) = (18,9 м, 6,8 м).Векторы в трех измерениях
Чтобы указать положение точки в пространстве, нам нужны три координаты ( x , y , z ), где координаты x и y определяют местоположение на плоскости, а координата z дает вертикальное положение выше или ниже плоскости. Трехмерное пространство имеет три ортогональных направления, поэтому нам нужны не два, а три единичных вектора для определения трехмерной системы координат..
2,19
Если мы знаем координаты его начала b (xb, yb, zb) b (xb, yb, zb) и его конца e (xe, ye, ze) e (xe, ye, ze), то его скалярные компоненты равны полученные путем взятия их разностей: AxAx и AyAy задаются уравнением 2.13, а компонент z —
Az = ze−zb.Az = ze − zb.2,20
Величина получается путем обобщения уравнения 2.15 на три измерения:
A = Ax2 + Ay2 + Az2. A = Ax2 + Ay2 + Az2.2,21
Это выражение для величины вектора получено в результате двойного применения теоремы Пифагора.Как видно на рис. 2.22, диагональ в плоскости xy имеет длину Ax2 + Ay2Ax2 + Ay2, и ее квадрат прибавляется к квадрату Az2Az2, чтобы получить A2A2. Обратите внимание, что когда -компонент z равен нулю, вектор полностью лежит в плоскости xy , и его описание сокращается до двух измерений.
Обратите внимание, что когда -компонент z равен нулю, вектор полностью лежит в плоскости xy , и его описание сокращается до двух измерений.
Рис. 2.22 Вектор в трехмерном пространстве — это векторная сумма трех его векторных компонентов.
Пример 2.7
Взлет дрона
Во время взлета IAI Heron (рисунок 2.23), его положение относительно поста управления — 100 м над землей, 300 м к востоку и 200 м к северу. Минутой позже он находится на высоте 250 м над землей, 1200 м к востоку и 2100 м к северу. Каков вектор смещения дрона по отношению к диспетчерской вышке? Какова величина его вектора смещения?Рис. 2.23 Дрон IAI Heron в полете. (Источник: SSgt Рейнальдо Рамон, ВВС США)
Стратегия
Возьмем начало декартовой системы координат за диспетчерскую вышку., который указывает вверх от земли. Первое положение дрона — это начало (или, что то же самое, начало) вектора смещения, а его второе положение — конец вектора смещения.Решение
Мы идентифицируем b (300,0 м, 200,0 м, 100,0 м) и e (1200 м, 2100 м, 250 м) и используем уравнение 2.13 и уравнение 2.20, чтобы найти скалярные компоненты вектора смещения дрона. : {Dx = xe − xb = 1200.0m − 300.0m = 900.0m, Dy = ye − yb = 2100.0m − 200.0m = 1900.0m, Dz = ze − zb = 250.) м / с, какова величина вектора скорости дрона? .

 circ =|overline<α>||overline<β>|cdot 0=0$
circ =|overline<α>||overline<β>|cdot 0=0$
 Вектор перпендикулярен векторам и , то есть и ;
Вектор перпендикулярен векторам и , то есть и ;
Leave A Comment