Задачи по теме «Сила Лоренца, сила Ампера»
1. Два первоначально покоившихся электрона ускоряются в электрическом поле: первый проходит разность потенциалов U, второй — 2 U. Ускорившиеся электроны попадают в однородное магнитное поле, линии индукции которого перпендикулярны скорости движения электронов. Найдите отношение радиусов кривизны траекторий первого и второго электронов.
2. Радиусы окружностей, по которым движутся α-частица и электрон (масса первой в 4 раза больше)
3. Два электрона А и В движутся в однородном магнитном поле, при этом вектора их скоростей перпендикулярны вектору магнитной индукции. Отношение кинетических энергий электронов ЕА/ЕВ =4. Найдите RА/ RВ.
4. Электрон, обладая кинетической энергией 1,6∙10-12 Дж, движется по окружности в однородном магнитном поле с индукцией 1,5 Тл. Чему равен радиус его окружности?
6. Протон движется по окружности в магнитном поле с индукцией 10-3Тл. За какое время он совершит полный оборот?
7. Протон, влетевший со скоростью v в однородное магнитное поле перпендикулярно его силовым линиям, движется по окружности с периодом Т. Каким будет период обращения атома гелия, состоящего из двух протонов и двух нейтронов, влетевшего таким же образом и с такой же скоростью в это поле?
8. Протон, влетевший со скоростью v в однородное магнитное поле перпендикулярно его силовым линиям, движется по окружности радиуса R. Каким будет радиус траектории атома гелия, состоящего из двух протонов и двух нейтронов, влетевшего таким же образом и с такой же скоростью в это поле?
9. Как меняется радиус траектории электрона, движущегося в однородном магнитном поле перпендикулярно вектору магнитной индукции, при уменьшении его кинетической энергии в 4 раза?
Как меняется радиус траектории электрона, движущегося в однородном магнитном поле перпендикулярно вектору магнитной индукции, при уменьшении его кинетической энергии в 4 раза?
10. Протон и электрон, обладая одинаковыми кинетическими энергиями, влетают в однородное магнитное поле перпендикулярно его силовым линиям. Определите отношение радиусов траекторий протона и электрона. Отношение масс этих частиц равно 1836.
11. Протон и электрон, обладая одинаковыми скоростями, влетают в однородное магнитное поле перпендикулярно его силовым линиям. Определите отношение радиусов траекторий протона и электрона.
12. Найдите модуль импульса частицы с зарядом q, движущейся в однородном магнитном поле с индукцией В по окружности радиусом R.
Л.р. №8 Движение заряженных частиц в магнитном поле
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 1 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
ЛАБОРАТОРНАЯ РАБОТА № 9
ДВИЖЕНИЕ ЗАРЯЖННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ
Учебная цель занятия
Применение движения заряженных частиц в электрических и магнитных полях получило широкое распространение в науке и технике. К приборам подобного рода относятся электронно-лучевые трубки, ускорители элементарных частиц, массспектрометры и многие другие.
Содержание лабораторной работы
В данной лабораторной работе необходимо изучить движение заряженной частицы в магнитном поле.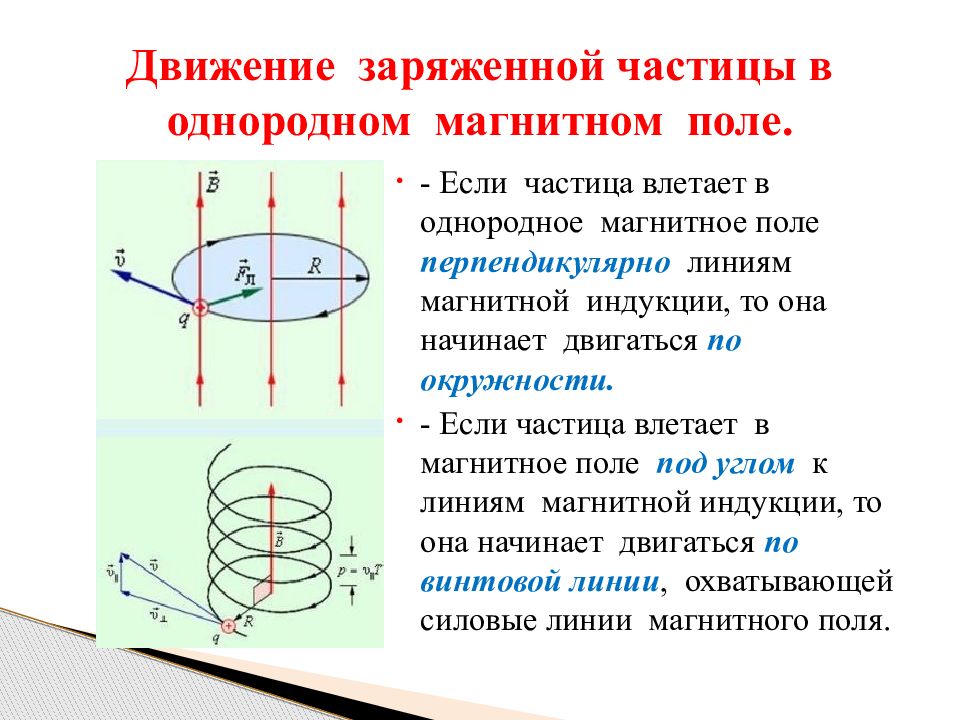 Задавая такие параметры, как проекции вектора скорости и индукцию магнитного поля, можно в видеть как изменяется траектория движения заряженной частицы, каков радиус её вращения, можно вычислить период обращения. Необходимо построить графики следующих зависимостей: гироскопического радиуса и периода обращения частицы от проекции скорости на ос х; циклотронной частоты и периода обращения от значения индукции магнитного поля; длины шага от значении проекции вектора скорости на ось х. Все зависимости строятся при условии, что третий параметр, задаваемый в модели остаётся постоянным или равен нулю.
Задавая такие параметры, как проекции вектора скорости и индукцию магнитного поля, можно в видеть как изменяется траектория движения заряженной частицы, каков радиус её вращения, можно вычислить период обращения. Необходимо построить графики следующих зависимостей: гироскопического радиуса и периода обращения частицы от проекции скорости на ос х; циклотронной частоты и периода обращения от значения индукции магнитного поля; длины шага от значении проекции вектора скорости на ось х. Все зависимости строятся при условии, что третий параметр, задаваемый в модели остаётся постоянным или равен нулю.
Базовый материал
Повторить, а при необходимости изучить теоретические вопросы базового материала:
1.Савельев Курс физики, т.2
2.Сивухин Общий курс физики, т.3
3.Матвеев Курс физики, т.3
4.Грабовский Курс физики
5.Лекционный материал
Подготовка к занятию
Для успешного выполнения и сдачи работы необходимо подготовить бланк отчёта по работе, подготовить ответы на контрольные вопросы, знать понятия тока, магнитного пол, законы Био-Савара и Ампера, выражение для силы Лоренца.
Входной контроль
1. Какой величиной характеризуется магнитное поле? В чём она измеряется?
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 2 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
2.Какая сила действует на движущийся заряд в магнитном поле? Как она называется?
3.Чему равна сила, действующая со стороны магнитного поля, на покоящуюся заряженную частицу?
4.Записать закон Био-Савара.
5.Как направлена сила, действующая на движущуюся заряженную частицу? Сформулируйте правило буравчика.
6.Какую работу совершает сила Лоренца при движении заряда?
7.Какая сила действует на проводник с током в магнитном поле?
8.Изобразите силовые линии прямолинейного проводника с током.
9.Как взаимодействуют два параллельных бесконечно длинных проводника с
током?
10.Какие величины задаются в модели? Вычисляются?
Теоретическое введение и исходные данные
Уравнение движения частицы, меющей массу ь и заряд й, движущегося со скоростью вв постоянном магнитном поле с индукцией В, имеет следующий вид:
|
|
| (1) |
|
| ||
где | — сила, действующая на движущуюся частицу в магнитном поле, | ||
называемая силой Лоренца. Это векторное уравнение необходимо спроектировать на оси прямоугольной декартовой системы координат. Получим три скалярных уравнения.
Пусть вектор индукции магнитного поля направлен вдоль оси :
Отсюда, согласно правилу определения составляющих векторного произведения, следует:
,
,
Таким образом, уравнение (1) приводится к системе дифференциальных уравнений:
,
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 3 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
,
,
Отсюда видно, что остаётся постоянной составляющая скорости, параллельная оси , т.е. вдоль которой направлено магнитное поле.
Можно также непосредственно обнаружить и другую особенность данного движения: остаётся также постоянной кинетическая энергия
Так как
Потому что векторное произведение перпендикулярно к вектору скорости. Следовательно, магнитное поле не изменяет кинетическую энергию свободной частицы. Из постоянства кинетической энергии мы делаем вывод, что величина также постоянна. Этот результат наводит на мысль искать решение выражающее равномерное круговое движение, при котором составляющие скорости по осям x и y
изменяются по синусоидальному закону с разностью фаз | . |
Решение системы уравнений движения (2) будем искать в следующем виде: | |
, |
|
, | (3) |
Это – уравнения кругового движения. Из них следует:
,
,
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
Инженерно-технический институт КГУ, кафедра физики. | стр. 4 из | |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
И после подстановки решений (3) система уравнений принимает вид:
,
(4)
Эти уравнения тождественно выполняются при условии, что:
А этим соотношенем определяется так называемая циклортронная (гироскопическая, ларморовская) частота, т.е. частота движения заряженной частицы в магнитном поле. Уравнения (4) удовлетворяются при любом значении .
Рисунок 1. Положительный заряд q, движущийся с начальной скоростью v, перпендикулярной к индукции В однородного магнитного поля, описывает
окружность радиусом |
| с постоянной по абсолютной величине |
|
скоростью V
Уравнение для циклотронной частоты можно получить и элементарным способом. Направленная внутрь траектории частицы магнитная сила создаёт центростремительное (направленное внутрь) ускорение, необходимое для кругового
Направленная внутрь траектории частицы магнитная сила создаёт центростремительное (направленное внутрь) ускорение, необходимое для кругового
движения этой частицы. Величина центростремительного ускорения равна |
| или |
| ||
. Следовательно, |
|
|
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 5 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
,
Или
Откуда получаем
Найдём уравнение траектории частицы в магнитном поле. Изменние положения частицы в заивисимости от времени можно определить, интегрируя уравнения движения (3), положив в них равным :
Отсюда видно, что проекция траектории частицы на плоскость xy представляет собой
окружность с центром в точке | . Радиус этой окружности равен | ||||
|
|
|
|
| . |
|
|
| |||
Этот радиус называется | гироскопическим радиусом или циклотронным | ||||
(ларморовским)радиусом. |
|
|
|
|
|
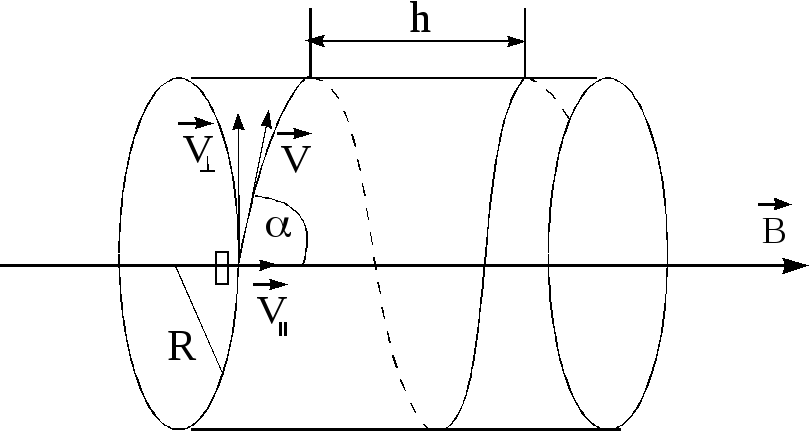
Рисунок 2. Положительный заряд q описывает в однородном магнитном поле с индукцией В спираль с постоянным шагом. При этом параллельная вектору В составляющая скорости заряда, остается постоянной
При этом параллельная вектору В составляющая скорости заряда, остается постоянной
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 6 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
Траектория частицы представляет собой спираль, ось которой направлена параллельно магнитной идукции; составляющая скорости частицы, параллельная вектору В, остаётся постоянной.
Заметим следующее
|
|
| , |
|
| ||
Где | — импульс частицы в плоскости, перпендикулярной к . Это важное | ||
соотношение; выполняется и в релятивистской области скоростей, если вместо подставить в него релятивистский импульс. Поэтому можно применять это соотношение для определния импульсов частиц с очень высокой энергией. Рассмотрим примеры
1.Гироскопическая частота Какова гироскопическая частота электрона в магнитном поле с индукцией 1,1 Тл
(величина поля 10-15 Тл типична для магнитных полей обычных электромагнитов с железным сердечником)? Согласно формуле для циклотрнонной частоты, имеем:
Частотак периодического движения, равна:
Соответствующая длина электромагнитной волны в свободном пространстве равна:
ц |
|
|
| м |
|
| |||
| ц | |||
Гироскопическая частота протона относится к гироскопической частоте электрона в том же самом магнитном поле так же, как масса элетрона к массе протона (1836 раз):
Направление круговогодвижения электрона в магнитном поле противоположно направлению движения протона, потому чт их заряды имеют противоположнве знаки.
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 7 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
2.Гироскопический радиус Каков равдиус траектории электрона, движущегося в циклотроне со скоростью
м/с в плоскости, перпендиуклярной к вектору магнитной индукции В, величина которого равна 1,1 Тл?
Применяя уравнение |
|
|
| , найдём: |
|
|
Гироскопический радиус протона, движущегося с той же скоростью, больше в Мр/m раз:
Рисунок 3 Полученная в водородной пузырьковой камере фотография траектории электрона, движущегося с большой скоростью в магнитном поле. Электрон входит в поле зрения внизу слева. Теряя свою энергию на ионизацию водородных молекул, электрон замедляет движение. Когда уменьшается скорость электрона, уменьшается и радиус кривизны его траектории в магнитном поле. Поэтому траектория имеет форму спирали. (Радиа ионная
лабо ато ия и . Лоу ен а)
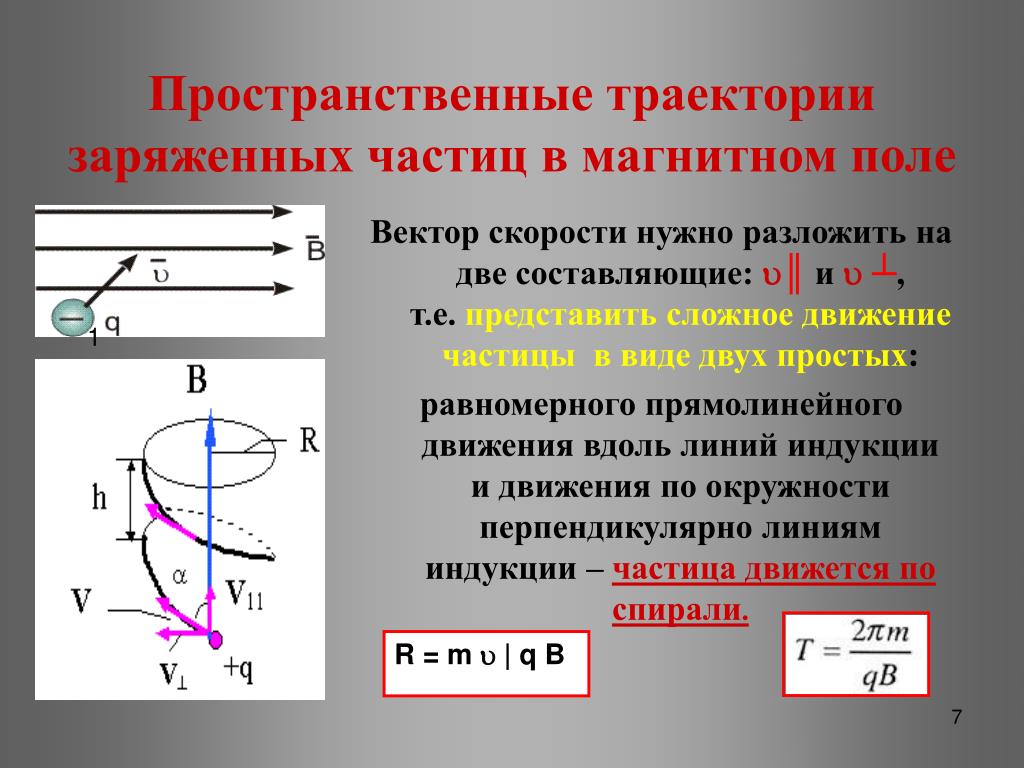
Рассмотрим случай, когда скорость частицы направлена под углом к магнитному полю. Представим скорость в виде , где — скорость вдоль поля, а — перпендикулярно к нему. Движения с этими скоростями независимы. Первое есть равномерное прямолинейное движение вдоль поля сос скоростью
Лабораторная |
| СМК КГУ | Редакция | ||
работа № |
| Движение заряженных частиц в магнитном поле | 1 |
|
|
|
| Инженерно-технический институт КГУ, кафедра физики. | стр. 8 из | ||
|
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
|
|
, второе – равномерное движение по окружности вокруг поля с угловой | |||||
частотой, | равное гироскопической. Радиус этой окружности равен |
|
| . В | |
|
| ||||
результате сложение обоих движений возникает движежние по спирали, ось которой параллельна магнитному полю.
Порядок выполнения работы
Задание 1 1. Сделать описание модели в соответствие с таблицей 1
|
| Таблица 1 |
|
| Величины |
| Задаваемые | Вычисляемые |
Пределы
изменения
Единица
измерения
2.Получить формулу для гироскопического радиуса
3.Задать значение проекции вектора скорости на ось z равной нулю
4.Установить значение вектора магнитной индукции равной в соответствии с таблицей 2
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 9 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
Таблица 2
№ п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Индукция | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,5 | 1,7 | 1,8 | 2,0 |
магнитного |
|
|
|
|
|
|
|
|
|
|
поля |
|
|
|
|
|
|
|
|
|
|
5. Изменяя значение проекции вектора скорости на ось х, записывать значения гироскопического радиуса, число полных оборотов и времени (соответствующее полному количеству оборотов) в таблицу 3
Изменяя значение проекции вектора скорости на ось х, записывать значения гироскопического радиуса, число полных оборотов и времени (соответствующее полному количеству оборотов) в таблицу 3
|
|
|
|
|
|
| Таблица 3 |
№ | Vz | Vx | Индук | Число | Время, t | Период, | Гир. |
|
|
| ция, B | оборотов, |
| T | Радиус, |
|
|
|
| N |
|
| R |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
6. Вычислить период обращения частицы: T=t/N
Вычислить период обращения частицы: T=t/N
7.Построить график зависимости гироскопического радиуса и периода обращения от начальной скорости (проекции на ось х)
8.Получить формулу для циклотронной частоты
9.Построить график зависимости циклотронной частоты и периода обращения от
скорости при определённом значении индукции поля 10.В какую сторону движется заряд при положительном и отрицательном значении
индукции поля 11.Сделать вывод о зависимости гироскопического радиуса, циклотронной частоты
и периода обращения от величины проекции скорости на ось х
Задание 2
Лабораторная | СМК КГУ | Редакция |
работа № | Движение заряженных частиц в магнитном поле | 1 |
| Инженерно-технический институт КГУ, кафедра физики. | стр. 10 из |
| Утверждена на заседании кафедры физики января 2010, протокол №1 | 13 |
1.Задать значение проекции вектора скорости на ось z равной нулю
2.Установить значение проекции вектора скорости на ось х в соответствии с таблицей 4
Таблица 4
№ п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Скорость | 1,0 | 1,7 | 2,3 | 3,0 | 3,7 | 4,3 | 5,0 | 5,7 | 6,3 | 8 |
по оси x |
|
|
|
|
|
|
|
|
|
|
3. Изменяя индукция магнитного поля В, записывать значения гироскопического радиуса, число полных оборотов и времени (соответствующее полному количеству оборотов) в таблицу 5
Изменяя индукция магнитного поля В, записывать значения гироскопического радиуса, число полных оборотов и времени (соответствующее полному количеству оборотов) в таблицу 5
|
|
|
|
|
|
| Таблица 5 |
№ | Vz | Индукция, | Vx | Число | Время, t | Период, | Гир. |
|
| B |
| оборотов, |
| T | Радиус, |
|
|
|
| N |
|
| R |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
4. Вычислить период обращения частицы: T=t/N
Вычислить период обращения частицы: T=t/N
5.Построить график зависимости гироскопического радиуса и периода обращения от величины вектора магнитной индукции
6.Построить график зависимости циклотронной частоты и периода обращения от вектора магнитной индукции при определённом значении скорости
7.Сделать вывод о зависимости гироскопического радиуса, циклотронной частоты и периода обращения от величины магнитного поля
8.Сделать вывод о траектории движения частицы в отсутствие составляющей вектора скорости по оси z
Задание 3
%PDF-1.4 % 117 0 obj > endobj 116 0 obj > endobj 114 0 obj > endobj 1599 0 obj >stream Acrobat Distiller 7.0 (Windows)**D:20050906171414Acrobat PDFMaker 7.0 for Word2006-12-16T13:31:24+03:002006-12-16T13:31:22+03:002006-12-16T13:31:24+03:00uuid:48fa14ff-aad9-45de-9754-f2fc68c114d9uuid:6d817f01-a4ae-4987-9de3-3184296e6f88
2
ГЛАВА 3. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ЭЛЕКТРОМАГНИТНЫХ ПОЛЯХ
ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ЭЛЕКТРОМАГНИТНЫХ ПОЛЯХ
Движение каждого из электронов, поставленных эмиттером (катодом), в рабочем объёме происходит под действием внешних полей и , созданных потенциальным электродами и токовыми катушками, и поля , созданного всеми остальными электронами. На рис. 3.1 показано поле , созданное парой плоских электродов и поля , созданные в точке e четырьмя электронами. Эти электроны распределены по всему рабочему объёму и образуют пространственный или объёмный заряд (ПЗ или ОЗ).
Рис.3.1 Внешнее поле и поле пространственного заряда
Уравнение движения электрона даётся вторым законом Ньютона
(3.1)
Поле есть сумма кулоновских полей, созданных в точке каждым из движущихся электронов. Оно определяется их мгновенными положениями , которые как раз и должны находиться из (3.1). Поэтому задача сводится к решению системы из N обыкновенных дифференциальных уравнений
Решить её можно только численно с помощью компьютера, да и то при числе частиц N, не превышающем . Поэтому используют другой подход. Считают, что поле создаётся непрерывно распределённым зарядом с локальной плотностью
(3.2)
где – так называемая — функция Дирака, отличная от нуля только в точке расположения j— го электрона . Потенциал поля пространственного заряда удовлетворяет уравнению Пуассона
(3.3)
(3. 4)
4)
В большинстве случаев плотность пространственного заряда такова, что . Тогда взаимным влиянием электронов друг на друга можно пренебречь. Все они будут двигаться одинаково, то есть по подобным траекториям, в полях , .
Разнообразие конфигураций полей в реальных приборах не слишком велико. Их можно свести к следующим базовым конфигурациям:
— постоянное однородное электрическое поле ;
— переменное однородное электрическое поле ;
— постоянное однородное магнитное поле ;
— скрещенные постоянные поля и ;
— постоянное неоднородное магнитное поле .
Рассмотрим движение одиночного электрона в этих полях.
3.1. ДВИЖЕНИЕ ЭЛЕКТРОНА В ПОСТОЯННОМ ОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Рассмотрим два частных, но часто встречающихся, случая.
3.1.1. НАЧАЛЬНАЯ СКОРОСТЬ ЭЛЕКТРОНА ПЕРПЕНДИКУЛЯРНА ПОЛЮ.
Такая конфигурация обеспечивает отклонение электрона. Поле создаётся парой плоских электродов шириной и бесконечной длины, к которым приложена разность потенциалов . Пусть расстояние между электродами равно , тогда , (рис. 3.2). Электрон влетает в поле в момент времени в точке со скоростью , направленной по оси .
Рис. 3.2. Отклонение электрона полем, перпендикулярным скорости
Уравнение движения электрона запишем в проекциях на оси координат
(3.5)
Общие решения уравнений (3.5) находятся элементарно,
Постоянные интегрирования получаем из начальных условий
Таким
образом, (3. 6)
6)
Исключив время , получим уравнение траектории
(3.7)
Это уравнение параболы.
3.1.2. НАЧАЛЬНАЯ СКОРОСТЬ ЭЛЕКТРОНА РАВНА НУЛЮ ИЛИ НАПРАВЛЕНА ПО ПОЛЮ
Такая конфигурация обеспечивает ускорение электрона при переносе его между двумя электродами (катодом и сеткой, двумя сетками, рис. 3.3).
Рис. 3.3. Ускорение электрона продольным полем
Из уравнения движения и начальных условий , находим
(3.8)
(3.9)
Полагая в (3.8) , получим уравнение для времени пролёта электрона между электродами
или
При из первого уравнения находим
(3.10)
При из второго уравнения имеем
(3.11)
Ускоряющее напряжение во многих случаях таково, что , то есть приобретаемая электроном энергия намного меньше начальной кинетической энергии. Тогда, разлагая квадратный корень в (3.11) по правилу , получим
Время пролёта — важный параметр прибора, используемый при анализе его реакции на переменную разность потенциалов между электродами.
3.2. ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРЕМЕННОМ ОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Пусть между плоскими электродами в предыдущей
конфигурации приложено переменное напряжение . Начальную скорость в момент положим равной нулю. Дважды интегрируя
уравнение движения электрона , находим
Начальную скорость в момент положим равной нулю. Дважды интегрируя
уравнение движения электрона , находим
(3.12)
Полагая в (3.12) , получим уравнение для времени пролёта,
(3.13)
В (3.13) время пролёта входит только в виде произведения
(3.14)
где — период изменения напряжения между электродами. Безразмерный параметр называется углом пролёта электрона. Он показывает изменение фазы напряжения за время движения электрона между электродами. Если фаза изменяется на , то поле меняет направление на противоположное, например, с ускоряющего на тормозящее. Линейная частота при этом равна
(3.15)
Для её вычисления надо в (3.15) подставить , найденное из уравнения (3.13). Решить это трансцендентное уравнение можно только численно. Поэтому сделаем грубую оценку, подставив из (3.10),
Примем , , тогда
Это граница между ВЧ и СВЧ диапазонами. При , и изменение фазы напряжения не сказывается на движении электронов. Они движутся так, как в постоянном поле с мгновенным значением напряжённости. Это область классической низкочастотной электроники, которую мы и будем изучать. Если же , то . Движение электронов очень сильно зависит от соотношения между фазой напряжения и моментом начала движения . Это уже область СВЧ электроники, которой мы не коснёмся.
Принципиальные различия реакции прибора на низкие и
сверхвысокие частоты можно проиллюстрировать графически, если построить по
формулам (3.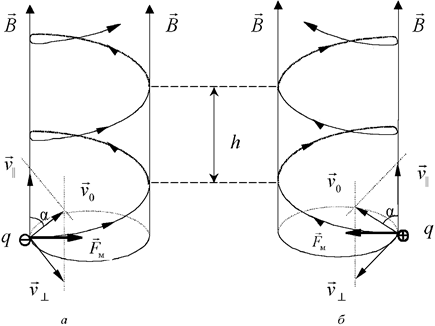 8) и (3.12) временные зависимости положения электронов,
влетающих в поле в различные моменты . Эти графики называются пространственно-временными диаграммами.
8) и (3.12) временные зависимости положения электронов,
влетающих в поле в различные моменты . Эти графики называются пространственно-временными диаграммами.
На рис. 3.4 показаны пространственно-временные диаграммы движения электронов под действием постоянного напряжения.
Рис. 3.4. Пространственно-временные диаграммы движения
электронов при постоянном напряжении.
Видно, что все электроны, не зависимо от времени начала движения , достигают второго электрода.
Иначе выглядят пространственно-временные диаграммы движения электронов под действием переменного напряжения (рис.3.5). Время пролёта возрастает по сравнению с предыдущим случаем даже при синфазном с полем начале движения. При возрастает ещё больше. Некоторые электроны достигают второго электрода после нескольких колебаний. Другие вообще не достигают его, а возвращаются назад.
Рис. 3.5. Пространственно-временные диаграммы движения
электронов при переменном напряжении .
, — период изменения .
Таким образом, движение электрона в сверхвысокочастотном электрическом поле существенно отличается от его движения в медленно меняющемся поле.
3.3. ФИЗИЧЕСКАЯ ПРИРОДА ТОКОВ В ЭЛЕКТРОННЫХ ПРИБОРАХ
На любом участке замкнутой цепи, включающей
электронный прибор, ток в данный момент одинаков по величине и направлению. Но
на разных участках физическая природа тока может быть, и, как правило, является
различной. Рассмотрим простейшую замкнутую цепь из вакуумного диода и источника
питания. Диод есть прибор с двумя электродами – катодом и анодом. Катод эмиттирует
электроны в рабочий объём. На анод подаётся положительный потенциал, создающий
ускоряющее поле и обеспечивающий собирание электронов (рис. 3.6).
3.6).
С поверхности катода истекает ток эмиссии. Он определяется главным образом внутренними процессами в катоде. Энергия электронов, с которой они покидают катод, намного меньше , поэтому её можно полагать равной нулю. Тогда все эмиттированные электроны начинают движение в рабочем объёме с нулевой начальной скоростью.
.
Рис. 3.6 Токи в электронном приборе
Под действием поля электроны приобретают к моменту времени скорость
Они образуют так называемый конвекционный ток или ток переноса. Конвекционный ток обусловлен перемещением носителей заряда на макроскопические расстояния. Плотность конвекционного тока равна произведению объёмной плотности заряда на мгновенную скорость электронов ,
Одиночный электрон создаёт конвекционный ток
Ток во внешней цепи прибора, например, в анодном выводе, не является конвекционным. Он обусловлен не макроскопическим переносом электронов, а поляризацией электродов электронами, движущимися в рабочем объёме. Рассмотрим слой электронов толщиной в сечении рабочего объёма (рис. 3.7).
Рис. 3.7. Поляризация электродов конвекционным током
На единицу площади он содержит заряд . Этот заряд создаёт на катоде и аноде поляризационные заряды и такие, что
(3.16)
Поляризация
ослабляет поле у катода и усиливает его у анода. Если в отсутствие заряда на катоде и аноде напряжением создаются заряды на единицу площади, то при наличии заряда плотность заряда на катоде
равна , а на аноде — . Перераспределение поля
происходит таким образом, что работа по перемещению единичного заряда от катода
к аноду остаётся равной , то есть
Перераспределение поля
происходит таким образом, что работа по перемещению единичного заряда от катода
к аноду остаётся равной , то есть
(3.17)
Подставив поля у катода и у анода в (3.17), получим связь между и ,
(3.18)
Из (3.16) и (3.18) находим выражения для поляризационных зарядов
(3.19)
По мере перемещения заряда , создающего конвекционный ток, заряд на катоде убывает, а заряд на аноде увеличивается. Такое изменение поляризационных зарядов происходит за счёт смещения многих электронов в проводниках на небольшие по атомным масштабам расстояния. Это смещение, восстанавливающее электронейтральность, называется максвелловской релаксацией. Ток во внешней цепи равен скорости изменения полного заряда на одном из электродов. Полный заряд на аноде равен , а ток в анодном выводе
(3.20)
Он состоит из двух компонент. Первая компонента есть ток перезарядки ёмкости анод-катод. При . Вторая компонента
(3.21)
есть так называемый наведённый ток, индуцированный в выводе зарядом . Наведённый ток, созданный всеми зарядами из рабочего объёма, равен
Наведённый ток в пересчёте на единицу площади конвекционного потока равен среднему значению плотности конвекционного тока в рабочем объёме,
Конвекционный
ток в любом сечении рабочего объёма должен оставаться одинаковым по величине и
равным току эмиссии, .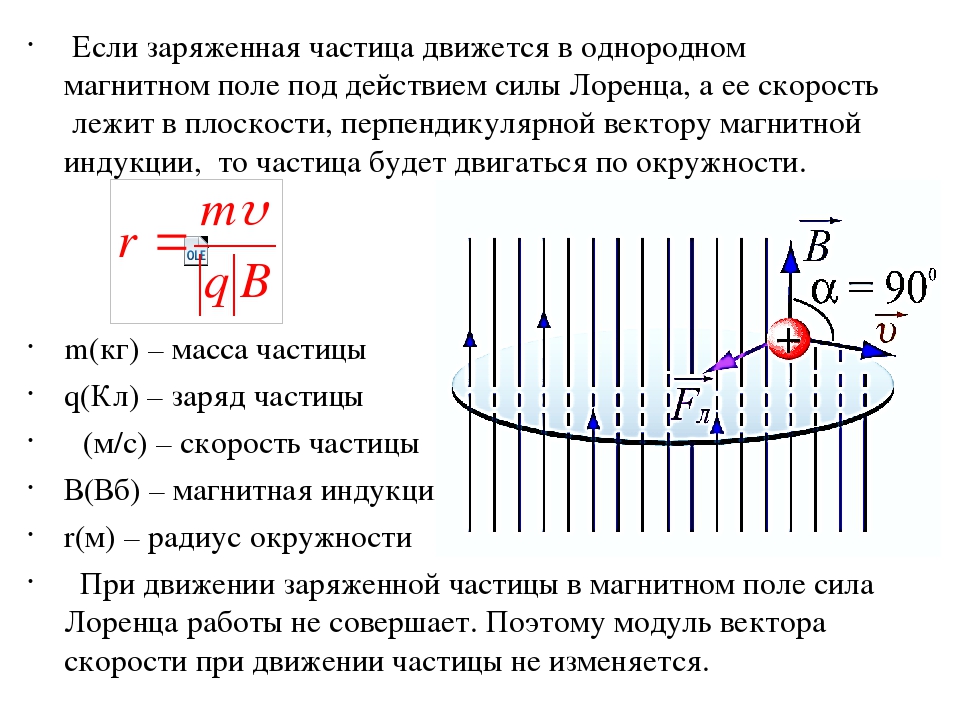 Поэтому
Поэтому
(3.22)
Таким образом, постоянный конвекционный ток индуцирует во внешней цепи равный себе наведённый ток. Это обычная ситуация в «классической» низкочастотной электронике.
Пусть теперь переменный конвекционный ток создаётся потоком электронов переменной плотности , влетающих в рабочий объём с постоянной скоростью . По определению,
,
Заряд в слое индуцирует наведённый ток
Выбирая начало координат посредине между катодом и анодом, суммарный наведённый ток запишем в виде
(3.23)
Параметр называется коэффициентом взаимодействия электронного потока с полем. При значении угла пролёта , а наведённый ток вовсе не содержит переменной составляющей, хотя в конвекционном токе она присутствует. Но при , и наведённый ток воспроизводит конвекционный ток. Этот пример ещё раз подчёркивает отличие низкочастотной электроники от электроники сверхвысоких частот.
Таким образом, полный ток, протекающий во внешней цепи любого электронного прибора, имеет две основные составляющие:
1. Наведённый ток, обусловленный движением зарядов в междуэлектродном пространстве;
2. Ёмкостной ток, обусловленный перезарядкой междуэлектродной ёмкости
Только при или ток во внешней цепи точно равен конвекционному току. Поэтому в низкочастотной электронике обычно не делают различия между конвекционным и наведённым током.
3.4 ДВИЖЕНИЕ ЭЛЕКТРОНА В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Однородное магнитное поле всюду имеет одинаковую
величину и направление. Выберем систему координат так, чтобы ось z была направлена по полю. Тогда вектор имеет только одну компоненту, . Пусть электрон начинает
движение в момент из начала координат со скоростью . Уравнение (3.1) запишем в
проекциях на оси координат,
Выберем систему координат так, чтобы ось z была направлена по полю. Тогда вектор имеет только одну компоненту, . Пусть электрон начинает
движение в момент из начала координат со скоростью . Уравнение (3.1) запишем в
проекциях на оси координат,
Из сразу следует, что вдоль оси z электрон движется равномерно с начальной скоростью ,
(3.25)
Уравнения и можно проинтегрировать по t,
,
Величина имеет размерность обратного времени. Она называется ларморовской или циклотронной частотой. Первым термином отмечен вклад в науку английского физика Джозефа Лармора (1857 – 1942). Постоянные и находим из начальных условий,
,
В системе уравнений
естественно перейти к искомым функциям и :
Исключив из первого уравнения, получим уравнение гармонических колебаний, , решение которого имеет вид
Постоянные А и В снова найдём из начальных условий
,
Таким образом,
находим интегрированием,
, ,
Соотношения , задают траекторию электрона в параметрическом
виде.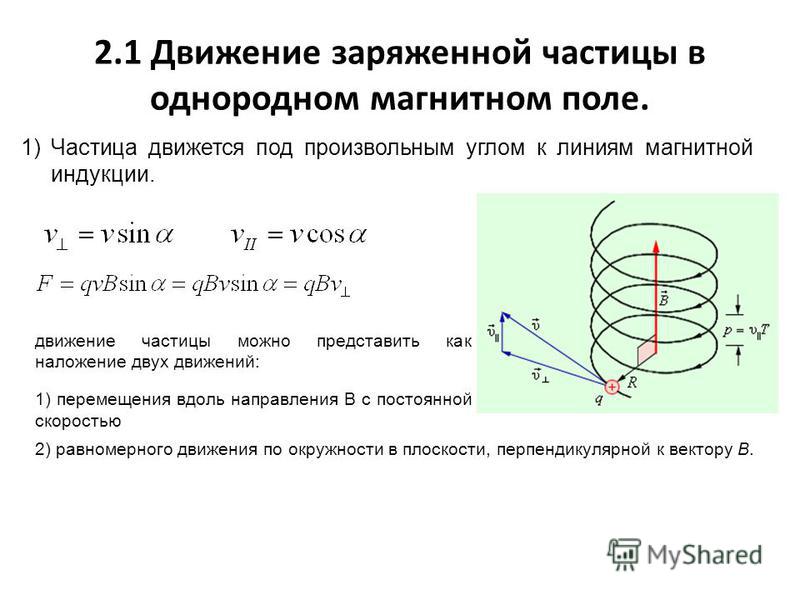 Удобно исключить из них время t. Для этого возведём оба соотношения в квадрат и
сложим их,
Удобно исключить из них время t. Для этого возведём оба соотношения в квадрат и
сложим их,
или (3.27)
Получили уравнение проекции траектории на плоскость XY. Она представляет собой окружность с ларморовским радиусом
(3.28)
с центром в точке .
Таким образом, ларморовская частота есть частота вращения электрона вокруг силовой линии магнитного поля. Она не зависит от начальной скорости электрона. Радиус же окружности пропорционален компоненте скорости, перпендикулярной полю. Если одновременно в начале координат влетают в поле электроны с разными , то при они одновременно будут возвращаться в ту же точку после 1, 2, 3, … оборотов (рис.3.8)
Рис. 3.8. Траектории электронов при .
При траектория электрона будет винтовой линией, навитой на магнитную силовую линию (рис.3.9).
Рис. 3.9. Траектория электрона при
3.5. ДВИЖЕНИЕ ЭЛЕКТРОНА В СКРЕЩЕННЫХ ПОЛЯХ
Пусть поле направлено по оси , то есть , а поле — под произвольным углом к . Электрон начинает движение из начала координат со скоростью (рис. 3.10).
Рис. 3.10. Скрещенные поля и
Аналогично предыдущему пункту запишем уравнение движения
в проекциях на оси координат
Из последнего уравнения следует закон равномерно ускоренного движения электрона параллельно магнитному полю
(3. 29)
29)
Через и обозначены z-компоненты электрического поля и начальной скорости соответственно.
Первое уравнение продифференцируем один раз и исключим из него с помощью второго уравнения
Интегрируя полученное уравнение,
и исключая постоянную с помощью начальных условий,
,
получим
Аналогично для получается уравнение
Из (3.30) немедленно следует, что выражения в скобках гармонически зависят от времени,
(3.31)
(3.31) есть параметрическое уравнение проекции траектории электрона на плоскость . Постоянные определим из начальных условий:
Возведя уравнения (3.31) в квадрат и сложив их, получим уравнение траектории в виде
(3.32)
где (3.33)
(3.34)
Согласно уравнению (3.32), в плоскости , перпендикулярной магнитному полю, электрон движется по окружности с ларморовским радиусом
При этом центр окружности перемещается согласно уравнениям , . Скорость этого движения
направлена перпендикулярно векторам и , поскольку . Движущийся центр ларморовской окружности называется ведущим центром, а само его движение – поперечным дрейфом.
Таким образом, движение электрона в скрещенных электрическом и магнитном полях можно представить в виде суммы трёх движений – ускоренного движения параллельно магнитному полю, вращения по ларморовской окружности и дрейфа со скоростью
(3. 35)
35)
Проекция траектории на плоскость показана на рис. 2.4.11 для случая (магнитная сила слабее электрической), и на рис. 3.12 – для случая (магнитная сила превосходит электрическую).
Рис. 3.11. Поперечный дрейф электрона при .
Рис. 3.12. Поперечный дрейф электрона при .
Формулу (3.35) можно обобщить на случай, когда на электрон вместо электрического поля действует однородная сила любой природы, например, гравитационная, если подставить в неё определение электрического поля ,
(3.36)
Из (3.36) следует, что если на частицы с противоположными зарядами сила действует в одном направлении, то дрейфуют они в противоположных направлениях, тогда как в электрическом поле поперечный дрейф и электронов, и ионов происходит в одном направлении.
3.6. ДВИЖЕНИЕ ЭЛЕКТРОНА В НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Движение электрона в неоднородном магнитном поле описывается уравнением
(3.37)
При произвольной зависимости магнитной индукции от координат получить его точное решение в замкнутом виде нельзя. Для конкретной конфигурации поля траектория электрона может быть найдена численными методами. Однако они не позволяют проанализировать решение качественно и дать наглядную интерпретацию изменения траектории при изменении поля. Поэтому физиками были разработаны приближённые методы решения уравнения (3.37), основанные на его упрощении.
При описании движения электрона в сильном неоднородном магнитном поле используют следующий подход. По аналогии с движением в скрещенных полях считают, что оно состоит из суммы движения по ларморовской окружности радиуса вокруг силовой линии и перемещения центра этой окружности ,
(3. 38)
38)
Рассмотрим два вида неоднородных магнитных полей.
1. Силовые линии поля суть прямые, но величина поля (плотность силовых линий) изменяется в пространстве. В этом случае градиент поля всюду перпендикулярен . Если ларморовский радиус столь мал, что поле на расстоянии изменяется слабо, то есть
то можно разложить в ряд Тейлора
Тогда уравнение (3.37) примет вид
Второе слагаемое в правой части после усреднения по промежутку времени может быть приведено к виду , где есть магнитный момент кругового тока площадью , созданного вращающимся электроном. По определению,
Таким образом, в среднем градиент магнитного поля действует как однородная сила . Следовательно, он вызывает градиентный магнитный дрейф со скоростью
(3.39)
Физически градиентный дрейф обусловлен тем, что ларморовский радиус обратно пропорционален величине локального магнитного поля . Траектория электрона подобна показанной на рис. 3.12.
2. Градиент магнитного поля параллелен полю. В этом случае силовые линии искривлены. Их возможная топология показана на рис.3.13. Она называется «магнитной бутылкой».
Рис.3.13. «Магнитная бутылка»
На
электрон, движущийся в направлении горлышка бутылки и обладающий ненулевой
перпендикулярной компонентой скорости , действует тормозящая сила . Если градиент достаточно
велик, то она может затормозить электрон вплоть до исчезновения параллельной
компоненты скорости , а затем ускорить его в
противоположном направлении.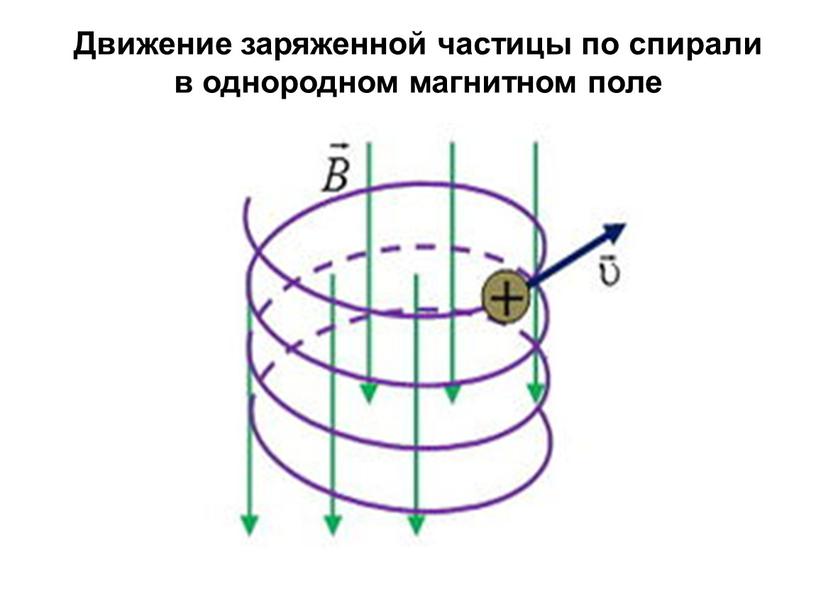 Электрон как бы отражается от области с большей
плотностью силовых линий. Поэтому горлышко бутылки называют магнитным зеркалом.
Отражение имеет место, если поля в точке начала движения и в точке отражения связаны соотношением
Электрон как бы отражается от области с большей
плотностью силовых линий. Поэтому горлышко бутылки называют магнитным зеркалом.
Отражение имеет место, если поля в точке начала движения и в точке отражения связаны соотношением
(3.40)
Кривизна — траектория — электрон
Кривизна — траектория — электрон
Cтраница 1
Кривизна траектории электронов будет увеличиваться, как показано на рис. 74, до тех пор, пока при некоторой напряженности поля H Hk электронный ток в анодной цепи совсем не прекратится. [1]
Радиус кривизны траектории электрона определим исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца F. [2]
Сравните радиусы кривизны траектории электрона и протона, если: а) двигаясь с одинаковой скоростью и, они влетают в однородное магнитное поле с индукцией 0 1 Тл перпендикулярно к силовым линиям; б) пройдя одну и ту же разность потенциалов, они влетают в магнитное поле. [3]
Наличие осевого магнитного поля позволяет по кривизне траектории электронов измерять их импульсы. [4]
В однородном магнитном поле электрон движется по окружности определенного радиуса. Уменьшается или увеличивается радиус кривизны траектории электрона при медленном возрастании индукции магнитного поля. [5]
В однородном магнитном поле электрон движется по окружности определенного радиуса. Уменьшается или увеличивается радиус кривизны траектории электрона при медлен-ном возрастании индукции магнитного поля. [6]
Почему на фотопластинке, полученной при работе с пузырьковой камерой, треки электронов малой энергии представляют собой спирали. Другими словами, почему радиус кривизны траектории электрона меняется в постоянном магнитном поле, в котором помещена камера.
[7]
Другими словами, почему радиус кривизны траектории электрона меняется в постоянном магнитном поле, в котором помещена камера.
[7]
При наложении поперечного магнитного поля, перпендикулярного электрическому полю в темном пространстве, электроны пересекают темное пространство не по прямой, а по искривленной траектории, в результате чего толщина этой области уменьшается. Это оси бенно важно, когда кривизна траектории электронов достаточно велика, так что электроны, эмнттированные с катода, не достигают края области отрицательного свечения. Следовательно, практическое использование ионного распыления с поперечным магнитным полем не представляет интереса. [8]
Магнитное поле, индукция которого В 5 гс, направлено перпендикулярно электрическому полю, на — пряженность которого Е 10 в.см. Пучок электронов, летящих с некоторой скоростью и, влетает в простран-и ство, где расположены эти поля, причем скорость электронов перпендикулярна плоскости, в которой лежат векторы Е и В. Найти: 1) скорость электронов v, если при одновременном действии обоих полей пучок электронов не испытывает отклонения, 2) радиус кривизны траектории электронов при условии включения одного магнитного поля. [9]
Пучок электронов, летящих с некоторой скоростью и, влетает в пространство, где расположены эти поля, причем скорость электронов перпендикулярна плоскости, в которой лежат век — торы Е и В. Найти: 1) скорость электронов и, если при одновременном действии обоих полей пучок электронов не испытывает отклонения, 2) радиус кривизны траектории электронов при условии включения одного магнитного поля. [10]
Фактически / — фокусное расстояние тонкой магнитной линзы, действие которой эквивалентно действию поля рассеяния. Расстояние f отсчитывается от начала однородной области. В первом приближении оптическая сила линзы зависит лишь от угла падения и радиуса кривизны траектории электрона в однородном поле, но не зависит от характера поля рассеяния.
[11]
Расстояние f отсчитывается от начала однородной области. В первом приближении оптическая сила линзы зависит лишь от угла падения и радиуса кривизны траектории электрона в однородном поле, но не зависит от характера поля рассеяния.
[11]
Страницы: 1
Движение заряженной частицы в магнитном поле — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Опишите, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении через магнитное поле.Что произойдет, если это поле будет однородным при движении заряженной частицы? По какому пути следует частица? В этом разделе мы обсуждаем круговое движение заряженной частицы, а также другое движение, возникающее в результате попадания заряженной частицы в магнитное поле.
Самый простой случай имеет место, когда заряженная частица движется перпендикулярно однородному полю B ((рисунок)). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица следует по кривой траектории в магнитном поле.Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость.
Отрицательно заряженная частица движется в плоскости бумаги в области, где магнитное поле перпендикулярно бумаге (обозначено маленькими буквами, такими как хвосты стрелок). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)
Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)В этой ситуации магнитная сила обеспечивает центростремительную силу. Заметив, что скорость перпендикулярна магнитному полю, величина магнитной силы уменьшается до Поскольку магнитная сила F обеспечивает центростремительную силу, мы имеем
Решение для r дает
Здесь r — радиус кривизны пути заряженной частицы с массой m и зарядом q , движущейся со скоростью v , перпендикулярной магнитному полю с напряженностью B .Время прохождения заряженной частицы по круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. Исходя из этого и (рисунок), мы можем получить период движения как
.Если скорость не перпендикулярна магнитному полю, то мы можем сравнить каждую составляющую скорости отдельно с магнитным полем. Компонент скорости, перпендикулярный магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
, где — угол между v и B .Компонент, параллельный магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, что также показано на (Рисунок). Параллельное движение определяет шаг p спирали, который представляет собой расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
В результате получается винтообразное движение, как показано на следующем рисунке.
Заряженная частица, движущаяся со скоростью, отличной от направления магнитного поля.Компонента скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой. Шаг — это расстояние по горизонтали между двумя последовательными кругами. Результирующее движение — спиральное.
Пока заряженная частица движется по спирали, она может попасть в область, где магнитное поле неоднородно. В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля.Частица может отразиться до того, как войдет в область с более сильным магнитным полем. Это похоже на волну на струне, которая движется от очень легкой тонкой струны к твердой стене и отражается назад. Если отражение происходит с обоих концов, частица оказывается в так называемой магнитной бутылке.
Захваченные частицы в магнитных полях обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли. Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (частицы высокой энергии, приходящие извне Солнечной системы), чтобы выяснить, похож ли он на поток, измеренный на Земле.Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в космическом пространстве. Полярные сияния, как и знаменитое полярное сияние (северное сияние) в Северном полушарии ((Рисунок)), представляют собой прекрасные проявления света, излучаемого, когда ионы рекомбинируют с электронами, входящими в атмосферу, когда они вращаются по спирали вдоль силовых линий магнитного поля. (Ионы — это в основном атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния наблюдались также на других планетах, таких как Юпитер и Сатурн.
(a) Радиационные пояса Ван Аллена вокруг Земли захватывают ионы, образующиеся в результате попадания космических лучей в атмосферу Земли. (b) Великолепное зрелище северного сияния, или северного сияния, сияет в северном небе над Беар-Лейк недалеко от базы ВВС Эйлсон, Аляска. Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота. (кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
Beam Deflector Исследовательская группа занимается изучением короткоживущих радиоактивных изотопов.Им необходимо разработать способ транспортировки альфа-частиц (ядер гелия) от места их создания к месту, где они столкнутся с другим материалом с образованием изотопа. Луч альфа-частиц изгибается в области под углом 90 градусов с однородным магнитным полем 0,050 Тл ((Рисунок)). а) В каком направлении следует приложить магнитное поле? (б) Сколько времени требуется альфа-частицам, чтобы пройти через область однородного магнитного поля?
Установка отражателя балки, вид сверху.
Стратегия
- Направление магнитного поля показано RHR-1.Ваши пальцы указывают в направлении v , а большой палец должен указывать в направлении силы, влево. Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно указывать вниз.
- Период движения альфа-частицы по окружности
Поскольку частица движется только по четверти круга, мы можем взять 0,25-кратный период, чтобы найти время, необходимое для обхода этого пути.
Решение
- Давайте начнем с фокусировки на альфа-частице, входящей в поле в нижней части изображения.Сначала покажите пальцем вверх по странице. Чтобы ваша ладонь открывалась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны менять ориентацию, пока они не будут указывать на страницу.
 Это направление приложенного магнитного поля.
Это направление приложенного магнитного поля. - Период движения заряженной частицы по кругу вычисляется с использованием заданных в задаче массы, заряда и магнитного поля. Получается, что это
Однако для данной задачи альфа-частица обходит четверть круга, поэтому время, необходимое для этого, составит
Значение. Это время может быть достаточно быстрым, чтобы добраться до материала, который мы хотели бы бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп и продолжает испускать альфа-частицы.Если бы мы могли усилить магнитное поле, приложенное к области, это сократило бы время еще больше. Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
Проверьте свое понимание Однородное магнитное поле величиной 1,5 Тл направлено горизонтально с запада на восток. (а) Какова магнитная сила, действующая на протон в момент, когда он движется вертикально вниз в поле со скоростью, равной (б) Сравните эту силу с массой протона w .
а. к югу; б.
Сводка
- Магнитная сила может создавать центростремительную силу и заставлять заряженную частицу двигаться по круговой траектории радиусом
- Период кругового движения заряженной частицы, движущейся в магнитном поле, перпендикулярном плоскости движения, равен
- Спиральное движение возникает, если скорость заряженной частицы имеет компоненту, параллельную магнитному полю, а также компоненту, перпендикулярную магнитному полю.
Концептуальные вопросы
В данный момент электрон и протон движутся с одинаковой скоростью в постоянном магнитном поле. Сравните магнитные силы на этих частицах. Сравните их ускорения.
Величина магнитных сил протона и электрона одинакова, поскольку они имеют одинаковый заряд. Однако направления этих сил противоположны друг другу. Ускорения противоположны по направлению, и электрон имеет большее ускорение, чем протон, из-за его меньшей массы.
Однако направления этих сил противоположны друг другу. Ускорения противоположны по направлению, и электрон имеет большее ускорение, чем протон, из-за его меньшей массы.
Обязательно ли увеличение величины однородного магнитного поля, через которое проходит заряд, увеличение магнитной силы, действующей на заряд? Обязательно ли изменение направления поля означает изменение силы, действующей на заряд?
Электрон проходит через магнитное поле, не отклоняясь. Что вы сделаете по поводу магнитного поля?
Магнитное поле должно быть направлено параллельно или антипараллельно скорости.
Если заряженная частица движется по прямой, можно ли сделать вывод об отсутствии магнитного поля?
Как определить, какой полюс электромагнита северный, а какой южный?
Компас указывает на северный полюс электромагнита.
Проблемы
Электрон космических лучей движется перпендикулярно магнитному полю Земли на высоте, где напряженность поля равна Каков радиус круговой траектории, по которой движется электрон?
(a) Зрители «Звездного пути» слышали о двигателе на антиматерии на корабле Starship Enterprise . Одна из возможностей для такого футуристического источника энергии — хранить заряженные частицы антивещества в вакуумной камере, циркулирующие в магнитном поле, а затем извлекать их по мере необходимости.Антивещество уничтожает обычную материю, производя чистую энергию. Какая напряженность магнитного поля необходима, чтобы удерживать антипротоны, движущиеся по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но имеют противоположный (отрицательный) заряд. (b) Можно ли получить такую напряженность поля с помощью современных технологий или это футуристическая возможность?
(a) Ион кислорода-16 с массой движется перпендикулярно магнитному полю 1,20 Тл, что заставляет его двигаться по дуге окружности с 0. 231-метровый радиус. Какой положительный заряд на ионе? б) Каково отношение этого заряда к заряду электрона? (c) Обсудите, почему соотношение, найденное в (b), должно быть целым числом.
231-метровый радиус. Какой положительный заряд на ионе? б) Каково отношение этого заряда к заряду электрона? (c) Обсудите, почему соотношение, найденное в (b), должно быть целым числом.
а. б. 3; c. Это отношение должно быть целым числом, потому что заряды должны быть целыми числами основного заряда электрона. Никаких бесплатных сборов со значениями меньше, чем этот базовый сбор, не существует, и все сборы являются целыми числами, кратными этому базовому сбору.
Электрон в телевизионном электронно-лучевой трубке движется со скоростью 1 мс в направлении, перпендикулярном полю Земли, которое имеет напряженность а) электрическое поле какой напряженности должно быть приложено перпендикулярно полю Земли, чтобы электрон двигался по прямой линии? (b) Если это делается между пластинами, разделенными 1.00 см, какое напряжение приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом для защиты от внешних магнитных полей и исключения необходимости в такой коррекции.)
(а) С какой скоростью протон будет двигаться по круговой траектории того же радиуса, что и электрон в предыдущем упражнении? б) Каким был бы радиус пути, если бы протон имел ту же скорость, что и электрон? (c) Каким был бы радиус, если бы протон имел такую же кинетическую энергию, что и электрон? (г) Тот же импульс?
(а) 3.27 x 10 4 м / с (б) 12,525 м (в) 292 м (г) 6,83 м.
(a) Какое напряжение будет ускорять электроны до скорости (b) Найдите радиус кривизны пути протона, ускоренного через этот потенциал в поле 0,500 Тл, и сравните его с радиусом кривизны электрона, ускоренного через такой же потенциал.
Альфа-частица движется по круговой траектории радиусом 25 см в однородном магнитном поле величиной 1,5 Тл. А) Какова скорость частицы? б) Какова кинетическая энергия в электрон-вольтах? (c) Через какую разность потенциалов должна быть ускорена частица, чтобы придать ей эту кинетическую энергию?
Частица с зарядом q и массой m ускоряется из состояния покоя через разность потенциалов V , после чего встречает однородное магнитное поле B . Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?
Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?
Глоссарий
- космические лучи
- состоит из частиц, которые происходят в основном за пределами Солнечной системы и достигают Земли
- винтовой ход
- суперпозиция кругового движения с прямолинейным движением, за которым следует заряженная частица, движущаяся в области магнитного поля под углом к полю
Движение заряженной частицы в магнитном поле
Electric vs.Магнитные силы
И электрические, и магнитные силы влияют на траекторию заряженных частиц, но качественно по-разному.
Цели обучения
Сравните влияние электрического и магнитного полей на заряженную частицу
Ключевые выводы
Ключевые точки
- Сила, действующая на заряженную частицу из-за электрического поля, направлена параллельно вектору электрического поля в случае положительного заряда и антипараллельно в случае отрицательного заряда.Это не зависит от скорости частицы.
- Напротив, магнитная сила, действующая на заряженную частицу, ортогональна вектору магнитного поля и зависит от скорости частицы. Правило правой руки можно использовать для определения направления силы.
- Электрическое поле может действовать на заряженную частицу, в то время как магнитное поле не действует.
- Сила Лоренца — это комбинация электрической и магнитной сил, которые часто рассматриваются вместе в практических приложениях.
- Линии электрического поля генерируются на положительных зарядах и заканчиваются на отрицательных. Силовые линии изолированного заряда направлены прямо радиально наружу. Электрическое поле касается этих линий.
- Силовые линии магнитного поля в случае магнита генерируются на северном полюсе и заканчиваются на южном полюсе. Магнитные полюса не существуют изолированно.
 Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.
Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.
Ключевые термины
- ортогональные : из двух объектов под прямым углом; перпендикулярны друг другу.
Электрические силы против магнитных
Сила, создаваемая как электрическими, так и магнитными силами, будет влиять на движение заряженных частиц. Однако результирующее изменение траектории частиц будет качественно отличаться между двумя силами. Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их влияние на заряженную частицу.
Электростатическая сила и магнитная сила на заряженной частице
Напомним, что в статическом неизменном электрическом поле E сила, действующая на частицу с зарядом q, будет:
[латекс] \ text {F} = \ text {qE} [/ латекс]
Где F, — вектор силы, q — заряд, а E — вектор электрического поля. Обратите внимание, что направление F идентично E в случае позитивистского заряда q и в противоположном направлении в случае отрицательно заряженной частицы.{2}} [/ латекс]
Следует подчеркнуть, что электрическая сила F действует параллельно электрическому полю E . Ротор электрической силы равен нулю, т.е .:
[латекс] \ bigtriangledown \ times \ text {E} = 0 [/ латекс]
Следствием этого является то, что электрическое поле может работать, и заряд в чистом электрическом поле будет следовать по касательной к линии электрического поля.
Напротив, напомним, что магнитная сила, действующая на заряженную частицу, ортогональна магнитному полю, так что:
[латекс] \ text {F} = \ text {qv} \ times \ text {B} = \ text {qvBsin} \ theta [/ latex]
, где B — вектор магнитного поля, v — скорость частицы, а θ — угол между магнитным полем и скоростью частицы. Направление F можно легко определить с помощью правила правой руки.
Направление F можно легко определить с помощью правила правой руки.
Правило правой руки : Магнитные поля действуют на движущиеся заряды. Эта сила — одна из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки – 1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Если скорость частицы выровнена параллельно магнитному полю или равна нулю, магнитная сила будет равна нулю.Это отличается от случая электрического поля, где скорость частицы не имеет никакого отношения в любой данный момент к величине или направлению электрической силы.
Угловая зависимость магнитного поля также заставляет заряженные частицы двигаться перпендикулярно линиям магнитного поля по кругу или по спирали, в то время как частица в электрическом поле будет двигаться по прямой линии вдоль линии электрического поля.
Еще одно различие между магнитными и электрическими силами состоит в том, что магнитные поля не объединяются, , поскольку движение частицы является круговым и, следовательно, заканчивается в одном и том же месте.Мы выражаем это математически как:
[латекс] \ text {W} = \ oint \ text {B} \ cdot \ text {dr} = 0 [/ latex]
Лоренц Форс
Сила Лоренца — это объединенная сила, действующая на заряженную частицу, вызванная как электрическим, так и магнитным полями, которые часто рассматриваются вместе для практических приложений. Если частица с зарядом q движется со скоростью v в присутствии электрического поля E и магнитного поля B , то на нее будет действовать сила:
[латекс] \ text {F} = \ text {q} [\ text {E} + \ text {vBsin} \ theta] [/ latex]
Линии электрического и магнитного поля
Выше мы кратко упомянули, что движение заряженных частиц относительно силовых линий различается в зависимости от того, имеем ли мы дело с электрическими или магнитными полями. Есть некоторые заметные различия между концептуальными представлениями силовых линий электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы представляем себе, что силовые линии тем плотнее упакованы, чем больше заряды. Хорошо видно, что ротор электрической силы равен нулю.
Есть некоторые заметные различия между концептуальными представлениями силовых линий электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы представляем себе, что силовые линии тем плотнее упакованы, чем больше заряды. Хорошо видно, что ротор электрической силы равен нулю.
Электрическое поле, создаваемое точечными зарядами : электрическое поле, окружающее три различных точечных заряда: (а) положительный заряд; (б) отрицательный заряд равной величины; (c) больший отрицательный заряд.
Если задействовано несколько зарядов, силовые линии формируются на положительных зарядах и заканчиваются на отрицательных.
В случае магнитов силовые линии формируются на северном полюсе (+) и заканчиваются на южном полюсе (-) — см. Рисунок ниже.Однако магнитные «заряды» всегда идут парами — магнитных монополей (изолированных северных или южных полюсов) не существует. Вихрь магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться по спирали вокруг этих силовых линий до тех пор, пока частицы имеют ненулевую составляющую скорости, направленную перпендикулярно силовым линиям.
Модель магнитного полюса : Модель магнитного полюса: два противоположных полюса, Северный (+) и Южный (-), разделенные расстоянием d, создают H-поле (линии).
Магнитное поле может также создаваться током, силовые линии которого представляют собой концентрические круги вокруг токоведущего провода. Магнитная сила в любой точке в этом случае может быть определена с помощью правила правой руки, и она будет перпендикулярна обоим. ток и магнитное поле.
При постоянной скорости получается прямая
Если скорость заряженной частицы параллельна магнитному полю, результирующая сила отсутствует и частица движется по прямой линии.
Цели обучения
Определить условия, при которых частица движется по прямой в магнитном поле
Ключевые выводы
Ключевые точки
- Первый закон движения Ньютона гласит, что если объект не испытывает чистой силы, то его скорость постоянна.
- Частица с постоянной скоростью будет двигаться по прямой в пространстве.
- Если скорость заряженной частицы полностью параллельна магнитному полю, магнитное поле не будет оказывать на частицу силы и, таким образом, скорость останется постоянной.
- В случае, если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Ключевые термины
- прямолинейное движение : движение, которое происходит в одном направлении
Постоянная скорость обеспечивает прямолинейное движение
Вспомните первый закон движения Ньютона. Если объект не испытывает чистой силы, то его скорость постоянна: объект либо находится в состоянии покоя (если его скорость равна нулю), либо он движется по прямой с постоянной скоростью (если его скорость отлична от нуля).
Во многих случаях частица может не испытывать чистой силы. Частица могла существовать в вакууме вдали от любых массивных тел (которые проявляют гравитационные силы) и электромагнитных полей. Или на частицу могут действовать две или более силы, уравновешенные таким образом, что результирующая сила равна нулю. Так обстоит дело, скажем, с частицей, подвешенной в электрическом поле, электрическая сила которого точно уравновешивает гравитацию.
Если результирующая сила, действующая на частицу, равна нулю, то ускорение обязательно равно нулю в соответствии со вторым законом Ньютона: F = ma.Если ускорение равно нулю, любая скорость частицы будет поддерживаться бесконечно (или до тех пор, пока результирующая сила не станет равной нулю). Поскольку скорость является вектором, направление остается неизменным вместе со скоростью, поэтому частица движется в одном направлении, например, по прямой.
Заряженные частицы, движущиеся параллельно магнитным полям
Сила, которую заряженная частица «ощущает» из-за магнитного поля, зависит от угла между вектором скорости и вектором магнитного поля B .Напомним, что магнитная сила составляет:
Нулевая сила, когда скорость параллельна магнитному полю : В приведенном выше случае магнитная сила равна нулю, потому что скорость параллельна силовым линиям магнитного поля.
[латекс] \ text {F} = \ text {qvBsin} \ theta [/ latex]
Если магнитное поле и скорость параллельны (или антипараллельны), то sinθ равен нулю и сила отсутствует. В этом случае заряженная частица может продолжать прямолинейное движение даже в сильном магнитном поле.Если находится в диапазоне от 0 до 90 градусов, то составляющая v , параллельная B , остается неизменной.
Круговое движение
Поскольку магнитная сила всегда перпендикулярна скорости заряженной частицы, частица будет совершать круговое движение.
Цели обучения
Опишите условия, которые приводят к круговому движению заряженной частицы в магнитном поле
Ключевые выводы
Ключевые точки
- Магнитное поле не работает, поэтому кинетическая энергия и скорость заряженной частицы в магнитном поле остаются постоянными.{2}} {\ text {r}} [/ latex].
- Решение для r выше дает гриорадиус, или радиус кривизны траектории частицы с зарядом q и массой m, движущейся в магнитном поле с напряженностью B. Тогда гриорадиус определяется как [латекс] \ text {r} = \ frac {\ text {mv}} {\ text {qB}} [/ latex].
- Циклотронная частота (или, что то же самое, гирочастота) — это количество циклов, которые частица совершает вокруг своего кругового цикла каждую секунду, и определяется как [latex] \ text {f} = \ frac {\ text {qB}} {2 \ пи \ текст {м}} [/ латекс].
Ключевые термины
- гирорадиус : Радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.

- циклотронная частота : частота заряженной частицы, движущейся перпендикулярно направлению однородного магнитного поля B (постоянная величина и направление). Дается равенством центростремительной силы и магнитной силы Лоренца.
Круговое движение заряженной частицы в магнитном поле
Магнитные силы могут заставлять заряженные частицы двигаться по круговой или спиральной траектории.Ускорители элементарных частиц удерживают протоны на круговых траекториях с помощью магнитной силы. Космические лучи будут следовать по спирали при встрече с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). На фотографии пузырьковой камеры на рисунке ниже показаны заряженные частицы, движущиеся по таким искривленным траекториям. Изогнутые траектории заряженных частиц в магнитных полях являются основой ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре.показывает путь, пройденный частицами в пузырьковой камере.
Пузырьковая камера : Следы пузырьков создаются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в изображении пузырьковой камеры этим художником. Существует сильное магнитное поле, перпендикулярное странице, которое вызывает искривленные траектории частиц. Радиус пути можно использовать для определения массы, заряда и энергии частицы.
Итак, вызывает ли магнитная сила круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу.Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость. Это типично для равномерного кругового движения. Самый простой случай возникает, когда заряженная частица движется перпендикулярно однородному B-полю, как показано на рисунке. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение. ) Здесь магнитная сила (Лоренц сила) обеспечивает центростремительную силу
) Здесь магнитная сила (Лоренц сила) обеспечивает центростремительную силу
Круговое движение заряженной частицы в магнитном поле : отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиками — как хвосты стрелок) .{2}} {\ text {r}} [/ latex]
решение для r дает
[латекс] \ text {r} = \ frac {\ text {mv}} {\ text {qB}} [/ latex]
Здесь r , называемый гирорадиусом или циклотронным радиусом, представляет собой радиус кривизны пути заряженной частицы с массой м и зарядом q , движущейся со скоростью v перпендикулярно магнитному полю прочность B . Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Компонент скорости, параллельный полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Мы рассмотрим последствия этого случая в следующем разделе, посвященном спиральному движению.
Частица, совершающая круговое движение из-за однородного магнитного поля, называется циклотроном резонанс .Этот термин происходит от названия циклотронного ускорителя частиц, показанного на рисунке. Циклотронная частота (или, что то же самое, гирочастота) — это количество циклов, которые частица совершает вокруг своего кругового контура каждую секунду, и может быть найдена путем решения для v выше и подставив частоту обращения так, чтобы
Циклотрон : Французский циклотрон, произведенный в Цюрихе, Швейцария, в 1937 г.
[латекс] \ text {f} = \ frac {\ text {v}} {2 \ pi \ text {r}} [/ latex]
становится
[латекс] \ text {f} = \ frac {\ text {qB}} {2 \ pi \ text {m}} [/ latex]
Циклотронная частота тривиально выражается в радианах в секунду как
.
[латекс] \ omega = \ frac {\ text {qB}} {\ text {m}} [/ latex].
Спиральное движение
Винтовое движение возникает, когда вектор скорости не перпендикулярен вектору магнитного поля.
Цели обучения
Опишите условия, которые приводят к спиральному движению заряженной частицы в магнитном поле
Ключевые выводы
Ключевые точки
- Ранее мы видели, что круговое движение возникает, когда скорость заряженной частицы перпендикулярна магнитному полю. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.
- Если скорость не перпендикулярна магнитному полю, мы учитываем только компонент v, который перпендикулярен полю при проведении наших вычислений.
- Компонент скорости, параллельный полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Это вызывает спиральное движение.
- Заряды могут двигаться по спирали вдоль силовых линий. Если сила магнитного поля увеличивается в направлении движения, поле будет оказывать силу, замедляющую заряды и даже меняющую их направление.Это называется магнитным зеркалом.
Ключевые термины
- спиральное движение : движение, которое создается, когда один компонент скорости постоянен по величине и направлению (т. Е. Прямолинейное движение), в то время как другой компонент постоянен по скорости, но равномерно изменяется по направлению (т. Е. Круговое движение. ). Это суперпозиция прямолинейного и кругового движения.
- магнитное зеркало : Конфигурация магнитного поля, при которой напряженность поля изменяется при движении вдоль силовой линии.Эффект зеркала приводит к тенденции заряженных частиц отскакивать от области сильного поля.
Спиральное движение
В разделе о круговом движении мы описали движение заряженной частицы с вектором магнитного поля, направленным перпендикулярно скорости частицы.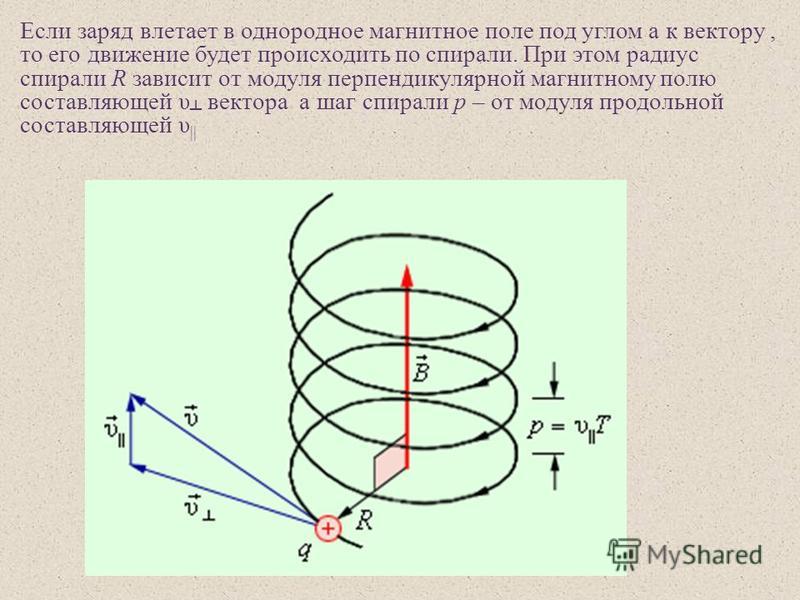 В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой данный момент, что приводит к круговому движению. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.быстро рассматривает эту ситуацию в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой данный момент, что приводит к круговому движению. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.быстро рассматривает эту ситуацию в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
Круговое движение заряженной частицы в магнитном поле : отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиками — как хвосты стрелок) . Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине.2} {\ text {r}} [/ latex]
[латекс] \ text {F} = \ text {qvBsin} \ theta = \ text {qv} _ {\ perp} \ text {B} [/ latex]
Компонент скорости, параллельный полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Это производит спиральное движение (т.е. спиральное движение), а не круговое движение.
показывает, как электроны, движущиеся не перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Компонент скорости, параллельный линиям, не изменяется, поэтому заряды вращаются по спирали вдоль силовых линий.Если напряженность поля увеличивается в направлении движения, поле будет оказывать силу, замедляющую заряды (и даже меняющую их направление), образуя своего рода магнитное зеркало.
Спиральное движение и магнитные зеркала : Когда заряженная частица движется вдоль силовой линии магнитного поля в область, где поле становится сильнее, частица испытывает силу, которая уменьшает составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии и переворачивает его, образуя «магнитное зеркало».«
Движение заряженных частиц в магнитных полях связано с такими разными вещами, как северное сияние или австралийское сияние (северное и южное сияние) и ускорители частиц. Заряженные частицы, приближающиеся к линиям магнитного поля, могут быть захвачены спиральными орбитами вокруг линий, а не пересекать их. , как показано выше. Некоторые космические лучи, например, следуют за линиями магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере.Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются составной частью радиационного фона; следовательно, они дают более высокую дозу излучения на полюсах, чем на экваторе.
Заряженные частицы, приближающиеся к линиям магнитного поля, могут быть захвачены спиральными орбитами вокруг линий, а не пересекать их. , как показано выше. Некоторые космические лучи, например, следуют за линиями магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере.Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются составной частью радиационного фона; следовательно, они дают более высокую дозу излучения на полюсах, чем на экваторе.
Заряженные частицы движутся по спирали вдоль линий магнитного поля Земли : Энергичные электроны и протоны, составляющие космических лучей, исходящие от Солнца и дальнего космоса, часто следуют за линиями магнитного поля Земли, а не пересекают их.(Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом в смысле стержневого магнита.)
Примеры и приложения
Циклотроны, магнетроны и масс-спектрометры представляют собой практические технологические приложения электромагнитных полей.
Цели обучения
Обсудить применение масс-спектрометров, движение заряженных частиц в циклотроне и то, как микроволны генерируются в магнетроне с резонатором.
Ключевые выводы
Ключевые точки
- Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории.Частицы удерживаются на спиральной траектории статическим магнитным полем и ускоряются быстро меняющимся электрическим полем.
- Магнетрон с резонатором представляет собой мощную вакуумную лампу, которая генерирует микроволны, используя взаимодействие потока электронов с магнитным полем. Магнетрон находит применение в радарах, обогреве и освещении.
- Масс-спектрометры измеряют отношение массы к заряду заряженных частиц с помощью электромагнитных полей для разделения частиц с разными массами и / или зарядами.
 Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца.
Ключевые термины
- циклотрон : ускоритель ранних частиц, в котором заряженные частицы генерировались в центральном источнике и ускорялись по спирали наружу посредством фиксированного магнитного и переменного электрического поля.
- масс-спектрометр : устройство, используемое в масс-спектрометрии для определения массового состава данного вещества.
- магнетрон : устройство, в котором электроны заставляют резонировать в камере особой формы и, таким образом, производить микроволновое излучение; используется в радарах и микроволновых печах.
Примеры и приложения — Движение заряженной частицы в магнитном поле
Обзор
Напомним, что заряженные частицы в магнитном поле будут двигаться по круговой или спиральной траектории в зависимости от совмещения их вектора скорости с вектором магнитного поля. Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, включая циклотрон и синхротрон, магнетрон с резонатором и масс-спектрометр.
Циклотроны и синхротроны
Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории. Частицы удерживаются на спиральной траектории статическим магнитным полем и ускоряются быстро меняющимся (радиочастотным) электрическим полем.
Cyclotron Sketch : Рисунок частицы, ускоряемой в циклотроне и выбрасываемой через канал.
Циклотроны ускоряют пучки заряженных частиц с помощью высокочастотного переменного напряжения, которое прикладывают между двумя электродами D-образной формы (также называемыми «деээ»).Дополнительное статическое магнитное поле прикладывается перпендикулярно плоскости электрода, позволяя частицам повторно встречаться с ускоряющим напряжением много раз в одной и той же фазе. Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
[латекс] \ text {f} = \ frac {\ text {qB}} {2 \ pi \ text {m}} [/ latex]
с релятивистской массой м и его зарядом q . Эта частота задается равенством центростремительной силы и магнитной силы Лоренца.Частицы, инжектируемые около центра магнитного поля, увеличивают свою кинетическую энергию только при рециркуляции через зазор между электродами; таким образом, они движутся наружу по спирали. Их радиус будет увеличиваться до тех пор, пока частицы не попадут в цель по периметру вакуумной камеры или не покинут циклотрон с помощью лучевой трубки, что позволит их использовать. Частицы, ускоренные циклотроном, можно использовать в терапии частицами для лечения некоторых типов рака. Кроме того, циклотроны являются хорошим источником пучков высоких энергий для ядерно-физических экспериментов.
Синхротрон является усовершенствованием циклотрона, в котором ведущее магнитное поле (изгибание частиц по замкнутому пути) зависит от времени, синхронизировано с пучком частиц с увеличивающейся кинетической энергией. Синхротрон — одна из первых концепций ускорителей, которые позволяют создавать крупномасштабные объекты, поскольку изгиб, фокусировка пучка и ускорение могут быть разделены на разные компоненты.
Полостной магнетрон
Магнетрон с резонатором представляет собой мощную вакуумную лампу, которая генерирует микроволны, используя взаимодействие потока электронов с магнитным полем.Все магнетроны с резонатором состоят из горячего катода с высоким (непрерывным или импульсным) отрицательным потенциалом, создаваемым высоковольтным источником постоянного тока. Катод встроен в центр вакуумированной лопастной круглой камеры. Магнитное поле, параллельное нити накала, создается постоянным магнитом. Магнитное поле заставляет электроны, притянутые к (относительно) положительной внешней части камеры, двигаться по спирали наружу по круговой траектории, что является следствием силы Лоренца. По краю камеры расположены цилиндрические полости.Полости открыты по своей длине и соединяют общее пространство полости. Когда электроны проходят мимо этих отверстий, они создают резонансное высокочастотное радиополе в полости, которое, в свою очередь, заставляет электроны группироваться в группы.
По краю камеры расположены цилиндрические полости.Полости открыты по своей длине и соединяют общее пространство полости. Когда электроны проходят мимо этих отверстий, они создают резонансное высокочастотное радиополе в полости, которое, в свою очередь, заставляет электроны группироваться в группы.
Схема магнетрона с резонатором : Сечение магнетрона с резонансным резонатором. Магнитные силовые линии параллельны геометрической оси этой конструкции.
Размеры полостей определяют резонансную частоту и, следовательно, частоту излучаемых микроволн.Магнетрон — это автоколебательное устройство, не требующее никаких внешних элементов, кроме источника питания. Магнетрон находит практическое применение в радарах, обогреве (как основной компонент микроволновой печи) и освещении.
Масс-спектрометрия
Масс-спектрометрия — это аналитический метод измерения отношения массы к заряду заряженных частиц. Он используется для определения массы частиц и определения элементного состава образца или молекулы.
Масс-анализаторы разделяют ионы в соответствии с их отношением массы к заряду.Следующие два закона управляют динамикой заряженных частиц в электрическом и магнитном полях в вакууме:
[латекс] \ text {F} = \ text {Q} (\ text {E} + \ text {v} \ times \ text {B}) [/ latex] (сила Лоренца)
[латекс] \ text {F} = \ text {ma} [/ latex]
Приравнивая приведенные выше выражения для силы, приложенной к иону, получаем:
[латекс] (\ text {m} / \ text {Q}) \ text {a} = \ text {E} + \ text {v} \ times \ text {B} [/ latex]
Это дифференциальное уравнение вместе с начальными условиями полностью определяет движение заряженной частицы в терминах m / Q.Есть много типов масс-анализаторов, использующих статические или динамические поля, а также магнитные или электрические поля, но все они работают в соответствии с приведенным выше дифференциальным уравнением.
На следующем рисунке показан один тип масс-спектрометра.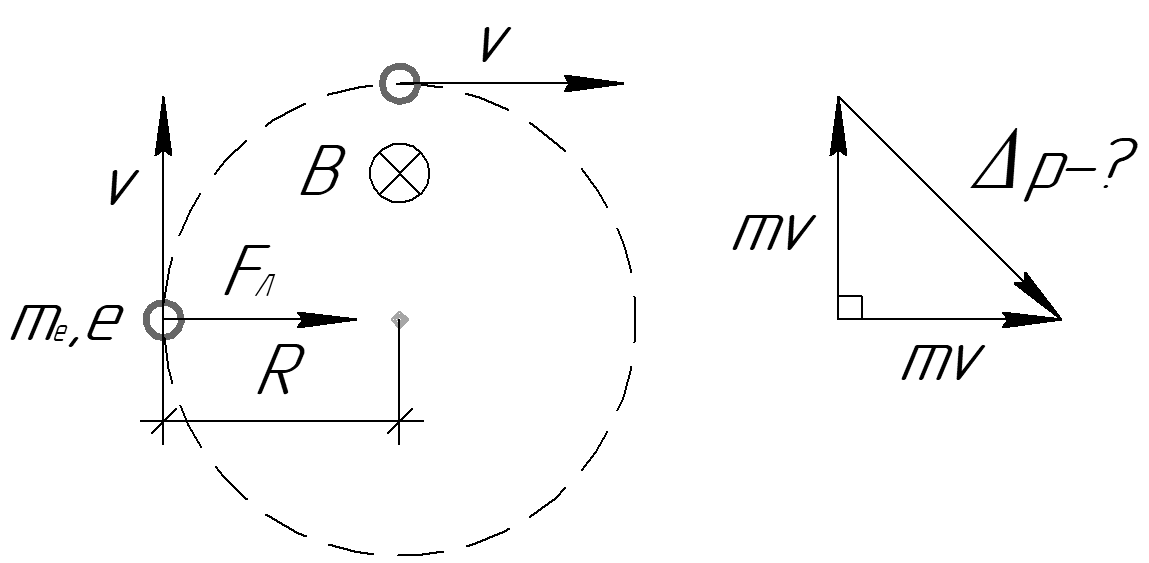 Отклонения частиц зависят от отношения массы к заряду. В случае изотопного диоксида углерода каждая молекула имеет одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы.Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительные содержания могут быть выведены путем подсчета количества частиц каждой данной массы.
Отклонения частиц зависят от отношения массы к заряду. В случае изотопного диоксида углерода каждая молекула имеет одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы.Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительные содержания могут быть выведены путем подсчета количества частиц каждой данной массы.
Масс-спектрометрия : Схема простого масс-спектрометра с масс-анализатором секторного типа. Он предназначен для измерения соотношения изотопов диоксида углерода (IRMS), как в дыхательном тесте с мочевиной углерода-13.
AP Physics 2 — AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
11.3 Движение заряженной частицы в магнитном поле — University Physics Volume 2
Учебные цели
К концу этого раздела вы сможете:
- Объясните, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Опишите, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении через магнитное поле. Что произойдет, если это поле будет однородным при движении заряженной частицы? По какому пути следует частица? В этом разделе мы обсуждаем круговое движение заряженной частицы, а также другое движение, возникающее в результате попадания заряженной частицы в магнитное поле.
Что произойдет, если это поле будет однородным при движении заряженной частицы? По какому пути следует частица? В этом разделе мы обсуждаем круговое движение заряженной частицы, а также другое движение, возникающее в результате попадания заряженной частицы в магнитное поле.
Самый простой случай имеет место, когда заряженная частица движется перпендикулярно однородному полю B (рисунок 11.7). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение.Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица следует по кривой траектории в магнитном поле. Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость.
Рис. 11.7. Отрицательно заряженная частица движется в плоскости бумаги в области, где магнитное поле перпендикулярно бумаге (обозначено маленькими × ··· × — как хвосты стрелок).Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)В этой ситуации магнитная сила создает центростремительную силу Fc = mv2r.Fc = mv2r. Учитывая, что скорость перпендикулярна магнитному полю, величина магнитной силы уменьшается до F = qvB.F = qvB. Поскольку магнитная сила F обеспечивает центростремительную силу Fc, Fc, мы имеем
Решение для r дает
Здесь r — радиус кривизны пути заряженной частицы с массой m и зарядом q , движущейся со скоростью v , перпендикулярной магнитному полю с напряженностью B . Время прохождения заряженной частицы по круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. Основываясь на этом и уравнении 11.4, мы можем получить период движения как
Время прохождения заряженной частицы по круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. Основываясь на этом и уравнении 11.4, мы можем получить период движения как
11,6
Если скорость не перпендикулярна магнитному полю, то мы можем сравнить каждую составляющую скорости отдельно с магнитным полем. Компонент скорости, перпендикулярный магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
vperp = vsinθ, vpara = vcosθ.vperp = vsinθ, vpara = vcosθ.11,7
, где θθ — угол между v и B . Компонент, параллельный магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, что также показано в уравнении 11.7. Параллельное движение определяет шаг p спирали, который представляет собой расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
В результате получается винтообразное движение, как показано на следующем рисунке.
Рис. 11.8 Заряженная частица движется со скоростью, отличной от направления магнитного поля. Компонента скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой. Шаг — это расстояние по горизонтали между двумя последовательными кругами. Результирующее движение — спиральное.
Пока заряженная частица движется по спирали, она может попасть в область, где магнитное поле неоднородно.В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля. Частица может отразиться до того, как войдет в область с более сильным магнитным полем. Это похоже на волну на струне, которая движется от очень легкой тонкой струны к твердой стене и отражается назад. Если отражение происходит с обоих концов, частица оказывается в так называемой магнитной бутылке.
Если отражение происходит с обоих концов, частица оказывается в так называемой магнитной бутылке.
Захваченные частицы в магнитных полях обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли.Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (частицы высокой энергии, приходящие извне Солнечной системы), чтобы выяснить, похож ли он на поток, измеренный на Земле. Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в космическом пространстве. Полярные сияния, как и знаменитое полярное сияние (северное сияние) в Северном полушарии (рис. 11.9), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, входящими в атмосферу, когда они движутся по спирали вдоль силовых линий магнитного поля.(Ионы — это в основном атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
Рис. 11.9 (a) Радиационные пояса Ван Аллена вокруг Земли захватывают ионы, произведенные космическими лучами, падающими на атмосферу Земли. (b) Великолепное зрелище северного сияния, или северного сияния, сияет в северном небе над Беар-Лейк недалеко от базы ВВС Эйлсон, Аляска.Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота. (кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
Пример 11.2
Дефлектор луча
Группа исследователей занимается изучением короткоживущих радиоактивных изотопов. Им необходимо разработать способ транспортировки альфа-частиц (ядер гелия) от места их создания к месту, где они столкнутся с другим материалом с образованием изотопа. Пучок альфа-частиц (m = 6.64 · 10−27 кг, q = 3,2 · 10−19C) (m = 6,64 · 10−27 кг, q = 3,2 · 10−19C) изгибается через 90-градусную область с однородным магнитным полем 0,050 Тл (рисунок 11. 10) . а) В каком направлении следует приложить магнитное поле? (б) Сколько времени требуется альфа-частицам, чтобы пройти через область однородного магнитного поля?
10) . а) В каком направлении следует приложить магнитное поле? (б) Сколько времени требуется альфа-частицам, чтобы пройти через область однородного магнитного поля?Рисунок 11.10 Вид сверху на установку дефлектора балки.
Стратегия
- Направление магнитного поля показано RHR-1. Ваши пальцы указывают в направлении v , а большой палец должен указывать в направлении силы, влево.Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно указывать вниз.
- Период движения альфа-частицы по окружности
Поскольку частица движется только по четверти круга, мы можем взять 0,25-кратный период, чтобы найти время, необходимое для обхода этого пути.
Раствор
- Давайте начнем с фокусировки на альфа-частице, входящей в поле в нижней части изображения. Сначала покажите пальцем вверх по странице.Чтобы ваша ладонь открывалась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны менять ориентацию, пока они не будут указывать на страницу. Это направление приложенного магнитного поля.
- Период движения заряженной частицы по кругу вычисляется с использованием заданных в задаче массы, заряда и магнитного поля. Это оказывается T = 2πmqB = 2π (6,64 · 10−27 кг) (3,2 · 10−19C) (0,050T) = 2,6 · 10−6s.T = 2πmqB = 2π (6,64 · 10−27 кг) (3,2 · 10−19C) ( 0.050T) = 2,6 × 10-6 с. Однако для данной задачи альфа-частица проходит четверть круга, поэтому время, необходимое для этого, будет равно t = 0,25 × 2,61 × 10–6 с = 6,5 × 10–7 с. t = 0,25 × 2,61 × 10–6 с = 6,5 × 10–7 с.
Значение
Это время может быть достаточно быстрым, чтобы добраться до материала, который мы хотели бы бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп и продолжает испускать альфа-частицы. Если бы мы могли усилить магнитное поле, приложенное к области, это сократило бы время еще больше.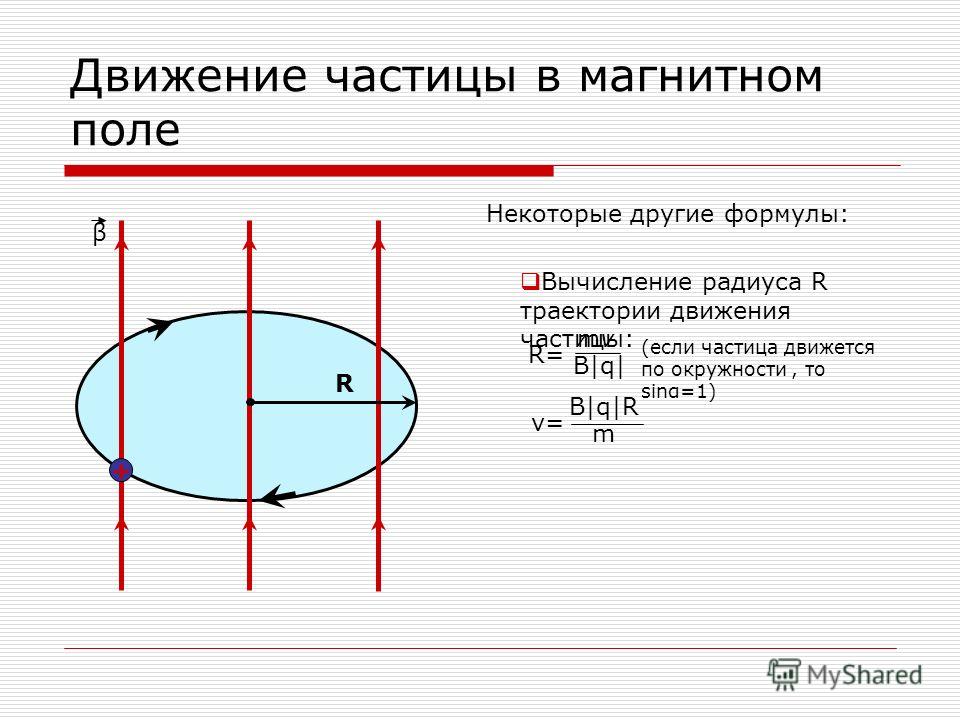 Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.Проверьте свое понимание 11,2
Однородное магнитное поле величиной 1,5 Тл направлено горизонтально с запада на восток. (а) Какая магнитная сила действует на протон в момент, когда он движется вертикально вниз в поле со скоростью 4 × 107 м / с? 4 × 107 м / с? (b) Сравните эту силу с массой протона w .
Пример 11.3
Движение по спирали в магнитном поле
Протон входит в однородное магнитное поле 1.0 × 10–4T1.0 × 10–4T со скоростью 5 × 105 м / с и 5 × 105 м / с. Под каким углом должно быть магнитное поле относительно скорости, чтобы шаг результирующего спирального движения был равен радиусу спирали?Стратегия
Шаг движения относится к параллельной скорости, умноженной на период кругового движения, тогда как радиус относится к перпендикулярной составляющей скорости. После установки равных друг другу радиуса и шага найдите угол между магнитным полем и скоростью или θ.θ.Решение
Шаг задается уравнением 11.8, период — уравнением 11.6, а радиус кругового движения — уравнением 11.5. Обратите внимание, что скорость в уравнении радиуса связана только с перпендикулярной скоростью, в которой происходит круговое движение. Поэтому мы подставляем синусоидальную составляющую общей скорости в уравнение радиуса, чтобы приравнять шаг и радиус: p = rv∥T = mv⊥qBvcosθ2πmqB = mvsinθqB2π = tanθθ = 81,0 °. p = rv∥T = mv⊥qBvcosθ2πmqB = mvsinθqB2π = tanθθ = 81.0 °.Значение
Если бы этот угол был 0 °, 0 °, была бы только параллельная скорость, и спираль не образовалась бы, потому что не было бы кругового движения в перпендикулярной плоскости. Если бы этот угол был 90 °, 90 °, было бы только круговое движение, и не было бы движения кругов, перпендикулярных движению. Это то, что создает спиральное движение.
электромагнетизм — Движение электрона, ускоряющегося в однородном магнитном поле
Весь вопрос сформулирован прекрасно, но позвольте мне все же пересмотреть эти формулировки.
Насколько мне известно, когда электроны движутся перпендикулярно однородному магнитному полю, сила Лоренца заставляет электрон совершать круговое движение.
Сила Лоренца — это выражение наблюдаемого явления, когда движущиеся заряды отклоняются под действием магнитного поля (движутся или не по отношению к заряду, но обязательно не параллельно траектории заряда). Сила Лоренца является результатом отклонения зарядов магнитными полями, а не причиной отклонения.
Такой подход приводит нас к вопросу, как взаимодействуют магнитное поле и движущийся заряд. С вашим следующим предложением вы близки. Вы подробно описываете, что происходит во взаимодействии.
Когда этот электрон совершает круговое движение, он испускает электромагнитное излучение, поэтому он движется по спиральной траектории с непрерывно уменьшающимся радиусом орбиты.
Помимо электрического заряда у электрона есть собственное магнитное поле. Электроны — магнитные диполи. Теперь взаимодействие между прибывающими электронами и внешним магнитным полем происходит естественным образом. Внешнее поле выравнивает эти диполи параллельно своему собственному полю.
Неопределенность в описании того, что вызывает силу Лоренца (отклонение зарядов), заключается в следующем.
Вызывает ли выравнивание магнитного диполя электрона его отклонение (эффект гироскопа), а боковое ускорение вызывает испускание фотона?
Или выравнивание магнитного диполя электрона вызывает испускание фотона, и электрон отклоняется его моментом отдачи?
В любом случае связь между испусканием фотона и потерей кинетической энергии очевидна.
Поскольку этот электрон испускает электромагнитное излучение, его энергия должна уменьшаться.
\ circ $, либо под углом $ \ theta $.В первом случае его путь приводит к круговой траектории, а во втором случае образуется спиральная траектория.
Теперь мы хотим ответить на этот вопрос: почему заряженные частицы движутся по спирали?
Как только заряженная частица входит в магнитное поле $ B $ под некоторым углом $ \ theta $, ее скорость можно разложить на параллельную и вертикальную составляющие относительно $ \ vec {B} $, которые равны $ v _ {\ parallel} = v \, \ cos \ theta $ и $ v _ {\ bot} = v \, \ sin \ theta $.
Однородное магнитное поле $ B $ не прикладывает никакой силы к заряженной частице (скажем, электрону) в параллельном направлении, равном $ F _ {\ parallel} = q \, v _ {\ parallel} \, B \ sin 0 = 0 $.{\ circ} = q \, v _ {\ bot} \, B $, что заставляет заряженную частицу равномерно двигаться по круговой траектории.
Эти два вышеуказанных движения, равномерное движение, параллельное полю $ B $ и равномерное круговое движение, перпендикулярное полю $ B $, создают фактический путь заряженной частицы в однородном магнитном поле $ B $, которое похоже на пружину и называется спиральной или винтовой.
Характеристики винтовой траектории:
Каждая спиральная траектория имеет три различных характеристики: радиус, период времени и шаг.{2}} R \\ \\ \ Rightarrow R & = \ frac {m \, v _ {\ bot}} {q \, B} \\ \\ & = \ frac {mv \, \ sin \ theta} {qB } \ end {align *} Где $ m $ — масса заряженной частицы.
Период времени: Время, необходимое для совершения одного оборота, получается путем определения средней скорости как \ begin {align *} v & = \ frac {\ Delta x} {\ Delta t} \\ \\ v _ {\ bot} & = \ frac {2 \ pi \, R} {T} \\ \\ \ Rightarrow T & = \ frac {2 \ pi \, R} {v _ {\ bot}} \\ \\ & = \ frac {2 \ pi} {q \, B} \, m \ end {align *}, где выше мы использовали предыдущую формулу для $ R $ и $ v _ {\ bot} = v \, \ sin \ theta $.Этот период также называется циклотронным периодом, а его частота является обратной величине периода по формуле \ [f = \ frac 1T = \ frac {q \, B} {2 \ pi \, m} \]
Шаг спирали: расстояние, пройденное параллельно магнитному полю $ B $ за один оборот, называется шагом спиральной траектории и получается как \ begin {align *} p & = v _ {\ parallel} \, T \\ & = (v \, \ cos \ theta) \, \ left (\ frac {2 \ pi \, m} {q \, B} \ right) \ end {align *} Таким образом, формула для шага спираль — $ p = \ frac {2 \ pi \, mv \, \ cos \ theta} {q \, B} $.
{\ circ} $ создается круговое движение.
Если скорость частицы имеет компоненты, параллельные и перпендикулярные однородному магнитному полю, то она движется по спирали. В параллельном случае сила на частицу отсутствует, а в перпендикулярном — центростремительное ускорение к центру. Последнее обновление: 02.09.2020
8.3 Движение заряженной частицы в магнитном поле — Введение в электричество, магнетизм и электрические схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Опишите, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении через магнитное поле.Что произойдет, если это поле будет однородным при движении заряженной частицы? По какому пути следует частица? В этом разделе мы обсуждаем круговое движение заряженной частицы, а также другое движение, возникающее в результате попадания заряженной частицы в магнитное поле.
Самый простой случай возникает, когда заряженная частица движется перпендикулярно однородному полю (рис. 8.3.1). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица следует по кривой траектории в магнитном поле.Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость.
(рисунок 8.3.1)
Рис. 8.3.1 Отрицательно заряженная частица движется в плоскости бумаги в области, где магнитное поле перпендикулярно бумаге (обозначено маленькой буквой s — как хвосты стрелок).Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)
В этой ситуации магнитная сила обеспечивает центростремительную силу. Учитывая, что скорость перпендикулярна магнитному полю, величина магнитной силы уменьшается до. Поскольку магнитная сила обеспечивает центростремительную силу, мы имеем
(8.3.1)
Решение для урожайности
(8.3.2)
Здесь — радиус кривизны пути заряженной частицы с массой и зарядом, движущейся со скоростью, перпендикулярной напряженности магнитного поля. Время прохождения заряженной частицы по круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. На основании этого и 8.3.1 мы можем получить период движения как
.(8.3.3)
Если скорость не перпендикулярна магнитному полю, то мы можем сравнить каждую составляющую скорости отдельно с магнитным полем. Компонент скорости, перпендикулярный магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
(8.3.4)
где — угол между и. Компонент, параллельный магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, также показанное на 8.3.4. Параллельное движение определяет шаг и спирали, то есть расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
(8.3.5)
В результате получается спиральное движение , как показано на следующем рисунке.
(рисунок 8.3.2)
Рис. 8.3.2 Заряженная частица движется со скоростью, отличной от направления магнитного поля. Компонента скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой.Шаг — это расстояние по горизонтали между двумя последовательными кругами. Результирующее движение — спиральное.
Пока заряженная частица движется по спирали, она может попасть в область, где магнитное поле неоднородно. В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля. Частица может отразиться до того, как войдет в область с более сильным магнитным полем. Это похоже на волну на струне, которая движется от очень легкой тонкой струны к твердой стене и отражается назад.Если отражение происходит с обоих концов, частица оказывается в так называемой магнитной бутылке.
Захваченные частицы в магнитных полях обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли. Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (частицы высокой энергии, приходящие извне Солнечной системы), чтобы увидеть, похож ли он на поток, измеренный на Земле.Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в космическом пространстве. Aurorae , как и знаменитое полярное сияние (северное сияние) в северном полушарии (рис. 8.3.3), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, входящими в атмосферу, когда они движутся по спирали вдоль силовых линий магнитного поля. (Ионы — это в основном атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния наблюдались также на других планетах, таких как Юпитер и Сатурн.
(рисунок 8.3.3)
Рис. 8.3.3 (a) Радиационные пояса Ван Аллена вокруг Земли захватывают ионы, произведенные космическими лучами, падающими на атмосферу Земли. (b) Великолепное зрелище северного сияния, или северного сияния, сияет в северном небе над Беар-Лейк недалеко от базы ВВС Эйлсон, Аляска.Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота.(кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
ПРИМЕР 8.3.1
Дефлектор луча
Группа исследователей занимается изучением короткоживущих радиоактивных изотопов. Им необходимо разработать способ транспортировки альфа-частиц (ядер гелия) от места их создания к месту, где они столкнутся с другим материалом с образованием изотопа. Луч альфа-частиц изгибается через область градусов с однородным магнитным полем (рис. 8.3.4). а) В каком направлении следует приложить магнитное поле? (б) Сколько времени требуется альфа-частицам, чтобы пройти через область однородного магнитного поля?
(рисунок 8.3,4)
Рисунок 8.3.4. Вид сверху на установку дефлектора балки.Стратегия
а. Направление магнитного поля показано RHR-1. Ваши пальцы указывают в направлении, а большой палец должен указывать в направлении силы, влево. Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно указывать вниз.
г. Период движения альфа-частицы по окружности
.(8.3.6)
Поскольку частица движется только по четверти круга, мы можем умножить этот период, чтобы найти время, необходимое для обхода этого пути.Решение
а. Начнем с того, что сфокусируемся на альфа-частице, входящей в поле в нижней части изображения. Сначала покажите пальцем вверх по странице. Чтобы ваша ладонь открывалась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны менять ориентацию, пока они не будут указывать на страницу. Это направление приложенного магнитного поля.
г. Период движения заряженной частицы по кругу рассчитывается с использованием заданных в задаче массы, заряда и магнитного поля.Получается
.Однако для данной задачи альфа-частица обходит четверть круга, поэтому время, необходимое для этого, составит
.Значение
Это время может быть достаточно быстрым, чтобы добраться до материала, который мы хотели бы бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп и продолжает испускать альфа-частицы. Если бы мы могли усилить магнитное поле, приложенное к области, это сократило бы время еще больше.Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
ПРОВЕРЬТЕ ПОНИМАНИЕ 8.2
Однородное магнитное поле магнитуды направлено горизонтально с запада на восток. (а) Какая магнитная сила действует на протон в момент, когда он движется вертикально вниз в поле со скоростью? б) Сравните эту силу с весом протона.
ПРИМЕР 8.3.2
Движение по спирали в магнитном поле
Протон входит в однородное магнитное поле со скоростью.Под каким углом должно быть магнитное поле относительно скорости, чтобы шаг результирующего спирального движения был равен радиусу спирали?
Стратегия
Шаг движения относится к параллельной скорости, умноженной на период кругового движения, тогда как радиус относится к перпендикулярной составляющей скорости. После установки равных друг другу радиуса и шага найдите угол между магнитным полем и скоростью или.
Решение
Шаг задается уравнением 8.3.5 период определяется уравнением 8.3.3, а радиус кругового движения задается уравнением 8.3.2. Обратите внимание, что скорость в уравнении радиуса связана только с перпендикулярной скоростью, в которой происходит круговое движение. Поэтому мы подставляем синусоидальную составляющую общей скорости в уравнение радиуса, чтобы приравнять шаг и радиус:
Значение
Если бы этот угол был, то имела бы только параллельная скорость и спираль не образовывалась бы, потому что не было бы кругового движения в перпендикулярной плоскости.Если бы этот угол был, то было бы только круговое движение, и не было бы движения кругов, перпендикулярных движению.


 Это направление приложенного магнитного поля.
Это направление приложенного магнитного поля. Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.
Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.
 Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца. \ circ $, либо под углом $ \ theta $.В первом случае его путь приводит к круговой траектории, а во втором случае образуется спиральная траектория.
\ circ $, либо под углом $ \ theta $.В первом случае его путь приводит к круговой траектории, а во втором случае образуется спиральная траектория.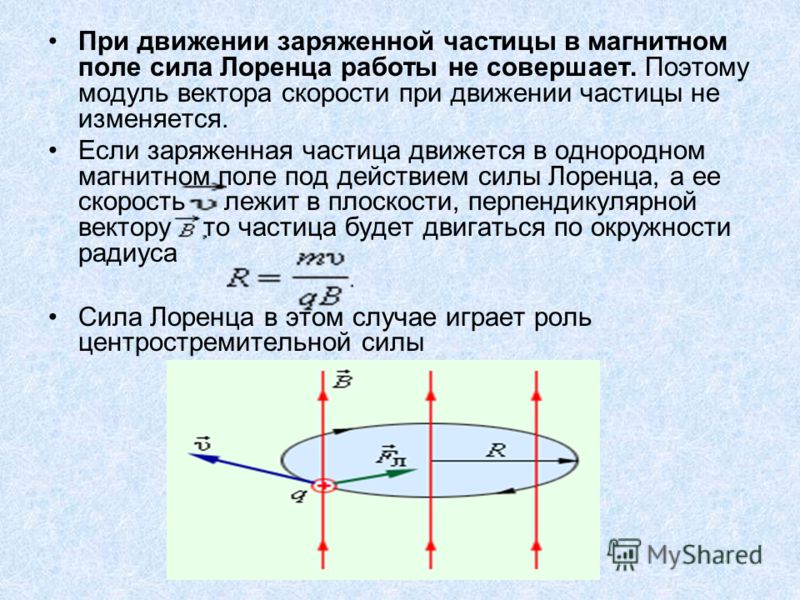 {\ circ} $ создается круговое движение.
{\ circ} $ создается круговое движение. Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)
Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.) Шаг — это расстояние по горизонтали между двумя последовательными кругами. Результирующее движение — спиральное.
Шаг — это расстояние по горизонтали между двумя последовательными кругами. Результирующее движение — спиральное.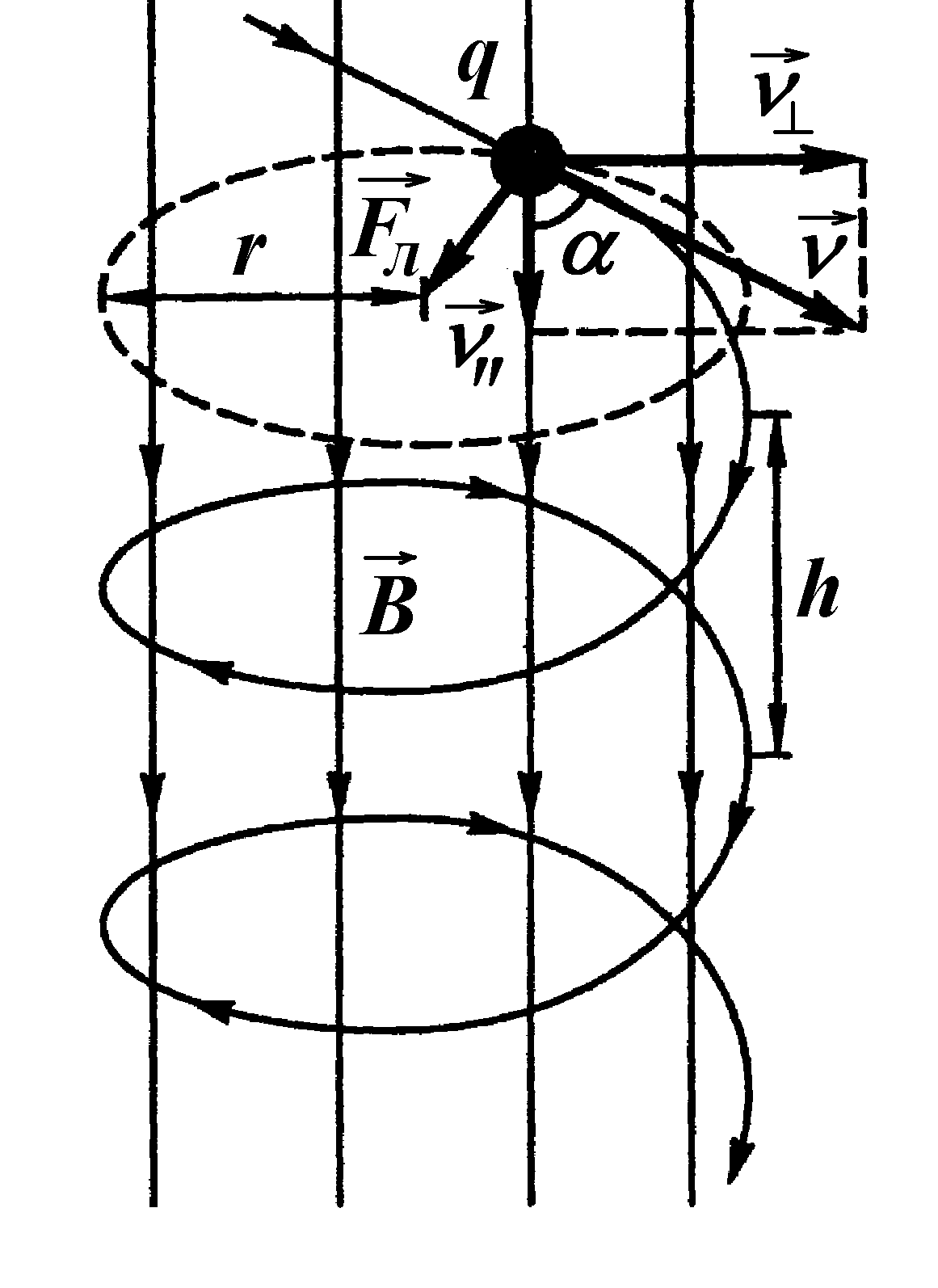 Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота.(кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота.(кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
.jpg)
Leave A Comment