Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математикеГеометрия (Планиметрия)Треугольники

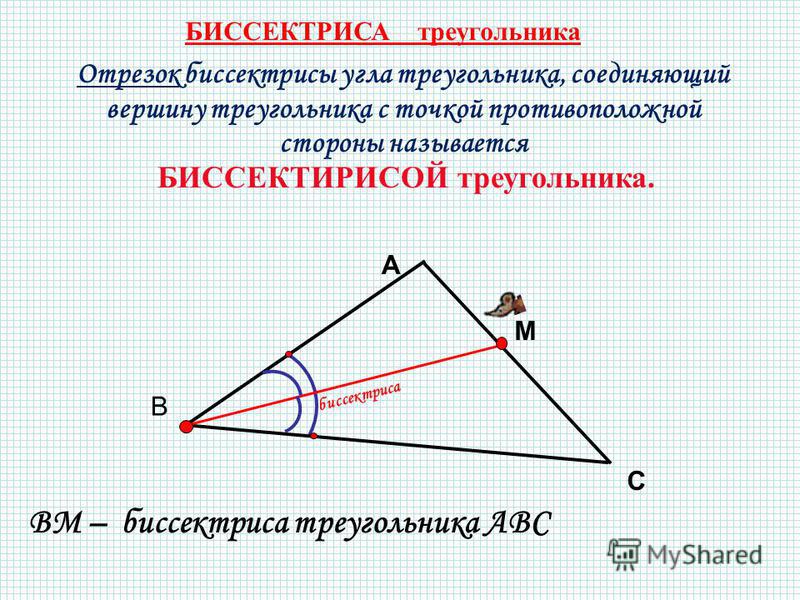
      Напомним, что биссектрисой угла называют луч, делящий угол пополам.

      Определение. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).

Рис.1

      Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.

      На рисунке 1 биссектрисой является отрезок AD.

      Теорема 1. Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

      Доказательство. Продолжим сторону AC треугольника ABC, изображенного на рисунке 1, за точку A. Проведем через точку B прямую, параллельную биссектрисе AD. Обозначим точку пересечения построенных прямых буквой E (рис. 2).

Рис.2

      Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD, поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD. Заметим также, что угол BEA равен углу DAC, поскольку эти углы являются соответственными при параллельных прямых EB и AD. Таким образом, угол EBA равен углу BEA, откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.

      Отсюда, воспользовавшись теоремой Фалеса, получаем:

что и требовалось доказать.

      Следствие 1. Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения

Рис.3

b = |AC|,   a = |BC|,   c = |AB|,   p = |BD|,   q = |DC|.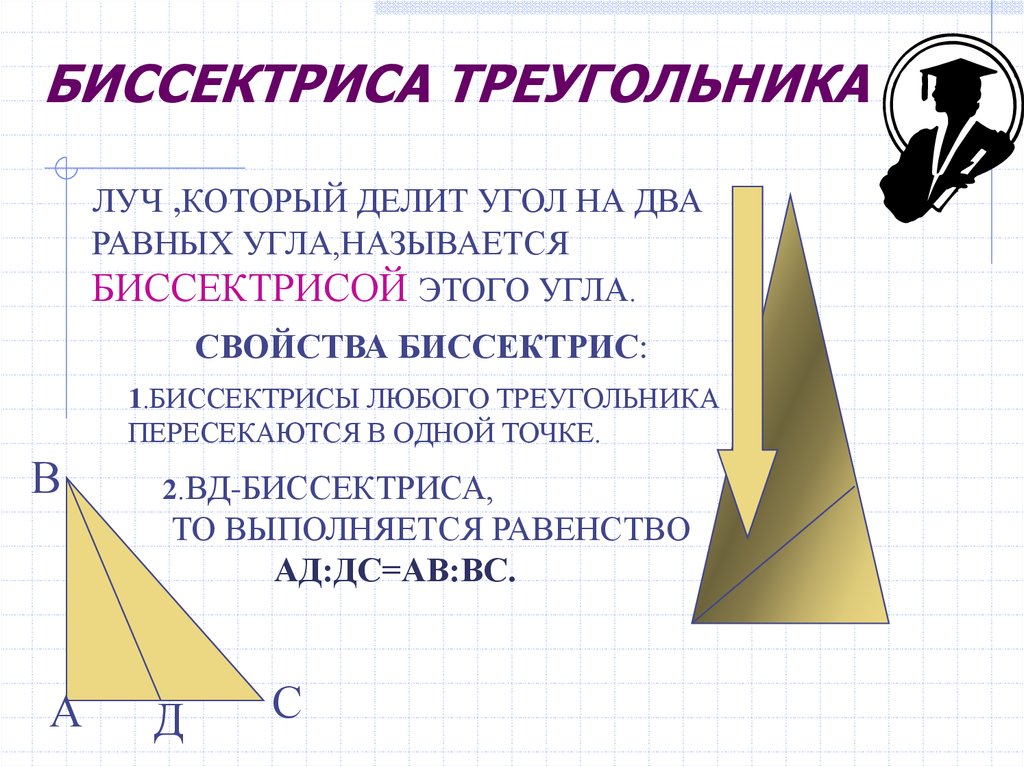

      Тогда

      Доказательство. Поскольку

то

что и требовалось доказать.

      Следствие 2. Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O.

Рис.4

      Тогда справедлива формула:

      Доказательство. Поскольку

то

что и требовалось доказать.

      Замечание. В любом треугольнике все три биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

      Теорема 2. Рассмотрим рисунок 5, который практически совпадает с рисунком 2.

Рис.5

      Тогда для длины биссектрисы справедлива формула:

      Доказательство. Из рисунка 5 следует формула

|EB| = 2c cos α .

      Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC, получаем:

что и требовалось доказать.

      Теорема 3. Длину биссектрисы треугольника (рис.6) можно найти по формуле:

      Доказательство. Рассмотрим рисунок 6

Рис.6

и воспользуемся теоремой косинусов:

      Теперь воспользуемся формулой «Косинус двойного угла»:

      Следовательно,

откуда с помощью Теоремы 2 получаем:

что и требовалось доказать.

      Задача. Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высотаCE.

Рис.7

Доказать, что выполнено равенство:

      Решение.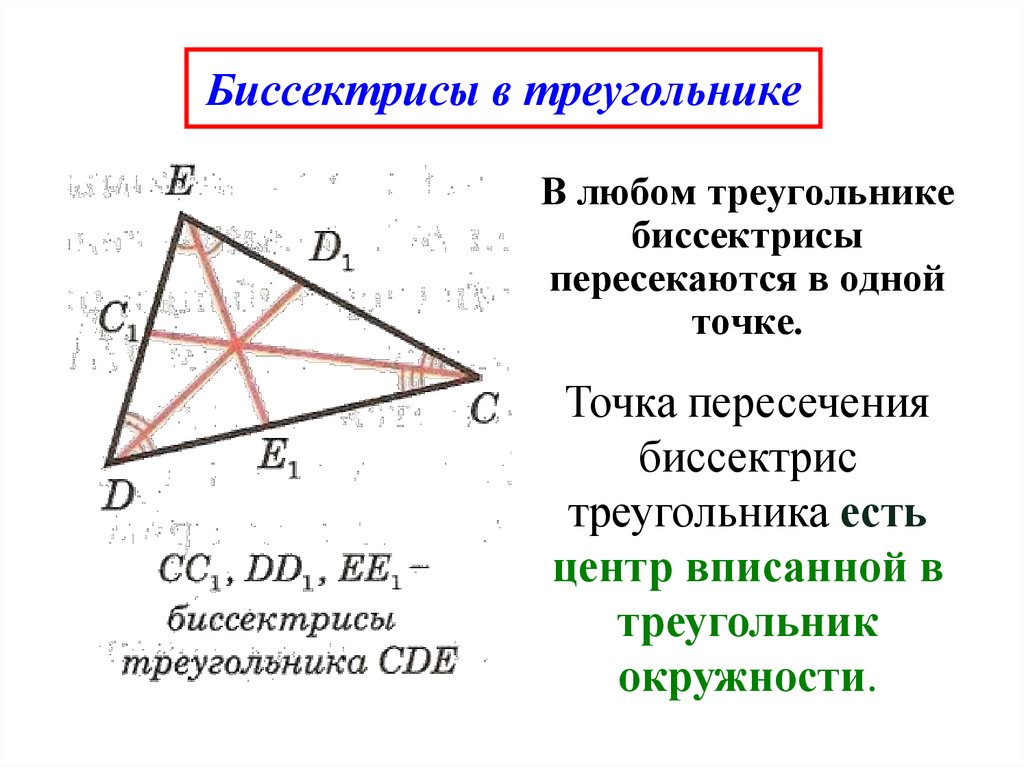 Поскольку CD – биссектриса угла ACB, то

      Поскольку CE – высота, то

      Следовательно,

что и требовалось доказать.

      Из решения этой задачи вытекает простое следствие.

      Следствие. Длины биссектрисы CD и высоты CE связаны следующей формулой:

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

свойства, доказательство, признаки и формулы

Что такое биссектриса треугольника — определение

Определение 1

Биссектриса угла — это луч, делящий угол пополам.

Определение 2

Биссектриса треугольника — это отрезок, который является частью биссектрисы угла треугольника и соединяет вершину треугольника с точкой на противоположной стороне.

Так как в треугольнике три угла, можно провести три биссектрисы.

Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Свойства биссектрисы

1. Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон.

2. Точка пересечения трех внутренних биссектрис любого треугольника является центром вписанной окружности.

3. Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону.

4. Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле:

5. Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

Доказательство теоремы

Теорема 1

Биссектриса при вершине треугольника делит противоположную сторону на два отрезки, пропорциональные сторонам, прилежащим к данной вершине.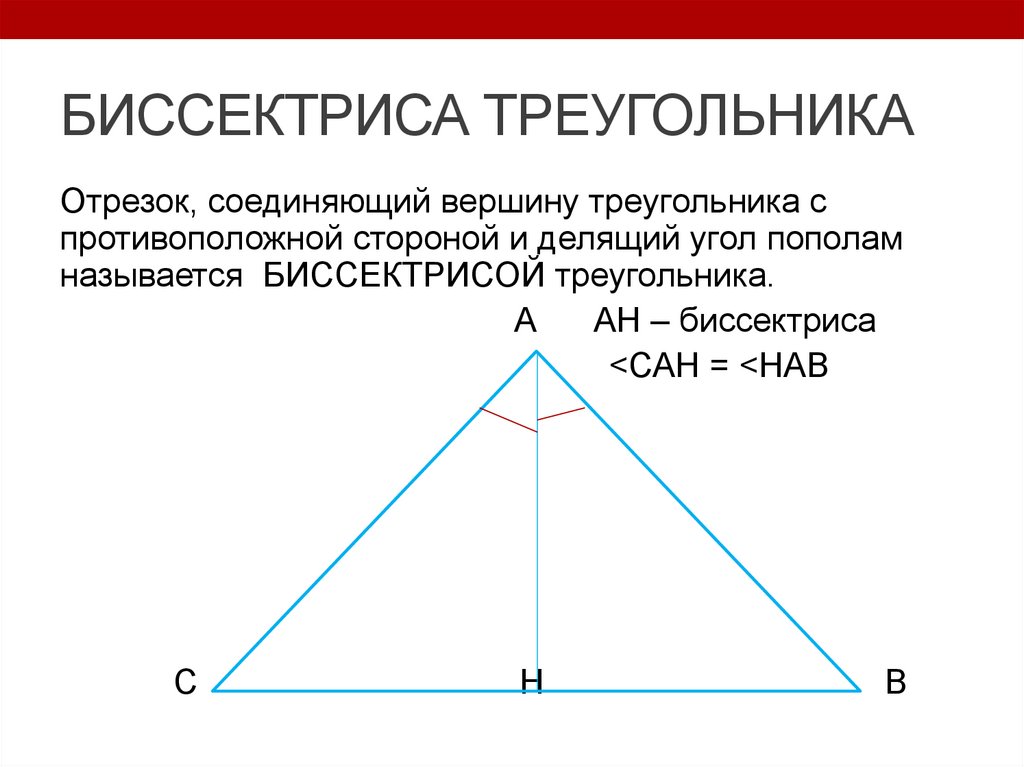

Доказательство через метод площадей

Из вершины A опущена биссектриса AD. Построим высоту треугольника AH. Найдем площади треугольников ABD и ACD:

S(ABD)=AH*BD/2

S(ACD)=AH*DC/2

S(ABD)/S(ACD)=(AH*BD/2)/(AH*DC/2)=BD/DC

С другой стороны, площадь треугольников можно найти по формулам:

S(ABD)=AB*AD*sinα/2

S(ACD)=AD*AC*sinα/2

S(ABD)/S(ACD)=(AB*AD*sinα/2)/(AD*AC*sinα/2)=AB/AC ⇒

BD/DC=AB/AC.

Доказательство через теорему синусов

Из вершины A в треугольнике ABC проведем биссектрису AD.

По теореме синусов для треугольников ABD и ACD:

AB/sin(180-δ)=BD/sinα

AC/sinδ=CD/sinα

(AB/sin(180-δ))/(AC/sinδ)=(BD/sinα)/(CD/sinα) ⇒

AB/AC=BD/DC.

Доказательство через подобие треугольников

Из вершины A в треугольнике ABC проведем биссектрису AD.

Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения L и K.

Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (∠ALB=∠AKC, ∠BAL=∠CAK). Тогда:

AB/AC=BL/CK

Треугольники BLD и CKD подобны, так как ∠BLD=∠CKD, а углы BDL и CDK равны как вертикальные. Тогда:

BD/CD=BL/CK ⇒

AB/AC=BD/DC.

Прямая и обратная теорема о свойстве биссектрисы угла

Теорема 2

Каждая точка биссектрисы неразвернутого угла равноудалена от сторон угла, то есть расстояния от точки М до АС и до ВС (сторон угла) равны.

Задан угол ∠BAC , AL — его биссектриса, точка М лежит на биссектрисе.

Доказать, что MK=MP.

Доказательство:

Расстояние от точки до прямой — это длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.

Треугольники AMK и AMP — прямоугольные. Они равны, так как имеют общую гипотенузу АМ, а углы ∠KAM  и ∠PAM  равны, так как AL — биссектриса угла ∠BAC.

Таким образом, прямоугольные треугольники равны по гипотенузе и острому углу, отсюда следует, что MK=MP=d.

Следовательно, точка на биссектрисе угла равноудалена от сторон этого угла.

Обратная теорема: если точка равноудалена от сторон неразвернутого угла, то она лежит на его биссектрисе.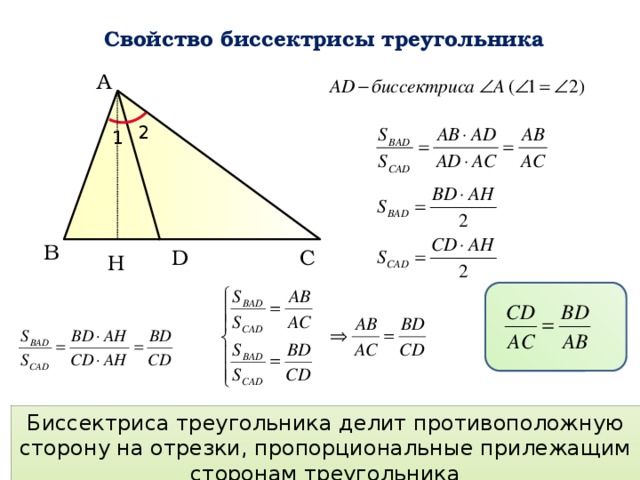

Задан неразвернутый угол BAC, точка М равноудалена от сторон угла.

Доказать, что точка М лежит на биссектрисе угла.

Доказательство:

Расстояние от точки до прямой — это длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.

Треугольники AMK и AMP — прямоугольные. Они равны, так как имеют общую гипотенузу АМ, катеты МК и МР равны по условию.

Таким образом, прямоугольные треугольники равны по гипотенузе и катету.

Из равенства треугольников следует равенство соответствующих элементов: против равных катетов лежат равные углы — значит, ∠KAM=∠PAM.

Следовательно, точка М лежит на биссектрисе данного угла.

Примеры решения задач

Задача 1

Даны стороны треугольника ABC :AB=16, AC=4, BC=18 . Найти отрезки, полученные делением биссектрисой большой стороны треугольника.

Решение:

Так как напротив большей стороны треугольника находится вершина A, то биссектриса AD делит сторону BC на отрезки BD и CD.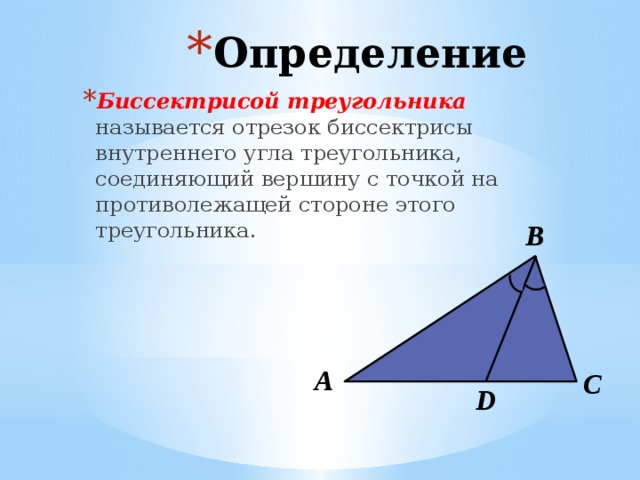 Тогда:

AB/AC=BD/CD

Обозначим BD=x. Тогда CD=BC−x=18−x. Подставим данные:

16/4=x/(18−x)

4=x/(18−x)

x=4(18−x)

x=72-4x

5x=72

x=14,4=BD

CD=BC−x=18−x=18-14,4=3,6.

Ответ:14,4 ; 3,6.

Задача 2

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найти длину биссектрисы, проведенной к гипотенузе.

Решение:

По теореме Пифагора:

BC2 = AB2 + AC2 = 62 + 82 = 100.

BC = 10 см.

По свойству 1 составляем пропорцию, приняв отрезок BD на гипотенузе за a (тогда DC =10-a):

BD/DC=AB/AC

a/(10-a)=6/8

8a=60-6a

14a=60

a≈4

BD=4, DC =10-a=10-4=6.

По свойству 4 вычислим длину биссектрисы:

AD2 = AB*AC – BD*DC =6*8-4*6=24

AD≈4,9.

Ответ: 4,9 см.

Теорема о биссектрисе угла — Доказательство, Обратное, Формула, Примеры

Теорема о биссектрисе угла утверждает, что биссектриса угла треугольника делит противоположную сторону на два отрезка, которые пропорциональны двум другим сторонам треугольника. Биссектриса угла — это луч, который делит данный угол на два угла равной величины. Давайте узнаем больше о теореме биссектрисы угла в этой статье.

о биссектрисах угла
1. Что такое теорема о биссектрисе угла?
2. Доказательство теоремы о биссектрисе
3. Теорема, обратная теореме о биссектрисе угла
4. Формула теоремы о биссектрисе угла
5. Часто задаваемые вопросы по теореме

Что такое теорема о биссектрисе угла?

Теорема о биссектрисе угла треугольника утверждает, что в треугольнике биссектриса любого угла будет делить противоположную сторону в отношении сторон, содержащих этот угол. Рассмотрим рисунок ниже:

Здесь PS — биссектриса ∠P. Согласно теореме о биссектрисе угла , PQ/PR = QS/RS или a/b = x/y.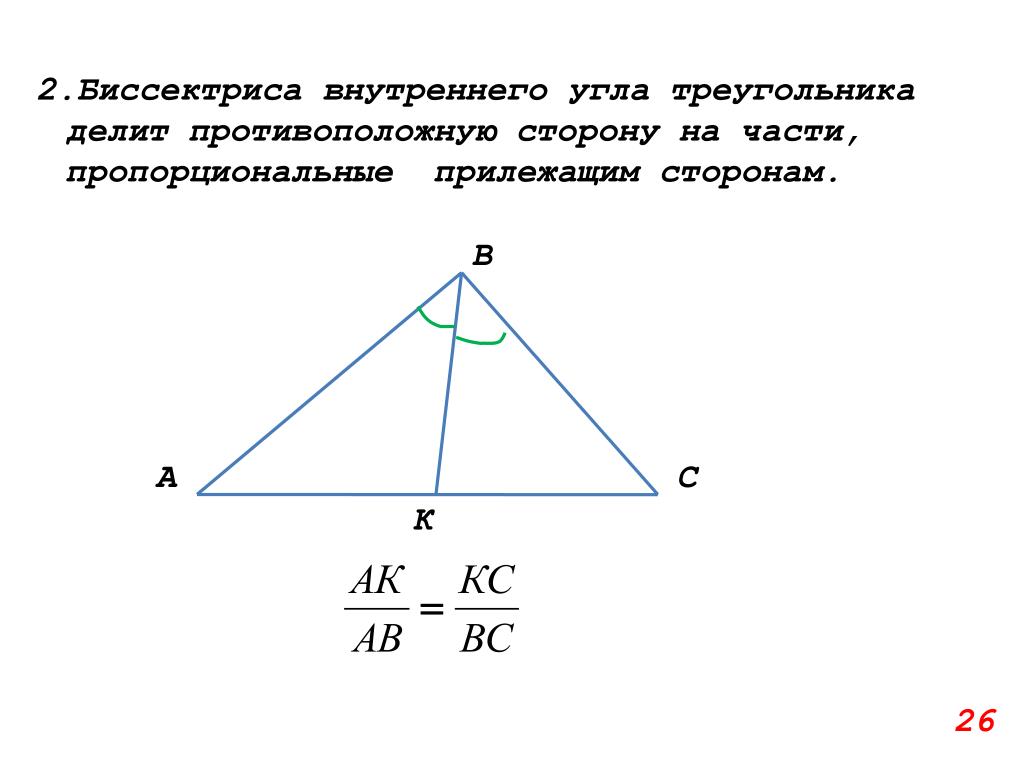

Биссектриса угла — это прямая или луч, который делит угол в треугольнике на две равные части. Основные свойства биссектрисы угла заключаются в том, что любая точка биссектрисы угла равноудалена от сторон угла, а биссектриса угла делит противоположную сторону треугольника в отношении прилежащих сторон, что известно как угол свойство биссектрисы треугольника.

Доказательство теоремы о биссектрисе

Утверждение: В треугольнике биссектриса любого угла будет делить противолежащую сторону в отношении сторон, содержащих этот угол. Давайте посмотрим на доказательство этого.

Нарисуйте луч CX, параллельный AD, и продолжите BA, чтобы пересечь этот луч в точке E. стороны в разных точках, две другие стороны делятся в таком же отношении.

В ΔCBE DA параллелен CE.

BD/DC = BA/AE ⋯ (1)

Теперь нам осталось доказать, что AE = AC.

Отметим углы на рисунке выше.

Поскольку DA параллелен СЕ, имеем

∠DAB = ∠CEA (соответствующие углы) —— (2)

∠DAC = ∠ACE (чередующиеся внутренние углы) —— (3)

Так как AD является биссектрисой ∠BAC, мы имеем ∠DAB = ∠DAC —- (4).

Из (2), (3) и (4) мы можем сказать, что ∠CEA = ∠ACE. Это делает ΔACE равнобедренным треугольником. Так как стороны, противоположные равным углам, равны, то AC = AE.

Замените AC на AE в уравнении (1).

BD/DC = BA/AC

Отсюда доказано.

Теорема, обратная теореме о биссектрисе угла

Теорема, обратная биссектрисе угла, утверждает, что если стороны треугольника удовлетворяют следующему условию: «Если линия, проведенная из вершины треугольника, делит противоположную сторону на две части так, что они пропорциональны двум другим сторонам треугольника, треугольник», это означает, что точка на противоположной стороне этого угла лежит на его биссектрисе угла. Здесь нам известно, что стороны пропорциональны, и отсюда мы пришли к выводу, что прямая/луч/отрезок является биссектрисой соответствующего угла. Это известно как обратная теорема о биссектрисе угла в геометрии.

Посмотрите на изображение ниже, чтобы понять его визуально.

Формула теоремы о биссектрисе угла

Теорема о биссектрисе угла треугольника гласит, что «в треугольнике биссектриса любого угла будет делить противоположную сторону в отношении сторон, содержащих этот угол». Отсюда мы можем записать формулу теоремы о биссектрисе угла треугольника как

\(\dfrac{\text{BD}}{\text{DC}} = \dfrac{\text{AB}}{\text{AC} }\)

► Похожие темы

Ниже перечислены несколько интересных тем, связанных с теоремой о биссектрисе угла треугольника.

  • Теорема о биссектрисе перпендикуляра
  • Построение биссектрисы угла
  • Теорема о сходстве треугольников
  • Теорема о внешнем угле

Часто задаваемые вопросы по теореме

о биссектрисах угла

Что такое теорема о биссектрисах треугольника?

Теорема о биссектрисе угла треугольника гласит, что «Биссектриса любого угла внутри треугольника делит противоположную сторону на две части, пропорциональные двум другим сторонам треугольника, которые содержат этот угол».

Какая формула теоремы о биссектрисе угла?

Пусть AD — биссектриса ∠A в ΔABC. Согласно формуле теоремы о биссектрисе угла, BD/DC = AB/AC.

Чем похожи теорема о делителях сторон и теорема о биссектрисе угла?

Единственное сходство между теоремой о делителях сторон и теоремой о биссектрисе угла заключается в том, что обе теоремы связаны с пропорциями длин сторон треугольника.

Как использовать теорему о биссектрисе угла?

Теорему о биссектрисе угла треугольника можно использовать для нахождения недостающих длин сторон треугольника. Он устанавливает отношения между сторонами.

Что является обратной теоремой о биссектрисе угла?

Если линия или луч AD проведены в ΔABC так, что BD/DC = AB/AC, то AD делит ∠A пополам. Это утверждение обратной теоремы о биссектрисе угла.

Как доказать теорему о биссектрисе угла?

Чтобы доказать теорему о биссектрисе угла, нам нужно продолжить стороны треугольника и построить рядом с ним еще один треугольник.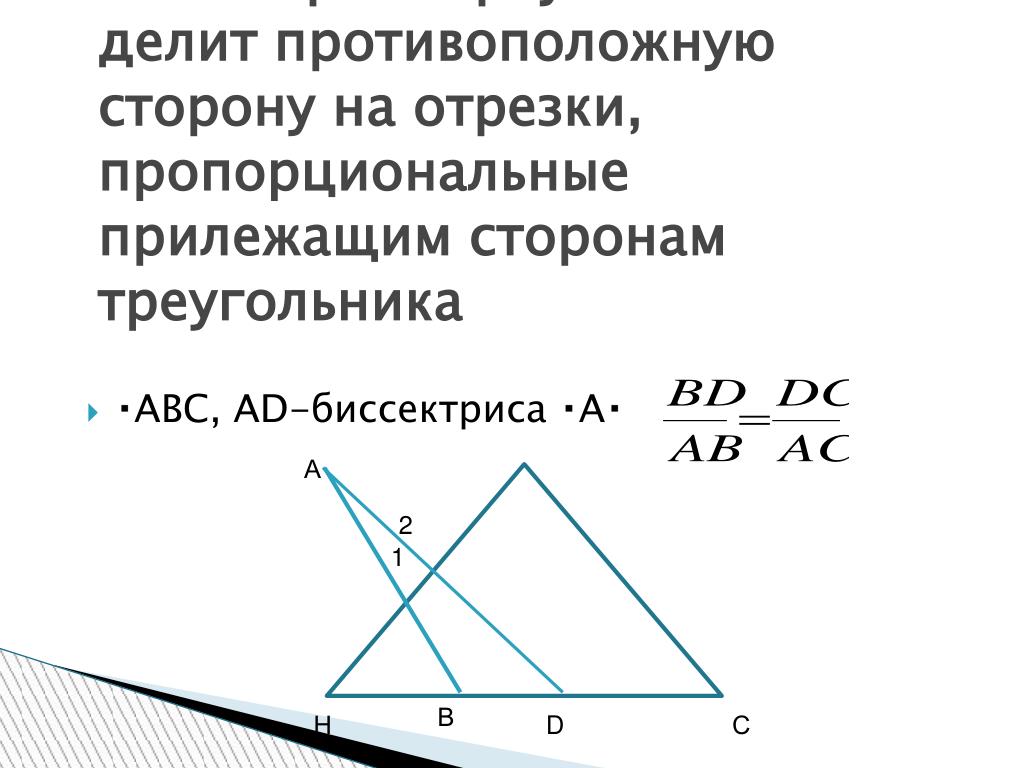 Затем мы используем основную теорему пропорциональности, чтобы установить соотношение между сторонами нарисованного треугольника.

Объяснение урока: Теорема о биссектрисе угла и ее обращение

В этом объяснении мы научимся использовать теорема о биссектрисе угла и ее обращение для нахождения недостающей стороны длина в треугольнике.

В треугольнике биссектриса внутреннего угла пересекает сторону напротив угла, который разбивает сторону на два отрезка меньшего длины. Что можно сказать о соотношении длин этих отрезки линии? Ответ на этот вопрос дает теорема о биссектрисе угла. что мы сейчас констатируем.

Теорема: биссектриса внутреннего угла Теорема

Если внутренний угол треугольника делится пополам, биссектриса делит противоположной стороны на отрезки, длины которых имеют то же отношение, что и длины необщих смежных сторон соответствующего угла, разделенного пополам.

То есть

Докажем эту теорему.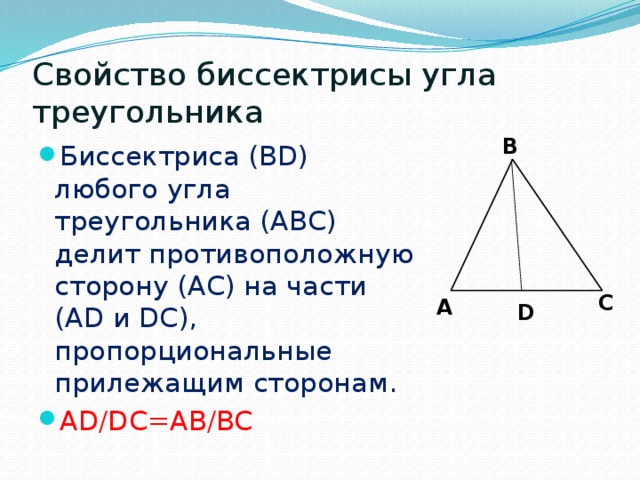 Начнем с рисования ⃖⃗𝐴𝐸 из вершины 𝐴 так, чтобы параллельно ⃖⃗𝐶𝐷. Затем мы расширяем 𝐵𝐶 после точки 𝐶 до ⃖⃗𝐵𝐶 пересекается с ⃖⃗𝐴𝐸 в точке 𝐸.

Поскольку 𝐶𝐷 — биссектриса угла ∠𝐵𝐶𝐴, мы знаем, что два отмеченных угла в диаграммы в вершине 𝐶 конгруэнтны. Кроме того, поскольку ⃖⃗𝐴𝐸⫽⃖⃗𝐶𝐷,

  • ∠𝐵𝐶𝐷 и ∠𝐵𝐸𝐴 соответственные углы, поэтому они равны,
  • ∠𝐷𝐶𝐴 и ∠𝐶𝐴𝐸 являются противоположными углами, так они конгруэнтны.

Это приводит к тому, что все четыре отмеченных угла на схеме выше равны конгруэнтный. Заметим, что в △𝐵𝐴𝐸 имеем две параллельные линии, ⃖⃗𝐴𝐸 и ⃖⃗𝐷𝐶, которые пересекаются двумя секущими, 𝐵𝐴 и 𝐵𝐸, так что у нас есть 𝐵𝐷𝐷𝐴=𝐵𝐶𝐶𝐸.

Наконец, мы замечаем, что △𝐴𝐶𝐸 — это равнобедренный треугольник, потому что 𝑚∠𝐶𝐴𝐸=𝑚∠𝐶𝐸𝐴, что означает 𝐶𝐸=𝐶𝐴. Следовательно, 𝐵𝐷𝐷𝐴=𝐵𝐶𝐶𝐴.

Перезапись 𝐵𝐷=𝐷𝐵 и 𝐵𝐶=𝐶𝐵 потенциальных клиентов к утверждению теоремы.

В нашем первом примере мы применим биссектрису внутреннего угла Теорема нахождения недостающих длин в треугольнике.

Пример 1. Нахождение неизвестных длин сторон треугольника с помощью биссектрисы угла Теорема

На рисунке 𝐴𝐷 делит пополам ∠𝐵𝐴𝐶, 𝐵𝐷=8, 𝐷𝐶=11, а периметр △𝐴𝐵𝐶 равен 57. Определите длины 𝐴𝐵 и 𝐴𝐶.

Ответ

Нам дано, что 𝐴𝐷 — это биссектриса внутреннего угла при ∠𝐴 в треугольник 𝐴𝐵𝐶. Вспоминаем биссектрису внутреннего угла теорема. Если внутренний угол треугольника делится пополам, то биссектриса делит противоположную сторону на отрезки, длины которых равны отношение как длины необщих смежных сторон соответствующих разделенный пополам угол. На приведенной схеме это означает 𝐷𝐶𝐵𝐷=𝐴𝐶𝐴𝐵.

Так как нам дано 𝐵𝐷=8 и 𝐷𝐶=11, это означает 118=𝐴𝐶𝐴𝐵.

Также известно, что периметр треугольника 𝐴𝐵𝐶 равно 57.

Напомним, что периметр многоугольника равен сумме длин сторон многоугольника. Это ведет к 𝐴𝐵+𝐵𝐶+𝐴𝐶=57.

Так как точка 𝐷 делится 𝐵𝐶 на два меньших отрезка, 𝐵𝐷 и 𝐷𝐶, мы можем заменить 𝐵𝐶=𝐵𝐷+𝐷𝐶 писать 𝐴𝐵+𝐵𝐷+𝐷𝐶+𝐴𝐶=57.

Подставляя 𝐵𝐷=8 и 𝐷𝐶=11, получаем

𝐴𝐵+8+11+𝐴𝐶=57𝐴𝐵+𝐴𝐶=38. (1)

Напомним полученное ранее уравнение 118=𝐴𝐶𝐴𝐵, который можно переставить на

𝐴𝐶=118𝐴𝐵. (2)

Подставляя это выражение в уравнение (1) и упрощая, имеем 𝐴𝐵+𝐴𝐶=38𝐴𝐵+118𝐴𝐵=38198𝐴𝐵=38𝐴𝐵=819×38=16.

Мы можем подставить это значение в уравнение (2) чтобы получить 𝐴𝐶=118𝐴𝐵=118×16=22.

Следовательно, 𝐴𝐵=16,𝐴𝐶=22.

Давайте рассмотрим другой пример, где мы идентифицируем неизвестный термин с помощью этой теоремы.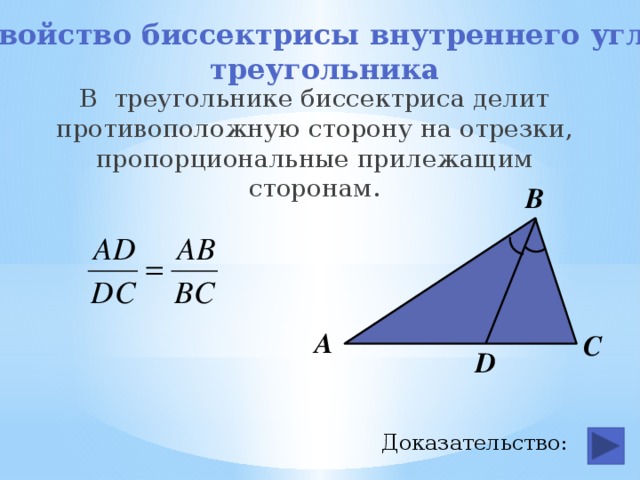

Пример 2. Использование теоремы о биссектрисе угла для формирования и решения алгебраическое уравнение

Учитывая, что 𝐴𝐶=10, 𝐶𝐷=6, 𝐴𝐵=𝑥+9 и 𝐵𝐷=𝑥+5, найти числовое значение 𝑥.

Ответ

Нам дано, что 𝐴𝐷 — это биссектриса внутреннего угла в точке 𝐴 в треугольнике 𝐴𝐵𝐶. Вспомним теорему о биссектрисе внутреннего угла который связывает отношение длин отрезков, связанных с биссектриса угла. На этой диаграмме эта теорема говорит нам 𝐷𝐶𝐵𝐷=𝐴𝐶𝐴𝐵.

Мы можем подставить заданные длины и выражения в это уравнение, чтобы писать 6𝑥+5=10𝑥+9.

Крест умножая и упрощая, получаем 6(𝑥+9)=10(𝑥+5)6𝑥+54=10𝑥+506𝑥−10𝑥=50−54−4𝑥=−4𝑥=1.

В предыдущих двух примерах мы применяли теорему об отношении линии отрезки, относящиеся к биссектрисе внутреннего угла треугольника. утверждение, обратное этой теореме, также верно. Точнее, рассмотрим треугольник 𝐴𝐵𝐶, где нам дается точка 𝐷 на сторона 𝐵𝐶.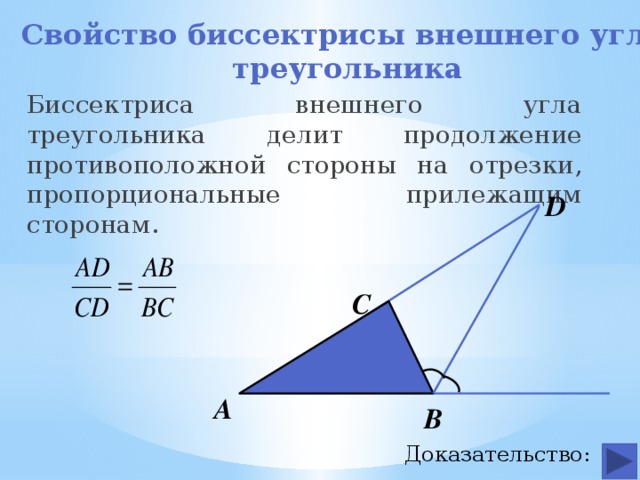

Если нам известно, что длины отрезков удовлетворяют 𝐷𝐵𝐷𝐶=𝐴𝐵𝐴𝐶, мы знаем, что точка 𝐷 лежит на биссектрисе внутреннего угла в вершине 𝐴 треугольника 𝐴𝐵𝐶.

Обратимся теперь к аналогичной теореме о биссектрисе для внешнего угол треугольника.

Теорема: Теорема о биссектрисе внешнего угла

Рассмотрим ∠𝐵𝐶𝐸, который является внешним углом треугольника 𝐴𝐵𝐶 в вершине 𝐶 делится пополам 𝐶𝐷, пересекающая продолжение стороны треугольник напротив ∠𝐶, который 𝐴𝐵, в точке 𝐷, как показано на следующую схему.

У нас есть следующие идентификаторы: 𝐷𝐵𝐷𝐴=𝐶𝐵𝐶𝐴.

Доказательство этой теоремы сложнее, чем доказательство внутренней биссектрисы. теорема, хотя идеи схожи. Докажем эту теорему. Мы начните с рисования ⃖⃗𝐷𝐸 из вершины 𝐷 так, чтобы он был параллелен ⃖⃗𝐵𝐶. Эта параллельная линия пересекается с продолжение стороны 𝐴𝐶 в точке 𝐸, как показано на схеме ниже.

Заметим, что углы ∠𝐶𝐷𝐸 и ∠𝐷𝐶𝐵 — противоположные углы относительно две параллельные линии; следовательно, они конгруэнтны. Это делает треугольник 𝐸𝐷𝐶 равнобедренный. С 𝐵𝐶 и 𝐷𝐸 параллельны, мы видим, что треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 подобны. В В частности, это потому, что два треугольника имеют общий угол при 𝐴, а две другие пары углов являются соответствующими углами относительно параллельных прямых.

Это означает, что для некоторой положительной константы 𝑟 имеем 𝐴𝐵𝐴𝐷=𝑟,𝐴𝐶𝐴𝐸=𝑟,𝐵𝐶𝐷𝐸=𝑟.

Если мы возьмем уравнение 𝐴𝐶𝐴𝐸=𝑟, мы можем написать 𝐴𝐶=𝑟𝐴𝐸=𝑟(𝐴𝐶+𝐶𝐸).

Поскольку мы знаем, что △𝐸𝐷𝐶 равнобедренный, у нас есть 𝐶𝐸=𝐷𝐸. Это ведет к

𝐴𝐶=𝑟(𝐴𝐶+𝐷𝐸). (3)

Теперь мы можем изменить уравнение 𝐵𝐶𝐷𝐸=𝑟 написать 𝐷𝐸=𝐵𝐶𝑟. Подставив это в правую часть уравнения (3), получаем 𝑟(𝐴𝐶+𝐷𝐸)=𝑟𝐴𝐶+𝐵𝐶𝑟=𝑟𝐴𝐶+𝐵𝐶.

Следовательно,

𝐴𝐶=𝑟𝐴𝐶+𝐵𝐶.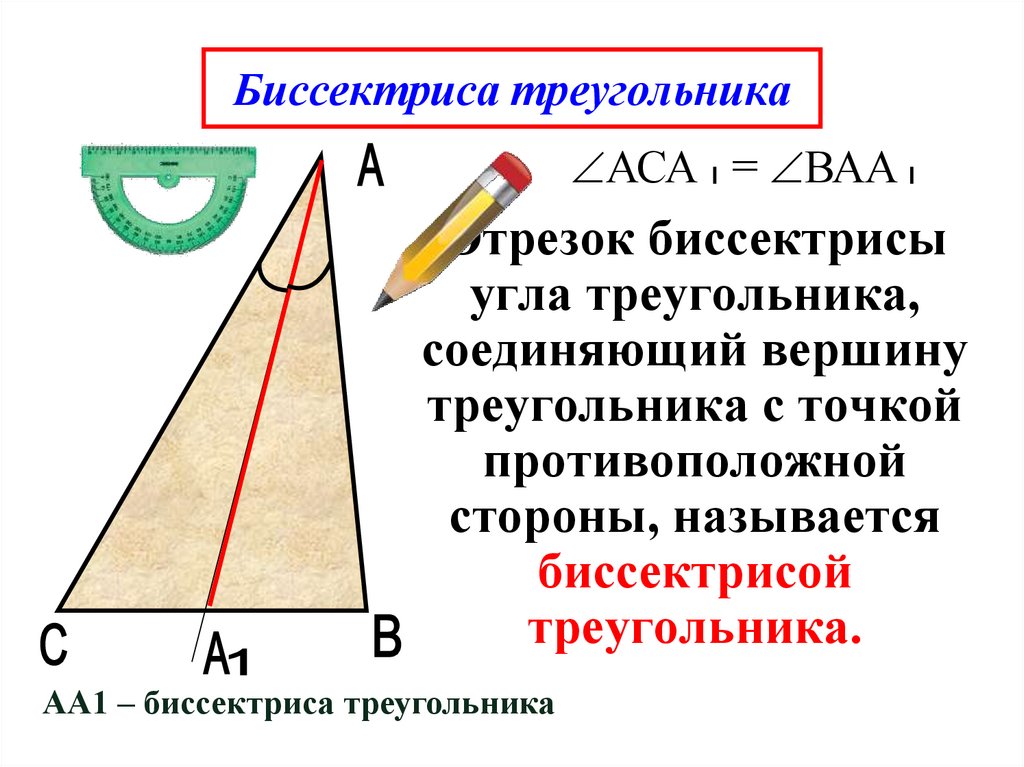 (4)

Теперь мы можем подставить 𝑟=𝐴𝐵𝐴𝐷 в (4) писать 𝐴𝐶=𝐴𝐵𝐴𝐷×𝐴𝐶+𝐵𝐶.

Умножая обе части уравнения на 𝐴𝐷 и переставляя, получаем 𝐴𝐶om𝐴𝐷 = 𝐴𝐵om𝐴𝐶+𝐵𝐶om𝐴𝐷𝐴𝐶 = 𝐴𝐷 — 𝐴𝐵 𝐴𝐵 = 𝐵𝐶om𝐴𝐷𝐴𝐶 (𝐴𝐷 — 𝐴𝐵) = 𝐵𝐶> 𝐴𝐷𝐴𝐶om𝐵𝐷 = 𝐵𝐶om𝐴𝐷.

Эквивалент желаемого соотношения 𝐷𝐵𝐷𝐴=𝐶𝐵𝐶𝐴, что доказывает теорему.

Рассмотрим пример, где мы применим биссектрису внешнего угла Теорема нахождения недостающей длины в треугольнике.

Пример 3. Нахождение неизвестных длин сторон треугольника с помощью биссектрисы угла Теорема

Учитывая, что 𝐴𝐵=60, 𝐴𝐶=40, и 𝐵𝐶=31, что такое 𝐶𝐷?

Ответ

На схеме указано, что 𝐴𝐷 — биссектриса экстерьера угол при 𝐴 треугольника 𝐴𝐵𝐶. Мы вспомните теорему о биссектрисе внешнего угла, которая дает тождество 𝐷𝐶𝐷𝐵=𝐴𝐶𝐴𝐵.

Так как 𝐷𝐵=𝐷𝐶+𝐶𝐵, мы можем написать 𝐷𝐶𝐷𝐶+𝐶𝐵=𝐴𝐶𝐴𝐵.

Нам даны длины 𝐴𝐵=60, 𝐴𝐶=40, и 𝐵𝐶=31, что мы можем подставить в уравнение выше написать 𝐷𝐶𝐷𝐶+31=4060.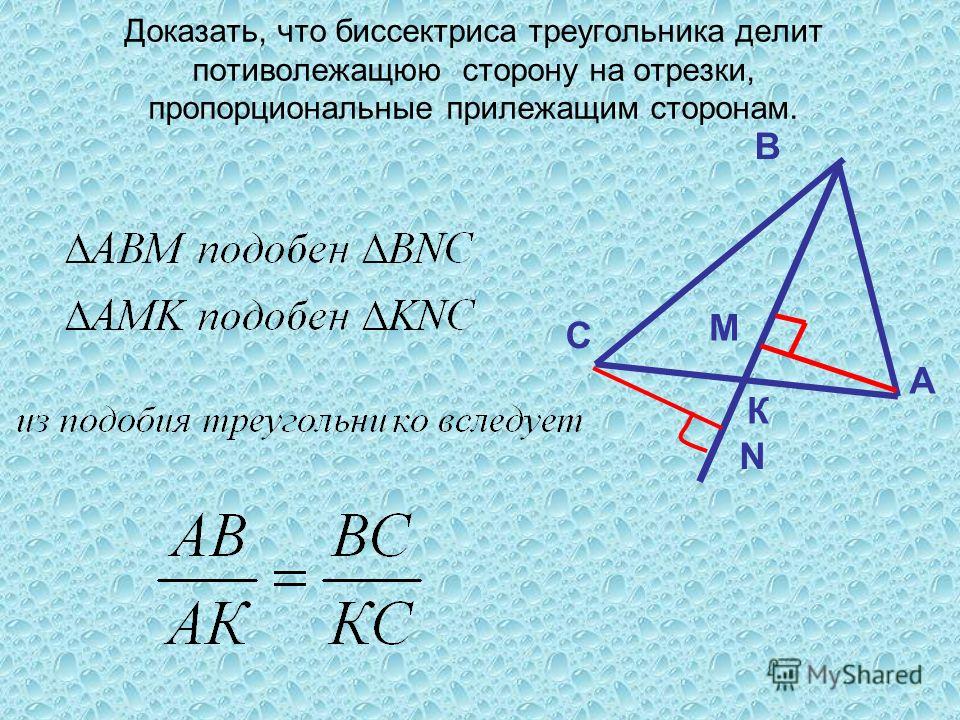

Приведенное выше уравнение имеет одну неизвестную длину, 𝐷𝐶, что совпадает с длиной 𝐶𝐷, которую мы находясь в поиске. Умножение креста и упрощение полученного уравнение, получаем 60𝐶𝐷=40(𝐶𝐷+31)60𝐶𝐷=40𝐶𝐷+124020𝐶𝐷=1240𝐶𝐷=124020=62.

Следовательно, 𝐶𝐷=62.

В следующем примере мы применим обе теоремы для внутренней и биссектрисы внешнего угла треугольника, найти отношение площадей два треугольника.

Пример 4. Нахождение отношения площадей двух треугольников с помощью угла Теорема о биссектрисе

Если 𝐴𝐵=30 см, 𝐵𝐶=40см, и 𝐴𝐶=45см, найдите отношение между районы △𝐴𝐸𝐷 и △𝐴𝐸𝐶.

Ответ

Рассмотрим площади двух треугольников 𝐴𝐸𝐷 и 𝐴𝐸𝐶. Мы знаем, что площадь треугольника данный 0,5××.baselengthcorrespondingheight

Высота обоих треугольников определяется длиной отрезка. из вершины 𝐴, пересекающейся перпендикулярно линия 𝐸𝐶. Назовем эту высоту ℎ, как показано на следующей диаграмме.

Длина основания треугольника 𝐴𝐸𝐷 равна 𝐸𝐷, а длина основания треугольника 𝐴𝐸𝐶 это 𝐸𝐶. Следовательно, площадь △𝐴𝐸𝐷=12𝐸𝐷×ℎ,△𝐴𝐸𝐶=12𝐸𝐶×ℎ.

Так как 12ℎ является общим фактором в обеих областях, отношение двух площадей можно записать как 𝐸𝐷∶𝐸𝐶.

Ни одна из этих длин не предусмотрена, поэтому вернемся к нашему заданному диаграмма. Мы видим, что 𝐴𝐷 биссектриса внутреннего угла при 𝐴 треугольника 𝐴𝐵𝐶 а еще это 𝐴𝐸 биссектриса внешнего угла при 𝐴 треугольника 𝐴𝐵𝐶. Напомним теоремы об отношении прямых отрезки, относящиеся к биссектрисам внутреннего и внешнего углов треугольника. Теоремы сообщают нам следующие тождества: 𝐷𝐶𝐷𝐵=𝐴𝐶𝐴𝐵,𝐸𝐵𝐸𝐶=𝐴𝐵𝐴𝐶.

Мы можем заменить данные длины 𝐴𝐵=30см, 𝐵𝐶=40см, и 𝐴𝐶=45см написать

𝐷𝐶𝐷𝐵=4530=32,𝐸𝐵𝐸𝐶=3045=23. (5)(6)

Поскольку мы знаем, что 𝐸𝐶=𝐸𝐵+𝐵𝐶, мы можем подставьте это выражение в уравнение (6) выше, чтобы написать 𝐸𝐵𝐸𝐵+𝐵𝐶=23.

Мы можем перекрестно умножить это уравнение и заменить 𝐵𝐶=40 см, чтобы получить 3𝐸𝐵=2(𝐸𝐵+𝐵𝐶)3𝐸𝐵=2𝐸𝐵+2𝐵𝐶3𝐸𝐵−2𝐸𝐵=2×40𝐸𝐵=80.см

Мы также знаем, что 𝐵𝐷+𝐷𝐶=𝐵𝐶, что означает 𝐷𝐶=𝐵𝐶−𝐵𝐷=40−𝐷𝐵. Замена этого выражение в уравнение (5), 40−𝐷𝐵𝐷𝐵=32.

Упрощение дает 2(40−𝐷𝐵)=3𝐷𝐵80−2𝐷𝐵=3𝐷𝐵80=2𝐷𝐵+3𝐷𝐵5𝐷𝐵=80𝐷𝐵=16 см

Наконец, 𝐷𝐶=40−𝐷𝐵=40−16=24.cm

Теперь мы можем вычислить 𝐸𝐷=𝐸𝐵+𝐵𝐷=80+16=96,𝐸𝐶=𝐸𝐷+𝐷𝐶=96+24=120.cmcm

Это означает, что отношение 𝐸𝐷∶𝐸𝐶 можно записать как 96∶120. Разделив каждую часть на 24, это соотношение равно эквивалентно 4∶5.

Отсюда соотношение площадей △𝐴𝐸𝐷 и △𝐴𝐸𝐶 равно 4∶5.

До сих пор мы обсуждали соотношение длин отрезки, относящиеся к биссектрисе внутреннего или внешнего угла треугольник.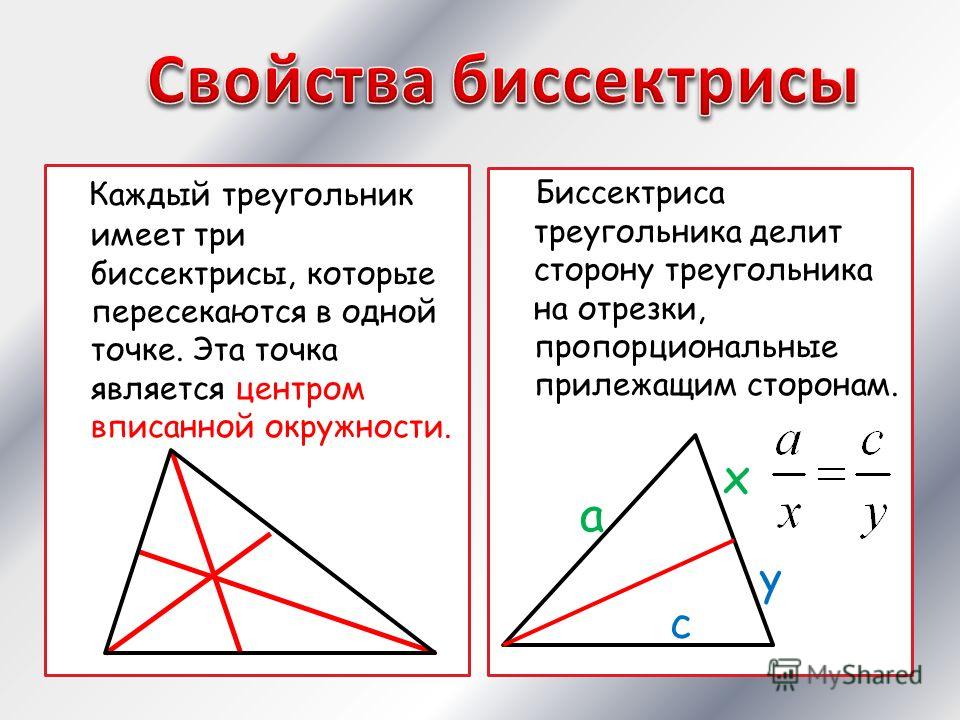 Теперь рассмотрим теорему, касающуюся длины отрезок биссектрисы угла.

Теорема: Длина биссектрисы угла в треугольнике

В любом треугольнике 𝐴𝐵𝐶, если 𝐶𝐷 биссектриса угла 𝐶, то имеем

Докажем эту теорему. Начнем с добавления окружности, описывающей треугольник выше, а также добавление точки пересечения 𝐸 между линией 𝐶𝐷 и кругом.

На диаграмме выше мы знаем, что два зеленых угла при вершине 𝐶 конгруэнтны, так как 𝐶𝐷 — биссектриса ∠𝐴𝐶𝐵. Заметим также, что углы при вершинах 𝐵 и 𝐸 вписанные углы, стягиваемые по общей дуге 𝐴𝐶. Напомним, что все углы, опирающиеся на общий дуги имеют одинаковую меру, что говорит нам о том, что два красных угла в диаграммы совпадают. Затем △𝐶𝐵𝐷 и △𝐶𝐸𝐴 делят две пары конгруэнтных углов, что означает, что это подобные треугольники. Следовательно, 𝐶𝐷𝐶𝐴=𝐶𝐵𝐶𝐸.

Пишем 𝐶𝐸=𝐶𝐷+𝐷𝐸, имеем 𝐶𝐷𝐶𝐴=𝐶𝐵𝐶𝐷+𝐷𝐸.

Перемножая и упрощая как прежде, получаем

𝐶𝐷 (𝐶𝐷+𝐷𝐸) = 𝐶𝐵om𝐶𝐴𝐶𝐷+𝐶𝐷om𝐷𝐸 = 𝐶𝐵om𝐶𝐴𝐶𝐷 = 𝐶𝐵om𝐶𝐴 -𝐶𝐷 𝐶𝐷t𝐷𝐸.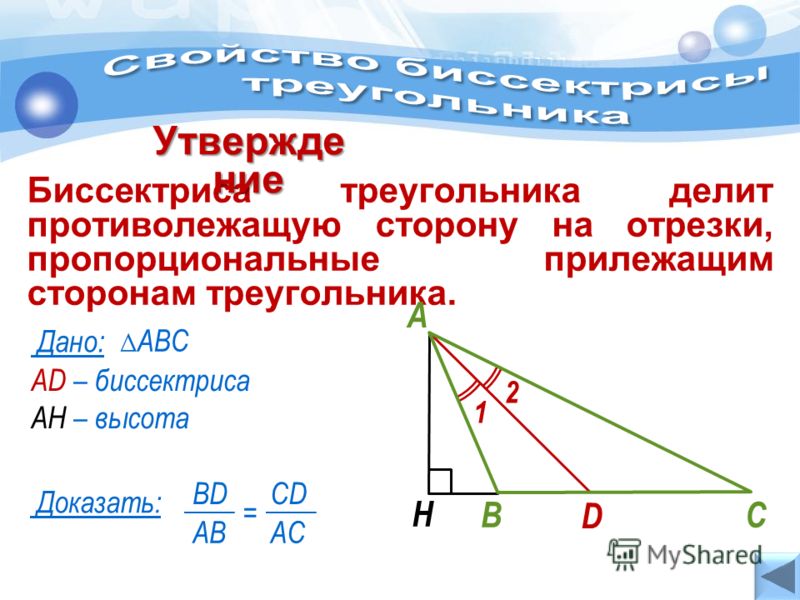  (7)

Мы отмечаем здесь, что положительный квадратный корень из обеих частей этого уравнение не даст желаемой формулы. В частности, термин 𝐶𝐷⋅𝐷𝐸 в правой части уравнения выше следует заменить на 𝐷𝐵⋅𝐷𝐴. Для того, чтобы оправдать это замены, нам нужно наблюдать еще одну пару подобных треугольников.

На диаграмме выше мы видим, что ∠𝐵𝐶𝐸 и ∠𝐵𝐴𝐸 — вписанные углы, опирающиеся на одной дуге, а значит, они конгруэнтны. Затем, △𝐶𝐵𝐷 и △𝐴𝐸𝐷 делят две пары конгруэнтных углы, значит, они подобны. Это дает нам 𝐶𝐷𝐷𝐴=𝐷𝐵𝐷𝐸, что приводит к 𝐶𝐷⋅𝐷𝐸=𝐷𝐵⋅𝐷𝐴.

Теперь мы можем подставить выражение правой части уравнения (7) писать 𝐶𝐷=𝐶𝐵⋅𝐶𝐴−𝐷𝐵⋅𝐷𝐴.

Извлечение положительного квадратного корня из обеих частей этого уравнения дает 𝐶𝐷=√𝐶𝐵⋅𝐶𝐴−𝐷𝐵⋅𝐷𝐴, что доказывает теорему.

В последнем примере мы применим эту теорему, чтобы найти длину биссектриса внутреннего угла треугольника.

Пример 5. Нахождение неизвестной длины стороны в треугольнике с помощью биссектрисы угла Теорема

В треугольнике 𝐴𝐵𝐶 𝐴𝐵=76см, 𝐴𝐶=57см, и 𝐵𝐷=52см. Учитывая, что 𝐴𝐷 делит пополам ∠𝐴 и пересекается 𝐵𝐶 в 𝐷 определите длину 𝐴𝐷.

Ответ

Напомним, что если 𝐴𝐷 делит пополам ∠𝐴 в треугольнике 𝐴𝐵𝐶, у нас есть 𝐴𝐷=√𝐴𝐶⋅𝐴𝐵−𝐷𝐶⋅𝐷𝐵.

Из вопроса мы знаем длины 𝐴𝐶, 𝐴𝐵, и 𝐷𝐵. Следовательно, чтобы найти 𝐴𝐷, мы должны сначала найди 𝐷𝐶. Чтобы найти эту длину, вспомним еще одну теорему о биссектриса угла: если внутренний угол треугольника делится пополам, то биссектриса делит противоположную сторону на отрезки, длины которых равны отношение как длины необщих смежных сторон соответствующих разделенный пополам угол. На приведенной схеме это означает 𝐷𝐶𝐵𝐷=𝐴𝐶𝐴𝐵.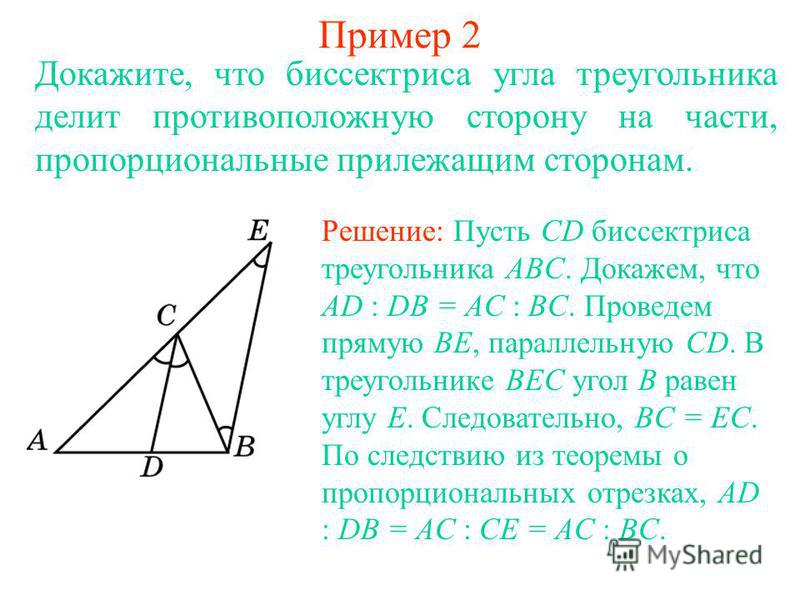

Подставляя данные длины в это уравнение, 𝐷𝐶52=5776𝐷𝐶=5776⋅52=39.cm

Теперь мы можем подставить эту длину и другие заданные длины в формула длины биссектрисы угла: 𝐴𝐷=√𝐴𝐶⋅𝐴𝐵−𝐷𝐶⋅𝐷𝐵=√57⋅76−39⋅52=48.cm

Следовательно, длина 𝐴𝐷 равна 48 см.

Рассмотрим расширение этой теоремы о длине биссектрисы угла, где мы рассматриваем длину биссектрисы внешнего угла треугольника.

Теорема: длина биссектрисы внешнего угла треугольника

В любом треугольнике 𝐴𝐵𝐶, если 𝐶𝐷 — биссектриса угла 𝐶, то имеем 𝐶𝐷=√𝐷𝐵⋅𝐷𝐴−𝐶𝐵⋅𝐶𝐴.

Эту теорему можно доказать, используя предыдущую теорему в сочетании с другими теоремами о биссектрисе угла, которые мы мы узнали до сих пор, хотя мы не будем включать доказательство в это объяснение.

Рассмотрим пример, в котором мы должны использовать теоремы о биссектрисе внешнего угла, чтобы найти недостающие длины в треугольник.

Пример 6.

Нахождение неизвестной длины стороны в треугольнике с помощью теоремы о биссектрисе внешнего угла 𝑥 и 𝑦.

Ответ

Напомним, что если 𝐴𝐷 делит пополам внешний угол при ∠𝐴 в треугольнике 𝐴𝐵𝐶, то имеем 𝐴𝐷=√𝐷𝐶⋅𝐷𝐵−𝐴𝐶⋅𝐴𝐵.

Заметим, что 𝐴𝐷 на диаграмме равно 𝑥. Нам это дано 𝐴𝐶=10 и 𝐴𝐵=15, но длины 𝐷𝐶=𝑦+4 и 𝐷𝐵=6+(𝑦+4)=𝑦+10 нужно рассчитать, найдя 𝑦.

Чтобы найти 𝑦, мы можем использовать теорему о биссектрисе внешнего угла, которая дает нам другое соотношение между длинами сторон треугольника, внешний угол которого делится пополам. А именно, они связаны следующее соотношение: 𝐴𝐶𝐴𝐵=𝐷𝐶𝐷𝐵.

Подставляя данные длины, имеем 1015=𝑦+4𝑦+10.

Мы можем решить это для 𝑦, перемножив и переставив, чтобы получить 10(𝑦+10)=15(𝑦+4)10𝑦+100=15𝑦+6040=5𝑦𝑦=8.

Теперь, когда у нас есть 𝑦, вернемся к исходному уравнению. Замена в заданных длинах и 𝑦=8, мы имеем 𝐴𝐷=√𝐷𝐶⋅𝐷𝐵−𝐴𝐶⋅𝐴𝐵𝑥=√(𝑦+10)⋅(𝑦+4)−15⋅10=√18⋅12−150=√66.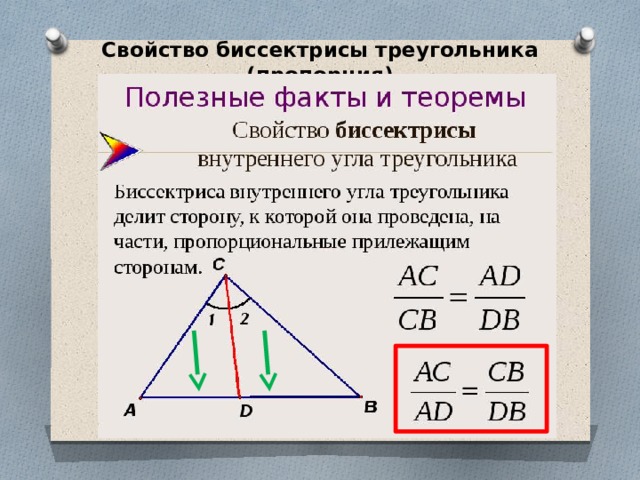

В итоге 𝑥=√66 и 𝑦=8.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые моменты

  • Если внутренний угол треугольника делится пополам, биссектриса делит противоположную сторону на отрезки, длины которых имеют то же отношение, что и длины необщих смежных сторон соответствующего угла, разделенного пополам.
    То есть,
  • Обратное утверждение вышеприведенной теоремы также верно. Точнее, рассмотреть треугольник 𝐴𝐵𝐶, где нам дана точка 𝐷 сбоку 𝐵𝐶.
    Если нам дано, что длины отрезков удовлетворяют 𝐷𝐵𝐷𝐶=𝐴𝐵𝐴𝐶, мы знаем, что точка 𝐷 лежит на биссектрисе внутренний угол при вершине 𝐴 в треугольнике 𝐴𝐵𝐶.
  • Рассмотрим ∠𝐵𝐶𝐸, внешний угол треугольника 𝐴𝐵𝐶 в вершине 𝐶 делится пополам 𝐶𝐷, пересекающая продолжение стороны треугольник напротив ∠𝐶, который 𝐴𝐵, в точке 𝐷, как показано на следующей диаграмме.