К числу 15 допишите слева и справа по одной цифре: К числу 15 допишите слева и справа по одной цифре так, чтобы получившееся число было кратно 15. Сколько решений имеет задача?

Номер №89 — ГДЗ по Математике 6 класс: Мерзляк А.Г.

войтирегистрация

1. Ответкин
2. Решебники
3. 6 класс
4. Математика
5. Мерзляк
6. Номер №89

НАЗАД К СОДЕРЖАНИЮ

2014г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №89 по учебнику Математика. 6 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. 2014г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №89 по учебнику Математика. 6 класс. Учебник / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, под редакцией В.Е. Подольского. Вентана-Граф. 4 издание, дополненное. 2019г.

Условие 20142019г.

Cменить на 2014 г.

Cменить на 2019 г.

К числу 15 допишите слева и справа по одной цифре так, чтобы получившееся число было кратно 15. Сколько решений имеет задача?

К числу 15 допишите слева и справа по одной цифре так, чтобы получившееся число было кратно 15. Сколько решений имеет задача?

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

Решение 4

Решение 4

Решение 5

Решение 5

Решение 6

Решение 6

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С. И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN.INFO

Классы

Предметы

Мерзляк 6 класс — § 3.

Признаки делимости на 9 и на 3

• Ответы к учебнику для 6 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Вопросы к параграфу

1. Как узнать, делится ли число нацело на 9?

Надо посчитать сумму цифр числа. Если сумма цифр делится на 9, то и само число делится на 9.

Например:

• В числе 387 сумма цифр равна 3 + 8 + 7 = 18 — делиться на 9. Значит и само число должно делиться на 9. Действительно, 387 : 9 = 43 — число делится на 9 нацело.
• В числе 115 сумма цифр равна 1 + 1 + 5 = 7 — не делится на 9. Значит и само число не должно делиться на 9. Действительно, 115 : 9 = 12 (ост. 7).

2. Как по записи натурального числа определить, кратно оно 3 или нет?

Надо посчитать сумму цифр числа. Если сумма цифр делится на 3, то и само число делится на 3.

Например:

• В числе 285 сумма цифр равна 2 + 8 + 5 = 15 — делиться на 3. Значит и само число должно делиться на 3. Действительно, 285 : 3 = 95 — число делится на 3 нацело.
• В числе 460 сумма цифр равна 4 + 6 + 0 = 10 — не делится на 3. Значит и само число не должно делиться на 3. Действительно, 460 : 3 = 153 (ост. 1).

Решаем устно

1. Буквой n обозначили некоторое чётное число. Чётным или нечётным является число:

1. n + 1 — нечётное число
2. n + 2 — чётное число

2. Какой цифрой оканчивается произведение:

1) 1 • 2 • 3 • 4 • 5 • 6 • 7 — цифрой 0, так как в произведении есть множители 2 и 5, которые дают произведению 0 на конце.

2) 1 • 3 • 5 • 7 • 9 • 11 • 13 — цифрой 5, так как в произведении есть цифра 5, но нет цифры 2. Значит произведение будет кратно 5, но не кратно 10.

3. Какие из чисел 184, 162, 243, 145, 210, 144, 153, 105, 230, 201 делятся нацело:

1) на 2

184, 162, 210, 144, 230 — все чётные числа.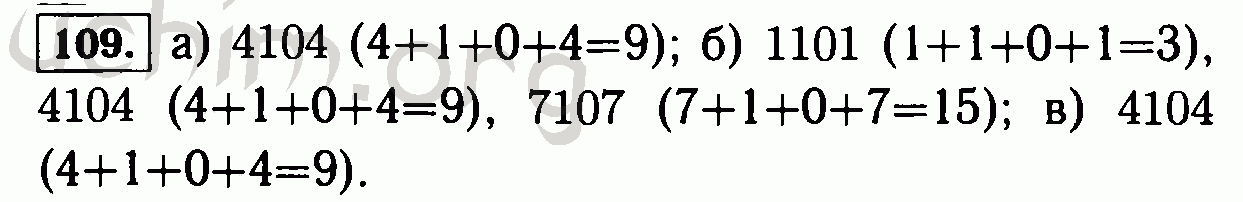

2) на 5

145, 210, 105, 230 — все числа, оканчивающиеся на 5 или на 0.

3) на 10

210, 230 — все числа, оканчивающиеся на 0.

4) на 3

162, 243, 210, 144, 153, 105, 201 — все числа, сумма цифр которых делится на 3.

5) на 9

162, 243, 144, 153 — все числа, сумма цифр которых делится на 9.

4. Какое из чисел 2 045, 4 750, 7 254, 6 225 делится нацело на 3, но не делится на 2?

6 225 — так как это нечётное число, сума цифр которого делится на 3.

5. Какую из цифр 5, 8, 2, 1 надо поставить вместо звёздочки, чтобы число 5 6*5 было кратным 9?

• 5 + 6 + 5 = 16
• Ближайшее кратное 9 число, большее 16 — это 18.
• Значит нам не хватает цифры 2 (18 — 2 = 16).

Ответ: 5 625.

6. Сколько существует двузначных чисел, кратных числу:

1) 5

Это все двузначные числа, оканчивающиеся на 0 или на 5:

• 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95 — всего 18 чисел.

2) 9

Это все двузначные числа, сумма цифр которых делится на 9:

• 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 — всего 10 чисел.

Упражнения

73. Заполните таблицу (поставьте знак «+» в случае утвердительного ответа или знак «—» в ином случае).

74. Заполните таблицу (поставьте знак «+» в случае утвердительного ответа или знак «—» » ином случае).

75. Из чисел 8 937, 6 585, 37 828, 44 292, 9 462, 58 395, 23 646 выпишите те, которые делятся нацело:

1) на 3

8 937, 6 585, 44 292, 9 462, 58 395, 23 646 — так как сумма их цифр делится на 3.

2) на 9

8 937 — так как сумма цифр этого числа делится на 9.

3) на 3 и на 2

44 292, 9 462, 23 646 — так как это чётные числа и сумма их цифр делится на 3.

76. Из чисел 7 826, 1 215, 4 075, 2 880, 3 921, 9 319, 6 072, 8 142 выпишите те, которые делятся нацело:

1) на 3

1 215, 2 880, 3 921, 6 072, 8 142 — так как сумма цифр этих чисел делится на 3.

2) на 9

1 215, 2 880 — так как сумма цифр этих чисел делится на 9.

3) на 9 и на 5

1 215, 2 880 — так как эти числа заканчиваются на 0 или на 5, а сумма их цифр делится на 9. 

77. Найдите все значения у, кратные:

1) числу 3, при которых верно неравенство 143 < у < 162

144, 147, 150, 153, 156, 159

2) числу 9, при которых верно неравенство 92 < у < 128

99, 108, 117, 126.

78. Найдите все значения m, кратные:

1) числу 3, при которых верно неравенство 324 < m < 345

327, 330, 333, 336, 339, 342.

2) числу 9, при которых верно неравенство 423 < m < 480

432, 441, 450, 459, 468, 477.

79. Вместо звёздочки поставьте такую цифру, чтобы получилось число, кратное 3 (рассмотрите все возможные случаи):

1) 54 84*

54 840, 54 843, 54 846, 54 849.

2) 3*6 393

306 393, 336 393, 366 393, 396 393.

3) 7 9*8

7 908, 7 938, 7 968, 7 998.

80. Вместо звёздочки поставьте такую цифру, чтобы получилось число, кратное 9 (рассмотрите все возможные случаи):

1) 62 8*1

62 811

2) 57* 582

570 582, 579 582.

3) 7 *51

7 551

81. Запишите:

1. наименьшее число, для записи которого используется только цифра 2 и которое делится нацело на 3  — 222
2. наименьшее трёхзначное число, которое делится нацело на 9 — 108

82. Какую цифру можно поставить вместо звёздочки в записи 6 27*. чтобы полученное число делилось нацело и на 3, и на 5?

Цифру 0, чтобы получилось число 6 270:

• сумма цифр этого числа равна 15, то есть делится на 3;
• на конце этого числа цифра 0, то есть делится на 5.

83. Какую цифру можно поставить вместо звёздочки в записи 21 85*. чтобы полученное число делилось нацело на 3, но не делилось нацело на 2?

Цифру 5, чтобы получилось число 21 855:

• сумма цифр этого числа равна 21, то есть делится на 3;
• это число нечётное, то есть не делится на 2.

84. Какую цифру можно поставить вместо звёздочки в записи 3 47*, чтобы полученное число делилось нацело и на 2, и па 3?

Цифру 4, чтобы получилось число 3 474:

• это чётное число, то есть делится на 2;
• сумма цифр этого числа равна 18, то есть делится на 3.

85. Запишите наименьшее:

1. четырёхзначное число, кратное 3 — 1 023;
2. пятизначное число, кратное 9 — 10 249;
3. шестизначное число, кратное 3 и 2 — 102 354;
4. четырёхзначное число, кратное 5 и 9 — 1 035.

Цифры в записи числа не могут повторяться.

86. Запишите наибольшее четырёхзначное число, которое делится нацело:

1. на 2 и на 3 — 9 996; 
2. на 3 и на 5 — 9 990; 
3. на 3 и на 10 — 9 990;
4. на 2 и на 9 — 9 990.

87. Какое наименьшее число надо прибавить к данному, чтобы получить число, кратное 9:

1. 1 275 — число 3, так как 1 275 + 3 = 1 278 — делится на 9;
2. 3 333 — число 6, так как 3 333 + 6 = 3 339 — делится на 9; 
3. 25 718 — число 4, так как 25 718 + 4 = 25 722 — делится на 9; 
4. 987 652 — число 8, так как 987 652 + 8 = 987 660 — делится на 9;
5. 10 203 040 — число 8, так как 10 203 040 + 8 = 10 203 048 — делится на 9;
6. 19 191 919 191 — число 3, так как 19 191 919 191 + 3 = 19 191 919 194 — делится на 9.

88. Запишите, используя по одному разу каждую из цифр 0, 1. 4, 7, наибольшее и наименьшее четырёхзначные числа, кратные 15.

• Наибольшее четырёхзначное число, состоящее из цифр 0, 1, 4, 7 и кратное 15 — 7 410, так как оно делится и на 5, и на 3.
• Наименьшее четырёхзначное число, состоящее из цифр 0, 1, 4, 7 и кратное 15 — 1 470, так как оно делится и на 5, и на 3.

89.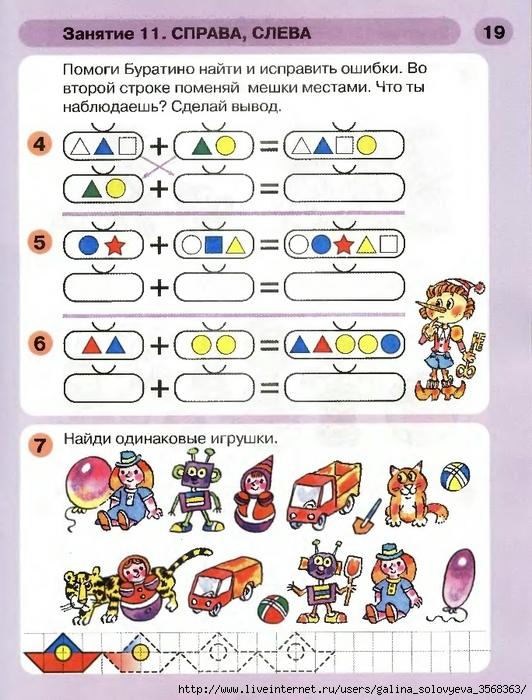 К числу 15 допишите слева и справа по одной цифре так, чтобы получившееся число было кратно 15. Сколько решений имеет задача?

Чтобы число было кратно 15, надо чтобы оно делилось на 5 и на 3:

• на 5 делятся числа, в конце которых стоит 0 или 5;
• на 3 делятся числа, сумма цифр которых делится на 3.

Значит подходят числа:

• 3 150, 6 150, 9 150,
• 1 155, 4 155, 7 155.

Ответ: Задача имеет 6 решений: 3 150, 6 150, 9 150, 1 155, 4 155, 7 155.

90. К числу 34 припишите слева и справа по одной цифре так. чтобы получившееся число было кратно 45. Сколько решений имеет задача?

Чтобы число было кратно 45, надо чтобы оно делилось на 5 и на 9:

• на 5 делятся числа, в конце которых стоит 0 или 5;
• на 9 делятся числа, сумма цифр которых делится на 9.

Значит подходят числа:

• 2 340
• 6 345

Ответ: Задача имеет 2 решения: 2 340, 6 345.

91.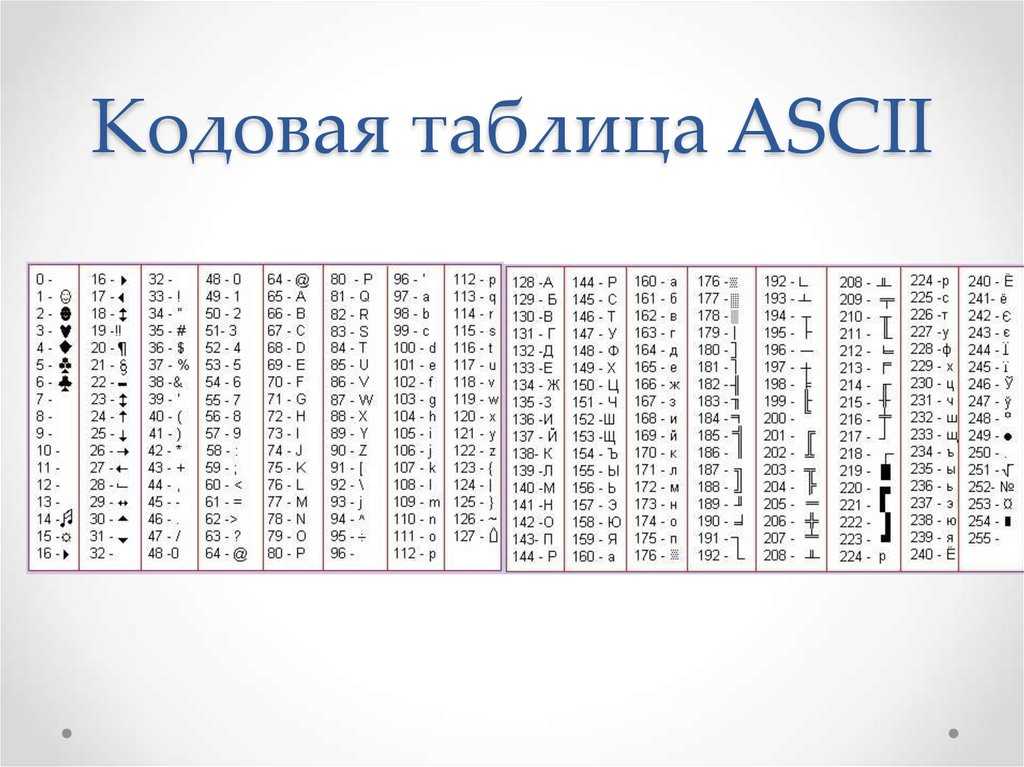 Вместо звёздочек поставьте такие цифры, чтобы четырёхзначное число *74* делилось нацело на 18. Найдите все решения.

Чтобы число было делилось нацело на 18, надо чтобы оно делилось на 2 и на 9:

• на 2 делятся все чётные числа, то есть числа оканчивающиеся на 0, 2, 4, 6 и 8;
• на 9 делятся числа, сумма цифр которых делится на 9.

Значит подходят числа:

• 7 740,
• 5 742,
• 3 744,
• 1 746,
• 8 748.

Ответ: Задача имеет 5 решения: 7 740, 5 742, 3 744, 1 746, 8 748.

92. Вместо звёздочек поставьте такие цифры, чтобы четырёхзначное число 3 *4* делилось нацело на 9. Найдите все решения.

• Чтобы число делилось нацело на 9, надо чтобы сумма его цифр делилась на 9.
• Мы знаем, что в числе 3 * 4* уже есть цифры 3 и 4. Сумма этих цифр равна 3 + 4 = 7.
• Значит сумма оставшихся цифр может быть равна 2 либо 11.
• Подойдут следующие варианты:
  • 3 042, 3 141, 3 240 — в которых сумма дописанных цифр равна 2, а общая сумма чисел равна 9;
  • 3 249, 3 348, 3 447, 3 546, 3 645, 3 744, 3 843, 3 942 — в которых сумма дописанных цифр равна 11, а их общая сумма равна 18.

93. Папа Карло купил три пакета кефира, пачку масла за 45 сольдо, несколько буханок хлеба по 24 сольдо, шесть коробков спичек. Может ли вся покупка стоить 200 сольдо?

Пусть папа Карло заплатил за покупку:

• 3a сольдо за кефир, если он купил 3 пачки кефира по а сольдо за каждую;
• 45 сольдо за масло;
• 24b сольдо за хлеб, если он купил b буханок хлеба по 24 сольдо за каждую;
• 6c сольдо за спички, если он купил 6 коробков по с сольдо за каждый.

Предположим, что такая покупка могла стоить ровно 200 сольдо. Тогда можно записать:

• 3а + 45 + 24b + 6с = 200

Мы видим, что каждое из слагаемых кратно 3. Значит можно записать:

• 3 • а + 3 • 15 + 3 • 8b + 3 • 2с = 200

Согласно распределительному свойству умножения, мы можем вынести число 3 за скобку:

• 3 • (а + 15 + 8b + 2с) = 200

Чтобы найти сумму в скобках, придётся 200 : 3

• (а + 15 + 8b + 2с) = 200 : 3

Это невозможно, так как 200 не делится на 3 нацело.  

Значит наше предположение неверно и такая покупка не могла стоить 200 сольдо.

Ответ: Вся покупка не может стоить 200 сольдо.

94. Сначала вычислили сумму цифр числа, равного произведению 1 • 2 • 3 • … • 999 • 1 000. Потом вычислили сумму цифр полученного числа. Так поступали до тех пор, пока не получили однозначное число. Что это за число?

Как мы видим, в данном произведении находятся множители кратные всем натуральным числам, в том числе и кратные 2, 3, 5, 9 и 10. 

• Это значит, что произведение будет чётным числом, оканчивающимся на 0.
• Кроме того, сумма цифр этого числа будет делиться на 3 и 9, согласно признаку делимости чисел на 3 и на 9.
• Отметим, что не все числа, делящиеся на 3, делятся и на 9, но все числа делящиеся на 9 точно делятся на 3. Так что для нас важно, что установить, что произведение будет точно делиться на 9.

Так как сумма цифр числа произведения делится на 9, то и число, обозначающее эту сумму цифр тоже будет обязательно делиться на 9.  

После многократного повторения такого действия в результате останется число, сумма цифр которого равна 9.

Это значит, что в результате получиться число 9.

Ответ: 9.

95. Рома и Дима записывают девятнадцатизначное число, используя только цифры 1, 2 и 4. Первую цифру пишет Рома, вторую — Дима, третью — снова Рома и так далее по очереди. Рома хочет получить в результате число, кратное 3. Может ли Дима помешать ему это сделать?

Представим, как могут развиваться события: 

Вариант 1:

1 ход: Рома может поставить любую цифру, например 1;

2 ход: Дима хочет помешать и ставит цифру, которая сделает число не кратным 3, например 4;

3 ход: Рома видит, что сумма записанных цифр равна 5 и ставит цифру 1 или цифру 4, что позволит ему исправить ситуацию.

Игра продолжается и каждый раз Дима делает сумму цифр не кратную 3, а Рома исправляет ситуацию.

19 ход. Рома ходит последним и делает сумму цифр полученного числа кратную 3.

Рома выигрывает, поскольку он ходит последним, а цифр 1, 2 и 4 ему достаточно, чтобы сделать кратным число, некратное 3.

Вариант 2:

1 ход: Рома может поставить любую цифру, например 1;

2 ход: Дима, несмотря на своё намерение помешать, делает так, чтобы сумма записанных цифр была кратна 3;

3 ход: Роме приходится писать любую цифру, так как ни одно из разрешённых цифр не кратно 3.

Игра продолжается и каждый раз Дима делает сумму цифр кратную 3, а от действий Ромы ничего не зависит.

18 ход. Дима опять делает так, чтобы сумма записанных цифр была кратна 3.

19 ход. Рома проигрывает, так как какие бы из цифр 1, 2 или 4 он не записал, сумма всех цифр уже не будет кратной 3.

Вывод:

Для того, чтобы Дима смог помешать Роме, ему надо «поддаться» и на каждом ходу сделать сумму цифр кратную 3. Тогда Рома, который ходит последним, не сможет исправить ситуацию.

Ответ: да, Дима сможет это сделать.

Упражнения для повторения

96. Как изменится — увеличится или уменьшится — и на сколько девятизначное число, последняя цифра которого 0, а предпоследняя — 5, если эти две цифры поменять местами?

Пусть все неизвестные цифры этого девятизначного числа будут спрятаны за х. Тогда можно записать:

• исходное девятизначное число — ххххххх50
• новое девятизначное число — ххххххх05

Мы видим, что исходное число больше, чем новое. Выполним вычитание столбиком:

Ответ: число уменьшится на 45.

97. Река Иртыш на 598 км длиннее реки Оби. Найдите длину каждой из этих рек, если их общая длина равна 7 898 км.

Пусть длина Оби х км, тогда длина Иртыша (х + 598 км). Можем составить уравнение:

х + (х + 598) = 7 898
2х + 598 = 7 898
2х = 7 898 — 598
2х = 7 400
х = 7 400 : 2
х = 3 700 (км) — длина Оби.

3 700 + 598 = 4 298 (км) — длина Иртыша.

Ответ: длина Иртыша — 4 298 км, а длина Оби — 3 700 км.

98. По маршруту Орёл — Тула — Москва выехал автомобиль. Какое расстояние между Орлом и Тулой, если оно на 5 км больше расстояния между Тулой и Москвой, а длина всего маршрута составляет 345 км?

Пусть х км расстояние между Тулой и Москвой. Тогда (х + 5) — расстояние между Орлом и Тулой. Можем составить уравнение:

х + (х + 5) = 345
2х + 5 = 345
2х = 345 — 5
2х = 340
х = 340 : 2
х = 170 (км) — расстояние межу Тулой и Москвой.

170 + 5 = 175 (км) — расстояние между Орлом и Тулой.

Ответ: между Москвой и Тулой 175 км.

99. Вычислите:

Готовимся к изучению новой темы

100. Упростите выражение, заменив произведение одинаковых множителей степенью:

101. Найдите значение выражения:

102. Запишите число 64 в виде степени с основанием:

1) 8

2) 4

3) 2

Задача от мудрой совы

103. В чемпионате страны по футболу принимают участие 16 команд, каждая из которых имеет свой стадион. Все команды должны сыграть между собой, причём в каждом туре проводятся 8 игр. Можно ли составить расписание туров так, чтобы каждая команда по очереди играла на своём стадионе и на стадионе соперника?

Предположим, что возможно составить такое расписание. Для удобства разделим команды на 2 группы: красную и синюю. По 8 команд в каждой.

• 1, 3, 5 и 7 тур: Команды красной группы играют на своём поле с командами из синей группы, то есть синие будут играть на поле соперника.
• 2, 4, 6 и 8 тур: Команды синей группы играют на своём поле с командами из красной группы, то есть красные будут играть на поле соперника.

После 8 тура получится, что любая команда из красной группы уже сыграла с каждой командой из синей группы и наоборот.

Это значит, что дальше команды из красной группы должны играть между собой, а команды из синей группы — между собой.

Но, так как все команды одной группы одинаково чередовали свой и чужой стадион, то получиться, что у одного из соперников порядок чередования нарушится. Например, если должны сыграть 1 и 2 команда из красной группы, то они будут играть на стадионах:

1. свой — чужой — свой — чужой — свой — чужой — свой — чужой — свой;
2. свой — чужой — свой — чужой — свой — чужой — свой — чужой — чужой.

То есть второй команде из красной группы придётся 2 раза подряд сыграть на стадионе соперника. 

Это противоречит нашему предположению. Значит такое расписание составить невозможно.

Ответ: нет, невозможно.

• Ответы к учебнику для 6 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Как добавлять начальные нули к числам или тексту с неравной длиной

Итог: Узнайте, как написать простую формулу для добавления нулей перед числами или текстом в столбце, где значения имеют разную длину. Это также известно как дополнение чисел ведущими или предшествующими нулями.

Уровень навыка: Простой

Проблема: Как добавить нули в начале числа?

Меган задала отличный вопрос о том, как добавить нули обратно в начало некоторых идентификационных номеров. Это часто называют дополнением чисел нулями.

У нее есть список идентификаторов сотрудников, которые когда-то были текстом с начальными нулями. Однако текстовые значения были преобразованы в числа, а нули в начале каждого числа были удалены.

Нам нужно добавить нули обратно, чтобы мы могли выполнить поиск в другой таблице. Эта таблица содержит столбец идентификационных номеров, хранящихся в виде текста с ведущими нулями.

Решение №1: Заполнение чисел с помощью функции ТЕКСТ

В этом примере числа в столбце А имеют разную длину, и нам нужно преобразовать их в 6-значные числа.

Есть несколько способов решить эту проблему, и использование функции ТЕКСТ, вероятно, является самым простым.

На следующем рисунке показано, как написать формулу ТЕКСТ для преобразования значения в строку длиной 6 символов.

 =ТЕКСТ(A2, "000000") 

«000000» — это числовой формат, который преобразует число в 6-значное число. Нули в числовом формате являются заполнителями для чисел. Если существует число больше нуля, то будет отображаться это число, в противном случае будет отображаться ноль.

Таким образом, эта простая формула добавит правильное количество нулей в начале значения, чтобы создать 6-значное число. Важно отметить, что формула возвращает текстовое значение . Это похоже на число, но t тип данных на самом деле текст .

Это означает, что мы можем использовать его в функции поиска, такой как ВПР или ПОИСКПОЗ, для поиска идентификатора сотрудника в таблице данных и возврата имени сотрудника.

Решение №2. Заполнение цифр или текста с помощью функции ПРАВИЛЬНО

Иногда числа, которые нам нужно дополнить, также содержат текст. В этом случае функция ТЕКСТ не будет работать, поскольку она применяет формат числа .

Функция ПРАВИЛЬНО может помочь нам, когда значения содержат числа ИЛИ текст . Он работает для обоих и является хорошим универсальным решением.

Шаг 1. Добавьте начальные нули

Первый шаг — добавьте такое же количество начальных нулей в начале числа. В этом примере самое короткое число в столбце A состоит из 3 цифр. Поэтому мы добавим 3 нуля перед всеми числами, чтобы убедиться, что каждое число состоит как минимум из 6 цифр.

Некоторые номера будут длиннее 6 цифр, и пока это нормально.

Шаг 2: Используйте функцию ПРАВИЛЬНО, чтобы удалить лишние нули

Теперь мы можем использовать функцию ПРАВИЛЬНО, чтобы вернуть 6 цифр или символов с правой стороны значения.

Это в основном удаляет все лишние нули, которые мы добавили перед числами на первом шаге.

Объедините это в одну простую формулу, чтобы добавить ведущие нули

Я разбил ее на два шага, чтобы объяснить формулу. Однако шаги можно объединить в одну простую формулу.

Эта простая формула добавит правильное количество нулей в начале значения, чтобы создать 6-значное число. Важно отметить, что формула возвращает текстовое значение . Это похоже на число, но t тип данных на самом деле текст .

Альтернативные решения для заполнения чисел

Другой альтернативой является применение пользовательского форматирования чисел. Это отобразит значение в виде 6-значного числа. Однако это НЕ изменит значение. Значение в ячейке по-прежнему будет исходным числом, которое содержит менее 6 символов. Поэтому мы НЕ сможем использовать отформатированное значение в нашей формуле поиска.

Мы также можем использовать вложенную формулу ЕСЛИ, функцию ПРАВИЛЬНО или функцию ВЫБОР для выполнения той же задачи, что и функция ТЕКСТ. Все эти альтернативы будут более длинными и сложными формулами.

Как вы вводите цифры или текст?

У вас есть более сложный сценарий, в котором вам нужно дополнить числа? Мы всегда так делаем, верно…? 🙂

Пожалуйста, оставьте комментарий ниже с вашим сценарием или любыми вопросами или предложениями. Спасибо!

3.3.4 Двоичная арифметика

Учись

Двоичные дополнения

• В двоичной системе счисления или системе счисления с основанием 2 есть только две цифры, 0 и 1 .
• Это означает, что в отличие от десятичной системы счисления 1 + 1 не равно 2 , это равно 10 .
• Ознакомьтесь со следующими правилами, которые применяются при сложении двоичных чисел. вместе:
  • 0 + 0 = 0
  • 0 + 1 = 1
  • 1 + 0 = 1
  • 1 + 1 = 10 ( 0 и содержат 1 )
  • 1 + 1 + 1 = 11 ( 1 и содержат 1 )
• Двоичное сложение можно выполнить с помощью сложения столбцов. Поскольку наибольшее значение, которое может иметь однозначное двоичное число, равно 1, что угодно превышающее это, должно быть перенесено в следующую колонку (2) в таблица значений мест с основанием 2:

	32	16	8	4	2	1
						1
+						1
Ответить					1	0
Переносится					1

• Посмотрите, как 0101 и 0111 были сложены вместе с помощью столбца дополнение в примере ниже:

	32	16	8	4	2	1
			0	1	0	1
+			0	1	1	1
Ответить			1	1	0	0
Переносится			1	1	1

• 1 + 1 = 10 и 10 + 1 = 11 поэтому:
• 1 + 1 + 1 = 11

Ошибки переполнения

• Ошибка переполнения возникает при ответе на двоичное сложение уравнение больше, чем ЦП способен обрабатывать.
• Например, процессор с разрядностью 8 бит может обрабатывать двоичные данные. номера до 11111111 . Однако, если добавить еще один бит, чтобы дать 100000000 , 9-битный ответ, процессор проигнорирует 1 и выведет 00000000 , что неверно.

Объяснение двоичного сложения

• В следующем видео показано, как выполнить двоичное сложение.

Badge It

Silver — выполните следующие бинарные дополнения:

1

	128	64	32	16	8	4	2	1
	0	0	1	1	1	0	1	1
+	0	1	0	1	0	0	0	1
Ответить
Переносится

2

	128	64	32	16	8	4	2	1
	0	1	0	0	1	1	1	1
	0	1	0	1	0	1	1	1
+	1	0	0	1	0	1	0	0
Ответить
Переносится

3

	128	64	32	16	8	4	2	1
	1	1	0	1	0	0	1	1
	1	1	1	0	1	1	1	1
+	0	0	0	1	0	1	0	0
Ответить
Переносится

Загрузка в представление данных — двоичная арифметика: серебро на BourneToLearn

Learn It

Двоичные сдвиги

• В двоичной системе счисления или системе счисления с основанием 2 значение цифры изменяется в степени двойки, когда его место в числе смещается влево (Умножение) или направо (разделенный)
• В следующей таблице показано, как двоичные числа сдвигаются в степени из двух:

	Сдвиг влево	Сдвиг вправо
Смена 1 место	Умножить на 2	Разделить на 2
Смена 2 места	Умножить на 4	Разделить на 4
Смена 3 места	Умножить на 8	Разделить на 8

Сдвиг влево (умножение) двоичного числа)

• Если двоичное число сдвинуто влево, это эквивалентно умножение числа на 2 для каждого сдвига влево.
• Например: если мы сдвинем на два разряда влево:

0

0

0

0

1

1

1

1

<—————————————————

• Это дает нам двоичное число:

0

0

1

1

1

1

0

0

• (Примечание: мы заполняем пустые бинарные позиции 0s при переходе к слева)
• Исходное двоичное число имеет значение 15 (т. е. 8 + 4 + 2 + 1 = 15).
• После сдвига на две позиции влево значение равно 60 (т.е. 32 + 16 + 8 + 2 + 1 = 15). Это умножается на 4 или 2 ²

Сдвиг вправо (деление) двоичного числа)

• Если двоичное число сдвинуто вправо, это эквивалентно деление числа на 2 для каждого сдвига влево.
• Например: если мы сдвинем на три разряда вправо:

0

1

1

1

0

0

0

0

—————————————————>

• Это дает нам двоичное число:

0

0

0

0

1

1

1

0

• Исходное двоичное число имеет значение 112 (т. е. 64 + 32 + 16 = 112).
• После сдвига на три позиции вправо значение равно 14 (т.е. 8 + 4 + 2 = 14). Число было разделено на 8 и стало 2 ³ .
• (Примечание: мы заполняем пустые бинарные позиции 0s по мере перехода к справа)

Badge It

Золото — Запишите результаты после следующих операций сдвига и запишите десятичные значения до и после сдвигов:

 1. Двоичное число 11001100 сдвинуто на ДВА знака вправо.
2. Двоичное число 00011001 сдвинуто на ДВА знака влево.
3. Двоичное число 11001000 сдвинуто на ТРИ знака вправо.
4. Двоичное число 00000111 сдвинуто на ЧЕТЫРЕ разряда влево.
5. Двоичное число 10000000 сдвинуто на ПЯТЬ знаков вправо.
 

Загрузка в представление данных — двоичная арифметика: Золото на BourneToLearn

Точность двоичного сдвига с умножением/делением на степень двойки

• Этот метод позволяет легко умножать и делить двоичные числа.