20 задач по электродинамике. Вариант 3
Тест содержит 20 заданий (Э1–Э20). К каждому заданию дается 4 варианта ответа, из которых правильный только один.
Внимательно прочитайте каждое задание и предлагаемые варианты ответа. Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа.
Выбрав нужный вариант ответа под номером выполняемого вами задания (Э 1–Э 25), кликните мышкой в кружочке, соответствующем выбранному вами ответу.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
За выполнение каждого задания дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
 При одном сопротивлении реостата вольтметр показывает 6 В, амперметр 1 А (см. рисунок). При другом сопротивлении реостата показания приборов: 4 В и 2 А. Чему равно внутреннее сопротивление источника тока? Амперметр и вольтметр считать идеальными. При одном сопротивлении реостата вольтметр показывает 6 В, амперметр 1 А (см. рисунок). При другом сопротивлении реостата показания приборов: 4 В и 2 А. Чему равно внутреннее сопротивление источника тока? Амперметр и вольтметр считать идеальными. |
0,5 Ом
1 Ом
1,5 Ом
2 Ом
Э2. Две проволоки одинаковой длины из одного и того же материала включены последовательно в электрическую цепь. Сечение первой проволоки в 3 раза больше сечения второй. Количество теплоты, выделяемое в единицу времени в первой проволоке,
в 3 раза меньше, чем во второй
в 9 раза больше, чем во второй
в 3 раз меньше, чем во второй
Э3.
Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. При перемещении по какой траектории электрическое поле совершает меньшую работу?
При перемещении по какой траектории электрическое поле совершает меньшую работу?
I
II
III
работа одинакова при движении по всем траекториям
Э4. При прохождении электромагнитных волн в воздухе происходят колебания
молекул воздуха
плотности воздуха
напряженности электрического и индукции магнитного полей
концентрации кислорода
Э5. Контур АВСD находится в однородном магнитном поле, линии индукции которого направлены перпендикулярно плоскости чертежа от наблюдателя (см. рисунок, вид сверху). Магнитный поток через контур будет меняться, если контур
движется в направлении к наблюдателю
поворачивается вокруг стороны АВ
движется в плоскости рисунка
Э6. На рисунке приведен график зависимости силы тока от времени в колебательном контуре. На каком из графиков правильно показан процесс изменения заряда конденсатора?
На рисунке приведен график зависимости силы тока от времени в колебательном контуре. На каком из графиков правильно показан процесс изменения заряда конденсатора?
Э7. Как изменится сопротивление цепи, изображенной на рисунке, при замыкании ключа K?
уменьшится
увеличится
не изменится
уменьшится или увеличится в зависимости от соотношения между сопротивлениями R1 и R2
Э8. Узкий пучок белого света в результате прохождения через стеклянную призму расширяется, и на экране наблюдается разноцветный спектр. Это явление объясняется тем, что призма
поглощает свет с некоторыми длинами волн
окрашивает белый свет в различные цвета
преломляет свет с разной длиной волн по-разному, разлагая его на составляющие
изменяет частоту волн
Э9.
и в газах, и в электролитах – только ионами
в газах – только ионами, в электролитах – ионами и электронами
в газах – электронами и ионами, в электролитах – только ионами
и в газах, и в электролитах – только электронами
Э10. На штепсельных вилках некоторых бытовых электрических приборов имеется надпись: «6 А, 250 В». Определите максимальную допустимую мощность электроприборов, которые можно включать, используя такие вилки.
1500 Вт 41,6 Вт 1,5 Вт 0,024 Вт
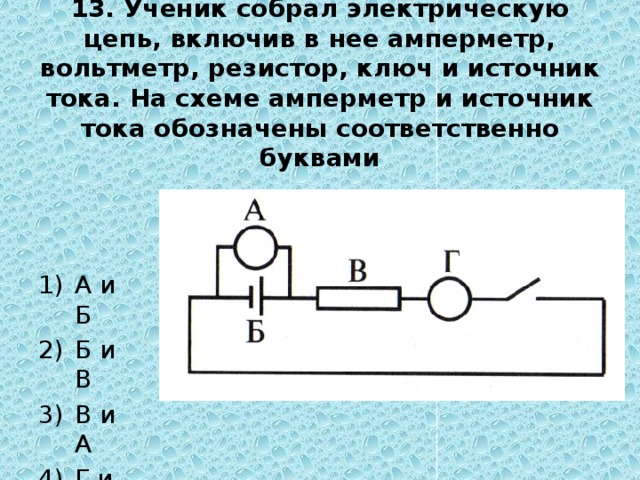
Э11. На рисунке показан участок цепи постоянного тока, содержащий 3 лампочки накаливания. Если сопротивление каждой лампочки 24 Ом, то сопротивление всего участка цепи
72 Ом
48 Ом
36 Ом
8 Ом
Э12. Как инфракрасное излучение воздействует на живой организм?
Как инфракрасное излучение воздействует на живой организм?
вызывает фотоэффект
охлаждает облучаемую поверхность
нагревает облучаемую поверхность
способствует загару
Э13. Участок цепи состоит из трех последовательно соединенных резисторов, сопротивления которых равны r, 2r и 3r. Сопротивление участка уменьшится в 1,5 раза, если убрать из него
первый резистор второй резистор третий резистор первый и второй резисторы
Э14. При прохождении по проводнику электрического тока силой 5 А в течение 2 мин совершается работа 150 кДж. Чему равно сопротивление проводника?
0,02 Ом 50 Ом 3 кОм 15 кОм
Э15. Какое утверждение о взаимодействии трех изображенных на рисунке заряженных частиц является правильным?
1 и 2 отталкиваются, 2 и 3 притягиваются, 1 и 3 отталкиваютсяь
1 и 2 притягиваются, 2 и 3 отталкиваются, 1 и 3 отталкиваются
1 и 2 отталкиваются, 2 и 3 притягиваются, 1 и 3 притягиваются
1 и 2 притягиваются, 2 и 3 отталкиваются, 1 и 3 притягиваются
Э16.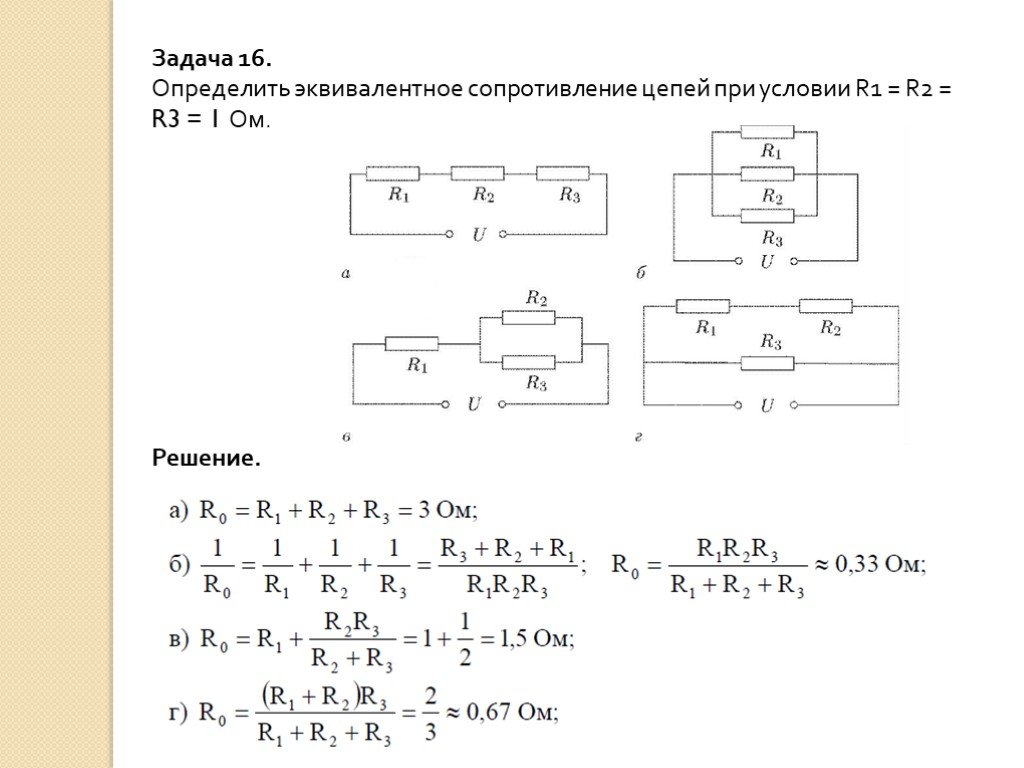
отклонение магнитной стрелки вблизи проводника с током
взаимодействие двух проводов с током
появление тока в замкнутой катушке при опускании в нее постоянного магнита
возникновение силы, действующей на проводник с током в магнитном поле
Э17. На рисунке показан ход светового луча через стеклянную призму. Показатель преломления стекла n определяется отношением длин отрезков
CD/AB
AB/CD
OB/OD
OD/OB
Э18. На рисунке (вид сверху) показана картина линий индукции магнитного поля прямого проводника с током. В какой из четырех точек индукция магнитного поля наименьшая?
в точке а
в точке б
в точке в
в точке г
Э19.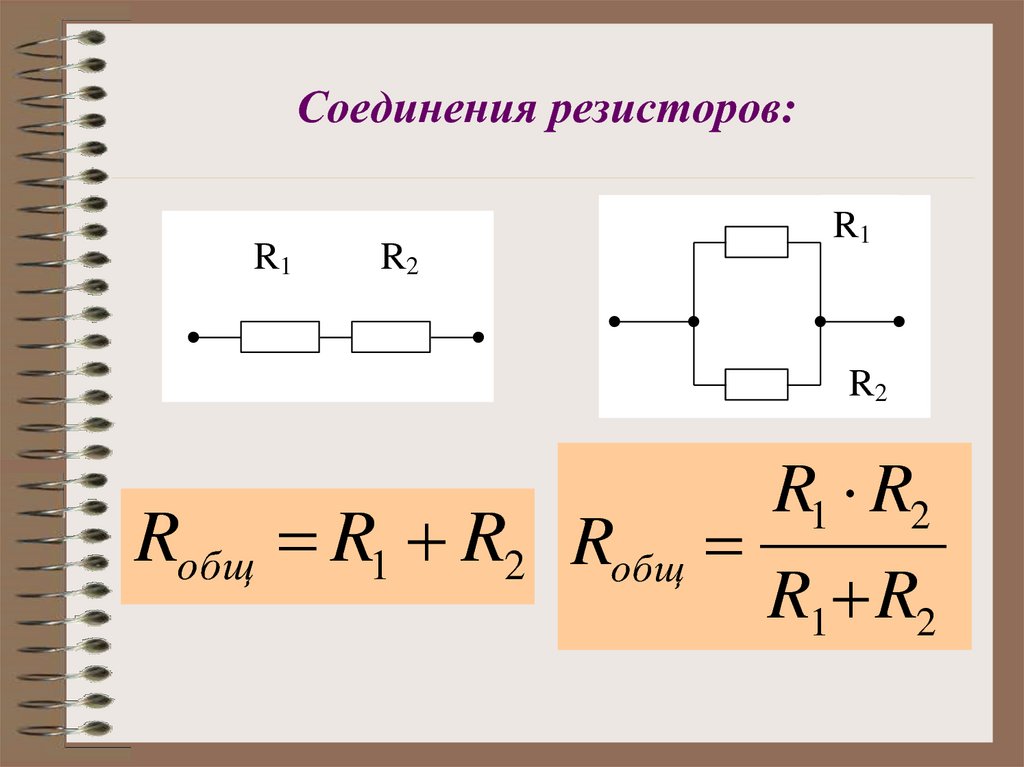 Изучая закономерности соединения резисторов, ученик собрал электрическую цепь, изображенную на рисунке. Какая энергия выделится во внешней части цепи при протекании тока в течение 10 минут? Необходимые данные указаны на схеме. Амперметр считать идеальным.
Изучая закономерности соединения резисторов, ученик собрал электрическую цепь, изображенную на рисунке. Какая энергия выделится во внешней части цепи при протекании тока в течение 10 минут? Необходимые данные указаны на схеме. Амперметр считать идеальным.
60 Вт
960 Вт
1800 Вт
3600 Вт
Э20. Дифракционная решетка с периодом 10-5 м расположена параллельно экрану на расстоянии 1,8 м от него. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 20,88 см от центра дифракционной картины при освещении решетки нормально падающим пучком света длиной волны 580 нм? Считать sinα = tgα.
0 1 2 3
Входная контрольная работа по физике ( 10 класс)
Входная контрольная работа 10класс
1 вариант
А1. Яблоко массой 0,3 кг падает с дерева. Выберите верное утверждение.
Выберите верное утверждение.
1) Яблоко действует на Землю силой 3 Н, а Земля не действует на яблоко.
2) Земля действует на яблоко с силой 3 Н, а яблоко не действует на Землю.
3) Яблоко и Земля не действуют друг на друга.
4) Яблоко и Земля действуют друг на друга с силой ЗН.
А2. С помощью простого механизма
1) можно получить выигрыш в силе, но нельзя получить выигрыш в работе
2) нельзя получить выигрыш в силе, но можно получить выигрыш в работе
3) можно получить выигрыш и в силе, и в работе
4) нельзя получить выигрыша ни в силе, ни в работе
А3. Автомобиль массой 2 103 кг движется равномерно по мосту. Скорость автомобиля равна 5 м/с. Чему равна кинетическая энергия автомобиля? 1) 105 Дж 2) 104 Дж 3) 2,5 · 104 Дж 4) 5 103 Дж
А4. При силе тока в электрической цепи 0,6 А сопротивление лампы равно 5 Ом. Мощность электрического тока, выделяющаяся на нити лампы, равна 1) 0,06 Вт 2) 1,8 Вт 3) 3 Вт 4) 15 Вт
А5. Радиоактивный изотоп нептуния после одного α-распада превращается в изотоп
Радиоактивный изотоп нептуния после одного α-распада превращается в изотоп
С1.На покоящееся тело массой 0,2кг действует в течении 5с сила 0,1Н. Какую скорость приобретает тело и какой путь оно пройдет за указанное время.
С2.Линейная скорость некоторой точки на грампластинке 0,3м/с, а центростремительное ускорение 0,9м/с2. Найдите расстояние этой точки от оси вращения.
С3.Вагон массой 30т движется со скоростью 2м/с по горизонтальному участку дороги сталкивается и сцепляется с помощью автосцепки с неподвижным вагоном массой 20т. Чему равна скорость совместного движения вагонов.
2вариант
А1. Двое учеников стоя, на роликовых коньках, держатся за одну веревку, протянутую между ними. Когда они начинают вдвоем вытягивать веревку, первый начинает двигаться с ускорением а. С каким ускорением движется второй, если его масса в 2 раза меньше? Силой трения между роликами коньков и землей можно пренебречь.
1) 2а 2) а 3) 2а/3 4) а/2
А2. . С помощью системы блоков
. С помощью системы блоков
1) нельзя получить выигрыша ни в силе, ни в работе
2) нельзя получить выигрыш в силе, но можно получить выигрыш в работе
3) можно получить выигрыш и в силе, и в работе
4) можно получить выигрыш в силе, но нельзя получить выигрыш в работе
А3. Изучая закономерности соединения резисторов, ученик собрал электрическую цепь (см. рис.) и измерил силу тока в ней. Какова работа электрического тока на резисторах при протекании тока в течение 1 мин?
1) 3 Дж 2) 6 Дж 3) 24 Дж 4) 1440 Дж
А4. Скорость автомобиля массой 1000 кг при торможении изменяется в соответствии с графиком, представленным на рисунке. Чему равна кинетическая энергия автомобиля через 20 с после начала торможения?
1) 8 ·105Дж 2) 4 ·105 Дж 3) 2 · 105Дж 4) 105 Дж
А5. Радиоактивный изотоп полония превращается в стабильное ядро полония в результате радиоактивных распадов: 1) одного β 2) одного а и двух β 3) двух а и одного β 4) двух а и двух β
1. Мяч массой 0,5кг после удара, длящегося 0,02с, приобретает скорость 10м/с. Найдите силу удара.
Мяч массой 0,5кг после удара, длящегося 0,02с, приобретает скорость 10м/с. Найдите силу удара.
2.Конькобежец движется со скоростью 10 м/с по окружности радиусом 20м. Определите его центростремительное ускорение.
3.Две тележки, движущиеся на встречу друг другу, со скоростью 0,2м/с и 0,4м/с сталкиваются и начинают двигаться вместе. Найдите скорость тележек после взаимодействия. Массы тележек соответственно равны 600кг и 350кг.
А1
А2
А3
А4
А5
С1
С2
С3
1вариант
4
1
3
2
1
2,5м/с;6,25м
0,1м
1,2м/с
2вариант
1
4
4
3
2
250Н
5м/с2
0,02м/с
Просмотр содержимого документа
«Входная контрольная работа по физике ( 10 класс) »
Входная контрольная работа 10класс
1 вариант
А1. Яблоко массой 0,3 кг падает с дерева.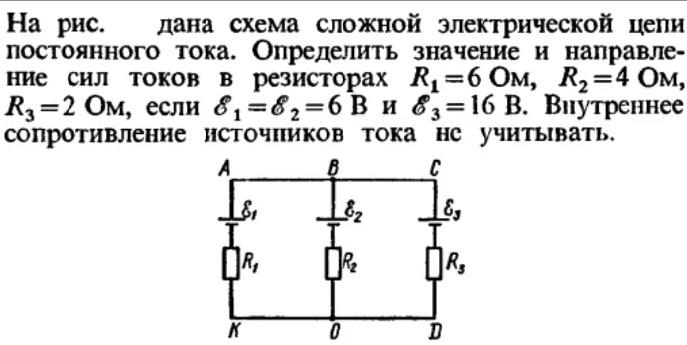 Выберите верное утверждение.
Выберите верное утверждение.
1) Яблоко действует на Землю силой 3 Н, а Земля не действует на яблоко.
2) Земля действует на яблоко с силой 3 Н, а яблоко не действует на Землю.
3) Яблоко и Земля не действуют друг на друга.
4) Яблоко и Земля действуют друг на друга с силой ЗН.
А2. С помощью простого механизма
1) можно получить выигрыш в силе, но нельзя получить выигрыш в работе
2) нельзя получить выигрыш в силе, но можно получить выигрыш в работе
3) можно получить выигрыш и в силе, и в работе
4) нельзя получить выигрыша ни в силе, ни в работе
А3. Автомобиль массой 2 103 кг движется равномерно по мосту. Скорость автомобиля равна 5 м/с. Чему равна кинетическая энергия автомобиля? 1) 105 Дж 2) 104 Дж 3) 2,5 · 104 Дж 4) 5 103 Дж
А4. При силе тока в электрической цепи 0,6 А сопротивление лампы равно 5 Ом. Мощность электрического тока, выделяющаяся на нити лампы, равна 1) 0,06 Вт 2) 1,8 Вт 3) 3 Вт 4) 15 Вт
А5. Радиоактивный изотоп нептуния после одного α-распада превращается в изотоп
Радиоактивный изотоп нептуния после одного α-распада превращается в изотоп
С1.На покоящееся тело массой 0,2кг действует в течении 5с сила 0,1Н. Какую скорость приобретает тело и какой путь оно пройдет за указанное время.
С2.Линейная скорость некоторой точки на грампластинке 0,3м/с, а центростремительное ускорение 0,9м/с2. Найдите расстояние этой точки от оси вращения.
С3.Вагон массой 30т движется со скоростью 2м/с по горизонтальному участку дороги сталкивается и сцепляется с помощью автосцепки с неподвижным вагоном массой 20т. Чему равна скорость совместного движения вагонов.
2вариант
А1. Двое учеников стоя, на роликовых коньках, держатся за одну веревку, протянутую между ними. Когда они начинают вдвоем вытягивать веревку, первый начинает двигаться с ускорением а. С каким ускорением движется второй, если его масса в 2 раза меньше? Силой трения между роликами коньков и землей можно пренебречь.
1) 2а 2) а 3) 2а/3 4) а/2
А2. . С помощью системы блоков
. С помощью системы блоков
1) нельзя получить выигрыша ни в силе, ни в работе
2) нельзя получить выигрыш в силе, но можно получить выигрыш в работе
3) можно получить выигрыш и в силе, и в работе
4) можно получить выигрыш в силе, но нельзя получить выигрыш в работе
А3. Изучая закономерности соединения резисторов, ученик собрал электрическую цепь (см. рис.) и измерил силу тока в ней. Какова работа электрического тока на резисторах при протекании тока в течение 1 мин?
1) 3 Дж 2) 6 Дж 3) 24 Дж 4) 1440 Дж
А4. Скорость автомобиля массой 1000 кг при торможении изменяется в соответствии с графиком, представленным на рисунке. Чему равна кинетическая энергия автомобиля через 20 с после начала торможения?
1) 8 ·105Дж 2) 4 ·105 Дж 3) 2 · 105Дж 4) 105 Дж
А5. Радиоактивный изотоп полония превращается в стабильное ядро полония в результате радиоактивных распадов: 1) одного β 2) одного а и двух β 3) двух а и одного β 4) двух а и двух β
1. Мяч массой 0,5кг после удара, длящегося 0,02с, приобретает скорость 10м/с. Найдите силу удара.
Мяч массой 0,5кг после удара, длящегося 0,02с, приобретает скорость 10м/с. Найдите силу удара.
2.Конькобежец движется со скоростью 10 м/с по окружности радиусом 20м. Определите его центростремительное ускорение.
3.Две тележки, движущиеся на встречу друг другу, со скоростью 0,2м/с и 0,4м/с сталкиваются и начинают двигаться вместе. Найдите скорость тележек после взаимодействия. Массы тележек соответственно равны 600кг и 350кг.
А1 | А2 | А3 | А4 | А5 | С1 | С2 | С3 | |
1вариант | 4 | 1 | 3 | 2 | 1 | 2,5м/с;6,25м | 0,1м | 1,2м/с |
2вариант | 1 | 4 | 4 | 3 | 2 | 250Н | 5м/с2 | 0,02м/с |
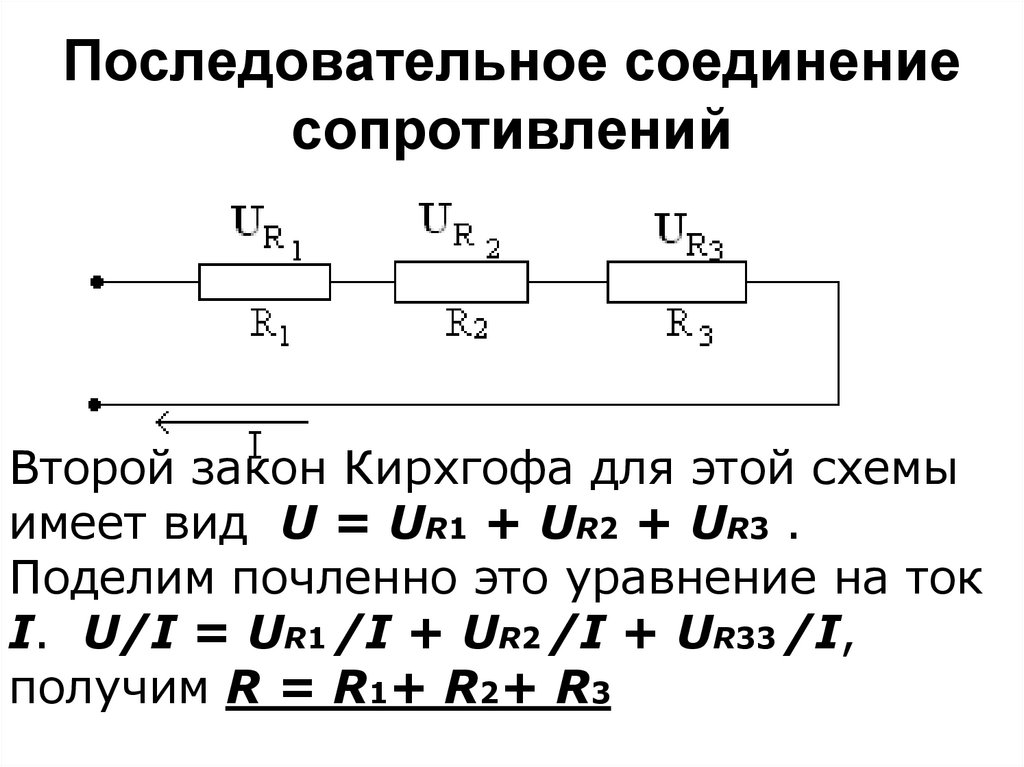
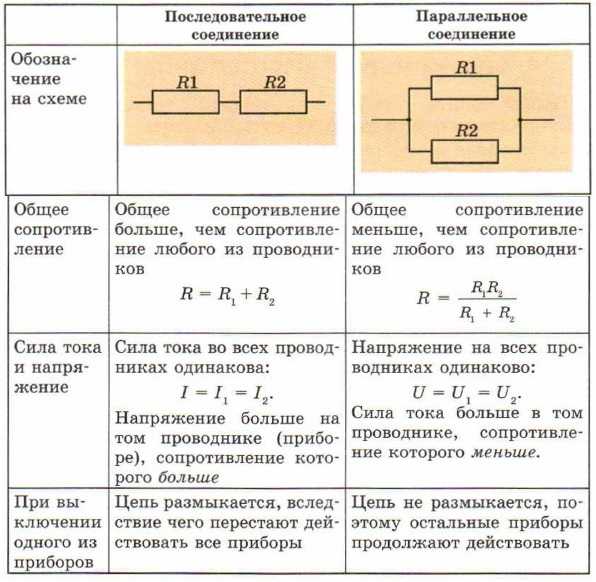
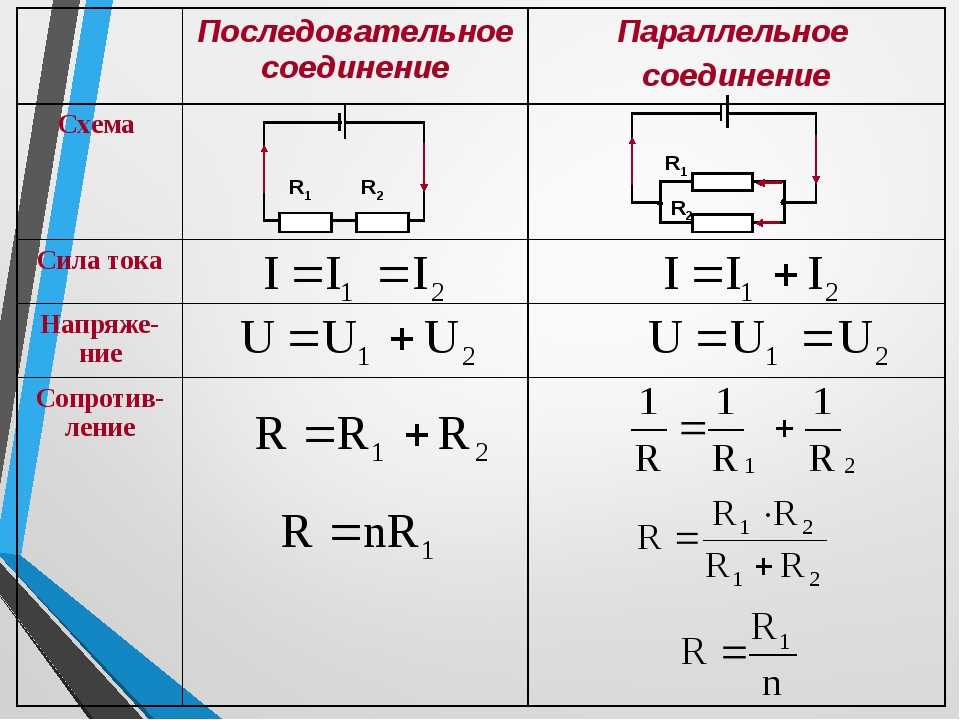
Учебное пособие по физике: последовательные цепи
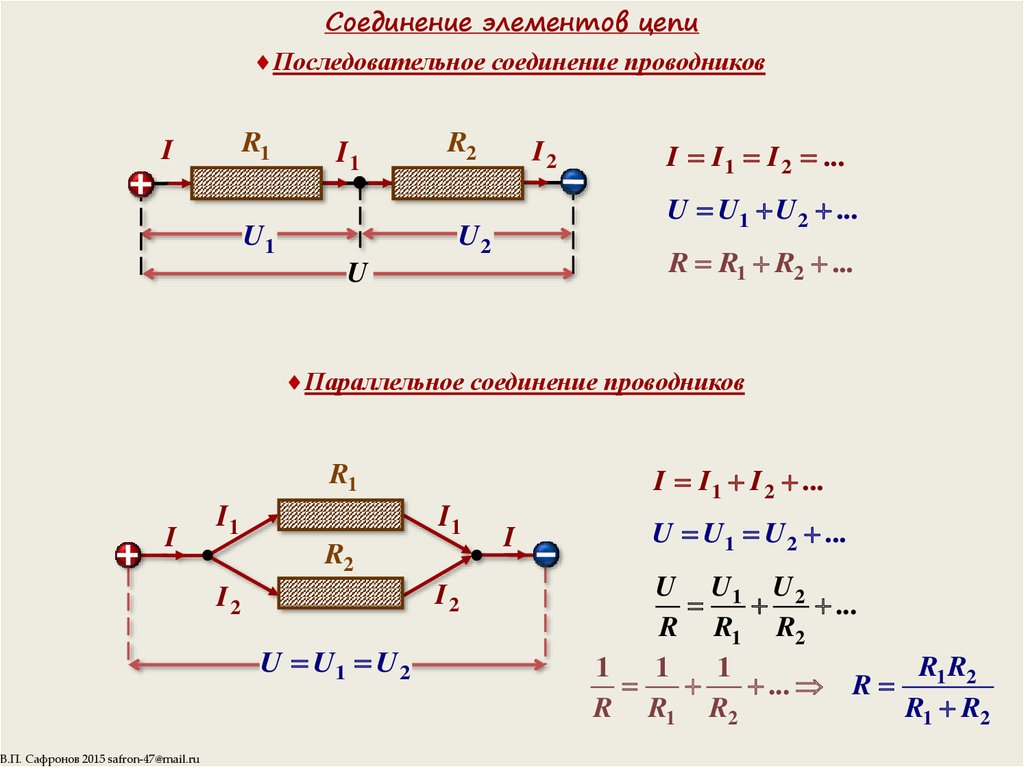
Как упоминалось в предыдущем разделе урока 4, два или более электрических устройства в цепи могут быть соединены последовательно или параллельно.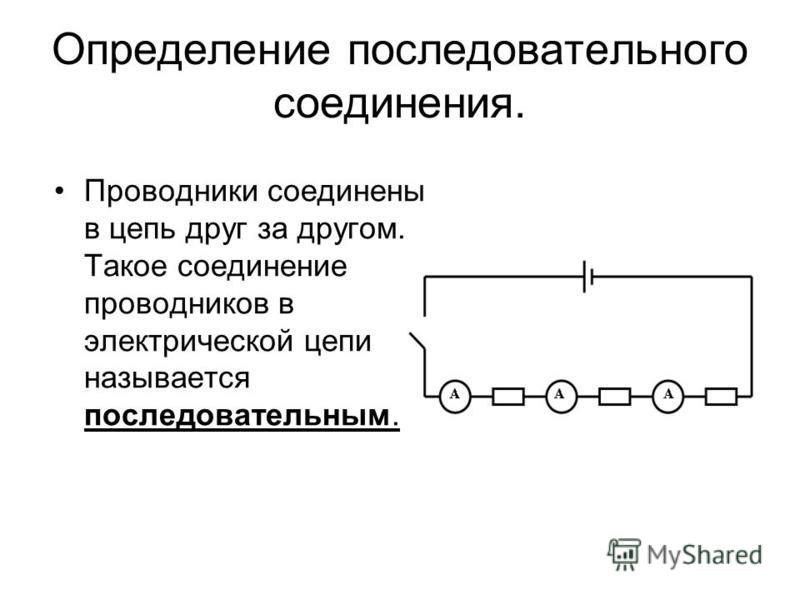 Когда все устройства соединены с помощью последовательных соединений, цепь называется последовательной цепью . В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может пройти через внешнюю цепь. Каждый заряд, проходящий через петлю внешней цепи, будет последовательно проходить через каждый резистор.
Когда все устройства соединены с помощью последовательных соединений, цепь называется последовательной цепью . В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может пройти через внешнюю цепь. Каждый заряд, проходящий через петлю внешней цепи, будет последовательно проходить через каждый резистор.
В предыдущем разделе урока 4 было проведено краткое сравнение и противопоставление последовательной и параллельной цепей. В этом разделе было подчеркнуто, что добавление большего количества резисторов в последовательную цепь приводит к довольно ожидаемому результату в виде увеличения общей сопротивление. Поскольку в цепи есть только один путь, каждый заряд сталкивается с сопротивлением каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это повышенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).
Эквивалентное сопротивление и ток
Заряды текут вместе по внешней цепи со скоростью, которая везде одинакова. Ток в одном месте не больше, чем в другом. Фактическая величина тока обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая качает заряд, наличие двух 6-омных резисторов, соединенных последовательно, будет эквивалентно наличию в цепи одного 12-омного резистора. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом будет эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. А наличие четырех резисторов на 6 Ом последовательно было бы эквивалентно наличию в цепи одного резистора на 24 Ом.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для расчета эквивалентного сопротивления (R экв. ) выглядит следующим образом:
Для последовательных цепей математическая формула для расчета эквивалентного сопротивления (R экв. ) выглядит следующим образом:
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных последовательно.
Больше практикиСоздавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Ток в последовательной цепи везде одинаков. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами так, что в одном месте его меньше, чем в другом. Заряды можно представить себе как марширующие вместе по проводам электрической цепи, везде марширующие с одинаковой скоростью. Ток — скорость, с которой течет заряд, — везде одинакова. Это то же самое на первом резисторе, что и на последнем резисторе, как и в батарее. Математически можно написать
Заряд НЕ расходуется резисторами так, что в одном месте его меньше, чем в другом. Заряды можно представить себе как марширующие вместе по проводам электрической цепи, везде марширующие с одинаковой скоростью. Ток — скорость, с которой течет заряд, — везде одинакова. Это то же самое на первом резисторе, что и на последнем резисторе, как и в батарее. Математически можно написать
, где I 1 , I 2 и I 3 , Iccount Thurn. Thuousth Ara The Arach значения в отдельных местах резисторов.
Эти значения тока легко рассчитать, если известно напряжение батареи и известны значения отдельных сопротивлений. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.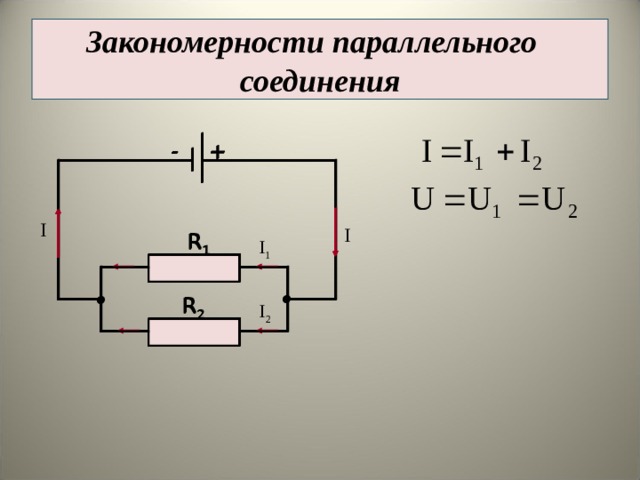
Electric Potential Difference and Voltage Drops
Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию заряду для его перемещения через ячейку и создания разности электрических потенциалов на двух концах внешней цепи. Ячейка на 1,5 вольта создаст разность электрических потенциалов во внешней цепи 1,5 вольта. Это означает, что электрический потенциал на положительной клемме на 1,5 вольт больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольта электрического потенциала. Эта потеря электрического потенциала называется падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. д.) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от 1,5-вольтовой ячейки, оснащена более чем одним резистором, то суммарная потеря электрического потенциала составляет 1,5 вольта. На каждом резисторе есть падение напряжения, но сумма этих падений напряжения составляет 1,5 вольта — столько же, сколько номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:
д.) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от 1,5-вольтовой ячейки, оснащена более чем одним резистором, то суммарная потеря электрического потенциала составляет 1,5 вольта. На каждом резисторе есть падение напряжения, но сумма этих падений напряжения составляет 1,5 вольта — столько же, сколько номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:
Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. что вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам придется использовать приведенное выше уравнение. Батарея изображается своим обычным схематическим символом, а ее напряжение указывается рядом с ним. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.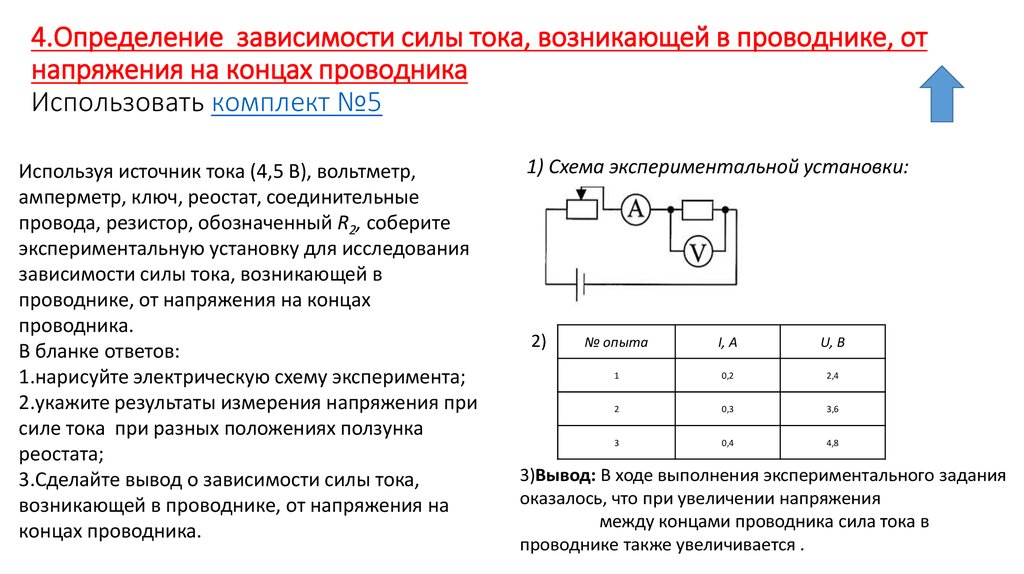
Ранее в Уроке 1 обсуждалось использование диаграммы электрического потенциала. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.
Схема, показанная на схеме выше, питается от 12-вольтового источника питания. В цепи последовательно соединены три резистора, каждый из которых имеет свое падение напряжения. Отрицательный знак разности электрических потенциалов просто означает, что при прохождении через резистор происходит потеря электрического потенциала. Обычный ток направляется по внешней цепи от положительного вывода к отрицательному. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, место А на схеме соответствует положительной клемме или клемме с высоким потенциалом.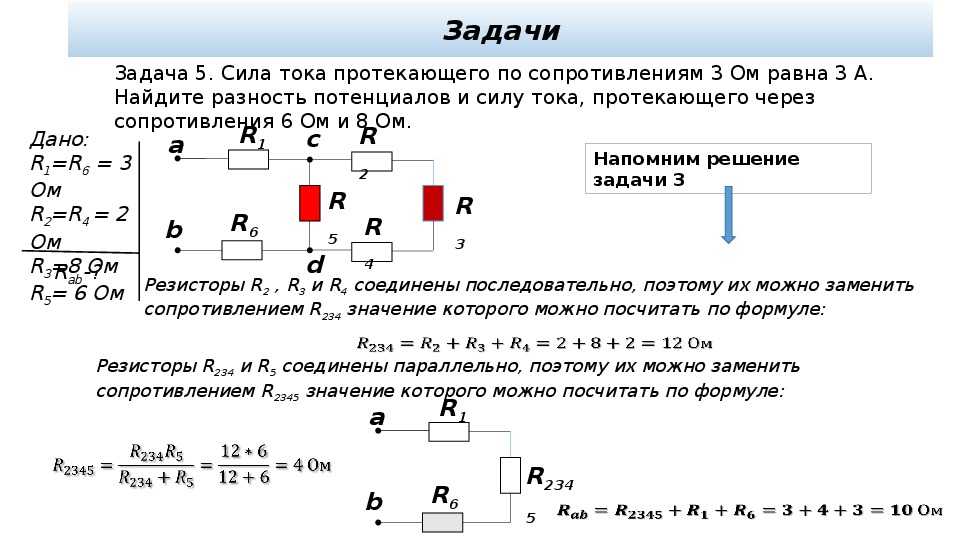 Место A находится под напряжением 12 вольт, а место H (отрицательная клемма) находится под напряжением 0 вольт. Проходя через аккумулятор, заряд приобретает 12 вольт электрического потенциала. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются за три этапа, каждый из которых соответствует протеканию через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда. Поскольку точки А и В разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через его первый резистор, он теряет 3 В электрического потенциала и падает до 9 В.V в точке C. Поскольку точка D отделена от точки C простым проводом, она имеет фактически тот же электрический потенциал 9 В, что и C.
Место A находится под напряжением 12 вольт, а место H (отрицательная клемма) находится под напряжением 0 вольт. Проходя через аккумулятор, заряд приобретает 12 вольт электрического потенциала. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются за три этапа, каждый из которых соответствует протеканию через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда. Поскольку точки А и В разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через его первый резистор, он теряет 3 В электрического потенциала и падает до 9 В.V в точке C. Поскольку точка D отделена от точки C простым проводом, она имеет фактически тот же электрический потенциал 9 В, что и C.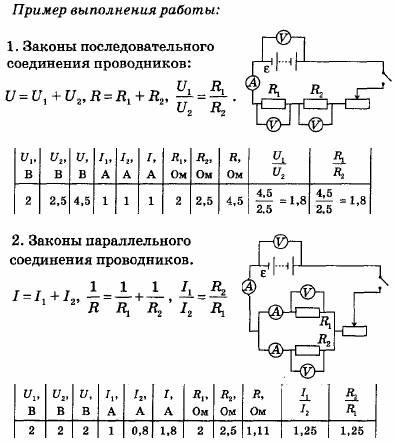 Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает вниз. до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет фактически тот же электрический потенциал 2 В, что и E. Наконец, когда заряд проходит через последний резистор, он теряет 2 В электрического тока. потенциала и падает до 0 В в точке G. В точках G и H заряду не хватает энергии, и ему требуется повышение энергии, чтобы снова пройти через внешнюю цепь. Повышение энергии обеспечивается аккумулятором по мере того, как заряд перемещается от H к A.
Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает вниз. до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет фактически тот же электрический потенциал 2 В, что и E. Наконец, когда заряд проходит через последний резистор, он теряет 2 В электрического тока. потенциала и падает до 0 В в точке G. В точках G и H заряду не хватает энергии, и ему требуется повышение энергии, чтобы снова пройти через внешнюю цепь. Повышение энергии обеспечивается аккумулятором по мере того, как заряд перемещается от H к A.
В уроке 3 закон Ома (ΔV = I • R) был представлен как уравнение, связывающее падение напряжения на резисторе с сопротивлением резистора и током на резисторе. Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсуждавшимися на этой странице, возникает большая идея.
В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.
Поскольку ток в последовательной цепи везде одинаков, значение I ΔV = I • R одинаково для каждого из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) зависит от изменения сопротивления. Везде, где сопротивление наибольшее, падение напряжения будет наибольшим на этом резисторе. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.
Математический анализ последовательных цепей
Приведенные выше принципы и формулы можно использовать для анализа последовательной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в последовательной цепи. Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока в батарее (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока в батарее (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
Теперь, когда известно эквивалентное сопротивление батареи можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:
Значение тока 1,5 ампера — это ток в месте расположения батареи.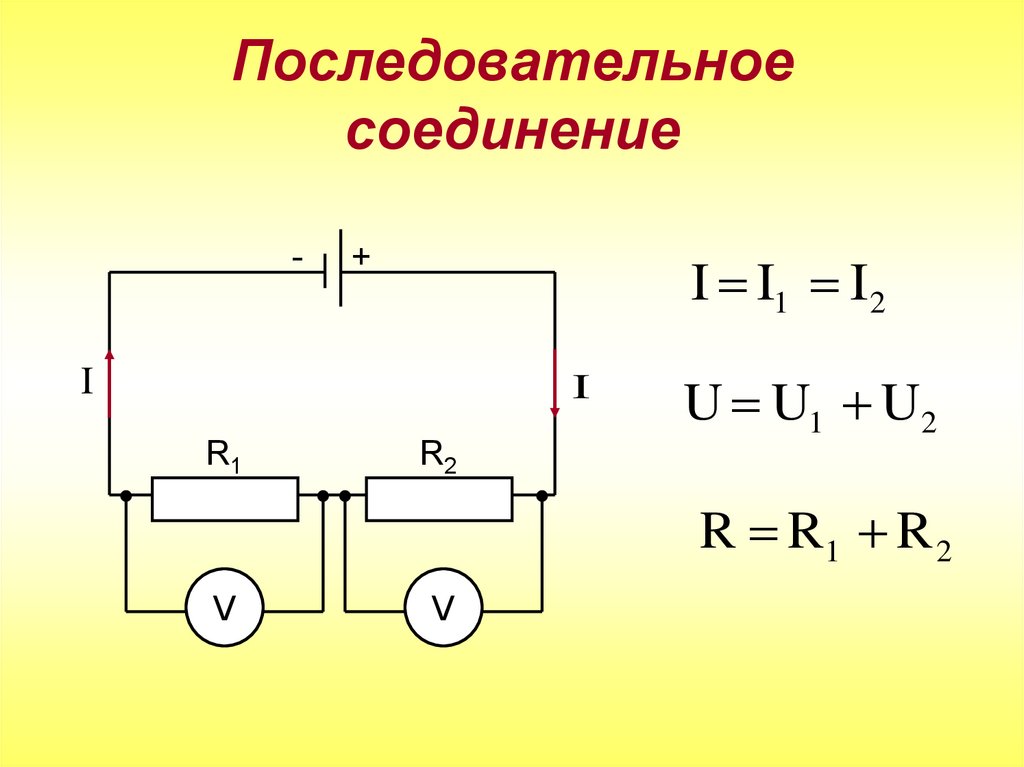 Для последовательной цепи без мест разветвления ток везде одинаков. Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Следовательно, 1,5 ампера — это значение I 1 , I 2 и I 3 .
Для последовательной цепи без мест разветвления ток везде одинаков. Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Следовательно, 1,5 ампера — это значение I 1 , I 2 и I 3 .
Осталось определить три значения — падение напряжения на каждом из отдельных резисторов. Закон Ома снова используется для определения падения напряжения на каждом резисторе — это просто произведение тока на каждом резисторе (рассчитанного выше как 1,5 ампера) и сопротивления каждого резистора (указанного в условии задачи). Расчеты показаны ниже.
ΔV 1 = (1,5 А) • (17 Ом) ΔV 1 = 25,5 В | ΔV 2 = (1,5 А) • (12 Ом) ΔV 2 = 18 В | ΔV 3 = (1,5 А) • (11 Ом) ΔV 3 = 16,5 В |
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма падений напряжения на каждом отдельном резисторе равна номинальному напряжению батареи.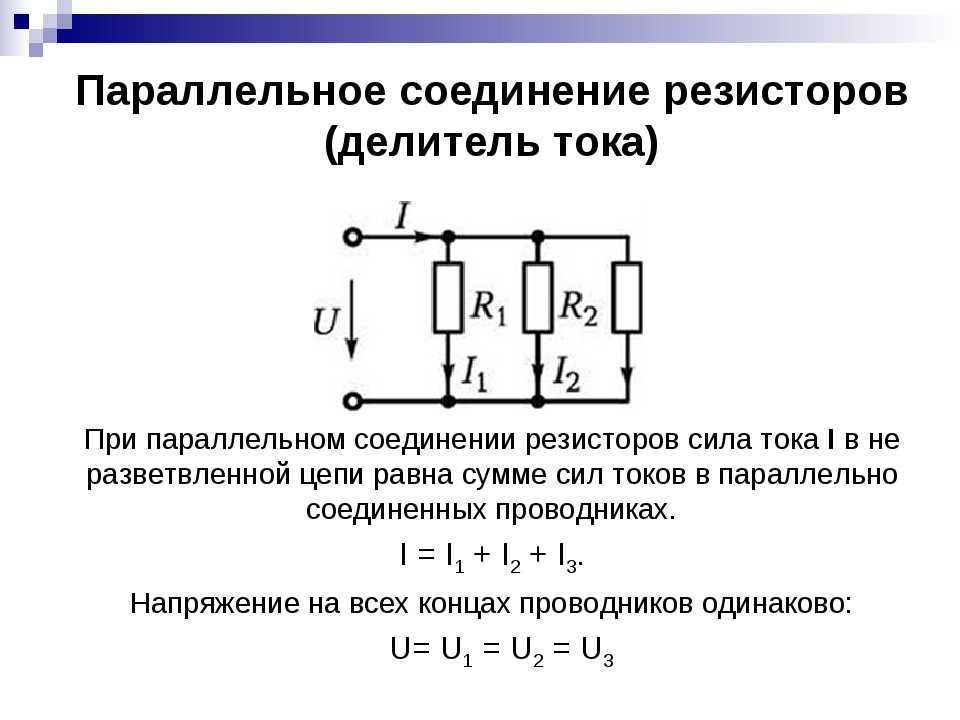 Другими словами, является ли ΔV батарея = ΔV 1 + ΔV 2 + ΔV 3 ?
Другими словами, является ли ΔV батарея = ΔV 1 + ΔV 2 + ΔV 3 ?
Является ли 60 В = 25,5 В + 18 В + 16,5 В?
Является ли 60 В = 60 В?
Да!!
Математический анализ этой последовательной цепи включал сочетание концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать понятия, что ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ. В следующей части урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход смешивания понятий с уравнениями будет столь же важен для этого анализа.
Мы хотели бы предложить .
 ..
.. Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).
Посетите: DC Circuit Builder
1. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:
Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:
a. Два последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.
б. Три последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.
с. Три последовательно соединенных резистора сопротивлением 5 Ом обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
2. При увеличении количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается неизменным) и ток в цепи __________ (увеличивается, уменьшается, остается неизменным).
3. Рассмотрим следующие две схемы последовательных цепей. Для каждой диаграммы используйте стрелки, чтобы указать направление условного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.
4. Три одинаковые лампочки подключены к D-ячейке, как показано справа. Какое из следующих утверждений верно?
а. Все три лампочки будут иметь одинаковую яркость.б. Лампочка между X и Y будет самой яркой.
в. Лампочка между Y и Z будет самой яркой.
д. Лампочка между Z и батареей будет самой яркой.
5. Три одинаковые лампочки подключены к батарейке, как показано справа. Какие корректировки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все, что применимо.
Три одинаковые лампочки подключены к батарейке, как показано справа. Какие корректировки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все, что применимо.
а. Увеличьте сопротивление одной из лампочек.б. Увеличьте сопротивление двух лампочек.
в. Уменьшите сопротивление двух лампочек.
д. Увеличьте напряжение батареи.
эл. Уменьшите напряжение батареи.
ф. Снимите одну из лампочек.
6. Три одинаковые лампочки подключены к батарейке, как показано справа. W, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Разность потенциалов между X и Y больше, чем между Y и Z.б. Разность потенциалов между X и Y больше, чем между Y и W.
в. Разность потенциалов между Y и Z больше, чем между Y и W.
д. Разность потенциалов между X и Z больше, чем между Z и W.
эл. Разность потенциалов между X и W больше, чем на аккумуляторе.
ф. Разность потенциалов между X и Y больше, чем между Z и W.
7. Сравните схемы X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на одном резисторе в цепи X.
a. меньше чемб. больше
в. то же, что
8. Батарея 12 В, резистор 12 Ом и лампочка подключены, как показано на схеме X ниже. Резистор на 6 Ом добавляется к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано на рисунке. Лампочка появится ____.
а. диммер в контуре Xб. диммер в цепи Y
в. одинаковая яркость в обоих контурах
9. Три резистора соединены последовательно.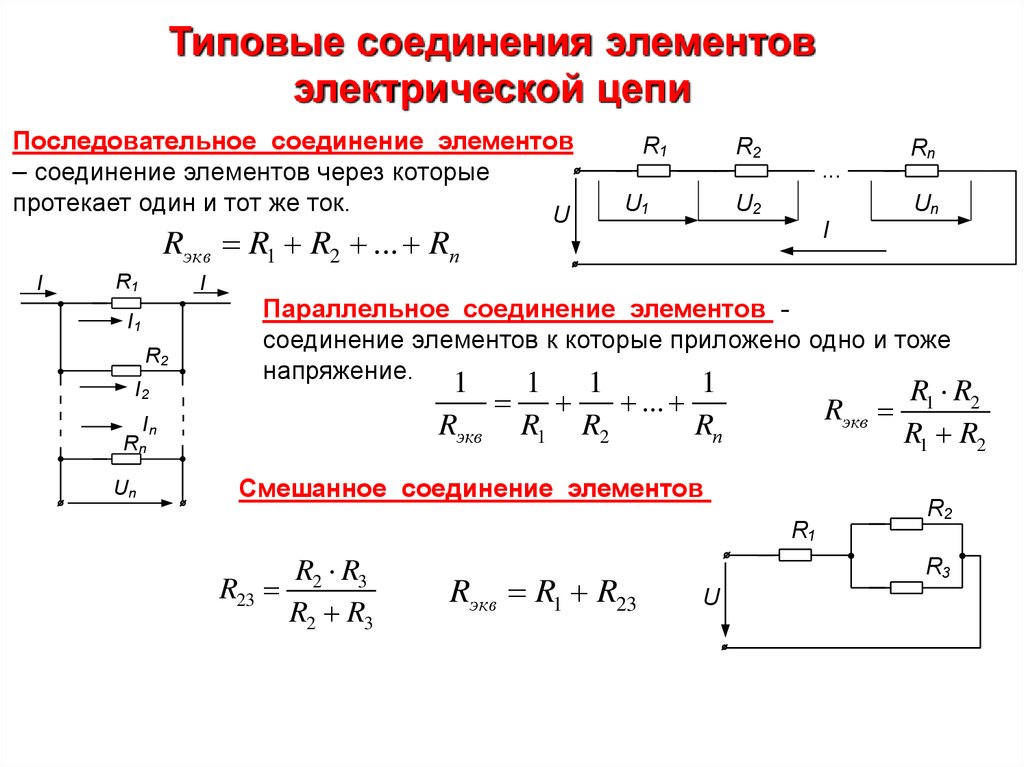 Если поместить в цепь с 12-вольтовым источником питания. Определить эквивалентное сопротивление, общий ток цепи, падение напряжения и ток на каждом резисторе.
Если поместить в цепь с 12-вольтовым источником питания. Определить эквивалентное сопротивление, общий ток цепи, падение напряжения и ток на каждом резисторе.
Следующий раздел:
Учебник по физике: параллельные цепи
Как упоминалось в предыдущем разделе урока 4, два или более электрических устройства в цепи могут быть соединены последовательно или параллельно. Когда все устройства соединены с помощью параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство размещается в своем отдельном отделение . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи. Каждый заряд, проходящий через петлю внешней цепи, пройдет через один резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел заряд делает выбор в отношении того, через какое ответвление следует пройти на обратном пути к терминалу с низким потенциалом.
Короткое сравнение и противопоставление последовательной и параллельной цепей было сделано в предыдущем разделе Урока 4. В этом разделе подчеркивалось, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату в виде меньшего общего сопротивление. Поскольку существует несколько путей, по которым может течь заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому можно направить заряд через основную область сопротивления в цепи. Это уменьшенное сопротивление в результате увеличения количества ответвлений приведет к увеличению скорости протекания заряда (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платной дорогой. Пункт взимания платы является основным местом сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов взимания платы в пределах их собственной ветки на платной дороге обеспечит больше путей для движения автомобилей через пункт взимания платы.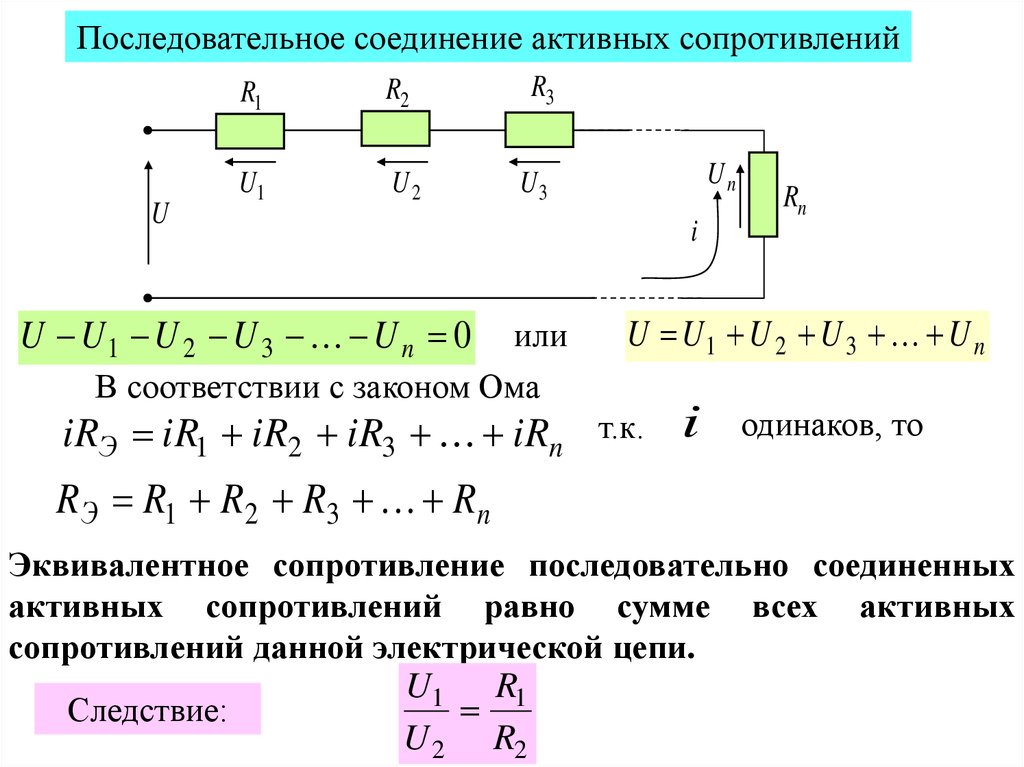 Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Эти дополнительные пункты взимания платы снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Ток
Скорость, с которой заряд течет по цепи, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами таким образом, чтобы ток в одном месте был меньше, чем в другом. В параллельной цепи заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Тем не менее, если взять в целом, общая сумма тока во всех ветвях при суммировании равна сумме тока в точках за пределами ветвей. правило, что ток везде тот же до сих пор работает, только с изюминкой. Ток вне ветвей равен сумме токов в отдельных ветвях. Это все тот же ток, только разделенный на более чем один путь.
В форме уравнения этот принцип можно записано как
 ..
.. , где I —
, где I —
, где I —
, где I —
, где I . общая сумма тока вне ветвей (и в аккумуляторе) и I 1 , I 2 и I 3 представляют ток в отдельных ветвях цепи.
На протяжении всего этого модуля широко использовалась аналогия между потоком заряда и потоком воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Течение заряда в проводах аналогично течению воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах разделяется на отдельные ветви. В каждой , узел (место разветвления), вода идет двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ответвлениях за пределами узла.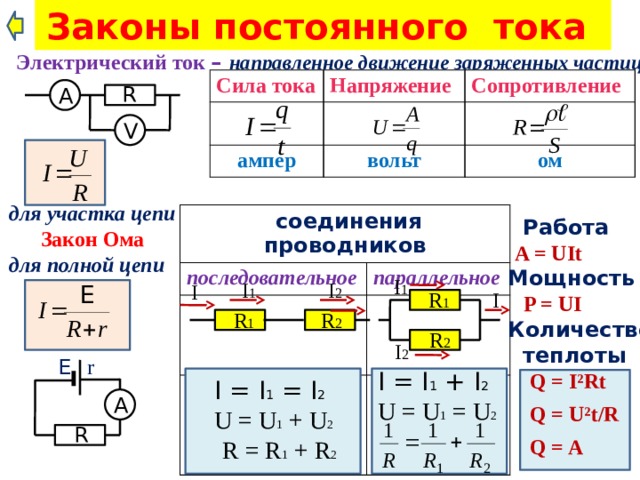 Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел.
Точно так же, когда две или более ветвей впадают в узел, скорость, с которой вода вытекает из узла, будет равна сумме скоростей потока в отдельных ветвях, впадающих в узел.
Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд течет в узел, равна сумме скоростей потока в отдельных ветвях за пределами узла. Это показано в примерах, показанных ниже. В примерах вводится новое обозначение схемы — буква А, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая незначительное сопротивление потоку заряда.
На схеме А показаны два резистора, соединенных параллельно с узлами в точках А и В. Заряд течет в точку А со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой через резистор 2. Ток в ответвлении с резистором 1 равен 2 ампера, а ток в ответвлении с резистором 2 равен 4 ампера.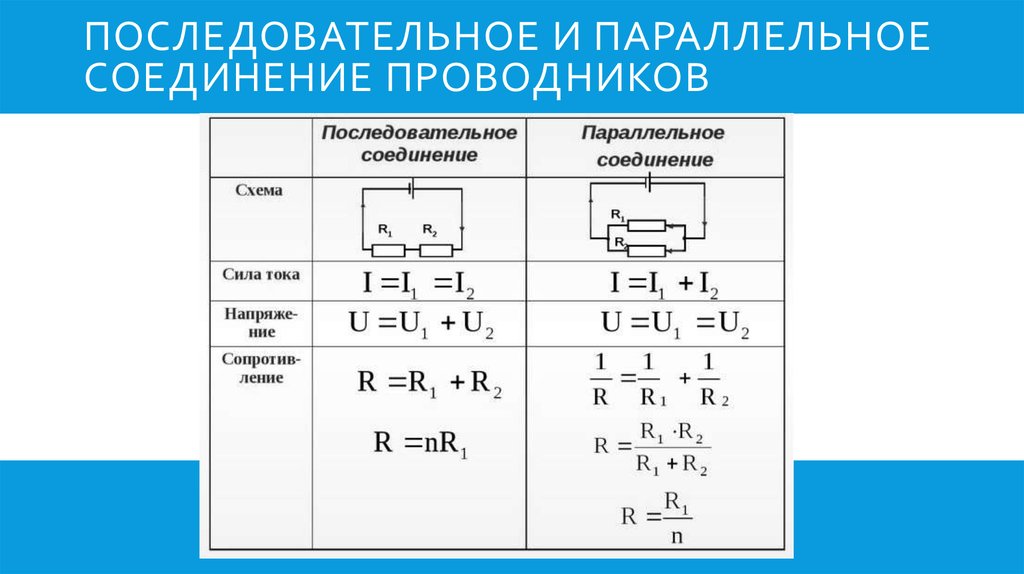 После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях.
После того, как эти две ветви снова встречаются в точке B и образуют единую линию, сила тока снова становится равной 6 ампер. Таким образом, мы видим, что справедлив принцип, согласно которому ток вне ветвей равен сумме токов в отдельных ветвях.
6 ампер = 2 ампера + 4 ампера
Схема B, приведенная выше, может быть немного сложнее, если на ней три резистора расположены параллельно. На диаграмме идентифицированы четыре узла, обозначенные A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторы 2). и 3). Ток 12 ампер делится на путь 2 ампера (через резистор 1) и путь 10 ампер (направленный к точке B). В точке Б происходит дальнейшее разделение потока на два пути — один через резистор 2, другой через резистор 3. Ток силой 10 ампер, приближающийся к точке В, разделяется на 6-амперный путь (через резистор 2) и 4-амперный путь.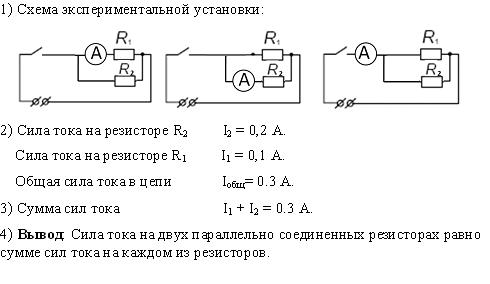 -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.
-амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера и что сумма значений тока в отдельных ветвях равна току вне ветвей.
12 ампер = 2 ампера + 6 ампер + 4 ампера
Можно также провести анализ потока в точках C и D, и видно, что сумма расходов потока, направляющихся в эти точки, равна расходу, который находится непосредственно за этими точками.
Эквивалентное сопротивление
Фактическая величина тока всегда обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая двух резисторов, размещенных на параллельных ветвях, каждый из которых имеет одинаковое значение сопротивления 4 Ом. Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора.
Поскольку схема предлагает два равно путям для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь оказывает сопротивление 4 Ом любому заряду, проходящему через нее, только половина всего заряда, протекающего через цепь, встретит сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая качает заряд, наличие двух 4-омных резисторов, включенных параллельно, было бы эквивалентно наличию в цепи одного 2-омного резистора. Точно так же наличие двух резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 3 Ом. А наличие двух 12-омных резисторов параллельно было бы эквивалентно наличию в цепи одного 6-омного резистора.
Теперь давайте рассмотрим еще один простой случай с тремя параллельными резисторами, каждый из которых имеет одинаковое сопротивление 6 Ом. С тремя 90 529 равными 90 530 путями для прохождения заряда через внешнюю цепь, только одна треть заряда выберет прохождение через данную ветвь.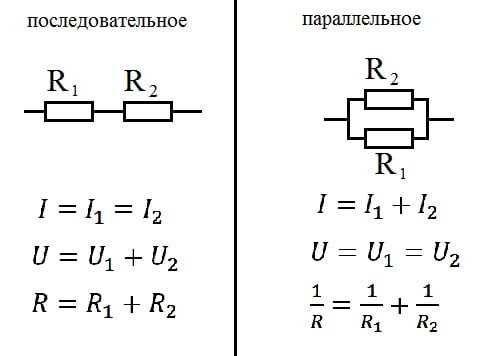 Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора.
Каждая отдельная ветвь оказывает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи равно 2 Ом. Что касается батареи, которая качает заряд, наличие трех резисторов 6 Ом параллельно будет эквивалентно наличию в цепи одного резистора 2 Ом. Таким же образом присутствие трех 9Параллельное подключение резисторов сопротивлением Ω эквивалентно наличию в цепи одного резистора сопротивлением 3 Ω. А наличие трех 12-омных резисторов параллельно будет эквивалентно наличию в цепи одного 4-омного резистора.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи. Для параллельных цепей математическая формула расчета эквивалентного сопротивления (R Уравнение ) IS
 ..
.. , где R 1 , R 2222222222222222222222222. 2 и R 3 — значения сопротивления отдельных резисторов, соединенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, когда все пути оказывают одинаковое сопротивление отдельному заряду, проходящему через них. Простые случаи выше были выполнены без использования уравнения. Тем не менее, уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления. Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.
1/R экв. Использование калькулятора… 1/R экв. = 0,25 Ом -1 Ч экв. = 1 / (0,25 Ом -1 ) R экв. = 4,0 Ом
| |
1/R экв. = 1/(5,0 Ом) + 1/(7,0 Ом) + 1/(12 Ом) Использование калькулятора… 1/R экв. = 0,42619 Ом-1 R экв. = 1 / (0,42619 Ом -1 ) R экв. = 2,3 Ом |
Ваша очередь попробовать
Нужно больше практики? Используйте Два резистора параллельно виджет ниже, чтобы попробовать некоторые дополнительные проблемы.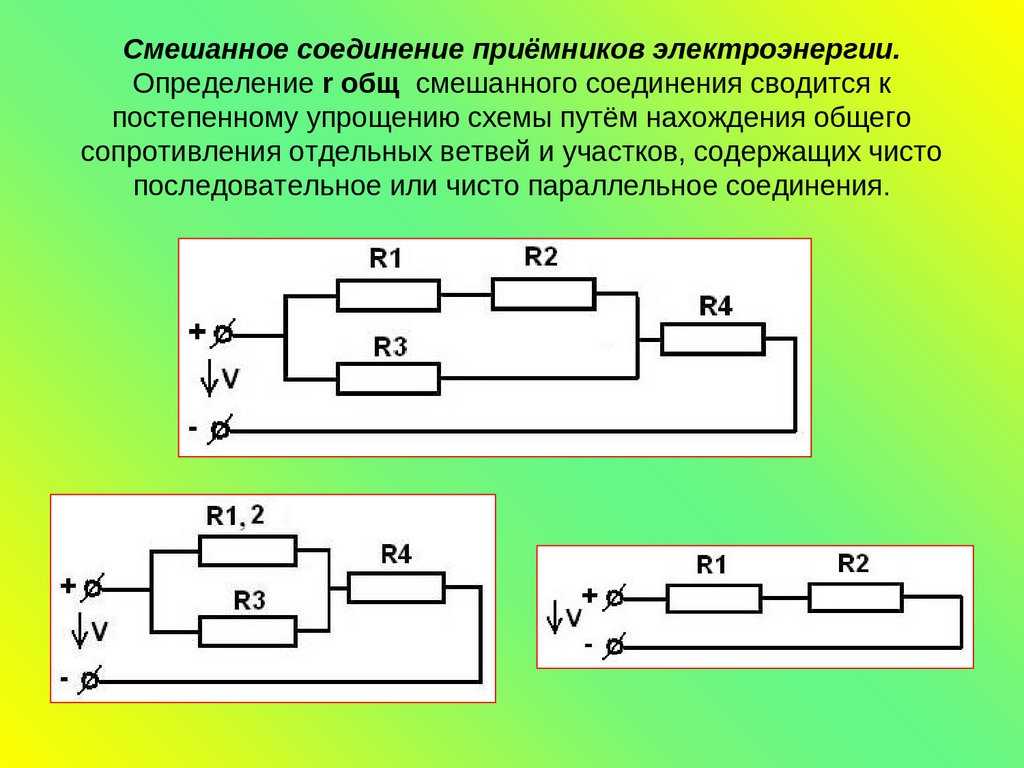 Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления.
Введите любые два значения сопротивления, которые вы хотите. Используйте свой калькулятор, чтобы определить значения R eq . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте сколько угодно раз с разными значениями сопротивления.
В разделе «Схемы» учебника «Класс физики» подчеркивалось, что любое повышение напряжения, полученное за счет заряда батареи, теряется из-за заряда, когда он проходит через резисторы внешний контур. Общее падение напряжения во внешней цепи равно приросту напряжения при прохождении заряда по внутренней цепи. В параллельной цепи заряд не проходит через каждый резистор; скорее, он проходит через один резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое оно выбирает для прохождения должно быть равно напряжению батареи.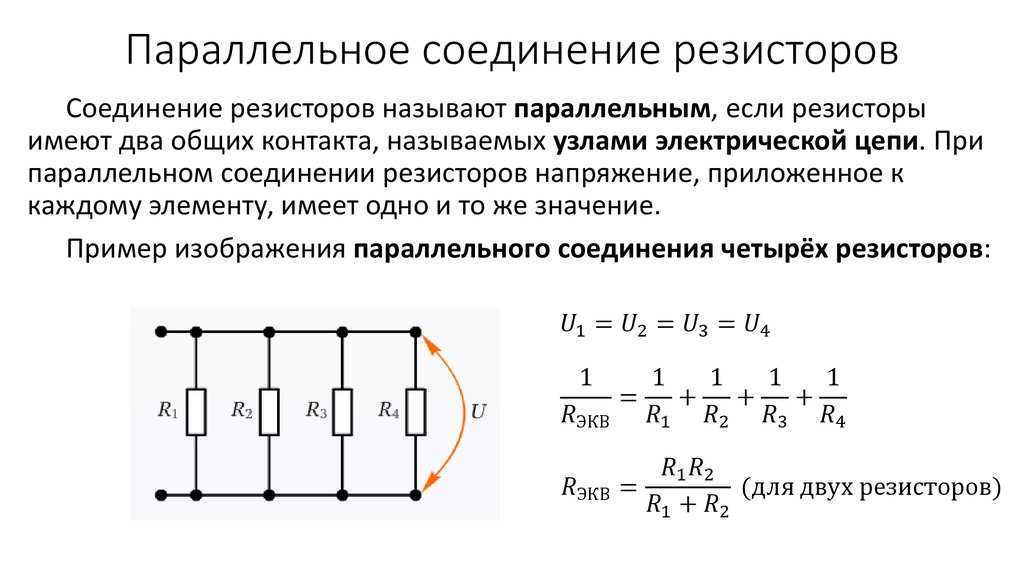 В виде уравнения этот принцип будет выражен как
В виде уравнения этот принцип будет выражен как
от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, столкнется только с одним из этих трех резисторов и, таким образом, столкнется с одним падением напряжения в 12 вольт.
Диаграммы электрических потенциалов были представлены в Уроке 1 этого модуля и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.
Как показано на диаграмме электрических потенциалов, положения A, B, C, E и G находятся под высоким электрическим потенциалом. Один заряд выбирает только один из трех возможных путей; таким образом, в положении B один заряд будет двигаться к точке C, E или G, а затем пройдет через резистор, который находится в этой ветви. Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.
Один заряд выбирает только один из трех возможных путей; таким образом, в положении B один заряд будет двигаться к точке C, E или G, а затем пройдет через резистор, который находится в этой ветви. Заряд не теряет своего высокого потенциала до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F, либо от G к H. Как только он проходит через резистор, заряд возвращается почти к 0 вольт и возвращается к отрицательному клемму аккумулятора для повышения напряжения. В отличие от последовательных цепей, заряд в параллельной цепи сталкивается с единичным падением напряжения на своем пути через внешнюю цепь.
Ток через данную ветвь можно предсказать, используя уравнение закона Ома и падение напряжения на резисторе и сопротивление резистора. Поскольку падение напряжения одинаково на каждом резисторе, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением испытывает наибольший ток. В этом смысле можно сказать, что заряд (как у людей) выбирает путь наименьшего сопротивления. В форме уравнения это можно записать как
В этом смысле можно сказать, что заряд (как у людей) выбирает путь наименьшего сопротивления. В форме уравнения это можно записать как
Этот принцип иллюстрируется схемой, показанной ниже. Произведение I•R одинаково для каждого резистора (и равно напряжению батареи). Но ток в каждом резисторе разный. Ток больше там, где сопротивление наименьшее, а ток меньше там, где сопротивление больше.
Математический анализ параллельных цепей
Приведенные выше принципы и формулы можно использовать для анализа параллельной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в параллельной цепи.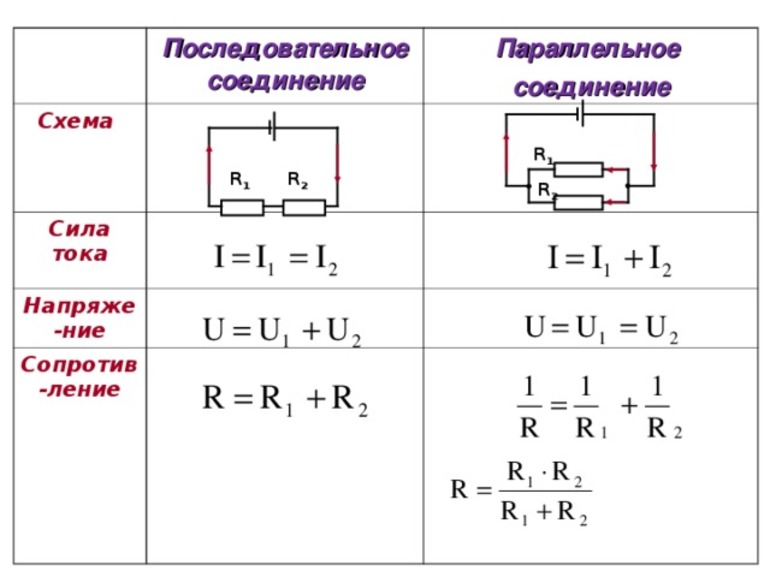 Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I tot ), а также падения напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
1 / R экв. = 0,23306 Ом -1
R экв. = 1 / (0,23306 Ом -1 )
R экв = 4,29Ом
(округлено от 4,29063 Ом)
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:
Расчет показан здесь:
I to = 14,0 ампер
(округлено от 13,98396 ампер)
Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом данном проходе через внешнюю цепь. То есть падение напряжения на каждом из трех резисторов такое же, как напряжение, полученное в батарее:
Осталось определить три значения — ток в каждом из отдельных резисторов. Закон Ома используется еще раз для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 вольт), деленное на сопротивление каждого резистора (данное в условии задачи). Расчеты показаны ниже.
Расчеты показаны ниже.
I 1 = (60 В) / (17 Ом) I 1 = 3,53 А | I 2 = (60 В) / (12 Ом) I 2 = 5,00 ампер | I 3 = (60 В) / (11 Ом) I 3 = 5,45 А |
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). Другими словами, я tot = I 1 + I 2 + I 3 ?
Является ли 14,0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?
Является ли 14,0 ампер = 13,98 ампер?
Да!!
(Разница в 0,02 ампера является просто результатом предварительного округления значения I до от 13,98. )
)
Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать концепцию, что падение напряжения на каждом из трех резисторов равно напряжению батареи и что сумма тока в каждом резисторе равна общему току. Это понимание необходимо для завершения математического анализа. В следующей части урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие последовательно.
Больше практики Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.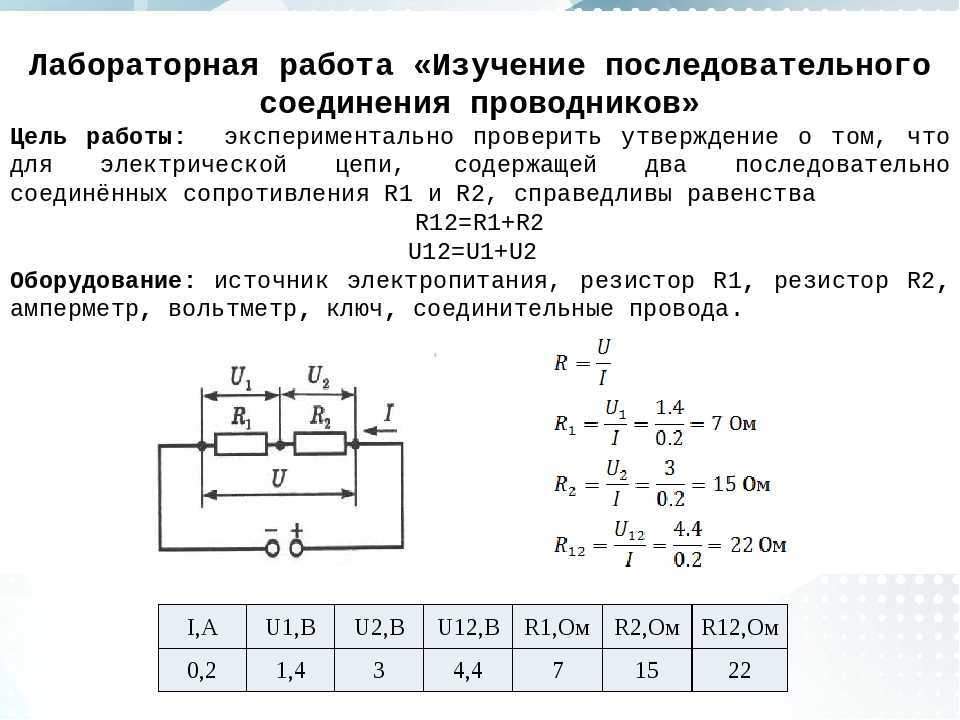
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).
Посетите: DC Circuit Builder
1. По мере того, как в цепь параллельно добавляются все новые и новые резисторы, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается) и общий ток цепи ____________ (увеличивается, уменьшается).
2. Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Ток Y больше тока Q.б. Ток на Y больше, чем ток на P.
в. Ток в Y больше, чем ток в Z.
д. Ток на P больше, чем ток на Q.
е. Ток на Q больше, чем ток на P.
ф. Ток одинаков во всех местах.
3. Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах) ток будет …
Три одинаковые лампочки подключены к D-элементу, как показано ниже. P, Q, X, Y и Z представляют местоположения вдоль цепи. В каком месте(ах) ток будет …
a. … такой же, как у X?б. … так же, как в Q?
в. … такой же, как у Y?
д. … меньше, чем на Q?
эл. … меньше, чем у P?
ф. … вдвое больше, чем у Z?
г. … в три раза больше, чем у Y?
4. Какие корректировки можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все, что применимо.
а. Увеличьте сопротивление лампы X.б. Уменьшите сопротивление лампы X.
в. Увеличьте сопротивление лампы Z.
д. Уменьшить сопротивление лампы Z.
эл. Увеличьте напряжение ячейки (как-то).
ф. Уменьшить напряжение ячейки (каким-то образом).
г. Снимите лампу Y.
.
5. Аккумулятор 12 В, резистор 12 Ом и резистор 4 Ом подключены, как показано на рисунке. Ток в резисторе сопротивлением 12 Ом в _____ раз больше, чем у резистора сопротивлением 4 Ом.
Аккумулятор 12 В, резистор 12 Ом и резистор 4 Ом подключены, как показано на рисунке. Ток в резисторе сопротивлением 12 Ом в _____ раз больше, чем у резистора сопротивлением 4 Ом.
а. 1/3
б. 1/2
в. 2/3
д. то же, что
эл. 1,5 раза
ф. дважды
г. три раза
ч. четыре раза
6. Аккумулятор 12 В, резистор 12 Ом и резистор 4 Ом подключены, как показано на рисунке. Падение напряжения на резисторе 12 Ом в ____ раз меньше, чем на резисторе 4 Ом.
а. 1/3
б.
1/2
в. 2/3
д. то же, что
эл. 1,5 раза
ф. дважды
г. трижды
ч. четыре раза
7. Аккумулятор 12 В и резистор 12 Ом подключены, как показано на схеме. Резистор на 6 Ом добавляется к резистору на 12 Ом, чтобы создать схему Y, как показано на рисунке. Падение напряжения на резисторе сопротивлением 6 Ом в цепи Y равно ____ падения напряжения на резисторе в цепи X.
a. больше, чемб. меньше
в. то же, что
8. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:
a.Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
б. Три резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
с. Три резистора 8 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом соединены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом соединены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом включены параллельно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.
9. На основании ваших ответов на приведенный выше вопрос дополните следующее утверждение:
Общее или эквивалентное сопротивление трех параллельно соединенных резисторов будет _____.


 = 1/(12 Ом) + 1/(12 Ом) + 1/(12 Ом)
= 1/(12 Ом) + 1/(12 Ом) + 1/(12 Ом) 1/2
1/2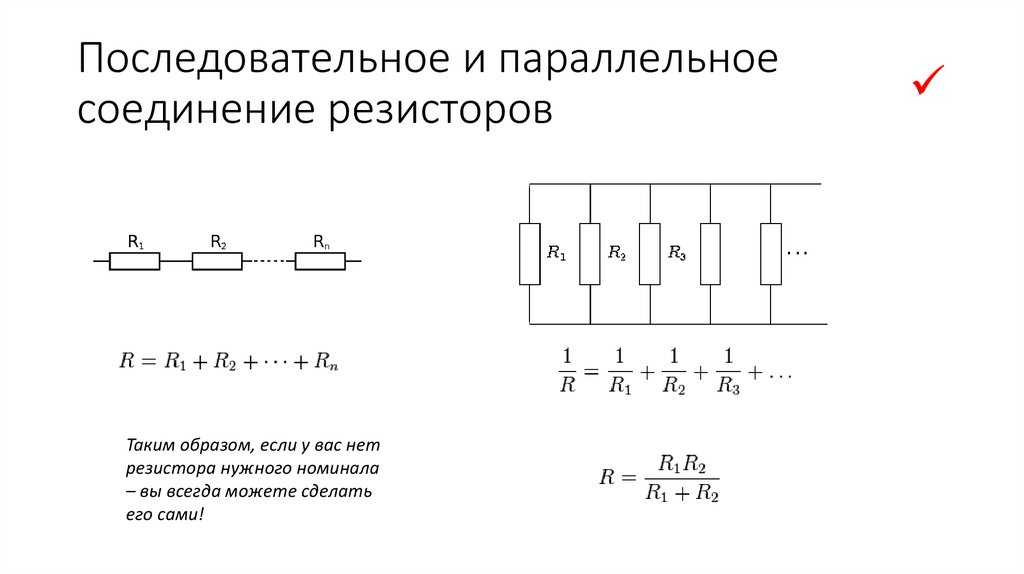 Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
Два резистора 6 Ом, включенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
Leave A Comment