Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.

Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
опрос)
(фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график.

- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 | |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6.
Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
цена основного деления: 1.
 Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2. 3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7.
Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14.Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.
Экстремумы функции (Лекция №9)
Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке.
Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2 минимум. Аналогично для точки x4.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее
значения во всех точках некоторого интервала, содержащего точку x0, т. е. если существует такая
окрестность точки x0, что для всех x≠x0,
принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
е. если существует такая
окрестность точки x0, что для всех x≠x0,
принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция
имеет в точке максимум, то это не означает, что в этой точке функция имеет
наибольшее значение во всей области определения.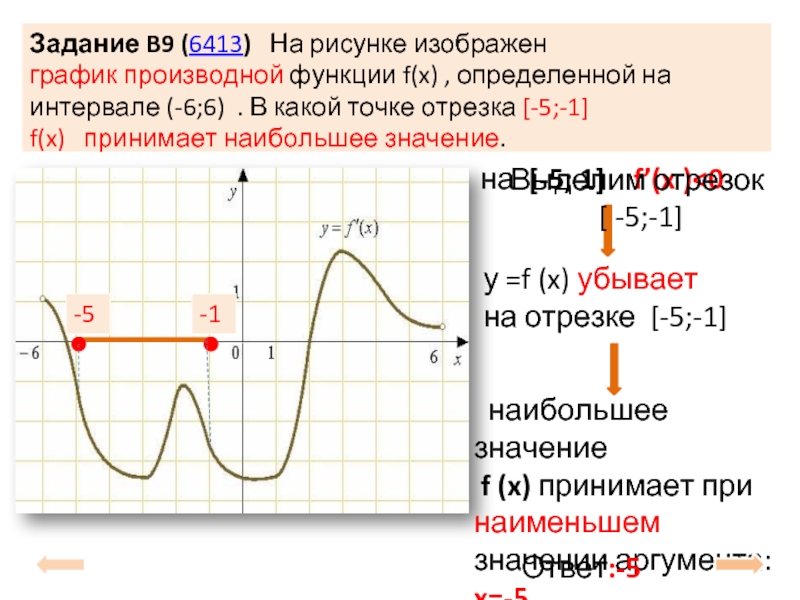 На рисунке, рассмотренном выше,
функция в точке x1 имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x1. В частности, f(x1) < f(x4)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
На рисунке, рассмотренном выше,
функция в точке x1 имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x1. В частности, f(x1) < f(x4)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. Но тогда
Переходя в этих
неравенствах к пределу при Δx→ 0 и учитывая, что производная f ‘(x0)
существует, а следовательно предел, стоящий слева, не
зависит от того как Δx → 0,
получаем: при Δx → 0
– 0 f’(x0)
≥ 0 а при Δx → 0
+ 0 f’(x0)
≤ 0. Так как f ‘(x0)
определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x0) = 0.
Так как f ‘(x0)
определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x0) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
- y=|x|.
Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.
-
Функция не имеет производной при x=0, так как обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.

-
Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x0 мы знаем, что f ‘(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум.
Например. .
Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.

Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x0 функция имеет максимум.
 Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.Таким образом, если
- f ‘(x)>0 при x<x0 и f ‘(x)<0 при x> x0, то x0 – точка максимума;
- при x<x0 и f ‘(x)>0 при x> x0, то x0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x0f ‘(x)>0 для x< x0, f ‘(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x) — f(x0) = f ‘(c)(x- x0), где c лежит между x и x0.

- Пусть x < x0. Тогда c< x0 и f ‘(c)>0. Поэтомуf ‘(c)(x- x0)<0и, следовательно,
f(x) — f(x0)<0,т.е. f(x)< f(x0).
- Пусть x > x0. Тогда c> x0 и f ‘(c)<0. Значитf ‘(c)(x- x0)<0. Поэтому f(x) — f(x0)<0,т.е.f(x) < f(x0).
Таким образом, для всех значений x достаточно близких к x0f(x) < f(x0). А это значит, что в точке x0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f ‘(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства
f ‘(x)<0 при x< x1, f ‘(x)>0 при x> x1.

Тогда слева от точки x1 функция возрастает, а справа убывает, следовательно, при x = x1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x2 и x3.
Схематически все вышесказанное можно изобразить на картинке:Правило исследования функции y=f(x) на экстремум
- Найти область определения функции f(x).
- Найти первую производную функции f ‘(x).
- Определить критические
точки, для этого:
- найти действительные корни уравнения f ‘(x)=0;
- найти все значения x при которых производная f ‘(x) не существует.
- Определить знак
производной слева и справа от критической точки. Так как знак производной
остается постоянным между двумя критическими точками, то достаточно определить
знак производной в какой-либо одной точке слева и в одной точке справа от
критической точки.

- Вычислить значение функции в точках экстремума.
Примеры. Исследовать функции на минимум и максимум.
- . Область определения функции D(y)=R.
Найдем производную заданной функции
Определим критические точки . Производная не существует при х2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.
-
Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
- Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
- Вычислить значения функции на концах отрезка при x = a, x = b.
- Из всех полученных значений выбрать наибольшее и наименьшее.
Примеры.
- Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].
Найдем критические точки функции.

Вычислим значения функции в найденной точке и на концах заданного отрезка.
Итак,
- Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].
- Чему равна наименьшая площадь боковой поверхности
прямого кругового конуса объема 3π?
По теореме Пифагора
.
Следовательно, .
.
Найдем критические точки функции S: S‘ = 0, т.е.
Покажем, что при найденном значении h функция Sбок достигает минимума.
.
Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Пусть r – радиус основания цилиндра, h – высота.
Нам нужно максимизировать объем цилиндра .

Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что . Отсюда .
, по смыслу задачи 0≤h≤2R.
.
Покажем, что при найденном значении h функция V принимает наибольшее значение.
Определение домена и диапазона по графику
Результаты обучения
- Поиск домена и диапазона по графику и уравнению.
- Укажите домен и диапазон функций инструментария.
Другой способ определить домен и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси [latex]x[/latex]. Диапазон — это набор возможных выходных значений, которые показаны на оси [latex]y[/latex]. Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения.
Мы можем заметить, что граф простирается по горизонтали от [латекс]-5[/латекс] вправо без границ, так что домен равен [латекс]\левый[-5,\infty \правый)[/латекс]. Вертикальный экстент графика — это все значения диапазона [latex]5[/latex] и ниже, поэтому диапазон равен [latex]\left(\mathrm{-\infty },5\right][/latex]. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011
Пример: поиск домена и диапазона на графике
Найдите домен и диапазон функции [latex]f[/latex].
Показать решение
Пример: нахождение области определения и диапазона по графику добычи нефти
Найдите область определения и диапазон функции [latex]f[/latex].
(кредит: модификация работы Управления энергетической информации США)
Показать решение
Попробуйте
Имея график, определите домен и диапазон, используя интервальную нотацию.
Показать раствор
Вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Домен и диапазон функций инструментария
Теперь мы вернемся к нашему набору функций набора инструментов, чтобы определить домен и диапазон каждой из них.
Для постоянной функции [latex]f\left(x\right)=c[/latex] область определения состоит из всех действительных чисел; ограничений на ввод нет. Единственным выходным значением является константа [latex]c[/latex], поэтому диапазоном является набор [latex]\left\{c\right\}[/latex], содержащий этот единственный элемент. { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
{ 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
Для обратной функции [латекс]f\left(x\right)=\frac{1}{x}[/latex] мы не можем делить на 0, поэтому мы должны исключить 0 из области определения. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон также не будет включать 0. В нотации построителя наборов мы могли бы также написать [латекс]\влево\{х|\текст{ }х\ne 0\вправо \}[/latex], множество всех вещественных чисел, не равных нулю. 9{2}}[/latex], мы не можем делить на [latex]0[/latex], поэтому мы должны исключить [latex]0[/latex] из домена. Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Для функции квадратного корня [latex]f\left(x\right)=\sqrt[]{x}[/latex] мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или выше. Диапазон также исключает отрицательные числа, поскольку квадратный корень из положительного числа [latex]x[/latex] определяется как положительный, хотя квадрат отрицательного числа [latex]-\sqrt{x}[/latex] также дает нам [латекс]x[/латекс].
Для функции кубического корня [latex]f\left(x\right)=\sqrt[3]{x}[/latex] домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция).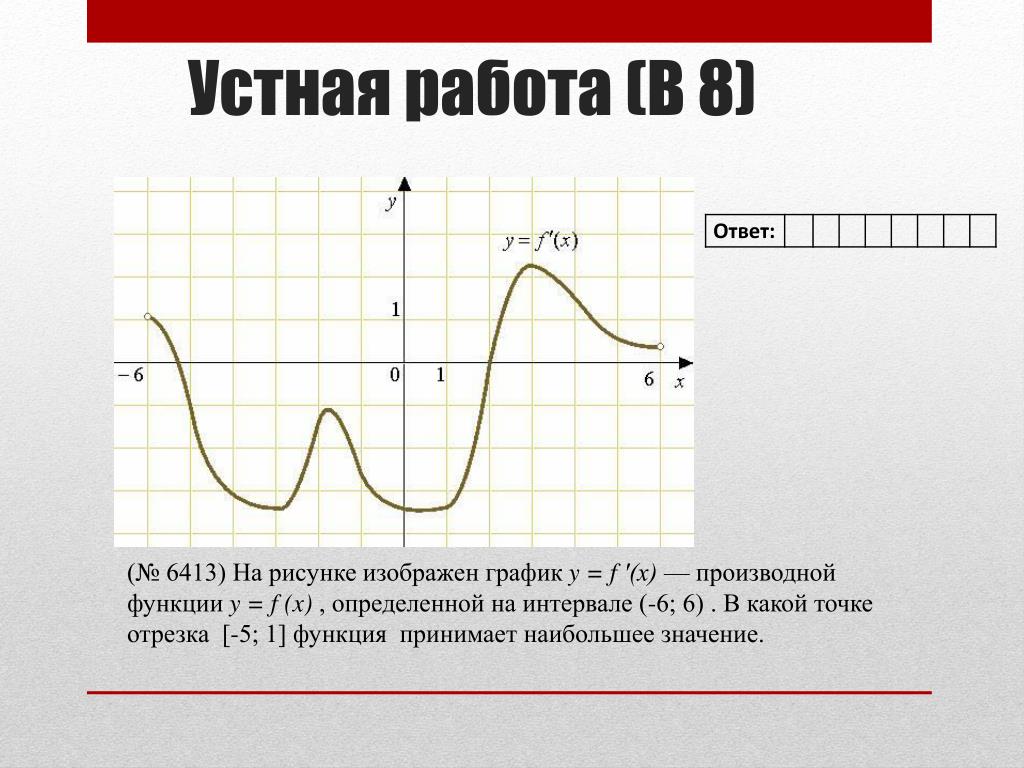
Попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Упорядоченные пары, линейный график… Пошаговое решение математических задач
8.1 Упорядоченные пары
Уравнения, такие как d = 60t, {Iota} = 0,05P и y = 2x + 3, представляют отношения между парами переменных. Например, в первом уравнении, если t = 3, то d = 60 * 3 = 180. Понимая, что t — первое, а d — второе, мы можем записать пару (3, 180) для представления t = 3 и d = 180. Пара (8,180) называется упорядоченной парой. Очевидно, (180, 3) отличается от (3, 180), если t — первое число, а d — второе число.
Говорят, что (3, 180) удовлетворяет уравнению или является решением уравнения d=60t. Точно так же (100, 5) удовлетворяет {Iota} = 0,05P, где P = 100 и {Iota} = 0,05 (100) = 5 . Кроме того, (2, 7) удовлетворяет y = 2x + 3, где x = 2 и y=2*2+3=7.
В упорядоченной паре, скажем (x, y), x называется первым компонентом, а y называется вторым компонентом.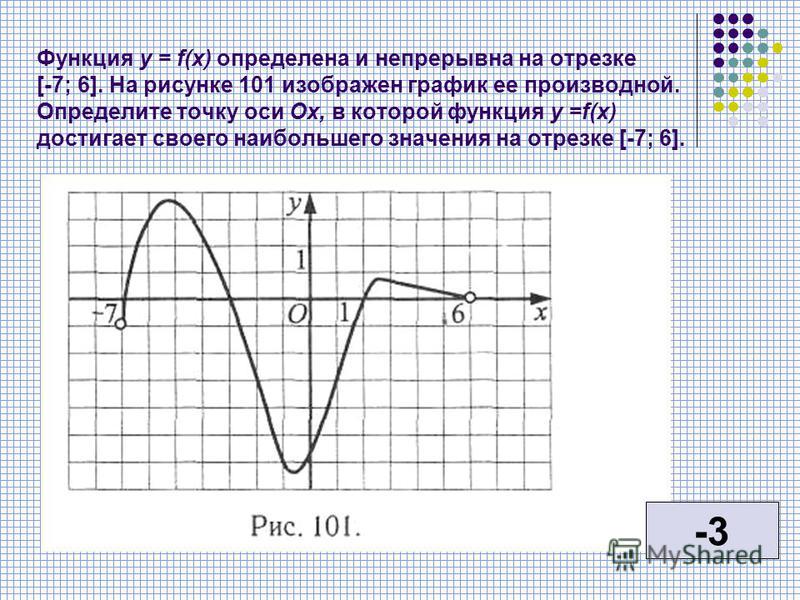 Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,
Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,
выберите x=1, тогда y=2*1+3=5
выберите x= -2, тогда y=2(-2)+3= -1
выберите x=1/2, тогда y=2 (1/2)+3=4
Все упорядоченные пары (1,5), (-2, -1) и (1/2, 4) удовлетворяют уравнению y = 2x + 3.
Приписанная переменная к первому компоненту также называется независимой переменной, а переменная, присвоенная второму компоненту, называется зависимой переменной. Таким образом, мы связываем (x, y) с y = 2x + 3, а y «зависит» от значений, присвоенных x.
Мы также можем записать пары в виде таблиц. Выбор значений независимой переменной произволен.
d=60 т
| т | д |
| 5 | 60*5=300 |
| 10 | 60*10=600 |
| 12 | 60*12=720 |
| 15 | 60*15=900 |
{Йота}=0,5P
| P | {Йота} |
| 100 | 0,05*(100)=5 |
| 200 | 0,05(200)=10 |
| 500 | 0,05(500)=25 |
| 1000 | 0,05(1000)=50 |
y=2x+3
| x | и |
| -2 | 2(-2)+3=-1 |
| -1 | 2(-1)+3=1 |
| 0 | 2(0)+3=3 |
| 3 | 2(3)+3=9 |
Другим обозначением, обычно используемым в математике для представления зависимой переменной, является обозначение функции.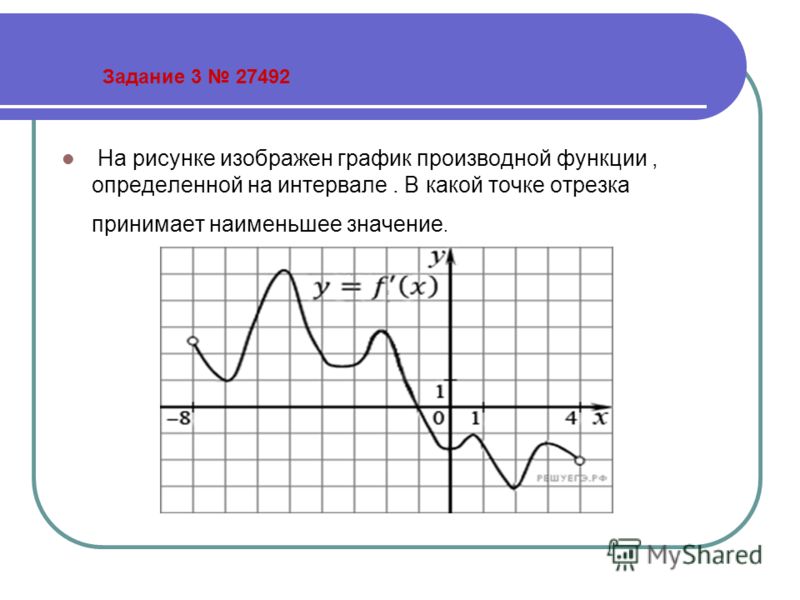 Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например,
Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например,
если f(x)=2x-5
то f(1)=2*1-5=-3
f(3)=2*3-5=1
90 010 f(6) =2*6-5=7и f(-1)=2(-1)-5=-7
(Примечание: f(x) не означает умножение f на x. f(x) — самостоятельная запись.)
Благодаря работе Рене Декарта (1596-1650) мы можем представить упорядоченные пары как точек на плоскости путем построения графика в декартовой системе координат. В этой системе две числовые линии пересекаются под прямым углом и делят плоскость на четыре квадранта. Начало, обозначенное упорядоченной парой (0, 0), является точкой пересечения. Горизонтальная числовая линия называется горизонтальной осью или осью x. Вертикальная числовая линия называется вертикальной осью или осью Y. Точки, лежащие на любой из осей, не находятся ни в одном квадранте. Они просто расположены на оси (см. рис. 8.1).
Другими словами, каждой точке соответствует одна упорядоченная пара действительных чисел, а каждой упорядоченной паре действительных чисел соответствует одна точка.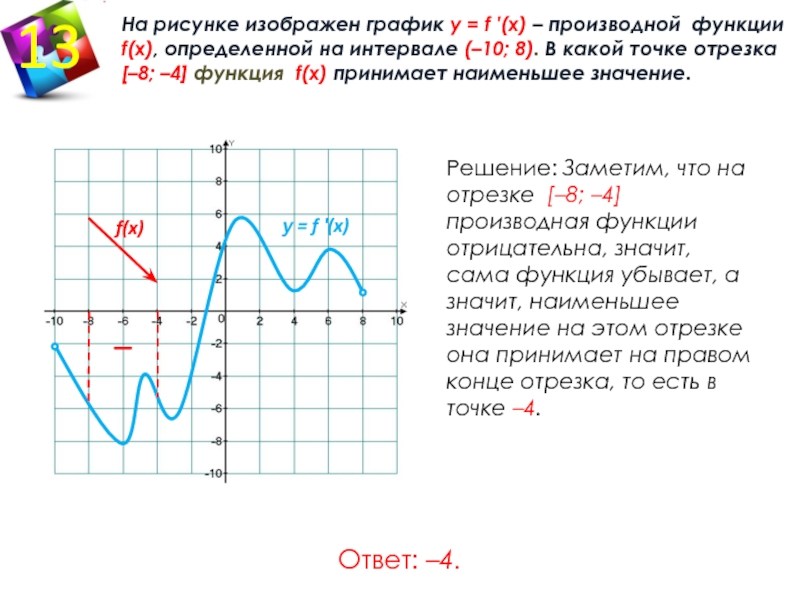 Это важное соотношение является краеугольным камнем декартовой системы координат.
Это важное соотношение является краеугольным камнем декартовой системы координат.
Графики точек A(2, 1), B(-2, 3), C(-3, -2), D(l, -2) и {эпсилон}=(3, 0) показано на рисунке 8.2. (Примечание: упорядоченная пара действительных чисел и соответствующая точка на графике часто используются для обозначения друг друга. Таким образом, упорядоченная пара (2,1) и точка (2,1) взаимозаменяемы.)
1 и 2
1.{(-2,1),(0,2),(1,3) , (2, -3)}
2. {(-1,3),(0,1),(1,-1),(2,-3),(3,-5)}
3. Если f(x)=-2x+1, найти f(-1),f(0),f(1),f(2) и f(3).
f(1)=-2(-1)+1=3
f(0)=-2(0)+1=1
f(1)=-2(1)+1=-1
f(2)=-2(2)+1=-3
F (3) =-2 (3) + 1 = -5
8.2 Графические линейные уравнения
Предположим, что мы хотим график точек, которые удовлетворяют уравнению y = 2x + 3. существует конечное число таких точки. Мы построим график пяти, чтобы попытаться найти закономерность (см.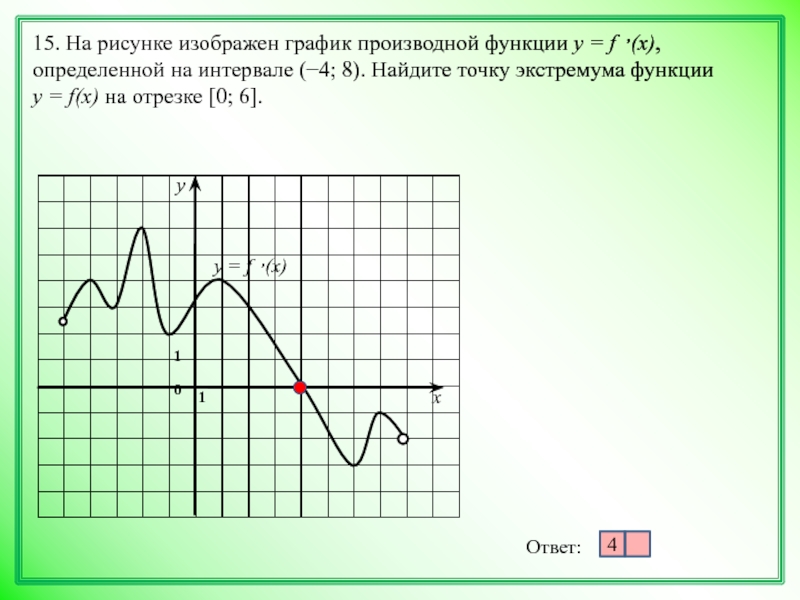 рис. 8.3).
рис. 8.3).
Пять точек на рис. 8.3 лежат на одной прямой. На самом деле они лежат на прямой, и любая упорядоченная пара, удовлетворяющая уравнению y = 2x + 3, также будет лежать на этой прямой.
От чего зависит, будут ли точки, удовлетворяющие уравнению, лежать на прямой? Точки, удовлетворяющие любому уравнению вида
Ax+By=C
будет лежать на прямой. Уравнение называется линейным уравнением и считается стандартной формой уравнения прямой. Мы можем записать уравнение y = 2x + 3 в стандартной форме -2x + y = 3.
| x | 2х+3=у |
| 0 | 2(0)+3=3 |
| -1 | 2(-1)+3=1 |
| 1/2 | 2(1/2)+3=4 |
| 1 | 2(1)+3=5 |
| -2 | 2(-2)+3=-1 |
Рис. прямой линии, для определения всего графика необходимо всего две точки.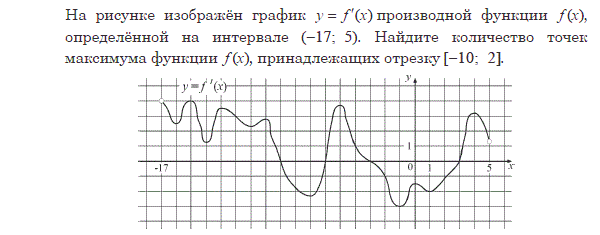 (Две точки определяют линию.) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
(Две точки определяют линию.) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
Примеры
1. Нарисуйте график линейного уравнения x + 3y = 6.
x=0
0+3y=6
900 10 y=2x=3
3+3y= 6
3y=3
y=1
Две точки на графике — (0, 2) и (3, 1). Возможно, вы выбрали еще два. Избегайте выбора двух точек близко друг к другу.
2. Нарисуйте график линейного уравнения 2x-5y=10
x=5
2*5-5y=10
10-5y=10
-5y=10
y=0
x=0
2*0-5y=10
0-5y=10
y=-2
x=-5
2( -5) -5y = 10
-10-5y = 10
-5y = 20
y = -4
График Три балла-хорошая идея, просто чтобы убедиться, что график находится в правильном положении.
Хотя выбор значений для x или y может быть произвольным, установка значения x = 0 найдет точку на графике, где линия пересекает ось y. Эта точка называется y-перехватом. Точка пересечения с осью X — это точка, которую можно найти, приняв y = 0. Эти две точки обычно легко найти, и они часто используются в качестве двух точек для построения графика линейного уравнения.
Эта точка называется y-перехватом. Точка пересечения с осью X — это точка, которую можно найти, приняв y = 0. Эти две точки обычно легко найти, и они часто используются в качестве двух точек для построения графика линейного уравнения.
Примеры
Нарисуйте следующие линейные уравнения, найдя точки пересечения по осям x и 90 107 точек пересечения по оси y.
1. 3y+2x=6
x=0→y=2
y=0→x=3
Посмотрим как наш математический решатель генерирует график этого уравнения и подобных линейных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою проблему
2. 3y-2x=6
x=0→y=2
y=0→x=-3
Поскольку x-координата y-координаты всегда равна 0, мы условимся называть y-координату y-перехват. В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
Пример
Нарисуйте следующее линейное уравнение: y — 3x = 0
y-3x=0
x=0→y=0
x=2→y=6
Давайте посмотрите, как наш математический решатель генерирует график этого уравнения и подобных линейных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
8.3 Формы пересечения наклона и точки-наклона
Плотнику дали набор чертежей дома, которые предусматривают крышу 5:12. Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)
То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)
Рисунок 8.4
Что, если еще одна крыша должна быть 7:12? Стал бы плотник строить крышу так, чтобы на каждые 7 дюймов подъема приходилось 12 дюймов прогона? Конечно. Отношение подъема к бегу будет 7/12 (см. рис. 8.5). 9Рис. 8.5
Для прямой линии отношение подъема к длине называется наклоном линии.
slope=(подъем)/(набег)
График линейного уравнения y=3x-1 показан на рис. 8.6. Как вы думаете, что такое наклон линии?
Рис. 8.6
Чтобы вычислить уклон, найдите любые две точки на линии, затем найдите подъем и уклон, используя эти две точки (см. рис. 8.7а). (Коэффициент подъема
1=8
х= -1 y=3(-1)-1=-3-1=-4
Теперь, используя P_1(-1, -4) и P_2(3, 8), координаты P_3 равны (3, -4 ), как показано на рисунке 8.7b. P_3 имеет те же координаты x, что и P_2, и те же координаты, что и P_1.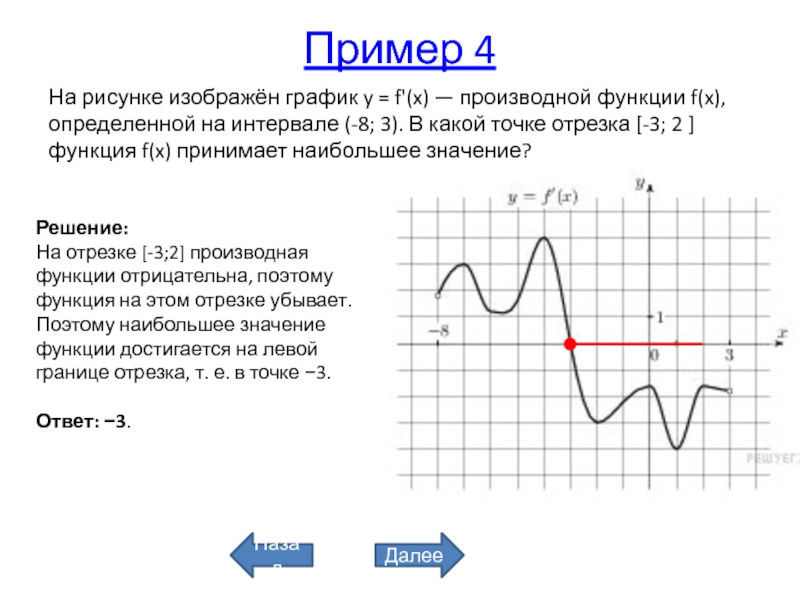
(Примечание. Обозначение P_1 читается как «P sub 1», а 1 называется нижним индексом . Точно так же P_2 читается как «P sub 2», а P_3 читается как «P sub 3».)
Для линии y=3x-1,
наклон=(подъем)/(разгон)=(8-(-4))/(3-(-1))
=12/4=3
Теперь найдите наклон линии y=3x+2. Найдите две точки на линии и рассчитайте соотношение: подъем/спуск
Например,
x=0 y=3*0+2=0+2=2
x=1 y=3*1+2= 3+2=5
Таким образом, P_1(0, 2), P_2(1, 5) и P_3(1, 2) показаны на рис. 8.8.
Обратите внимание, что две линии y = 3x — 1 и y = 3x + 2 имеют одинаковый наклон, равный 3. (См. рис. 8.9..) Это означает, что прямые параллельны. Все прямые с одинаковым наклоном параллельны. Все линии на рис. 8.9 имеют наклон 3 и параллельны.
Используя индексную запись, мы можем вывести формулу для наклона любая линия. Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.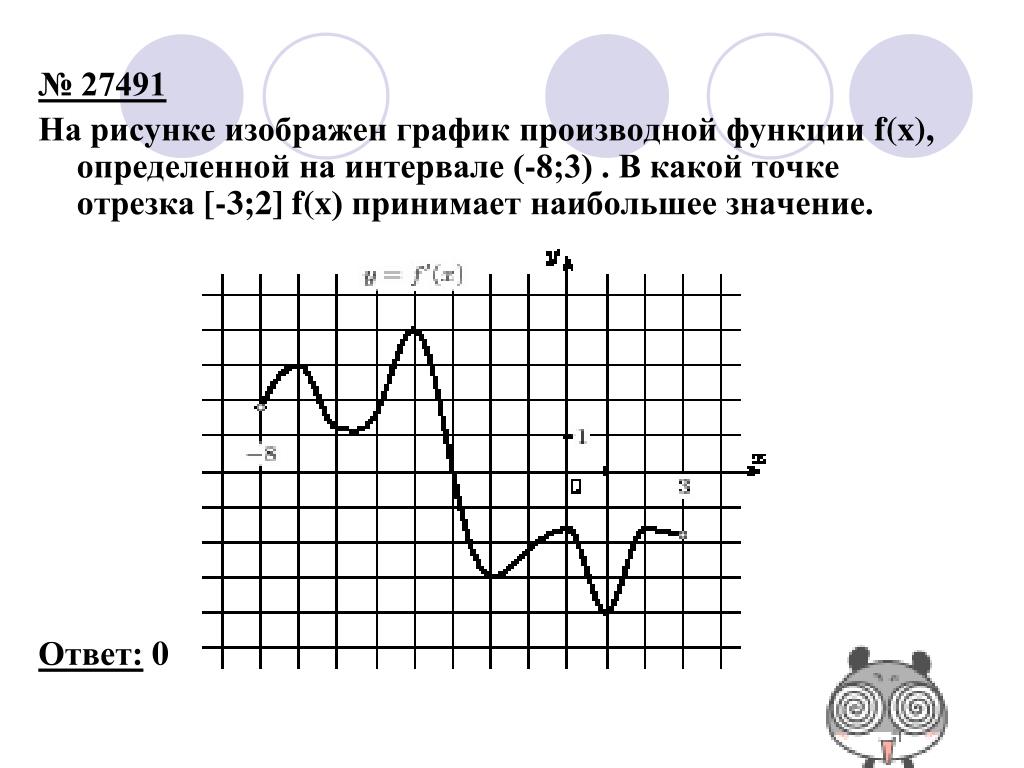 10, и можно вычислить наклон.
10, и можно вычислить наклон.
наклон=(подъем)/(бег)=(y_2-y_1)/(x_2-x_1) 92=6
-6+3y_2=6
3y_2=12
y_2=4
(x_1,y_1)=(0,2) и x_2, y_2)=(-3,4)
наклон= (y_2-y_1)/(x_2-x_1)=(4-2)/(-3-0)=2/(-3)=-(2/3)
2. Предположим, что порядок точек в пример 1 изменен. То есть (x_1,y_1)=(-3,4) и (x_2,y_2) = (0, 2). Будет ли это влиять на наклон?
slope=(y_2-y_1)/(x_2-x_1)=(2-4)/(0-(-3))=-2/(3)=-(2/3)
Изменение порядка точки не имеют значения при расчете наклона. И числитель, и знаменатель меняют знак, поэтому дробь имеет одинаковое значение. В примере 1 2/-3=-(2/3), а в примере 2 -2/3=-(2/3). Важной процедурой является то, что координаты должны вычитаться в одном и том же порядке как в числителе, так и в знаменатель.
В общем случае
slope=(y_2-y_1)/(x_2-x_1)=(y_1-y_2)/(x_1-x_2)
Отрицательный наклон для линии 2x + 3y = 6 означает, что линия наклоны (или уклоны) вниз вправо (см. рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
slope=-2/3=-(2/3)
Рис. 5). Начните с точки (4, 5) и найдите другую точку на линии, используя наклон как (подъем)/(спуск)=3/4.
Четыре единицы вправо (бег) и три единицы вверх (подъем) от (4, 5) дадут еще одну точку на линии. Из (4, 5) вы могли переместиться на 4 единицы влево и на 3 единицы вниз или на 8 единиц вправо, а затем на 6 единиц вверх. Просто двигайтесь так, чтобы отношение подъема к бегу было 3 к 4, и вы найдете вторую точку на графике. (Для отрицательного наклона двигайтесь либо вправо, а затем вниз, либо влево, а затем вверх.)
Решите уравнение 2x+3y=6 относительно y.
2x+3y=6
3y=-2x+6
(3y)/3=(-2x+6)/3
y=(-2x)/3+6/3
y=-(2/3x)+ 2
Обратите внимание, что коэффициент x,-(2/3) совпадает с наклоном линии. Кроме того, для линий, обсуждавшихся ранее, y = 3x-1 и y = 3x + 2, наклон каждой линии был равен 3, что является коэффициентом x. Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Предположим, что уравнение решено относительно y и y=mx+b. Пусть (x_1,y_1) и (x_2,y_2) — две точки на прямой. (x_1!=y_1) Тогда
y_1=mx_1+b and y_2=mx_2+b
slope=(y_2-y_1)/(x_2-x_1)=((mx_2+b)-(mx _1+б)) /(x_2-x_1)
=(mx_2+b-mx_1-b)/(x_2-x_1)=(mx_2-mx_1)/(x_2-x_1)
=
Наклон m, коэффициент x , в виде y = mx + b
Для прямой y = mx + b пусть x=0. Тогда y=m*0+b=b и y = b является точкой пересечения с осью y. Поскольку m — наклон, а b — точка пересечения с осью y, мы приходим к следующему определению.
y = mx + b называется формой наклона и пересечения для уравнения прямой; m — наклон, а b — точка пересечения с осью y.
Найдите наклон (м) и точку пересечения по оси y b каждой из следующих линий, переписав уравнение в форме наклона и точки пересечения.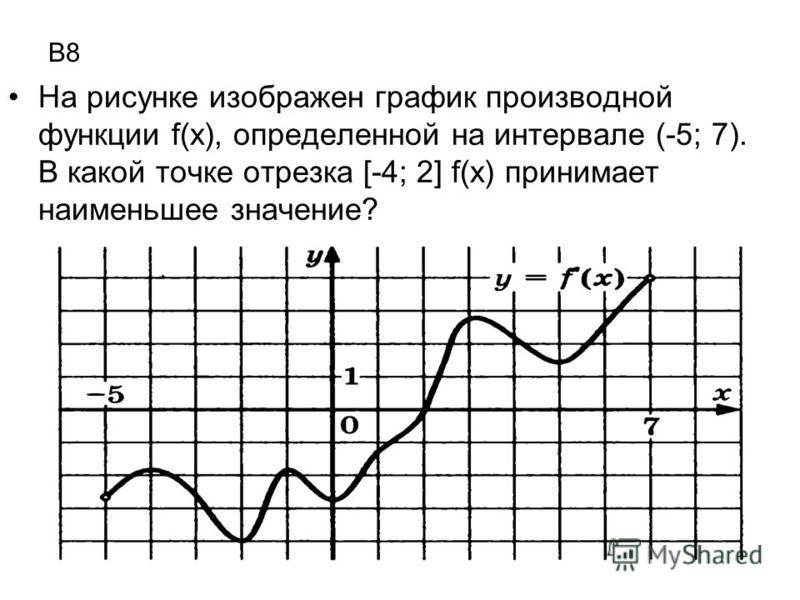 Затем начертите линию.
Затем начертите линию.
1. 2x+3y=3
3y=-2x+3
y=(-2x+3)/3
y=-(2 /3x)+1
м=-(2/3 )
y-отрезок = 1.
2. x-2y=6
x=6+2y
x-6=2y
(x-6)/2=y
1/2x-3=y 9 0011
м=1/2 b=-3
3 . -4x+2y=7
2y=4x+7
y=(4x+7)/2
y=2x+7/2
m=2 b=7/2
Если линия должна иметь определенный наклон и проходить через определенную точку, уравнение, представляющее линию, можно найти, как показано на следующем рисунке.
Пусть линия имеет наклон § и проходит через точку (1, 5). Если (x, y) представляет точку на линии, то наклон, рассчитанный с использованием (1, 5) и (x, y), должен составлять 2/3. то есть
(y-5)/(x-1)=2/3
В другой форме,
y-5=2/3(x-1)
фиксированная точка (x_1,y_1) может быть представлена в виде строка
; m — наклон, а (x_1,y_1) — фиксированная точка.
Примеры
1. Найдите уравнение прямой, имеющей наклон m=3/4 и проходящей через точку (4,5).
y-y_1=m(x-x_1)
y-5=3/4(x-4) (уравнение в форме точка-наклон)
или y-5=3/4x-3
y=3/4x+2 (уравнение в форме наклона-отрезка)
или 4y=3x+8
-3x+4y=8 (уравнение в стандартной форме, Ax+By=C)
2 . Найдите уравнение прямой, проходящей через две точки (- 1, -3) и (5, -2).
m=(y_2-y_1)/(x_2-x_1)=(-2-(-3))/(5-(-1))=(-2+3)/(5+1)=1/ 6Найдите m, используя формулу для наклона .
Используя форму точка-наклон (любая точка (-1, -3 или (5, -2) даст тот же результат)
y-(-2)=1/6(x-5)
y+ 2=1/6(x-5) (уравнение в форме точка-наклон)
или y+2=1/6x-5/6
y=1/6x-17/6 (уравнение в
или 6y=x-17
17=x-6y (уравнение в стандартной форме, Ax+By=C)
Любая из трех основных форм уравнения прямой допустима В любом случае, если ответ дан в форме, отличной от вашей, вы должны быть в состоянии признать уравнения эквивалентными. 0011
0011
Давайте посмотрим, как наш математический решатель создает графики прямых линий и посмотрим на разный наклон линий. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
8.4 Горизонтальные и вертикальные линии
Рассмотрите уравнение y = 3. Если x = 5, чему равно y? Если х = -2, чему равно у? Если х=0, чему равно у? В каждом случае y = 3. Все точки (5, 3), (-2, 3) и (0,3) удовлетворяют условию y = 3. x может иметь любое значение, но y должен быть x. Чтобы подчеркнуть этот факт, уравнение y = 3 можно записать как 0x + y = 3 или y = 0x + 3. График уравнения y = 3 представляет собой горизонтальную линию, и каждая координата y равна 3 (см. рис. 8.12). .)
Рис. 8.12
Каков наклон линии y = 3? Записав уравнение в форме y = 0x + 3, наклон равен 0. Кроме того, по формуле для наклона с использованием (-2, 3) и (5, 3), наклон действительно равен 0:
slope = m=(y_2-y_1)/(x_2-x_1)=(3-3)/(5-(2))=0/7=0
Каковы графики уравнений y = -2 и y = 3 /2? Обе являются горизонтальными линиями с наклоном 0.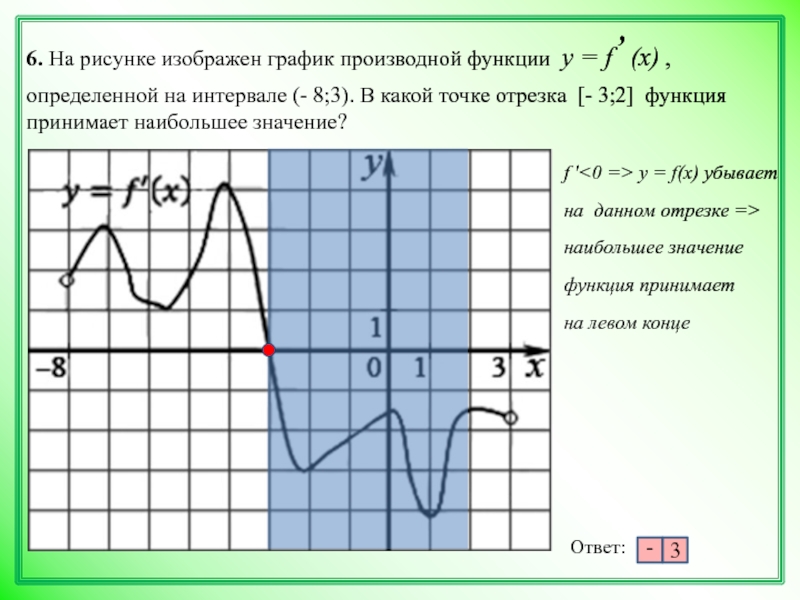 На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
Каков наклон линии x = 2 ? Чтобы ответить на этот вопрос, воспользуемся формулой наклона и двумя точками (2, 4) и (2, -3):
slope = m=(y_2-y_1)/(x_2-x_1)=(4-( -3))/(2-2)=7/0 undefined
Наклон не определен, потому что 0 не может быть знаменателем. Это верно для любой вертикальной линии. Графики уравнений вида x = a представляют собой вертикальные линии без наклона (или с неопределенным наклоном). Обратите внимание на то различие, что горизонтальные линии ((y = b)) имеют нулевой наклон, а вертикальные линии (x = a)) не имеют наклона. И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме, Ax + By = C, обсуждаемого в разделе 8.2. 9Рисунок 8.14
И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме, Ax + By = C, обсуждаемого в разделе 8.2. 9Рисунок 8.14
Примеры
Следуя линейным уравнениям, найдите наклон линии, если он существует, и начертите линию.
1. 2y=5
y=5/2
m=0
2. x +6=0
x=-6
без наклона
3. x+y= 0
y=-x
m=-1
8.5 Расстояние между двумя точками
Каково расстояние между двумя точками P_1(2, 3) и P_2(6, 3)? Каково расстояние между точками P_3 (-1, -4) и P_4 (-1, 1)? (См. рис. 8.15.)
расстояние (от P_1 до P_2)=6-2=4?
Это верно, так как точки P_1 и P_2 лежат на одной горизонтальной линии и имеют одинаковую координату y. Вы нашли
расстояние (от P_3 до P_4)=1-(-4)=5?
Это верно, поскольку точки P_3 и P_4 лежат на одной вертикальной линии и имеют одинаковую координату x.
Для расстояния от P_1 до P_2 почему бы не взять
расстояние (от P_1 до P_2) = 2-6=-4?
Причина в том, что термин расстояние означает положительное число. Как можно гарантировать положительное число после вычитания координат? Ответ состоит в том, чтобы взять абсолютное значение разности координат. Расстояние между двумя точками обозначается d.
Для P_1(x_1,y_1) и P_2(x_2,y_1) на горизонтальной линии,
Для P_1(x_1,y_1) и P_2(x_1,y_2) на вертикальной линии ,
Примеры
1. Найдите расстояние d между двумя точками (5, 7) и (-3, 7). Поскольку точки лежат на горизонтальной линии (они имеют одинаковую координату y),
или
2. Найдите расстояние d между двумя точками (2, 8) и 2,-(1/2 ). Поскольку точки находятся на вертикальной линии (они имеют одинаковую x:координату),
или
Что делать, если точки не лежат на вертикальной или горизонтальной прямой? Действительно, это более общий случай. Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух сторон.
Чтобы найти расстояние между двумя точками P_1(-1, 2) и P_2(5, 4), примените теорему Пифагора и рассчитайте длину гипотенузы, как показано на рис. 8.16. 92)
=корень(1/16+1)
=корень(1/16+16/16)
=корень(17/16)
9001 0 3. Докажите, что треугольник, определяемый точками A(- 2, 1), B(3,4) и C(1, -4) — равнобедренный треугольник. У равнобедренного треугольника две равные стороны.Решение:
Длина отрезка – это расстояние между точками A и B. Обозначим это расстояние через . Таким образом, чтобы показать, что треугольник ABC равнобедренный, нам нужно показать, что = или что = . Если ни одно из этих соотношений не верно, то треугольник не имеет двух равных сторон и не является равнобедренным.


 Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики. Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шрифт
установим размер шрифта 8пт. 3
3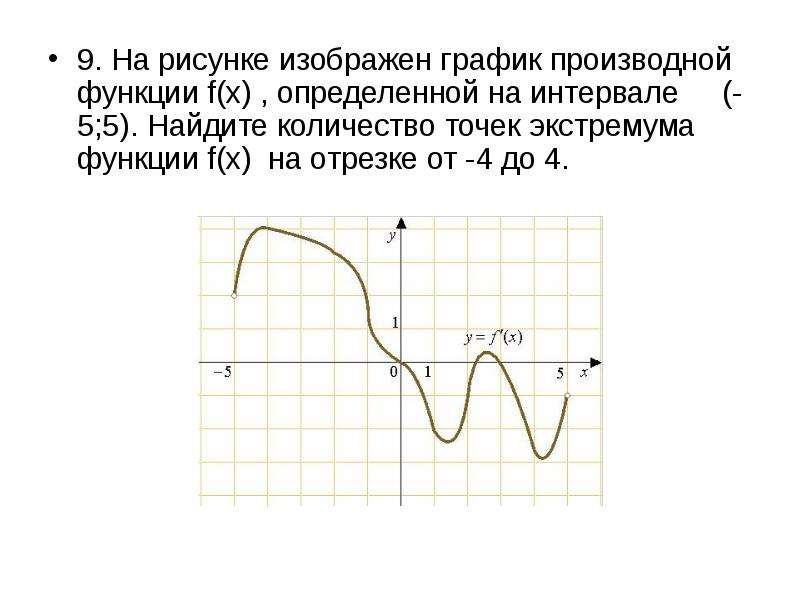 Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики. Верхний колонтитул слева: график функции у = x3
Верхний колонтитул слева: график функции у = x3
 Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.




Leave A Comment