Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
- Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время.
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
3. Развивающая раскраска для детей — Смешные рисунки из фигур
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.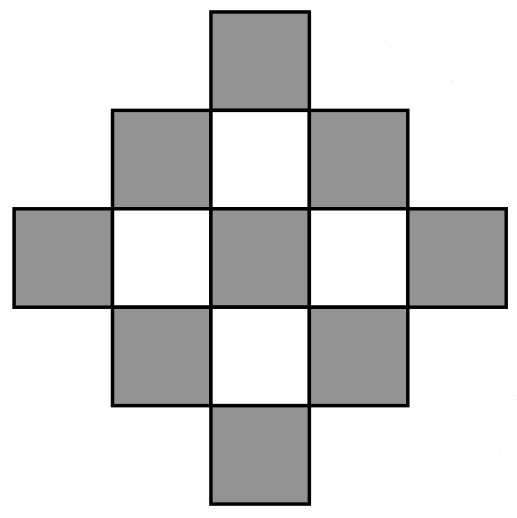
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить.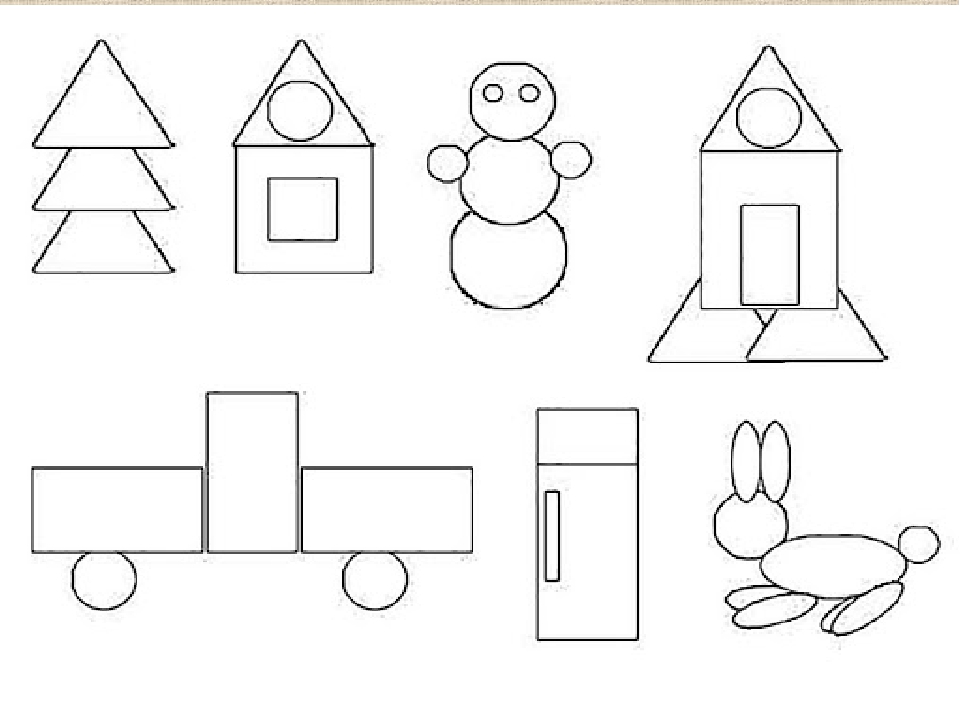 Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 10 для дошкольников
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Рисунок квадрата в перспективе | СПЛАЙН
ЦЕЛЬ ЗАДАНИЯ. Понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.
ПОСТАНОВКА ЗАДАНИЯ. Изобразите в перспективе горизонтальный и вертикальный квадраты.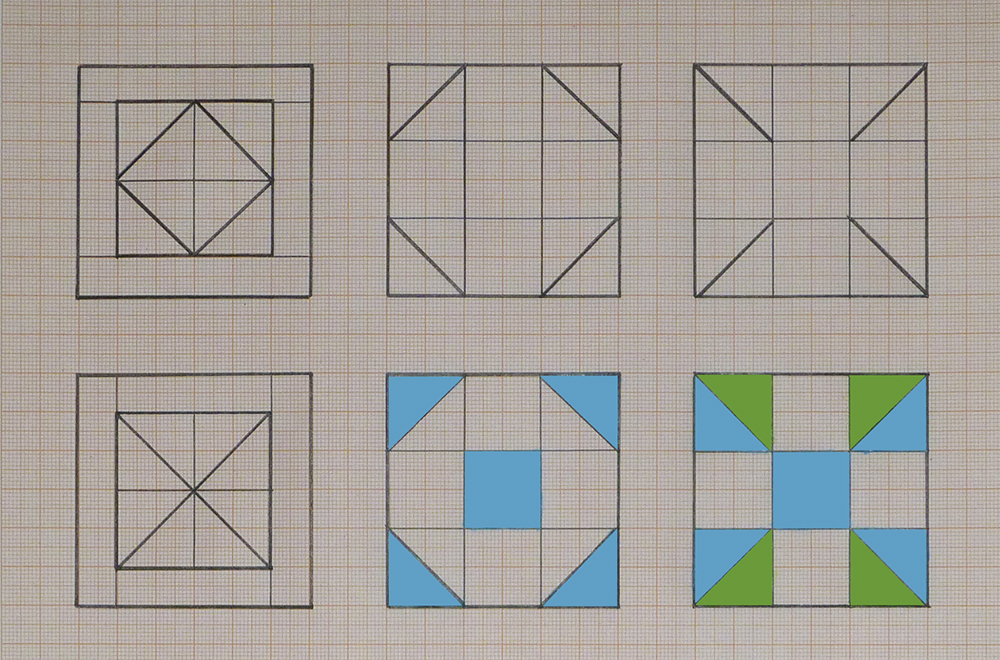
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности – две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю – больше, дальний – меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр – малую ось эллипса – ровно пополам.
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую – сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию – малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию – малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Фигуры из геометрических фигур. Картинки для детей, дошкольников, 1-2 класс. Шаблоны для аппликаций
Фигуры и цвета малыши начинают изучать с самого детства с помощью различных методик, в частности, через аппликации. Эти аппликации складываются из геометрических фигур, которые ребенок приклеивает к картонной или бумажной основе.
С какого возраста можно начинать учить с ребенком геометрические фигуры
По мнению ученых, обучать малыша следует с самого рождения, при этом его проводят в несколько этапов:
- После рождения малыш почти ничего не запоминает, однако приучается смотреть на мир во всех его аспектах. В это время рекомендуется разговаривать с младенцем, проговаривая каждую фигуру, читать небольшие детские стихи, петь песни.
- Когда ребенку исполнится 6 месяцев, он постарается узнать о мире побольше. Для этого он будет трогать и покусывать предметы. Важно подобрать правильные игрушки. Подойдет набор мягких квадратов, на которых нарисованы цветы, бабочки, птички.
- Следующий этап начинается тогда, когда малыш учится говорить. Необходимо проговаривать все названия фигур, начиная с самых простых (круг, треугольник, квадрат). Затем придет черед трапеции, прямоугольника и других. На этом этапе поможет игрушечная пирамидка, пластмассовые кубики, из которых строят башню, и рисование.

Таким образом, обучение можно с рождения ребенка, используя разные методики.
Изучение геометрических фигур: названия, форма, цвет, размер
С возрастом ребенок должен узнавать все больше фигур и цветов.
К 2 годам необходимо знать:
- треугольник;
- квадрат;
- круг.
В этом же возрасте нужно знать основные цвета:
- синий;
- красный;
- желтый;
- зеленый;
- белый.
Некоторые дети в 2 года знают несколько больше цветов:
- оранжевый;
- фиолетовый;
- черный;
- розовый.
К 6 годам ребенок узнает о более сложных, комбинированных цветах и оттенках, знакомится с составными (состоящими из основных) фигурами.
Дети обучаются через игры, они бывают разной сложности, поэтому давать их ребенку рекомендуется в следующей последовательности:
- Нарисованные на картоне круги, треугольники, квадраты разных размеров и цветов.
 Называйте изображения своими именами, проговаривая их вслух.
Называйте изображения своими именами, проговаривая их вслух. - Нарисовать на картоне только контуры фигур, причем все контуры должны быть разных цветов, чтобы малыш обводил их соответствующими цветами, раскрашивал и проговаривал названия вслух. В возрасте от 2 лет следует начинать сравнивать размеры.
- Вырезать фигуры и разложить на видных местах в доме, чтобы малыш искал рисунки. Каждый раз, когда ребенок находит изображение, он должен назвать следующие характеристики: фигуру, цвет и размер.
- Игровые наборы, предназначенные для изучения выше перечисленного. Например, пирамидка, грибы разных цветов и размеров на подставке, мозаика и другие. Такие игры развлекут ребенка, привлечет его внимание.
- Поиск геометрических фигур в окружающем мире. Например, стол – это прямоугольник, шкатулка – квадрат, а мячик – круг. Рекомендуется рассматривать и более сложные формы: стакан – цилиндр, а праздничный колпак – пирамида.

Разработано множество методик, предназначенных для изучения фигур и цветов. Они рассчитаны для детей разного возраста, а также учитывают их любимые занятия.
Изучение сложных геометрических фигур с помощью простых: польза занятий для детей
Фигуры из геометрических фигур, или составные фигуры, проще изучать через простые формы. Необходимо вырезать несколько квадратов, кругов и треугольников и складывать их.
Примеры составления сложных фигур:
- Трапеция: квадрат + 2 треугольника.
- Прямоугольник: 2 и более квадратов.
- Ромб: 2 равных треугольника.
- Параллелограмм: 2 квадрата + 2 равных треугольника.
Ребенок должен быть полностью вовлечен в процесс обучения, в противном случае обучение будет бесполезным. Обучение в формате игры – лучший способ привлечь внимание ученика и сделать процесс интересным. Делая открытия самостоятельно, малыш пожелает продолжить обучение.
Уроки начертательной геометрии для детей
Начертательная геометрия направлена на развитие пространственного мышления. Ребенок учится представлять сложные объемные фигуры, раскладывая их на простые и плоские. Задания предусматривают не только выбор правильных ответов, но и объяснение своего выбора и почему другие ответы неверны.
Ребенок учится представлять сложные объемные фигуры, раскладывая их на простые и плоские. Задания предусматривают не только выбор правильных ответов, но и объяснение своего выбора и почему другие ответы неверны.
Дорисовать фигуру по образцу
Закрепить урок поможет рисование.
Что нужно сделать:
- Показать ребенку фигуры, рассказать о них, привести примеры вещей соответствующей формы, которые находятся в комнате.
- Распечатать бланки, на которых пунктирной линией изображены недорисованные фигуры (пример бланка приведен выше).
- Задание: продолжить пунктир, сказать, которое изображение является кругом, квадратом, прямоугольником.
- Обговорить получившиеся результаты.
Вместо пунктирных линий могут быть и обычные, но прерывающиеся. Это упрощенный вариант упражнения. Чтобы усложнить задание, необходимо распечатать бланк, на котором часть фигуры закрашена, но не повторяет контуры. Это запутает малыша.
Кроме дорисовывания, появляется необходимость закрасить оставшуюся часть фигуры.
Обведение фигуры по точкам
Упражнение по соединению точек развивает воображение, позволяя представить, какие точки нужно соединить, чтобы получилась заданная фигура. Этот навык развивает способность к выполнению заданий по образцу, что пригодится в школе. Ребенок должен рисовать карандашом, чтобы он мог исправить ошибки.
Как делать упражнение:
- Распечатать бланки заданий.
- На каждом бланке слева представлен образец рисунка, а справа множество точек, из которых нужно составить такой же рисунок.
- Ребенок должен заметить, что точки разные: есть точки с крестиками, черные точки и белые. Одинаковые точки соединять нельзя.
- Справа точек больше, чем нужно – некоторые останутся вне рисунка.
Поиск геометрических фигур на изображении
Фигуры из геометрических фигур привлекают внимание детей. Им становится интересно, как же разделить сложный рисунок на простой, а простой собрать в сложный.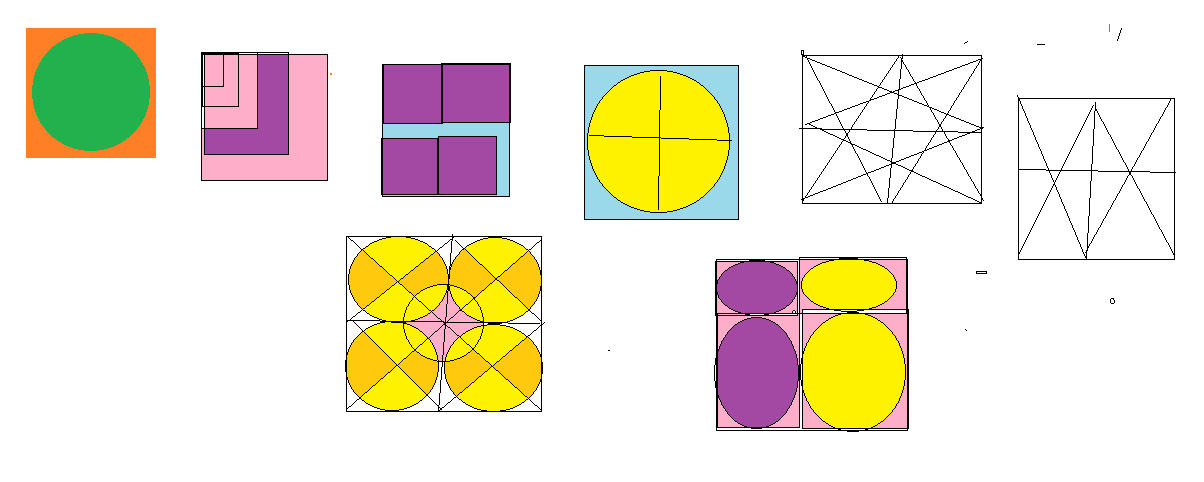 В этом задание предлагается найти круги, квадраты, треугольники. В усложненном варианте добавляются прямоугольники, трапеции, овалы и ромбы.
В этом задание предлагается найти круги, квадраты, треугольники. В усложненном варианте добавляются прямоугольники, трапеции, овалы и ромбы.
Легкий рисунок «бабочка» для девочек:
- Круги разных размеров – туловище.
- 2 пары одинаковых треугольников – нижние и верхние крылья.
- По 2 штуки маленьких, средних и больших кругов – украшение крыльев.
В рисунке «дом» можно найти:
- Квадрат – основная часть дома.
- Прямоугольник – дверь.
- Два круга или овала – окна.
- Маленький круг – дверная ручка.
- Треугольник – крыша.
Усложненный рисунок «кораблик»:
- Трапеция – корпус корабля.
- 3 круга – окна кают.
- 2 прямоугольника разных размеров – возвышение на палубе.
- Треугольники – паруса.
Рисунок «робот»:
- Квадрат – тело робота.
- 2 равных прямоугольника – ноги.
- 2 одинаковых равносторонних треугольника – ступни.

- 2 равных ромба – кнопки на теле робота.
- Длинный прямоугольник – плечи.
- 2 круга, 2 прямоугольника и 2 круга – руки.
- Небольшой квадрат – лицо.
- 2 маленьких круга – глаза.
- Треугольник – нос.
- Тонкий прямоугольник – рот.
- Трапеция (в длине должна быть больше квадрата лица) – шляпа.
Примеры рисунков расположены по степени сложности (от легкого к сложного).
Раскрашивание геометрических фигур
Задание развивает пространственное мышление, так как ребенок должен закрасить фигуры так, чтобы одна перекрывала другую.
Как проводить упражнение:
- Нарисовать на листе бумаги пары круг-квадрат, треугольник-круг, квадрат-треугольник и другие так, чтобы их концы пересекались, перекрывая друг друга.
- Предоставить ребенку лист и цветные карандаши.
- Попросить малыша раскрасить фигуры так, чтобы одна из пары находилась сверху друг друга, проговаривая вслух цвета.
Чтобы облегчить задачу, необходимо заранее показать ребенку объемные фигуры, дать ему возможность подвигать их и поиграть.
Пазл из геометрических фигур: как сложить нужные формы
Фигуры из геометрических фигур ребенку поможет научиться собирать игра в пазлыФигуры из геометрических фигур не сразу понятны малышам. Для упрощения обучения рекомендуется собирать своеобразные «пазлы».
Как проводить первый вариант упражнения:
- Распечатать бланки, на которых сверху нарисованы простые фигуры, а внизу несколько сложных форм.
- Ребенок должен найти, какой из вариантов на нижней части листа совмещает в себе все перечисленные формы на верхней части листа.
- Также необходимо объяснить получившиеся ответы.
Вначале следует давать простые рисунки, в которых фигуры соединяются без наклона. Также форма может содержать только квадраты или только треугольники.
Упражнение развивает фантазию и ориентацию в плоскости фигур.
Группировка простых фигур в сложные
Это задание обратно предыдущему.
Как выполнять упражнение:
- Распечатать на картоне несколько кругов, квадратов, треугольников и трапеций, вырезать их.

- Задача ребенка – составить как можно больше разных форм, состоящих из перечисленных выше фигур.
- Чтобы выучить цифры, необходимо считать каждый вид фигур.
Чтобы усложнить задачу, ребенок должен составить определенный рисунок (птицу, корабль).
Второй вариант выполнения упражнения:
- Показать ребенку закрашенное изображение и предоставить фигуры, необходимые для составления этого рисунка.
- Задача заключается в составлении идентичного изображения.
Этот вариант предназначен для детей от 6 лет.
Примеры и пошаговые инструкции для создания аппликаций из геометрических фигур
В зависимости от возраста ребенка аппликации выполняют по-разному:
- До 2,5 лет дети не умеют вырезать, поэтому это делает взрослый. На усмотрение взрослого, приклеивать бумажные детали к картону может ребенок или сам взрослый. Во втором случае, следует советоваться с малышом, куда именно приклеить деталь.

- От 2,5 до 5 лет дети умеют вырезать ножницами, но делают это неровно, поэтому при необходимости следует исправлять неровности.
- От 5 лет дети учатся ровно резать, поэтому участие взрослого в процесс создания аппликации минимально.
В маленьком возрасте малыш старается упростить форму, которую видит. Например, облака, похожие на кудри, упрощаются до овала.
Для детей 3-5 лет
Привлечь маленьких детей могут необычные картинки и процесс их создания. Аппликация «Ежик» нестандартна, но проста в создании. В качестве иголок используются ладошки из коричневой или черной бумаги.
Их можно сделать двумя способами:
- Приложить ладошку ребенка к бумаге с обратной стороне листа и обвести простым карандашом. Вырезать ладошку по контуру.
- Раскрасить ладошку малыша краской и приложить к бумаге. Контуры обводить не следует. Вырезать деталь.
Понадобится 4 ладошки.
Также понадобятся следующие детали:
- «Лодочка», состоящая из овала и кривого треугольника. Эта деталь послужит телом и носом ежика.
- Небольшой круг – кончик носа.
- Красный полукруг – рот.
- Белый полукруг – часть глаза.
- Маленький черный круг – зрачок.
- Круг с подрезанными верхней и нижней частью зеленого цвета – яблоко.
- Темно-зеленые ромбы – 2 листа яблока.
- Деталь, похожая на капсулу белого цвета – ножка гриба.
- Коричневый полукруг – шляпка гриба.
- Четыре трапеции разных размеров – ноги.
Детали следует приклеивать в той последовательности, в которой они перечислены выше. При этом 2 ладошки расположены пальцами вверх, одна – по диагонали, последняя – вбок.
Конец тела располагается около последней ладошки.
Аппликация «Объемная божья коровка»:
- Половина черного овала – голова.
- Два красных или розовых круга – тело.
 Круги нужно согнуть пополам: одну половину приклеить к картону, вторую оставить. Половину второго круга приклеить рядом с первой так, чтобы из приклеенной части образовался круг.
Круги нужно согнуть пополам: одну половину приклеить к картону, вторую оставить. Половину второго круга приклеить рядом с первой так, чтобы из приклеенной части образовался круг. - Черные круги – точки. Они располагаются как на приклеенных, так и на отступающих частях тела.
- Покупные глаза разного размера.
- Усики и круги на их концах дорисовать черным фломастером.
Картина привлекает своим объемом. Ребенок может поиграть с выступающими частями божьей коровки.
Как сделать аппликацию «цветочная поляна»:
- Раскрасить картонный лист зеленой краской.
- Небольшой квадрат сложить 4 раза так, чтобы получился квадрат меньшего размера. Обрезать 3 угла (кроме угла сгиба). Разогнуть лист.
- В центр получившихся из квадрата лепестков приклеить круг контрастного цвета.
- Сделать несколько цветков.
- Приклеить цветы на раскрашенный лист картона.
Картина получится многоцветной, поэтому ребенку станет интересно рассмотреть цветы поближе.
Для учеников 1 класса
Первоклассники способны создавать более сложные аппликации, используя новые материалы.
Аппликация «Сирень»:
- Раскрасить картонный лист акварельной краской. При желании, можно сделать плавный переход от одного цвета к другому (от красного к фиолетовому, от фиолетового к синему или от синего к бледно-голубому).
- Дать фону подсохнуть.
- Вырезать прямоугольник и круг для вазы.
- Приклеить к основе сначала прямоугольник, а круг – сверху него.
- Вырезать из гофрированной бумаги зеленого цвета 4 тонкие короткие полоски. Эти полоски будут стеблями.
- Равномерно приклеить стебли к концу вазы.
- Вырезать из цветной салфетки 6 деталей овальной или яйцеобразной формы. Эти детали помогут обозначить границы соцветий сирени.
- Приклеить детали рядом со стеблями. Так как соцветий больше, чем стеблей, необходимо соотнести 4 соцветия со стеблями, а остальные приклеить по краям вазы.

- Разрезать салфетки на маленькие квадраты.
- Некоторые квадрату скомкать, остальные сначала порвать, а потом скомкать.
- Смазать соцветие клеем, распределить на нем комочки из салфеток.
- Повторить пункты 9-11 для остальных соцветий.
- Вырезать 6 листов из гофрированной бумаги: 4 приклеить на стебли, остальные – по краям.
- В некоторых местах объемных соцветий нанести пятна розовой акварельной краски.
Выполнить аппликацию «Гусеница» под силу каждому ребенку в 7 лет. Процесс создания занимает немного времени, поэтому подойдет, чтобы занять ребенка на небольшой период времени.
Как делать:
- Вырезать несколько разноцветных кругов одинакового размера.
- Приклеить на картон круги друг за другом. При желании, расположить круги с подъемами, будто гусеница ползет.
- На первом кругу нарисовать улыбку, приклеить глаза и дорисовать ресницы.
- Приклеить рожки – два треугольника.
Для детей 2-4 класса
Фигуры, изученные детьми до 11 лет, позволяют создавать сложные и интересные рисунки. Составление комбинаций из геометрических фигур и вырезание мелких деталей развивает мелкую моторику. В частности, этому способствует аппликация «Мыши».
Составление комбинаций из геометрических фигур и вырезание мелких деталей развивает мелкую моторику. В частности, этому способствует аппликация «Мыши».
Детали, необходимые для первой мыши:
- Серый полукруг – тело.
- 2 черных круга разных размеров – нос и глаз.
- 2 одинаковых серых круга – уши.
- 2 отрезка черной проволоки – усы.
- Отрезок белой толстой нити – хвост.
Сначала следует приклеивать к основе одно ухо, затем тело, которое немного перекрывает ухо, затем остальные детали.
Детали, необходимые для второй мыши:
- Серый овал с заостренными концами – тело.
- 2 серых круга – уши.
- 2 маленьких черных круга – глаза.
- Черный круг большего размера – нос.
- 2 отрезка черной проволоки – усы.
- Отрезок толстой белой нити – хвост.
Кусок сыра – равносторонний желтый треугольник. Его необходимо сложить пополам и склеить. На двойном треугольнике нарисовать круги и вырезать с помощью маникюрных ножниц.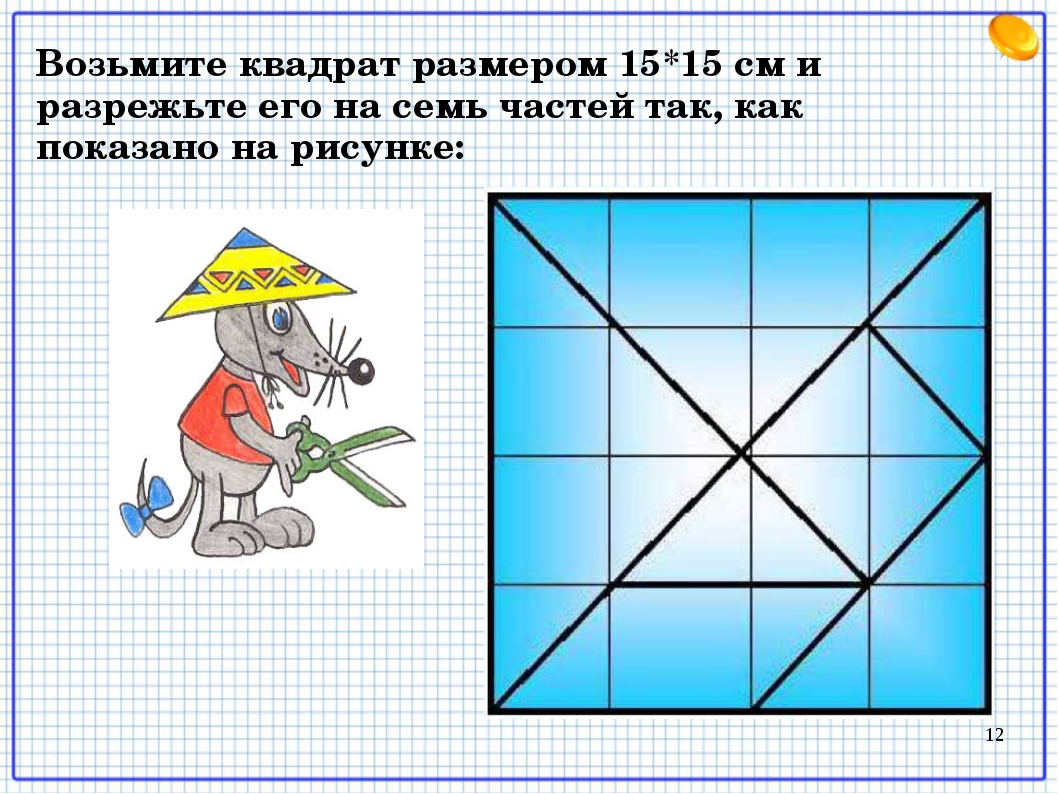 Нижнюю часть треугольника обрезать так, чтобы треугольник оказался равносторонним.
Нижнюю часть треугольника обрезать так, чтобы треугольник оказался равносторонним.
Как расположить элементы на листе:
- Приклеить сыр так, чтобы угол был направлен в верхнюю правую диагональ.
- Первую мышь приклеить над сыром ближе к основанию. Хвост опустить вниз и вправо так, чтобы он находился на сыре.
- Вторую мышь расположить под сыром ближе к его концу так, чтобы нос почти упирался в край сыра.
В качестве фона может выступать не только однотонный картон, но и картон с необычным орнаментом (клетка рубашки или круги). Дети в возрасте 8-10 лет способны комбинировать разные элементы, создавая сложные сюжеты.
Чтобы создать аппликацию «Космос», необходимо сделать следующие модели ракет:
- Вырезать корпус ракеты, который показан на фото ниже.
- Вырезать 3 круга контрастного цвета одинакового размера.
- Вырезать 3 круга меньшего размера.
- В каждый круг из пункта 2 приклеить по одному кругу из пункта 3.
 Получатся окна.
Получатся окна. - Приклеить окна на корпус ракеты.
Вторая модель ракеты:
- Вырезать корпус ракеты по фото.
- Вырезать два круга разного размера.
- Вклеить в маленький круг в большой.
- Вырезать овал, разрезать его на 4 части (2 части – крылья ракеты).
- Приклеить окно и крылья к корпусу ракеты.
Необходимо сделать несколько ракет и приклеить к листу так, чтобы они летели в разных направлениях. Оставшуюся площадь заполнить небольшими кругами и звездами. В мультфильмах из хвоста ракет вырывается огонь или дым, который можно изобразить овалами или спиральной деталью.
Геометрическая аппликация «Транспорт»
Фигуры из геометрических фигур складываются в полноценные картины при их правильном распределении.
Ниже рассмотрены аппликации разных видов транспорта. Аппликация «Поезд» состоит из вагонов двух типов: первого вагона и остальных. Вначале перечислены фигуры, необходимые для первого вагона.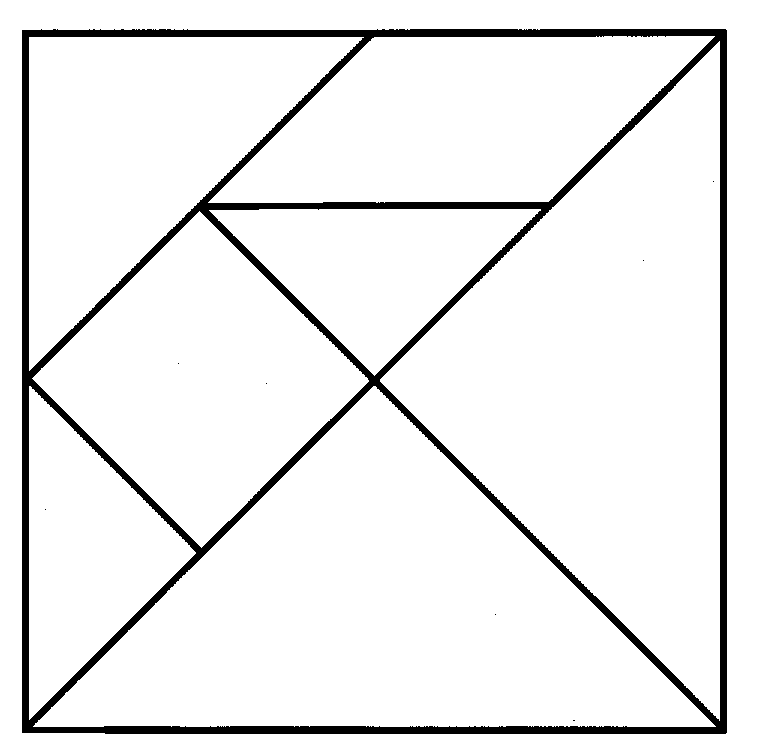
| Аппликация | Фигуры, которые используются в процессе создания аппликации | Часть транспорта, которую изображает фигура | Особенности расположения |
| «Поезд» | Прямоугольник | Корпус | Полукруг находится слева от прямоугольника |
| Полукруг | |||
| Большой и маленький прямоугольники | Кабина водителя | Один из прямоугольников — окно | |
| Треугольник | Труба | Часть фигуры перекрывается прямоугольником корпуса | |
| Треугольник меньшего размера | Фонарь | Частично перекрыт полукругом корпуса | |
| Прямоугольник | Основа для колес | Клеится под корпусом | |
| 3 круга | Колеса | Располагаются под корпусом, крепятся на прямоугольник | |
| Круг большего размера | Колесо | Клеится под кабиной водителя, частично ее перекрывая | |
| Тонкие прямоугольники | Цепи, соединяющие вагоны | — | |
| Прямоугольники | Вагоны | — | |
| По 4 круга 1 вагон | |||
| «Автобус» | Большой прямоугольник | Корпус | — |
| 2 круга | Колеса | Перекрывают часть корпуса, располагаются ближе к краям прямоугольника | |
| 2 прямоугольника | Двери | Располагаются около колес | |
| 4 более тонких прямоугольника | Окна дверей | На каждую дверь 2 окна | |
| 2 квадрата | Окна на корпусе | Квадратные окна располагаются по краям от дверей, а прямоугольное окно – между ними | |
| Прямоугольник | |||
| «Корабль» | Треугольник с обрезанными краями | Основная часть корабля | — |
| 3 круга | Окна | — | |
| Тонкий длинный прямоугольник | Палка, на которую крепятся паруса | Клеится левее середины основного треугольника | |
| Треугольник | Паруса | Клеятся с двух сторон от палки | |
| Полукруг | |||
| Квадрат | Флаг | Располагается в верхней части палки | |
| Прямоугольные треугольники | |||
| «Грузовик» | 2 прямоугольника разных размеров | Кабина водителя и передняя часть | Меньший прямоугольник крепится сбоку от большого |
| Квадрат | Окно | — | |
| Прямоугольник | Кузов | — | |
| 2 круга | Колеса | Один круг располагается под кабиной водителя, а второй – под кузовом. Часть кругов перекрывает ту часть грузовика, к которому крепится. Часть кругов перекрывает ту часть грузовика, к которому крепится. | |
| Треугольник | Груз | — |
Аппликации из геометрических фигур «Животные»
Животных могут изобразить даже самые маленькие.
Аппликация «Мартышка» состоит из следующих фигур:
- Овал – тело.
- 4 тонких овала – руки и ноги.
- Изогнутый тонкий овал – хвост.
- Круг – лицо.
- 4 круга (2 маленьких и 2 средних) – уши.
- Круг – нос.
- 2 белых и 2 черных круга – глаза.
Аппликация «Медведь» состоит из тех же фигур, но в качестве ушей используются 2 полукруга, а хвост не виден.
Аппликация «Цыпленок»:
- Вырезать 2 овала и приклеить на расстоянии друг от друга. Эти овалы станут крыльями.
- Вырезать желтый овал – тело будущего цыпленка. Приклеить тело между крыльями так, чтобы оно перекрывало часть крыльев.
- Сверху приклеить круг – лицо цыпленка.

- Вырезать маленький оранжевый круг. Внутрь приклеить еще более маленький черный круг.
- Склеенные круги приклеить на лицо сбоку, будто цыпленок смотрит вправо или влево.
- Вырезать 3 красных треугольника.
- Один треугольник приклеить сбоку от лица рядом с глазом – этот треугольник будет клювом.
- Остальные треугольники приклеить под телом – это лапы птицы.
- Один прямоугольный желтый треугольник приклеить с той стороны, где не расположен клюв. Этот треугольник – хвост.
Чтобы составить полноценную картину, необходимо добавить траву, состоящую из овалов разных размеров и длины, рядом с лапами цыпленка. Таким образом, птица будто бегает по полю.
Аппликация слон складывается из следующих деталей:
- Круг – тело.
- Прямоугольники – ноги.
- Полукруги – ступни.
- Тонкий треугольник – хвост.
- Полукруг большего размера – ухо.
- Небольшой круг – голова.
- Прямоугольник – хобот.

- Белый и черный круги – глаз.
Рекомендуется дать ребенку выбрать самостоятельно, какое животное он хочет изобразить и как хочет это сделать.
Рисунки из геометрических фигур: задания для детей
Изучив геометрические фигуры, ребенку необходимо понять, как их комбинировать в сложные рисунки.
Фигуры из геометрических фигур – первый этап изучения. Второй этап – складывание фигур в рисунки окружающих предметов.
Варианты упражнений на знание геометрических фигур:
- Распечатать бланк, на котором изображены различные предметы. Задача ребенка – назвать фигуры, которые он видит в представленных предметах.
- Разделить лист на 2 части. В левой части нарисовать по пары из двух одинаковых фигур. Упражнение заключается в том, что ребенок должен нарисовать в правой части фигуры, которые можно получить из пар фигур слева (2 прямоугольных треугольника – прямоугольник).
- Распечатать бланки, на которых изображены различные предметы (поезд, корабль, елка с шариками). Задание: посчитать количество каждой из фигур на рисунках.
- Распечатать бланки, на которых нарисованы картинки и задано определенное количество какой-либо фигуры. Необходимо найти рисунок, на котором присутствует указанное количество заданной фигуры.
Перечисленные выше задания помогают ребенку запомнить фигуры и научиться правильно считать. С геометрическими фигурами ребенок начинает знакомиться с самого рождения, узнавая все больше информации об окружающем мире. Обучение рекомендуется проводить в форме игры, составляя с ребенком разные комбинации из фигур.
Автор: mariamur1
Оформление статьи: Натали Подольская
Видео про геометрические фигуры
Как сделать фигуры из геометрических фигур — поделки для детей в этом видео:
Геометрия для детей» src=»https://www.youtube.com/embed/I5vSCY4-bR4?wmode=transparent&rel=0&feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Квадрат и его свойства, диагонали квадрата, площадь квадрат, теорема
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
- Все углы квадрата — прямые, все стороны квадрата — равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.
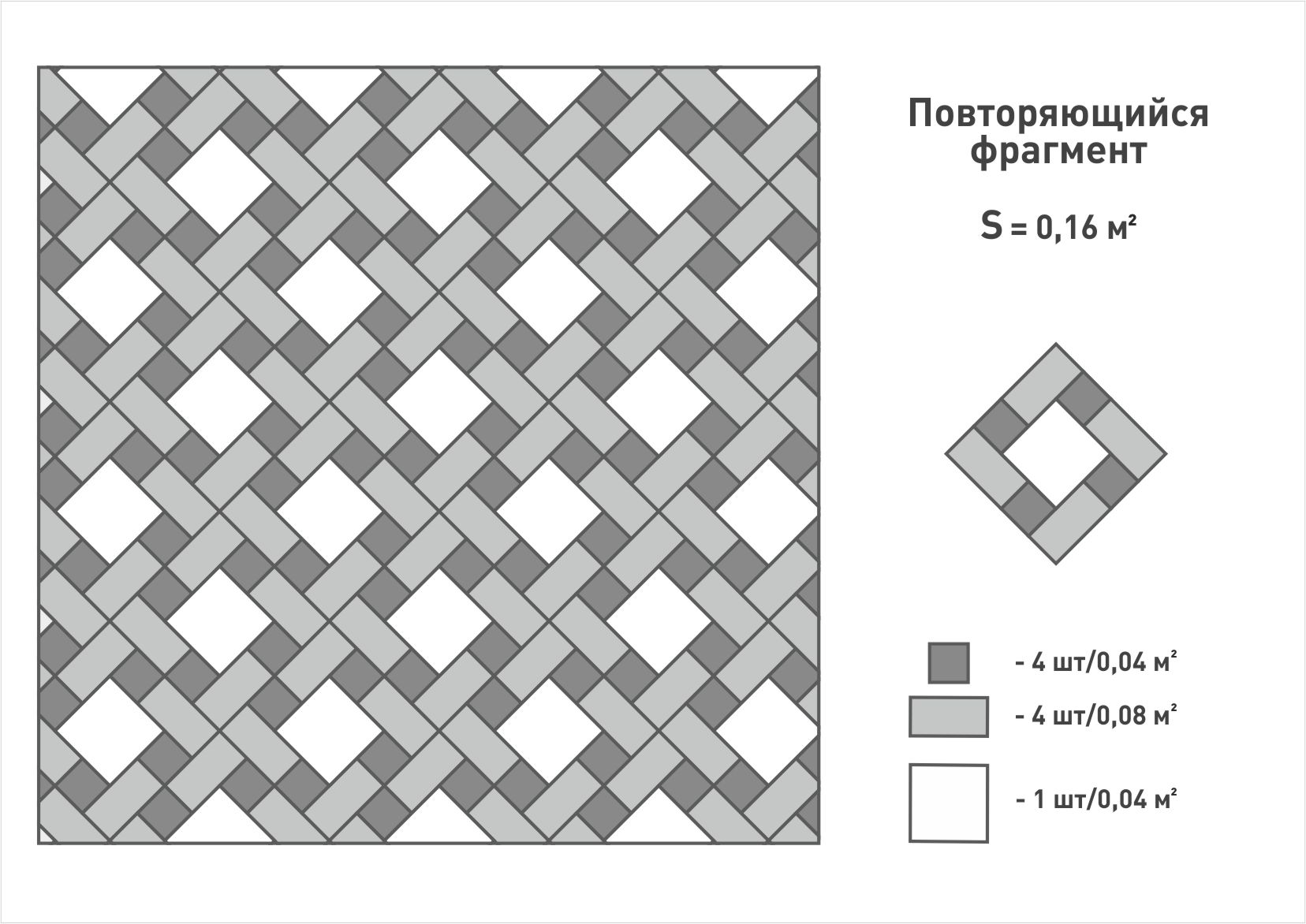
Площадь квадрата, очевидно, равна квадрату его стороны: .
Диагональ квадрата равна произведению его стороны на , то есть
.
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
1. Найдите сторону квадрата, диагональ которого равна .
Мы знаем, что . Тогда .
2. Найдите радиус окружности, описанной около квадрата со стороной, равной .
Очевидно, радиус окружности равен половине диагонали квадрата.
Ответ: .
3. Найдите сторону квадрата, описанного около окружности радиуса .
Диаметр окружности равен стороне квадрата.
Ответ: .
4. Найдите радиус окружности, вписанной в квадрат , считая стороны квадратных клеток равными .
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Ответ: .
5. Найдите радиус окружности, вписанной в четырехугольник . В ответе укажите
.
Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, . Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .
Ответ: .
Рисунок 4 квадраты внутри друг друга
К этой проблеме можно подойти несколькими различными способами, используя черепаху. Хотя очевидным ответом, по-видимому, являются вложенные циклы для рисования квадратов, ниже приведены некоторые другие способы думать об этом.
Во-первых, используя turtle.circle(steps=4) . Программа circle может рисовать произвольные правильные многоугольники включая квадраты хотя вам придется внести коррективы относительно позиционирования:
import turtle
def drawSquares(myTurtle, sideLength, nSquares, distanceApart):
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x - sideLength/ 2, y - sideLength / 2) # adjust so current x, y is center
myTurtle. pendown()
myTurtle.setheading(-45) # by default square would be sitting on corner instead of on side
for _ in range(nSquares):
radius = sideLength * 2**0.5 / 2
myTurtle.circle(radius, steps=4)
sideLength -= 10
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
yertle = turtle.Turtle()
yertle.penup()
yertle.goto(60, 60)
yertle.pendown()
drawSquares(yertle, 200, 4, 10)
turtle.done()
pendown()
myTurtle.setheading(-45) # by default square would be sitting on corner instead of on side
for _ in range(nSquares):
radius = sideLength * 2**0.5 / 2
myTurtle.circle(radius, steps=4)
sideLength -= 10
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
yertle = turtle.Turtle()
yertle.penup()
yertle.goto(60, 60)
yertle.pendown()
drawSquares(yertle, 200, 4, 10)
turtle.done()
Для моих оставшихся примеров я собираюсь принять тот же вызывающий код и просто представить модифицированные подпрограммы drawSquares() . Я считаю, что рекурсивное решение @PVNRT’s было превосходным, хотя я бы немного скорректировал его следующим образом:
def drawSquares(myTurtle, sideLength, nSquares, distanceApart):
if nSquares < 1:
return
for _ in range(4):
myTurtle.forward(sideLength)
myTurtle. left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
drawSquares(myTurtle, sideLength - distanceApart, nSquares - 1, distanceApart)
left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
drawSquares(myTurtle, sideLength - distanceApart, nSquares - 1, distanceApart)
Мой личный любимый способ решения такого рода проблем — использовать штамповку вместо рисования . Это чрезвычайно быстрое решение:
def drawSquares(yourTurtle, sideLength, nSquares, distanceApart):
myTurtle = yourTurtle.clone() # clone turtle so we don't have to restore changes
myTurtle.shape("square") # modify turtle shape for stamping
myTurtle.fillcolor(turtle.bgcolor()) # modify turtle fill color for stamping
for _ in range(nSquares):
myTurtle.turtlesize(sideLength / 20) # magic number 20 is default stamp size
myTurtle.stamp()
sideLength -= distanceApart
И, наконец, очевидное решение с использованием вложенных циклов, которое не должно быть столь очевидным теперь, когда вы увидели, что есть и другие подходы:
def drawSquares(myTurtle, sideLength, nSquares, distanceApart):
for n in range(nSquares):
for _ in range(4):
myTurtle. forward(sideLength)
myTurtle.left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
sideLength -= distanceApart
forward(sideLength)
myTurtle.left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
sideLength -= distanceApart
Одним из слабых мест в спецификации OP было значение аргументов x & Y. Я оставил их с пониманием того, что квадраты рисуются в текущем x & y. OP рассматривал их как верхний правый угол рисунка, который не согласуется ни с чем в черепахе. Я решил сделать их либо нижним левым, либо центральным (для решений на основе круга и штамповки.)
Под «Черным квадратом» Малевича обнаружили два цветных рисунка :: Впечатления :: РБК Стиль
О результатах последних исследований «Черного квадрата» было объявлено 11 ноября на международной конференции, посвященной 100-летию картины, сообщает телеканал «Культура».
Научный сотрудник отдела научной экспертизы Третьяковской галереи Екатерина Воронина рассказала, что картину просветили рентгеновскими лучами, а кроме того, под микроскопом были рассмотрены кракелюры — трещины краски на поверхности «Черного квадрата». Сквозь них отчетливо просвечивался другой слой краски.
Сквозь них отчетливо просвечивался другой слой краски.
«Черный квадрат» в Третьяковской галерее
Ранее предполагалось, что под слоем черной краски скрывается другое изображение. «Мы выяснили, что таких изображений не одно, а два. И доказали, что первоначальное изображение — это кубофутуристическая композиция, а лежащая под «Черным квадратом» — это протосупрематическая композиция», — заявила Екатерина Воронина.
Изображения, скрытые под «Черным квадратом»
стали видны в результате просвечивания рентгеновскими лучами
По ее словам, почти полностью удалось расшифровать и надпись, которую Казимир Малевич сделал на картине, впоследствии закрашенной «Черным квадратом». Фраза, по мнению ученых, звучит как «Битва негров в темной пещере». Таким образом работу Малевича можно считать аллюзией на картину 1882 года французского писателя и журналиста Альфонсо Алле. Более чем за четверть века до «Черного квадрата», в 1882–1884 годах, Алле изобрел свою «монохромную живопись» и написал картину «Битва негров в темной пещере глубокой ночью».
Таким образом работу Малевича можно считать аллюзией на картину 1882 года французского писателя и журналиста Альфонсо Алле. Более чем за четверть века до «Черного квадрата», в 1882–1884 годах, Алле изобрел свою «монохромную живопись» и написал картину «Битва негров в темной пещере глубокой ночью».
Все подробности проведенных исследований «Черного квадрата» будут опубликованы в специальном издании, которое появится в продаже в ближайшие 10 дней, сообщила «Русской службе новостей» генеральный директор Третьяковской галереи Зельфира Трегулова.
В 2015 году самая известная картина Каземира Малевича отмечает свое 100-летие. «Черный квадрат» входит в цикл супрематических работ художника, в которых он исследовал базовые возможности цвета и композиции. По замыслу Малевича, «Черный квадрат» являлся частью триптиха, в который также вошли «Черный круг» и «Черный крест».
Позднее Малевич выполнил несколько авторских повторений «Черного квадрата». Сейчас известны четыре варианта картины, различающиеся рисунком, фактурой и цветом. В Третьяковской галерее хранится именно подлинник 1915 года, с которого впоследствии делались повторения.
Сейчас известны четыре варианта картины, различающиеся рисунком, фактурой и цветом. В Третьяковской галерее хранится именно подлинник 1915 года, с которого впоследствии делались повторения.
Рисунок укладки паркета, елочка, разбежка, шашка, квадрат, плетенка
Вступление
Штучный или наборный паркет благодаря особенностям конструкции и своим размерам можно укладывать по самым различным рисункам. Каждый рисунок укладки подбирается по дизайну помещения и важен для общего вида отделки.
В отделке жилого помещения имеет значение каждая деталь, даже кажущаяся малой. Порой в малом сосредоточено не только эстетика, но и качество ремонта. Например, розетки и выключатели. Вы можете вложить деньги в дорогостоящие материалы для отделки пола и стен, но не уделить должное внимание выключателям и розеткам и получить головную боль при их эксплуатации. Розетки шведской компании Werkel от официального дилера на сайте https://werkel.pro/, удовлетворит не только самые придирчивые требования по дизайну, но отличается высочайшим качеством и продолжительной эксплуатацией.
Название рисунков укладки наборного паркета
Можно выделить десять основных, стандартных рисунков укладки наборного паркета:
- Палуба или Разбежка или Номер один;
- Ёлочка;
- Двойная и тройная ёлочка;
- Шашка;
- Дополнительный фриз;
- Рисунок «Шведка»;
- Плетёнка;
- Корзинка;
- Квадрат простой;
- Петербургский рисунок.
Рисунок укладки паркета «Разбежка», «Палуба», «Номер один», «Первый номер»
Рисунок «Разбежка» или профессиональное название «Первый номер» это наиболее распространенный рисунок укладки паркета, имеющий большое распространение с советских времен.
Этот вид укладки наборного паркета надежен и практичен. Плашки, уложенные по рисунку «Разбежка» со всех четырех сторон скреплены между собой замками на всей поверхности паркетного ковра. Это создает единое, монолитное покрытие пола.
Паркет по рисунку «Разбежка» укладывается вдоль стен, по интенсивному ходу движения или по направлению падения света.
Само название «Разбежка» происходит от технологии укладки. Каждый следующий ряд, смещается по отношению к предыдущему. Причем, смещение можно сделать, строго в половину плашки или хаотично. При этом нужно помнить, что рисунок «Разбежка» в половину плашки, увеличивает расход паркета на 10-15% по сравнению с хаотичной укладкой.
Также рисунок «Разбежка» можно использовать при диагональной укладки паркета. Диагональная укладка это укладка в направлении по диагонали квадратных или прямоугольных помещений. Здесь также нужно учитывать, что диагональная укладка паркета, также увеличивает расход на 5-7 %.Тесть для укладки паркета в разбежку по диагонали со смещением на пол плашки, нужно на 20% больше материала, чем на укладку в прямую разбежку, с хаотичной укладкой.
Рисунок «Разбежка» это самый дешевый метод укладки штучного паркета, а при укладки вдоль стен с хаотичным расположением плашек и самый экономный, по закупке материала, метод укладки штучного паркета.
Рисунок укладки паркета Елочка
Рисунок укладки штучного паркета «Елочка», также очень распространен. Я бы назвал рисунок «Елочка» классическим рисункам укладки паркета.
При укладки паркета Елочкой на разные плашки падает свет под разными углами. Из-за этого, создается впечатление, что плашки паркета имеют разные фактуры. Но это лишь игра света. Правда, елочкой укладывается и разнофактурная древесина.
Рисунок «Елочка» применяется как для укладки вдоль стен, так и по диагонали. Укладка «Елочкой» вдоль стен начинается от центра, и обрез производится у стен. «Елочка» по диагонали обычно не центруется, потому-то, во-первых, центровка при такой укладке не видна, а во-вторых, обрезных краев при такой укладки нет.
Паркет для укладки по рисунку «Елочка» прямая нужно закупать на 7 -10 % больше, чем площадь комнаты. Для укладка «Елочкой» по диагонали, запас должен быть 3- 5 %.
Рисунок для укладки паркета «Елочка двойная» и «Елочка тройная»
Эти два вида «Елочки» используются для визуального увеличения ширины паркетных клепок. Эти рисунки аналогичны простой елочки, только каждая сторона паркетного рисунка, собирается не из одной клепки, а из двух или из трех. Так визуально увеличивается ширина плашки, но длинна остается неизменной.
При выборе рисунка «Елочка двойная» и «Елочка тройная» большое значение имеет цветовая и фактурная подборка клепок паркета. Клепки, собираемые в двойки и тройки должны подбираться заранее и подходить друг к другу.
При применении рисунка «Елочка двойная» и «Елочка тройная» запас паркета, должен быть около 20%.
Рисунок для укладки паркета «Шашка»
Рисунок для укладки паркета «Шашка» это еще один не сложный рисунок укладки штучного паркета. Рисунок «Шашка» это квадраты, собранные из клепок паркета и уложенные с поворотом в 90° по отношению друг к другу.
При такой укладке, на свету играют целые квадраты из плашек. Для усиления эффекта квадратной укладки, применяют разнофактурный паркет. Например, орех и ясень. Это создает контрастирующий эффект при любом освещении.
Рисунок «Шашка» укладывается по диагонали и параллельно стенам.
Но при выборе для укладки «Шашка» нужно понимать следующие нюансы.
Для укладки типа «Шашка» нужны половина паркетин с правым замком, а половина с левым. Упаковка паркета, как раз содержит половину правых паркетин, а половину левых. Трудности возникают при желании разнофактурной укладки паркета шашкой. Получается, что при разнофактурной укладки шашкой, половина упаковок паркета, становятся не нужны. Это нужно понимать и искать фирму укладчик, которая сможет переделать часть замков паркетин, изготовив другие пазы и гребни.
Запас на подпил при таком рисунке, от 0 до 15%.Наиболее популярен метод укладки «Шашка» под углом 45°.
И еще одно. Для укладки паркета по рисунку «Шашка» нужно правильно выбрать размер паркетин. Длина паркетин должна делиться на ее ширину без остатка. Например, подойдет паркет:50×400;60×420 мм. Это нужно для сборки правильных квадратов для укладки.
Дополнительный фриз
Дополнительный фриз на ковре паркета это специально сделанная паркетная дорожка, уложенная перпендикулярно к стене. Все клепки фриза скрепляются между собой по длинной стороне, а короткой стороной (торцом) они соединяются с полосами , обрамляющими основное «зеркало» паркета, наподобие рамки.
Делается фриз из тех же пород дерева, что и основное зеркало. Фриз великолепно выделяет основной рисунок паркета, создавая своеобразную паркетную рамку. Это особенно актуально в помещениях неправильной формы, с различными выступами и нишами.
Фризы могут укладываться по рисунку «Елочка».
Рисунок для укладки паркета «Шведка»
Рисунок «Шведка» похож на рисунок «Разбежка», только каждый ряд состоит не из одной, а из двух паркетин. Причем каждая пара паркетин, отделяется от другой, поперечной короткой клепкой.
После укладки первого ряда, второй ряд укладывается со смещением в половину паркетной пары.
Укладка по рисунку «Шведка» не относится к экономичным. Минимальный запас паркета на распиловку 3-5%.Но практика показывает, необходимость 10 % запаса паркета, а для неправильных помещений 20-25 %.
Кроме большого расхода при укладки рисунком «Шведка», паркетное полотно получается не монолитным, торцевые короткие планки не соединяются в паз.
Для решения этой проблемы, нужно изготавливать специальные соединительные пазы, по месту укладки, что значительно увеличивает стоимость работ.
Рисунок для укладки паркета «Плетенка»
«Плетенка» это самый распространенный и востребованный способ художественной укладки паркета. Рисунок основан на переплетении пар и троек паркетин. Делается «Плетенка» из двух и трех пород паркета. Несмотря на свою простоту, масса его разновидностей позволяют создавать оригинальные рисунки укладки.
Особо выделяется однопородная «Плетенка», под названием «Павловская». В этом рисунке паркетины переплетаются не парами и тройками, а по одной.
Запас паркета при покупке для рисунка «Плетенка» 20-25 %.
Рисунок для укладки паркета «Корзинка»
Рисунок «Корзинка», это замкнутая «Плетенка», образующая рисунок напоминающий корзину. Отличие в том, что переплетение прямоугольников происходит не по центру, а по краям. Это создает один замкнутый квадрат со вставкой по центру.
Выполняется корзинка из двух и из одной породы паркета.
Рисунок для укладки паркета «Квадрат»
Рисунок для паркета «Квадрат» делается на основе рисунка «Шашки». Отличий в том, что каждая шашка обрамляется в отдельную рамку, «обноску»
Обноска делается из другой породы древесины. Каждый квадрат рисунка разворачивается под 90° по отношению к предыдущему. Укладывется паркет по рисунку квадрат, как параллельно по стенам, так и по диагонали.
Рисунок для укладки паркета «Петербургский»
Этот рисунок по-другому называют «Петербургский стиль». Основа этого рисунка, рисунок «Квадрат». Отличаю в толщине обноски. Обноска «Петербургского» рисунка делается в две или три паркетины.
При трехжильной обноске центральная жила делается более тонкой и контрастной по сравнению с другими.
Это только основные рисунки укладки паркета.Благодаря своей уникальности из наборногопаркета можно выложить практически любой рисунок.Сложные рисунки укладки паркета называют винтаж.
Фотогаллерея с рисунками паркета
©Opolax.ru
Другие статьи раздела: Паркетные работы
Простое пошаговое руководство по передаче или увеличению изображений — Art is Fun
как использовать метод сетки для увеличения или передачи изображения
Это
Page 9 15-страничного руководства, объясняющего, как раскрашивать фотореалистично.Метод сетки — недорогой, низкотехнологичный способ воспроизвести и / или увеличить изображение, которое вы хотите нарисовать или нарисовать. Метод сетки может занять довольно много времени, в зависимости от того, насколько большой и детализированной будет ваша картина.Хотя этот процесс не такой быстрый, как использование проектора или переводной бумаги, он имеет дополнительное преимущество, помогая улучшить ваши навыки рисования и наблюдения.
Вкратце, метод сетки включает в себя рисование сетки на вашей эталонной фотографии, а затем рисование сетки с равным соотношением на вашей рабочей поверхности (бумага, холст, деревянная панель и т. Д.). Затем вы рисуете изображение на своем холсте, сосредотачиваясь на одном квадрате за раз, пока все изображение не будет перенесено. Когда вы закончите, вы просто стираете или закрашиваете линии сетки и начинаете работать над своей картиной, которая теперь будет в идеальных пропорциях! Ура.
Чтобы использовать метод сетки, вам понадобится линейка , бумажная копия вашего контрольного изображения и карандаш для рисования линий на изображении. Вам также понадобится рабочая поверхность, на которую вы будете переносить фотографию, например, бумага, холст, деревянная панель и т. Д.
Чтобы нарисовать линии сетки на бумаге , я бы рекомендовал использовать механический карандаш , поэтому что вы можете получить тонкую точную линию. Обязательно рисуйте сетку очень легко, чтобы ее можно было легко стереть, когда закончите.
Чтобы нарисовать линии сетки на холсте или дереве , я бы посоветовал использовать тонкий кусок заостренного угля . Опять же, убедитесь, что вы сделали линии сетки как можно более светлыми, чтобы их было легко стереть, когда вы закончите. Преимущество использования угля на холсте или дереве вместо карандаша в том, что уголь можно легко стереть бумажным полотенцем или тряпкой, тогда как карандаш труднее стереть.
При рисовании сеток важно помнить, что они должны иметь соотношение 1: 1 .Это очень важно — иначе ваш рисунок будет искажен! По сути, соотношение 1: 1 означает, что у вас будет такое же количество линий на холсте, что и на эталонной фотографии, и что в обоих случаях линии должны быть расположены на равном расстоянии друг от друга — идеальные квадраты.
Запутались? Это довольно просто, как только вы освоитесь. Давайте посмотрим на метод сетки в действии, и он станет более понятным.
Допустим, вы хотите нарисовать следующее изображение:
Бесплатное руководство по рисованию — Как рисовать от руки с квадратными сетками для рисования
Привет, меня зовут Колин Брэдли,
Я считаю, что все хотели бы рисовать.Не просто рисовать, а точно рисовать , они хотели бы копировать свои собственные фотографии и создавать прекрасные произведения искусства.
В викторианскую эпоху художники разбивали свои рисунки на сетку, чтобы обеспечить правильные пропорции и перспективы. Несколько лет назад мне нужно было сделать то же самое, и я создал свой собственный продукт — квадратные сетки для рисования.
Они снова помогли мне создать точные контурные рисунки, которые я использую пастельными карандашами и другими средствами.Я начал продавать эти сетки 20 лет назад, и с тех пор тысяч студентов по всему миру добились успеха.
В этом курсе я покажу вам, как использовать наши сетки или любую другую систему с координатной сеткой для создания точных и точных контурных чертежей из ваших собственных фотографий.
Я покажу вам 3 примера: портрет, животное и пейзаж. Я также покажу вам, как вы можете использовать сетки для увеличения ваших изображений, что особенно полезно, если вы работаете с меньшей фотографией.
При использовании сеток вы не только поймете перспективу и пропорции, но и улучшите свою способность свободной руки.
Этот курс бесплатный , и мы рекомендуем вам попробовать этот метод рисования.
______________
В этом курсе вы узнаете, как использовать квадратную сетку для рисования для точного копирования ваших собственных изображений .
Вы узнаете, как накладывать более мелкие сетки, чтобы воспроизвести мелкие детали в глазах и зданиях.
Использование квадратного рисунка Система научит вас перспективе, пропорциям и создаст мышечную память для рисования от руки.
В этом курсе Колин покажет вам, как использовать систему рисования квадратов для:
- Рисование портретов
- Рисование животных
- Рисование пейзажей
- Масштабирование ваших рисунков
- Перенос ваших рисунков с помощью графитового угля
Рисование основных форм | Справка SketchUp
Многие модели начинаются с основных форм.В SketchUp инструменты фигур помогают рисовать прямоугольники, круги и многоугольники. Вы найдете эти инструменты на панели инструментов «Приступая к работе», на панели инструментов «Рисование» и на панели инструментов «Большой набор инструментов».
Рисование прямоугольника или квадрата
В SketchUp прямоугольники можно рисовать практически где угодно:
- На плоскости
- На вертикальной плоскости
- На существующих забоях
- Отдельно от существующей геометрии (выровнено по плоскости осей)
- На основе существующей геометрии
Чтобы нарисовать прямоугольник с помощью инструмента «Прямоугольник», выполните следующие действия:
- Выберите инструмент Прямоугольник () на панели инструментов или нажмите клавишу R .Курсор изменится на карандаш с прямоугольником.
Совет: Чтобы начать сначала в любой момент во время этих шагов, нажмите Esc .
- Щелкните, чтобы установить первую угловую точку прямоугольника. .
- Щелкните, чтобы установить первую угловую точку прямоугольника. Чтобы выровнять плоскость вашего прямоугольника с определенной осью чертежа или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе.
- Щелкните, чтобы установить первую угловую точку прямоугольника.Чтобы выровнять плоскость вашего прямоугольника с определенной осью чертежа или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе. Если вы предпочитаете рисовать прямоугольник из центра, нажмите клавишу Ctrl (Windows) или клавишу Option (macOS).
- Переместите курсор по диагонали, чтобы найти нужный размер и форму прямоугольника. Чтобы нарисовать прямоугольник с точными размерами, используйте поле «Измерения», в котором при перемещении курсора отображаются размеры вашего прямоугольника.Чтобы помочь вам разместить прямоугольник относительно осей рисования или другой геометрии, механизм вывода SketchUp отображает на экране подсказки. Когда появится нужный вывод, переходите к шагу 4. Выводы в поле «Измерения» и в инструменте «Прямоугольник» объясняются немного позже в этом разделе.
- Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника. Ваша фигура отображается с лицом, как показано на следующем рисунке.
- Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника.Или, если вы рисуете прямоугольник из центра, щелкните еще раз, чтобы установить любую угловую точку. Ваша фигура отображается с лицом, как показано на следующем рисунке.
Когда вы рисуете прямоугольник, поле «Измерения» помогает вам моделировать в точности следующим образом:
- Установите длину и ширину. Введите значение длины, запятую, значение ширины и нажмите Введите . Например, введите 8 ‘, 20’ и нажмите . Введите . Если вы вводите только число или числа, SketchUp использует текущую настройку единиц измерения документа.Вы также можете изменить настройку единиц измерения документа, указав британские (например, 1’6 «) или метрические (например, 3,652 м ) единицы.
- Укажите только длину или ширину. Если ввести значение и запятую ( 3 ‘, ), новое значение будет применено к первому измерению, а второе измерение не изменится. Точно так же, если вы введете запятую, а затем значение (, 3 ’), изменится только второе измерение.
- Измените положение прямоугольника на отрицательные числа. Если вы вводите отрицательное значение ( –24, –24 ), SketchUp применяет это значение в направлении, противоположном тому, которое вы указали при рисовании.
Совет: Нет необходимости щелкать поле Измерения перед вводом значения. Во время рисования поле «Измерения» ждет, когда вы введете точные измерения, если вы захотите это сделать. Кроме того, пока вы не выберете другой инструмент или не нарисуете другой прямоугольник, вы можете использовать поле «Измерения», чтобы изменять размеры прямоугольника сколько угодно раз.
Примечание: Если вы используете неанглийскую клавиатуру, используйте запятую для обозначения десятичного разряда и точку с запятой для разделения размеров. Например, вы можете ввести две стороны прямоугольника как: 7,6 м; 4,3 м
Когда вы перемещаете курсор с выбранным инструментом «Прямоугольник», механизм вывода SketchUp отображает следующие подсказки:
Необходимо выровнять плоскость прямоугольника с осью чертежа или другой геометрией? Клавиши со стрелками могут помочь, как описано в следующей таблице.
| Ключ-модификатор | : фиксирует плоскость прямоугольника так, чтобы он совпадал с… | Как это выглядит на экране |
|---|---|---|
| Стрелка влево | Зеленая ось | |
| Стрелка вверх | Голубая ось | |
| Стрелка вправо | Красная ось | |
| Стрелка вниз | Предполагаемая геометрия |
На видео вы можете увидеть эти функции инструмента «Прямоугольник» в действии.
Рисование повернутого прямоугольника
Инструмент «Повернутый прямоугольник» может пригодиться, когда вам нужно нарисовать прямоугольник, грань которого находится под углом к красной, зеленой или синей осям SketchUp по умолчанию или к другой геометрии.
Как и инструмент «Прямоугольник», инструмент «Повернутый прямоугольник» позволяет создавать точные прямоугольники и квадраты и выводить на экран выводы, которые помогут вам при рисовании. Однако, когда вы создаете прямоугольник с помощью инструмента «Повернутый прямоугольник», вы также располагаете прямоугольник под углом.На следующем рисунке показан пример прямоугольника, созданного с помощью инструмента «Прямоугольник с поворотом».
Чтобы создать повернутый прямоугольник, выполните следующие действия:
- На панели инструментов в меню «Инструменты для фигур» выберите инструмент «Прямоугольник с поворотом» (). Или выберите Draw> Shapes> Rotated Rectangle в строке меню.
- (Необязательно) Нажмите клавишу со стрелкой, чтобы задать плоскость для повернутого прямоугольника в соответствии с таблицей, приведенной ранее в этой статье. Например, нажмите клавишу со стрелкой влево, чтобы ограничить плоскость вашего повернутого прямоугольника зеленой плоскостью.
- Щелкните один раз, чтобы задать первый угол прямоугольника.
- Создайте первый край вашего повернутого прямоугольника. Сделать это можно двумя способами:
- Введите точное измерение и нажмите Введите .
- Или переместите курсор в то место, где вы хотите разместить вторую конечную точку этого ребра, используя механизм вывода SketchUp, чтобы расположить конечную точку относительно осей или другой геометрии, как показано на следующем рисунке, а затем щелкните.
Совет: Вы можете использовать несколько клавиш-модификаторов при выполнении этого шага. Удерживайте нажатой клавишу Shift , чтобы ограничить первый край его текущим направлением. Клавиша Alt (Windows) или Command (macOS) блокирует плоскость транспортира. Или клавиши со стрелками снова могут помочь вам выровнять первый край по оси. Просто нажмите кнопку со стрелкой, соответствующую желаемому выравниванию, как объяснялось ранее в этом разделе. Например, нажмите клавишу со стрелкой вправо, чтобы ограничить первый край так, чтобы он был выровнен по красной оси.
- На этом этапе вы устанавливаете ширину и угол вашего прямоугольника. Вы можете установить эти значения несколькими способами:
- Введите угол и ширину в поле «Измерения», следуя подсказке.
- Введите ширину и угол в поле «Измерения», следуя подсказке.
- Переместите транспортир, чтобы установить угол, и переместите курсор от центра транспортира, чтобы установить ширину, как показано на следующем рисунке.Чтобы ограничить угол, удерживайте нажатой клавишу Shift . Щелкните, чтобы завершить создание повернутого прямоугольника.
Совет: Нажмите клавишу Alt (Windows) или Command (macOS), чтобы установить базовую линию транспортира в текущем положении курсора, а затем переместите курсор, чтобы измерить угол от установленной базовой линии. Этот метод полезен, если вы хотите измерить угол от точки, отличной от базовой линии, установленной на шаге 3. Появится пунктирная линия, чтобы вы могли увидеть новую базовую линию.
Примечание. , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения». Например, вы можете ввести угол и ширину второй кромки как 43,2; 8,2 м , чтобы получить угол 43,2 градуса и длину 8,2 метра.
Примечание. , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения».Например, вы можете ввести ширину и угол второй кромки как 8,2 м; 43,2 , чтобы получить ширину 8,2 метра и угол 43,2 градуса.
Рисование круга или эллипса
Прежде чем рисовать круг, полезно понять, как SketchUp создает объекты круга:
- Объекты окружности имеют радиус и соединяют несколько отрезков линии.
- Эти сегменты действуют как одна линия в том смысле, что они могут определять край грани и разделять грань.Кроме того, при выборе одного сегмента выделяется весь круговой объект. Механизм вывода
- SketchUp по-прежнему видит сегменты в круге. Итак, если вы наведете указатель мыши на окружность объекта круга, вы увидите выводы конечной и средней точки.
Чтобы нарисовать круг, выполните следующие действия:
- На панели инструментов выберите инструмент Окружность () в раскрывающемся меню рядом с инструментом Прямоугольник. Или нажмите клавишу C . Курсор изменится на карандаш с кружком, а в поле «Измерения» будет указано количество сторон по умолчанию: 24, как показано на рисунке.Чтобы изменить количество сторон, вы можете ввести значение сейчас или подождать, пока не закончите рисовать круг.
- Щелкните, чтобы разместить центральную точку круга. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
- Щелкните, чтобы разместить центральную точку круга. Чтобы выровнять плоскость вашего круга с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию.Например, стрелка вверх выравнивает плоскость круга по синей оси. Подробную информацию см. В таблице в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
- Переместите курсор из центральной точки, чтобы определить радиус круга. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Нажмите Esc в любой момент, чтобы начать все заново.
- Щелкните, чтобы закончить круг. SketchUp создает лицо в форме круга, как показано на рисунке.
- (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый круг, вы можете использовать поле «Измерения», чтобы изменить радиус круга или количество сторон следующим образом:
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . В качестве альтернативы вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или — , чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавишу Ctrl (Microsoft Windows) и клавишу + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
- Чтобы изменить радиус: Введите число и единицу измерения (при желании), например 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните . Совет: Диалоговое окно «Информация об объекте» предлагает удобный способ редактировать значения сторон и радиуса в любое время. Дополнительные сведения см. В разделе «Редактирование фигур» далее в этой статье.
Чтобы нарисовать эллипс или овал, выполните следующие действия:
- Нарисуйте окружность с помощью инструмента Окружность .
- Выберите инструмент Масштаб ().
- Щелкните круг. Вокруг круга отображается ограничивающая рамка с восемью зелеными ручками.
- Щелкните одну из средних ручек (не одну из угловых) и переместите мышь, чтобы превратить круг в эллипс, как показано здесь.
- Нажмите еще раз, когда закончите масштабировать круг.
Рисование многоугольника
Вы можете создавать полигональные объекты с помощью инструмента «Многоугольник». (В этом нет ничего удивительного.) Тем не менее, вот несколько фактов, которые вы можете не знать о многоугольниках, но которые полезно знать при их рисовании:
- В SketchUp многоугольник имеет радиус и 3 или более сторон. Таким образом, размер вашего многоугольника измеряется от центральной точки, а количество сторон определяет тип рисованного многоугольника. Пятиугольник в виде 5 сторон; восьмиугольник имеет 8 сторон.
- Многоугольники действуют как одна линия, так как они могут определять край грани, а также разделять грань. При выборе одной стороны многоугольника выделяется весь многоугольник.
- Механизм вывода SketchUp интерпретирует каждую сторону многоугольника как сегмент. Когда вы наводите курсор на многоугольник, вы видите конечную точку, среднюю точку и исходные точки.
- Вы можете рисовать многоугольники на гранях или отдельно от существующей геометрии.
Чтобы нарисовать многоугольник, выполните следующие действия:
- Выберите инструмент Многоугольник () на панели инструментов.Курсор изменится на карандаш с многоугольником. В поле «Измерения» указано текущее количество сторон. Чтобы изменить количество сторон многоугольника, вы можете ввести числовое значение сейчас или дождаться завершения рисования.
- Щелкните, чтобы разместить центральную точку многоугольника. В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
- Щелкните, чтобы разместить центральную точку многоугольника. Чтобы выровнять плоскость вашего многоугольника с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, соответствующую желаемому выравниванию.Например, стрелка вверх выровняет плоскость многоугольника по синей оси. Подробнее см. В предыдущей таблице в разделе «Рисование прямоугольника или квадрата». В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
- Переместите курсор из центральной точки, чтобы определить радиус многоугольника. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Чтобы указать радиус, введите значение и нажмите Введите .Вы также можете нажать Esc , чтобы начать все заново.
- Щелкните второй раз, чтобы закончить многоугольник. Здесь вы видите 5-сторонний многоугольник.
- (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый многоугольник, вы можете использовать поле Измерения, чтобы изменить радиус или количество сторон следующим образом:
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
- Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . В качестве альтернативы вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или — , чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавишу Ctrl (Microsoft Windows) и клавишу + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
- Чтобы изменить радиус: Введите число и единицу измерения (при желании), например 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните .
Совет: Хотя инструмент «Многоугольник» работает аналогично инструменту «Круг», разница между инструментами становится очевидной, когда вы нажимаете / вытягиваете круг или многоугольник в трехмерную форму.Края круга выглядят гладкими, но края многоугольника имеют четкие стороны, как показано здесь.
В этом видеоролике вы можете увидеть, как инструменты «Круг» и «Многоугольник» демонстрируют все свои трюки.
Редактирование форм
Диалоговое окно «Информация об объекте» позволяет изменить радиус или стороны круга или многоугольника в любое время после создания формы. Вот как:
- Щелкните правой кнопкой мыши край (не грань) круга или многоугольника, который вы хотите отредактировать.
- Выберите Entity Info из появившегося контекстного меню, как показано здесь.
- На панели «Информация об объекте» щелкните поле Radius или Segments , измените значение и нажмите , введите (Microsoft Windows) или Return (Mac). После того, как вы нажмете Enter или Return, ваша форма немедленно отобразит ваши изменения.
SketchUp не позволяет изменять ширину или длину прямоугольника в любое время.Если вы уже выбрали другой инструмент или нарисовали дополнительные прямоугольники, вам нужно стереть прямоугольник, который вы хотите изменить, и перерисовать его. Подробнее см. Рисование прямоугольника. Или измените размер прямоугольника с помощью инструмента «Масштаб», если вам не нужно вводить точные размеры.
Конечно, вы можете сделать гораздо больше, чем просто изменить размер фигуры. Вы можете превратить 2D-форму в 3D-форму с помощью инструмента Push / Pull. Вы можете искажать формы с помощью инструмента «Перемещение» или масштабировать всю или часть модели.
Простой рисунок с черепахой — Введение в программирование на Python
Введение
«Черепаха» — это функция Python, такая как доска для рисования, которая позволяет вам командовать черепаху, чтобы нарисовать ее повсюду!
Вы можете использовать такие функции, как черепаха.вперед (...) и черепаха. слева (...) который может перемещать черепаху.
Прежде чем использовать черепаху, ее необходимо импортировать. Рекомендуем поиграться сначала с ним в интерактивном интерпретаторе, так как есть дополнительная работа требуется, чтобы он работал из файлов. Просто зайдите в свой терминал и введите:
Примечание
Ничего не видите в Mac OS? Попробуйте ввести команду типа turtle.forward (0) и глядя, открылось ли новое окно за вашим
командная строка.
Примечание
Вы работаете с Ubuntu и получаете сообщение об ошибке «Нет модуля с именем
_tkinter »? Установите недостающий пакет с помощью sudo apt-get install
python3-tk
Примечание
Хотя может возникнуть соблазн просто скопировать и вставить то, что написано на эту страницу в ваш терминал, мы рекомендуем вам вводить каждую команду. Печатание дает вам синтаксис под ваши пальцы (наращивая мышечную память!) и даже может помочь избежать странных синтаксических ошибок.
Черепаха .вперед (...) функция сообщает черепахе двигаться вперед
на заданное расстояние. turtle.left (...) принимает число градусов, которое вы
хотите повернуть влево. Еще есть черепаха . назад (...) и черепаха. Правая (...) тоже.
Примечание
Хотите начать все заново? Вы можете ввести turtle.reset () , чтобы очистить рисунок.
что ваша черепаха сделала до сих пор. Мы более подробно остановимся на turtle.reset () совсем немного.
Стандартная черепаха представляет собой просто треугольник. Это не весело! Давай сделаем черепаху
вместо этого с помощью команды turtle.shape () :
Настолько симпатичнее!
Если вы поместите команды в файл, вы могли бы узнать, что черепаха
окно исчезает после того, как черепаха закончит свое движение. (Это потому
Python выходит, когда ваша черепаха закончит двигаться. Поскольку окно черепахи
принадлежит Python, он также уходит.) Чтобы этого не произошло, просто положите черепаха.exitonclick () внизу файла. Теперь окно остается открытым
пока вы не нажмете на нее:
импортная черепаха turtle.shape («черепаха») черепаха вперед (25) turtle.exitonclick ()
Примечание
Python — это язык программирования, в котором горизонтальный отступ текста важный. Мы узнаем все об этом позже в главе «Функции». но пока просто имейте в виду, что случайные пробелы или табуляции перед любой строкой кода Python может вызвать непредвиденную ошибку. Вы даже можете попробовать добавить один чтобы проверить, как питон будет жаловаться!
Рисование квадрата
Примечание
От вас не всегда ожидают, что вы сразу узнаете ответ.Учиться методом проб и ошибок! Поэкспериментируйте, посмотрите, что делает Python, когда вы ему рассказываете разные вещи, что дает красивое (хотя иногда неожиданные) результаты и что дает ошибки. Если ты хочешь сохранить играть с тем, что вы узнали, что создает интересное результаты, это тоже нормально. Не стесняйтесь пробовать и терпеть неудачу и учиться от него!
Упражнение
Нарисуйте квадрат как на следующем рисунке:
Для квадрата вам, вероятно, понадобится прямой угол, равный 90 градусам.
Решение
черепаха.вперед (50) черепаха слева (90) черепаха вперед (50) черепаха слева (90) черепаха вперед (50) черепаха слева (90) черепаха вперед (50) черепаха слева (90)
Примечание
Обратите внимание, как черепаха начинается и заканчивается в одном и том же месте и в одном направлении, до и после рисования квадрат. Это полезное соглашение, оно упрощает чтобы нарисовать несколько фигур позже.
Бонус
Если вы хотите проявить творческий подход, вы можете изменить свою форму с помощью черепаха.width (...) и turtle.color (...) функций. Как ты
использовать эти функции? Прежде чем вы сможете использовать функцию, вам необходимо знать
его подпись (например, что ставить между скобками и что те
это означает.) Чтобы узнать это, вы можете ввести help (turtle.color) в
Оболочка Python. Если текста много, Python поместит текст справки
в пейджер , который позволяет листать вверх и вниз. Нажмите кнопку q клавиша для выхода из пейджера.
Подсказка
Вы видите такую ошибку:
NameError: имя 'черепаха' не определено
при попытке просмотреть справку? В Python вам нужно импортировать имена перед тем, как вы
могут ссылаться на них, поэтому в новой интерактивной оболочке Python вам потребуется import turtle до help (turtle.color) будет работать.
Еще один способ узнать о функциях — просмотреть онлайн-документацию.
Осторожно
Если вы что-то неправильно нарисовали, вы можете приказать черепахе стереть свою чертежную доску.
с черепахой .reset () или отмените последний шаг с помощью turtle.undo () .
Подсказка
Как вы могли прочитать в справке, вы можете изменить цвет с помощью черепаха. Цвет ( цветовая строка ) . К ним относятся, но не ограничиваются
«Красный», «зеленый» и «фиолетовый». См. Это руководство по цветам для получения более подробной информации.
список.
Если вы хотите установить значение RGB, обязательно запустите turtle.colormode (255) первый. Тогда, например, вы можете запустить turtle.цвет (215, 100, 170) от до
установить розовый цвет.
Как нарисовать невозможный квадрат
Простое, пошаговое руководство по рисованию невозможного квадратаНажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Невозможный квадрат — это тип невозможного объекта, также известный как невозможная фигура или неразрешимая фигура. Это тип оптической иллюзии, в которой трехмерный рисунок интерпретируется глазами и мозгом как трехмерный объект.Однако его геометрия такова, что он не может существовать в трехмерном пространстве.
Невозможный квадрат в этом руководстве по рисованию основан на треугольнике Пенроуза, невозможном объекте, созданном шведским художником Оскаром Реутерсвардом в 1934 году. Поэтому его иногда называют квадратом Пенроуза.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
Обратите внимание на углы, под которыми кажется, что стороны квадрата ориентированы. Затем обратите внимание, как эти углы соединяются.Невозможность фигуры сбивает с толку и почти столетие делает ее популярным арт-объектом.
Оптические иллюзии, такие как невозможный квадрат, используют затенение, чтобы обмануть мозг. Обратите внимание на более темный и светлый оттенок, который указывает на тени. Наши предыдущие знания углов также добавляют иллюзии. Даже после того, как осознана невозможность объекта, кажущаяся трехмерная природа остается.
Интересно, что можно создавать другие фигуры Пенроуза или невозможные формы, включая пятиугольники, шестиугольники и восьмиугольники.Однако по мере увеличения количества сторон оптическая иллюзия становится менее разительной. Фигуры не кажутся «невозможными», а деформированы, скручены или заплетены.
Хотите нарисовать невозможный квадрат? Это простое пошаговое руководство по рисованию фигур поможет вам. Все, что вам понадобится, это лист бумаги и карандаш, маркер или ручка. Вы также можете раскрасить законченный рисунок.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Невозможный треугольник, Невозможный куб и Звезда.
Разблокируйте БЕСПЛАТНЫЕ и ПЕЧАТНЫЕ уроки рисования и раскрашивания! Узнать большеПошаговая инструкция по рисованию невозможного квадрата
Рисование невозможного квадрата — шаг 11. Начните с рисования прямой вертикальной линии. Это указывает на одну сторону квадрата. От нижней части этой линии вытяните короткую прямую диагональную линию. Затем от конца этой линии протяните более длинную прямую на противоположной диагонали. Эти линии образуют угол и нижнюю сторону квадрата.
Рисование невозможного квадрата — шаг 22. Вытяните длинную прямую вертикальную линию вверх от нижней части квадрата. От этой линии вытяните более короткую прямую диагональную линию. Затем соедините это с исходной линией, используя длинную прямую линию.
Рисование невозможного квадрата — шаг 33. Проведите прямую вертикальную линию вниз от самого верхнего угла фигуры. Не продолжайте эту линию до нижней части квадрата.
Рисование невозможного квадрата — шаг 44.Нарисуйте прямую диагональную линию, отходящую от предыдущей. Эта линия должна быть параллельна низу квадрата, очерчивая верх нижнего сегмента.
Рисование невозможного квадрата — шаг 55. Проведите прямую линию вверх от конца предыдущей линии. Эта линия должна быть параллельна стороне квадрата, но обратите внимание, что она дальше от внешней линии, чем предыдущие линии.
Рисование невозможного квадрата — шаг 66.От конца предыдущей линии проведите короткую прямую, параллельную вершине квадрата. Затем проведите более короткую прямую линию вверх от конца этой линии.
Рисование невозможного квадрата — шаг 77. От конца предыдущей линии проведите прямую линию, параллельную вершине квадрата. Затем проведите прямую линию вниз до самого нижнего угла квадрата.
Рисование невозможного квадрата — шаг 88. Теперь вы закончите обрисовывать внутреннюю часть квадрата.Из внутреннего угла фигуры, заключенной на предыдущем шаге, проведите прямую вертикальную линию.
Рисование невозможного квадрата — шаг 99. Из предыдущей линии проведите прямую линию, чтобы пересечь противоположный край внутренней части квадрата. Соедините внутренний угол со следующим ближайшим углом, чтобы завершить невозможную форму.
Завершите чертеж «Невозможный квадрат»10. Раскрасьте свой невозможный квадрат. Затем ознакомьтесь с нашими руководствами по рисованию искусственных объектов, чтобы научиться рисовать больше невозможных фигур.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
Учебник по рисованию для печати
Нарисуйте квадрат и прямоугольник в черепахе — Python
Нарисуйте квадрат и прямоугольник в черепахе — Python
Предварительные требования: Основы программирования Turtle
turtle — это встроенный модуль в Python. Обеспечивает рисование с помощью экрана (картон) и черепахи (ручка).Чтобы что-то нарисовать на экране, нам нужно переместить черепаху (ручку). Для перемещения черепахи есть несколько функций, например, вперед (), назад () и т. Д.
Площадь чертежа:
Python3
|
Ввод:
100
Выход:
Второй подход (с использованием цикла):
Python3
|
Ввод:
100
Выход:
Прямоугольник чертежа:
Python3
|
Ввод:
100 120
Выход:
Второй подход (с использованием цикла):
Python3
|
Ввод:
100 120
Выход:
С этого момента вы, должно быть, научились рисовать различные основные геометрические иллюстрации, такие как круг, квадрат, прямоугольник.Итак, давайте применим эти знания, чтобы построить что-то, что вы действительно сможете использовать при создании игр, например, давайте нарисуем человека, используя базовые знания геометрии.
Вот код для этой реализации: —
Python3
|
Выход:
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .
Упражнение: Рисование квадратов
Для этого упражнения вам понадобится сетка из точек, карандаш и мозг.
Давайте узнаем, сколько квадратов вы можете сделать на разных сетках:
Примечание. «1 на 1» означает, сколько сторон (а не сколько точек).
Итак, попробуем порисовать несколько квадратов и посчитайте сколько:
1 по 1
| Ну, это просто, есть только один: |
2 пользователем 2
| Это тоже кажется простым. Их четверо, не так ли? | ||
| Но
подождите, это не полный ответ. Есть и более крупный один: |
Что делает всего пять квадратов - четыре 1 на 1 квадратик и один 2 на 2 кв
Твоя очередь!
3 пользователя 3
Подсказка: Для в случае 3 на 3 вы ожидаете получить квадраты 1 на 1, 2 на 2 квадрата и 3 на 3 квадрата. Сколько каждого?
Теперь можно приступить к заполнению таблицы:
| Сколько квадратов 1 на 1 | Сколько квадратов 2 на 2 | Сколько квадратов 3 на 3 | Сколько квадратов 4 на 4 | Сколько квадратов 5 на 5 | Итого | |
| 1 пользователем 1 сетка: | 1 | 1 | ||||
| 2 пользователем 2 Сетка: | 4 | 1 | 5 | |||
| 3 пользователем 3 Сетка: | ||||||
| 4 пользователем 4 Сетка: | ||||||
| 5 пользователем 5 Сетка: |
Вы что-нибудь заметили в числах в таблице?
Они все квадратные номера:
- 1 2 = 1 ,
- 2 2 = 4 ,
- 3 2 = 9 ,
- и др...
и найдены итоги сложив квадратные числа.
Формула спасения ...!
На самом деле существует формула для сложения первых n квадратных чисел:
S n = n (n + 1) (2n + 1) / 6
Пример: количество квадратов в корпусе
5 на 5Попробуйте подставить n = 5 в формулу:
S n = n (n + 1) (2n + 1) / 6
S 5 = 5 × (5 + 1) × (2 × 5 + 1) / 6
S 5 = 5 × 6 × 11/6
S 5 = 55
Итак, мы вроде решили вопрос.Ура!
Но подождите ... это еще не все!
Я сказал, что тебе нужно использовать свои мозги. Вернемся к случаю 2 на 2:
2 пользователя 2
Есть еще один квадрат, этот:
Почему квадрат? У него четыре равные стороны и четыре прямых угла, так что это квадрат.
Итак, что делает всего шесть квадратов.
Четыре 1 на 1 квадратик, один 2 на 2 квадрата и один х х кв.
Какое значение имеет x ? Мы можем использовать Пифагора Теорема, чтобы найти это:
x 2 = 1 2 + 1 2 = 1 + 1 = 2
Итак, x = √2
Итак, у нас четыре 1 на 1 квадратов , один 2 на 2 квадрата и на один √2 на √2 квадрат .
Твоя очередь!
3 на 3
- Есть еще квадраты?
ДА ! Вы можете их найти?
4 на 4 и 5 на 5
Также попробуйте сетку 4 на 4 и сетку 5 на 5
По мере продвижения вы найдете такие квадраты:
Каковы длины сторон этих квадратов?
Вы можете использовать Pythagoras ' Теорема, чтобы решить это самостоятельно
В каждом случае, сколько вы получите по каждому?
Вот таблица, которая вам поможет:
| Сколько 1 по 1 | Сколько 2 на 2 | Сколько 3 на 3 | Сколько 4 на 4 | Сколько 5 на 5 | Сколько √2 на √2 | Сколько √5 на √5 | Сколько √8 на √8 | Сколько √10 на √10 | Сколько √13 на √13 | Сколько √17 на √17 | Итого | |
| Сетка 1 на 1: | 1 | 1 | ||||||||||
| 2 пользователем 2 Сетка: | 4 | 1 | 1 | 6 | ||||||||
| 3 пользователем 3 Сетка: | ||||||||||||
| 4 пользователем 4 Сетка: | ||||||||||||
| 5 пользователем 5 Сетка: |
Продвинутый
Можете ли вы найти формулу для расчета количества квадратов с длины, которые являются квадратными корнями?
Можете ли вы тогда найти формулу для общего количества квадратов в каждый случай?
Есть ли еще квадраты, которые мы пропустили?
Заключение
То, что сначала казалось простым упражнением, оказалось быть довольно сложным.


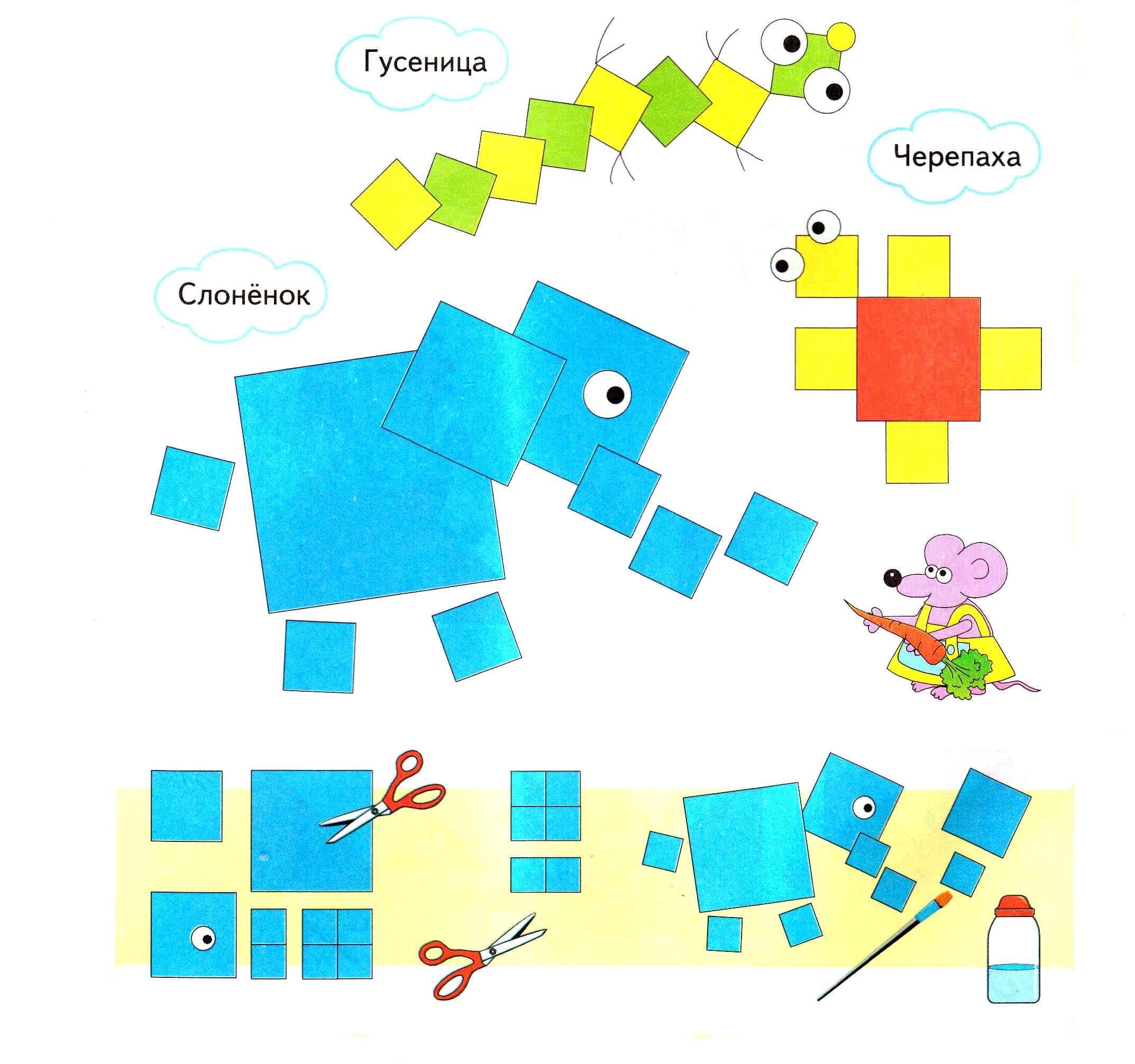 Называйте изображения своими именами, проговаривая их вслух.
Называйте изображения своими именами, проговаривая их вслух.
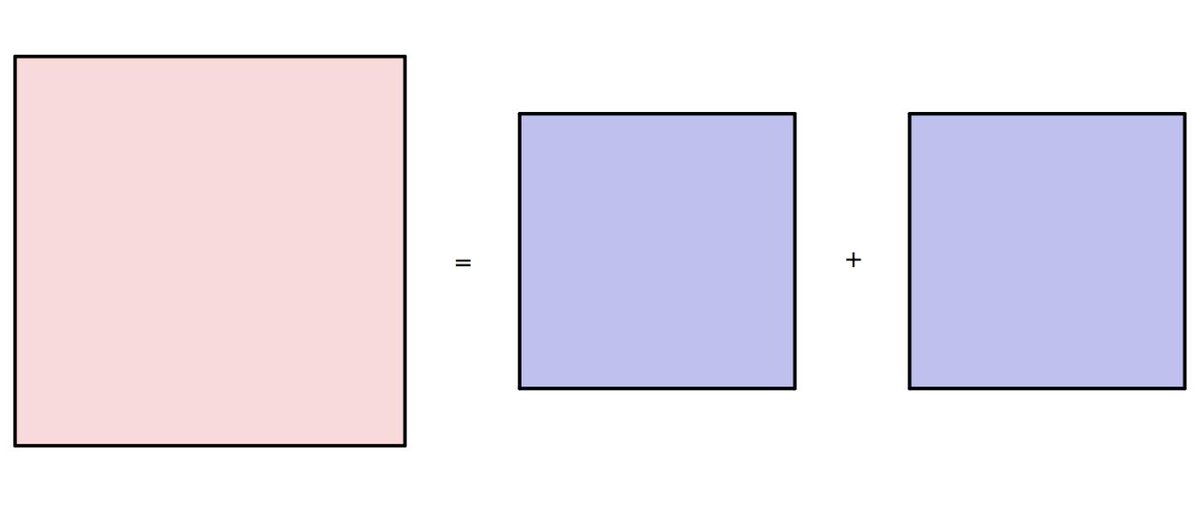
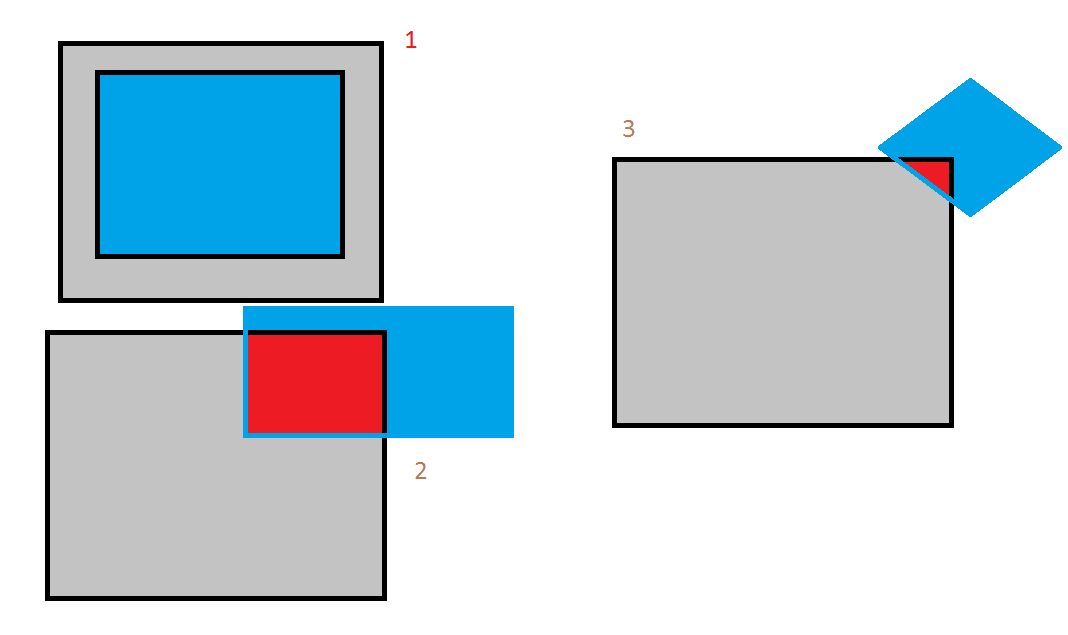
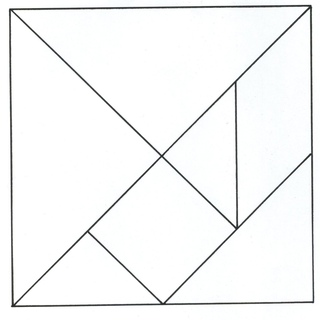
 Круги нужно согнуть пополам: одну половину приклеить к картону, вторую оставить. Половину второго круга приклеить рядом с первой так, чтобы из приклеенной части образовался круг.
Круги нужно согнуть пополам: одну половину приклеить к картону, вторую оставить. Половину второго круга приклеить рядом с первой так, чтобы из приклеенной части образовался круг.
 Получатся окна.
Получатся окна.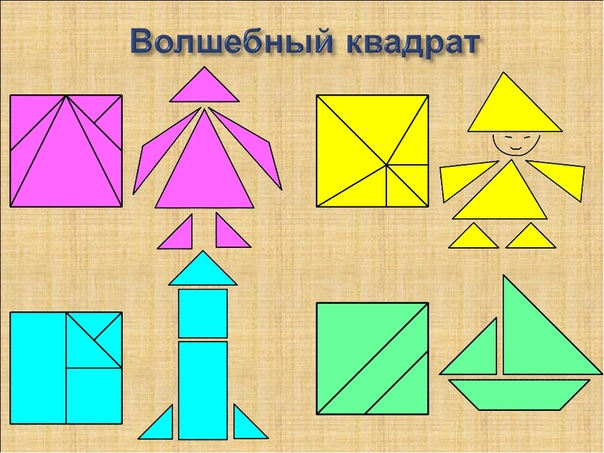

 pendown()
myTurtle.setheading(-45) # by default square would be sitting on corner instead of on side
for _ in range(nSquares):
radius = sideLength * 2**0.5 / 2
myTurtle.circle(radius, steps=4)
sideLength -= 10
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
yertle = turtle.Turtle()
yertle.penup()
yertle.goto(60, 60)
yertle.pendown()
drawSquares(yertle, 200, 4, 10)
turtle.done()
pendown()
myTurtle.setheading(-45) # by default square would be sitting on corner instead of on side
for _ in range(nSquares):
radius = sideLength * 2**0.5 / 2
myTurtle.circle(radius, steps=4)
sideLength -= 10
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
yertle = turtle.Turtle()
yertle.penup()
yertle.goto(60, 60)
yertle.pendown()
drawSquares(yertle, 200, 4, 10)
turtle.done()
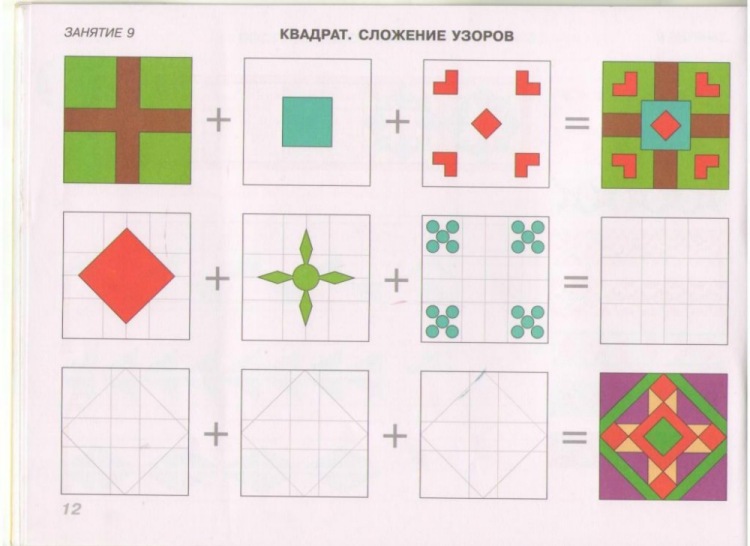 left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
drawSquares(myTurtle, sideLength - distanceApart, nSquares - 1, distanceApart)
left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
drawSquares(myTurtle, sideLength - distanceApart, nSquares - 1, distanceApart)
 forward(sideLength)
myTurtle.left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
sideLength -= distanceApart
forward(sideLength)
myTurtle.left(90)
myTurtle.penup()
x, y = myTurtle.position()
myTurtle.goto(x + distanceApart / 2, y + distanceApart / 2)
myTurtle.pendown()
sideLength -= distanceApart
Leave A Comment