Интеграл от скорости по времени – Интегрирование уравнений движения / Habr

§ 4. Расстояние как интеграл

Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено?

Таблица 8.4 • скорость падающего шара

v₁, тогда по формуле s= v₁t можно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В результате мы получим много маленьких отрезков, которые в сумме дадут весь путь. Таким образом, путь является суммой скоростей, умноженных на отдельные интервалы времени, или s = vt,
где греческая буква  (сигма) означает суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени, скажем t_i, умноженные на t:

(8.6)

причем каждый последующий момент t_i+1 находится по правилу t_i+1=t_i+t. Но расстояние, полученное этим методом, не будет точным, поскольку скорость за время t все же изменяется. Выход из этого положения заключается в том, чтобы брать все меньшие и меньшие интервалы t, т. е. разбивать время движения на все большее число все меньших отрезков. В конце концов мы придем к следующему, теперь уже точному выражению для пройденного пути:

(8.7)

Математики придумали для этого предела, как и для дифференциала, специальный символ. Значок  превращается в d, напоминая о том, что интервал времени сколь угодно мал, а знак суммирования превращается в ∫ — искаженное большое S, первая буква латинского слова «Summa». Этот значок назван интегралом. Таким образом, мы пишем

s=∫v(t)dt, (8.8)

v(t), так что один оператор (d/dt) «уничтожает» другой (∫). Это дает возможность получать формулы для интегралов путем обращения формул для дифференциалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами можете составить таблицу интегралов.

Любая функция, заданная в аналитическом виде, т. е. выражающаяся через комбинацию известных нам функций, дифференцируется очень просто — вся операция выполняется чисто алгебраически, и в результате мы всегда получаем какую-то известную функцию. Однако интеграл не от всякой функции можно записать в аналитическом виде. Разумеется, для каждого частного интеграла всегда сначала пытаются найти такую функцию, которая, будучи продифференцирована, давала бы функцию, стоящую после знака интеграла (она называется подынтегральной). Однако это не всегда удается сделать. В таких случаях интеграл вычисляют просто суммированием, т. е. вычисляют суммы типа (8.6) со все меньшими и меньшими интервалами, пока не получат результат с достаточной точностью.

studfiles.net

Обзор методов вычисления интегралов по времени и пространству

Интегрирование — один из важнейших математических инструментов, особенно в численном моделировании. Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования.

Важность интегралов

В COMSOL используется метод конечных элементов, который преобразует описывающее некоторый процесс уравнение в частных производных в интегральное уравнение — другими словами, в слабую форму (weak form). При детальном и глубоком изучении формулировок, используемых в интерфейсах COMSOL, вы обнаружите, что множество граничных условий реализованы через интегралы. В качестве наиболее характерных примеров можно привести условия

Total heat flux (Общий тепловой поток) или Floating potential (Плавающий потенциал). Вычисление интегралов также играет ключевую роль в процессе постобработки результатов, поскольку COMSOL рассчитывает большое количество вспомогательных величин через интегралы, например энергию электрического поля, скорость потока или общий тепловой поток. Разумеется, пользователи вольны использовать интегрирование в COMSOL в своих целях, и в этой статье мы объясним вам, как это делать максимально эффективно.

Вычисление интегралов в узле Derived Values

Интеграл общего вида имеет форму

\int_{t_0}^{t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t

где [t_0,t_1] — это временной интервал, \Omega — это пространственная область, а F(u) — это произвольное выражение, включающее зависимую переменную u и произвольные функции от нее, в том числе производные по пространству, времени, а также любой другой величине.

Наиболее удобный способ вычисления интегралов — использование узла Derived Values (Расчет выражений) в разделе Results (Результаты) ленты Ribbon или дерева модели (Лента Ribbon отсутствует в том случае, если ваш компьютер работает не под управлением ОС Windows®).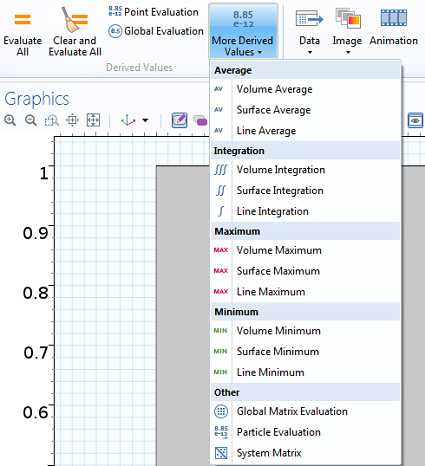

Добавление операций расчета пространственных интегралов по объему, поверхности или линии в узле Derived Values (Расчет выражений)

Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных (data set). В поле Expression (Выражение) вводится подынтегральная функция, включающая зависимые или производные переменные. Для данных расчета во временной области пространственный интеграл вычисляется на каждом временном шаге. В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл.

Пример настроек вычисления интегралов по поверхности (Surface Integration) с дополнительным вычислением интеграла по времени в разделе Data Series Operations.

Оператор Average (Усреднение) — еще одна операция в разделе Derived Values, связанная с вычислением интегралов. Оператор вычисляет интеграл и делит его на объем, площадь или длину выбранной области. Операция Averageв узле Data Series Operations аналогично вводит деление на продолжительность временного диапазона. Операторы узла Derived Values — важный инструмент, однако их можно использовать только во время постобработки, а значит с их помощью можно рассчитать далеко не любой интеграл. Именно поэтому в COMSOL представлены другие более мощные и гибкие инструменты для вычисления интегралов. Мы продемонстрируем их работу на представленном ниже модельном примере.

Вычисление пространственного и временного интегралов для демо-модели из области теплопередачи

Рассмотрим простую модель теплопередачи: двумерный единичный квадрат из алюминия в (x,y)-плоскости. Температура верхней и правой сторон постоянна и равна комнатной (293.15 K), в то время как для левой и нижней границы задан общий входящий тепловой поток (General inward heat flux), составляющий 5 000 W/m^2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже.

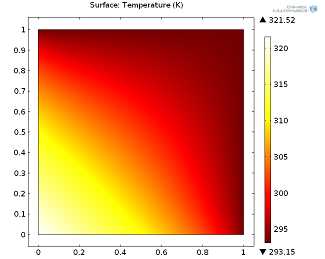
Стационарное решение, нажмите на изображение для увеличения.

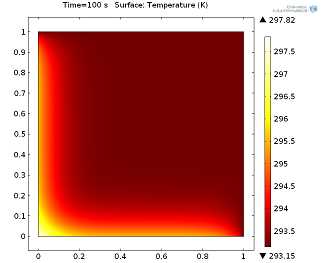
Нестационарное решение (для момента времени 100 секунд), нажмите на изображение для увеличения.

Вычисление пространственного интеграла с использованием операторов узла Component Coupling

Операторы узла Component Coupling (Сопряжение компонентов) используются в тех случаях, когда, например, в одном выражении объединяются несколько интегралов, или интегралы требуются в процессе вычислений, или требуется множество контурных интегралов. Операторы данного узла определяются в разделе Definitions (Определения). На этом этапе режультат использования оператора не просчитывается, а указываются только их название и выборки областей.

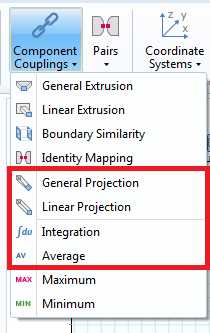
Добавление операторов через узел Component Couplings

В нашем примере мы для начала хотим вычислить пространственный интеграл для стационарного распределения температуры, равный

\int_{\Omega}T(x,y)\ \mathrm{d}x\mathrm{d}y = 301.65

В пакете COMSOL оператор вычисления интеграла по умолчанию получает имя intop1.

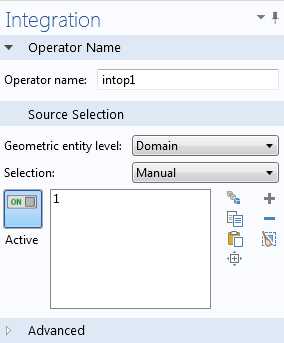
Окно настроек оператора интегрирования.

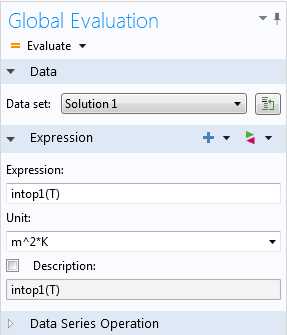
Расчет результата интегрирования через оператор.

Теперь давайте рассмотрим, как оператор интегрирования может использоваться непосредственно в процессе расчета модели. С его помощью мы могли бы, например, выяснить, какая нагревательная мощность потребуется для получения средней температуры 303.15 К, то есть температуры, на 10 К превышающей температуру окружающей среды. Прежде всего нам необходимо вычислить разницу между требуемым и действительным средними значениями. Среднее значение вычисляется путем деления интеграла от T на интеграл от постоянной функции 1, который равен площади области. Нетрудно догадаться, что вычисление подобного вида легко выполнить с помощью представленного в COMSOL оператора Average (Усреднение), см. комментарии выше. По умолчанию данный оператор получает название aveop1. Обратите внимание, что среднее значение для области в нашем примере совпадает с интегралом, т.к. область имеет единичную площадь. Соответствующая разность равна

303.15-\int_{\Omega}T(x,y)\mathrm{d} x\mathrm{d} y = 1.50

Далее нам необходимо найти значение General heat flux (Общий тепловой поток) на левой и нижней границах, при котором была бы достигнута требуемая средняя температура. Для этого мы введем дополнительную степень свободы под названием q_hot и дополнительное ограничение в качестве глобального уравнения (Global Equation). Общий входящий тепловой поток (General inward heat flux) тогда перезадается через переменную q_hot.

Добавление дополнительной степени свободы (переменной) и глобального уравнения, для неяного подбора средней температуры, равной 303.15 K.

Решение данной сопряженной системы с помощью стационарного исследования дает значение q_{hot}=5 881.30 W/m^2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К.

Вычисление неопределенного интеграла посредством оператора интегрирования

В своих обращениях в службу поддержки пользователи часто задают один и тот же вопрос: как рассчитать неопределенный пространственный интеграл? Для этой цели нам также пригодится оператор интегрирования, задаваемый через Component Couplings. Нахождение неопределенного интеграла — операция, обратная дифференцированию. Неопределенный интеграл позволяет вычислять площади произвольных областей, ограниченных графиками функций. Одна из самых важных прикладных задач — вычисление вероятностей в статистическом анализе. Для того чтобы это продемонстрировать, мы зафиксируем y=0 и обозначим неопределенный интеграл от T(x,0) как u(x). Это значит, что \frac{\partial u}{\partial x}=T(x,0). Тогда неопределенный интеграл имеет вид

u(\bar x) = \int_0^{\bar x}T(x,0)\mathrm{d} x

Здесь мы используем \bar x, чтобы отличать переменную интегрирования от внешней переменной. В отличие от представленных выше интегралов, результатом интегрирования является функция, а не скалярная величина. Нам необходимо указать для ПО, что для каждого значения \bar x\in[0,1] соответствующее значение u(\bar x) вычисляется при помощи интеграла. В среде COMSOL это можно легко сделать всего за три шага. Во-первых, потребуется логическое выражение для переписывания интеграла в виде

u(\bar x) = \int_0^1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x

Во-вторых, нам понадобится оператор вычисления интеграла, который будет действовать на нижней границе области из примера. Давайте обозначим его как intop2. В-третьих, мы должны отличать переменную интегрирования от внешней переменной. Принятые обозначения для такого случая: x называется источником (source), а \bar x — точкой назначения (destination). При использовании операторов интегрирования доступен встроенный оператор dest, который позволяет явно оглашать, что соответствующее выражение не относится к переменным интегрирования. Точнее, это значит, что в COMSOL \bar x=dest(x). Объединив логическое выражение с оператором dest, мы получим выражение вида T*(x<=dest(x)), которое является именно тем входным выражением, которое требуется для intop2. Объединив все вместе, мы можем вычислить неопределенный интеграл, воспользовавшись выражением intop2(T*(x<=dest(x))). Результат данной операции можно проиллюстрировать следующим графиком:

Как построить график неопределенного интеграла с помощью оператора интегрирования, оператора dest и логического выражения.

В пакете COMSOL дополнительно доступны еще два оператора вычисления интеграла, а именно общая проекция (general projection) и линейная проекция (linear projection). Эти операторы можно использовать для получения множества контурных интегралов в любом направлении в области. Другими словами, вычисление интеграла производится только вдоль одного измерения. В результате мы получаем функцию размерности на единицу меньше, чем размерность области. Для двухмерного примера результатом будет одномерная функция, которая может быть рассчитана на любой границе. Более подробная информация об использовании данных операторов будет представлена в одной из следующих публикаций в нашем компоративном блоге.

Вычисление пространственного интеграла посредством дополнительного физического интерфейса

Наиболее гибким способом вычисления пространственных интегралов является техника с добавлением дополнительного PDE-интерфейса. Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных

\frac{\partial u}{\partial x}=T(x,y)

с граничным условием типа Дирихле u=0 на левой границе. Расчет такого уравнения проще всего реализовать в физическом (математическом) интерфейсе Coefficient Form PDE (Дифференциальное уравнение в частных производных, коэффициентная форма записи), который потребует следующих настроек:

Вычисление пространственного интеграла посредством дополнительного PDE-интерфейса.

Зависимая переменная u представляет собой неопределенный интеграл по x и доступна в процессе расчета модели и в постобработке. Помимо гибкости, дополнительным преимуществом данного подхода является точность, так как интеграл рассчитывается не вспомогательными инструментами на основе уже определенного распределения переменной, а непосредственно в процессе расчета с учетом алгоритмов оценки погрешностей и т.п.

Вычисление временного интеграла посредством встроенных операторов

Мы уже упоминали узел Data Series Operations, который можно использовать для вычисления интеграла по времени. Другой крайне полезный способ вычисления интеграла по времени обеспечивается встроенными операторами timeint и timeavg для вычисления интеграла или среднего значения по времени, соответственно. Данные инструменты доступны при постобработке результатов, используются для вычисления интеграла от любого выражения (зависящего от времени) на заданном временном интервале. В нашем примере мы рассчитаем среднее значение температуры в диапазоне от 90 до 100 секунд, то есть:

\frac{1}{10}\int_{90}^{100}T(x,y,t)\ \mathrm{d} t

На поверхностном графике ниже представлен результирующий интеграл, являющийся функцией пространственных переменных (x,y):

Использование оператора timeavg – оператора вычисления интеграла по времени.

Схожие операторы существуют для вычисления интегралов на сферических зонах, а именно ballint, circint, diskint и sphint.

Вычисление временного интеграла посредством дополнительного физического интерфейса

В случае если временные интегралы нужно использовать непосредственно в модели в процессе расчета, вам будет необходимо задать их как дополнительные зависимые переменные. Аналогично представленному выше примеру с интерфейсом Coefficient Form PDE, это можно сделать, добавив ODE-интерфейс из раздела Mathematics. Предположим, например, что на каждом временном шаге требуется вычислять интеграл от величины общего теплового потока на промежутке от старта до текущего момента, который показывает накопленную энергию. Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.

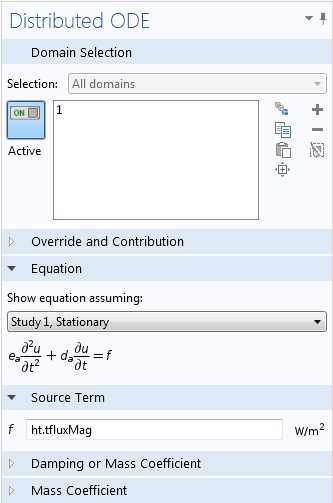
Использование дополнительного ODE-интерфейса для вычисления интеграла по времени.

В чем польза подобной техники? Полученный интеграл можно повторно использовать в других физических интерфейсах, поля в которых могут зависеть от накопленной в системе энергии. Более того, полученный резултат будет мгноменно доступен для всех видов постобработки, что удобнее и быстрее, чем использование встроенных операторов. Рекомендуем ознакомится с моделью Carbon Deposition in Hetereogeneous Catalysis (Образование сажевых отложений при гетерогенном катализе), в которой ОДЕ в области используется для вычисления пористости катализатора при наличии химических реакций в виде нестационарной полевой переменной.

Вычисление интеграла от аналитических функций и выражений

До сих пор мы демонстрировали, каким образом вычислять интеграл от искомых переменных в процессе расчета или при постобработке. Но не касались случая взятия интегралов от аналитических функций или выражений. Для этой операции в среде COMSOL доступен встроенный оператор integrate(expression, integration variable, lower bound, upper bound).

Выражение может представлять собой любую одномерную функцию, например sin(x). При этом допускается включение дополнительных переменных, например sin(x*y). Второй параметр определяет, по какой переменной вычисляется интеграл. Например, integrate(sin(x*y),y,0,1) выдает функцию переменной x, потому что интегрирование выполняется только по переменной y. Обратите внимание, что данный оператор также может использоваться для работы с аналитическими функциями, заданными в узле Definitions (Определения) текущего компонента.

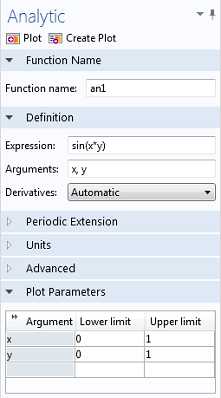
Добавление аналитической функции.

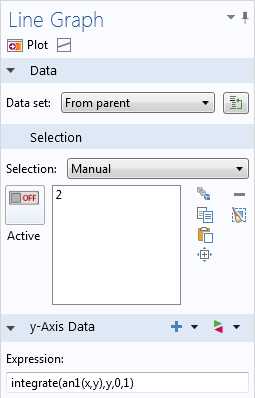
Вычисление интеграла от аналитической функции.

Материалы для дальнейшего изучения

www.comsol.ru

§ 4. Расстояние как интеграл

Таблица 8.4 • скорость падающего шара

Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90 км/час, то замедляется, затем где-то останавливается у светофора и т.д.? Сделать это нетрудно. Нужно использовать ту же идею и выражать полное расстояние через бесконечно малые его части. Пусть в первую секунду скорость будет v₁, тогда по формуле s= v₁t можно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В результате мы получим много маленьких отрезков, которые в сумме дадут весь путь. Таким образом, путь является суммой скоростей, умноженных на отдельные интервалы времени, или s = vt, где греческая буква  (сигма) означает суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени, скажем t_i, умноженные на t:

(8.6)

(8.7)

s=∫v(t)dt, (8.8)

где v(t) — скорость в момент t. Сама же операция суммирования этих членов называется интегрированием. Она противоположна операции дифференцирования в том смысле, что производная этого интеграла равна v(t), так что один оператор (d/dt) «уничтожает» другой (∫). Это дает возможность получать формулы для интегралов путем обращения формул для дифференциалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами можете составить таблицу интегралов.

studfiles.net

Расстояние как интеграл — GrandKid

Расстояние как интеграл. Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено? Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90 км/час, то замедляется, затем где-то останавливается у светофора и т. д.? Сделать это нетрудно. Нужно использовать ту же идею и выражать полное расстояние через бесконечно малые его части.

Пусть в первую секунду скорость будет υ₁, тогда по формуле ∆s = υ₁∆t можно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В результате мы получим много маленьких отрезков, которые в сумме дадут весь путь. Таким образом, путь является суммой скоростей, умноженных на отдельные интервалы времени, или s = ∑υ∆t, где греческая буква ∑ (сигма) означает суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени, скажем t

i умноженные на ∆t:

причем каждый последующий момент t_i+lнаходится по правилу t_i+1= t_i+ ∆t. Но расстояние, полученное этим методом, не будет точным, поскольку скорость за время ∆t все же изменяется. Выход из этого положения заключается в том, чтобы брать все меньшие и меньшие интервалы ∆t, т. е. разбивать время движения на все большее число все меньших отрезков. В конце концов мы придем к следующему, теперь уже точному выражению для пройденного пути:

Математики придумали для этого предела, как и для дифференциала, специальный символ. Значок ∆ превращается в d, напоминая о том, что интервал времени сколь угодно мал, а знак суммирования превращается в ∫ —искаженное большое S, первая буква латинского слова «Summa». Этот значок назван интегралом. Таким образом, мы пишем

где υ(t) —скорость в момент t. Сама же операция суммирования этих членов называется интегрированием. Она противоположна операции дифференцирования в том смысле, что производная этого интеграла равна υ(t), так что один оператор (d/dt) «уничтожает» другой (∫). Это дает возможность получать формулы для интегралов путем обращения формул для дифференциалов: интеграл от функции, стоящей в правой колонке табл. 8.3, будет равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами можете составить таблицу интегралов.

grandkid.ru

&nbsp&nbsp&nbsp&nbsp Определенный интеграл. Теорема существования.

&nbsp&nbsp&nbsp&nbsp Решение многих важных задач геометрии и физики (определение площади, работы, массы, пути) приводит к одной и той же последовательности действий над известными функциями и их аргументами.
&nbsp&nbsp&nbsp&nbsp Если отвлечься от физического смысла переменных и от их обозначений, то указанная последовательность действий состоит в следующем:
&nbsp&nbsp&nbsp&nbsp 1) Интервал $[a, b]$, в котором задана непрерывная функция $f(x)$, разбивается на $n$ частичных интервалов при помощи точек $$x_{0}=a,x_{1},x_{2},…,x_{n-1},x_{n}=b.$$
&nbsp&nbsp&nbsp&nbsp 2) Значение функции $f(\xi _{i})$ в какой-нибудь точке $\xi _{i}\in [x_{i-1},x_{i}]$ умножается на длину этого интервала $x_{i}-x_{i-1}$, т.е. составляется произведение $f(\xi _{i})(x_{i}-x_{i-1}).$
&nbsp&nbsp&nbsp&nbsp 3) Берется сумма $I_{n}$ всех этих произведений $$I_{n}=f(\xi _{1})(x_{1}-x_{0})+f(\xi _{2})(x_{2}-x_{1})+…+f(\xi _{n})(x_{n}-x_{n-1})=\sum_{i=1}^{n}{f(\xi _{i})(x_{i}-x_{i-1})}$$
или, если обозначить $x_{i}-x_{i-1}$ через $\Delta x_{i}$,

$$I_{n}=\sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$

(1)

&nbsp&nbsp&nbsp&nbsp 4) Находится предел $I$ суммы $I_{n}$ при стремлении к нулю длины наибольшего частичного интервала, и следовательно, при $n\rightarrow \propto$, т.е. $$I=\lim I_{n}=\lim \sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$
&nbsp&nbsp&nbsp&nbsp В рассмотренных выше четырех конкретных задачах этот предел $I$ измеряет соответственно площадь, работу, путь, массу. В общем слк=учае он называется определенным интегралом или просто интегралом от функции $f(x)$ в пределах от $a$ до $b$ и обозначается так: $$I=\int_{a}^{b}{f(x)dx}$$
и читается: интеграл от от $a$ до $b$ $f(x)$ на $dx$. Следовательно, по определению $$\int_{a}^{b}{f(x)dx}=\lim \sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$
Сумма (1) называется $n$-й интегральной суммой.
&nbsp&nbsp&nbsp&nbsp Определение. Определенным интегралом называется предел, к которому стремится $n$-я интегральная сумма (1) при стремлении к нулю длины наибольшего частичного интервала.
&nbsp&nbsp&nbsp&nbsp Как и в неопределенном интеграле, функция $f(x)$ — подынтегральная функция, выражение $f(x)dx$ — подынтегральное выражение и переменная $x$ — переменная интегрирования. Интервал $[a, b]$ называется интервалом интегрирования, число $a$ — нижний, а число $b$ — верхний пределы интеграла.
&nbsp&nbsp&nbsp&nbsp Сам процесс образования определенного интеграла показывает, что символ $\int_{a}^{b}{f(x)dx}$ есть некоторе число. Величина его зависит только от вида подынтегральной функции и от чисел $a$ и $b$, определяющих интервал интегрирования. Переменная интегрирования $x$ служит лишь для удобного обозначения определенного интеграла; ничего не изменится, если переменную интегрирования обозначить другой буквой, например $t$ или $u$: $$\int_{a}^{b}{f(x)dx}=\int_{a}^{b}{f(t)dt}=\int_{a}^{b}{f(u)du}.$$
&nbsp&nbsp&nbsp&nbsp Внешняя общность записи определенного и неопределенного интегралов подчеркивает тесную связь между ними, хотя определенный интеграл есть число, а неопределенный интеграл — совокупность первообразных функций.
&nbsp&nbsp&nbsp&nbsp Итак, совершенно очевидный результат $$\int_{a}^{b}{dx}=b-a,$$ который следует из того, что любая интегральная сумма для функции $f(x)\equiv 0$ равна $b-a$: $$\sum_{i=1}^{n}{\Delta x_{i}}=x_{1}-x_{0}+x_{2}-x_{1}+…+x_{n}-x_{n-1}=x_{n}-x_{0}=b-a.$$
&nbsp&nbsp&nbsp&nbsp Применяя определение интеграла, можно сделать такие выводы:
&nbsp&nbsp&nbsp&nbsp 1) Площадь криволинейной трапеции равна интегралу от ординаты линии, ограничивающей трапецию, взятому по основанию: $$s=\int_{a}^{b}{f(x)dx}.$$
&nbsp&nbsp&nbsp&nbsp 2) Работа, произведенная силой, равна интегралу от силы, взятому по пути: $$A=\int_{0}^{S}{f(S)dS}.$$
&nbsp&nbsp&nbsp&nbsp 3) Путь, пройденный телом, равен интегралу от скорости, взятому по времени: $$S=\int_{T_{1}}^{T_{2}}{f(t)dt}.$$
&nbsp&nbsp&nbsp&nbsp 4) Масса, распределенная на линии, равна интегралу от плотности, взятому по длине линии: $$m=\int_{0}^{s}{f(s)ds}.$$
&nbsp&nbsp&nbsp&nbsp Теорема существования определенного интеграла. Если функция $f(x)$ непрерывна в замкнутом интервале $[a, b]$, то ее $n$-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т.е. определенный интеграл $\int_{a}^{b}{f(x)dx}$, не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.
&nbsp&nbsp&nbsp&nbsp Интегральные суммы, составленные при различных разбиениях интервала интегрирования и различных выборах точек $\xi$, могут отличаться друг от друга весьма значительно. Сформулированная выше теорема показывает, что для непрерывных функций разница между этими суммами стирается по мере возрастания числа точек деления и убывания длины наибольшего частичного интервала, совсем исчезая в пределе.

2012-11-04 • Просмотров [ 4011 ]

primat.org

Интеграл — скорость — Большая Энциклопедия Нефти и Газа, статья, страница 1

Интеграл — скорость

Cтраница 1

Интеграл скоростей wz, направленных к загрузочному концу бассейна по dz, дает расход конвекционного потока, а интеграл скоростей w z, направленных в сторону выработочного конца бассейна по dz, — — сумму конвекционного и выработочного потока. [1]

В выражении (4.18) интеграл скорости выделения тепла по температуре берется по всей области, в которой скорость реакции отлична от нуля. Вследствие быстрого уменьшения скорости реакции при падении температуры основное слагаемое дает сравнительно узкий интервал температуры, примыкающий к температуре горения. [3]

Назовем течение жидкости, образующее поле скоростей v, безвихревым, если интеграл скорости вдоль любой замкнутой кривой равен нулю. В этом случае будем также и самое поле обозначать как безвихревое. Тогда мы можем высказать следующую теорему: поле градиента скаляра ср всегда — поле безвихревое. [5]

Интегральные реакторы представляют собой трубчатые проточные аппараты; в данном случае концентрации компонентов меняются по длине реактора, и, следовательно, выходные показатели являются интегралом скоростей процесса по всем элементарным объемам аппарата. [7]

При движении любой системы тел, находящихся под действием взаимных сил притяжения, или сил, направленных к неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые, описываемые различными телами, а равно их скорости необходимо таковы, что сумма произведений отдельных масс на интеграл скорости, умноженной на элемент кривой, является максимумом или минимумом — при условии, что первые и последние точки каждой кривой рассматриваются как заданные, так что вариации координат, соответствующих этим точкам, равны нулю. [8]

При движении любой системы тел, находящихся под действием взаимных сил притяжения, или сил, направленных к неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые, описываемые различными телами, а равно их скорости, необходимо таковы, что сумма произведений отдельных масс на интеграл скорости, умноженной на элемент кривой, является максимумом или минимумом — при условии, что первые и последние точки каждой кривой рассматриваются как заданные, так что вариации координат, соответствующих этим точкам, равны нулю. [9]

Указанное свойство, найденное Эйлером при движении изолированных тел, которое представлялось присущим только этим телам, я, пользуясь принципом сохранения живых сил, распространил на движение любой системы тел, действующих друг на друга каким угодно образом; отсюда вытекает новый общий принцип, согласно которому сумма произведений масс на интегралы скоростей, умноженных на элементы пройденных путей, является всегда максимумом или минимумом. [10]

Указанное свойство, найденное Эйлером при движении изолированных тел, которое представлялось присущим только этим телам, я, пользуясь принципом сохранения живых сил, распространил на движения любой системы тел, действующих друг на друга каким угодно образом; отсюда вытекает новый общий принцип, согласно которому сумма произведений масс на интегралы скоростей, умноженных на элементы пройденных путей, является всегда максимумом или минимумом. [11]

Данные о кинетике гомогенных жидких систем обычно получают, проводя опыты в периодически действующем реакторе ( реже — в проточном), а данные о кинетике гетерогенных систем для реакций, проходящих в газовой фазе, — в проточных реакторах ( трубках) на малой длине слоя катализатора ( дифференциальный реактор) или по всей длине слоя катализатора ( интегральный реактор — выходные характеристики являются интегралом скоростей процесса по всем элементарным объемам аппарата) или же в циркуляционных установках. [12]

Данные о кинетике гомогенных жидких систем обычно получают, проводя опыты в периодически действующем реакторе и реже в проточном, а данные о кинетике гетерогенных систем, реакций, проходящих в газовой фазе, — в проточных реакторах ( трубках) на малой длине слоя катализатора ( дифференциальный реактор) или по всей длине слоя катализатора ( интегральный реактор, так как выходные характеристики являются интегралом скоростей процесса по всем элементарным объемам аппарата) или же в циркуляционных установках. [13]

Однако указанные применения носят слишком специальный характер, чтобы на них можно было построить доказательство общего принципа; кроме того, они несколько неопределенны и произвольны, что придает некоторую ненадежность и выводам, которые можно было бы сделать на их основании о точности самого принципа. Поэтому мне кажется, что было бы неправильно изложенный в таком виде принцип ставить в один ряд с теми принципами, которые были указаны выше. Существует, однако, и другой способ его применения, более общий и более точный, который один только и заслуживает внимания математиков. Первую идею этого принципа дал Эйлер в конце своего сочинения De isoperimetricis, напечатанного в Лозанне в 1744 г.; он показал, что при траекториях, описанных под действием центральных сил, интеграл скорости, умноженный на элемент кривой, всегда является максимумом или минимумом. [14]

При систематическом изложении механики этот принцип отходит у Лагранжа на второй план. Эта формулировка такова: при движении любой системы тел, находящихся под действием взаимных сил притяжения, или сил, направленных к неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые, описываемые различными телами, а равно их скорости необходимо таковы, что сумма произведений отдельных масс иа интеграл скорости, умноженной на элемент кривой, является максимумом или минимумом — при условии, что первые и последние точки каждой кривой рассматриваются как заданные. [15]

Страницы: 1

www.ngpedia.ru

Решение интегралов. Рассказываем, как решать интегралы.

Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная диференциированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

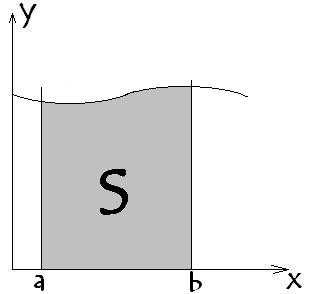
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:

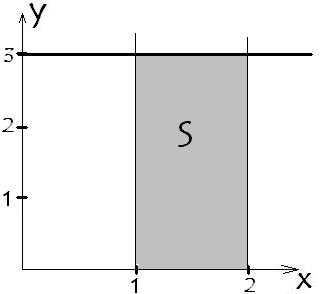
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:

Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.

F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов: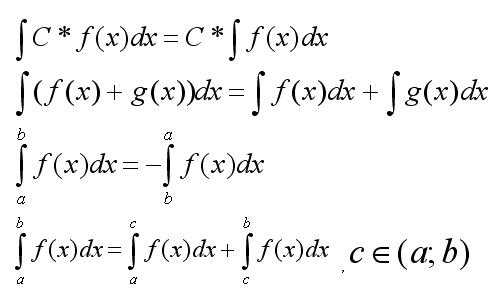

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной.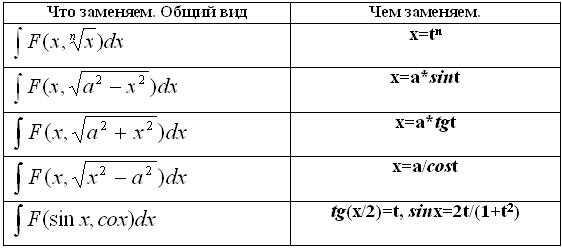

Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой.

Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выважения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin²+cos²=1
m,n – четные, sin²x=(1-cos2x)/2 и cos²x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg²x=1/cos²x — 1

С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1:
Решить интеграл:

Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.

Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:

Проверим решение(найдем производную):

Пример 2. Решаем интеграл

Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t⁵. t⁵ = x+5 . Получаем.

Но dx нужно тоже заменить на t. x= t⁵ — 5, dx = (t⁵ — 5)’ = 5t⁴. Подставляем:

Интеграл из таблицы. Считаем:

Подставляем в ответ вместо t ,

Решение интеграла:

Пример 3. Решение интеграла:

Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

В данном случае коэфециент ? перед интегралом получился в результате замены dx на ?*d(2x+1). Если вы найдете производные x’ = 1 и ?*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.

В итоге получаем:

Для закрепления темы интегралов рекомендуем также посмотреть видео.

В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.

Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.

Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

§ 4. Расстояние как интеграл