Информатика 10 класс формула шеннона: Конспект урока по информатике и ИКТ в 10 классе. Тема: Формула Шеннона.

План-конспект урока по информатике «Измерение информации (формулы Хартли и Шеннона)» (10 класс)

Урок информатики (10класс)

Тема: Измерение информации (формулы Хартли и Шеннона)

Цели: ввести понятие «количество информации», сформировать у учащихся понимание вероятности, равновероятных событий, не равновероятных событий, научить находить количество информации.

Ход урока

1. Организационный момент

Приветствие

Проверка присутствующих

Сообщение темы и целей урока

2. Изучение нового материала

1. Существует два подхода к определению информации. Один из них называется содержательный или вероятностный. Из названия можно сделать вывод, что количество информации зависит от ее содержания.

Задание 1 (устно)

Определите количество информации с позиции «информативно» или «не информативно».

1. Столица России – Москва (не инф., т.к. уже знаем).

2. Сумма квадратов катетов равна квадрату гипотенузы (не инф., уже знаем).

3. Эйфелева башня имеет высоту 300 метров и вес 9000 тонн (инф.).

4. Дифракцией света называется совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью (не инф., т.к. непонятно).

Сообщение несет больше информации, если в нем содержатся новые и понятные сведения. Такое сообщение называется

информативным.

Следует отличать понятия информация и информативность.

— Содержит ли учебник физики 10 класса информацию? (да)

— Для кого он будет информативным – для ученика 10 класса или 1 класса? (для ученика 10 класса)

Вывод: количество информации зависит от информативности.

Информативность можно обозначить 1, не информативная информация равна 0. Но это не даёт точного определения количества информации.

Существует 2 подхода при определении количества информации – содержательный и алфавитный. Содержательный применяется для измерения информации, используемой человеком, а алфавитный – компьютером.

Компьютер не понимает смысла информации, поэтому для её измерения нужен другой подход. Информация передаётся с помощью сигналов. Горит зелёный свет – можно переходить улицу, горит красный – стой. Поднял руку на уроке – учитель понял, что ты можешь ответить на его вопрос. В этих примерах сигнал имеет два состояния, их двух вариантов мы выбираем один.

Сообщение содержит информацию, если оно приводит к уменьшению неопределенности наших знаний.

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.

(Выделенное курсивом учащиеся записывают в тетрадь).

Для количественного выражения любой величины необходимо определить единицу измерения. Например, для измерения длины выбран определенный эталон метр, массы – килограмм.

Минимальная единица информации называется бит.

1 бит – это такое количество информации, уменьшающее неопределенность знаний в два раза.

Чтобы закодировать все символы нужна комбинация из 8 нулей и единиц, подобный набор называют двоичным кодом и это составляет

1 байт = 8 бит = 1 символ.

1 килобайт=1024 байт

1 мегабайт=1024 килобайт

1 гигабайт=1024 мегабайт

1 терабайт=1024 гигабайт

Для человека получение новой информации приводит к расширению знаний, или к уменьшению неопределенности. Например, сообщение о том, что завтра среда, не приводит к уменьшению неопределенности, поэтому оно не содержит информацию.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. Мы знаем до броска, что может произойти одно из двух событий – монета окажется в одном из двух положений: «орел» или «решка». После броска наступает полная определенность (визуально получаем информацию о том, что выпал, например, «орел»). Информационное сообщение о том, что выпал «орел» уменьшает нашу неопределенность в 2 раза, так как получено одно из двух информационных сообщений.

В окружающей действительности достаточно часто встречаются ситуации, когда может произойти больше, чем 2 равновероятных события. Так, при бросании шестигранного игрального кубика – 6 равновероятных событий. Событие выпадение одной из граней кубика уменьшает неопределенность в 6 раз. Чем больше начальное число событий, тем больше неопределенность нашего знания, тем больше мы получим информации при получении информационного сообщения.

2. Алфавитный подход к измерению информации

Суть алфавитного подхода к измерению информации определяется по количеству использованных для ее представления знаков некоторого алфавита. Например, если при представлении числа XVIII использовано 5 знаков римского алфавита, то это и есть количество информации. То же самое число, т. е. ту же самую информацию, можно записать в десятичной системе (18). Как видим, получается 2 знака, т. е. другое значение количества информации.

Алфавит – конечный набор символов, используемых для представления информации.

Мощность алфавита – число символов в алфавите.

(записать определение в тетрадь)

Для того чтобы при измерении одной и той же информации получалось одно и то же значение количества информации, необходимо договориться об использовании определенного алфавита. Так как в технических системах применяется двоичный алфавит, то его же используют для измерения количества информации.

Количество знаков в алфавите N=2, N=2 ⁱ , I – количество информации, I = 3 бита.

N=2 ^{i, где N – мощность алфавита, количество символов в алфавите,}

i — информационный вес каждого символа, измеряется в битах. I – информационный объем текста, высчитывается по формуле. I=K*i, где К – количество символов в тексте.

Чем большее количество знаков в алфавите, тем большее количество информации несет 1 знак алфавита.

3. Содержательный подход к измерению информации

N = 2 ^I, где N – количество возможных событий, I – количество информации.

Задача № 1. Сколько бит информации несет сообщение о том, что из колоды карт достали даму пик?

Ответ: 32=2 ^I, т.е. I=5 бит

а) Если события равновероятны, то для измерения количества информации используется формула Хартли:

N = 2^I

N – количество возможных событий,

I – количество информации (в битах).

б) Если события имеют различную вероятность, используется формула Шеннона:

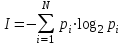
I – количество информации;

N – количество возможных событий;

Р_i – вероятность отдельных событий.

4. Физкультминутка. (1 мин.)

Задание

Заполнить пропуски числами:

а)

__Гб=1536 Мб=__Кбайт

Решение:

1536 Мб=1536:1024 Гб=1,5 Гб

б) 512 Кб=2_ байт=2_ бит

512 Кб= 512*1024 байт=524288 байт или 2⁹*2¹⁰=2¹⁹ байт

2¹⁹ байт=2¹⁹*2³ бит=2²² бит, так как в 1 байте 8 бит или 2³

5. Решение задач

1) В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?

Решение:

т.к. вытаскивание любого из шаров равновероятно, то количество информации вычисляется по формуле 2^I=N, где I – количество информации, а N – количество шаров. Тогда 2

I=32, отсюда I = 5 бит.

2) Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?

Решение:

Поскольку выбор одной дорожки из 4-х равновероятен, то количество информации определяется по формуле: 2^I=N, где I – количество информации, а N=4 – количество дорожек. Тогда 2^I=4, отсюда I=2 бита.

3) При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?

Решение:

Поскольку выбор числа равновероятен из заданного диапазона, то количество информации определяется по формуле 2^I=N, где I=6 бит, а N – количество чисел в искомом интервале. Отсюда: 2⁶=N, N=64.

4) В корзине 15 яблок, 15 груш и 30 слив. Сколько бит информации несет сообщение о том, что выбранный из корзины фрукт – яблоко?

Решение:

1. Найдем общее количество фруктов: 15 + 15 +30 = 60.

2. Найдем вероятность выбора каждого из фруктов:

р_я = 15/60 = ¼

р_г = 15/60 = ¼

р_с = 30/60 = ½

3. Найдем количество информации:

I = — (1/4*log₂1/4 + 1/4*log₂1/4 + 1/2*log₂1/2) = — (1/4*(-2) + ¼*(-2) + ½*(-1)) = ½ + ½ + ½ = 0,5 + 0,5 + 0,5 = 1,5 бита

6. Закрепление нового материала. Решение задач на определение количества информации. (15 мин.)

№ 1. Определите самостоятельно количество информации, которое несет 1 буква русского алфавита.

Ответ: буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению информации).

№ 2. Два текста содержат одинаковое число символов. Первый текст составлен в алфавите мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличается количество информации в этих текстах?

Ответ: 1) 32=2 ⁱ , I = 5 бит

2) 64 = 2 ⁱ , I = 6 бит

7. Подведение итогов урока (5 мин.)

— Какие существуют подходы к определению количества информации?

Ответ: существует 2 подхода к измерению количества информации – смысловой и технический или алфавитный.

— В чем состоит отличие одного подхода от другого?

Ответ: при смысловом подходе количество информации – мера уменьшения неопределенности знания при получении информационного сообщения, при алфавитном – количество знаков в сообщении * количество информации, которое несет 1 знак алфавита.

— Назовите единицы измерения информации от самых маленьких до самых больших.

Ответ: бит, байт, Кб, Мб, Гб, Тб.

— На какую величину отличается байт от Кб, Кб от Мб, Мб от Гб?

Ответ: 1024 (2¹⁰).

— Сколько битов содержится в 1 байте?

Ответ: 8.

— Что такое бит при смысловом и алфавитном подходе к определению количества информации?

Ответ: при смысловом подходе бит – уменьшение неопределенности знания в 2 раза при получении информационного сообщения;

при алфавитном подходе бит – информационная емкость одного знака при двоичном кодировании.

3. Домашнее задание

§ 3, 4, задание 5-9 (с. 33-34) письменно.

Заполнить пропуски числами: 5 Кб = ___ байт = ___ бит;

___ Кб = ___ байт = 2¹³ бит.

Формула Шеннона, объяснение и пример задачи

Формула Шеннона (Информационная энтропия)

Данная формула также как и формула Хартли, в информатике  применяется для высчитывания общего количество информации при различных вероятностях.

В качестве примера различных не равных вероятностей можно привести выход людей из казармы в военной части. Из казармы могут выйти как и солдат, так и офицер, и даже генерал. Но распределение cолдатов, офицеров и генералов в казарме разное, что очевидно, ведь солдатов будет больше всего, затем по количеству идут офицеры и самый редкий вид будут генералы. Так как вероятности не равны для всех трех видов военных, для того чтобы подсчитать сколько информации займет такое событие и используется формула Шеннона.

Для других же равновероятных событий, таких как подброс монеты (вероятность того что выпадет орёл или решка будет одинаковой — 50 %) используется формула Хартли. 

Интересуешься информатикой? Читайте нашу новую лекцию системы счисления

Теперь, давайте рассмотрим применение этой формулы на конкретном примере:

В каком сообщений содержится меньше всего информации (Считайте в битах):

1. Василий сьел 6 конфет, из них 2 было барбариски. 
2. В комьютере 10 папок, нужный файл нашелся в 9 папке.
3. Баба Люда сделала 4 пирога с мясом и 4 пирога с капустой. Григорий сьел 2 пирога.
4. В Африке 200 дней сухая погода, а 165 дней льют муссоны. африканец охотился 40 дней в году.

В этой задаче обратим внимания что 1,2 и 3 варианты, эти варианты считать легко, так как события равновероятны. И для этого мы будем использовать формулу Хартли  I = log₂N (рис.1) А вот с 4 пунком где видно, что распределение дней не равномерно(перевес в сторону сухой погоды), что же тогда нам в этом случае делать? Для таких событий и используется формула Шеннона или информационной энтропии: I = — ( p₁log₂ p₁ + p₂ log₂ p₂ + . . . + p_N log₂ p_N), (рис.3)

ФОРМУЛА КОЛИЧЕСТВА ИНФОРМАЦИ (ФОРМУЛА ХАРТЛИ, РИС.1 )

В которой:

• I — количество информации
• p — вероятность того что это события случиться

Далее чтобы узнать p необходимо поделить количество интересующих нас событий на общее количество возможных вариантов. 

Интересующие нас события в нашей задаче это

1. Было две барбариски из шести (2/6)
2. Была одна папка в которой нашлась нужный файл по отношению к общему количеству (1/10)
3. Всего пирогов было восемь из которых сьедено григорием два (2/8)
4. и последнее сорок дней охоты по отношению к двести засушливым дням и сорок дней охоты к сто шестидесяти пяти  дождливым дням. (40/200) + (40/165)

таким образом получаем что:

ФОРМУЛА ВЕРОЯТНОСТИ ДЛЯ СОБЫТИЯ.

Где K — это интересующие нас событие, а N общее количество этих событий, также чтобы проверить себя вероятность того или иного события не может быть больше единицы. (потому что вероятных событий всегда меньше)

ФОРМУЛА ШЕННОНА ДЛЯ ПОДСЧЕТА ИНФОРМАЦИИ (РИС.3)

Вернемся к нашей задаче и посчитаем сколько информации содержится.

Кстате, при подсчёте логарифма удобно использовать сайт  — https://planetcalc.ru/419/#

• Для первого случая — 2/6 = 0,33 = и далее Log₂ 0,33 = 1.599 бит
• Для второго случая — 1/10 = 0,10  Log₂ 0,10 = 3.322 бит
• Для третьего — 2/8 = 0,25 = Log₂ 0,25 = 2 бит
• Для четвертого — 40/200 + 40/165 = 0.2 и 0,24 соотвественно, далее считаем по формуле -(0,2 * log₂ 0,2) +-(o.24 * log₂ 0.24) = 0.95856 бит

Таким образом ответ для нашей задачи получился 4.

Вот таким образом и используется формула Шеннона при подсчёте информации. Если у вас есть какие либо вопросы, или что то Вам не понятно можете задать вопросы в комментариях. (отвечаю оперативно)

---

4.7 / 5 ( 3 голоса )

---

Помогая проекту BEST-EXAM, вы делаете образование более доступным для каждого человека, внесите и вы свой вклад —
поделитесь этой статьей в социальных сетях!

Формула Шеннона ℹ️ определение, условия применения главной информационной теории, значение, онлайн-калькулятор, примеры решения задач

Информационная теория

Обработка информации — важная техническая задача, чем, например, преобразование энергии из одной формы в другую. Важнейшим шагом в развитии теории информации стала работа Клода Шеннона (1948). Логарифмическое измерение количества данных было первоначальной теорией, и прикладными задачами по коммуникации в 1928 году. Наиболее известным является вероятностный подход к измерению информации, на основе которого представлен широкий раздел количественной теории.

Отличительная черта вероятностного подхода от комбинаторного состоит в том, что новые предположения об относительной занятости любой системы в разных состояниях и общего количества элементов не учитываются. Ряд информации взят из отсутствия неопределённости в выборе различных возможностей. В основе такого подхода лежат энтропийные и вероятностные множества.

Основная теорема Шеннона о кодировании

Важный практический вопрос при обработке информации — какова мощность системы передачи данных. Можно получить определённый ответ, используя уравнение Шеннона. Оно позволяет точно понять информационную пропускную способность любого сигнального канала. Формула Шеннона в информатике: I = — (p1log2 p1 + p2 log2 p2 +. + pN log2 pN)

Основная теория Шеннона о кодировании для дискретного канала с помехой, приведённая здесь без доказательства, аналогична теореме канала не имеющего помех: если источник данных с энтропией H (Z), а канал связи имеет ширину полосы C, то сообщения, сгенерированные источником, всегда могут быть закодированы так, чтобы их скорость передачи vz была произвольно близка к значению: vzm = C | H (Z).

Не существует метода кодирования, который бы позволял передавать со скоростью, превышающей vzm, и с произвольно низкой вероятностью ошибки. Другими словами, если поток информации: H ‘(Z) = vz * H (Z) <= C. Тогда можно выбрать специальный код, что позволяет передавать всю информацию с произвольно низкой вероятностью ошибки. При H ‘(Z)> C он не существует.

Стоит рассмотреть сигнал, который эффективно передаётся (т. е. без избыточности) в виде зависящего от времени аналогового напряжения. Картина изменения в течение определённого интервала T позволяет приёмнику выявить, какое из возможных сообщений было фактически отправлено.

Используя идею межсимвольного влияния, можно сказать, что, поскольку нет избыточности значения будут независимыми при условии, и они достаточно далеки друг от друга, чтобы их стоило отбирать отдельно. По сути, невозможно сказать, что одно из значений просто от знания другого. Конечно, для любого сообщения оба типа данных заранее определяются содержанием.

Но получатель не может знать, какое из всех возможных сообщений прибыло, пока оно не пришло. Если приёмник заранее знает, какое напряжение, должно быть, передано, то само сообщение не дало бы никакой новой информации! То есть получатель не будет знать больше после его прибытия, чем раньше.

Это приводит к замечательному выводу:

• Сигнал, который эффективно передаёт информацию, будет меняться и непредсказуем.
• Эффективный сигнал очень похож на случайный шум.

Именно поэтому случайный шум может привести к ошибкам в полученном сообщении. Статистические свойства эффективного сигнала аналогичны. Если шум был явно разным, приёмник мог легко отделить информацию и избежать каких-либо неполадок. Поэтому для обнаружения и исправления ошибок нужно сделать реальный сигнал менее «шумоподобным».

Условие применения формулы Шеннона — избыточность, создаёт предсказуемые отношения между различными участками сигнального устройства. Хотя это снижает эффективность передачи информации в системе, но помогает отличать детали сигнала от случайного шума. Здесь обнаружена максимально возможная информационная пропускная способность системы. Поэтому нужно избегать избыточности и позволять сигналу иметь «непредсказуемые» качества, которые делают его статистически похожим на случайный шум.

Передача сигналов

Реальный сигнал должен иметь конечную мощность. Следовательно, для этого набора сообщений должен быть некоторый максимально возможный уровень мощности. Это значит что напряжение тока сигнала ограничено к некоторому ряду. Это также означает, что мгновенное напряжение сигнала, должно быть, ограничено и не выступает за пределы диапазона. Аналогичный аргумент должен быть верен и для шума. Поскольку предполагается, что система эффективна, можно ожидать, сигнал и шум будут иметь аналогичные статистические свойства.

Это означает:

1. Если долго наблюдать за сигналом или шумом, можно обнаружить, что их колебания уровня имеют одинаковое отношение пикового/среднеквадратичного напряжения.
2. Во время типичного сообщения колебания напряжения шума будут ограничены некоторым диапазоном.

При передаче сигналов в присутствии шума нужно стараться, чтобы сигнал был больше и свести к минимуму эффекты шума. Поэтому можно ожидать, что система передачи информации применится и обеспечит, чтобы для каждого типичного сообщения сила почти равнялось некоторому максимальному значению.

Это означает, что в такой системе, большинство сообщений будет одинаковый уровень мощности. В идеале каждое ИС должно иметь одинаковый, максимально возможный уровень мощности. На самом деле можно повернуть этот аргумент с ног на голову и сказать, что «типичны» только сообщения со средними силами, подобными этому максимуму. Те, что обладают гораздо более низкими способностями, необычны — то есть редки.

Определённое уравнение

Сигнал и шум не коррелированны, то есть они не связаны каким-либо образом, который позволит предсказать один из них. Суммарная мощность, получаемая при объединении этих некоррелированных ИС, по-видимому, случайно изменяющихся величин, задаётся.

Поскольку сигнал и шум статистически аналогичны, их комбинация будет иметь то же значение форм-фактора, что и сам сигнал или шум. Потому можно ожидать, что комбинированный сигнал и шум, как правило, будут ограничены диапазоном напряжения.

Стоит рассмотреть теперь разделение этого диапазона на полосы одинакового размера. (т. е. каждая из этих полос будет охватывать ИС.) Чтобы предоставить другую метку для каждой полосы, нужны символы или цифры. Поэтому всегда можно указать, какую полосу занимает уровень напряжения в любой момент с точки зрения B-разрядного двоичного числа. По сути, этот процесс является ещё одним способом описания того, что происходит, когда берут цифровые образцы с B-разрядным аналоговым преобразователем, работающим в общем диапазоне.

Нет никакого реального смысла в выборе значения, которое настолько велико. Это потому что шум кубика будет просто иметь тенденцию рандомизировать фактическое напряжение на эту сумму, делая любые дополнительные биты бессмысленными. В результате максимальное количество битов информации, которую можно получить относительно уровня в любой момент, будет определено.

Уравнение Шеннона может использовать:

1. Максимально возможную скорость передачи информации по заданному каналу или системе.
2. Передачу данных определяется полосой пропускания, уровнем сигнала и шума.
3. Поэтому ИС называется законом информационной пропускной способности канала.

При передаче информации некоторые параметры используемых сигналов могут приобретать случайный символ в канале связи, например, из-за многолучевого распространения радиоволн, гетеродинирующих сигналов. В результате амплитуда и начальная фаза данных являются случайными. Согласно статистической теории связи, эти особенности сигналов необходимы для их оптимальной обработки, они определяют как структуру приёмника, так и качество связи.

Хартли понимал информационное получение как подбор одного вида данных из набора равновероятного сообщения и определил объём, содержащейся ВС, как логарифм N. Выполняются примеры решения по формуле Хартли в информатике: N = mn.

Помехи разложения всегда присутствуют в границе любого реального сигнала. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно предположить, что все сигналы передаются неискажёнными.

В этом случае средний объём информации, переносимой одним символом, можно считать расчётным: J (Z; Y) = Хапр (Z) — Хапест (Z) = Хапр (Y). Поскольку функция H (Y) = H (Z) и H (Y / Z) = 0, а индекс max {J (Z; Y)} = Hmax (Y) — максимальная энтропия источника класса сигнала, возникающая в результате распределения символов Y: p (y1) = p (y2) = … = p (ym) = 1 / My, т. е. Hmax (Y) = logaMy.

Следовательно, главная дискретная ширина полосы таблицы без информации о помехах в единицу времени равна: Cy = Vy • max {J (Z; Y)} = Vy • Hmax (Y) = Vy • logaMy или записываться Ck = Vk • logaMy. Где буква Mk — должно быть максимально возможное количество уровней, разрешённых для передачи по этому каналу (конечно, может обозначаться Mk = My).

Согласно теореме, метод кодирования онлайн, который может использоваться и позволяет:

• с данными согласно уравнению H (x) ≤ C — передать всю информацию, сгенерированную источником с ограниченным размером буфера калькулятора;
• в случае H (x)> C такого способа кодирования не существует, поскольку требуется буфер, объём которого определяется избыточной производительностью источника по ширине полосы канала, умноженной на время передачи.

Вероятностный подход к определению вычисления объёма информации — математический вывод формулы Шеннона не является удовлетворительным для метода оценки роли энтропии, отражения элементов системы и может не применяться. Как общий информатический объект невозможно допустить единый способ измерения и его правила.

План-конспект урока по информатике и икт (10 класс) по теме: Разработка урока информатики по теме «Измерение информации» (10 класс)

Урок информатики  (10класс)

Тема: Измерение информации (формулы Хартли и Шеннона)

Цели: ввести понятие «количество информации», сформировать у учащихся понимание вероятности, равновероятных событий, не равновероятных событий, научить находить количество информации.

Ход урока

1. Организационный момент

Приветствие

Проверка присутствующих

Сообщение темы и целей урока

2. Изучение нового материала

1. Существует два подхода к определению информации. Один из них называется содержательный или вероятностный. Из названия можно сделать вывод, что количество информации зависит от ее содержания.

Задание 1 (устно)

Определите количество информации в следующих сообщениях с позиции «много» или «мало». Содержат ли сообщения новые и понятные сведения?

1. Столица России – Москва.
2. Сумма квадратов катетов равна квадрату гипотенузы.
3. Дифракцией света называется совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью.
4. Эйфелева башня имеет высоту 300 метров и вес 900 тонн.

Сообщение несет больше информации, если в нем содержатся новые и понятные сведения. Такое сообщение называется информативным.

— Содержит ли информацию учебник физики за 10 класс?

— Для кого он будет информативным – для ученика 10 класса или 1 класс?

2. Рассмотрим понятие информативности с другой стороны. Если некоторое сообщение является информативным, следовательно, оно дает нам знания или уменьшает неопределенность наших знаний.

Пример.

Мы бросаем монету и пытаемся угадать, какой стороной она упадет на поверхность. Возможен один результат из двух: монета окажется в положении «орел» или «решка». Каждое из этих двух событий окажется равновероятным, т.е. ни одно из них не имеет преимущества перед другим.

Перед броском монеты мы точно не знаем, как она упадет. Это событие предсказать невозможно, т.е. перед броском существует неопределенность нашего знания (возможно одно событие из двух). После броска наступает полная определенность знания, т.к. мы получаем зрительное сообщение о положении монеты. Это зрительное сообщение уменьшает неопределенность нашего знания в два раза, т.к. из двух равновероятных событий произошло одно.

3. Единицы измерения информации.

Наименьшая единица измерения информации – 1 бит.

1 бит  — это количество информации, уменьшающее неопределенность знаний в два раза.

1 байт = 8 бит;

1 Кбайт = 210 байт = 1024 байт;

1 Мбайт = 210 Кбайт = 1024 Кбайт;

1 Гбайт = 210 Мбайт = 1024 Мбайт 

Задание 2.

Заполнить пропуски числами:

а)__Гб=1536 Мб=__Кбайт

Решение:

1536 Мб=1536:1024 Гб=1,5 Гб

1. 1536 Мб= 1536*1024 Кб=1 572 864 Кб

б) 512 Кб=2_ байт=2_ бит

512 Кб= 512*1024 байт=524288 байт или 29*210=219 байт

219 байт=219*23 бит=222 бит, так как  в 1 байте 8 бит или 23

4. Измерение информации.

а) Если события равновероятны, то для измерения количества информации используется формула Хартли:

N = 2I

N – количество возможных событий,

I – количество информации (в битах).

б)  Если события имеют различную вероятность, используется формула Шеннона:

I – количество информации;

N – количество возможных событий;

Рi – вероятность отдельных событий.

5. Решение задач

1) В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?

1. Решение:

т.к. вытаскивание любого из шаров равновероятно, то количество информации вычисляется по формуле 2I=N, где I – количество информации, а N – количество шаров. Тогда 2I=32, отсюда I = 5 бит.

2) Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?

2. Решение:

Поскольку выбор одной дорожки из 4-х равновероятен, то количество информации определяется по формуле: 2I=N, где I – количество информации, а N=4 – количество дорожек. Тогда 2I=4, отсюда I=2 бита.

3) При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?

3. Решение:

Поскольку выбор числа равновероятен из заданного диапазона, то количество информации определяется по формуле 2I=N, где I=6 бит, а N – количество чисел в искомом интервале. Отсюда: 26=N, N=64.

4) В корзине 15 яблок, 15 груш и 30 слив. Сколько бит информации несет сообщение о том, что выбранный из корзины фрукт – яблоко?

Решение:

1. Найдем общее количество фруктов: 15 + 15 +30 = 60.
2. Найдем вероятность выбора каждого из фруктов:

ря = 15/60 = ¼

рг = 15/60 = ¼

рс = 30/60 = ½

3. Найдем количество информации:

I = — (1/4*log21/4 + 1/4*log21/4 + 1/2*log21/2) = — (1/4*(-2) + ¼*(-2) + ½*(-1)) = ½ + ½ + ½ = 0,5 + 0,5 + 0,5 = 1,5 бита

3. Домашнее задание

§ 2.2, 2.4, задание 2.1, 2.2 (с. 78) письменно.

Заполнить пропуски числами: 5 Кб = ___ байт = ___ бит;

___ Кб = ___ байт = 213 бит.

бит

байт

Кбайт

Мбайт

Гбайт

: 1024

: 1024

: 1024

: 8

Презентация на тему «Формула Шеннона»

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Количество информации и вероятность. Пример 1. В коробке имеется 50 шаров.Из них 40 белых и 10 черных.Какова вероятность того, что при вытаскивании «не глядя» попадется белый шар, черный шар? Решение. Пусть рч-вероятность попадания при вытаскивании черного шара, Рб-вероятность попадания белого шара. Тогда Рч=10/50=0,2 рб=40/50=0,8 Вероятность попадания белого шара в 4 раза больше, чем черного.

2 слайд Описание слайда:

Формула для вычислений количества информации в случае различных вероятностей событий предложил К.Шеннон в 1948 году. I-количество информации N-количество возможных событий Рi-вероятность i-го события.

3 слайд Описание слайда:

Этот подход к определению количества информации называется вероятностным. Если события равновероятны, то количество информации, которое мы получаем, достигает максимального значения и формула имеет вид I=log2N

4 слайд Описание слайда:

Количественная зависимость между вероятностью события (р) и количеством информации в сообщении о нем (i) выражается формулой: i=log2(1/p)

5 слайд Описание слайда:

Пример. Определим количество информации в сообщении о попадании белого шара и черного: iб=log2(1/0,8)=log2(1,25)=0,32192 iч=log2(1/0,2)=log25=2,321928

6 слайд Описание слайда:

Пример . В алфавите племени МУМУ всего 4 буквы(А,У,М,К), один знак препинания(точка) и для разделения слов используют пробел.Подсчитали, что в популярном романе «Мумука» содержится всего 10000 знаков, из них: букв А-4000, букв У-1000, букв М-2000, букв К-1500, точек-500, пробелов-1000.Какой объем информации содержит книга?

7 слайд Описание слайда:

Решение. Подсчитаем частоту встречаемости каждого символа во всем тексте книги(т.е. Вероятность) и информационные веса символом: Буква А: pA= 4000/10000=0,4; iA=log2(1/0,4)=1,321928 и т.д. Общий объем информации в книге вычислим как сумму произведений информационного веса каждого символа на число повторений этого символа в книге: I=iA*nA+…=

8 слайд Описание слайда:

Задачи. №1. В корзине лежат 8 черных шаров и 24 белых.Сколько информации несет сообщение о том, что достали черный шар? №2. В коробке лежат 64 цветных карандаша.Сообщение о том, что достали белый шар, несет 4 бита информации. Сколько белых карандашей было в корзине? №3. В классе 30 человек.За контрольную по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Иванов получил четверку?

9 слайд Описание слайда:

№4. За четверть ученик получил 100 оценок. Сообщение о том, что он получил четверку, несет 2 бита информации.Сколько четверок ученик получил за четверть? №5.Для ремонта школы использовали белую, синюю и коричневую краски. Израсходовали одинаковое количество банок белой и синей краски. Сообщение о том, что закончилась банка белой краски, несет 2 бита информации. Синей краски израсходовали 8 банок. Сколько банок коричневой краски было израсходовали на ремонт школы?

10 слайд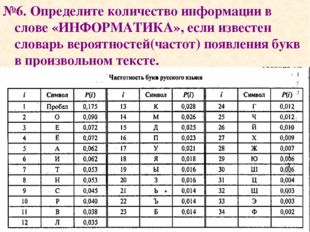 Описание слайда:

№6. Определите количество информации в слове «ИНФОРМАТИКА», если известен словарь вероятностей(частот) появления букв в произвольном тексте.

11 слайд Описание слайда:

№7. На остановке останавливаются автобусы с разными номерами. Сообщение о том, что к остановке подошел автобус с номером 1 несет 4 бит информации. Вероятность появления на остановке автобуса с номером 2 в 2 раза меньше, чем вероятность появления автобуса с номером 1. Сколько информации несет сообщение о появлении на остановке автобуса с номером 2?

12 слайд Описание слайда:

Домашнее задание. №1. Возьмите произвольный текст на английском языке(3-4 страницы) и составьте частотный словарь английского языка. Определите, какое количество информации несет каждая буква этого словаря. №2. Используя результат предыдущей задачи, определите количество информации с слове «INFORMATION».

13 слайд Описание слайда:

Самостоятельная работа. Вариант 1. В корзине лежат 32 клубка шерсти. Среди них-4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти? Вариант 2. В ящике лежат перчатки (белые и черные).Среди них- 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько всего пар перчаток было в ящике?

14 слайд Описание слайда:

Вариант 3. Известно, что в ящике лежат 20 шаров. Из них10-черных, 5 белых, 4-желтых и 1 красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар, белый шар, желтый шар, красный шар? Вариант 4. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?

15 слайд Описание слайда:

Определите количество информации в фразе «ПОВТОРЕНИЕ-МАТЬ УЧЕНИЯ»

16 слайд Описание слайда:

Ответы. Вариант 1. 3 бит Вариант 2. 32 пары Вариант 3. 1 бит, 2 бит, 2,32бит, 4,32 бит Вариант 4. 24 шара.

Курс профессиональной переподготовки

Учитель информатики

Курс профессиональной переподготовки

Учитель математики и информатики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-036073

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Информация и вероятность. Формула Хартли. Формула Шеннона

Содержание урока

Формула Хартли

Задачи

Информация и вероятность

Вопросы и задания

Задачи

Формула Шеннона

Вопросы и задания

Задачи

Формула Хартли

Вы знаете, что при выборе из двух возможных вариантов количество полученной информации равно 1 биту. Если количество вариантов N равно 2^I, то количество информации при выборе одного из них равно I битов. А как вычислить количество информации, если количество вариантов не равно степени числа 2?

Ответить на этот вопрос стало возможно только после того, как вы изучили логарифмы в курсе математики. Из формулы

N = 2^I

сразу следует, что I — это степень, в которую нужно возвести 2, чтобы получить N, т. е. логарифм:

I = log₂ N.

Эта формула называется формулой Хартли в честь американского инженера Ральфа Хартли, который предложил её в 1928 г.

Пусть, например, на лётном поле стоят 10 самолётов (с номерами от 1 до 10) и известно, что один из них летит в Санкт-Петербург.

Сколько информации в сообщении «Самолёт № 2 летит в Санкт-Петербург»? У нас есть 10 вариантов, из которых выбирается один, поэтому по формуле Хартли количество информации равно

I = log₂ 10 ≈ 3,322 бита.

Обратите внимание, что для значений N, которые не равны целой степени числа 2, количество информации в битах — дробное число.

С помощью формулы Хартли можно вычислить теоретическое количество информации в сообщении. Предположим, что алфавит (полный набор допустимых символов) включает 50 символов (в этом случае говорят, что мощность алфавита равна 50). Тогда информация при получении каждого символа составляет

I = log₂ 50 ≈ 5,644 бита.

Если сообщение содержит 100 символов, его общий информационный объём примерно равен

5,644 • 100 = 564,4 бита.

В общем случае объём сообщения длиной L символов, использующего алфавит из N символов, равен I = L • log₂ N.

Такой подход к определению количества информации называют алфавитным. Конечно, на практике невозможно использовать для кодирования символа нецелое число битов, поэтому используют первое целое число, которое больше теоретически рассчитанного значения. Например, при использовании алфавита из 50 символов каждый символ будет закодирован с помощью 6 битов (50 ≤ 2⁶ = 64).

Сколько разных сообщений можно передать, если известен алфавит и длина сообщения? Предположим, что для кодирования сообщения используются 4 буквы, например «А», «Б», «В» и «Г», и сообщение состоит из двух символов. Поскольку каждый символ может быть выбран 4 разными способами, на каждый вариант выбора первого символа есть 4 варианта выбора второго. Поэтому общее число разных двухбуквенных сообщений вычисляется как 4 • 4 = 4² = 16. Если в сообщение добавить ещё один символ, то для каждой из 16 комбинаций первых двух символов третий можно выбрать четырьмя способами, так что число разных трёхсимвольных сообщений равно 4 • 4 • 4 = 4³ = 64.

В общем случае, если используется алфавит из N символов, то количество разных возможных сообщений длиной L символов равно Q = N^L.

Следующая страница Задачи

Cкачать материалы урока

Презентация по информатике на тему «Вероятностный подход к измерению информации» (10 класс)

Инфоурок › Информатика ›Презентации›Презентация по информатике на тему «Вероятностный подход к измерению информации» (10 класс)

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Тема: Вероятностный подход к определению количества информации. Формула Шеннона. Цель: Научиться определять количество информации через вероятность?

2 слайд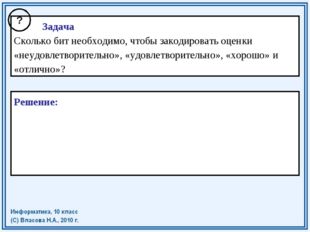 Описание слайда:

Задача Сколько бит необходимо, чтобы закодировать оценки «неудовлетворительно», «удовлетворительно», «хорошо» и «отлично»? ? Решение: N=4 – равновероятные события 2i=N 2i=4  i=2 (бита) – необходимо для кодирования оценки.

3 слайд Описание слайда:

N – количество равновероятных событий I – количество информации, что произошло одно из N событий (бит) ! Сообщение уменьшающее неопределённость знаний в 2 раза несёт 1 бит информации. !

4 слайд Описание слайда:

В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар? В корзине лежит 11 шаров разного цвета. Сколько информации несет сообщение, что достали красный шар?

5 слайд Описание слайда:

Логарифмом числа b по основанию а (a>0, a≠1) называется показатель степени, в которую надо возвести число а, чтобы получилось b. !

6 слайд Описание слайда:

Вычислите: ?

7 слайд Описание слайда:

формула Хартли Эта формула была выведена в 1928 г. американским инженером Р.Хартли и носит его имя.

8 слайд Описание слайда:

В корзине лежат 8 чёрных и 24 белых шара. а) Сколько информации несёт сообщение, что из корзины достали чёрный шар? б) Сколько информации несёт сообщение, что из корзины достали шар?

9 слайд Описание слайда:

В корзине лежат 8 чёрных и 24 белых шара. а) Сколько информации несёт сообщение, что из корзины достали чёрный шар? А – достать чёрный шар В – достать белый шар n – количество возможных событий n=32 m – количество интересующих событий mA=8 mB=24 pi – вероятность отдельного события В корзине лежат 8 чёрных и 24 белых шара. а) Сколько информации несёт сообщение, что из корзины достали чёрный шар? !

10 слайд Описание слайда:

Какие события могут произойти при подбрасывании монеты? Сколько этих событий? Какие это события (равновероятные или нет)? Найдите вероятность этих событий. Что можно сказать про эти вероятности? Выразите p через N, где p-вероятность, а N- количество равновероятных событий? Выразите из формулы N. Запишите формулу Хартли и N замените.

11 слайд Описание слайда:

количество информации, через вероятность В корзине лежат 8 чёрных и 24 белых шара. а) Сколько информации несёт сообщение, что из корзины достали чёрный шар? Найдите вероятность события, что достали чёрный шар? Подставьте её в формулу. !

12 слайд Описание слайда:

В корзине лежат 8 чёрных и 24 белых шара. б) Сколько информации несёт сообщение, что из корзины достали шар? формула Клода Шеннона ! I – количество информации n – количество возможных событий pi – вероятность отдельных событий

Курс профессиональной переподготовки

Учитель информатики

Курс профессиональной переподготовки

Учитель математики и информатики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-127272

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Калькулятор энтропии Шеннона | Теория информации

Как рассчитать энтропию? — формула энтропии

Формула энтропии Шеннона:

H (x) = -Σ n i = 1 [P (x i ) * log b P (x i )] = Σ n i = 1 [P (x i ) * журнал b (1 / P (x i ))]

Где

• Σ n i = 1 — оператор суммирования для вероятностей от i до n .
• P (x i ) — вероятность одного события.

В теории информации энтропия состоит из нескольких единиц. Это зависит от того, каково основание логарифма — b . Обычно, когда мы имеем дело с компьютерами, он равен 2 , а единица измерения известна как бит (также называемая шенноном ). Наш калькулятор энтропии Шеннона использует эту основу. Когда основание равно числу Эйлера , e , энтропия измеряется в натс .Если это 10 , то это dit , ban или hartley .

Давайте воспользуемся формулой энтропии Шеннона в примере:

1. У вас есть последовательность номеров: 1035830701 .
2. У каждого отдельного символа своя вероятность появления:

• п (1) = 2/10 .
• п (0) = 3/10 .
• п (3) = 2/10 .
• п (5) = 1/10 .
• п (8) = 1/10 .
• п (7) = 1/10 .

3. Энтропия Шеннона равна:

• H = p (1) * log 2 (1 / p (1)) + p (0) * log 2 (1 / p (0)) + p (3) * log 2 ( 1 / p (3)) + p (5) * журнал 2 (1 / p (5)) + p (8) * журнал 2 (1 / p (8)) + p (7) * журнал 2 (1 / п (7)) .
• После ввода значений:
• H = 0,2 * лог 2 (1 / 0,2) + 0.3 * log 2 (1 / 0,3) + 0,2 * log 2 (1 / 0,2) + 0,1 * log 2 (1 / 0,1) + 0,1 * log 2 (1 / 0,1) + 0,1 * журнал 2 (1 / 0,1) .
• H = 2,44644 ​​.

Знайте, что вы умеете вычислять энтропию Шеннона самостоятельно! Продолжайте читать, чтобы узнать некоторые факты об энтропии!

.

сжатие — формула энтропии Шеннона. Помогите моему замешательству

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира

.

формул алгебры для класса 10

• • Классы
    • Класс 1-3
    • Класс 4-5
    • Класс 6-10
    • Класс 11-12
  • КОНКУРСНЫЙ ЭКЗАМЕН
    • BNAT 000 NC
      • 000 NC Книги
        • Книги NCERT для класса 5
        • Книги NCERT для класса 6
        • Книги NCERT для класса 7
        • Книги NCERT для класса 8
        • Книги NCERT для класса 9
        • Книги NCERT для класса 10
        • Книги NCERT для класса 11
        • Книги NCERT для класса 12
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT 9000 9000
        • NCERT Exemplar Class
          • Решения RS Aggarwal, класс 12
          • Решения RS Aggarwal, класс 11
          • Решения RS Aggarwal, класс 10
          90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • RD Sharma Class 6 Решения
          • Решения RD Sharma
          Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • PHYSICS
          • Механика
          • Оптика
          • Термодинамика Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • MATHS
          • Теорема Пифагора
          0004
          • 000300030004
          • Простые числа
          • Взаимосвязи и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Деление фракций
        • 000
        • 000
        • 000
        • 000
        • 000
        • 000 Microology
        • 000
        • 000 Microology
        • 000 BIOG3000
          FORMULAS
          • Математические формулы
          • Алгебраические формулы
          • Тригонометрические формулы
          • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы
            • 0003000 PBS4000
            • 000300030002 Примеры калькуляторов химии
            Класс 6
            • Образцы бумаги CBSE для класса 7
            • Образцы бумаги CBSE для класса 8
            • Образцы бумаги CBSE для класса 9
            • Образцы бумаги CBSE для класса 10
            • Образцы бумаги CBSE для класса 11
            • Образцы бумаги CBSE чел для класса 12
          • CBSE Контрольный документ за предыдущий год
            • CBSE Контрольный документ за предыдущий год Класс 10
            • Контрольный документ за предыдущий год CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Class 11 Physics
            • Решения HC Verma, класс 12, физика
          • Решения Лакмира Сингха
            • Решения Лакмира Сингха, класс 9
            • Решения Лакмира Сингха, класс 10
            • Решения Лакмира Сингха, класс 8
          • Заметки CBSE
          • , класс
            CBSE Notes
            Примечания CBSE класса 7
            • Примечания CBSE класса 8
            • Примечания CBSE класса 9
            • Примечания CBSE класса 10
            • Примечания CBSE класса 11
            • Примечания CBSE класса 12
            • Примечания к редакции CBSE
              • Примечания к редакции
              • CBSE
              • Примечания к редакции класса 10 CBSE
              • Примечания к редакции класса 11 CBSE 9000 4
              • Примечания к редакции класса 12 CBSE
            • Дополнительные вопросы CBSE
              • Дополнительные вопросы по математике класса 8 CBSE
              • Дополнительные вопросы по науке 8 класса CBSE
              • Дополнительные вопросы по математике класса 9 CBSE
              • Дополнительные вопросы по науке класса 9 CBSE
              Дополнительные вопросы по математике для класса 10
              • Дополнительные вопросы по науке, класс 10 по CBSE
            • CBSE, класс
              • , класс 3
              • , класс 4
              • , класс 5
              • , класс 6
              • , класс 7
              • , класс 8
              • , класс 9 Класс 10
              • Класс 11
              • Класс 12
            • Учебные решения
          • Решения NCERT
            • Решения NCERT для класса 11
              • Решения NCERT для класса 11 по физике
              • Решения NCERT для класса 11 Химия
              Решения для биологии класса 11
              • Решения NCERT для математики класса 11
              9 0003 NCERT Solutions Class 11 Accountancy
              • NCERT Solutions Class 11 Business Studies
              • NCERT Solutions Class 11 Economics
              • NCERT Solutions Class 11 Statistics
              • NCERT Solutions Class 11 Commerce
            • NCERT Solutions For Class 12
              • NCERT Solutions For Класс 12 по физике
              • Решения NCERT для химии класса 12
              • Решения NCERT для класса 12 по биологии
              • Решения NCERT для класса 12 по математике
              • Решения NCERT Класс 12 Бухгалтерия
              • Решения NCERT, класс 12, бизнес-исследования
              • Решения NCERT, класс 12 Экономика
              • NCERT Solutions Class 12 Accountancy Part 1
              • NCERT Solutions Class 12 Accountancy Part 2
              • NCERT Solutions Class 12 Micro-Economics
              • NCERT Solutions Class 12 Commerce
              • NCERT Solutions Class 12 Macro-Economics
            • NCERT Solutions For Класс 4
              • Решения NCERT для математики класса 4
              • Решения NCERT для класса 4 EVS
            • Решения NCERT для класса 5
              • Решения NCERT для математики класса 5
              • Решения NCERT для класса 5 EVS
            • Решения NCERT для класса 6
              • Решения NCERT для математики класса 6
              • Решения NCERT для науки класса 6
              • Решения NCERT для социальных наук класса 6
              • Решения NCERT для класса 6 Английский
            • Решения NCERT для класса 7
              • Решения NCERT для класса 7 Математика
              • Решения NCERT для класса 7 Наука
              • Решения NCERT для класса 7 по социальным наукам
              • Решения NCERT для класса 7 Английский
            • Решения NCERT для класса 8
              • Решения NCERT для класса 8 Математика
              • Решения NCERT для класса 8 Science
              • Решения NCERT для социальных наук 8 класса
              • Решение NCERT ns для класса 8 Английский
            • Решения NCERT для класса 9
              • Решения NCERT для социальных наук класса 9
            • Решения NCERT для математики класса 9
              • Решения NCERT для математики класса 9 Глава 1
              • Решения NCERT для Математика класса 9 Глава 2
              • Решения NCERT для математики класса 9 Глава 3
              • Решения NCERT для математики класса 9 Глава 4
              Решения NCERT
              • для математики класса 9 Глава 5
              • Решения NCERT для математики класса 9 Глава 6
              • Решения NCERT для Математика класса 9 Глава 7
              • Решения NCERT для математики класса 9 Глава 8
              Решения NCERT
              • для математики класса 9 Глава 9
              Решения NCERT
              • для математики класса 9 Глава 10
              • Решения NCERT для математики класса 9 Глава 11
              • Решения NCERT для Математика класса 9 Глава 12
              • Решения NCERT для математики класса 9 Глава 13
              Решения
              • NCERT для математики класса 9 Глава 14
              • Решения NCERT для математики класса 9 Глава 15
            • Решения NCERT для науки класса 9
              • Решения NCERT для науки класса 9 Глава 1
              • Решения NCERT для науки класса 9 Глава 2
              • Решения NCERT для класса 9 Наука Глава 3
              • Решения NCERT для Науки Класса 9 Глава 4
              • Решения NCERT для Науки Класса 9 Глава 5
              • Решения NCERT для Науки Класса 9 Глава 6
              • Решения NCERT для Науки Класса 9 Глава 7
              • Решения NCERT для Класса 9 Наука Глава 8
              • Решения NCERT для Науки Класса 9 Глава 9
              • Решения NCERT для Науки Класса 9 Глава 10
              • Решения NCERT для Науки Класса 9 Глава 12
              • Решения NCERT для Науки Класса 9 Глава 11
              • Решения NCERT для Класса 9 Наука Глава 13
              • Решения NCERT для класса 9 Наука Глава 14
              • Решения NCERT для класса 9 по науке Глава 15
            • Решения NCERT для класса 10
              • Решения NCERT для класса 10 по социальным наукам
            • Решения NCERT для математики класса 10
              • Решения NCERT для математики класса 10 Глава 1
              • Решения NCERT для математики класса 10 Глава 2
              • Решения NCERT для математики класса 10 Глава 3
              • Решения NCERT для математики класса 10 Глава 4
              • Решения NCERT для математики класса 10 Глава 5
              • Решения NCERT для математики класса 10 Глава 6
              • Решения NCERT для математики класса 10 Глава 7
              • Решения NCERT для математики класса 10 Глава 8
              • Решения NCERT для математики класса 10 Глава 9
              Решения NCERT
              • для математики класса 10 Глава 10
              Решения
              • NCERT для математики класса 10 Глава 11
              • Решения NCERT для математики класса 10 Глава 12
              • Решения NCERT для математики класса 10 Глава 13
              • NCERT Sol Решения NCERT для математики класса 10 Глава 14
              • Решения NCERT для математики класса 10 Глава 15
            • Решения NCERT для науки класса 10
              • Решения NCERT для науки класса 10 Глава 1
              • Решения NCERT для науки класса 10 Глава 2
              • Решения NCERT для науки класса 10, глава 3
              • Решения NCERT для науки класса 10, глава 4
              • Решения NCERT для науки класса 10, глава 5
              • Решения NCERT для науки класса 10, глава 6
              • Решения NCERT для науки класса 10, глава 7
              • Решения NCERT для науки 10 класса, глава 8
              • Решения NCERT для науки класса 10 Глава 9
              • Решения NCERT для науки класса 10 Глава 10
              • Решения NCERT для науки класса 10 Глава 11
              • Решения NCERT для науки класса 10 Глава 12
              • Решения NCERT для науки 10 класса Глава 13
              • Решения NCERT для науки 10 класса Глава 14
              • Решения NCERT для науки 10 класса Глава 15
              • Решения NCERT для науки 10 класса Глава 16
            • Учебный план NCERT
            • NCERT
          • Commerce
            • Class 11 Commerce Syllabus
              ancy Account
              • Программа бизнес-исследований 11 класса
              • Учебная программа по экономике 11 класса
            • Учебная программа по коммерции 12 класса
              • Учебная программа по бухгалтерии 12 класса
              • Учебная программа по бизнесу 12 класса
              • Учебная программа по экономике
              • 9000 9000
                • Образцы документов по коммерции класса 11
                • Образцы документов по коммерции класса 12
                • TS Grewal Solutions
                  • TS Grewal Solutions Class 12 Accountancy
                  • TS Grewal Solutions Class 11 Accountancy
                • Отчет о движении денежных средств
                • Что такое Entry eurship
                • Защита прав потребителей
                • Что такое основной актив
                • Что такое баланс
                • Формат баланса
                • Что такое акции
                • Разница между продажами и маркетингом
              • ICSE
                • Документы
                • ICSE
                • Вопросы ICSE
                • ML Aggarwal Solutions
                  • ML Aggarwal Solutions Class 10 Maths
                  • ML Aggarwal Solutions Class 9 Maths
                  • ML Aggarwal Solutions Class 8 Maths
                  • ML Aggarwal Solutions Class 7 Maths
                  • ML 6 Maths
                  • ML 6 Maths
                • Selina Solutions
                  • Selina Solutions для класса 8
                  • Selina Solutions для Class 10
                  • Selina Solutions для Class 9
                • Frank Solutions
                  • Frank Solutions для математики класса 10
                  • Frank Solutions для математики класса 9
                • Класс ICSE 9000 2
                • ICSE Class 6
                • ICSE Class 7
                • ICSE Class 8
                • ICSE Class 9
                • ICSE Class 10
                • ISC Class 11
                • ISC Class 12
            • IAS
              Exam
              • IAS
              • Civil
              • Сервисный экзамен
              • Программа UPSC
              • Бесплатная подготовка к IAS
              • Текущие события
              • Список статей IAS
              • Пробный тест IAS 2019
                • Пробный тест IAS 2019 1
                • Пробный тест IAS 2019 2
            • Экзамен KPSC KAS
            • Экзамен UPPSC PCS
            • Экзамен MPSC
            • Экзамен RPSC RAS ​​
            • TNPSC Group 1
            • APPSC Group 1
            • Экзамен BPSC
            • WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
            • Вопросник UPSC 2019
              • Ключ ответов UPSC 2019
            • Коучинг IAS
              • IA S Coaching Бангалор
              • IAS Coaching Дели
              • IAS Coaching Ченнаи
              • IAS Coaching Хайдарабад
              • IAS Coaching Mumbai
          • JEE
            • BYJU’SEE
            • 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
            • Вопросник JEE
            • Биномиальная теорема
            • Статьи JEE
            • Квадратичное уравнение
          • NEET
            • Программа BYJU NEET
            • NEET 2020
            • NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
            • Поддержка
              • Разрешение жалоб
              • Служба поддержки
              • Центр поддержки
          • Государственные советы
            • GSEB
              • GSEB Syllabus
              • GSEB4
              • GSEB3 Образец статьи
              GSEB3 004
              • MSBSHSE
                • MSBSHSE Syllabus
                • MSBSHSE Учебники
                • Образцы статей MSBSHSE
                • Вопросники MSBSHSE
              • AP Board
                • APSCERT
                • Syll
                • AP 9000SC4
                • Syll
                • AP
                • Syll 9000SC4
                • Syll
                • Syll
              • MP Board
                • MP Board Syllabus
                • MP Board Образцы документов
                • Учебники MP Board
              • Assam Board
                • Assam Board Syllabus
                • Assam Board Учебники 9000 9000 Board4 BSEB
                  • Bihar Board Syllabus
                  • Bihar Board Учебники
                  • Bihar Board Question Papers
                  • Bihar Board Model Papers
                • BSE Odisha
                  • Odisha Board Syllabus
                  • Odisha Board Syllabus
                  • Odisha Board Syllabus
                  • Программа PSEB
                  • Учебники PSEB
                  • Вопросы PSEB
                • RBSE
                  • Rajasthan Board Syllabus
                  • RBSE Учебники
                  • RBSE Question Papers
                • HPBOSE
                • HPBOSE
                • HPBOSE
                • JKBOSE
                  • Программа обучения JKBOSE
                  • Образцы документов JKBOSE
                  • Шаблон экзамена JKBOSE
                • TN Board
                  • TN Board Syllabus
                  • TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
                    • Программа JAC
                    • Учебники JAC
                    • Вопросники JAC
                  • Telangana Board
                    • Telangana Board Syllabus
                    • Telangana Board Учебники
                    • Papers Telangana Board Учебники
                    • Учебный план KSEEB
                    • Типовой вопросник KSEEB
                  • KBPE
                    • Учебный план KBPE
                    • Учебники KBPE
                    • Документы по KBPE
                  • 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
                • Совет по Западной Бенгалии
                  • Учебный план Совета по Западной Бенгалии
                  • Учебники для Совета по Западной Бенгалии
                  • Вопросы для Совета по Западной Бенгалии
                • UBSE
                • TBSE
                • Гоа Совет
                • 000
                • NBSE0003 Board
                • Manipur Board
                • Haryana Board
              • Государственные экзамены
                • Банковские экзамены
                  • Экзамены SBI
                  • Экзамены IBPS
                  • Экзамены RBI
                  • IBPS

                    03

                    Экзамены SSC

                    9SC2

                  • SSC GD
                  • SSC CPO 900 04
                  • SSC CHSL
                  • SSC CGL
                • Экзамены RRB
                  • RRB JE
                  • RRB NTPC
                  • RRB ALP
                • O Экзамены на страхование
                • LIC4
                • LIC4 9000 ADF UPSC CAPF
                • Список статей государственных экзаменов
              • Обучение детей
                • Класс 1
                • Класс 2
                • Класс 3
              • Академические вопросы
                • Вопросы по физике
                • Вопросы по химии
                • Вопросы по химии
                • Вопросы
                • Вопросы науки
          ,

          Объяснение квадратичной формулы | Purplemath

          Purplemath

          Часто самый простой способ решить « ax ² + bx + c = 0» для значения x — это разложить на множители квадратичный коэффициент, установить каждый коэффициент равным нулю и затем решить каждый фактор. Но иногда квадратичная величина слишком беспорядочная, или она вообще не учитывается, или вам просто не хочется вводить множители.Хотя факторинг не всегда может быть успешным, квадратная формула всегда может найти решение.

          Квадратичная формула использует « a », « b » и « c » из « ax ² + bx + c », где « a », » b «и c » — это просто числа; они представляют собой «числовые коэффициенты» квадратного уравнения, которые они дали вам решить.

          MathHelp.com

          

          Квадратичная формула выводится из процесса завершения квадрата и официально записана как:

          Квадратичная формула: для ax ² + bx + c = 0, значения x , которые являются решениями уравнения, даются как:

          Чтобы квадратичная формула работала, ваше уравнение должно иметь форму «(квадратичная) = 0».Кроме того, «2 a » в знаменателе Формулы находится под всем, что указано выше, а не только под квадратным корнем. И внизу это «2 a «, а не просто «2». Убедитесь, что вы осторожны, чтобы не уронить квадратный корень или «плюс / минус» в середине ваших вычислений, иначе я могу гарантировать, что вы забудете «вставить их обратно» в свой тест, и вы запутаетесь себя вверх. Помните, что « b ² » означает «квадрат ВСЕГО из b , включая его знак», поэтому не оставляйте b ² отрицательным, даже если b отрицательное, потому что квадрат негатива — это позитив.

          Другими словами, не будьте небрежны и не пытайтесь сокращать путь, потому что это только навредит вам в долгосрочной перспективе. Поверьте мне в этом!

          Вот несколько примеров того, как работает квадратичная формула:

          Это квадратичное значение множителя:

          x ² + 3 x — 4 = ( x + 4) ( x — 1) = 0

          … Итак, я уже знаю, что решения: x = –4 и x = 1. Как мое решение будет выглядеть в квадратичной формуле? Используя a = 1, b = 3 и c = –4, мое решение выглядит так:

          Тогда, как и ожидалось, решение будет x = –4, x = 1.

          ---

          Предположим, у вас есть ax ² + bx + c = y , и вам предлагается вставить ноль для y . Соответствующие значения x являются интерцепциями x на графике. Таким образом, решение ax ² + bx + c = 0 для x означает, среди прочего, что вы пытаетесь найти x -перехватов.Поскольку было два решения для x ² + 3 x — 4 = 0, тогда на графике должно быть два интерцепта x . Построив график, мы получим кривую ниже:

          Как видите, точки пересечения x (красные точки выше) соответствуют решениям, пересекая ось x на x = –4 и x = 1.Это показывает связь между построением графиков и решением: когда вы решаете «(квадратичный) = 0», вы находите точки пересечения x графика. Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для решения квадратичной, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые интервалы x имеют те же десятичные значения, что и делать решения, предоставленные квадратной формулой.

          Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вы должны проверить, были ли вычисленные и нанесенные на график значения достаточно близкими; не ожидайте точного совпадения.

          ---

          • Решите 2 x ² — 4 x — 3 = 0. При необходимости округлите ответ до двух десятичных знаков.

          Нет множителей при (2) (- 3) = –6, которые в сумме дают –4, поэтому я знаю, что эту квадратичную нельзя разложить на множители. Я буду применять квадратичную формулу. В этом случае a = 2, b = –4 и c = –3:

          Тогда ответ будет x = –0.58, x = 2,58 с округлением до двух десятичных знаков.

          Предупреждение: «Решение», «корни» или «нули» квадратичной функции обычно должны быть в «точной» форме ответа. В приведенном выше примере точная форма — это квадратный корень из десяти. Вам нужно будет получить приближение калькулятора, чтобы построить график пересечений по оси x или упростить окончательный ответ в текстовой задаче. Но если у вас нет веских причин думать, что ответ должен быть округленным, всегда используйте точную форму.

          Сравните решения 2 x ² — 4 x — 3 = 0 с интерцепциями x на графике:

          Как и в предыдущем примере, интервалы x соответствуют нулям из квадратичной формулы. Это всегда правда. «Решения» уравнения — это также точки пересечения x соответствующего графика.

          ---

          URL: https: // www.purplemath.com/modules/quadform.htm

          ,