Самостоятельная работа по физике 11 класс «Механические колебания»

Механические колебания (11 класс) Вариант 1.

1. По графику найти амплитуду и период колебаний, определить частоту, циклическую частоту, написать уравнение гармонических колебаний.

2. Ускорение свободного падения на поверхности Луны равно 1,6 м/с2. Какой длины должен математический маятник, чтобы его период колебаний на Луне был равен 4,9 с?

3. Если уменьшить массу колеблющегося груза на 30 г, то период колебаний уменьшится в 2 раза. Найдите первоначальную массу груза.

4.Уравнение гармонических колебаний частицы имеет вид x=0,04Sin(0,25п+2), где х – в метрах, t –время в секундах. Определите амплитуду, период и частоту колебаний частицы.

5. Определите амплитуду гармонических колебаний тела, если его полная энергия 0, 04Дж, а жёсткость пружины, к которой прикреплено тело, равно 2Н/м.

6. Груз массой 400гр совершает колебания на пружине жёсткостью 250Н/м, амплитуда колебаний 15см. Найдите полную механическую энергию колебаний и наибольшую скорость. В каком положении она достигается?

_____________________________________________________________________________

Механические колебания (11 класс) Вариант 2.

1. Тело совершает гармоническое колебание по закону х(t)=20·sinπt. Определите амплитуду, период, частоту, циклическую частоту колебаний. Нарисуйте график колебаний.

2. Груз массой 9,86 кг колеблется на пружине, имея период колебаний 2с. Чему равна жёсткость пружины? Какова частота колебаний груза?

3. За одно и то же время один математический маятник делает 40 колебаний, а второй 30. Какова длина каждого маятника, если разность их длин 7 см?

4.Груз массой 400гр совершает колебания на пружине жёсткостью 250Н/м. Амплитуда колебаний 15см. найдите полную механическую энергию колебаний и наибольшую скорость.

5. В неподвижном лифте висит маятник, период колебаний которого 1с. С каким ускорением движется лифт, если период колебаний этого маятника стал равным 1.1с?

6. Груз массой 4кг совершает горизонтальные колебания под действием пружины жёсткостью 75Н/м. При каком смещении груза от положения равновесия модуль его скорости равен 5м/с, если в положении равновесия модуль его скорости равен 10м/с?

Механические колебания (11 класс) Вариант 3.

1. По графику найти амплитуду и период колебаний, определить частоту, циклическую частоту, написать уравнение гармонических колебаний.

2. Математический маятник длиной 99,5 см за одну минуту совершал 30 полных колебаний. Определить период колебания маятника и ускорение свободного падения в том месте, где он находится.

3. За одно и то же время один пружинный маятник делает 10 колебаний, а второй — на пружине с той же жесткостью – 20 колебаний. Определите массы грузов маятников, если сумма их масс равна 3 кг.

4.Шарик, движущийся горизонтально под действием пружины, совершает свободные гармонические колебания. Полная энергия равна 0.6Дж. На расстоянии 3см от положения равновесия упругая сила, действующая на шарик со стороны пружины, равна 10Н. Определите амплитуду колебаний.

5. Нитяной маятник, совершая свободные колебания, поднимается на высоту 20см от положения равновесия. Определите скорость маятника при прохождении положения равновесия.

6. Один математический маятник имеет период колебаний 3с, а другой- 4с. Каков период колебаний математического маятника, длина которого равна сумме длин указанных маятников.

____________________________________________________________________________

Механические колебания (11 класс) Вариант 4.

1. Тело совершает гармоническое колебание по закону х(t)=0,4·cos5πt. Определите амплитуду, период, частоту, циклическую частоту колебаний. Нарисуйте график колебаний.

2. Найти массу груза, который на пружине жёсткостью 250 Н/м делает 20 колебаний за 16с.

3. Из двух математических маятников один совершил 10 колебаний, а другой за то же время 6 колебаний. Найдите длину каждого маятника, если сумма их длин равна 42,5 см.

4.Колеблющийся на нити металлический шарик, проходит положение равновесия со скоростью 0,8м/с. Определите максимальную высоту, на которую поднимается шарик от положения равновесия.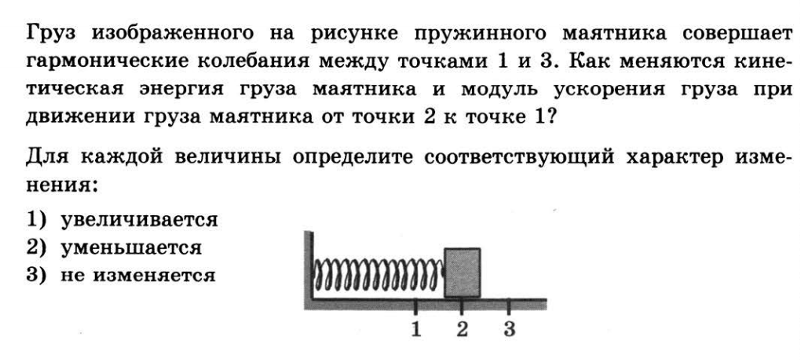

5. Груз массой 3кг, совершает горизонтальные колебания под действием пружины жёсткостью 80Н/м. при каком смещении груза от положения равновесия модуль его скорости равен 6м/с, если в положении равновесия модуль его скорости равен 12м/с?

6. Как изменится период колебаний математического маятника, если его перенести с Земли на Луну (gз=9,8 м/с2; gл=1,6 м/с2;).

Математический, пружинный маятники. Период, частота, амплитуда колебаний. Тест

Всего вопросов: 15

Вопрос 1. Чему равен период колебаний маятника длиной 1 м? Ускорение свободного падения примите равным 9,81 м/с2.

Вопрос 2. Чему равна циклическая (круговая) частота колебаний груза массой 200 г, подвешенного к пружине жесткостью 0,05 Н/м?

Вопрос 3. Найти массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за 16 с.

Вопрос 4. Груз висит на пружине и колеблется с периодом 0,5 с. На сколько укоротится (см) пружина, если снять с нее груз?

Вопрос 5. При увеличении длины математического маятника на 10 см его период колебаний увеличился на 0,1 с. Каким был начальный период колебаний?

Вопрос 6. Колебания математического маятника происходят по закону (м). Определите длину его нити подвеса.

Вопрос 7. На какой промежуток времени отстанут за сутки маятниковые часы вследствие вращения Земли, если их с полюса перенести на экватор? Считайте, что на полюсе часы шли точно.

Вопрос 8. Определите время отставания маятниковых часов за сутки, если их поднять на высоту 5 км над поверхностью Земли.

Вопрос 9. Груз массой 4 кг совершает горизонтальные колебания под действием пружины жесткостью 75 Н/м. При каком смещении груза от положения равновесия модуль его скорости равен 5 м/с, если в положении равновесия модуль его скорости равен 10 м/с?

Вопрос 10.

К пружине подвешено тело массой 2 кг. Если к нему присоединить тело массой 300 г, то пружина растянется еще на 2 см. Каков будет период колебаний, если трехсотграммовый довесок снять и предоставить телу массой 2 кг колебаться?

Вопрос 11. Как изменится период колебаний маятника при перенесении его с Земли на Марс, если масса Марса в 9,3 раза меньше массы Земли, а радиус Марса в 1,9 раза меньше радиуса Земли? (В ответ запишите отношение).

Вопрос 12. При пожаре человек массой 60 кг прыгает из окна с высоты 10 м на специальную сетку, растягиваемую пожарными. При этом сетка прогибается на 0,8 м. Определите, на сколько прогнется сетка при прыжке с высоты 25 м.

Вопрос 13. Во сколько раз изменится период колебаний груза, подвешенного на резиновом жгуте, если отрезать ¾ длины жгута и подвесить на его оставшуюся часть тот же груз? (В ответ запишите отношение)

Вопрос 14. В неподвижном лифте висит маятник, период колебаний которого 1 с. С каким ускорением движется лифт, если период колебаний этого маятника стал равным 1,1 с? В каком направлении движется лифт?

Вопрос 15. Определите период малых колебаний математического маятника длиной 15 см, подвешенного к потолку вагона, движущегося горизонтально с ускорением 5 м/с

2.

Колебания и простое гармоническое движение: задачи 2

Проблема : В какой момент при колебании пружины действует сила на массу самый большой?

Напомним, что F = — кх . Таким образом, сила, действующая на массу, будет наибольшей, когда смещение блока является максимальным, или когда x = ± x м .

Проблема : Каков период колебаний груза массой 40 кг на пружине с постоянным к = 10 Н/м?

Мы получили, что T = 2 Π . Чтобы найти период колебания мы просто подставляем в это уравнение:

T = 2 Π = 4 Π секунд

Какие бы начальные условия не были заданы системе, период колебания будут такими же. Обратите внимание еще раз, что период, частота и угловой частоты являются свойствами системы, а не условий, наложенных на нее. система.

Проблема :

К пружине с постоянной силой 18 Н/м прикреплен груз массой 2 кг. Это тогда сместится в точку х = 2. Сколько времени потребуется, чтобы брусок добраться до точки х = 1?

Для этой задачи мы используем уравнения синуса и косинуса, которые мы вывели для простых гармоническое движение. Напомним, что

х = х m cos( σt ). Нам дано х и х м в вопросе и должны вычислить σ , прежде чем мы сможем найти t . Мы знаем, однако, что независимо от начального смещения, σ = = = = 3. Таким образом, мы можем подставляем наши значения:

= cos σt
=		 cos3 т
3 т = cos -1
t = = 0,35 секунды

Эта задача была простым примером того, как использовать наши уравнения для простых гармоническое движение.

Проблема :

Масса 4 кг, прикрепленная к пружине, совершает колебания с периодом 2 секунды. Каков период колебаний, если к пружине прикреплен груз массой 6 кг?

Чтобы найти период колебаний, нам нужно знать только м и к . Нам дано м и надо найти к на весну. Если масса 4 кг совершает колебания с периодом 2 секунд, мы можем вычислить k из следующего уравнения:

Т = 2 Π

Подразумевая, что

к = = = 4 Π 2

Теперь, когда у нас есть k , легко вычислить период для другой массы:

Т = 2 Π = 2 Π = = 2,45 секунды

Из этой проблемы можно сделать общее утверждение: большая масса, прикрепленная к данная пружина будет колебаться с более длительным периодом.

Проблема :

Через нее проходит груз массой 2 кг, совершающий колебания на пружине с постоянной силой 4 Н/м. точка равновесия со скоростью 8 м/с. Чему равна энергия системы при эта точка? Из вашего ответа выведите максимальное смещение,

x м г. масса.

Когда масса находится в точке равновесия, потенциальная энергия не сохраняется. весна. Таким образом, вся энергия системы является кинетической и может быть вычислена легко:

К = mv 2 = (2)(8) 2 = 64 Дж

Поскольку это полная энергия системы, мы можем использовать этот ответ для рассчитать максимальное перемещение груза. Когда блок максимально смещена, она находится в состоянии покоя, и вся энергия системы запасается в виде потенциальная энергия пружины, равная

U = кх м 2 . Так как энергия сохраняется в системе, мы можем связать ответ, который мы получили для энергии при одном положение с энергией в другом:

E f = E o
кх м 2 = mv 2 = 642
x м = = = 4 метра

Мы использовали энергетические соображения в этой задаче во многом так же, как когда мы впервые столкнулись с сохранением энергии — линейно ли движение, круговые или колебательные, наши законы сохранения остаются мощными инструментами.

Предыдущий раздел

Гармоническое движение

Гармоническое движение

Говорят, что объект, движущийся вдоль оси X, демонстрирует простое гармоническое движение , если его положение как функция времени изменяется как

x(t) = x 0 + A cos(ωt + φ).

Объект колеблется вокруг положения равновесия x 0 . Если мы выбираем начало нашей системы координат так, что x 0 = 0, тогда смещение x от положения равновесия как функция времени определяется выражением

x(t) = A cos(ωt + φ).

А — амплитуда колебаний, т. е. максимальное смещение объекта из положения равновесия либо в положительное или отрицательное направление x. Простое гармоническое движение повторяется. период T — это время, за которое объект совершить одно колебание и вернуться в исходное положение. угловая частота ω определяется как ω = 2π/T. Угловая частота измеряется в радианах в секунду. Обратная сторона период частота f = 1/T. частота f = 1/T = ω/2π движения дает число полных колебаний в единицу времени. Измеряется в герцах (1 Гц = 1/с).

Скорость объекта как функция времени определяется как

v(t) = dx(t)/dt = -ω A sin(ωt + φ),

а ускорение дается

a(t) = dv(t)/dt = -ω 2 A cos(ωt + φ) = -ω 2 x.

Величина φ называется фазовой постоянной . Он определяется начальными условиями движения. Если при t = 0 объект имеет максимальное смещение в положительном направлении x, тогда φ = 0, если он имеет максимальное смещение в отрицательном направлении x, тогда φ = π. Я толстый t = 0 частица движется через положение равновесия с максимальным скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна позвонил в фаза .

На рисунке ниже положение и скорость представлены как функция времени. для колебательного движения с периодом 5 с. Амплитуда и максимальная скорость имеют условные единицы. Положение и скорость вне фазы . Скорость равна нулю при максимальном смещении, и смещение равно нулю на максимальной скорости.


Для простого гармонического движения ускорение a = -ω 2 x равно пропорционально смещению, но в обратном направлении. Простой гармоническое движение — ускоренное движение . Если объект демонстрирует простое гармоническое движение, на него должна действовать сила. объект. Сила

F = ma = -mω 2 х.

Он подчиняется закону Гука , F = -kx, при k = mω 2 .

Ссылка: простая гармоническое движение (Youtube)

F = ma = md 2 x/dt 2 с F = -kx приводит к второму порядку дифференциальное уравнение

d 2 х/dt 2 = -(к/м)х.

Теперь мы знаем, как решить это уравнение. Решение

x(t) = Acos(ωt + φ), где ω 2 = k/m.

Решение дифференциального уравнения второго порядка включает две константы интеграция. Здесь этими константами являются A и φ. Они определяются начальными условиями задачи.

Одни и те же уравнения имеют одни и те же решения. Всякий раз, когда вы сталкиваетесь с дифференциальное уравнение вида d 2 x/dt 2 = -b 2 x, вы знаете что решение x(t) = Acos(ωt + φ), при ω = b.

Сила пружины подчиняется закону Гука. Предположим, что объект прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит сила на объект. Эта сила пропорциональна смещению х тела. пружинит из положения равновесия и движется в направлении, противоположном смещение.

Ф = -кх

Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.

a = -(к/м)х

Он набирает скорость по мере продвижения к положению равновесия, потому что его ускорение направлено в сторону его скорости. Когда он находится в равновесии положение, ускорение равно нулю, но объект имеет максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться. вниз, потому что ускорение теперь в направлении, противоположном направлению от его скорости. Пренебрегая трением, он останавливается, когда пружина сжимается на расстояние А, а затем ускоряется обратно к равновесию позиция. Он снова промахивается и останавливается в исходном положении, когда пружина растягивается на расстояние A. Движение повторяется. Объект колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой частота движения

ω = √(к/м),

период

Т = 2π√(м/к),

и частота

f = (1/(2π))√(к/м).

Резюме:

Если единственная сила, действующая на тело массой m, является силой закона Гука,
F = -kx
тогда движение объекта представляет собой простое гармоническое движение.
Если x — смещение от равновесия, мы имеем

.

х(t) = Acos(ωt + φ),
v(t) = -ωAsin(ωt + φ),
a(t) = -ω2Acos(ωt + φ) = -ω2x.
ω = (к/м) ½ = 2πf = 2π/T.

А = амплитуда
ω = угловая частота
f = частота
Т = период
φ = фазовая постоянная

Проблема:

Частица совершает простые гармонические колебания, так что ее перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6) где x в сантиметрах, t в секундах. При t = 0 найти
(а) смещение частицы,
(б) его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.

Решение:

  • Обоснование:
    Анализ простого гармонического движения.
    x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота, φ = фазовая постоянная.
    v(t) = -ω A sin(ωt + φ), a(t) = -ω 2 A cos(ωt + φ) = -ω 2 x.
  • Детали расчета:
    (a) Смещение как функция времени: x(t) = Acos(ωt + ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
    Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
    (b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
    (c) Ускорение при t = 0 равно a(0) = -ω 2 (5 см)cos(π/6) = -17,3 см/с 2 .
    (d) Период движения T = 2π/ω = π с, а амплитуда равна 5 см.
Проблема:

Частица массой 20 г движется в простом гармоническом движении с частотой 3 колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл его движение?
(b)  Какова его максимальная скорость? Где это происходит?
(с) Найдите максимальное ускорение частицы. Где в движении делает происходит максимальное ускорение?

Решение:

  • Рассуждение:
    Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ).
  • Детали расчета:
    (a) Общее расстояние d, которое проходит частица за один цикл, равно от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
    (b) Максимальная скорость частицы
    v макс. = ωA = 2πfA = 2π 15 см/с = 0,94 м/с.
    Частица имеет максимальную скорость при прохождении через положение равновесия.
    (c) Максимальное ускорение частицы равно
    и макс. = ω 2 А = (2πf) 2 А = 17,8 м/с 2 .
    Частица имеет максимальное ускорение в точках поворота, где имеет максимальное водоизмещение.
Проблема:

Груз массой 1 кг, прикрепленный к пружине с постоянной силой 25 Н/м, совершает колебания на горизонтальная дорожка без трения. При t = 0 масса выходит из состояния покоя при x = -3 см, то есть пружина сжата на 3 см. Пренебречь массой весны. Найти
(а) период его движения,
(б) максимальное значение его скорости и ускорения и
(в) перемещение, скорость и ускорение как функция времени.

Решение:

  • Обоснование:
    Для простого гармонического движения
    x(t) = Acos(ωt + φ),
    v(t) = -ωAsin(ωt + φ),
    a(t) = -ω2Acos(ωt + φ) = -ω2x.
    ω = (к/м) ½ = 2πf = 2π/T.
  • Детали расчета:
    (a) Период равен T = 2π(m/k) ½ = 2π(1 с 2 /25) ½ = 1,26 с.
    (b)  Угловая скорость ω = (к/м) ½ = 5/с.
    Максимальная скорость v max = ωА = 15 см/с.
    Максимальное ускорение частицы составляет макс. = ω 2 А = 0,75 м/с 2 .
    (в) x(t) = Acos(ωt + φ) = (3 см)cos((5/с)t + π) = -(3 см)cos((5/с)t),
    v(t) = -ωAsin(ωt + φ) = (15 см/с)sin((5/с)t),
    a(t) = -ω 2 Acos(ωt + φ) = (0,75 м/с 2 )cos((5/с)t).

Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В равновесия пружина растянута на расстояние x 0 = mg/k. Если масса смещается из положения равновесия вниз, а пружина растягивается дополнительное расстояние x, то полная сила, действующая на массу, равна mg — k(x 0 + x) = -kx направлена ​​в сторону положения равновесия.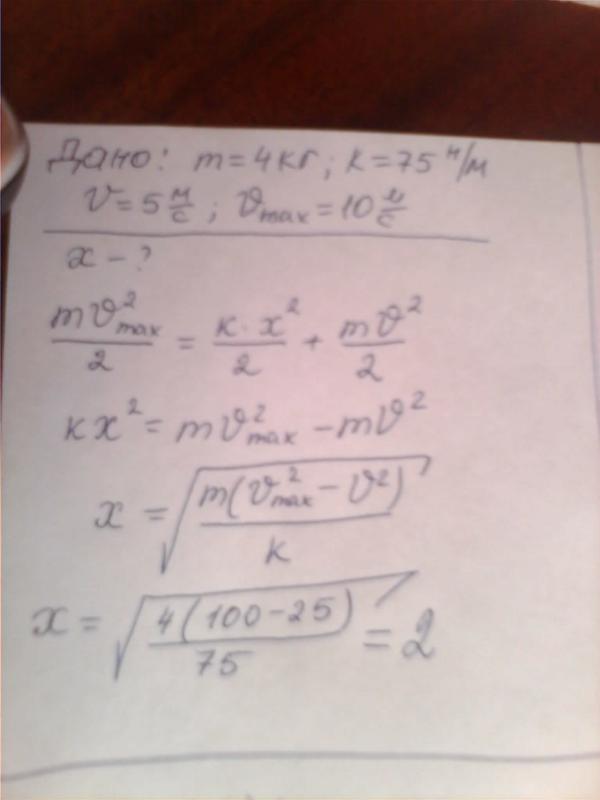 Если масса смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg — k(x 0 — х) = кх, направленный к положению равновесия. Масса будет выполнять простые гармонические движения. Угловая частота ω = (к/м) ½ то же для массы, колеблющейся на пружине в вертикальном или горизонтальном положении. Но равновесная длина пружины, вокруг которой она колеблется, различна для вертикальное положение и горизонтальное положение.

Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально на столе без трения.

Какова полная энергия объекта?

Кинетическая энергия объекта

K = ½mv 2 = ½mω 2 A 2 sin 2 (ωt + ф).

Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия U = ½kx 2 . Следовательно, потенциальная энергия объекта равна

.

U = ½kx 2 = ½mω 2 x 2 = ½mω 2 A 2 cos 2 (ωt + φ).

Полная механическая энергия объекта

E = K + U = ½mω 2 A 2 (sin 2 (ωt + φ) + cos 2 (ωt + φ)) = ½mω 2 A 2 .

Энергия E в системе пропорциональна квадрату амплитуды .

Е = ½ кА 2 .

Это постоянно меняющаяся смесь кинетической и потенциальной энергии.

Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω, восстанавливающая сила F = -mω 2 x подчиняется закону Гука и, следовательно, является консервативная сила . Мы можем определить потенциальную энергию U = ½mω 2 x 2 , а полная энергия объекта определяется выражением E = ½mω 2 А 2 .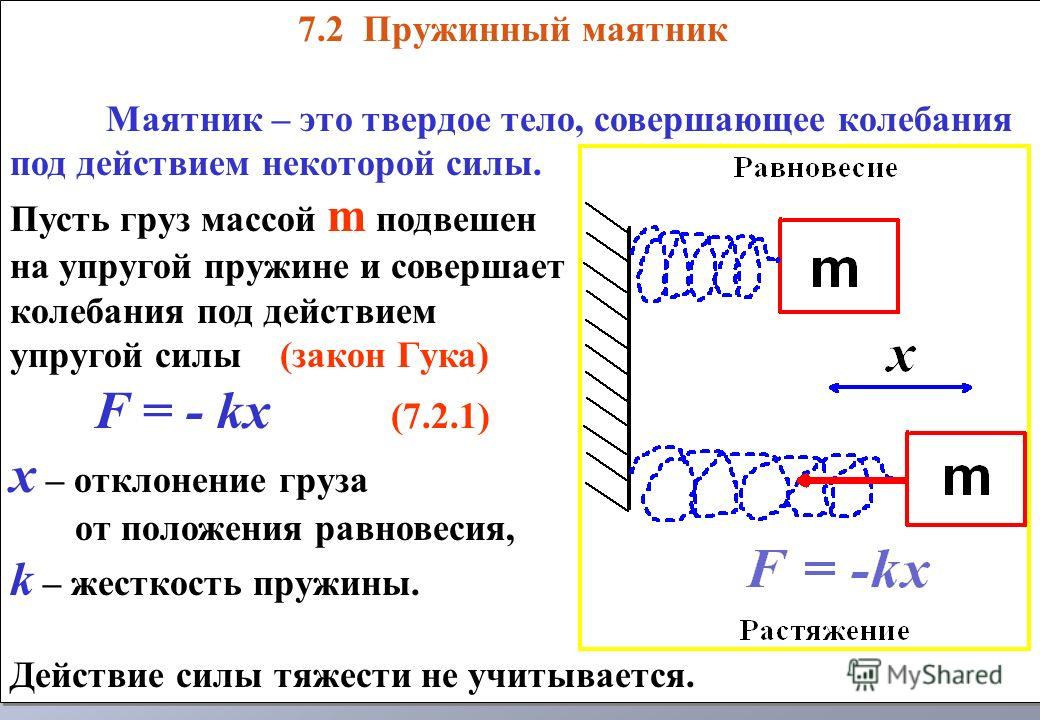

Проблема:

Частица, подвешенная на пружине, совершает колебания с угловой частотой 2 рад/с. Пружина подвешена к потолку кабины лифта и висит неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5 РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?

Решение:

  • Рассуждение:
    При движении в лифте с постоянной скоростью общая сила, действующая на масса равна нулю. Сила, действующая на пружину, по величине равна силе силы тяжести, действующей на массу, пружина имеет равновесную длину вертикальная пружина. Когда лифт внезапно останавливается, конец пружины крепятся к потолочным упорам. Однако масса имеет импульс, p = mv, и поэтому начинает растягивать пружину. Он движется через положение равновесия вертикальной пружины с ее максимальной скоростью v макс. = 1,5 м/с.
    Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ).