Графики зависимости пути от времени
Если траектория движения точки известна, то зависимость пути , пройденного точкой, от истекшего промежутка времени дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между и для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид . Составим таблицу пути и времени такого движения:
| t, с | 1 | 2 | 3 | 4 | 5 | 6 | … |
| s, м | 2 | 4 | 6 | 8 | 10 | 12 | … |
Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и пути и примем точку пересечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 18). Для «привязки» значений пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: пути и моменту , — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.
Рис. 18. График пути равномерного движения со скоростью 2 м/с
Рис. 19. К упражнению 12.1
В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.
Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.
Рис. 20. Графики пути равномерных движений со скоростями 2 и 3 м/с
Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе
Наклон графика зависит, конечно, не только от числового значения скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.
С помощью графиков пути можно легко решать разные задачи о движении. Для примера на рис. 18 штриховыми линиями показаны построения, необходимые для того, чтобы решить следующие задачи для данного движения: а) найти путь, пройденный за время 3,5 с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем (штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.
На графиках, описывающих равномерное прямолинейное движение, можно откладывать по оси ординат вместо пути координату движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси . Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.
Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущейся точки
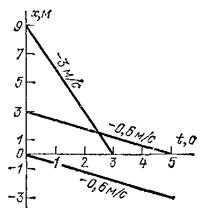
Рис. 23. Графики нескольких движений с отрицательными скоростями
Например, на рис. 22 прямая I есть график движения, происходящего с положительной скоростью 4 м/с (т. е. в направлении оси ), причем в начальный момент движущаяся точка находилась в точке с координатой м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой (прямая II). Прямая. III соответствует случаю, когда в момент движущаяся точка находилась в точке с координатой м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату в момент с.
Мы видим, что наклоны всех четырех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси вверх или вниз на соответственное расстояние.
Графики движений, происходящих с отрицательными скоростями (т. е. в направлении, противоположном направлению оси ), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата точки с течением времени уменьшается.
12.3. График пути для точки, движущейся со скоростью , отсекает на оси ординат отрезок . Как зависит от времени расстояние от начальной точки? Напишите формулу этой зависимости.
12.4. Точка, движущаяся со скоростью , в момент находится на расстоянии от начальной. Как зависит от времени расстояние ?
12.5. Точка, двигаясь равномерно вдоль оси , имела координаты м и м в моменты времени с и с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата в начальный момент. Найдите проекцию скорости на ось .
12.6. Найдите при помощи графика пути, когда и на каком расстоянии от точки А автомашину, вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через 20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая — со скоростью 60 км/ч.
12.7. Найдите при помощи графика пути, где и когда встретятся автомашины, вышедшие одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В, лежащих на расстоянии 100 км друг от друга.
Графики пути можно строить и для случаев, в которых тело движется равномерно в течение определенного промежутка времени, затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в течение первого часа со скоростью 20 км/ч, в течение второго часа — со скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.
12.8. Постройте график пути для движения, в котором за последовательные часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно суммарное перемещение тела?
sfiz.ru
Как построить график зависимости пути от времени — Науколандия
Построение графиков используют, чтобы показать зависимость одной величины от другой. При этом на одной оси откладывают изменение одной величины, а на другой оси — изменение другой величины. При прямолинейном равномерном движении скорость тела остается постоянной, меняются только время и зависимый от него пройденный путь. Поэтому наибольший интерес для такого движения представляет график, отражающий зависимость пути от времени.
При построении такого графика на одной из осей координатной плоскости отмечается изменение времени (t). Например, 1 с, 2 с, 3 с и т. д. Пусть это будет ось x. На другой оси (в данном случае y) отмечается изменение пройденного пути. Например, 10 м, 20 м, 30 м и т. д.
Начало системы координат принимается за начало движения. Это точка старта, в которой промежуток времени, потраченный на движение, равен нулю, и пройденный путь также равен нулю. Это первая точка графика зависимости пути от времени.
Далее на координатной плоскости находят вторую точку графика. Для этого для какого-либо времени пути находят пройденный за это время путь. Если скорость тела равна 30 м/с, то это может быть точка с координатами (1; 30) или (2; 60) и так далее.
После того, как вторая точка отмечена, проводят луч через две точки (первая — начало координат). Начало луча — это начало координат. Данный луч и является графиком зависимости пути от времени при прямолинейном равномерном движении. У луча нет конца, это говорит о том, что чем больше затраченное на путь время, тем больше будет пройденный путь.
Вообще говорят, что графиком зависимости пути от времени является прямая, проходящая через начало координат.
Чтобы доказать, что графиком является прямая, а, допустим, не ломаная линия, можно построить ряд точек на координатной плоскости. Например, если скорость равна 5 км/ч, то на координатной плоскости можно отметить точки (1; 5), (2; 10), (3; 15), (4; 20). Затем соединить их последовательно между собой. Вы увидите, что получится прямая.
Чем больше скорость тела, тем быстрее увеличивается пройденный путь. Если на одной и той же координатной плоскости начертить зависимости пути от времени для двух тел, движущихся с разными скоростями, то график тела, которое движется быстрее, будет иметь больший угол с положительным направлением оси времени.
Например, если одно тело движется со скоростью 10 км/ч, а второе — 20 км/ч, то на координатной плоскости можно отметить точки (1; 10) для одного тела и (1; 20) для другого. Понятно, что вторая точка находится дальше от оси времени, и прямая через нее образует больший угол, чем прямая через точку, отмеченную для первого тела.
Графики зависимости пути от времени при прямолинейном равномерном движении можно использовать для быстрого нахождения затраченного времени по известному значению пройденного пути или пути по известному времени. Для этого надо провести перпендикулярную линию из значения координатной оси, которое известно, до пересечения с графиком. Далее из полученной точки пересечения провести перпендикуляр к другой оси, получив тем самым искомое значение.
Кроме графиков зависимости пути от времени, можно построить графики зависимости пути от скорости и скорости от времени. Однако, так как при прямолинейном равномерном движении скорость постоянна, эти графики представляют собой прямые, параллельные осям пути или времени и проходящие на уровне заявленной скорости.
scienceland.info
Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:
s=v0t+at22, где \(а\) — это ускорение.
Сравним графики равномерного и равноускоренного движения:
Графики прямолинейного равномерного движения:
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость \(a(t)\) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график \(v(t)\) — прямая линия, параллельная оси времени.
Правило определения пути по графику \(v(t)\): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График \(s(t)\) — наклонная линия.

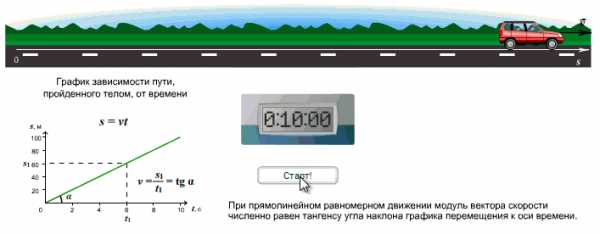
Графики равноускоренного движения:
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график \(a(t)\) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. Путь изменяется согласно линейной зависимости .
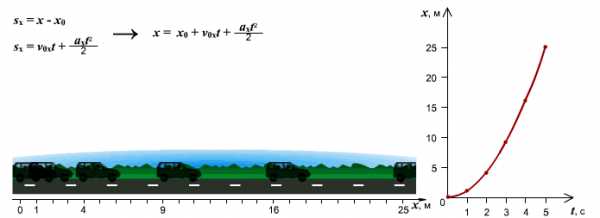
Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости: s=v0t+at22. В координатах зависимость имеет вид: x=x0+v0xt+axt22.
Графиком является ветка параболы.
Источники:
http://fizmat.by/kursy/kinematika/ravnouskorennoe
www.yaklass.ru
Вопрос 4
Равнопеременное движение. Уравнения скорости и перемещения при равнопеременном движении. Графическое представление равнопеременного движения.
Краткий ответ
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Скорость при равноускоренном движении по прямой — это начальная скорость тела плюс ускорение данного тела умноженное на время в пути
Перемещение при равноускоренном движении по прямой — это расстояние пройденное телом по прямой (расстояние между начальной и конечной точками движения)
Обозначения:
— Перемещение тела при равноускоренном движении по прямой
— Начальная скорость тела
— Скорость тела при равноускоренном движении по прямой
— Ускорение тела
— Время движения тела
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
Развернутый ответ Если скорость тела меняется, говорят, что оно движется неравномерно.Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.
Для характеристики неравномерного движения вводится понятие средней скорости:
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Скорость при равноускоренном движении по прямой — это начальная скорость тела плюс ускорение данного тела умноженное на время в пути
Перемещение при равноускоренном движении по прямой — это расстояние пройденное телом по прямой (расстояние между начальной и конечной точками движения)
Обозначения:
— Перемещение тела при равноускоренном движении по прямой
— Начальная скорость тела
— Скорость тела при равноускоренном движении по прямой
— Ускорение тела
— Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
— если известны начальная, конечная скорости движения и ускорение.
— если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
infofiz.ru
Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
Цели урока:
обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;
развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный (письменный) опрос, решение задач).
Связи:
межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные: равномерное и равноускоренное движение.
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
3. Объяснение нового материала.
Скачать этот видеоурок
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
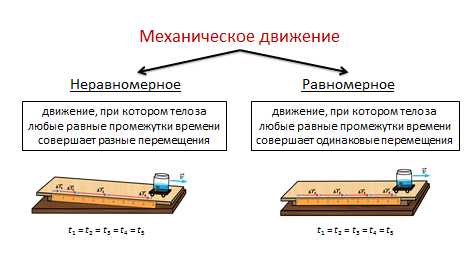
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.

Если движение равномерное, то:
1. Скорость тела не меняется с течением времени;
2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;
3. Уравнение перемещения имеет вид:
4. И — кинематическое уравнение равномерного движения.
Для равноускоренного:
1. Ускорение тела не изменяется с течением времени;
2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло
3. Уравнение скорости для равноускоренного движения имеет вид:
4. — уравнение перемещения для равноускоренного движения;
5. — кинематическое уравнение равноускоренного движения.
Для большей наглядности движение можно описывать с помощью графиков.
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.
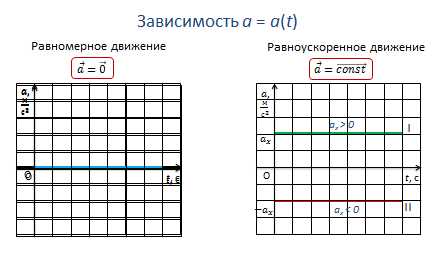
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.
Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.
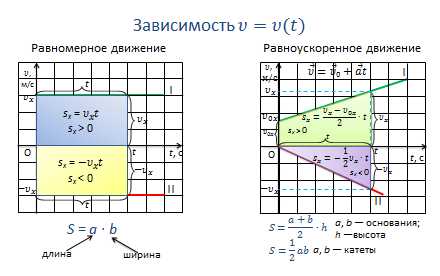
По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.
Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.
Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v0 + at, т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.
По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.
При этом проекция перемещения для первого тела будет положительной.
Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.
Проекция перемещения — отрицательна.
Теперь рассмотрим зависимость пройденного пути от времени.
Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.
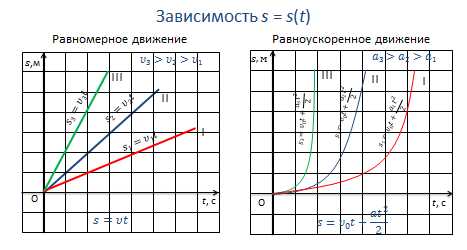
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.
При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
Теперь перейдем к рассмотрению зависимости перемещения от времени.
Рассмотрим равномерное движение.
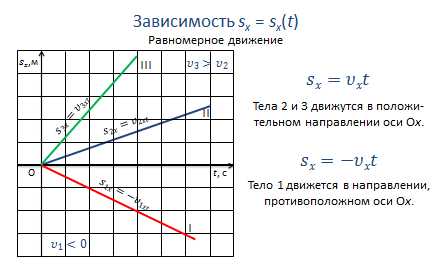
Т.к. при равномерном движении перемещение линейно зависит от времени (sx = υxt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.
А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.
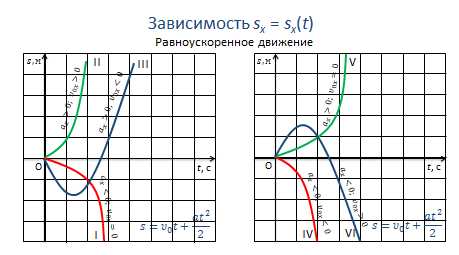
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.
Для 2-го тела ускорение и начальная скорость тела больше нуля.
Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.
У 4-го тела начальная скорость и ускорение меньше нуля.
Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.
И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.
И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).
Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.
График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.
В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
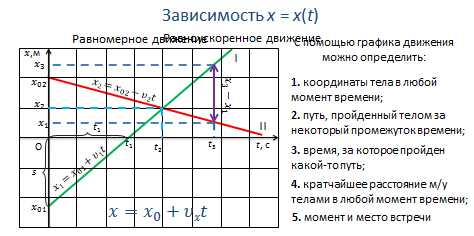
С помощью графика движения можно определить:
1. координаты тела в любой момент времени;
2. путь, пройденный телом за некоторый промежуток времени;
3. время, за которое пройден какой-то путь;
4. кратчайшее расстояние м/у телами в любой момент времени;
5. момент и место встречи и т. д.
По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).
При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.
4. Этап обобщения и закрепления нового материала
И так, сделаем главный вывод.
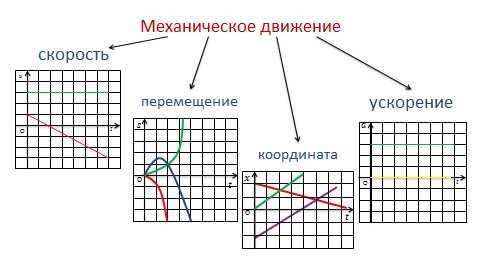
Механическое движение для большей наглядности можно описывать с помощью графиков:
1) Зависимости скорости от времени;
2) Зависимости ускорения от времени;
3) Зависимость координаты тела от времени;
4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
6. Домашнее задание.
videouroki.net
Всего вопросов: 20
Вопрос 1. На графике изображена зависимость скорости движения слона от времени. Чему равна скорость движения слона?
Вопрос 2. На рисунке изображен график зависимости координаты тела от времени движения.
Используя график, определите начальную координату тела.
Вопрос 3. Используя рисунок, определите характер и скорость движения тела.
Вопрос 4. Какой из приведенных ниже графиков соответствует равномерному движению?

Вопрос 5. Используя график зависимости пути от времени для равномерного прямолинейного движения тела, определите скорость тела.
Вопрос 6. Используя график зависимости пути от времени для равномерного прямолинейного движения тела, определите скорость тела.
Вопрос 7. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 8. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 9. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равномерно?
Вопрос 10. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси Ох, от времени. Чему равен модуль перемещения тела к моменту времени t=10 с?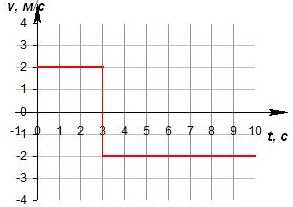
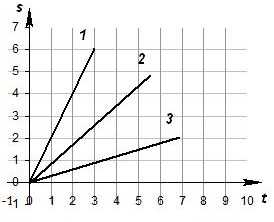
Вопрос 11. На рисунке представлены три графика зависимости пройденного пути от времени. Какое из тел двигалось с меньшей скоростью?
Вопрос 12. На рисунке представлен график зависимости координат от времени для трех тел. В каком из нижеприведенных соотношений между собой находятся скорости этих тел?
Вопрос 13. На рисунке представлен график зависимости координат от времени для трех тел. В каком из нижеприведенных соотношений находятся между собой абсолютные значения скоростей тел?
Вопрос 14. На рисунке приведены графики движения двух тел
Отношение скоростей равно:
Вопрос 15. Какой из нижеприведенных интервалов времени соответствует движению с наибольшей по модулю скоростью?
Вопрос 16. На рисунке представлен график зависимости скорости прямолинейного движения от времени. Перемещение и путь, пройденные точкой за 8 с движения, равны:
Вопрос 17. На рисунке приведена зависимость координаты тела от времени. Путь и перемещение тела за первые 3 с движения составляют:
Вопрос 18. На рисунке приведены графики движения велосипедиста I и мотоциклиста II в системе отсчета, связанной с землей. Определить скорость мотоциклиста относительно велосипедиста (в м/с).
Вопрос 19. Координата движущегося тела изменяется с течением времени так, как показано на рисунке. Какой из нижеприведенных графиков наиболее точно отражает зависимость проекции скорости этого тела от времени?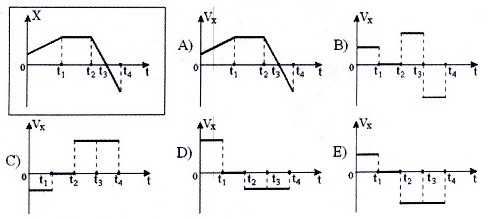
Вопрос 20. Какой из нижеприведенных графиков соответствует зависимости пройденного пути от времени, для тела проекция скорости которого изменяется так, как показано на рисунке? 
fizmat.by
Решение задач по теме «Графики пути и скорости при равномерном движении»
страница 1| Модуль Вариант 1 | Решение задач по теме «Графики пути и скорости при равномерном движении» | |
| Цель модуля. ОЗНАКОМИТЬСЯ с решениями простейших задач по данной теме. УМЕТЬ применять теоретические знания при решении задач по данной теме. УМЕТЬ применять теоретические знания при решении задач в нестандартных условиях. | ||
Учебный материал
| АОЗ о понятии «равномерное движение», формулах вычисления пути, времени и скорости, единицах измерения данных физических величин, графиках зависимостей пути и скорости от времени. Цель: ЗНАТЬ определение понятия «равномерное движение», формулы для вычисления пути, скорости и времени, единицы измерения данных величин. УМЕТЬ строить и читать графики зависимостей пути и скорости от времени. |
Ответьте на вопросы:
-
Какое движение называют равномерным? -
Что такое скорость? -
Какова формула скорости при равномерном прямолинейном движении? -
В каких единицах измеряется скорость? -
Что представляет уравнение равномерного прямолинейного движения? -
Как из уравнения движения найти время движения тела? -
Уравнение движения имеет вид s = 2,5t (м). Какую информацию мы можем извлечь из этой записи?
Решите задачи:
-
Выполните перевод единиц: 144 км/ч = ___ м/с. -
Выполните перевод единиц: 6 м/с = ___ км/ч. -
Скорость зайца 15 м/с, а дельфина – 18 км/ч. Кто из них движется быстрее? -
В течение 30 с поезд двигался равномерно со скоростью 72 км/ч. Какой путь он прошел за это время? -
За какое время плывущий по течению реки плот пройдет 15 км, если скорость течения 0,5 м/с? -
По графику пути (рис. 1) определите скорость движения тела. -
По графику скорости (рис. 2) определите путь. Пройденный телом за 6 с. Как представить числовое значение пути, используя график скорости? -
Скорость тела 18 м/с. Постройте график зависимости скорости от времени. Единицы масштаба выберите самостоятельно. -
Двигаясь прямолинейно и равномерно пешеход прошел 8 км за 2 часа. Постройте график зависимости пути от времени. Вычислите скорость пешехода и постройте график зависимости скорости от времени.
| Решение задач Цель: РЕШАТЬ простейших задачи по данной теме. РЕШАТЬ задачи по данной теме. РЕШАТЬ задачи в нестандартных ситуациях. |
Задача 1.
По графику пути (рис. 3) определите скорость движения тела.
Задача 2.
По графику скорости (рис. 4) определите путь, пройденный телом за 6 с. Как представить числовое значение пути, используя график скорости?
Задача 3.
Скорость тела 20 м/с. Постройте график зависимости скорости от времени. Единицы масштаба выберите самостоятельно.
З
5 см
адача 4.
Двигаясь прямолинейно и равномерно автомобиль проехал 240 км за 3 часа. Постройте график зависимости пути от времени. Вычислите скорость автомобиля и постройте график зависимости скорости от времени.
Задача 5.
Какова скорость катера, график движения которого представлен на рис. 5?
Задача 6.
По графикам движений тел (рис. 6) можно утверждать, что:
а) тела движутся по горкам разных наклонов;
б) что скорости обоих тел одинаковы;
в) скорость первого тела в 2,5 раза меньше скорости второго тела;
г) скорость первого тела в 2,5 раза больше скорости второго тела.
Постройте графики скорости движения тел.
Задача 7.
Двигаясь с постоянными скоростями, пешеход прошел 5,4 км за час, а велосипедист 200 м проехал за 20 с. Постройте в одной системе координат: а) графики скорости названных тел; б) графики пути за 20 с движения.
Задача 8.
На рисунке 7 представлены графики зависимости пути трех тел от времени. Как двигались эти тела? Определите скорости движения каждого тела, постройте графики зависимости скорости υ1, υ2, υ3 тел от времени.
Задача 9.
На рисунке 8 представлен график зависимости пути от времени. Как двигалось тело в течение времени движения? Определите путь s, пройденный телом, и скорости υ1, υ2, υ3 тела на всех участках движения.
Задача 10.
Используя график скорости движения тела (рис. 9), можно утверждать, что путь s1, пройденный за первые три секунды, и путь s2, пройденный за три последние секунды, связаны отношением:
а) s2 = 0,5s1;
б) s2 = 1,5s1;
в) s2 = s1;
г) s2 = 3s1.
Задача 11.
Упрощенный график скорости υ движения автомобиля приведен на рисунке 10. Охарактеризуйте движение автомобиля. Какие пути пройдены автомобилем на каждом участке движения? Какие детали графика опущены?
Задача 12.
Используя график скорости движения тела (рис. 11), можно доказать, что половина всего пути будет пройдена телом:
а) к концу 10-й секунды;
б) к концу 13-й секунды;
в) к концу 18-й секунды;
г) к концу 20-й секунды.
| Выходной контроль Цель: ПРОВЕРИТЬ усвоение учебных элементов. |
-
Какой из графиков соответствует графику зависимости пути от времени при равномерном прямолинейном движении? -
Определите по графику (рис.12) путь, который проехал велосипедист за 3 с.
-
12 м; -
9 м; -
6 м; -
3 м.
-
По графику (рис. 12) определите скорость движения в момент времени 3 с от начала движения.
-
27 м/с; -
12 м/с; -
3 м/с; -
0 м/с.
-
Какой из графиков скорости соответствует скорости велосипедиста, зависимость пути от времени которого представлена на рис. 12. -
Во сколько раз скорость движения лыжника Л (рис. 13) больше скорости движения пешехода П?
Наука никогда не решает вопроса, не поставив при этом десятка новых.
Джорж Бернард Шоу
| Подведение итогов Цель: ЗАПОЛНИТЬ лист контроля; ОЦЕНИТЬ знания. |
ЛИСТ КОНТРОЛЯ
| Учебный элемент | Ответ | Баллы | Результат |
| Решение задач | 1. v = 10 м/с 2. s = 30 м 3. 4. , 5. v ≈ 333,3 м/мин ≈5,5м/с 6. г. 7. 8. 9. s = 54 м, v1 = 3 м/с, v2 = 0 м/с, v3 = 6 м/с, v4 = 0 м/с 10. б 11. s1 = 50 м – равномерн., s2 = 75 м – равномерн., s3 = 0 м –не двигался, s4 = 38 м – не равномерн. 12. б | 2 2 2 4 4 3 3 3 4 5 8 8 | Поставьте себе итоговую оценку: 37-71 балла – «отлично» 17-36 балла – «хорошо»; 6-16 баллов – «зачет»; ≤5 баллов – «незачет». Сдайте лист контроля учителю. ОЦЕНКА ↓ |
| Выходной контроль | 1. г 2. б 3. в 4. в 5. в 3 раза | 2 2 2 2 4 | |
| Итого: | 71 | ||
То, что должно вознестись на самый верх, начинается в самом низу.
Гораций
Человек, который попадает в цель, — талант; человек, который попадает в цель невидимую, — гений.
Артур Шопенгауэр
ДИФФЕРЕНЦИРОВАННОЕ ДОМАШНЕЕ ЗАДАНИЕ
РЕФЛЕКСИЯ
Вырази своё отношение к изучаемому материалу:
| Тема неинтересна! | Очень интересная тема! | Нормальная тема |
Оцени уровень своих достижений на уроке с помощью смайлика:
| Отлично | Хорошо | Неудовлетворительно |
Вариант 1
страница 1
gymnazya.ru

Leave A Comment