График функции модуль х в квадрате – Построение функций, содержащих модули

Построение функций, содержащих модули

Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.

1. Начнем с построения графика

 

В “основе” его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график

Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:

Теперь необходимо умножить на два все ординаты, чтобы получить график функции

Наконец, сдвигаем график вверх на две единицы:

Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

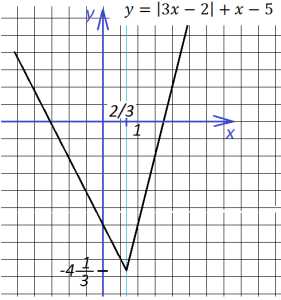
2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию

 

а в другой (левее) – график функции

Строим:

3. Следующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) – график по третьему уравнению:

Строим:

4. Теперь можем построить  график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

 при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

График этой функции, умноженной на два,

выглядит так:

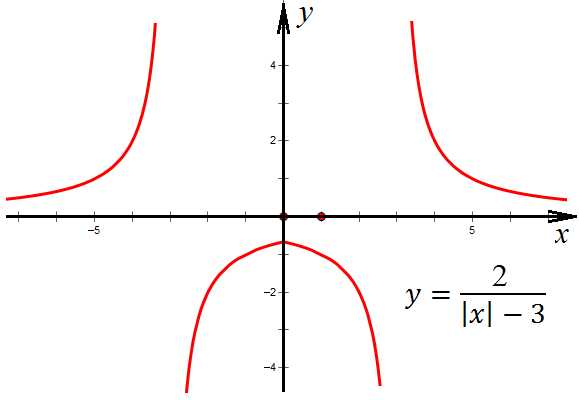
Теперь можно поднять график по оси у:

и тогда он будет таким: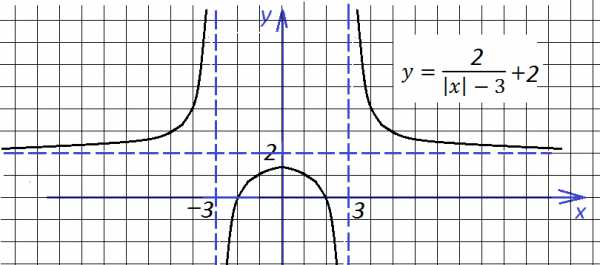

Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:

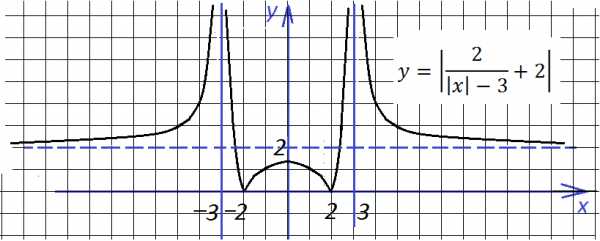
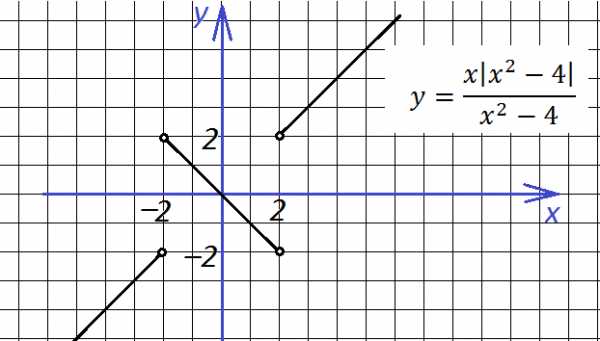
5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках  (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:

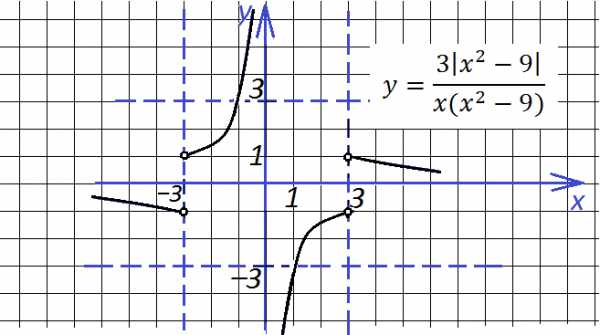
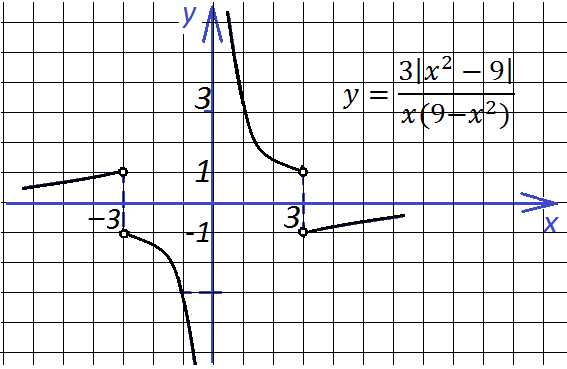
6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:

7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:

Первый:

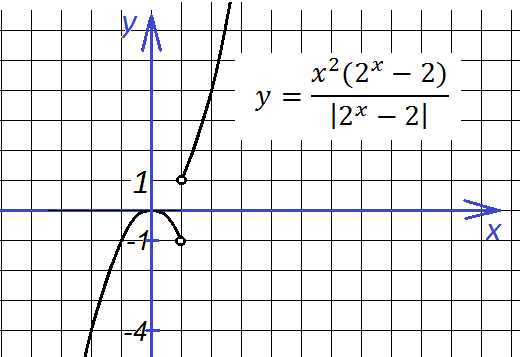
Второй:

 

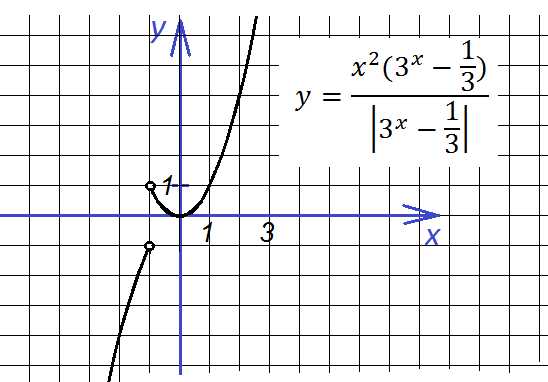
8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞)  так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

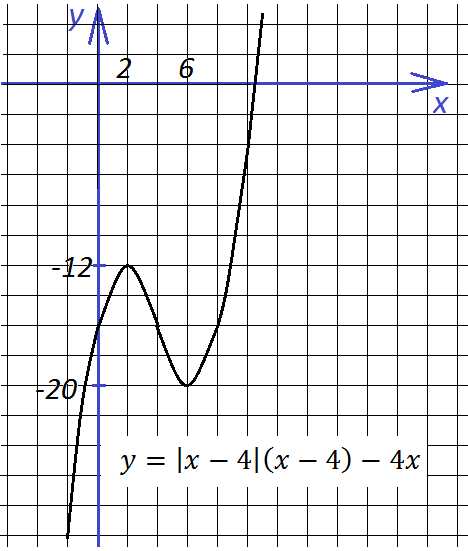
9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

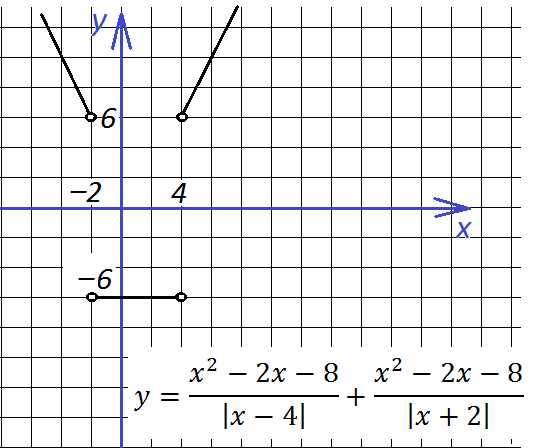
Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

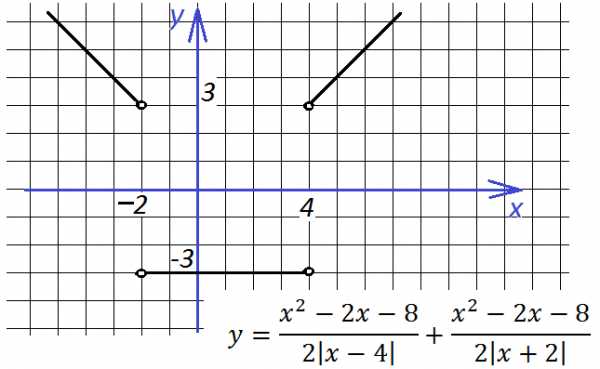
Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

10. Наконец, последний график мы построим для функции

Начнем построение с “базовой” для этого графика функции

она выглядит так:

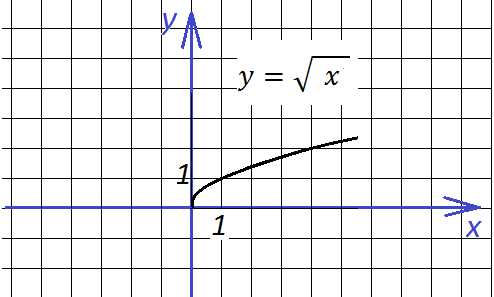
Далее добавим знак модуля под корень:

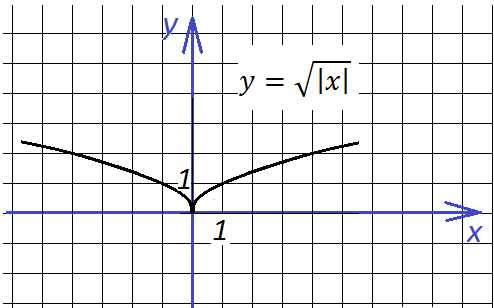
Теперь опустим этот график вниз на 4 единице по оси у:

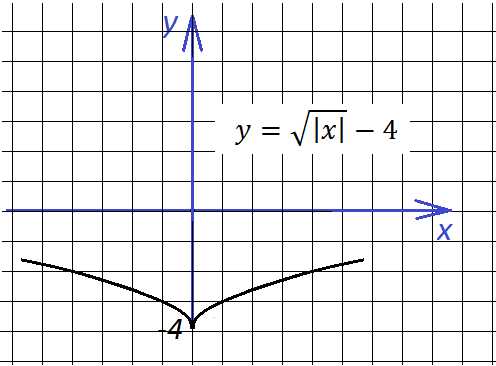
“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:

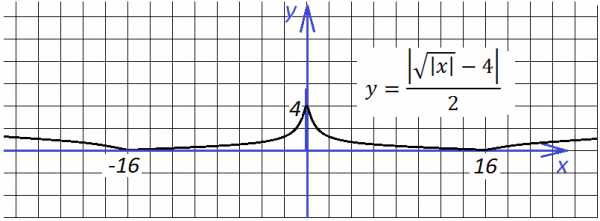
easy-physic.ru

Функция с модулем

Пример 1. Построить график функции y=||1-x²|-3|.
Построим график функции y=1-x² и применим к нему операцию «модуль» (часть графика, расположенная ниже оси OX симметрично отражается относительно оси OX).

Выполним сдвиг графика вниз на 3.

Применим операцию «модуль» и получим окончательный график функции y=||1-x²|-3|

Пример 2. Построить график функции y=||x²-2x|-3|.
В результате преобразования получаем y=|x²-2x|=|(x-1)²-1|. Построим график функции y=(x-1)²-1: строим параболу y=x² и выполняем сдвиг вправо на 1 и вниз на 1.

Применим к нему операцию «модуль» (часть графика, расположенная ниже оси OX симметрично отражается относительно оси OX).

Выполним сдвиг графика вниз на 3 и применим операцию «модуль», в результате получим окончательный график.

Пример 3. Построить график функции .
Чтобы раскрыть модуль, надо рассмотреть два случая:
1)x>0, тогда модуль раскроется со знаком «+» =
2)x=

Построим график для первого случая.

Отбросим часть графика, где x

Построим график для второго случая и аналогично отбросим часть, где x>0, в итоге получим.

Соединим два графика и получим окончательный.

Пример 4. Построить график функции .
Построим сначала график функции .Для этого удобно выделить целую часть, получим . Строя по таблице значений, получаем график.

Применим операцию модуль (часть графика, расположенная ниже оси OX симметрично отражается относительно оси OX). Получаем окончательный график

Пример 5. Построить график функции y=|-x²+6x-8|. Cначала упростим функцию до y=1-(x-3)² и построим её график

Теперь применим операцию «модуль» и отразим часть графика ниже оси OX, относительно оси OX

Пример 6. Построить график функции y=-x²+6|x|-8. Также упростим функцию до y=1-(x-3)² и построим её график

Теперь применим операцию «модуль» и отразим часть графика правее оси оY, в левую часть

Пример 7. Построить график функции . Построим график функции

Построим график функции

Выполним параллельный перенос на 3 единичных отрезка вправо и 2 вверх. График примет вид:

Применим операцию «модуль» и отразим часть графика правее прямой x=3 в левую полуплоскость.

Пример 8. Построить график функции . Построим график функции

Построим график функции

Построим график функции

Выполним параллельный перенос на 3 единичных отрезка вправо и 2 вверх. График примет вид:

Теперь применим операцию «модуль» и симметрично отразим часть графика правее оси OY

Пример 9. Построить график функции . Построим график функции из Примера 7,

Теперь применим операцию «модуль» ко всей функции

Пример 10. Построить график функции . Построим график функции из Примера 8,

Теперь применим операцию «модуль» ко всей функции

www.tofmal.ru

Методы построения графиков функций содержащих модуль

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (200,7 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Цель урока:

• повторить построение графиков функций содержащих знак модуля;
• познакомиться с новым методом построения графика линейно-кусочной функции;
• закрепить новый метод при решении задач.

Оборудование:

• мультимедиа проектор,
• плакаты.

Ход урока

Актуализация знаний

На экране слайд 1 из презентации.

Что является графиком функции y=|x| ? (слайд 2).

(совокупность биссектрис 1 и 2 координатных углов)

Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).

Рисунок 1

y=| x+3|

y=| x| +3

y=-2| x| -2

y=6-| x-5|

y=1/3| x-6| -3

Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x²-2x-3| (слайд 4)

Ученик: чтобы построить график данной функции нужно

— построить параболу y=x²-2x-3

— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)

Рисунок 2

Рисунок 3

Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x²-2|x|-3 (слайд 6).

Ученик: Чтобы построить график данной функции нужно:

— построить параболу.

— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)

Рисунок 4

Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x²-2|x|-3| (слайд 8).

Ученик: Чтобы построить график данной функции нужно:

— нужно построить параболу у=x²-2x-3

— строим у= x²-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ

— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)

Рисунок 5

Следующее задание выполняем письменно в тетрадях.

1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|

Ученик на доске с комментарием:

— находим нули подмодульных выражений х₁=-2, х₂=1, х₃=3

— разбиваем ось на промежутки

— для каждого промежутка запишем функцию

при х < -2, у=-х-4

при -2 х<1, у=х

при 1 х<3, у = 3х-2

при х 3, у = х+4

— строим график линейно-кусочной функции.

Мы с вами построили график функции используя определение модуля (слайд 10).

Рисунок 6

Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.

Метод вершин

Алгоритм:

1. Найдем нули каждого подмодульного выражения
2. Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
3. Нанесем точки на координатную плоскость и соединим последовательно

2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|

Учитель на доске, дети в тетрадях.

Метод вершин:

— найдем нули каждого подмодульного выражения;

— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа

х -3 -2 1 3 4

у -1 -2 1 7 8

— нанесем точки на координатную плоскость и соединим последовательно.

Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .

Рисунок 7

Каким же методом график получается быстрее и легче?

3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:

При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.

Следуем алгоритму; ученик на доске.

у=|х-2|-|х+1|

х₁=2, х₂=-1

у(-2)=4-1=3

у(-1)=3

у(2)=-3

у(3)=1-4=3, соединяем последовательно точки.

у_наиб = 3

4. Дополнительное задание

При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.

5. Домашняя работа

а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.

б) Построить график функции y=||x-1|-2|-3| .

16.02.2013

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

«Построение графика квадратной функции, содержащей модуль»

Разделы: Математика

---

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х²— 6x + 3.)

Цель.

• Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
• Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х² — 6х + 3. Найти нули функции.

Решение.

1. Направление “ветвей” параболы: если а = 1, а > 0, то “ветви” параболы направлены вверх.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

3. Уравнение оси симметрии: х = 3.

4. Нули функции: у(х) = 0, х² — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x _1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

Рис.1.

Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

Рис. 2.

2.у = |х| + 1. График функции на рисунке 3.

Рис.3.

3. у = |х + 1|. График функции рисунке 4.

Рис.4.

Вывод.

1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х² — 6|x| + 3,

б) у = |х² — 6х + 3|.

Решение.

а)

1.Построить график функции у = х²-6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

Рис.5.

б) 1. Построить график функции у = х² — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Рис. 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x² — 6|x| + 3|;

б) y = |x² — 6x + 3| — 3.

Решение.

а)

1. График функции у = х² + 6x + 3 отображаем относительно оси Оу, получается график функции у = х² — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Рис.7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

б)

1. График функции у = х² — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Рис.8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х² + 6x + 3 при х < 0 для точек у(0) = 3, у( — 1) = — 4.

График функции на рисунке 9.

Рис.9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х² + 6х + 3 при х 6.

1. Направление “ветвей” параболы: а = — 1, а < 0, “ветви” параболы направлены вниз.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х² — 6х + 3 при х = 7 у(7) = 10.

График на рис.10.

Рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Вид функции	Способ построения графика функции
1. у = f(|x|) 2. у = |f(x)| 3. у = |f(|x|)| 4. у = |f(x)| + a	1. Отобразить график функции у = f(x) симметрично относительно оси Оу. 2. Отобразить график функции у = f(x) симметрично относительно оси Ох. 3. Последовательно отобразить график функции у = f(x) симметрично относительно осей координат. 4. Параллельный перенос перенос графика функции у = |f(x)|на вектор {0;а}.

Группа 4.

Построить график функции:

а) у = х² — 5x + |x — 3|;

б) у = |x² — 5x| + x — 3.

Решение.

а) у = х² — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х² -6х + 3 при х 3,
затем график функции у = х² — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

Рис.11.

б) у = |х² — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.

График функции на рисунке 12.

Рис.12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х² — 5х + |x — 3||,

б) у= ||x² — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

 

Рис.13.

Рис. 14.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Рис.15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.

Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.

3. Задание на дом.

Построить графики функций с различным расположением модуля:

1. у = х² + 4х + 2;

2. у = — х² + 6х — 4.

4. Рефлексивно – оценочный этап.

1.Оценки за урок складываются из отметок:

а) за работу в группе;

б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Трудное ли домашнее задание?

Урок окончен.

11.11.2003

xn--i1abbnckbmcl9fb.xn--p1ai

Графики функций с модулем

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа

городского округа город Буй Костромской области

Графики функций

с модулем

Работу выполнила:

Торопова И.В. учитель математики

2004 г.

В курсе математики основной и средней школы незначительное место отводится построению графиков функций, аналитическое выражение которых содержит знак модуля. И поэтому учащиеся испытывают определённые затруднения при их построении.

Впервые с модулем числа учащиеся встречаются в курсе математики 6 класса, и больше не упоминается о нем до 9 класса, и немного заданий на построение графиков таких функций встречается в курсе алгебры и начала анализа 10 класса.

Поэтому, я считаю, что формировать навыки построения графиков функций, аналитическое выражение которых содержит знак модуля, можно начинать с учащимися 7 – 8 классов, проявляющими интерес к изучению математики на занятиях математического кружка или факультатива.

В 7 классе после изучения тем «Линейная функция» и « Прямая пропорциональность» стоит попробовать построить график функции y = |2х|.

Учащиеся уже хорошо умеют строить графики прямой пропорциональности и предварительно надо построить график функции

y = 2х, затем вспомнить с учащимися определение модуля числа и попросить их составить таблицу значений для функции y = |2х| (значения переменной х необходимо взять как положительные так и отрицательные), затем отметить полученные точки на координатной плоскости, соединить их и сравнить полученные графики, ответив на следующие вопросы:

а) Какие значения принимает функция y = |2х| при х≥0, х

б) чем сходны графики функций y = 2х и y = |2х|, чем различаются?

в) Можно ли получить график функции из графика функции y = 2х?
y = 2х y = |2х|

х	-3	-2	-1	0	1	2	3
y	-6	-4	-2	0	2	4	6

х	-3	-2	-1	0	1	2	3
y	6	4	2	0	2	4	6

Учащиеся заметят, что для построения графика функции y = |2х| можно построить график функции y = 2х, затем оставить без изменения часть графика при х≥0, а часть графика расположенную ниже оси х ( при х

Таких заданий можно подобрать много, а способные учащиеся вполне могут построить графики следующих функций: y = |х + 1|, y = |2х + 1|, используя выводы, полученные при построении графика функции y = |2х|.
y = | х + 1| y = |2х + 1|

В 8 классе учащиеся знакомятся с графиком обратной пропорциональности и продолжая формировать умения строить графики, сильным учащимся стоит

построить графики функций типа y = и y = , опираясь на знания, полученные при построении графиков функций, содержащих модуль

в 7 классе.

y = y =

В курсе алгебры 9 класса при изучении темы «Функция. Область определения и область значения функции» ребята знакомятся с графиком функции y = |х| , её областью определения и областью значения. Но заданий в учебнике под редакцией С.А. Теляковского с использованием функции

y = |х| нет, кроме №17 и то предлагаемого на дом. А вот в дидактических материалах для 9 класса авторов Ю.Н. Макарычева, Н.Г. Миндюка,

Л.М. Коротковой предлагаются задания из второго блока, способствующие развитию учащихся в алгоритмическом и логическом плане.

С-8 «График квадратичной функции»

Задание №6

Постройте график функции: а) y = |х| — 3 ; б) y = |х +3| .

y = |х| — 3 y = |х +3|

При построении данных графиков функций можно воспользоваться знаниями, полученными при преобразовании графиков функций y =aх²+n c одной стороны , т. е. график функции y = |х| — 3 можно получить из графика

y = |х| с помощью параллельного переноса вдоль оси Оy на три единицы масштаба вниз, а график функции y = |х +3| из графика функции y = |х| с помощью параллельного переноса вдоль оси Ох на три единицы масштаба влево. Затем сильных учащихся попросить сделать вывод о построении графиков функций вида y = |х| + n ; y = |х — m|.

n>0
y = |х — m| y = |х| + n

m

n

m>0

А с другой стороны (возможно учащиеся и этот способ вспомнят, который чаще всего и используется) построить график функции y = |х — m| можно из графика функции y = х – m , оставив без изменения все части графика, которые лежат выше оси абсцисс, а части расположенные ниже её отобразить симметрично.

С-14 «Графический способ решения систем уравнений» предлагается задание №5, также из второго блока.

Решите графически систему уравнений:

а) y =х² – 3

y = |х|
Ответ: (≈ -2,3; ≈2,3) (≈ 2,3; ≈2,3)

Учащиеся легко с этим заданием справляются, поэтому можно предложить

ёще ряд аналогичных заданий.

Задание: Изобразив схематически графики, выясните, имеет ли решение система уравнений и если имеет, то сколько:

а) y = х² – 3 б) y = х² – 3 в) y = х² – 3 г) y = х² – 3 д) y = х² – 3

y = |х| — 3 y = -|х| y = 4 — |х| y = -|х| — 3 y =-|х| — 4

(3 решения) (2 решения) (2 решения) (1 решение) (нет решения)

Решение.

а)

Отработав навыки построения графика квадратичной функции сильные учащиеся могут попробовать построить графики следующих функций:

а) y = |х²— 1|

Для построения достаточно сначала построить график функции y = х²— 1 , а на интервале (-1; 1) часть графика отобразить симметрично относительно оси абсцисс, остальную часть оставить без изменения.

Аналогичных заданий можно

подобрать достаточно много,

но после их выполнения необходимо

с учащимися сделать вывод о

построении графиков функций

вида y = |f(х)|.

Здесь же надо рассмотреть построение графиков функций вида y = f(|х|). т.е. графики функций содержащие модуль аргумента.

б) y = После его построения учащиеся заметят,

что данный график получается из графика

функции y =путем симметрии относительно уже оси Оy . Необходимо еще раз обратить внимание учащихся, что под знаком модуля находится аргумент и вновь сделать выводы.
в) y = х² — 6|х| + 4

Некоторые учащиеся заметят, что под знаком модуля стоит аргумент, учитывая что х² =|х|², тогда достаточно будет построить график функции для х≥0, а затем полученную кривую отобразить относительно оси у.

И закончить рассмотрение графиков функций в 9 классе, аналитическое выражение которых содержит знак модуля построением графиков вида

y = |f(|х|)|.

Предложить учащимся построить графики следующих функций:

а) y = |х| ; б) y = |х| — 1; в) y = | |х| — 1|.

Задания а) и б) легко учащиеся выполнят, но их выполнение должно натолкнуть их на мысль, что построение графика функции под в) следует выполнять поэтапно: строим график функции y = |х|, затем выполнить параллельный перенос вдоль оси Оу на одну единицу масштаба вниз и наконец, часть графика расположенного под осью Ох симметрично отобразить относительно её.

а) б) в)

Тренировочные упражнения:

а) y = | |2х|-3 | б) y = | 3|х| + 1| в) y =| х² — 4|х| + 3 |

г) y = |х| + х д) y = 2|х| + х е) y =+ 3

Вывод: Для построения графика функции y = |f(|х|)| надо построить график функции y = f(|х|), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс, а части, расположенные ниже её, отобразить симметрично относительно этой оси.

Такая работа с графиками закрепит знания учащихся о модуле числа и даст неплохие навыки для их построения.

В 10-11 классах эту работу следует продолжить, т.к. учащиеся основательно знакомятся со свойствами функций и их исследованием.

В 10 классе большое место отводится изучению тригонометрических функций и, конечно же, их графикам. Здесь можно такие задания:

1. Построить графики функций у = cos|x| и у = |cosx|.

Решение.

а)у = cos|x|, cos|x| = cosx, т.к. cos x = cos(-x). Следовательно, график данной функции тот же, что и график функции у = cosx;
б) у=- |cosx|, при cos x ≥ 0 у = cos x. Следовательно, на участке, где
cos x ≥ 0, график будет тот же, что и график функции у = cosx. При cos x у = — cosx. Следовательно, части графика функции у = cos x, расположенные
ниже оси абсцисс, зеркально отобразятся и будут расположены в верхней
полуплоскости.

2. Построить графики функций у = sin[x| и у = |sin x |.

Решение.

Чтобы построить график у = sin|x|, надо построить сначала график

у = sin х при х > 0, а затем построить кривую, симметричную с построенным графи­ком относительно оси ординат.

3. Построить график функции у = sin х + |sin х |.

4. Построить график функции у =tg|x|.

Решение.

Функция чётная, так как tg|-x| = tg|x|. При х > 0 график искомой функции тот же, что и график функции у = tg x.

5. Построить график функции у = |tgx|.

Решение.

Часть графика функции у = tgx, расположенную в верхней полуплоско­сти, оставить без изменений, а часть графика, расположенную в нижней полуплоскости, зеркально отобразить относительно оси ОХ.

В теме «Функции и их графики» при изучении нового материала и говоря о преобразовании графиков вновь вспомнить и о графиках функции у = |f(х)| и y = f(|х|):

а) график у = |f(х)| функции получается из графика функции у = f(х) сле­дующим образом: часть графика у = f(х), лежащая над осью Ох, сохраняет­ся, часть его, лежащая под осью Ох, отображается симметрично относи­тельно оси Ох:

б) график функции y = f(|х|) получается из графика функции у = f(х) так: при х≥0 график у = f(х) сохраняется, а при х 0 полученная часть графика отображается симметрично относительно оси Oу:

На следующем уроке рассмотреть построение нескольких таких графиков функций.

а) построить графики функций:

б) построить график функции у = |х-1| + |х+3|.

Решение.

Находим значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль: х — 1 = 0 или х + 3 = 0;

х= 1 или х = -3.

1) при х = -х+ 1-х-3 =-2х-2; у = -2х-2;

2) при -3= -х+ 1 +х + 3 = 4; у = 4;

3) при х>1, у = х-1+х + 3=2х + 2; у= 2х + 2.

В теме «Исследование функций» в учебнике «Алгебра и начала анализа» для учащихся 10-11 классов Колмогорова А.Н. включены функции, содержащие знак модуля, но таких заданий всего два — это №99(а, в), №55(а).

В качестве дополнительного задания на исследования тригонометрических функций сильным учащимся предложить построить график функции

у = 2 – sin| х+|

Решение.

1 способ. Строим график функции у = —sin|х|

Ось ординат переносим на +, а ось абсцисс — на -2.

2 способ. График имеет две ветви, уравнения которых различны.

1) если х+≥ 0, то есть х≥-, то у = 2 – sin( х+).

2) если х+0, то есть х, то у = 2 – sin( -(х+))= 2+ sin( х+).

Область определения функции — вся числовая прямая.

Область значения функции определим из условия -1≤– sin| х+|≤1

-1+2≤ у ≤ 1+2

1≤ у ≤3

Общая точка обеих ветвей графика: х= -; у=- sin| 0|+2=2: точка (-; 2).

Можно учащимся, конечно, предложить построить и исследовать графики таких функций, как у= arcsin| x| , у= arcsin| x-1|, у=arccos| x|, у= arctg| x|, но с этим заданием справятся только сильные учащиеся или проявляющие интерес к данной теме.

И закончить построение таких графиков функций в 11 классе рассмотрением графиков показательной и логарифмической функций типа:

у = 2^{| x|} у =| log _аx |

График функции у = 2^{x при х≥0 Строим график функции у = log _аx.}

И его зеркальное отображение На интервале (0;1) у = log _аx 0

относительно оси Оу дадут в (кривая расположена под осью Ох)

совокупности график заданной эта часть графика функции симмет

функции. рично отобразится относительно

оси Ох, а остальная часть останется

без изменения.

у = 2^{| x-1|} у = log | x |^|у = |log | x ||

Литература
1. Афанасьева Т.Л., Тапилина Л.А. Алгебра 10 класс (поурочные планы).- Волгоград . -2002. С.13-45.

2. Вирченко Н.А., Ляшко И.И., Швецов К.И. Графики функций: Справочник. –Киев: Наукова думка. -1979. — С.100-107.

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10-11 класса средней школы. – М.: Просвещение, 1990. – С. 47-54.
4. Макарычев Ю.Н. и др. Дидактические материалы по алгебре для 9 класса. – 5-е изд. – М.: Просвещение, 2000. – С. 10-19. 0>

www.megdu.ru

Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»

Разделы: Математика

---

“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”

Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.

Ход урока

I. Вводное слово учителя

Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х² математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.

Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.

Модуль и квадратичная функция

Построение графиков функций:

1. Y = АХ² + ВX + C,
2. Y = АХ² + ВX + C ,
3. Y = АХ² + ВХ + С

II. Устная работа

1) Дать определение модуля числа Х

2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).

3) Найти на рисунке график функции Y = –Х² + 4Х – 3.

4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?

5) Вспомнить, как построить график функции Y = Х

По определению модуля

График функции Y = Х симметричен относительно оси У.

III. Построение графиков функций:

Y = АХ² + ВX + C,

Y = АХ² + ВX + C,

Y = АХ² + ВХ + С

Работа проводится в группах, т.к. графики в К–1 в) и К–3 в) одинаковы, их необходимо сравнить и сделать вывод (всего 3 группы). Каждой группе выдается карточка, в ней 3 задания. Учащиеся должны построить графики квадратичной функции, содержащей модуль, используя определение модуля и сделать вывод: как построить график данной функции, используя график квадратичной функции и симметрию относительно осей координат.

Работа в группах.

Задание: построить график функции, используя:

а) определение модуля;
б) график функции Y = АХ² + ВХ + С;
в) симметрию относительно осей координат.

а) Y = Х² – 4 Х + 3
б) Y = Х² – 4 Х + 3
в) Y = Х² – 4 Х + 3

а) Y = Х² + 2 Х – 3
б) Y = Х² + 2 Х – 3
в) Y = Х² + 2 Х – 3

а) Y = –Х² + 4 Х – 3
б) Y = –Х² + 4 Х – 3
в) Y = –Х² + 4 Х – 3

IV. Учащиеся делают вывод о расположении графиков указанных функций

Вопрос: а) Как построить график функции Y = f (X)?

(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х< 0.
2 способ. Построить график функции Y = f (X) и отобразить правую часть графика симметрично относительно оси Y).

б) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).

в) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)

г) Почему графики функций Y = –Х² + 4X – 3 и Y = Х² – 4X + 3 одинаковы?

(Так как А = А , –А = А)

V.

У рассмотренных функций под знаком модуля была независимая переменная. Теперь рассмотрим функции, где под знаком модуля стоит либо сама функция, либо и функция, и независимая переменная одновременно, т.е. зависимости вида

Y = АХ² + ВX+ C и Y = АХ² + ВX + C

Приведем конкретные примеры.

а) Y = Х² – 4X+ 3

По определению

Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х² – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.

б) Y = Х² – 4X+ 3

Сначала строим график функции Y = Х² – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х² – 4X+ 3 , т.е. график функции Y = Х² – 4X+ 3 отображаем относительно оси Х.

VI. Творческое задание

Дана функция Y = Х² + 2X– 3

Выполнить всевозможные преобразования данной квадратичной функции с модулем.

10.03.2005

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai