Тест №2
2.1. Как называются разделы, на которые делится гидравлика?
а) гидростатика и гидромеханика;
б) гидромеханика и гидродинамика;
в) гидростатика и гидродинамика;
г) гидрология и гидромеханика.
2.2. Раздел гидравлики, в котором рассматриваются законы равновесия жидкости называется
а) гидростатика;
б) гидродинамика;
в) гидромеханика;
г) гидравлическая теория равновесия.
2.3. Гидростатическое давление — это давление присутствующее
а) в движущейся жидкости;
б) в покоящейся жидкости;
в) в жидкости, находящейся под избыточным давлением;
г) в жидкости, помещенной в резервуар.
2.4. Какие частицы жидкости испытывают наибольшее напряжение сжатия от действия гидростатического давления?
а) находящиеся на дне резервуара;
б) находящиеся на свободной поверхности;
в) находящиеся у боковых стенок резервуара;
г) находящиеся в центре тяжести рассматриваемого объема жидкости.
2.5. Среднее гидростатическое давление, действующее на дно резервуара равно
а) произведению глубины резервуара на площадь его дна и плотность;
б) произведению веса жидкости на глубину резервуара;
в) отношению объема жидкости к ее плоскости;
г) отношению веса жидкости к площади дна резервуара.
2.6. Первое свойство гидростатического давления гласит
а) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует от рассматриваемого объема;
б) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема;
г) гидростатическое давление неизменно во всех направлениях и всегда перпендикулярно в точке его приложения к выделенному объему.
2. 7. Второе свойство гидростатического давления гласит
7. Второе свойство гидростатического давления гласит
а) гидростатическое давление постоянно и всегда перпендикулярно к стенкам резервуара;
б) гидростатическое давление изменяется при изменении местоположения точки;
в) гидростатическое давление неизменно в горизонтальной плоскости;
2.8. Третье свойство гидростатического давления гласит
а) гидростатическое давление в любой точке не зависит от ее координат в пространстве;
б) гидростатическое давление в точке зависит от ее координат в пространстве;
в) гидростатическое давление зависит от плотности жидкости;
г) гидростатическое давление всегда превышает давление, действующее на свободную поверхность жидкости.
2.9. Уравнение, позволяющее найти гидростатическое давление в любой точке рассматриваемого объема называется
а) основным уравнением гидростатики;
в) основным уравнением гидромеханики;
г) основным уравнением гидродинамической теории.

2.10. Основное уравнение гидростатики позволяет
а) определять давление, действующее на свободную поверхность;
б) определять давление на дне резервуара;
в) определять давление в любой точке рассматриваемого объема;
г) определять давление, действующее на погруженное в жидкость тело.
2.11. Среднее гидростатическое давление, действующее на дно резервуара определяется по формуле
2.12. Основное уравнение гидростатического давления записывается в виде
2.13. Основное уравнение гидростатики определяется
а) произведением давления газа над свободной поверхностью к площади свободной поверхности;
б) разностью давления на внешней поверхности и на дне сосуда;
в) суммой давления на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев;
г) отношением рассматриваемого объема жидкости к плотности и глубине погружения точки.
2.14. Чему равно гидростатическое давление при глубине погружения точки, равной нулю
а) давлению над свободной поверхностью;
б) произведению объема жидкости на ее плотность;
в) разности давлений на дне резервуара и на его поверхности;
2.15. «Давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково»
а) это — закон Ньютона;
б) это — закон Паскаля;
в) это — закон Никурадзе;
г) это — закон Жуковского.
2.16. Закон Паскаля гласит
а) давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково;
б) давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям согласно основному уравнению гидростатики;
г) давление, приложенное к внешней поверхности жидкости равно сумме давлений, приложенных с других сторон рассматриваемого объема жидкости.
2.17. Поверхность уровня — это
а) поверхность, во всех точках которой давление изменяется по одинаковому закону;
б) поверхность, во всех точках которой давление одинаково;
в) поверхность, во всех точках которой давление увеличивается прямо пропорционально удалению от свободной поверхности;
г) свободная поверхность, образующаяся на границе раздела воздушной и жидкой сред при относительном покое жидкости.
2.18. Чему равно гидростатическое давление в точке А ?
а) 19,62 кПа;
б) 31,43 кПа;
в) 21,62 кПа;
г) 103 кПа.
2.19. Как приложена равнодействующая гидростатического давления относительно центра тяжести прямоугольной боковой стенки резервуара?
а) ниже;
б) выше;
в) совпадает с центром тяжести;
г) смещена в сторону.
2.20. Равнодействующая гидростатического давления в резервуарах с плоской наклонной стенкой равна
2.21. Точка приложения равнодействующей гидростатического давления лежит ниже центра тяжести плоской боковой поверхности резервуара на расстоянии
2.22. Сила гидростатического давления на цилиндрическую боковую поверхность по оси Оx равна
2.23. Сила гидростатического давления на цилиндрическую боковую поверхность по оси Oz равна
2.24. Равнодействующая гидростатического давления на цилиндрическую боковую поверхность равна
2. 25. Сила, действующая со стороны жидкости на погруженное в нее тело равна
25. Сила, действующая со стороны жидкости на погруженное в нее тело равна
2.26. Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется
а) устойчивостью;
б) остойчивостью;
в) плавучестью;
г) непотопляемостью.
2.27. Укажите на рисунке местоположение центра водоизмещения
а) 1;
б) 2;
в) 3;
г) 4.
2.28. Укажите на рисунке метацентрическую высоту
а) 1;
б) 2;
в) 3;
г) 4.
2.29. Для однородного тела, плавающего на поверхности справедливо соотношение
2.30. Вес жидкости, взятой в объеме погруженной части судна называется
а) погруженным объемом;
б) водоизмещением;
г) водопоглощением.
2.31. Водоизмещение — это
а) объем жидкости, вытесняемый судном при полном погружении;
б) вес жидкости, взятой в объеме судна;
в) максимальный объем жидкости, вытесняемый плавающим судном;
г) вес жидкости, взятой в объеме погруженной части судна.
2.32. Укажите на рисунке местоположение метацентра
а) 1;
б) 2;
в) 3;
г) 4.
2.33. Если судно возвращается в исходное положение после действия опрокидывающей силы, метацентрическая высота
а) имеет положительное значение;
в) равна нулю;
г) увеличивается в процессе возвращения судна в исходное положение.
2.34. Если судно после воздействия опрокидывающей силы продолжает дальнейшее опрокидывание, то метацентрическая высота
а) имеет положительное значение;
б) имеет отрицательное значение;
в) равна нулю;
г) уменьшается в процессе возвращения судна в исходное положение.
2.35. Если судно после воздействия опрокидывающей силы не возвращается в исходное положение и не продолжает опрокидываться, то метацентрическая высота
а) имеет положительное значение;
б) имеет отрицательное значение;
в) равна нулю;

2.36. По какому критерию определяется способность плавающего тела изменять свое дальнейшее положение после опрокидывающего воздействия
а) по метацентрической высоте;
б) по водоизмещению;
в) по остойчивости;
г) по оси плавания.
2.37. Проведенная через объем жидкости поверхность, во всех точках которой давление одинаково, называется
а) свободной поверхностью;
б) поверхностью уровня;
в) поверхностью покоя;
г) статической поверхностью.
2.38. Относительным покоем жидкости называется
а) равновесие жидкости при постоянном значении действующих на нее сил тяжести и инерции;
б) равновесие жидкости при переменном значении действующих на нее сил тяжести и инерции;
в) равновесие жидкости при неизменной силе тяжести и изменяющейся силе инерции;
г) равновесие жидкости только при неизменной силе тяжести.
2.39. Как изменится угол наклона свободной поверхности в цистерне, двигающейся с постоянным ускорением
а) свободная поверхность примет форму параболы;
б) будет изменяться;
в) свободная поверхность будет горизонтальна;
г) не изменится.
2.40. Во вращающемся цилиндрическом сосуде свободная поверхность имеет форму
а) параболы;
б) гиперболы;
в) конуса;
г) свободная поверхность горизонтальна.
2.41. При увеличении угловой скорости вращения цилиндрического сосуда с жидкостью, действующие на жидкость силы изменяются следующим образом
а) центробежная сила и сила тяжести уменьшаются;
б) центробежная сила увеличивается, сила тяжести остается неизменной;
в) центробежная сила остается неизменной, сила тяжести увеличивается;
г) центробежная сила и сила тяжести не изменяются.
Повторить тему
Ключи к тестам
Наверх страницы
Основы стереозрения / Хабр
В данной статье содержатся базовые сведения о математическом аппарате, используемом в стерео зрении. Идея ее написания появилась после того как я начал работать с методами стерео зрения, в частности использовать алгоритмы реализованные в OpenCV. Эти алгоритмы зачастую ссылаются на различные понятия, такие как «фундаментальная матрица», «эпиполярная геометрия», «триангуляция». Существуют очень хорошие книжки по компьютерному зрению, в которых описывается, в том числе и стерео зрение и все необходимые понятия, но в них, нередко, бывает представлено слишком много информации для новичка. Здесь же, в краткой форме изложены базовые сведения о том, как работает стерео зрение и основные связанные с ним необходимые понятия:
Эти алгоритмы зачастую ссылаются на различные понятия, такие как «фундаментальная матрица», «эпиполярная геометрия», «триангуляция». Существуют очень хорошие книжки по компьютерному зрению, в которых описывается, в том числе и стерео зрение и все необходимые понятия, но в них, нередко, бывает представлено слишком много информации для новичка. Здесь же, в краткой форме изложены базовые сведения о том, как работает стерео зрение и основные связанные с ним необходимые понятия:
- проективная геометрия и однородные координаты
- модель камеры
- эпиполярная геометрия (epiporal geomerty), фундаментальная и существенная матрицы (fundamental matrix, essential matrix)
- триангуляция стереопары точек
- карта глубины(depth map), карта смещений(disparity map) и идея, лежащая в основе ее вычисления
Практически весь материал статьи основан на книге «Multiple View Geometry in Computer Vision» by Hartley, R. I. and Zisserman, A., а раздел про построение карты глубины описан на основе материала из «Learning OpenCV» by Gary Bradski, Adrian Kaehler.
I. and Zisserman, A., а раздел про построение карты глубины описан на основе материала из «Learning OpenCV» by Gary Bradski, Adrian Kaehler.
Для понимания содержимого статьи достаточно иметь общее представление об аналитической геометрии и линейной алгебре: знать, что такое матрица, вектор, скалярное и векторное произведение.
В геометрии стерео зрения значительную роль играет проективная геометрия. К проективной геометрии есть несколько подходов: геометрический (подобно Евклидовой геометрии ввести понятие геометрических объектов, аксиом и из этого выводить все свойства проективного пространства), аналитический (рассматривать все в координатах, как в аналитическом подходе к Евклидовой геометрии), алгебраический.
Для дальнейшего изложения в основном понадобиться понимание аналитического подхода к проективной геометрии, и именно он и изложен ниже.
Точки проективной плоскости. Рассмотрим двухмерное проективное пространство (которое еще называется проективной плоскостью). В то время как на обычной Евклидовой плоскости точки описываются парой координат (x,y)T, на проективной плоскости точки описываются трехкомпонентным вектором (x,y,w)T. При этом для любого ненулевого числа a, векторы (x,y,w)T и (ax, ay, aw)T соответствуют одной и той же точке. А нулевой вектор (0,0,0)T не соответствует никакой точке и выкидывается из рассмотрения. Такое описание точек плоскости называется однородными координатами (homogeneous coordinates).
В то время как на обычной Евклидовой плоскости точки описываются парой координат (x,y)T, на проективной плоскости точки описываются трехкомпонентным вектором (x,y,w)T. При этом для любого ненулевого числа a, векторы (x,y,w)T и (ax, ay, aw)T соответствуют одной и той же точке. А нулевой вектор (0,0,0)T не соответствует никакой точке и выкидывается из рассмотрения. Такое описание точек плоскости называется однородными координатами (homogeneous coordinates).
Точкам проективной плоскости можно сопоставить точки обычной Евклидовой плоскости. Координатному вектору (x,y,w)T при w 0 сопоставим точку Евклидовой плоскости с координатами (x/w, y/w)T. Если же w = 0, т.е. координатный вектор имеет вид (x, y, 0T), то будем говорить, что эта точка в бесконечности. Таким образом, проективную плоскость можно рассматривать как Евклидовую плоскость, дополненную точками из бесконечности.
Таким образом, проективную плоскость можно рассматривать как Евклидовую плоскость, дополненную точками из бесконечности.
Перейти от однородных координат (x, y, w)T к обычным Евклидовым можно путем деления координатного вектора на последнюю компоненту и последующего ее отбрасывания (x,y,w)T (x/w,y/w)T. А от Евклидовых координат (x,y)T перейти к однородным можно за счет дополнения координатного вектора единичкой: (x,y)T (x,y,1)T
Прямые на проективной плоскости. Любая прямая на проективной плоскости описывается, подобно точке, трехкомпонентным вектором l = (a,b,c)T. Опять же вектор, описывающий прямую, определен с точностью до ненулевого множителя. При этом уравнение прямой будет иметь вид: lTx = 0.
В случае, когда a2 + b2 0 мы имеем аналог обычной прямой ax + by + c = 0. А вектор (0,0,w) соответствует прямой лежащей в бесконечности.
Трехмерное проективное пространство. По аналогии с проективной плоскостью, точки трехмерного проективного пространства определяются четырехкомпонентным вектором однородных координат (x,y,z,w)T. Опять же для любого ненулевого числа a, координатные вектора (x,y,z,w)T и (ax,ay,az,aw)T соответствуют одной и той же точке.
Как в случае проективной плоскости, между точками трехмерного Евклидова пространства и трехмерного проективного пространства можно установить соответствие. Вектору однородных координат (x,y,z,w)T при w 0 соответствует точка Евклодова пространства с координатами (x/w,y/w,z/w)T. А про точку с вектором однородных координат вида (x,y,z,0)T говорят, что она лежит в бесконечности.
А про точку с вектором однородных координат вида (x,y,z,0)T говорят, что она лежит в бесконечности.
Проективное преобразование. Еще одна вещь, которая потребуется для дальнейшего изложения — это проективные преобразования (homography, projective transformation — в англ. литературе). С геометрической точки зрения, проективное преобразование — это обратимое преобразование проективной плоскости (или пространства), которое переводит прямые в прямые. В координатах, проективное преобразование выражается в виде невырожденной квадратной матрицы H, при этом координатный вектор x переходит в координатный вектор x‘ по следующей формуле: x‘ = H x.
Рисунок 1: Модель камеры. C — центр камеры, Cp — главная ось камеры. Точка X трехмерного пространства проецируется в точку x — на плоскости изображения.
Современные CCD-камеры хорошо описываются с помощью следующей модели, называемой проективной камерой (projective camera, pinhole camera). Проективная камера определяется центром камеры, главной осью — лучом начинающимся в центре камеры и направленным туда, куда камера смотрит, плоскостью изображения — плоскостью на которую выполняется проецирование точек, и системой координат на этой плоскости. В такой модели, произвольная точка пространства X проецируется на плоскость изображения в точку x лежащую на отрезке CX, который соединяет центр камеры C с исходной точкой X (см. рис. 1).
Проективная камера определяется центром камеры, главной осью — лучом начинающимся в центре камеры и направленным туда, куда камера смотрит, плоскостью изображения — плоскостью на которую выполняется проецирование точек, и системой координат на этой плоскости. В такой модели, произвольная точка пространства X проецируется на плоскость изображения в точку x лежащую на отрезке CX, который соединяет центр камеры C с исходной точкой X (см. рис. 1).
Формула проецирования имеет простую математическую запись в однородных координатах:
x = P X
где X — однородные координаты точки пространства, x — однородные координаты точки плоскости, P — матрица камеры размера 3 4.
Матрица P выражается следующим образом P = KR[ I | —c] = K[R|t], где K — верхняя треугольная матрица внутренних параметров камеры размера 3 3 (конкретный вид приведен ниже), R — ортогональная матрица размера 3 3, определяющая поворот камеры относительно глобальной системы координат, I — единичная матрица размера 3 3, вектор c — координаты центра камеры, а t = Rc.
Стоит отметить, что матрица камеры определена с точностью до постоянного ненулевого множителя, который не изменит результатов проецирования точек по формуле x = P X. Однако этот постоянный множитель обычно выбирается так, что бы матрица камеры имела вышеописанный вид.
В самом простейшем случае, когда центр камеры лежит в начале координат, главная ось камеры сонаправлена оси Cz, оси координат на плоскости камеры имеют одинаковый масштаб (что эквивалентно квадратным пикселям), а центр изображения имеет нулевые координаты, матрица камеры будет равна P = K[I|0], где
У реальных CCD камер пикселы обычно незначительно отличаются от квадратных, а центр изображения имеет ненулевые координаты. В таком случае матрица внутренних параметров примет вид:
Коэффициенты f, x, y — называются фокусными расстояниями камеры (соответственно общим и вдоль осей x и y).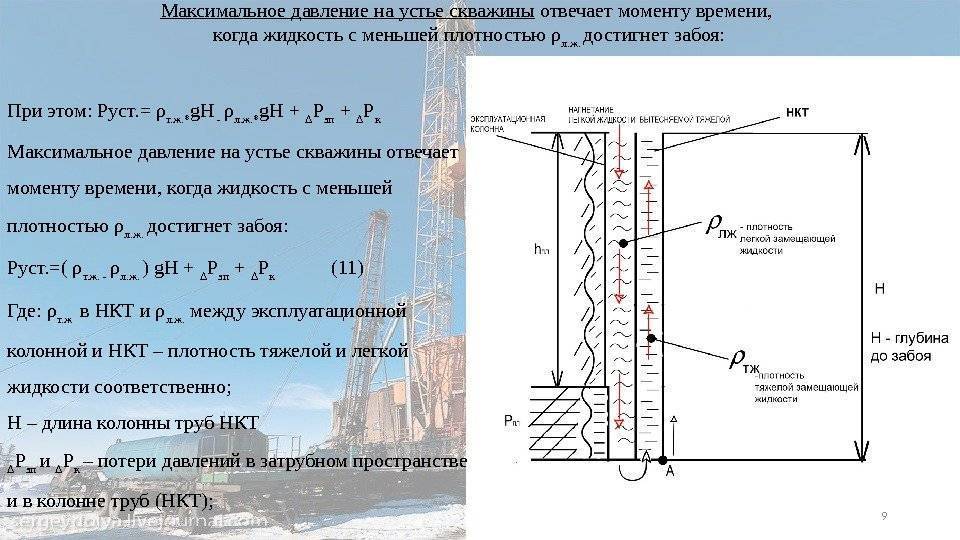
Помимо этого, в силу неидеальности оптики, на изображениях, полученных с камер, присутствуют искажения-дисторсии (distortion). Данные искажения имеют нелинейную математическую запись:
где k1, k2, p1, p2, k3 — коэффициенты дисторсии, являющиеся параметрами оптической системы; r2 = x‘2 + y‘2; (x‘, y‘) — координаты проекции точки относительно центра изображения при квадратных пикселях и отсутствии искажений; (x
Что такое измерение в математике? Определение, типы, формы, примеры
Определение
Размеры в математике — это мера размера или расстояния объекта, области или пространства в одном направлении. Проще говоря, это измерение длины, ширины и высоты чего-либо.
Размеры обычно выражаются следующим образом:
- Длина
- Ширина
- Ширина
- Высота или глубина
Типы фигур в зависимости от размеров
В зависимости от количества измерений, представленных на рисунке, его можно классифицировать на:
- Нуль-размерный
- Одномерный
- Двухмерный
- Трехмерный
- Нульмерный
Точка является нульмерным объектом, так как не имеет ни длины, ни ширины, ни высоты. У него нет размера. Он говорит только о местоположении.
У него нет размера. Он говорит только о местоположении.
- Одномерный
Для одномерной фигуры возможно только одно измерение. Отрезок линии, нарисованный на поверхности, является одномерным объектом, поскольку он имеет только длину и не имеет ширины.
- Две – размерные
Двумерные фигуры или объекты в геометрии представляют собой плоские плоские фигуры, имеющие два измерения – длину и ширину. Двумерные или двумерные формы не имеют толщины и могут быть измерены только с двух граней.
Квадрат, круг, прямоугольник и треугольник являются примерами двухмерных объектов. Мы можем классифицировать фигуры на основе их размеров.
Два измерения отмечены на двумерном графике с двумя осями: x и y. Ось x перпендикулярна или под углом 90° к оси y.
- Трехмерный
В геометрии трехмерные фигуры — это объемные фигуры или объекты или формы, имеющие три измерения — длину, ширину и высоту. В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.
В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.
Куб и прямоугольный параллелепипед являются примерами трехмерных объектов, поскольку они имеют длину, ширину и высоту.
Возьмем, к примеру, прямоугольный параллелепипед.
Атрибутами прямоугольного параллелепипеда являются грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.
Некоторые примеры трехмерных фигур:
Когда на графике отмечены три измерения, трехмерный график имеет три оси, а именно x, y и z. Каждая ось перпендикулярна или на 90° к другому.
Решаемые примеры О размерахВопрос 1: Сколько измерений имеет данная фигура?
Ответ: Фигура представляет собой кривую линию, проведенную из одной точки в другую и имеющую только одно измерение — длину.
Вопрос 2: Сколько измерений имеет данная фигура?
Ответ: Это точка или точка. Он вообще не имеет измерения, ни длины, ни ширины, ни ширины.
Он вообще не имеет измерения, ни длины, ни ширины, ни ширины.
Вопрос 3: Сколько измерений имеет шкала?
Ответ: Шкала имеет длину, ширину и толщину. Поэтому его можно назвать трехмерным.
Вопрос 4: Сколько размеров имеет цилиндрическое ведро для воды?
Ответ: Цилиндрический ковш имеет высоту, глубину и ширину. Таким образом, это трехмерная фигура.
Практические задачи на измерениях
1
Сколько измерений у объекта?
1
2
3
4
Правильный ответ: 3
Кубик Рубикса имеет длину, ширину и ширину. Он трехмерный.
2
Сколько измерений имеет данная фигура?
1
2
3
Правильный ответ: 2
Фигура представляет собой круг, длина и ширина которого измеряются между двумя точками на окружности.
3
Каков размерный тип объекта, который имеет только длину?
Один
Два
Три
Четыре
Правильный ответ: Один
Объект, имеющий только одно измерение, является одномерным.
4
Сколько размеров у ноутбука?
Ноль
Один
Два
Три
Правильный ответ: Три
Блокнот имеет длину, ширину и ширину. Итак, он трехмерный.
Заключение
Размеры обозначают размеры предмета или фигуры. Узнайте больше с SplashLearn , игровая платформа, которая делает математику, особенно геометрию, увлекательной с помощью различных игр и рабочих листов. Родители могут помочь своим детям легко учиться с помощью инновационных математических игр, которые легко решить и легко освоить.
Часто задаваемые вопросы о размерах
Что такое трехмерный квадрат?
Куб — это квадрат, нарисованный в трехмерном виде. У квадрата есть только длина и ширина, а у куба есть длина, ширина и ширина.
Как это называется, когда объект вообще не имеет размеров?
Это нульмерная фигура, и она не может быть объектом. Это просто точка на поверхности без измерения длины или ширины.
Это просто точка на поверхности без измерения длины или ширины.
Как можно выразить размеры вашей комнаты?
Комната представляет собой трехмерную структуру. Он должен иметь:
- Длина, измеренная по полу
- Высота от пола до потолка
- Ширина, измеренная по полу рядом с длиной.
Конспект лекций по восприятию: глубина, размер и форма
Конспект лекций по восприятию: глубина, размер и формаЧто нужно знать об этой лекции
- Бинокулярные признаки (вергенция, несоответствие)
- Бинокулярная диспарантность, скрещенная и нескрещенная диспарантность, зависимость от глубины и расстояния, гороптеры
- стереоскоп, стереограмма
- Стереограмма со случайными точками и проблема соответствия
- слияние, подавление, диплопия, бинокулярное соперничество
- несоответствие селективности бинокулярных нейронов в V1
- бинокулярное соперничество и нейронные корреляты зрительного восприятия
- Графические признаки глубины (текстура, затенение, перспектива и т.
 д.)
д.) - Постоянство размера
- Монокулярные физиологические признаки (размытие, аккомодация и т. д.)
- Сигналы движения (параллакс, кинетический эффект глубины)
Стереовидение
Stereopsis: по-гречески «четкий взгляд».Закройте один глаз и поднимите два указательных пальца, один как можно ближе к лицу, а другой как можно дальше. Зафиксируйте руку, расположенную дальше, и попеременно смотрите на сцену левым глазом, а затем правым. Как видите, расстояние между двумя пальцами в левом глазу отличается от правого; их относительное положение в двух сетчатках несопоставимо.
Бинокулярное несоответствие определяется как разница в расположении функции между изображением правого и левого глаза. Величина несоответствия зависит от глубины (то есть разницы в расстоянии до двух объектов и расстоянии до точки фиксации), и, следовательно, это сигнал, который зрительная система использует для определения глубины. Первым это понял Уитстон (1838). До этого люди были сбиты с толку, думали, что наличие двух глаз представляет собой проблему, потому что не могли понять, как можно видеть только одно изображение, когда смотришь на мир двумя глазами. Уитстон правильно указал на преимущество наличия двух глаз, чтобы видеть объекты в трехмерной глубине. Однако несоответствие также зависит от расстояния до точки фиксации, так что несоответствия необходимо дополнительно интерпретировать с использованием оценок расстояния фиксации.
Первым это понял Уитстон (1838). До этого люди были сбиты с толку, думали, что наличие двух глаз представляет собой проблему, потому что не могли понять, как можно видеть только одно изображение, когда смотришь на мир двумя глазами. Уитстон правильно указал на преимущество наличия двух глаз, чтобы видеть объекты в трехмерной глубине. Однако несоответствие также зависит от расстояния до точки фиксации, так что несоответствия необходимо дополнительно интерпретировать с использованием оценок расстояния фиксации.
Horopter: воображаемая трехмерная поверхность в комнате перед вами, которая включает в себя объект, на котором вы фиксируетесь, и все другие точки в трехмерном пространстве, которые проецируются на соответствующих позиции в двух сетчатках. Геометрический хороптер (множество точек с нулевой диспаратностью) представляет собой окружность, включающую точку фиксации и оптические центры (линзы) двух глаз.
Непересеченное несоответствие: Объект, находящийся дальше от вас, чем хороптор, имеет неперечеркнутое несоответствие.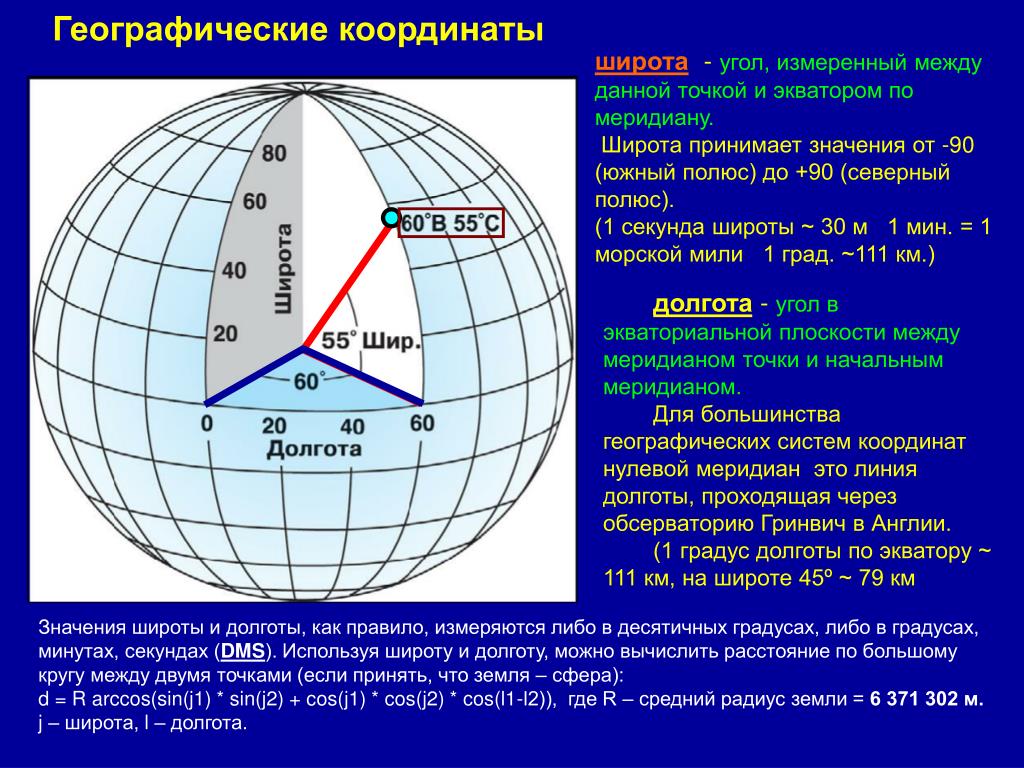 Вам придется развести (развести) глаза, чтобы зафиксироваться на нем. Он лежит дальше вправо с точки зрения правого глаза, чем с точки зрения левого глаза.
Вам придется развести (развести) глаза, чтобы зафиксироваться на нем. Он лежит дальше вправо с точки зрения правого глаза, чем с точки зрения левого глаза.
Пересечение несоответствий: Объект ближе, чем хороптор, пересек несоответствия. Вам придется скрестить (сойтись) глаза, чтобы зафиксироваться на нем. Это дальше влево с точки зрения правого глаза.
Стереоскоп: Одним из способов просмотра пар стереоизображений является использование зеркального стереоскопа. Если вы поместите свое лицо перед парой угловых зеркал и разместите два немного разных изображения по бокам, ваш левый глаз увидит левое изображение (E’), а ваш правый глаз увидит правое изображение (E ).
Стереограмма: Пара изображений (например, E/E’ выше), просматриваемых в стереоскоп (или красно-зеленый анаглиф). Два изображения на стереограмме немного отличаются друг от друга: элементы одного изображения смещены в немного разные позиции на другом изображении. Сдвиги имитируют различия, которые обычно существуют между представлениями настоящих трехмерных объектов.
Существует множество способов создания и просмотра стереограмм. Основная концепция состоит в том, чтобы представить два глаза слегка отличающимися друг от друга изображениями. Один из способов — наложить два полуизображения, одно красное, другое зеленое. Если смотреть через красно-зеленые очки, один глаз видит красное изображение, а другой глаз видит зеленое изображение.
Стереограммы были частью популярной культуры в каждом поколении, начиная с Уитстона. Стереоскопы Брюстера (другой дизайн, но та же концепция) были популярны примерно в 1900 году благодаря сфотографированным стереопарам. 3D-фильмы смотрели в красно-зеленых анаглифных очках в 1950-х годах. Современные 3D-фильмы обычно смотрят в поляризованных очках, а не в красно-зеленых, поэтому фильмы могут быть цветными. Еще один недавний метод — автостереограммы «волшебный глаз».
Стереограмма со случайными точками: Стереограмма со случайными точками была изобретена Белой Джулешем, психологом восприятия, оказавшим большое влияние за последние 30 лет. В приведенном ниже примере в анаглифных очках вы увидите квадратную поверхность, плавающую в глубине перед фоном. И квадрат переднего плана, и фон имеют маленькие точки, нарисованные на них в случайных местах.
В приведенном ниже примере в анаглифных очках вы увидите квадратную поверхность, плавающую в глубине перед фоном. И квадрат переднего плана, и фон имеют маленькие точки, нарисованные на них в случайных местах.
Это имеет важные последствия. Это означает, что:
- Вы можете видеть глубину по бинокулярному несоответствию без каких-либо других признаков глубины (параллакс движения, перспектива и т. д.),
- Вы можете видеть глубину без предварительного выделения очерченной формы или узнаваемого объекта. Это был удивительный результат, когда Юлес впервые обнаружил его. Это означает, что бинокулярная комбинация ранняя; он предшествует обработке узнаваемых форм/образов/объектов.
- Вы можете определить, какая точка в левом глазу соответствует (соответствует) какой точке в правом глазу при наличии множества потенциальных ложных совпадений. Предположительно совпадения выбираются таким образом, чтобы предполагаемая 3D-сцена была относительно плавной и непрерывной.

Чтобы построить стереограмму со случайными точками, вы сначала случайным образом размещаете набор точек на изображении. Затем сделайте две его копии. В одной копии сдвиньте область центрального квадрата влево, а в другой копии сдвиньте ту же область центрального квадрата вправо. Это оставляет дыры в каждом из изображений (оставшиеся от того места, откуда сместился квадрат). Заполните отверстия новыми случайными точками. Почему вы видите это в 3D? Сдвиг имитирует различия, которые обычно существуют между представлениями настоящих 3D-объектов. Дополнительные точки (X и Y выше) соответствуют тем частям фона, которые может видеть один глаз, но которые закрыты от поля зрения другого глаза квадратом переднего плана.
Как зрительная система видит глубину в стереограмме со случайными точками? Одна из гипотез состоит в том, что зрительная система сопоставляет признаки схожей формы, размера, контраста и т. д., чтобы оценить несоответствие. Но потенциальных совпадений может быть много. В принципе, каждая точка, присутствующая в одном ряду одного полуизображения, может иметь большое количество совпадений в другом полуизображении.
В принципе, каждая точка, присутствующая в одном ряду одного полуизображения, может иметь большое количество совпадений в другом полуизображении.
Эта проблема разрешения этой неоднозначности известна как проблема глобального стереопсиса , потому что мозг должен найти правильный общий (глобальный) набор совпадений. Он не может просто попытаться найти пару для каждой функции независимо. Глобальный стереопсис — проблема не только для стереограмм со случайными точками. Сцены природы (например, дерево с листьями, ковер и т. д.) имеют сходные черты. Зрительная система «решает» глобальную проблему стереоскопического зрения, используя дополнительные ограничения. Например, соседние точки на изображении обычно находятся в близких положениях по глубине, поэтому имеют почти такое же несоответствие.
Автостереограмма: Автостереограмма также известна как стимул «волшебный глаз». Хитрость заключается в том, чтобы отображать немного разные изображения для двух глаз. Автостереограмма работает за счет повторяющихся паттернов. Чтобы увидеть глубину в автостереограмме, нужно либо скрестить, либо развести глаза так, чтобы они фиксировались по отдельности на двух разных повторениях повторяющегося паттерна. Таким образом, вы эффективно получаете два разных изображения для двух глаз. Простой пример — иллюзия обоев. Если вы посмотрите на обои с вертикальными полосами и зафиксируете один глаз на одной полосе, а другой — на другой полосе, полоски будут казаться выступающими в глубине перед стеной. Это сложно сделать, потому что вам нужно зафиксировать точку, которая фактически находится перед изображением, фокусируясь/приспосабливаясь к самому изображению. Обратите внимание, что глубина, которую вы воспримете, будет противоположной при перекрестном объединении автостереограммы и при ее расходящемся объединении.
Автостереограмма работает за счет повторяющихся паттернов. Чтобы увидеть глубину в автостереограмме, нужно либо скрестить, либо развести глаза так, чтобы они фиксировались по отдельности на двух разных повторениях повторяющегося паттерна. Таким образом, вы эффективно получаете два разных изображения для двух глаз. Простой пример — иллюзия обоев. Если вы посмотрите на обои с вертикальными полосами и зафиксируете один глаз на одной полосе, а другой — на другой полосе, полоски будут казаться выступающими в глубине перед стеной. Это сложно сделать, потому что вам нужно зафиксировать точку, которая фактически находится перед изображением, фокусируясь/приспосабливаясь к самому изображению. Обратите внимание, что глубина, которую вы воспримете, будет противоположной при перекрестном объединении автостереограммы и при ее расходящемся объединении.
Стереослепота: 10% людей являются стереослепотами. Некоторые полностью стереослепы, некоторые слепы только к пересеченным или неперечеркнутым диспропорциям. Некоторая стереослепота вызвана косоглазием (блуждающим глазом). Если не лечить/фиксировать в очень раннем возрасте (младенчестве), бинокулярное зрение никогда не разовьется должным образом. У некоторых людей с косоглазием развивается амблиопия (иногда называемая ленивым глазом). Амблиопия – это корковая слепота. Амблиопия — это общий термин для обозначения дефицита зрения, который не имеет ничего общего с оптикой или строением глаза и сетчатки. При амблиопии мозг в основном игнорирует информацию от одного глаза. Другие люди с невылеченным косоглазием становятся альтернативными фиксаторами, которые могут видеть одним глазом, но никогда не используют их оба одновременно. То есть они сначала смотрят на вас левым глазом (пока правый глаз отведен), потом переключаются и смотрят на вас правым глазом (пока левый глаз отведен). В любом случае нет ни бинокулярного зрения, ни стереопсиса.
Некоторая стереослепота вызвана косоглазием (блуждающим глазом). Если не лечить/фиксировать в очень раннем возрасте (младенчестве), бинокулярное зрение никогда не разовьется должным образом. У некоторых людей с косоглазием развивается амблиопия (иногда называемая ленивым глазом). Амблиопия – это корковая слепота. Амблиопия — это общий термин для обозначения дефицита зрения, который не имеет ничего общего с оптикой или строением глаза и сетчатки. При амблиопии мозг в основном игнорирует информацию от одного глаза. Другие люди с невылеченным косоглазием становятся альтернативными фиксаторами, которые могут видеть одним глазом, но никогда не используют их оба одновременно. То есть они сначала смотрят на вас левым глазом (пока правый глаз отведен), потом переключаются и смотрят на вас правым глазом (пока левый глаз отведен). В любом случае нет ни бинокулярного зрения, ни стереопсиса.
Если вы записываете с помощью микроэлектрода от нейрона V1, в то время как животное просматривает ориентированные линии, представленные отдельно для двух глаз, и варьирует несоответствие, некоторые нейроны избирательны в отношении определенных несоответствий.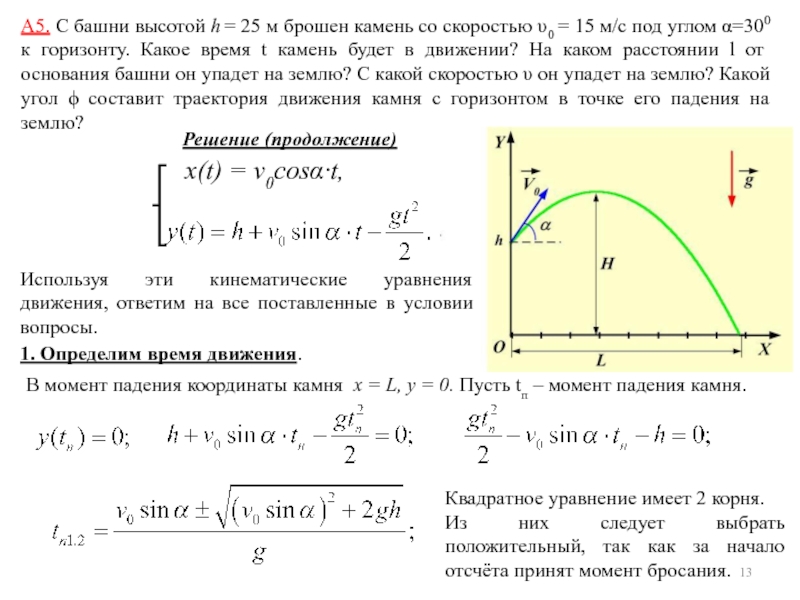
Этот нейрон вообще не реагирует, когда линия показывается одному глазу за раз. Чтобы получить ответ, линия должна быть предъявлена одновременно обоим глазам, она должна иметь правильную ориентацию, направление движения и правильное бинокулярное несоответствие, в данном случае несоответствие около 1/2 градуса угла зрения.
Нейроны различаются бинокулярным несоответствием, на которое они настроены. Это гистограмма, отображающая распределение несоответствий в предпочтениях. Многие нейроны настроены на нулевое несоответствие (на хоропторе), но, кроме того, есть нейроны, настроенные на диапазон скрещенных и неперекрещенных несоответствий. Возникающая картина заключается в том, что для каждого места в поле зрения существует набор нейронов, селективных для всех различных ориентаций, направлений движения и бинокулярных диспропорций. Один из способов, которым это может произойти, состоит в том, что нейрон имеет бинокулярное рецептивное поле, которое суммирует входные сигналы от слегка смещенных положений в двух глазах. Фьюжн
Фьюжн У вас два глаза и, следовательно, два поля зрения. Большой вопрос в начале 19 века (до Уитстона): у нас два глаза, почему мы не всегда видим два взгляда на мир? Ответ: два изображения объединяются в мозгу, образуя единый единый перцептивный опыт.
Зона слияния Пануна — это диапазон несоответствий или, что то же самое, диапазон глубин в трехмерном пространстве по обе стороны от гороптора, в котором зрительная система может успешно совместить два вида. Если несоответствие достаточно мало в пределах области слияния Панума, тогда зрительная система успешно объединяет два представления. Если несоответствие слишком велико, то нейроны в мозгу не могут с ним справиться, чтобы создать единое видение, и вы либо получаете: диплопия или подавление или бинокулярное соперничество .
Диплопия (двоение в глазах): смотреть на удаленный объект обоими открытыми глазами. Фиксируя этот объект, поместите указательный палец примерно на 6 дюймов перед своим лицом. Вы увидите два указательных пальца (один на изображении левого глаза и один на правом).
Вы увидите два указательных пальца (один на изображении левого глаза и один на правом).
Подавление: Это то, что обычно происходит, когда диспаратность сетчатки слишком велика (за пределами зоны слияния Panum). Доминирует взгляд одним глазом. Тот воспринимается. И взгляд другого глаза подавляется осознанием.
Бинокулярное соперничество: Это явление, с которым мы сталкиваемся, когда взгляды двух глаз сильно отличаются друг от друга. Взгляд одного глаза доминирует в течение нескольких секунд, а затем сменяется взглядом другого глаза. Например, если в один глаз предъявить горизонтальную решетку, а в другой глаз — вертикальную, то в восприятии можно сначала увидеть горизонтальную в течение нескольких секунд, затем смесь, затем вертикальную в течение нескольких секунд и т. д. Явление бинокулярного соперничества представляет особый интерес при изучении сознания/зрения, потому что физические стимулы (две решетки) не меняются, но сознательное восприятие резко меняется с течением времени. Более того, у нас нет сознательного контроля над восприятием; вы не можете силой воли заставить восприятие переключиться с одного на другое.
Более того, у нас нет сознательного контроля над восприятием; вы не можете силой воли заставить восприятие переключиться с одного на другое.
Сводка: Есть два способа иметь единое зрение. (1) Небольшое несоответствие приводит к слиянию и стереопсису. (2) Большое несоответствие часто приводит к подавлению взгляда одним глазом. Бинокулярное соперничество — это особый случай подавления, при котором подавление переключается между двумя точками зрения. Обратите внимание, что у вас может быть стереопсис в одной части поля зрения, диплопия в другой части поля зрения и соперничество/подавление в еще одной части поля зрения, и все это одновременно.
Бинокулярное соперничество в головном мозге Нейронные корреляты сознательного восприятия могут быть измерены экспериментально с использованием иллюзий восприятия, в которых восприятие отделено от физического стимула. Бинокулярное соперничество является примером такой иллюзии восприятия, которая использовалась для исследования нейронных коррелятов сознания. Бинокулярное соперничество возникает, когда разные зрительные стимулы предъявляются одновременно к каждому глазу. Как правило, осознание одного или другого стимула подавляется, так что мы сознательно осознаем один стимул в данный момент времени, а не оба одновременно. Взгляд одного глаза доминирует в сознании на несколько секунд, но сменяется взглядом другого глаза. Что делает бинокулярное соперничество таким замечательным, так это то, что перцептивный опыт колеблется, в то время как физический стимул остается постоянным. Из-за этой диссоциации бинокулярное соперничество предоставляет уникальную возможность для изучения нейронных коррелятов сознания.
Бинокулярное соперничество возникает, когда разные зрительные стимулы предъявляются одновременно к каждому глазу. Как правило, осознание одного или другого стимула подавляется, так что мы сознательно осознаем один стимул в данный момент времени, а не оба одновременно. Взгляд одного глаза доминирует в сознании на несколько секунд, но сменяется взглядом другого глаза. Что делает бинокулярное соперничество таким замечательным, так это то, что перцептивный опыт колеблется, в то время как физический стимул остается постоянным. Из-за этой диссоциации бинокулярное соперничество предоставляет уникальную возможность для изучения нейронных коррелятов сознания.
Согласно одной идее, бинокулярное соперничество возникает из-за того, что нейроны на ранних стадиях зрительной обработки реагируют на физические стимулы каждого глаза, тогда как нейроны на более поздних стадиях зрительной обработки включаются и выключаются и вызывают перцептивные изменения. Где-то между этими ранними и поздними стадиями нейронные сигналы, передающие один из двух стимулов, подавляются, как если бы существовали «ворота» к зрительному сознанию. V1 — это первое место в путях обработки зрительной информации мозга, где могут быть расположены эти «ворота», потому что это первое место, где сигналы от двух глаз объединяются.
V1 — это первое место в путях обработки зрительной информации мозга, где могут быть расположены эти «ворота», потому что это первое место, где сигналы от двух глаз объединяются.
Существуют ли такие ворота? Если да, то какие нейроны в мозге выполняют эту функцию? Локализованы ли нейроны в определенных областях мозга? Являются ли они особым типом клеток? Происходит ли стробирование за счет модуляции частоты возбуждения клеток или какого-либо другого компонента их ответов (например, синхронизации спайков, синхронного возбуждения)? Какие нейронные цепи и нейронные вычисления поддерживают конкуренцию между двумя стимулами?
Хотя у нас пока нет четких ответов на эти вопросы, мы начали изучать это в моей лаборатории с помощью фМРТ. Мы извлекли выгоду из интересного аспекта феномена восприятия; во время перцептивного чередования обычно воспринимается бегущая волна, в которой доминирование одного паттерна первоначально возникает в одном месте и постепенно расширяется, поскольку делает другой паттерн невидимым. Заметьте еще раз, что нет никакого физического изменения в стимуле, пока происходит это сознательное перцептивное изменение — все это происходит «в вашей голове». В этом эксперименте установлено, что перцептивные изменения во время бинокулярного соперничества сопровождаются волнами активности в первичной зрительной коре (V1). Опираясь на тот факт, что зрительная кора организована ретинотопически (нейроны в близлежащих местах зрительной коры реагируют на близлежащие места в зрительном поле), мы показали, что нейронная активность распространяется по подобластям зрительной коры таким образом, который коррелирует с динамическими перцептивными изменениями. опыт во время бинокулярного соперничества.
Заметьте еще раз, что нет никакого физического изменения в стимуле, пока происходит это сознательное перцептивное изменение — все это происходит «в вашей голове». В этом эксперименте установлено, что перцептивные изменения во время бинокулярного соперничества сопровождаются волнами активности в первичной зрительной коре (V1). Опираясь на тот факт, что зрительная кора организована ретинотопически (нейроны в близлежащих местах зрительной коры реагируют на близлежащие места в зрительном поле), мы показали, что нейронная активность распространяется по подобластям зрительной коры таким образом, который коррелирует с динамическими перцептивными изменениями. опыт во время бинокулярного соперничества.
В этом ролике показана демонстрация наших результатов. Правильно, пример временной последовательности перцептивного опыта наблюдателя. Слева: ответы фМРТ. Серая шкала, анатомическое изображение, проходящее через заднюю затылочную долю, примерно перпендикулярно шалькариновой борозде. Желтые блики, области серого вещества V1 превышают 75% пикового ответа. Обратите внимание на левое полушарие. Сначала реагирует нижняя губа борозды Calcarine, а затем верхняя губа борозды. Затем активность нижней губы борозды затухает раньше, чем активность верхней губы. Эта активность в мозге (слева) хорошо соответствует динамике перцептивных изменений (справа), учитывая ретинотопическую организацию V1 (нижняя губа шпорной борозды левого полушария соответствует верхнему правому квадранту поля зрения, а верхняя губа левой -полушарная шпорная борозда соответствует нижнему правому квадранту поля зрения). То же самое было бы очевидно в правом полушарии, но в другом срезе мозга. Красная кривая, ответы фМРТ, измеренные от субрегиона V1 (нижняя губа левого полушария Calcarine sulcus), ретинотопически соответствующего верхнему правому квадранту стимульного кольца. Зеленая кривая, ответы фМРТ, измеренные в субрегионе V1 (верхняя губа калькариновой борозды), ретинотопически соответствующей нижнему правому квадранту стимульного кольца. Желтый снова указывает, когда ответы в каждой подобласти превысили 75% их соответствующих пиков.
Обратите внимание на левое полушарие. Сначала реагирует нижняя губа борозды Calcarine, а затем верхняя губа борозды. Затем активность нижней губы борозды затухает раньше, чем активность верхней губы. Эта активность в мозге (слева) хорошо соответствует динамике перцептивных изменений (справа), учитывая ретинотопическую организацию V1 (нижняя губа шпорной борозды левого полушария соответствует верхнему правому квадранту поля зрения, а верхняя губа левой -полушарная шпорная борозда соответствует нижнему правому квадранту поля зрения). То же самое было бы очевидно в правом полушарии, но в другом срезе мозга. Красная кривая, ответы фМРТ, измеренные от субрегиона V1 (нижняя губа левого полушария Calcarine sulcus), ретинотопически соответствующего верхнему правому квадранту стимульного кольца. Зеленая кривая, ответы фМРТ, измеренные в субрегионе V1 (верхняя губа калькариновой борозды), ретинотопически соответствующей нижнему правому квадранту стимульного кольца. Желтый снова указывает, когда ответы в каждой подобласти превысили 75% их соответствующих пиков.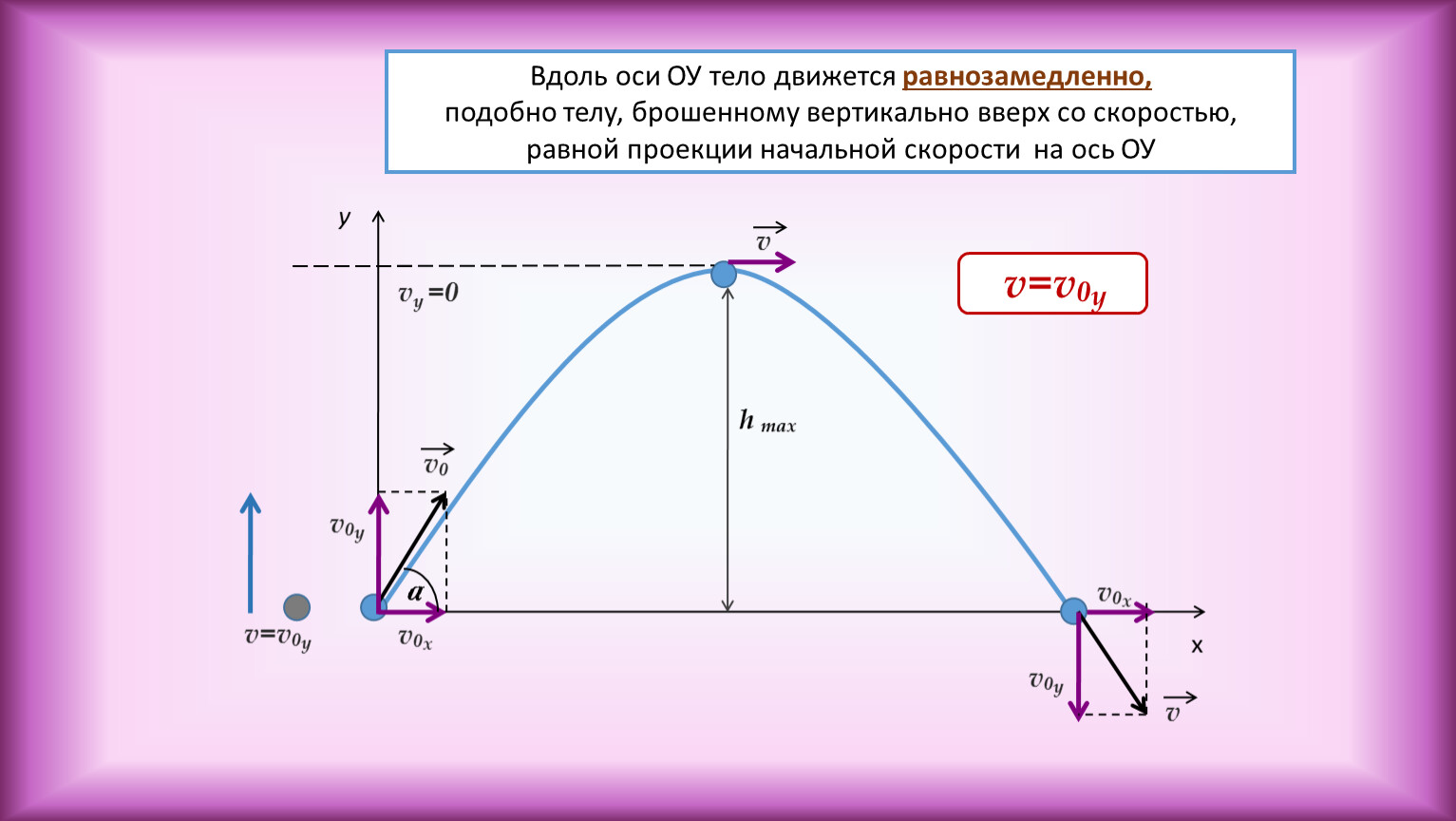 Зеленая кривая запаздывает во времени и больше по амплитуде, чем красная кривая, как и ожидалось от бегущей волны.
Зеленая кривая запаздывает во времени и больше по амплитуде, чем красная кривая, как и ожидалось от бегущей волны.
Действительно, активность в ряде областей мозга коррелирует с перцептивными чередованиями бинокулярного соперничества, включая не только первичную зрительную кору, но и области зрительной коры более высокого порядка в нижней височной доле, а также области теменной и префронтальной коры. Вполне вероятно, что эти разные области коры играют разные роли в зрительном восприятии во время бинокулярного соперничества.
Графические метки глубины
Когда открыт только один глаз, вы все равно видите с ощущением глубины, но между размером и расстоянием существует присущая двойственность.
Что делает зрительная система, чтобы справиться с этой неоднозначностью? Ваша зрительная система опирается на несколько сигналов для оценки/выведения расстояния, глубины и трехмерной формы. Существует большой набор таких сигналов: относительный размер, окклюзия, отбрасываемые тени, затенение, динамические тени (движение теней), воздушная перспектива, линейная перспектива, перспектива текстуры и высота в пределах изображения. Большинство из них основано на концепции, показанной выше: размер изображения объекта на сетчатке пропорционален размеру объекта, но обратно пропорционален расстоянию до объекта.
Большинство из них основано на концепции, показанной выше: размер изображения объекта на сетчатке пропорционален размеру объекта, но обратно пропорционален расстоянию до объекта.
Девушка слева на самом деле почти в два раза дальше от наблюдателя, чем мужчина справа. Однако, когда комната просматривается через глазок, реальных расстояний не видно. Поскольку вы воспринимаете двух людей как находящихся на одинаковом расстоянии от вас, тот, у кого угол зрения больше, кажется больше.
Текстура предоставляет 3 подсказки о форме/расстоянии:
- Элементы текстуры становятся более плотными с расстоянием.
- элементов текстуры становятся меньше с расстоянием
- ракурс (круги становятся овалами) при наклоне поверхности прочь.
Яркость поверхности зависит от ее ориентации относительно
источник света. Зрительная система предполагает, что свет исходит от
выше. Яркие пятна
кажутся наклоненными вверх лицом к свету.
Яркие пятна
кажутся наклоненными вверх лицом к свету.
Интерпретация формы по затенению взаимодействует с интерпретацией формы по контурам. Эти два изображения имеют одинаковое затенение, но разные ограничивающие контуры, и вы видите разные формы.
3 белых квадрата идентичны друг другу и расположены точно так же по отношению к сетке шахматной доски внизу. Отличаются только тени, создавая впечатление, что квадрат справа парит выше шахматной доски.
Линейная перспектива — еще один монокулярный признак глубины. Расстояние
между
rails постоянна в 3D-сцене, но становится все меньше и меньше в
изображение.
Это намек на дистанцию. Зрительная система использует это для сравнения
размеры объектов.
Две линии имеют одинаковую длину, но верхняя кажется больше.
потому что
воспринимается как находящееся дальше, и зрительная система компенсирует
в
перспектива. Эта компенсация расстояния в размерах интерпретации равна
известное как «постоянство размера».
По аналогии с постоянством яркости и контрастом яркости или постоянством цвета и цветовым контрастом мы также испытываем постоянство размера и контраст размера. Размер объекта интерпретируется относительно объектов вокруг него и в контексте других признаков (например, линейной перспективы) для размера и расстояния. Мужчина на картинках выше физически одинакового размера на обеих фотографиях (измерьте его), и слева он кажется нормальным, а справа крошечным. Центральные круги на рисунках ниже имеют одинаковый размер, но тот, что слева, выглядит больше, потому что он окружен маленькими кругами, а тот, что справа, меньше, потому что он окружен большими кругами.
Центральный принцип восприятия объектов заключается в том, что мы видим объекты в трехмерном мире. Если есть возможность интерпретировать рисунок или изображение как трехмерный объект, мы это делаем. Зрительная система компенсирует перспективу при оценке размера. Поразительно, что мы так этого не осознаем. Мы склонны интерпретировать форму и размер в 3D, часто не зная о 2D-размере. Две столешницы выше имеют точно такую же двухмерную форму на странице, за исключением жесткого поворота. Никто не поверит в это, когда впервые увидит иллюзию. Иллюзия показывает, что мы не видим двухмерную форму, нарисованную на странице, а вместо этого видим трехмерную форму объекта в пространстве.
Мы склонны интерпретировать форму и размер в 3D, часто не зная о 2D-размере. Две столешницы выше имеют точно такую же двухмерную форму на странице, за исключением жесткого поворота. Никто не поверит в это, когда впервые увидит иллюзию. Иллюзия показывает, что мы не видим двухмерную форму, нарисованную на странице, а вместо этого видим трехмерную форму объекта в пространстве.
Монокулярные физиологические сигналы
Когда мы фиксируем объект, мы обычно приспосабливаемся к объекту,
т. е. изменить силу хрусталика в наших глазах, чтобы сделать этот объект
в фокус. Аккомодационное усилие — слабый признак глубины. Как только мы
приспособленные к этому расстоянию, предметы, находящиеся намного ближе или дальше
от нас, чем это расстояние, не в фокусе на нашей сетчатке. Таким образом, размытие
является признаком того, что объекты находятся на другом расстоянии от
аккомодационное расстояние, хотя сигнал неоднозначен относительно того,
объекты ближе или дальше. Еще слабее, как сигналы глубины
(хотя теоретически полезны) являются искажения изображения, возникающие в результате
от астигматизма (роговица не является идеальной сферой) и хроматического
аберрация (когда желтый свет находится в фокусе, синий свет не в фокусе,
с заданного расстояния до объекта).

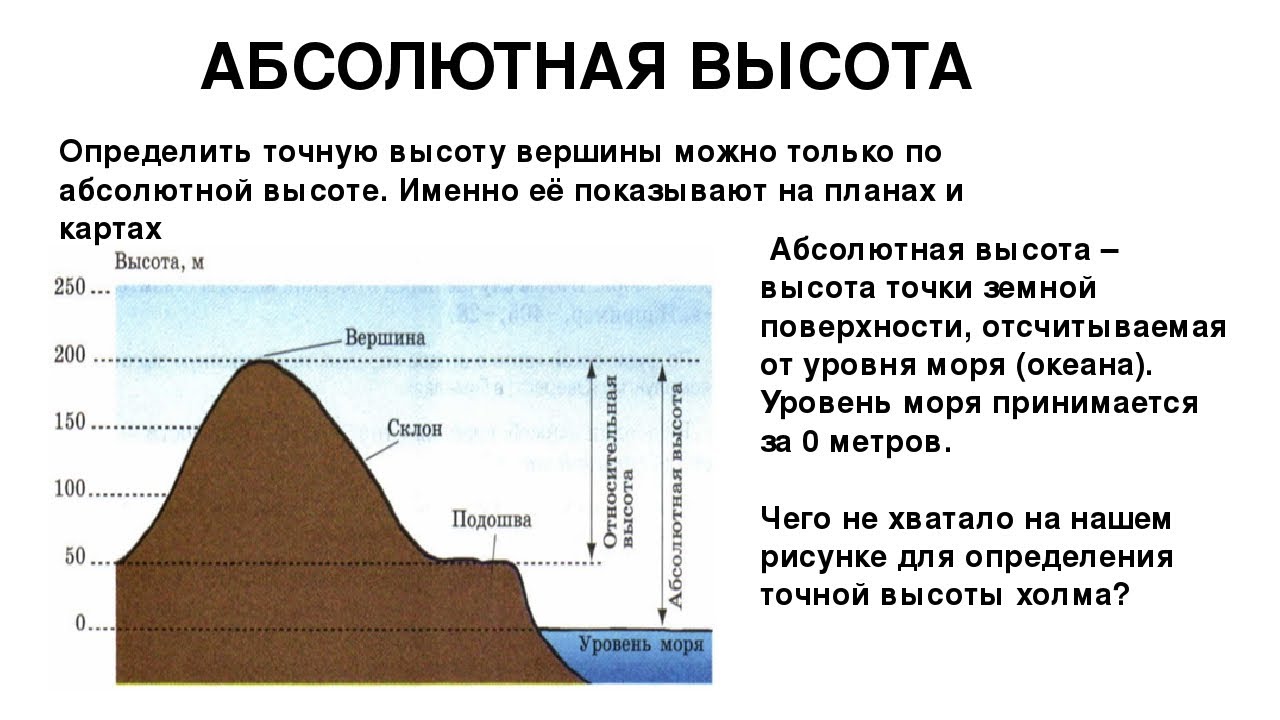 д.)
д.)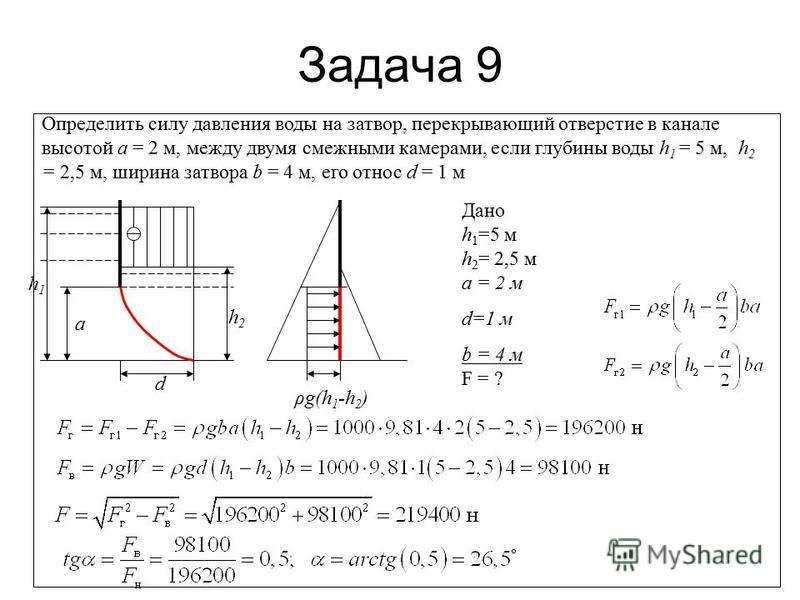
Leave A Comment