Гипотенуза прямоугольного треугольника равна 20 см а один из катетов равен 12: Гипотенуза прямоугольного треугольника равна 20 см.найдите его катеты ,если известно что один из них на…

Зачёт по теме «Теорема Пифагора»

9 июля 2022

В закладки

Обсудить

Жалоба

TG 4ЕГЭ

Пробные работы ОГЭ по математике

Практическая часть зачёта включает 4 варианта дифференцированных задач.

Задания 1 и 2 вариантов соответствуют обязательному уровню усвоению материала. Задания 3 и 4 вариантов представляют более сложные задания, требующие дополнительных знаний и более высокой вычислительной культуры. Представлены критерии оценивания и ответы к заданиям зачета.

На выполнение работы отводиться 45 минут.

tp.doc

Вариант 1

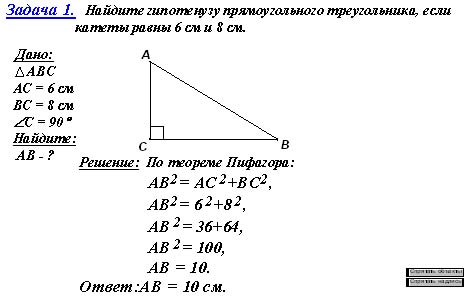
1. В прямоугольном треугольнике катеты равны 8 см и 6 см. Найдите гипотенузу этого треугольника.

2. Гипотенуза прямоугольного треугольника равна 13 см, а катет равен 12 см. Найдите другой катет.

3. Боковая сторона равнобедренного треугольника равна 17 см, его основание равно 16 см. Найдите высоту, проведенную к основанию.

4. Одна сторона прямоугольника равна 7 см, а диагональ равна 25 см.

Найдите периметр прямоугольника.

5. Катеты прямоугольного треугольника относятся как 3 : 4, гипотенуза равна 20 см. Найдите площадь этого треугольника.

Вариант 2

1. В прямоугольном треугольнике катеты равны 12 см и 5 см. Найдите гипотенузу этого треугольника.

2. В прямоугольном треугольнике один из катетов равен 7 см, гипотенуза равна 25 см. Найдите второй катет.

3. В равнобедренном треугольнике боковая сторона равна 10 см, его основание равно 12 см. Найдите высоту, проведенную к основанию треугольника.

4. Диагональ прямоугольника равна 13 см, одна из его сторон равна 5 см. Найдите периметр прямоугольника.

5. Катет прямоугольного треугольника равен 9 см, а гипотенуза и второй катет относятся как 5 : 4. Найдите площадь этого треугольника.

Вариант 3

1. В прямоугольном треугольнике катеты равны 15 см и 8 см. Найдите гипотенузу треугольника.

2. Диагонали ромба равны 10 см и 24 см. Найдите периметр ромба.

3. Катет прямоугольного треугольника равен 9 см, а гипотенуза больше второго катета на 3 см. Найдите периметр треугольника.

4. В равнобедренном треугольнике основание равно 24 см, высота, проведенная к основанию, равна 16 см. Найдите боковую сторону треугольника.

5. Найдите сторону равностороннего треугольника, если его высота равна 9 см.

Вариант 4

1. В прямоугольном треугольнике катеты равны 7см и 24 см. Найдите гипотенузу треугольника.

2. Катет прямоугольного треугольника равен 28 см. Разность двух других сторон равна 8 см. Найдите неизвестные стороны этого треугольника.

3. В равнобедренной трапеции основания равны 6 см и 12 см., боковая сторона равна 5 см. Найдите площадь трапеции.

4. Высота равностороннего треугольника равна 3 см. Найдите сторону этого равностороннего треугольника.

5. Расстояние от хорды к центру окружности 6 см, длина хорды 16 см. Найдите диаметр этой окружности.

Медиана к гипотенузе прямоугольного треугольника: свойства, задача

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

• Определение медианы прямоугольного треугольника
• Свойства медианы прямоугольного треугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Пример задачи

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми (<90°).

Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

• BC = 2AD
• AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

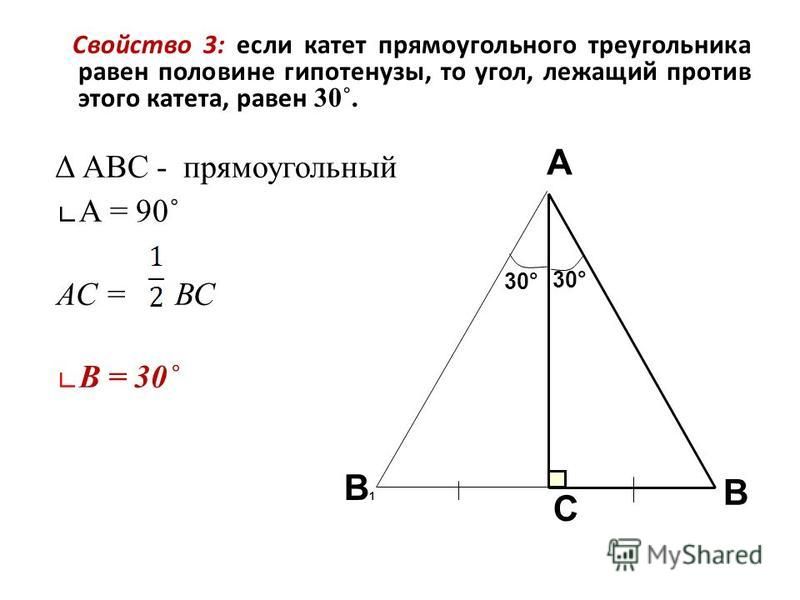
Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b² = с² – a² = 20² – 12² = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Гипотенуза треугольника.

Калькулятор

Создано Hanna Pamuła, PhD

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 20 ноября 2022 г.

Содержание:

• Что такое гипотенуза треугольника
• Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?
• Часто задаваемые вопросы

С помощью этого калькулятора гипотенузы вы быстро найдете самую длинную сторону прямоугольного треугольника. Если вы хотите узнать, что такое гипотенуза прямоугольного треугольника, как ее найти и что такое гипотенуза в формуле треугольника, вы найдете ответ ниже с простым примером, чтобы все прояснить. Не ждите больше; попробуйте этот калькулятор гипотенузы!

Что такое гипотенуза треугольника

Гипотенуза — это самая длинная сторона прямоугольного треугольника . Это сторона, противоположная прямому углу (90°). Длину гипотенузы можно найти, например, из теоремы Пифагора. Вы можете узнать больше об этом в нашем калькуляторе теоремы Пифагора.

Формула гипотенузы треугольника

В этом калькуляторе гипотенузы реализовано несколько формул — таким образом, мы убедились, что он подходит для различных сценариев, с которыми вы можете столкнуться. Вы можете найти гипотенузу:

1. Даны две стороны прямоугольного треугольника

Используйте теорему Пифагора для вычисления гипотенузы по сторонам прямоугольного треугольника. Извлеките квадратный корень из суммы квадратов:

• c = √(a² + b²)

2. Дан угол и одна сторона

• c = a / sin(α) = b / sin(β) , объясняется в нашем калькуляторе закона синусов.

3. Учитывая площадь и одну ветвь

Так как площадь прямоугольного треугольника равна a × b / 2 , то

• c = √(a² + b²) = √(a² + (площадь × 2 / a)²) = √( (площадь × 2 / b)² + b²) .

Чтобы узнать больше о вычислениях с прямоугольными треугольниками, посетите нашу область калькулятора прямоугольного треугольника и калькулятора сторон и углов прямоугольного треугольника.

Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?

Давайте посчитаем, какой длины должна быть лестница, если мы хотим спасти котенка с 10-футовой крыши. Калькулятор помогает найти длину лестницы от земли до края крыши, но не забывайте о той части лестницы, которая должна выходить за край!

1. Выберите вариант, необходимый для ваших расчетов . Мы знаем, что наша крыша имеет высоту 10 футов и что самый безопасный угол для лестницы составляет ~75,5°. Из выпадающего списка данного поля выберите вариант: угол ∡ и одна сторона .
2. Изменить единицы измерения на футы
   .

3. Введите указанные значения . Наша нога a имеет длину 10 футов, а угол α между лестницей и землей равен 75,5°.

4. Появляется

   Длина лестницы, гипотенуза прямоугольного треугольника ! Равен 10,33 фута.

   Также отображаются угол β = 14,5° и катет b = 2,586 фута. Вторая ножка также является важным параметром, так как она говорит вам, как далеко вы должны разместить лестницу от стены (точнее, от края крыши). Общий принцип, который следует запомнить, — это правило

   4:1 : на каждые четыре фута высоты по вертикали ножка лестницы должна отодвигаться от стены на один фут.

Часто задаваемые вопросы

Как найти гипотенузу с грехом?

1. Выполнить операцию sin над углом (не прямым углом).
2. Разделить длину стороны , противоположной углу, используемому в шаге 1, на результат шага 1.
3. Результатом является гипотенуза .

Всегда ли гипотенуза является самой длинной стороной?

Да, гипотенуза всегда является самой длинной стороной , но только для прямоугольных треугольников. В равнобедренных треугольниках две равные стороны называются катетами, а в равнобедренном треугольнике все стороны называются просто сторонами.

Как найти смежную и противоположную гипотенузу?

1. Найдите самую длинную сторону и назовите ее гипотенузой .
2. Вы можете найти смежную и противоположную стороны, только если выберете один угол меньше 90 градусов.
3. Смежное — это сторона, которая вместе с гипотенузой образует выбранный угол .
4. Противоположная сторона — это сторона, которая не образует выбранный угол .

Как найти высоту гипотенузы?

1. Нарисуйте высоту гипотенузы треугольника. Два новых треугольника, которые вы создали, подобны друг другу и основному треугольнику.
2. Разделите длину самой короткой стороны главного треугольника на гипотенузу главного треугольника.
3. Умножьте результат на длину оставшейся стороны, чтобы получить длину высоты.
4. В качестве альтернативы, углы внутри меньших треугольников будут такими же, как углы основного треугольника, так что вы можете выполнить тригонометрию чтобы найти его другим способом.

Что делать, если гипотенуза противоположна?

Если гипотенуза противоположна, то вы считаете неправильный угол — вы не можете использовать тригонометрию с прямым углом треугольника. Рассмотрим один из других углов. Это как смежный угол. Противоположная сторона будет той стороной, которая не образует этот угол.

Как построить прямую, перпендикулярную гипотенузе?

1. Приобретите циркуль, линейку и ручку или карандаш.
2. Установите циркуль на длину гипотенузы (или любую длину, если она остается постоянной).
3. Нарисуйте окружность с центром на одном из концов гипотенузы.
4. Нарисуйте еще один круг с центром на другом конце гипотенузы.
5. Нарисуйте линию, соединяющую две точки , где встречаются эти окружности. Эта линия перпендикулярна гипотенузе.

Как найти гипотенузу равнобедренного прямоугольного треугольника?

1. Найдите длину одной из сторон , не лежащих в гипотенузе .
2. Возведите в квадрат длину стороны.
3. Удвоить результат предыдущего шага.
4. Квадратный корень результат шага 3. Это длина гипотенузы .

Что такое теорема об угле гипотенузы?

Теорема об угле гипотенузы — это способ проверки конгруэнтности двух прямоугольных треугольников или нет. Он гласит, что если два прямоугольных треугольника имеют одинаковые гипотенузу и острый угол, то они равны.

Откуда произошло слово гипотенуза?

Слово гипотенуза происходит от древнегреческого hypoteinousa , что означает «растягивающаяся под (прямым углом)». Это, в свою очередь, происходит от гипо- «под» и теинеина «растягиваться». Еще одна вещь, за которую мы должны благодарить древних греков!

Как решить прямоугольный треугольник только с гипотенузой?

Вы не можете построить прямоугольный треугольник, используя только гипотенузу . Это связано с тем, что две другие стороны и углы все еще не определены, поэтому треугольник может иметь множество форм.

Hanna Pamuła, PhD

Гипотенуза

Посмотреть 18 похожих калькуляторов треугольников 🔺

30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… 15 more

мер гипотенузы20см прямоугольного треугольника. сумма длин ног 28 см. найти длину каждой стороны треугольника.

Квадратичные задачи

Элсион Л.

спросил 17.06.15

гипотенуза прямоугольного треугольника равна 20 см. сумма длин ног 28 см. найти длину каждой стороны треугольника.

Подписаться І 3

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Эндрю Д. ответил 17.06.15

Репетитор

5 (15)

Harvard Grad предлагает подготовку к экзаменам и репетиторство

См. таких репетиторов

Смотрите таких репетиторов

Allison,

 

Назовем смежные стороны прямоугольного треугольника a и b. 92-48)

a=12 или 16, что означает b=16 или 12 соответственно.

 

Таким образом, длины смежных сторон треугольника равны 12 и 16.

Голосовать за 1 Понизить

Подробнее

Отчет

Майкл Дж. ответил 17.06.15

Репетитор

5 (5)

Отлично упрощает сложные концепции и процессы

См. таких наставников

Смотрите таких репетиторов

Прямоугольный треугольник означает, что мы можем использовать теорему Пифагора. Мы знаем гипотенузу. Нам нужно найти стороны треугольника.

 

Пусть один катет = x

Пусть другой катет = y

Гипотенуза = 20 см

 

 

Напишите уравнения, представляющие информацию.

x + y = 28 сумм ног

x ² + Y ² = 20 ² Pythagorean Theoorem

Мы будем использовать эти равные.

 

x + y = 28               eq1

x ² + y ² = 400            eq2

 

 

У нас есть два уравнения с двумя разными переменными. Нам нужно объединить два уравнения в одно с одинаковыми переменными.

 

Подставьте eq1 в eq2. У нас будет eq2 через x.

x ² + (28 — x) ² = 400

x ² + (28 — x) (28 — x) = 400

962 x 2 2 2 2 2 2 2 2 2 2 2 2 . + 784 — 56x + x ² = 400

 

2x ² — 56x + 384 = 0

2 (x ² — 28x + 192) = 0

Установите термин в Круженел, равный Zero.

 

x ²  — 28x + 192 = 0

 

 

Умножьте уравнение, если возможно.

 

(x -12)(x — 16) = 0

 

x = 12         и        x = 16

 

3 9002. Оба положительные.

 

Подставьте эти значения x в eq1 соответственно.

y = 28 — x y = 28 — x

y = 28 — 12 y = 28 — 16

y = 16 y = 12

У нас есть пары ног:

x = 12 x = 16

y = 16 y = 12

Обратите внимание, что каждая пара ног имеет 16 и 12.