Постройте график функции y = |x| x – |x| – 6x

Задание.
Построить график функции y = |x|  x — |x|  — 6x.

Решение.
Обратим внимание на знак модуля, который содержит функция.
Как известно, переменная, которая стоит под знаком модуля, может принимать как отрицательные, так и положительные значения. В таком случае будет меняться и вся функция. Следовательно, необходимо исследовать оба варианта для переменной х.

1-й вариант. Переменная х — положительное число, то есть принимает значения от 0 до бесконечности.
Подставим в функцию положительное значение х и получим:

   

Получили уравнение параболы, ветви которой направлены вверх, так как перед х в квадрате стоит знак «плюс».
Найдем вершину этой параболы:

   

   

Получили точку вершины (3,5; 5,25).
Найдем точки пересечения с осями координат.
С осью Оу: х = 0

   

С осью Ох: у = 0

   

   

или
Получили две точки:
(0; 0) и (7; 0).

2-й вариант. Переменная х — отрицательное число, то есть принимает значения от минус бесконечности до 0.
Подставим в функцию отрицательное значение х и получим:

   

Получили уравнение параболы, ветви которой направлены вниз, так как перед х в квадрате стоит знак «минус».
Найдем вершину этой параболы:

   

   

Получили точку вершины (—2,5; —18,75).
Найдем точки пересечения с осями координат.
С осью Оу: х = 0

   

С осью Ох: у = 0

   

   

или
Получили две точки:
(0; 0) и (5; 0).
Нанесем полученные точки на координатную плоскость и проведем линию графика.

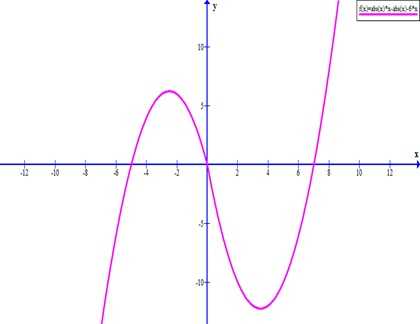
ru.solverbook.com

Постройте график функции y = 6/x

Задание.
Постройте график функции y = 6/x.
 
Решение.
Разберем последовательно как можно просто и без ошибок построить график любой функции.
Для этого первым делом рассмотрим функцию, график которой нужно построить.
Данная функция представлена в виде дроби целого известного числа и неизвестного, причем неизвестное стоит в знаменателе дроби. Вспоминаем математику начальных классов, когда учили, что делить нельзя только на ноль. Из этого делаем вывод, что неизвестное число х для заданной функции может быть каким угодно, кроме нуля. Теперь можно записать область значений переменной х:

   

Проверим, является ли функция четной. Для этого подставим —х в ее уравнение вместо х и сделаем вывод:

   

Получаем нечетную функцию. Для нас такая информация полезна тем, что график нечетной функции симметричен началу координат, то есть точке (0; 0).
Найдем точки, которые принадлежат графику, чтобы провести через них кривую. Выберем точки произвольно и подставим вместо х:

   

   

Точка (—3; —2)

   

   

Точка (—2; —3)

   

   

Точка (—1; —6)

   

   

Точка (1; 6)

   

   

Точка (2; 3)

   

   

Точка (3; 2)
Этих точек достаточно, чтобы построить гиперболу y = 6/x.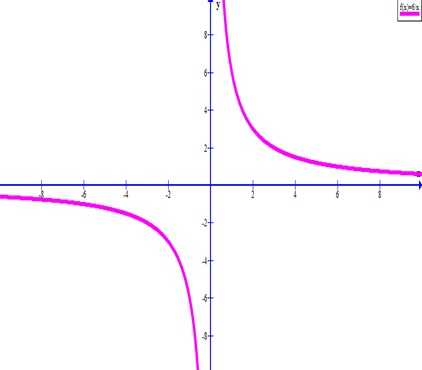

ru.solverbook.com

Постройте график функции y = 6/x

Задание.
Постройте график функции y = 6/x.

Решение.
Область определения любой функции — это значения переменной х, при которых функция не может существовать.
Обратим внимание на запись функции. Как известно, функция не существует, когда знаменатель равен нулю.

Областью определения являются значения, которые:

   

Что значит — функция не будет пересекать координатную ось Оу.
Определим четность или нечетность функции:

   

Это значит, что функция нечетная, то есть она симметрична началу координат.
Следовательно, достаточно построить одну ее часть, например, для положительных значений переменной х, а затем отобразить ее симметрично началу координат.
Подберем несколько точек, через которые будет проходить одна часть функции. Для этого выберем несколько положительных значений переменной х и найдем соответствующие им значения у:

   

   

   

   

   

   

   

   

   

   

   

   

Получили 6 точек с координатами , , , , , , которых будет достаточно для того, чтобы изобразить одну часть функции.
Нанесем эти точки на координатную плоскость и соединим плавной кривой, не забывая, что х не может быть равен нулю. Далее отобразим эту часть симметрично относительно точки (0; 0) и получим график заданной функции.

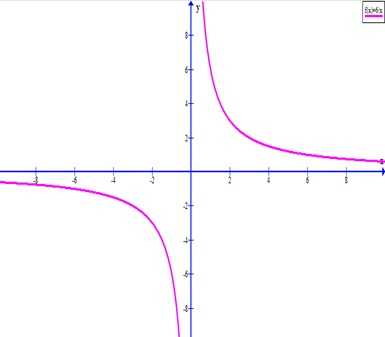
ru.solverbook.com

Ответы@Mail.Ru: постройте график функции y=x^2-|6x+7|

Функция чётная, поэтому её график симметричен относительно Оу. Построй график данной функции, не обращая внимания на модуль Ту часть графика, которая слева от оси Оу, сотри. Оставшуюся часть графика зеркально отрази от оси Оу на левую половину координатной плоскости График построен

Ого, какой сложный. Я Вам сочувствую. Всем сердцем. Держитесь и думайте!

по точкам от -3 до +3 левая часть — не знаю, а правая — обычная парабола на 7 клеточек вверх

Кривосиси получились:) <img src=»//otvet.imgsmail.ru/download/3452192_465a338130e95f35218b6de742fa5b1e_800.png» data-lsrc=»//otvet.imgsmail.ru/download/3452192_465a338130e95f35218b6de742fa5b1e_120x120.png» data-big=»1″>

x1+x2=6 x1=7 x1*x2=7 x2=-1 Только такое решение можно использовать или через дискриминант!! -1 и 7 это и есть ответ!

touch.otvet.mail.ru

постройте график функции y=x^2+6x+2. помогите пожалуйсто!

начнем с того, что это будет парабола, ветви направлены вверх далее находимкоординаты вершины параболы по формуле x=-b/2a=-6/2=-3 у=9-18+2=-7 (-3;-7) координаты вершины параболы далее чертишь таблицу со значениями, строишь параболу и график готов!!! вот в помощь сайт по построению графиков <a rel=»nofollow» href=»http://www.yotx.ru/default.aspx?clr0=000000&exp0=x^2+6x+2&mix=-10&max=10&asx=on&u=mm&nx=X&aiy=on&asy=on&ny=Y&iw=600&ih=400&ict=png&aa=on» target=»_blank»>http://www.yotx.ru/default.aspx?clr0=000000&exp0=x^2+6x+2&mix=-10&max=10&asx=on&u=mm&nx=X&aiy=on&asy=on&ny=Y&iw=600&ih=400&ict=png&aa=on</a>

поскольку х&#178; (коэффициент &gt;0) , =&gt; ветви вверх координаты х вершины= -b/2a (у тебя х= -6/2=-3) координаты у вершины — подсавляешь вместо х и находишь у: у=9-6*3+2=-7 теперь у тебя есть координаты вершины и направление ветвей включай свои художественные способности! 😉 P.S. можешь еще найти точки пересечения параболы с осью ОХ — получишь еще две точки=)

touch.otvet.mail.ru