Глава 2. Ускорение. Равноускоренное движение
Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло
(2.1) |
где и — скорости тела в конце и начале интервала времени .
Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости.
При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и .
Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации:
тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения.
В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).
Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача
Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (задача 2.1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5
Поэтому равноускоренному движению в задаче 2.1.5
При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями
(2.2) |
(2.3) |
где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.
В задаче 2.1.6 зависимость (2.2) в проекциях на ось , которая направлена параллельно ускорению и начало которой находится в точке начала движения, дает
Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что
Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что
В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид
где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).
Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела , проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .
 Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ
Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответЗависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид
где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ
Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (задача 2.2.1) используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема в зависимость скорости от времени дает
где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4).
Подстановка в эту формулу числовых значений дает (ответ 1).
Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной , отсчитанного от этой же точки, равно (
Скорость прямолинейного равноускоренного движения: график скорости
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле:
Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t. 2) в течение 4 секунд.
2) в течение 4 секунд.
Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость.
График проекции скорости тела при торможении
Если бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол.
Ниже представлен график такой ситуации.
Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Нужна помощь в учебе?
Предыдущая тема: Прямолинейное равноускоренное движение и ускорение
Следующая тема:   Перемещение при прямолинейном равноускоренном движении
| № | ВУЗЫ | Количество прет. БАК БАК |
Количество прет. МАГ |
| 1 | Astana IT University | 118 | |
| 2 | Алматы Менеджмент Университет | 1 | |
| 3 | Актюбинский региональный университет им.К.Жубанова | 32 | 1 |
| 4 | Алматинский технологический университет | 39 | 3 |
| 5 | Атырауский университет им.Х.Досмухамедов | 3 | |
| 6 | Алматинский университет энергетики и связи имени Гумарбека Даукеева | 95 | 4 |
| 7 | Баишев Университет | 1 | |
| 8 | Восточно-Казахстанский университет имени Сарсена Аманжолова | 5 | |
| 9 | Евразийский гуманитарный институт | 1 | |
| 10 | Евразийский технологический университет | 5 | |
| 11 | Казахский национальный женский педагогический университет | 2 | |
| 12 | Жетысуский университет имени И. Жансугурова Жансугурова |
1 | |
| 13 | Западно-Казахстанский аграрно-технический университет им.Жангир хан | 39 | |
| 14 | Универитет КАЗГЮУ имени М.С. Нарикбаева | ||
| 15 | КазГЮИУ Семей | 9 | |
| 16 | Казахстанский инженерно-технологический университет | 2 | |
| 17 | Казахский медицинский университет непрерывного образования | 1 | |
| 18 | Казахская национальная академия искусств имени Т.Жургенова | 42 | 3 |
| 19 | Казахстанско-Немецкий Университет | 3 | |
| 20 | Инновационный Евразийский университет | ||
| 21 | Карагандинский экономический университет Казпотребсоюза | 2 | |
| 22 | Карагандинский индустриальный университет | 15 | |
| 23 | Карагандинский университет имени академика Е. А.Букетова А.Букетова |
38 | 4 |
| 24 | Костанайский инженерно экономический университет им.М.Дулатова |
1 | |
| 25 | Кокшетауский университет им.Ш.Уалиханова | 42 | 1 |
| 26 | Казахский агротехнический университет им. С.Сейфуллина | 98 | 25 |
| 27 | Кызылординский университет имени Коркыт Ата | 1 | |
| 28 | Казахстанско-Российский медицинский университет | 8 | |
| 29 | Костанайский региональный университет им.А.Байтурсынова | 17 | 5 |
| 30 | Казахский Университет Путей Сообщения | 3 | |
| 31 | Медицинский университет г.Семей | 10 | |
| 32 | Казахская национальная академия хореографии | 3 | |
| 33 | Казахский национальный университет искусств | 12 | |
| 34 | Междунардный университет Астана | ||
| 35 | Южно-Казахстанский университет им. М. Ауэзова М. Ауэзова |
34 | 5 |
| 36 | Международный казахско-турецкий университет имени Х.А.Ясави | 13 | 1 |
| 37 | Международная образовательная корпорация | 25 | 2 |
| 38 | Медицинский университет Астана | 40 | |
| 39 | Университет «Нархоз» | 8 | |
| 40 | Египетский университет исламской культуры Нур-Мубарак | 26 | 3 |
| 41 | Рудненский индустриальный институт | 6 | |
| 42 | Северо-Казахстанский университет им. М. Козыбаева | 46 | 3 |
| 43 | Казахская академия спорта и туризм | 9 | |
| 44 | Университет «Туран» | 4 | 2 |
| 45 | Павлодарский педагогический университет | 17 | 2 |
| 46 | Западно-Казахстанский государственный университет им. М.Утемисова М.Утемисова |
6 | 3 |
| 47 | Университет «Туран-Астана» | 2 | |
| 48 | Казахский университет международных отношений и мировых языков им.Абылай хана | 16 | 5 |
| 49 | Университет Международного Бизнеса | 17 | 1 |
| 50 | Каспийский университет технологий и инжиниринга имени Ш.Есенова | 17 | |
| 51 | Университет имени Шакарима г.Семей | 12 | 2 |
| 52 | Южно-Казахстанская медицинская академия | 8 | |
| 53 | ВКТУ им.Д.Серикбаева | 21 | 1 |
| 54 | Западно-Казахстанский медицинский университет имени Марата Оспанова | 6 | |
| 55 | Казахский национальный исследовательский технический университет им. К.И. Сатпаева К.И. Сатпаева |
78 | 5 |
| 56 | Жезказганский университет имени О.А.Байконурова | 1 | |
| 57 | Казахский национальный педагогический университет имени Абая | 31 | 12 |
| 58 | Таразский региональный университет им. М.Х.Дулати | 42 | |
| 59 | Торайгыров университет | 56 | 2 |
| 60 | Карагандинский технический университет | 64 | 7 |
| 61 | Университет имени Сулеймана Демиреля | 3 | |
| 62 | МУИТ | 52 | 7 |
| 63 | Казахстанско-Британский технический университет | 52 | 4 |
| 64 | Казахский национальный университет им. Аль-Фараби Аль-Фараби |
44 | 6 |
| 65 | Международный университет туризма и гостеприимства | 6 | |
| 66 | Казахский университет технологии и бизнеса | 1 | |
| 67 | Казахская академия транспорта и коммуникации им. М.Тынышпаева | 12 | |
| 68 | Казахская национальная консерватория имени Курмангазы | 6 | |
| 69 | Евразийский национальный университет им. Л.Н. Гумилева | 84 | 9 |
| 70 | Казахский Национальный Аграрный Университет | 77 | 2 |
| 71 | Медицинский университет Караганды | 30 | |
| ВСЕГО | 1617 | 134 |
Динамика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы динамики
К оглавлению. ..
..
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы. Сила характеризуется тремя параметрами: точкой приложения, модулем (численным значением) и направлением. В Международной системе единиц (СИ) сила измеряется в Ньютонах (Н). Для измерения сил используют откалиброванные пружины. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра.
Для измерения сил используют откалиброванные пружины. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
1. Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
где: g — ускорение свободного падения, m — масса тела. Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
2. Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
3. Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
4. Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
5. Сила натяжения нити. Направлена вдоль нити от тела.
6. Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Проекции сил
К оглавлению…
В большинстве задач по динамике на тело действует больше чем одна сила. Для того чтобы найти равнодействующую всех сил в этом случае можно пользоваться следующим алгоритмом:
- Найдем проекции всех сил на ось ОХ и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось ОХ.
- Найдем проекции всех сил на ось OY и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось OY.
- Результирующая всех сил будет находится по формуле (теореме Пифагора):
При этом, обратите особое внимание на то, что:
- Если сила перпендикулярна одной из осей, то проекция именно на эту ось будет равна нулю.
- Если при проецировании силы на одну из осей «всплывает» синус угла, то при проецировании этой же силы на другую ось всегда будет косинус (того же угла). Запомнить при проецировании на какую ось будет синус или косинус легко.
 Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус.
Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус. - Если сила направлена в ту же сторону что и ось, то ее проекция на эту ось будет положительной, а если сила направлена в противоположную оси сторону, то ее проекция на эту ось будет отрицательной.
Законы Ньютона
К оглавлению…
Законы динамики, описывающие влияние различных взаимодействий на движение тел, были в одной из своих простейших форм, впервые четко и ясно сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год), поэтому эти законы также называют Законами Ньютона. Ньютоновская формулировка законов движения справедлива только в инерциальных системах отсчета (ИСО). ИСО – система отсчета, связанная с телом, движущимся по инерции (равномерно и прямолинейно).
Есть и другие ограничения на применимость законов Ньютона. Например, они дают точные результаты только до тех пор, пока применяются к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика).
Первый закон Ньютона (или закон инерции)
Формулировка: В ИСО, если на тело не действуют никакие силы или действие сил скомпенсировано (то есть равнодействующая сил равна нулю), то тело сохраняет состояние покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции. Итак, причиной изменения скорости движения тела целиком или его частей всегда является его взаимодействие с другими телами. Для количественного описания изменения движения тела под воздействием других тел необходимо ввести новую величину – массу тела.
Масса – это свойство тела, характеризующее его инертность (способность сохранять скорость постоянной). В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг). Масса тела – скалярная величина. Масса также является мерой количества вещества:
Второй закон Ньютона – основной закон динамики
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела и сила. Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила – является количественной мерой действия одного тела на другое.
Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила – является количественной мерой действия одного тела на другое.
Формулировка: Ускорение, приобретаемое телом в ИСО, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе этого тела:
Однако при решении задач по динамике второй закон Ньютона целесообразно записывать в виде:
Если на тело одновременно действуют несколько сил, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил. Если равнодействующая сила равна нолю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения, т.к. ускорение будет нулевым (первый закон Ньютона).
Третий закон Ньютона
Формулировка: В ИСО тела действуют друг на друга с силами, равными по модулю и противоположными по направлению, лежащими на одной прямой и имеющими одну физическую природу:
Эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга. Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Алгоритм решения задач по динамике
Задачи по динамике решаются с помощью законов Ньютона. Рекомендуется следующий порядок действий:
1. Проанализировав условие задачи, установить, какие силы действуют и на какие тела;
2. Показать на рисунке все силы в виде векторов, то есть направленных отрезков, приложенных к телам, на которые они действуют;
3. Выбрать систему отсчета, при этом полезно одну координатную ось направить туда же, куда направлено ускорение рассматриваемого тела, а другую – перпендикулярно ускорению;
4. Записать II закон Ньютона в векторной форме:
5. Перейти к скалярной форме уравнения, то есть записать все его члены в том же порядке в проекциях на каждую из осей, без знаков векторов, но учитывая, что силы, направленные против выбранных осей будут иметь отрицательные проекции, и, таким образом, в левой части закона Ньютона они будут уже вычитаться, а не прибавляться. В результате получатся выражения вида:
В результате получатся выражения вида:
6. Составить систему уравнений, дополнив уравнения, полученные в предыдущем пункте, в случае необходимости, кинематическими или другими простыми уравнениями;
7. Провести далее все необходимые математические этапы решения;
8. Если в движении участвует несколько тел, анализ сил и запись уравнений производится для каждого из них по отдельности. Если в задаче по динамике описывается несколько ситуаций, то подобный анализ производится для каждой ситуации.
При решении задач учитывайте также следующее: направление скорости тела и равнодействующей сил необязательно совпадают.
Сила упругости
К оглавлению…
Деформацией называют любое изменение формы или размеров тела. Упругими называют такие деформации, при которых тело полностью восстанавливает свою форму после прекращения действия деформирующей силы. Например, после того, как груз сняли с пружины, её длина в недеформированном состоянии не изменилась. При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При малых деформациях сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
где: k – жесткость тела, х – величина растяжения (или сжатия, деформации тела), оно равно разности между конечной и начальной длиной деформируемого тела. И не равно ни начальной ни конечной его длине в отдельности. Жесткость не зависит ни от величины приложенной силы, ни от деформации тела, а определяется только материалом, из которого изготовлено тело, его формой и размерами. В системе СИ жесткость измеряется в Н/м.
Утверждение о пропорциональности силы упругости и деформации называют законом Гука. В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
Таким образом, у каждого конкретного тела (а не материала) есть своя жесткость и она не изменяется для данного тела. Таким образом, если у Вас в задаче по динамике несколько раз растягивали одну и ту же пружину Вы должны понимать, что ее жесткость во всех случаях была одна и та же. С другой стороны если в задаче было несколько пружин разных габаритов, но, например, все они были стальные, то тем не менее у них у всех будут разные жесткости. Так как жесткость не является характеристикой материала, то ее нельзя найти ни в каких таблицах. Жесткость каждого конкретного тела будет либо Вам дана в задаче по динамике, либо ее значение должно стать предметом некоторых дополнительных изысканий при решении данной задачи.
При сжатии сила упругости препятствует сжатию, а при растяжении – препятствует растяжению. Рассмотрим также то, как можно выразить жесткость нескольких пружин соединенных определённым образом. При параллельном соединении пружин общий коэффициент жесткости рассчитывается по формуле:
При последовательном соединении пружин общий коэффициент жесткости может быть найден из выражения:
Вес тела
К оглавлению…
Силу тяжести, с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни в неправильном смысле, под весом подразумевается масса, однако это не так.
Весом тела называют силу, с которой тело действует на опору или подвес. Вес – сила, которая, как и все силы, измеряется в ньютонах (а не в килограммах), и обозначается P. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Согласно третьему закону Ньютона вес зачастую равен либо силе реакции опоры (если тело лежит на опоре), либо силы натяжении нити или силе упругости пружины (если тело висит на нити или пружине). Сразу оговоримся — вес не всегда равен силе тяжести.
Сразу оговоримся — вес не всегда равен силе тяжести.
Невесомость – это состояние, которое наступает, когда вес тела равен нолю. В этом состоянии тело не действует на опору, а опора на тело.
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Перегрузка рассчитывается по формуле:
где: P – вес тела, испытывающего перегрузку, P0 – вес этого же тела в состоянии покоя. Перегрузка – безразмерная величина. Это хорошо видно из формулы. Поэтому не верьте писателям-фантастам, которые в своих книгах измеряют ее в g.
Запомните, что вес никогда не изображается на рисунках. Он просто вычисляется по формулам. А на рисунках изображается сила натяжения нити либо сила реакции опоры, которые по третьему закону Ньютона численно равны весу, но направлены в другую сторону.
Итак, отметим еще раз три существенно важных момента в которых часто путаются:
- Несмотря на то, что вес и сила реакции опоры равны по величине и противоположны по направлению, их сумма не равна нулю.
 Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
Эти силы вообще нельзя складывать, т.к. они приложены к разным телам. - Нельзя путать массу и вес тела. Масса – собственная характеристика тела, измеряется в килограммах, вес – это сила действия на опору или подвес, измеряется в Ньютонах.
- Если надо найти вес тела Р, то сначала находят силу реакции опоры N, или силу натяжения нити Т, а по третьему закону Ньютона вес равен одной из этих сил и противоположен по направлению.
Сила трения
К оглавлению…
Трение – один из видов взаимодействия тел. Оно возникает в области соприкосновения двух тел при их относительном движении или попытке вызвать такое движение. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
где: μ – безразмерная величина, называемая коэффициентом трения покоя, а N – сила реакции опоры.
Если внешняя сила больше максимального значения силы трения, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения. Силу трения скольжения можно считать равной максимальной силе трения покоя.
Коэффициент пропорциональности μ поэтому называют также коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Коэффициент трения положителен и меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки их поверхностей. Таким образом коэффициент трения является неким конкретным числом для каждой конкретной пары взаимодействующих тел. Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Если в рамках решения задачи у Вас получается коэффициент трения больше единицы или отрицательный – Вы неправильно решаете эту задачу по динамике.
Если в условии задачи просят найти минимальную силу, под действием которой начинается движение, то ищут максимальную силу, под действием которой, движение ещё не начинается. Это позволяет приравнять ускорение тел к нулю, а значит значительно упростить решение задачи. При этом силу трения полагают равной ее максимальному значению. Таким образом рассматривается момент, при котором увеличение искомой силы на очень малую величину сразу вызовет движение.
Особенности решения задач по динамике с несколькими телами
К оглавлению…
Связанные тела
Алгоритм решения задач по динамике в которых рассматриваются несколько тел связанных нитями:
- Сделать рисунок.

- Записать второй закон Ньютона для каждого тела в отдельности.
- Если нить нерастяжима (а так в большинстве задач и будет), то ускорения всех тел будут одинаковы по модулю.
- Если нить невесома, блок не имеет массы, трение в оси блока отсутствует, то сила натяжения одинакова в любой точке нити.
Движение тела по телу
В задачах этого типа важно учесть, что сила трения на поверхности соприкасающихся тел действует и на верхнее тело, и на нижнее тело, то есть силы трения возникают парами. При этом они направлены в разные стороны и имеют равную величину, определяемую весом верхнего тела. Если нижнее тело тоже движется, то необходимо учитывать, что на него также действует сила трения со стороны опоры.
Вращательное движение
К оглавлению…
При движении тела по окружности независимо от того, в какой плоскости происходит движение, тело будет двигаться с центростремительным ускорением, которое будет направлено к центру окружности, по которой движется тело. При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
1. Выбрав оси, записать закон Ньютона в проекциях на каждую ось, для каждого из тел, участвующих в задаче, или для каждой из ситуаций, описываемых в задаче.
2. Если это необходимо, дополнить систему уравнений нужными уравнениями из других тем по физике. Особенно хорошо нужно помнить формулу для центростремительного ускорения:
3. Решить полученную систему уравнений математическими методами.
Так же есть ряд задач на вращение в вертикальной плоскости на стержне или нити. На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
Движение на нити. Так как нить только растягиваться, то при движении тела на нити в вертикальной плоскости в нити будет возникать только деформация растяжения и, как следствие, сила упругости, возникающая в нити, будет всегда направлена к центру окружности.
Движение тела на стержне. Стержень, в отличие от нити, может сжиматься. Поэтому в верхней точке траектории скорость тела, прикрепленного к стержню, может быть равна нулю, в отличии от нити, где скорость должна быть не меньше определенного значения, чтобы нить не сложилась. Силы упругости, возникающие в стержне, могут быть направлены как к центру окружности, так и в противоположную сторону.
Поворот машины. Если тело движется по твердой горизонтальной поверхности по окружности (например, автомобиль проходит поворот), то силой, которая удерживает тело на траектории, будет являться сила трения. При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
Закон всемирного тяготения. Спутники
К оглавлению…
Все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними. Таким образом закон всемирного тяготения в виде формулы выглядит следующим образом:
Такая запись закона всемирного тяготения справедлива для материальных точек, шаров, сфер, для которых r измеряется между центрами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной. В системы СИ он равен:
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле или другой планете. Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если же удалиться от поверхности Земли на некоторое расстояние h, то ускорение свободного падения на этой высоте станет равно (при помощи нехитрых преобразований можно также получить соотношение между ускорением свободного падения на поверхности планеты и ускорением свободного падения на некоторой высоте над поверхностью планеты):
Рассмотрим теперь вопрос об искусственных спутниках планет. Искусственные спутники движутся за пределами атмосферы (если таковая у планеты имеется), и на них действуют только силы тяготения со стороны планеты. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой орбите практически на нулевой высоте над планетой. Радиус орбиты таких спутников (расстояние между центром планеты и точкой где находится спутник) можно приближенно принять равным радиусу планеты Rп. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу планеты. Для спутников, движущихся по круговым траекториям на значительном удалении от планеты, гравитационное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника в таком случае находится с помощью формулы:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Если речь идёт о планете Земля, то нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Основы кинематики точки (Лекция 8)
Кинематикой называется та часть механики, в которой изучаются зависимости между величинами, характеризующими состояние систем, но не рассматриваются причины вызывающие изменение состояние движения.
Кинематика точки. Декартовы координаты.
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 31).
Рис.31.
Точка , где
– параметрические уравнения траектории.
где — единичные векторы (орты),
— непрерывны и 2 раза дифференцируемы; 2-е производные
– непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время:
или:
Введём понятия скорости и ускорения:
Рис.32.
т. М t
т. М’ t + t
(t — конечное).
Радиусы – векторы: t
t + t +
=
За время t (рис. 32):
(Направление по секущей MM’).
Скорость точки в момент времени t получается при t 0, то есть
(Направление по касательной и траектории точки)
Очевидно:
Проекции :
.
Модуль (длина):
Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
33).
Рис.33.
Совмещая начало векторов (t) и (t + t) в точке М => за t.
Среднее ускорение:
(направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при t 0, то есть
Очевидно:
Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы.
Часто их называют позиционными. Криволинейными они называются потому, что линии
вдоль которых меняется только одна координата, обычно бывают кривыми.
Криволинейными они называются потому, что линии
вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
Рис.34.
(x, y) – декартовы координаты.
(r, ) – полярные координаты.
Угол => от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos, y = r sin, где r 0; 0
(можно рассматривать и ).
Если r = const – концентрические окружности с центром в точке О.
Если = const – прямолинейные лучи из точки О.
Введём два орта:
Найдём производные по углу (рис. 35):
Рис.35.
(так как r = 1)
при ,
т. е. .
е. .
Далее:
при ,
т.е. .
При каждом дифференцировании по φ т. е. происходит поворот на угол .
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как , то
Но:
Очевидно:
Для ускорения:
.
Но: .
Очевидно:
Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
Дальше…
Движение с постоянным ускорением
При равноускоренном движении справедливы следующие уравнения, которые мы приводим без вывода:
| = o t + ½ t² | ⇒ | sx = υox t + ½ ax t² | ||
| sy = υoy t + ½ ay t² |
Как вы понимаете, векторная формула слева и две скалярные формулы справа равноправны. С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).
С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).
Зная, что sx = x – xo и sy = y – yo (см. § 12-е), из двух скалярных формул из правой верхней колонки получим уравнения для координат:
| x = xo + υox t + ½ ax t² | и | y = yo + υoy t + ½ ay t² |
Поскольку ускорение при равноускоренном движении тела постоянно, то координатные оси всегда можно расположить так, чтобы вектор ускорения был направлен параллельно одной оси, например оси Y. Следовательно, уравнение движения вдоль оси X заметно упростится:
x = xo + υox t + ( 0 ) и y = yo + υoy t + ½ ay t²
Обратите внимание, что левое уравнение совпадает с уравнением равномерного прямолинейного движения (см. § 12-ж). Это означает, что равноускоренное движение может «складываться» из равномерного движения вдоль одной оси и равноускоренного движения вдоль другой. Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).
Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).
Задача. Вытянув руки, девочка подбросила шар. Он поднялся на 80 cм и вскоре упал к ногам девочки, пролетев 180 cм. С какой скоростью шар был подброшен и какую скорость шар имел при ударе о землю?
Рекомендация. Для решения задач, в которых не дано время и не просят его найти, очень удобно применять не содержащую время формулу для квадрата проекции мгновенной скорости. Выведем эту формулу.
Возведём в квадрат обе части уравнения для проекции на ось Y мгновенной скорости: υy = υoy + ay t (см. § 12-и). Получим равенство:
υy² = ( υoy + ay t )² = υoy² + 2 υoy ay t + ay² t²
Вынесем за скобки множитель 2 ay только для двух правых слагаемых:
υy² = υoy² + 2 ay ( υoy t + ½ ay t² )
Заметим, что в скобках получилась формула для вычисления проекции перемещения: sy = υoy t + ½ ay t². Заменяя её на sy , получим:
| υy² = υoy² + 2 ay sy |
Решение. Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:
Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:
0 = υoy² + 2·(–g)·(+h) ⇒ υoy = ±√¯2gh = +4 м/с
Затем при начале движения из верхней точки вниз:
υy² = 0 + 2·(–g)·(–H) ⇒ υy = ±√¯2gh = –6 м/с
Ответ: шар был брошен вверх со скоростью 4 м/с, а в момент приземления имел скорость 6 м/с, направленную против оси Y.
Примечание. Надеемся, вы понимаете, что формула для квадрата проекции мгновенной скорости будет верна по аналогии и для оси X:
| υx² = υox² + 2 ax sx |
Если движение одномерное, то есть происходит только вдоль одной оси, можно пользоваться любой из двух формул в рамках.
К зачету физика 10-1
10 класс
Материалы к зачету по теме «
Основные законы механики «1. Механическое движение.
Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.
Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:
,
где — начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.
Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.
Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.
2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.
Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:
.
Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:
.
Координату тела находят по формуле:
.
Проекцию перемещения находят по формуле:
.
Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.
Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
.
| Так как | , то для координаты тела х имеем: |
При вычислениях по приведенным формулам знаки проекций векторов , а также знак начальной координаты х, определяются условием задачи и направлением оси координат.
3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение.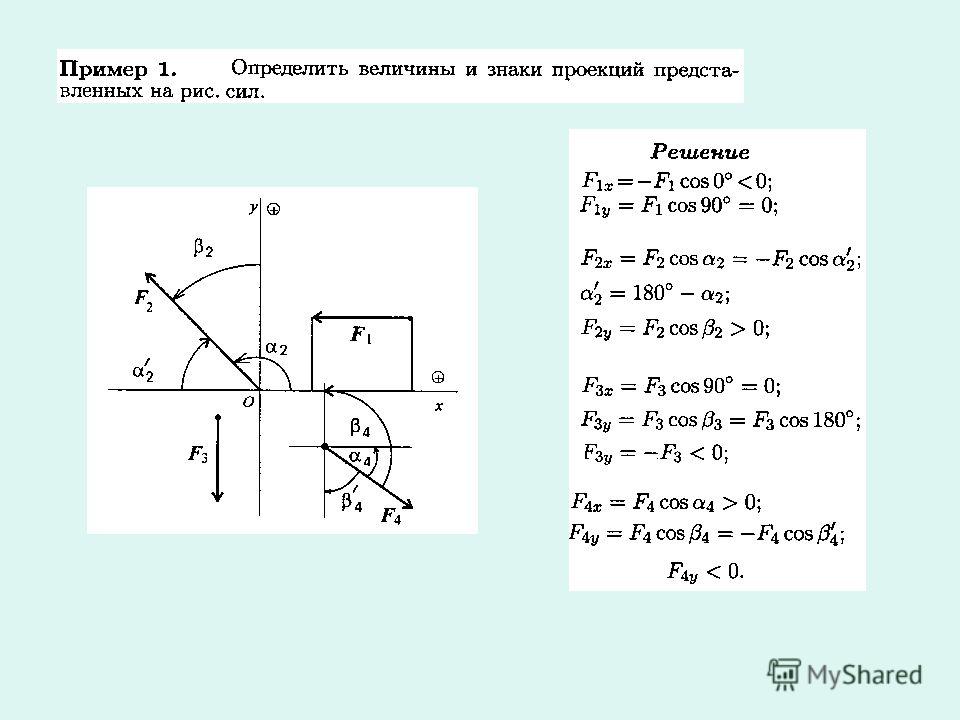 Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Связь между линейной и угловой скоростью выражается формулой:
,
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:
.
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.
Пример решения задачи:
1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.
Решите задачи самостоятельно:
1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?
2. 9 км/ч = … м/с; 10 м/с = … км/ч; 8 км/с = … км/ч, 54 км/ч = …м/с.
3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.
Попробуйте решить задачи из раздела «Кинематика»
вернуться на страницу «Физика» | вверх |
Движение снаряда | Безграничная физика
Основные уравнения и параболический путь
Движение снаряда — это форма движения, при которой объект движется по параболической траектории; путь, по которому следует объект, называется его траекторией.
Цели обучения
Оценить влияние угла и скорости на траекторию полета снаряда; получить максимальную высоту, используя смещение
Основные выводы
Ключевые моменты
- Объекты, которые проецируются с одной и той же горизонтальной поверхности и приземляются на нее, будут иметь вертикально симметричный путь.
- Время, необходимое для проецирования объекта и приземления, называется временем полета. Это зависит от начальной скорости снаряда и угла проекции.
- Когда снаряд достигает нулевой вертикальной скорости, это максимальная высота снаряда, а затем сила тяжести берет верх и ускоряет объект вниз.
- Горизонтальное смещение снаряда называется дальностью полета снаряда и зависит от начальной скорости объекта.
Ключевые термины
- траектория : путь тела, движущегося в пространстве.
- симметричный : проявление симметрии; наличие гармоничного или пропорционального расположения частей; имеющие соответствующие части или отношения.

Движение снаряда
Движение снаряда — это форма движения, при которой объект движется по двусторонне симметричной параболической траектории. Путь, по которому следует объект, называется его траекторией.Движение снаряда происходит только тогда, когда в начале траектории действует одна сила, после которой единственное препятствие — сила тяжести. В предыдущем разделе мы обсуждали, каковы различные компоненты объекта, движущегося снарядом. В этом атоме мы обсудим основные уравнения, которые идут вместе с ними в особом случае, когда начальные положения снаряда равны нулю (т.е. [latex] \ text {x} _0 = 0 [/ latex] и [latex] \ text { y} _0 = 0 [/ latex]).
Начальная скорость
Начальная скорость может быть выражена как компоненты x и компоненты y:
[латекс] \ text {u} _ \ text {x} = \ text {u} \ cdot \ cos \ theta \\ \ text {u} _ \ text {y} = \ text {u} \ cdot \ sin \ theta [/ latex]
В этом уравнении [latex] \ text {u} [/ latex] обозначает начальную величину скорости, а [latex] \ small {\ theta} [/ latex] обозначает угол полета снаряда.
Время полета
Время полета снаряда — это время от момента проецирования объекта до момента его достижения поверхностью. Как мы обсуждали ранее, [латекс] \ text {T} [/ latex] зависит от начальной величины скорости и угла полета снаряда:
[латекс] \ displaystyle {\ text {T} = \ frac {2 \ cdot \ text {u} _ \ text {y}} {\ text {g}} \\ \ text {T} = \ frac {2 \ cdot \ text {u} \ cdot \ sin \ theta} {\ text {g}}} [/ latex]
Разгон
При движении снаряда ускорение в горизонтальном направлении отсутствует.Ускорение [latex] \ text {a} [/ latex] в вертикальном направлении обусловлено только силой тяжести, также известной как свободное падение:
[латекс] \ displaystyle {\ text {a} _ \ text {x} = 0 \\ \ text {a} _ \ text {y} = — \ text {g}} [/ latex]
Скорость
Горизонтальная скорость остается постоянной, но вертикальная скорость изменяется линейно, потому что ускорение постоянно. В любой момент, [latex] \ text {t} [/ latex], скорость будет:
[латекс] \ displaystyle {\ text {u} _ \ text {x} = \ text {u} \ cdot \ cos {\ theta} \\ \ text {u} _ \ text {y} = \ text {u } \ cdot \ sin {\ theta} — \ text {g} \ cdot \ text {t}} [/ latex]
Вы также можете использовать теорему Пифагора, чтобы найти скорость:
[латекс] \ text {u} = \ sqrt {\ text {u} _ \ text {x} ^ 2 + \ text {u} _ \ text {y} ^ 2} [/ latex]
Рабочий объем
В момент времени t компоненты смещения равны:
[латекс] \ displaystyle {\ text {x} = \ text {u} \ cdot \ text {t} \ cdot \ cos \ theta \\ \ text {y} = \ text {u} \ cdot \ text {t } \ cdot \ sin \ theta- \ frac12 \ text {gt} ^ 2} [/ latex]
Уравнение для величины смещения: [латекс] \ Delta \ text {r} = \ sqrt {\ text {x} ^ 2 + \ text {y} ^ 2} [/ latex]. 2 \ theta} {2 \ cdot \ text {g}} [/ latex]
2 \ theta} {2 \ cdot \ text {g}} [/ latex]
Диапазон
Диапазон движения фиксируется условием [latex] \ small {\ sf {\ text {y} = 0}} [/ latex].2 \ cdot \ sin2 \ theta} {\ text {g}} [/ latex].
Диапазон траектории : Диапазон траектории показан на этом рисунке.
Снаряды под углом : Это видео дает четкое и простое объяснение того, как решить проблему со снарядами, запущенными под углом. Я стараюсь шаг за шагом пройти через эту сложную задачу до верстки, как решить ее очень понятным способом. На решение двухмерных кинематических задач нужно время, запишите, как я их решил.С наилучшими пожеланиями. Чтобы получить дополнительную помощь, посмотрите другие мои видео. Мир.
Решение проблем
При движении снаряда объект движется по параболической траектории; Путь, по которому следует объект, называется его траекторией.
Цели обучения
Определить, какие компоненты важны для определения движения снаряда объекта
Основные выводы
Ключевые моменты
- При решении задач, связанных с движением снаряда, мы должны помнить все ключевые компоненты движения и основные уравнения, которые им сопутствуют.
- Используя эту информацию, мы можем решать множество различных типов проблем, если мы можем анализировать предоставленную нам информацию и использовать основные уравнения для ее решения.
- Чтобы очистить два столба одинаковой высоты и выяснить, какое расстояние между ними, нам нужно помнить, что траектория имеет параболическую форму и что есть два разных момента, когда объект достигает высоты столбов .
- Когда мы имеем дело с объектом, летящим на наклонной плоскости, нам сначала нужно использовать данную информацию, чтобы переориентировать систему координат, чтобы объект запускался и падал на одну и ту же поверхность.
Ключевые термины
- переориентировать : заново сориентировать; повернуться лицом в другую сторону
Мы ранее обсуждали движение снаряда, его ключевые компоненты и основные уравнения. Используя эту информацию, мы можем решить множество проблем, связанных с движением снаряда. Прежде чем мы это сделаем, давайте рассмотрим некоторые ключевые факторы, которые будут влиять на решение проблемы.
Используя эту информацию, мы можем решить множество проблем, связанных с движением снаряда. Прежде чем мы это сделаем, давайте рассмотрим некоторые ключевые факторы, которые будут влиять на решение проблемы.
Что такое движение снаряда?
Движение снаряда — это движение объекта по двусторонне симметричной параболической траектории.Путь, по которому следует объект, называется его траекторией. Движение снаряда происходит только тогда, когда вначале действует одна сила, после которой единственное влияние на траекторию — это сила тяжести.
Каковы ключевые компоненты движения снаряда?
Ключевые компоненты, которые мы должны помнить для решения проблем движения снаряда:
- Начальный угол запуска, [латекс] \ theta [/ latex]
- Начальная скорость, [латекс] \ text {u} [/ latex]
- Время полета, [латекс] \ text {T} [/ latex]
- Ускорение, [латекс] \ text {a} [/ latex]
- Горизонтальная скорость, [латекс] \ text {v} _ \ text {x} [/ latex]
- Вертикальная скорость, [латекс] \ text {v} _ \ text {y} [/ latex]
- Смещение, [латекс] \ text {d} [/ latex]
- Максимальная высота, [латекс] \ text {H} [/ latex]
- Диапазон, [латекс] \ text {R} [/ latex]
youtube.com/embed/M8xCj2VPHas?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Как решить любую проблему движения снаряда (Метод Toolbox) : Представляем метод «Toolbox» для решения проблем движения снаряда! Здесь мы используем кинематические уравнения и модифицируем начальные условия, чтобы создать «набор инструментов» уравнений, с помощью которых можно решить классическую трехчастную задачу о движении снаряда.
Теперь давайте рассмотрим два примера проблем, связанных с движением снаряда.
Примеры
Пример 1
Допустим, вам дан объект, который должен расчистить две стойки одинаковой высоты, разделенные определенным расстоянием. Обратитесь к этому примеру. Снаряд метается со скоростью [латекс] 25 \ sqrt {2} [/ latex] м / с под углом 45 °. Если цель — очистить обе стойки, каждая высотой 30 м, найдите минимум: (а) положение катера на земле по отношению к стойкам и (б) расстояние между стойками. Для простоты используйте гравитационную постоянную 10. Проблемы любого типа в физике намного легче решить, если вы перечислите то, что вам известно («данность»).
Для простоты используйте гравитационную постоянную 10. Проблемы любого типа в физике намного легче решить, если вы перечислите то, что вам известно («данность»).
Диаграмма для примера 1 : Используйте этот рисунок как ссылку для решения примера 1. Проблема состоит в том, чтобы убедиться, что объект может очистить обе стойки.
Решение: Первое, что нам нужно сделать, это выяснить, в какое время [latex] \ text {t} [/ latex] объект достигает указанной высоты. Поскольку движение имеет параболическую форму, это произойдет дважды: один раз при движении вверх и еще раз, когда объект движется вниз.2} [/ латекс]
Мы можем использовать квадратное уравнение, чтобы найти, что корни этого уравнения равны 2s и 3s. Это означает, что снаряд достигнет 30 метров через 2 секунды, на пути вверх, и через 3 секунды, на пути вниз.
Пример 2
Объект запускается с основания склона под углом 30 °. Если угол пуска составляет 60 ° от горизонтали и скорость пуска составляет 10 м / с, каково общее время полета? Приведена следующая информация: [латекс] \ text {u} = 10 \ frac {\ text {m}} {\ text {s}} [/ latex]; [латекс] \ theta = 60 [/ латекс] °; [латекс] \ text {g} = 10 \ frac {\ text {m}} {\ text {s} ^ 2} [/ latex].
Диаграмма для примера 2 : Когда мы имеем дело с объектом, летящим на наклонной плоскости, нам сначала нужно использовать данную информацию, чтобы переориентировать систему координат, чтобы объект запускался и падал на одну и ту же поверхность.
Решение: чтобы учесть угол наклона, мы должны переориентировать систему координат так, чтобы точки проецирования и возврата находились на одном уровне. Угол проецирования по отношению к направлению [латекс] \ text {x} [/ latex] составляет [latex] \ theta — \ alpha [/ latex], а ускорение в [latex] \ text {y} [/ латекс] направление [латекс] \ текст {g} \ cdot \ cos {\ alpha} [/ латекс].Мы заменяем [latex] \ theta [/ latex] на [latex] \ theta — \ alpha [/ latex] и [latex] \ text {g} [/ latex] на [latex] \ text {g} \ cdot \ cos {\ alpha} [/ latex]:
[латекс] \ displaystyle {{\ text {T} = \ frac {2 \ cdot \ text {u} \ cdot \ sin (\ theta)} {\ text {g}} = \ frac {2 \ cdot \ text {u} \ cdot \ sin (\ theta- \ alpha)} {\ text {g} \ cdot \ cos (\ alpha)} = \ frac {2 \ cdot 10 \ cdot \ sin (60-30)} {10 \ cdot \ cos (30)}} = \ frac {20 \ cdot \ sin (30)} {10 \ cdot \ cos (30)} \\ \ text {T} = \ frac2 {\ sqrt3} \ text {s }} [/ latex]
Нулевой угол пуска
Объект, запущенный горизонтально на высоте [latex] \ text {H} [/ latex], проходит диапазон [latex] \ text {v} _0 \ sqrt {\ frac {2 \ text {H}} {\ text {g }}} [/ latex] во время полета [latex] \ text {T} = \ sqrt {\ frac {2 \ text {H}} {\ text {g}}} [/ latex].
Цели обучения
Объясните взаимосвязь между дальностью полета и временем полета
Основные выводы
Ключевые моменты
- Для нулевого угла пуска вертикальная составляющая начальной скорости отсутствует.
- Продолжительность полета до того, как объект упадет на землю, определяется как T = \ sqrt {\ frac {2H} {g}}.
- В горизонтальном направлении объект движется с постоянной скоростью v 0 во время полета.Диапазон R (в горизонтальном направлении) задается как: [latex] \ text {R} = \ text {v} _0 \ cdot \ text {T} = \ text {v} _0 \ sqrt {\ frac {2 \ текст {H}} {\ text {g}}} [/ latex].
Ключевые термины
- траектория : путь тела, движущегося в пространстве.
Движение снаряда — это форма движения, при которой объект движется по параболической траектории. Путь, по которому следует объект, называется его траекторией. Движение снаряда происходит при приложении силы в начале траектории запуска (после этого на снаряд действует только сила тяжести).
Одним из ключевых компонентов движения снаряда и траектории, по которой он следует, является начальный угол пуска . Угол, под которым запускается объект, определяет дальность, высоту и время полета объекта во время движения снаряда. показывает разные траектории для одного и того же объекта, запускаемого с одинаковой начальной скоростью и разными углами запуска. Как показано на рисунке, чем больше начальный угол запуска и максимальная высота, тем больше время полета объекта.
Траектории снаряда : Угол запуска определяет дальность и максимальную высоту, которую объект будет испытывать после запуска. На этом изображении показан путь того же объекта, запускаемого с одинаковой скоростью, но под разными углами.
Ранее мы обсуждали влияние различных углов запуска на дальность, высоту и время полета. Однако что будет, если нет угла, а объект просто запускается горизонтально? Имеет смысл запускать объект с определенной высоты ([latex] \ text {H} [/ latex]), иначе он не пролетел бы очень далеко, прежде чем ударился о землю. Давайте посмотрим, как перемещается объект, запущенный горизонтально на высоте [latex] \ text {H} [/ latex]. В нашем случае, когда [latex] \ alpha [/ latex] равно 0.
Давайте посмотрим, как перемещается объект, запущенный горизонтально на высоте [latex] \ text {H} [/ latex]. В нашем случае, когда [latex] \ alpha [/ latex] равно 0.
Движение снаряда : Снаряд движется по параболе. Начальный угол запуска равен [latex] \ alpha [/ latex], а скорость [latex] \ text {v} _0 [/ latex].
Продолжительность рейса
В начальной скорости нет вертикальной составляющей ([latex] \ text {v} _0 [/ latex]), потому что объект запускается горизонтально.2 [/ латекс]
Здесь [latex] \ text {T} [/ latex] — это продолжительность полета до того, как объект достигнет земли. Следовательно:
[латекс] \ displaystyle \ text {T} = \ sqrt {\ frac {2 \ text {H}} {\ text {g}}} [/ latex]
Диапазон
В горизонтальном направлении объект движется с постоянной скоростью [latex] \ text {v} _0 [/ latex] во время полета. Следовательно, диапазон [латекс] \ текст {R} [/ латекс] (в горизонтальном направлении) задается как:
[латекс] \ displaystyle \ text {R} = \ text {v} _0 \ cdot \ text {T} = \ text {v} _0 \ sqrt {\ frac {2 \ text {H}} {\ text {g }}} [/ latex]
Общий угол пуска
Начальный угол запуска (0-90 градусов) объекта, движущегося снарядом, определяет дальность, высоту и время полета этого объекта. 2 \ sin2 \ theta_ \ text {i}} {\ text {g}} [/ latex].2}) [/ латекс].
2 \ sin2 \ theta_ \ text {i}} {\ text {g}} [/ latex].2}) [/ латекс].
Ключевые термины
- траектория : путь тела, движущегося в пространстве.
Движение снаряда — это форма движения, при которой объект движется по двусторонне симметричной параболической траектории. Путь, по которому следует объект, называется его траекторией. Движение снаряда происходит только тогда, когда в начале траектории действует одна сила, после которой единственное препятствие — сила тяжести.
Одним из ключевых компонентов движения снаряда и траектории, по которой он следует, является начальный угол запуска.Этот угол может быть от 0 до 90 градусов. Угол, под которым запускается объект, определяет дальность, высоту и время полета, которые он будет испытывать при движении снаряда. показаны разные траектории одного и того же объекта, запущенного с одинаковой начальной скоростью под разными углами запуска. Как видно из рисунка, чем больше начальный угол запуска, тем ближе объект к максимальной высоте и тем больше время полета. Наибольшая дальность полета будет наблюдаться при угле пуска до 45 градусов.2 \ theta_ \ text {i}} {2 \ text {g}}}} \\ \ small {\ sf {\ text {T} = \ frac {2 \ text {v} _ \ text {i} sin \ тета} {\ text {g}}}} [/ latex]
Наибольшая дальность полета будет наблюдаться при угле пуска до 45 градусов.2 \ theta_ \ text {i}} {2 \ text {g}}}} \\ \ small {\ sf {\ text {T} = \ frac {2 \ text {v} _ \ text {i} sin \ тета} {\ text {g}}}} [/ latex]
где R — дальность полета, h — максимальная высота, T — время полета, v i — начальная скорость, θ i — начальный угол пуска, g — сила тяжести.
Теперь, когда мы понимаем, как угол запуска играет важную роль во многих других компонентах траектории объекта, движущегося снарядом, мы можем применить эти знания, чтобы заставить объект приземлиться там, где мы хотим. Если существует определенное расстояние d, на которое вы хотите, чтобы ваш объект прошел, и вы знаете начальную скорость, с которой он будет запущен, начальный угол запуска, необходимый для достижения этого расстояния, называется углом досягаемости.2})}} [/ латекс]
Ключевые моменты: дальность, симметрия, максимальная высота
Движение снаряда — это форма движения, при которой объект движется по параболической траектории. Путь, по которому следует объект, называется его траекторией.
Путь, по которому следует объект, называется его траекторией.
Цели обучения
Построить модель движения снаряда, указав время полета, максимальную высоту и дальность
Основные выводы
Ключевые моменты
- Объекты, которые проецируются с одной и той же горизонтальной поверхности и приземляются на нее, будут иметь путь, симметричный относительно вертикальной линии, проходящей через точку на максимальной высоте снаряда.
- Время, необходимое для проецирования объекта и приземления, называется временем полета. Это зависит от начальной скорости снаряда и угла проекции.
- Максимальная высота снаряда — это когда снаряд достигает нулевой вертикальной скорости. С этого момента вертикальная составляющая вектора скорости будет направлена вниз.
- Горизонтальное смещение снаряда называется дальностью полета снаряда и зависит от начальной скорости объекта.
- Если объект проецируется с одинаковой начальной скоростью, но с двумя дополнительными углами проецирования, дальность полета снаряда будет одинаковой.

Ключевые термины
- гравитация : Результирующая сила притяжения земных масс на поверхности Земли и центробежная псевдосила, вызванная вращением Земли.
- траектория : путь тела, движущегося в пространстве.
- двусторонняя симметрия : свойство быть симметричным относительно вертикальной плоскости
Что такое движение снаряда?
Движение снаряда — это форма движения, при которой объект движется по двусторонне симметричной параболической траектории.Путь, по которому следует объект, называется его траекторией. Движение снаряда происходит только тогда, когда в начале траектории действует одна сила, после которой единственное препятствие — сила тяжести. В этом атоме мы собираемся обсудить, каковы различные компоненты объекта в движении снаряда, мы обсудим основные уравнения, которые идут вместе с ними в другом атоме, «Основные уравнения и параболический путь»
Ключевые компоненты движения снаряда:
Время полета, Т:
Время полета снаряда в точности соответствует звуку. Это время от момента проецирования объекта до момента, когда он достигает поверхности. Время полета зависит от начальной скорости объекта и угла проекции, [латекс] \ тета [/ латекс]. Когда точка проекции и точка возврата находятся в одной горизонтальной плоскости, чистое вертикальное смещение объекта равно нулю.
Это время от момента проецирования объекта до момента, когда он достигает поверхности. Время полета зависит от начальной скорости объекта и угла проекции, [латекс] \ тета [/ латекс]. Когда точка проекции и точка возврата находятся в одной горизонтальной плоскости, чистое вертикальное смещение объекта равно нулю.
Симметрия:
Все снаряды движутся по двусторонне симметричной траектории, пока точки выброса и возврата происходят по одной и той же горизонтальной поверхности.Двусторонняя симметрия означает, что движение симметрично в вертикальной плоскости. Если бы вы провели прямую вертикальную линию от максимальной высоты траектории, она бы отразила себя вдоль этой линии.
Максимальная высота, H:
Максимальная высота объекта на траектории снаряда возникает, когда вертикальный компонент скорости, [latex] \ text {v} _ \ text {y} [/ latex], равен нулю. По мере того, как снаряд движется вверх, он движется против силы тяжести, и поэтому его скорость начинает замедляться.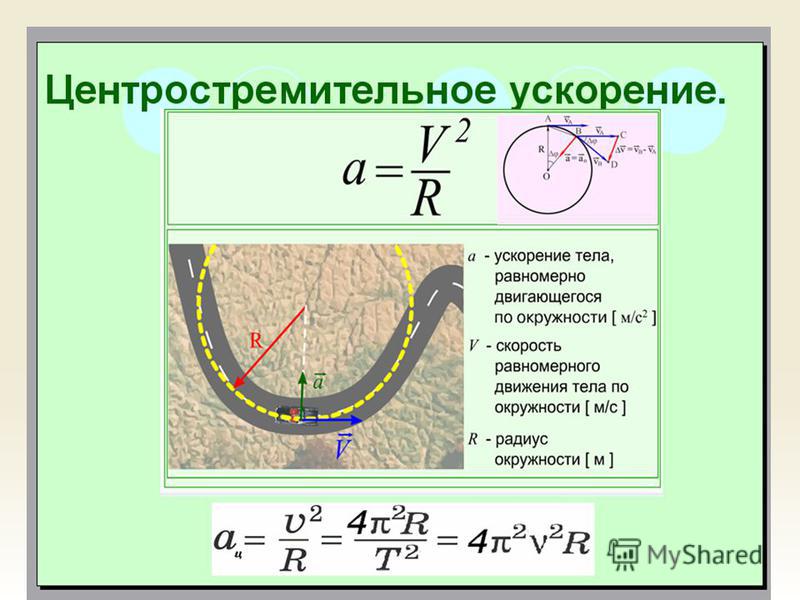 В конце концов вертикальная скорость достигнет нуля, и снаряд немедленно ускоряется вниз под действием силы тяжести. Когда снаряд достигает максимальной высоты, он начинает ускоряться вниз. Это также точка, в которой вы должны провести вертикальную линию симметрии.
В конце концов вертикальная скорость достигнет нуля, и снаряд немедленно ускоряется вниз под действием силы тяжести. Когда снаряд достигает максимальной высоты, он начинает ускоряться вниз. Это также точка, в которой вы должны провести вертикальную линию симметрии.
Дальность снаряда, R:
Дальность полета снаряда — смещение в горизонтальном направлении. В этом направлении нет ускорения, поскольку сила тяжести действует только вертикально. показывает линию диапазона.Подобно времени полета и максимальной высоте, дальность полета снаряда зависит от начальной скорости.
Диапазон : диапазон движения снаряда, как видно на этом изображении, не зависит от сил тяжести.
4.3 Движение снаряда — Университетская физика, том 1
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка снаряд запускается в воздух с начальной скоростью 70,0 м / с под углом 75,0 ° и 75,0 ° над горизонтом, как показано на рисунке 4. 13. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
13. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?Рис. 4.13. Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальные и вертикальные движения, в которых ax = 0ax = 0 и ay = −g.ay = −g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти желаемые величины.Решение
(a) Под «высотой» мы подразумеваем высоту или вертикальное положение y над начальной точкой. Наивысшая точка любой траектории, называемая апексом , достигается, когда vy = 0. vy = 0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2 = v0y2−2g (y − y0).vy2 = v0y2−2g (y − y0).
vy = 0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2 = v0y2−2g (y − y0).vy2 = v0y2−2g (y − y0).Поскольку y0y0 и vyvy оба равны нулю, уравнение упрощается до
0 = v0y2−2gy. 0 = v0y2−2gy.Решение y дает
Теперь мы должны найти v0y, v0y, составляющую начальной скорости в направлении y . Он задается формулами v0y = v0sinθ0, v0y = v0sinθ0, где v0v0 — начальная скорость 70,0 м / с, а θ0 = 75 ° θ0 = 75 ° — начальный угол. Таким образом,
v0y = v0sinθ = (70,0 м / с) sin75 ° = 67,6 м / sv0y = v0sinθ = (70,0 м / с) sin75 ° = 67,6 м / си и равно
у = (67.6 м / с) 22 (9,80 м / с2). Y = (67,6 м / с) 22 (9,80 м / с2).Таким образом, имеем
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательное. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом.На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом.На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других задачах физики, существует более одного способа решения, пока снаряд достигает своей наивысшей точки. В этом случае самый простой способ — использовать vy = v0y − gt.vy = v0y − gt. Поскольку vy = 0vy = 0 на вершине, это уравнение сводится к просто
или
t = v0yg = 67,6 м / с 9,80 м / с2 = 6,90 с. t = v0yg = 67,6 м / с 9,80 м / с2 = 6.90-е гг. Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что до взрыва снаряда проходит несколько секунд. Другой способ найти время — использовать y = y0 + 12 (v0y + vy) t.y = y0 + 12 (v0y + vy) t. Это оставлено вам в качестве упражнения.
Другой способ найти время — использовать y = y0 + 12 (v0y + vy) t.y = y0 + 12 (v0y + vy) t. Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивление воздуха незначительно, ax = 0ax = 0 и горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время, как задано формулой x = x0 + vxt, x = x0 + vxt, где x0x0 равно нулю.Таким образом,
, где vxvx — это составляющая скорости x , равная
. vx = v0cosθ = (70,0 м / с) cos75 ° = 18,1 м / с. vx = v0cosθ = (70,0 м / с) cos75 ° = 18,1 м / с.Время t для обоих движений одинаково, поэтому x равно
x = (18,1 м / с) 6,90 с = 125 м. x = (18,1 м / с) 6,90 с = 125 м. Горизонтальное движение — это постоянная скорость при отсутствии сопротивления воздуха. Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей. | s → | = 1252 + 2332 = 264m | s → | = 1252 + 2332 = 264m
Φ = tan − 1 (233125) = 61,8 °. Φ = tan − 1 (233125) = 61,8 °.
| s → | = 1252 + 2332 = 264m | s → | = 1252 + 2332 = 264m
Φ = tan − 1 (233125) = 61,8 °. Φ = tan − 1 (233125) = 61,8 °.
Обратите внимание, что угол для вектора смещения меньше, чем начальный угол запуска. Чтобы понять, почему это так, просмотрите Рис. 4.11, на котором показана кривизна траектории к уровню земли.
снарядов — Математика A-Level, версия
Данный раздел охватывает доработку снарядов.
Когда частица выбрасывается из земли, она будет следовать по изогнутой траектории, прежде чем упасть на землю.Насколько далеко перемещается частица, будет зависеть от скорости проецирования и угла проецирования.
Уравнения сувата могут быть адаптированы для решения задач, связанных со снарядами.
Разберем общий случай. Частица проецируется со скоростью u (м / с) под углом a к горизонтали:
Диапазон
Дальность (R) снаряда — это горизонтальное расстояние, которое он проходит во время движения.
Теперь s = ut + ½ at 2
Используя это уравнение по вертикали, мы получаем, что a = -g (ускорение свободного падения), а начальная скорость в вертикальном направлении — usina (путем разрешения).Следовательно:
Используя уравнение по горизонтали:
Помните, что нет ускорения по горизонтали, поэтому здесь a = 0.
Когда частица возвращается на землю, y = 0. Подставляя это в (1):
0 = utsina — ½ gt 2
t (usina — ½ gt) = 0
t = 0 или t = 2u sina (3)
g
Следовательно, когда x = R, t = 2u sina / g
Подставляя в (2):
R = ucosa (2u sina)
г
Следовательно, диапазон составляет
Время полета
Время, когда мяч находится в воздухе, определяется формулой (3).
Время полета =
Максимальный диапазон
Если частица проецируется с фиксированной скоростью, она перемещается на наибольшее расстояние по горизонтали, если она проецируется под углом 45 ° к горизонтали. Это связано с тем, что максимальное значение sin2a может быть равно 1, а sin2a = 1 при a = 45 °.
Это связано с тем, что максимальное значение sin2a может быть равно 1, а sin2a = 1 при a = 45 °.
Скорость
Скорость частицы в любой момент может быть вычислена по уравнению v = u + at.
Применяя это уравнение по горизонтали, мы находим:
Применяя его по вертикали, мы находим:
Чтобы определить скорость или направление частицы в любой момент движения, найдите горизонтальную и вертикальную составляющие скорости, используя приведенные выше формулы и используйте теорему Пифагора:
Пример
Ядро стреляет под углом 30 ° к горизонтали со скоростью 25 мс -1 .
а) Сколько времени осталось до удара?
б) Как далеко пролетит ядро, прежде чем ударится о землю?
а) Когда частица падает на землю, y = 0.
с = ut + ½ при 2
Применяя это уравнение по вертикали, когда частица ударяется о землю:
0 = 25Tsin30 — ½ gT 2 (где T — время полета)
Следовательно, T (25sin30 — ½ gT) = 0
Таким образом, T = 0 или T = (50sin30) / g
Следовательно, время полета 2. 55с (3сф)
55с (3сф)
b) Диапазон может быть найден исходя из горизонтального расстояния, пройденного частицей за время T, найденное в части (a)
с = ut + ½ при 2
Применяя это уравнение по горизонтали:
R = 25Tcos30
= 25 × 2,55 × 0,866
= 55,231 …
Следовательно, пройденное расстояние по горизонтали составляет 55,2 м (3sf)
Проблемы с горизонтально запущенными снарядами
Одна из сильных сторон физики — это ее способность использовать принципы физики для предсказания конечного результата движения объекта.Такие прогнозы делаются путем применения физических принципов и математических формул к заданному набору начальных условий. В случае снарядов студент-физик может использовать информацию о начальной скорости и положении снаряда, чтобы предсказать такие вещи, как, сколько времени снаряд находится в воздухе и как далеко снаряд уйдет. Физические принципы, которые необходимо применять, обсуждались ранее в Уроке 2. Используемые математические формулы обычно называются кинематическими уравнениями.Комбинирование этих двух параметров позволяет делать прогнозы относительно движения снаряда. На типичном уроке физики предсказательная способность принципов и формул чаще всего демонстрируется в задачах словесного рассказа, известных как задачи со снарядами.
Используемые математические формулы обычно называются кинематическими уравнениями.Комбинирование этих двух параметров позволяет делать прогнозы относительно движения снаряда. На типичном уроке физики предсказательная способность принципов и формул чаще всего демонстрируется в задачах словесного рассказа, известных как задачи со снарядами.
В этом курсе мы обсудим два основных типа проблем со снарядами. Хотя общие принципы одинаковы для каждого типа задач, подход будет отличаться из-за того, что задачи различаются по своим начальным условиям.Есть два типа проблем:
Тип проблемы 1:Снаряд запускается с начальной горизонтальной скоростью из возвышенного положения и следует параболической траектории к земле. К предсказуемым неизвестным относятся начальная скорость снаряда, начальная высота снаряда, время полета и горизонтальное расстояние снаряда.
Примеры проблем этого типа:
- Мяч для пула оставляет 0.
 Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления шара.
Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления шара. - Футбольный мяч отбрасывается горизонтально с холма высотой 22 метра и приземляется на расстоянии 35 метров от края холма. Определите начальную горизонтальную скорость футбольного мяча.
Тип проблемы 2:
Снаряд запускается под углом к горизонтали и поднимается вверх до пика при движении по горизонтали.Достигнув пика, снаряд падает с движением, симметричным его траектории вверх к пику. Предсказуемые неизвестные включают время полета, горизонтальную дальность и высоту снаряда, когда он находится на пике.
Примеры проблем этого типа:
- Футбольный мяч бьет ногой с начальной скоростью 25 м / с под углом 45 градусов к горизонту. Определите время полета, горизонтальное расстояние и максимальную высоту футбольного мяча.

- Прыгун в длину отрывается от земли с начальной скоростью 12 м / с под углом 28 градусов относительно горизонтали. Определите время полета, горизонтальное расстояние и максимальную высоту прыгуна в длину.
Второй тип проблем будет предметом следующей части Урока 2. В этой части Урока 2 мы сосредоточимся на первом типе проблем, которые иногда называют проблемами снарядов, запускаемых горизонтально.Три общих кинематических уравнения, которые будут использоваться для обоих типов задач, включают следующее:
d = v i • t + 0,5 * a * t 2
v f = v i + a • t
v f 2 = v i 2 + 2 * а • д
| где | d = смещение | a = ускорение | t = время |
| v f = конечная скорость | v i = начальная скорость |
Уравнения горизонтального движения снаряда
Приведенные выше уравнения хорошо подходят для движения в одном измерении, но снаряд обычно движется в двух измерениях — горизонтальном и вертикальном. Поскольку эти две составляющие движения не зависят друг от друга, необходимы две совершенно разные системы уравнений — одна для горизонтального движения снаряда, а другая — для его вертикального движения. Таким образом, три приведенных выше уравнения преобразуются в две системы из трех уравнений. Для горизонтальных составляющих движения уравнения:
Поскольку эти две составляющие движения не зависят друг от друга, необходимы две совершенно разные системы уравнений — одна для горизонтального движения снаряда, а другая — для его вертикального движения. Таким образом, три приведенных выше уравнения преобразуются в две системы из трех уравнений. Для горизонтальных составляющих движения уравнения:
x = v i x • t + 0,5 * a x * t 2
v f x = v i x + a x • t
v f x 2 = v i x 2 + 2 * a x • x
| где | x = горизонт. смещение смещение | a x = горизонт. разгон | t = время |
| v f x = конечный горизонт. скорость | v i x = начальный горизонт. скорость |
Из этих трех уравнений наиболее часто используется верхнее уравнение.Применение концепции снаряда к каждому из этих уравнений также привело бы к заключению, что любой член с x в нем будет сокращаться из уравнения, поскольку x = 0 м / с / с. После отмены терминов топор единственное уравнение полезности будет:
x = v i x • t
Для вертикальных составляющих движения три уравнения:
y = v iy • t + 0. 5 * ау * т 2
5 * ау * т 2
v fy = v iy + ay • t
v fy 2 = v iy 2 + 2 * ay • y
| где | y = верт. смещение | ау = верт. разгон | t = время |
| v fy = финальная верт.скорость | v iy = начальная верт. скорость |
В каждом из приведенных выше уравнений вертикальное ускорение снаряда составляет -9,8 м / с / с (ускорение свободного падения). Кроме того, для частного случая проблем первого типа (проблемы с снарядами горизонтального запуска) v iy = 0 м / с. Таким образом, любой член с v iy будет сокращаться из уравнения.
Таким образом, любой член с v iy будет сокращаться из уравнения.
Два набора из трех приведенных выше уравнений представляют собой кинематические уравнения, которые будут использоваться для решения задач движения снаряда.
Решение проблем с снарядамиЧтобы проиллюстрировать полезность приведенных выше уравнений при прогнозировании движения снаряда, рассмотрим решение следующей проблемы.
| Пример Мяч для пула оставляет 0.Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления шара. |
Решение этой проблемы начинается с приравнивания известных или заданных значений к символам кинематических уравнений — x, y, v ix , v iy , a x , a y и t. Поскольку информация по горизонтали и вертикали используется отдельно, разумно организовать данную информацию в два столбца — один столбец для горизонтальной информации и один столбец для вертикальной информации.В этом случае в постановке проблемы либо дается, либо подразумевается следующая информация:
Поскольку информация по горизонтали и вертикали используется отдельно, разумно организовать данную информацию в два столбца — один столбец для горизонтальной информации и один столбец для вертикальной информации.В этом случае в постановке проблемы либо дается, либо подразумевается следующая информация:
| Информация по горизонтали | Вертикальная информация |
| х = ??? v ix = 2,4 м / с a x = 0 м / с / с | y = -0.60 м v iy = 0 м / с a y = -9,8 м / с / с |
Как указано в таблице, неизвестной величиной является горизонтальное смещение (и время полета) шара для пула. Решение проблемы теперь требует выбора подходящей стратегии использования кинематических уравнений и известной информации для решения неизвестных величин. Практически всегда такая стратегия требует, чтобы одно из вертикальных уравнений использовалось для определения времени полета снаряда, а затем одно из горизонтальных уравнений использовалось для определения других неизвестных величин (или наоборот — сначала используйте уравнение по горизонтали, а затем по вертикали). Организованный список известных количеств (как в таблице выше) дает подсказки для выбора стратегии. Например, таблица выше показывает, что о вертикальном движении шара для пула известно три величины.Поскольку в каждом уравнении есть четыре переменных, знание трех переменных позволяет вычислить четвертую переменную. Таким образом, было бы разумно, чтобы вертикальное уравнение использовалось с вертикальными значениями для определения времени, а затем горизонтальные уравнения использовались для определения горизонтального смещения (x). Первое вертикальное уравнение (y = v iy • t + 0,5 • a y • t 2 ) позволит определить время. Как только соответствующее уравнение выбрано, физическая проблема трансформируется в проблему алгебры.
Практически всегда такая стратегия требует, чтобы одно из вертикальных уравнений использовалось для определения времени полета снаряда, а затем одно из горизонтальных уравнений использовалось для определения других неизвестных величин (или наоборот — сначала используйте уравнение по горизонтали, а затем по вертикали). Организованный список известных количеств (как в таблице выше) дает подсказки для выбора стратегии. Например, таблица выше показывает, что о вертикальном движении шара для пула известно три величины.Поскольку в каждом уравнении есть четыре переменных, знание трех переменных позволяет вычислить четвертую переменную. Таким образом, было бы разумно, чтобы вертикальное уравнение использовалось с вертикальными значениями для определения времени, а затем горизонтальные уравнения использовались для определения горизонтального смещения (x). Первое вертикальное уравнение (y = v iy • t + 0,5 • a y • t 2 ) позволит определить время. Как только соответствующее уравнение выбрано, физическая проблема трансформируется в проблему алгебры. Подстановкой известных значений уравнение принимает вид
Подстановкой известных значений уравнение принимает вид
Поскольку первый член в правой части уравнения сводится к 0, уравнение можно упростить до
-0,60 м = (-4,9 м / с / с) • т 2Если обе части уравнения разделить на -5,0 м / с / с, уравнение станет
0,122 с 2 = т 2Вычитая квадратный корень из обеих частей уравнения, можно определить время полета .
t = 0,350 с (округлено от 0,3499 с) После определения времени можно использовать горизонтальное уравнение для определения горизонтального смещения шара для пула. Напомним, из приведенной информации, v ix = 2,4 м / с и x = 0 м / с / с. Первое горизонтальное уравнение (x = v ix • t + 0,5 • a x • t 2 ) затем можно использовать для решения относительно «x». С выбранным уравнением физическая проблема снова превращается в проблему алгебры.Подстановкой известных значений уравнение принимает вид
С выбранным уравнением физическая проблема снова превращается в проблему алгебры.Подстановкой известных значений уравнение принимает вид
Поскольку второй член в правой части уравнения сводится к 0, уравнение можно упростить до
x = (2,4 м / с) • (0,3499 с)Таким образом,
x = 0,84 м (округлено от 0,8398 м)Ответ на указанную проблему заключается в том, что шар для пула находится в воздухе 0,35 секунды и приземляется на горизонтальном расстоянии 0.84 м от края бильярдного стола.
Следующая процедура резюмирует описанный выше подход к решению проблем.
- Внимательно прочтите проблему и перечислите известную и неизвестную информацию в терминах символов кинематических уравнений. Для удобства сделайте таблицу с горизонтальной информацией с одной стороны и вертикальной информацией с другой стороны.

- Укажите неизвестное количество, для устранения которого требуется проблема.
- Выберите уравнение по горизонтали или вертикали для определения времени полета снаряда.
- Определив время, используйте одно из других уравнений, чтобы найти неизвестное. (Обычно, если для определения времени используется горизонтальное уравнение, то для определения окончательной неизвестной величины можно использовать вертикальное уравнение.)
Одно предупреждение. Использование только четырех- и пятиэтапных процедур для решения физических задач — всегда опасный подход. Проблемы с физикой обычно просто проблемы! Хотя проблемы часто можно упростить, используя короткие процедуры, подобные описанной выше, не все проблемы можно решить с помощью описанной выше процедуры.Хотя шаги 1 и 2, указанные выше, имеют решающее значение для вашего успеха в решении проблем с горизонтально запускаемыми снарядами, всегда будет проблема, которая не подходит для формы . Решение проблем — это не приготовление пищи; это не просто следование рецепту. Скорее, решение проблем требует внимательного чтения, твердого понимания концептуальной физики, критического мышления и анализа и большого количества дисциплинированной практики. Никогда не отделяйте концептуальное понимание и критическое мышление от своего подхода к решению проблем.
Скорее, решение проблем требует внимательного чтения, твердого понимания концептуальной физики, критического мышления и анализа и большого количества дисциплинированной практики. Никогда не отделяйте концептуальное понимание и критическое мышление от своего подхода к решению проблем.
Футбольный мяч отбрасывается горизонтально с холма высотой 22 метра и приземляется на расстоянии 35 метров от края холма. Определите начальную горизонтальную скорость футбольного мяча.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно.Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо Turd the Target Interactive, либо нашего симулятора движения снаряда.
 Вы можете найти их обоих в разделе Physics Interactives на нашем сайте. В игре Turd the Target Interactive учащиеся пытаются помешать Birdman решить школьное футбольное поле, точно решая задачу с горизонтально запущенным снарядом.Симулятор движения снаряда позволяет учащемуся изучать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.
Вы можете найти их обоих в разделе Physics Interactives на нашем сайте. В игре Turd the Target Interactive учащиеся пытаются помешать Birdman решить школьное футбольное поле, точно решая задачу с горизонтально запущенным снарядом.Симулятор движения снаряда позволяет учащемуся изучать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.Projectile Motion
Projectile Motion3.3. Projectile Motion
Самый большой азарт в бейсболе — это хоумран. Движение мяча по изогнутой траектории в трибуны — это распространенный тип двумерного движения, называемого «движением снаряда».«Хорошее описание такого движения часто можно получить, если предположить, что сопротивление воздуха отсутствует.
ОБЗОР КОНЦЕПЦИИ Следуя подходу, описанному на рис. 3.6, мы рассматриваем горизонтальную и вертикальную части движения отдельно. В горизонтальном направлении или по оси x движущийся объект (снаряд) не замедляется при отсутствии сопротивления воздуха. Таким образом, компонент x скорости остается постоянным на своем начальном значении или v x = v 0x , а компонент x ускорения равен x = 0 м / с 2 .Однако в вертикальном направлении или в направлении y снаряд испытывает действие силы тяжести. В результате y-составляющая скорости v y не постоянна, а изменяется. Компонент y ускорения a y — это ускорение силы тяжести вниз. Если путь или траектория снаряда близка к поверхности земли, y имеет магнитуду 9,80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равны ускорению свободного падения, как это показано в краткой концепции на рисунке 3.8 резюмирует. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
Таким образом, компонент x скорости остается постоянным на своем начальном значении или v x = v 0x , а компонент x ускорения равен x = 0 м / с 2 .Однако в вертикальном направлении или в направлении y снаряд испытывает действие силы тяжести. В результате y-составляющая скорости v y не постоянна, а изменяется. Компонент y ускорения a y — это ускорение силы тяжести вниз. Если путь или траектория снаряда близка к поверхности земли, y имеет магнитуду 9,80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равны ускорению свободного падения, как это показано в краткой концепции на рисунке 3.8 резюмирует. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
|
| Пример 2 Пакет помощи при падении |
На рис. 3.9 показан самолет, движущийся горизонтально с постоянной скоростью +115 м / с на высоте 1050 м. Направления вправо и вверх были выбраны как положительные. Самолет выпускает «посылку», которая падает на землю по кривой траектории. Не обращая внимания на сопротивление воздуха, определите время, необходимое для того, чтобы пакет упал на землю.
Рассуждения Время, необходимое для того, чтобы пакет ударился о землю, — это время, за которое пакет упал с высоты 1050 м по вертикали. При падении он движется как вправо, так и вниз, но эти две части движения происходят независимо. Поэтому мы можем сосредоточиться исключительно на вертикальной части.Заметим, что первоначально упаковка движется в горизонтальном направлении или по оси x, а не по оси y, так что v 0y = 0 м / с. Кроме того, когда пакет ударяется о землю, компонент y его смещения составляет y = –1050 м, как показано на рисунке. Это ускорение свободного падения, поэтому y = –9,80 м / с 2 . Эти данные резюмируются следующим образом:
С этими данными можно использовать уравнение 3.5b () для определения времени спада.
Решение Поскольку v 0y = 0 м / с, это следует из уравнения 3.5b это и | ||||||||||||||||||||||
Свободно падающий пакет в Примере 2 набирает вертикальную скорость при спуске. Горизонтальная составляющая скорости, однако, сохраняет свое начальное значение v 0x = + 115 м / с на протяжении всего спуска. Поскольку самолет также движется с постоянной горизонтальной скоростью +115 м / с, он остается прямо над падающим пакетом. Пилот всегда видит пакет прямо под самолетом, как показано пунктирными вертикальными линиями на Рисунке 3.9 шоу. Этот результат является прямым следствием того факта, что упаковка не имеет ускорения в горизонтальном направлении. На самом деле сопротивление воздуха замедлит пакет, и он не останется непосредственно под самолетом во время снижения. Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке.Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета ударились о землю одновременно.
На самом деле сопротивление воздуха замедлит пакет, и он не останется непосредственно под самолетом во время снижения. Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке.Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета ударились о землю одновременно.
|
Не только пакеты на Рисунке 3. 10 достигают земли одновременно, но y-компоненты их скоростей также равны во всех точках на пути вниз. Однако пакет B ударяется о землю с большей скоростью, чем пакет A. Помните, что скорость — это величина вектора скорости, а скорость B имеет компонент x, а скорость A — нет. Величина и направление вектора скорости для пакета B в момент непосредственно перед тем, как пакет упадет на землю, вычислены в Примере 3.
10 достигают земли одновременно, но y-компоненты их скоростей также равны во всех точках на пути вниз. Однако пакет B ударяется о землю с большей скоростью, чем пакет A. Помните, что скорость — это величина вектора скорости, а скорость B имеет компонент x, а скорость A — нет. Величина и направление вектора скорости для пакета B в момент непосредственно перед тем, как пакет упадет на землю, вычислены в Примере 3.
| Пример 3 Скорость пакета Care |
Важной особенностью движения снаряда является что нет ускорения в горизонтальном направлении или в направлении оси x.В концептуальном примере 4 обсуждается интересное значение этой функции.
| Концептуальный пример 4 Я выстрелил пулей в воздух… |
Предположим, вы едете в кабриолете с опущенным верхом.
Обсуждение и решение Если бы сопротивление воздуха присутствовало, пуля замедлилась бы и она приземлилась бы позади вас, к задней части автомобиля. Однако сопротивление воздуха отсутствует, поэтому нужно более внимательно относиться к движению пули.Перед выстрелом из винтовки пуля, винтовка и автомобиль движутся вместе, поэтому пуля и винтовка имеют такую же горизонтальную скорость, что и автомобиль. Родственное домашнее задание: Концептуальный вопрос 12, проблема 34 | |||
Концептуальное моделирование 3. 1 1 |
| |
Часто снаряды, такие как футбольные мячи и бейсбольные мячи, запускаются в воздух под углом по отношению к земле.Зная начальную скорость снаряда, можно получить большой объем информации о движении. Например, в примере 5 показано, как рассчитать максимальную высоту, достигаемую снарядом.
| Пример 5 Высота начальной точки |
Также можно найти общее время или «время зависания», в течение которого футбольный мяч на рис. 3.12 находится в воздухе. Пример 6 показывает, как определить это время.
3.12 находится в воздухе. Пример 6 показывает, как определить это время.
| Пример 6 Время полета стартового снаряда |
Еще одна важная особенность движения снаряда называется «дальностью».«Дальность, как показано на рисунке 3.12, — это горизонтальное расстояние, пройденное между пуском и приземлением, при условии, что снаряд возвращается на тот же вертикальный уровень, на котором он был выпущен. Пример 7 показывает, как получить диапазон.
| Концептуальное моделирование 3.2 |
| |
| Пример 7 Диапазон начального удара |
Диапазон в предыдущем примере зависит от угла q , по которому выстреливается снаряд выше горизонтали. Когда сопротивление воздуха отсутствует, максимальный диапазон достигается при.
| Проверьте свое понимание 3 |
| ||
В примерах, рассмотренных до сих пор, использовалась информация о начальном местоположении и скорости снаряда для определения конечного местоположения и скорости. В примере 8 рассматривается противоположная ситуация и показано, как конечные параметры могут использоваться с уравнениями кинематики для определения начальных параметров.
Бейсболист выполняет хоумран, и мяч приземляется на сиденье слева, на 7,5 м выше точки, в которую он был нанесен. Он приземляется со скоростью 36 м / с под углом 28 ° от горизонтали (см. Рисунок 3.13). Не обращая внимания на сопротивление воздуха, найдите начальную скорость, с которой мяч покидает биту.
Рассуждения Чтобы найти начальную скорость, мы должны определить ее величину (начальная скорость v 0 ) и ее направление (угол q на чертеже). Эти величины связаны с горизонтальной и вертикальной составляющими начальной скорости (v 0x и v 0y ) соотношениями Решение
Поскольку сопротивление воздуха игнорируется, горизонтальная составляющая скорости v x остается постоянной на протяжении всего движения.
При определении v 0y мы выбираем знак плюса для квадратного корня, потому что вертикальный компонент начальной скорости указывает вверх на рис. 3.13, что является положительным направлением. Начальная скорость v 0 и угол q бейсбольного мяча равны | ||||||||||||||||||||||||||
| ||
При движении снаряда величина ускорения свободного падения существенно влияет на траекторию. Например, бейсбольный мяч или мяч для гольфа на Луне полетел бы намного дальше и выше, чем на Земле, если бы был запущен с той же начальной скоростью. Причина в том, что гравитация Луны примерно в шесть раз меньше земной.
В разделе 2.6 указывается, что определенные типы симметрии относительно времени и скорости присутствуют для свободно падающих тел. Эти симметрии также обнаруживаются в движении снарядов, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, рисунок 3.14 показывает, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
Эти симметрии также обнаруживаются в движении снарядов, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, рисунок 3.14 показывает, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
|
| Концептуальный пример 9 Два способа бросить камень |
| ./../../../art/common/example_line.gif» colspan=»2″> | |||
С вершины утеса над озером человек бросает два камня.Камни имеют одинаковую начальную скорость v 0 , но камень 1 бросается вниз под углом q ниже горизонтали, а камень 2 бросается вверх под тем же углом над горизонтом, как показано на рисунке 3.15. Не обращайте внимания на сопротивление воздуха и решите, какой камень ударяет в воду с большей скоростью.
Обсуждение и решение Мы можем предположить, что камень 1, брошенный вниз, ударится о воду с большей скоростью. Родственное домашнее задание: Задачи 37, 65 | |||
Во всех примерах этого раздела снаряды движутся по криволинейной траектории.В общем, если единственное ускорение вызвано действием силы тяжести, форму траектории можно представить как параболу.
| Тест самооценки 3.1 |
| |
| Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены. |
Движение в двух измерениях
Движение снаряда — движение под действием гравитация . Если мы будем стоять на краю крыши Науки
Строя и подбрасывая мяч вверх под углом, он движется вверх, а затем
вниз по вертикали, пока он движется по горизонтали.
Это движение снаряда .
Чтобы лучше понять движение снаряда, вернемся назад. а затем посмотрите на это глазами двух разных и особенных наблюдатели.
Какое движение видит дальний наблюдатель на земля?
Этот наблюдатель находится достаточно далеко, она потеряла восприятие глубины но ясно видно, как мяч поднимается и опускается. Она наблюдает бесплатно упасть, как если бы мяч был брошен прямо вверх.Это вертикальное перемещение с постоянным разгон .
Что движение видит наблюдатель над головой? Этот наблюдатель над головой достаточно высоко, чтобы он потерял восприятие глубины, но мог ясно видеть мяч перемещается по горизонтали. Он наблюдает горизонтальное движение с постоянным скорость .
Движение снаряда, таким образом, представляет собой комбинацию вертикального движения.
с постоянным ускорением (свободное падение, которое у нас уже есть
обсуждалось) и горизонтальное движение с постоянной скоростью (которую мы
тоже понимаю).
Пример
Чтобы упростить арифметику, воспользуемся приближением g = 10 м / с 2 и бросить мяч сверху Науки Постройте и посмотрите на его скорость и положение.
Мы бросаем мяч так, чтобы он двигался вверх с начальной вертикалью. скорость v yo = 20 м / с, поэтому он движется по горизонтали с начальной горизонтальной скоростью v xo = 15 м / с.
Мы могли бы также описать это как имеющую начальную скорость v o = 25 м / с под углом 53 ° от горизонтальный.Для углов, отсчитываемых от горизонтали, мы знать
v xo = v o cosv yo = v o sin
Посмотрите на горизонтальные компоненты; посмотрите на v x . Это горизонтальное движение с постоянной скоростью.
Посмотрите на вертикальные компоненты; посмотрите на v y ‘s. Это обычное, обычное свободное падение; это вертикальная скорость с
постоянное ускорение.
Это обычное, обычное свободное падение; это вертикальная скорость с
постоянное ускорение.
А теперь бросим мяч еще раз. На этот раз мы будем посмотрите на его положение или смещение.
Эти смещения происходят от x- и y-составляющих. уравнения,
x = x o + v xo t + 1 / 2 a x т 2и
y = y o + v лет t + 1 / 2 a y t 2Параболические траектории
Другой пример
Другие примеры
Забавно и интересно смотреть на такие вещи, как Maximum.
Высота или максимальное расстояние , называемое горизонтальным Диапазон .Но, пожалуйста, относитесь к этим как к интересным примерам, чтобы
быть решенными или выведенными, а не важными формулами
запомнил.
От плоскости , как дальше будет снаряд идти?
Начнем со стрельбы снарядом с начальной скоростью. v o , то есть с начальной скоростью v o при угол . Он начинается с начала координат (x o = 0, y o = 0). Как далеко он переместится на по горизонтали , прежде чем он вернется в исходное положение? исходное вертикальное положение (y = 0) снова.
Хотя может быть более удобным или более распространенным описанием начальная скорость v o по скорости v o и угол, проще и необходимо решать уравнения в терминах x- и y-компонент начальной скорости.
v xo = v o cosv yo = v o sin
Чтобы узнать , как далеко идет , мы должны сначала узнать как долго находится в воздухе.Один из способов — посмотреть, как долго
нужно, чтобы добраться до вершины. Вверху вертикальный компонент,
y-компонента скорости равна нулю. Мы могли бы найти время
требуется, чтобы v y исчезли. Потребуется дважды на этот раз подняться и спуститься на землю.
Вверху вертикальный компонент,
y-компонента скорости равна нулю. Мы могли бы найти время
требуется, чтобы v y исчезли. Потребуется дважды на этот раз подняться и спуститься на землю.
Возможно, более прямой подход — просто найти время требуется, чтобы вернуться на землю, чтобы вернуться к y = 0. Мы знаем вертикальное движение объясняется
y = y o + v лет t + 1 / 2 a y t 2с ускорением
а y = — ги
v лет = v o sinи
y o = 0Следовательно,
y = 0 + (v o sin) т — 1 / 2 г т 2Мы установим это равным нулю, y = 0, и решим для времени т,
(v o sin) т — 1 / 2 г т 2 = 0[(v o sin) t — 1 / 2 г t] t = 0
Есть два решения,
t = 0и
t до = t = (2 v o sin) / грамм Оба эти момента «верны». Первый, t = 0, относится к
начальный момент, когда снаряд ушел y = 0. Второй,
t до , относится ко времени, когда снаряд попадает обратно на y = 0; вот что интересно.
Первый, t = 0, относится к
начальный момент, когда снаряд ушел y = 0. Второй,
t до , относится ко времени, когда снаряд попадает обратно на y = 0; вот что интересно.
Как далеко, по горизонтали, переместился снаряд в этом время?
х = v х тДиапазон = X макс = x (t до ) = v xo t tot = (v o cos) (2 v o sin) / г
X макс. = 2 v o 2 cos грех / г
Так как это выражение содержит
потому что грехи
потому что = грех (90 o — ) это означает, что диапазон одинаков для угла и
для его дополнительного угла (90 o -).То есть при той же начальной скорости v o начальные углы
30 o и 60 o обеспечивают такой же диапазон. Начальные углы 20 o и 70 o обеспечивают
тот же диапазон.
Начальные углы 20 o и 70 o обеспечивают
тот же диапазон.
Мы можем немного поиграть с идентификаторами триггеров и вспомнить, что
2 cos грех = грех 2, чтобы переписать уравнение диапазона как
X макс = v o 2 sin 2 / граммИз этой формы уравнения дальности мы также можем видеть, что максимальное значение диапазона приходится на
знак равно 45 o, поскольку максимальное значение sin 2 равно 1.0 когда 2 90 o , или = 45 o .
Другой пример
Движение снаряда не обязательно должно начинаться и заканчиваться горизонтальная плоскость. Мы уже забросили мяч сверху Научный корпус и наблюдал, как он упал на землю на 25 м ниже. А теперь давайте бросим камень со дна обрыва и спросим, где он приземляется на землю выше.
Камень брошен с начальной скоростью 30 м / с под углом
60 o над горизонтом. Как показано на эскизе, это
брошен со дна каньона и поднимается в воздух, а затем приземляется
на плато, 20 м. выше дна каньона. Где это
ударился о землю? Или как далеко он проходит по горизонтали?
Как показано на эскизе, это
брошен со дна каньона и поднимается в воздух, а затем приземляется
на плато, 20 м. выше дна каньона. Где это
ударился о землю? Или как далеко он проходит по горизонтали?
Возможно, первое, что нужно сделать, — это переформулировать начальную скорость по составляющим; мы знаем
v xo = v o cosv xo = (30 м / с) (0,50)
v xo = 15 м / с
и
v лет = v o sinv лет = (30 м / с) (0.866)
v yo = 26 м / с
Прежде чем мы сможем ответить, «как далеко» он пролетел, проще спросить «как долго» оно витает в воздухе? Мы знаем, что его y-позиция задана по
y = y o + v лет t + 1 / 2 a y t 2 Нам нужно время, в течение которого координата y находится на плато,
y = 20 м.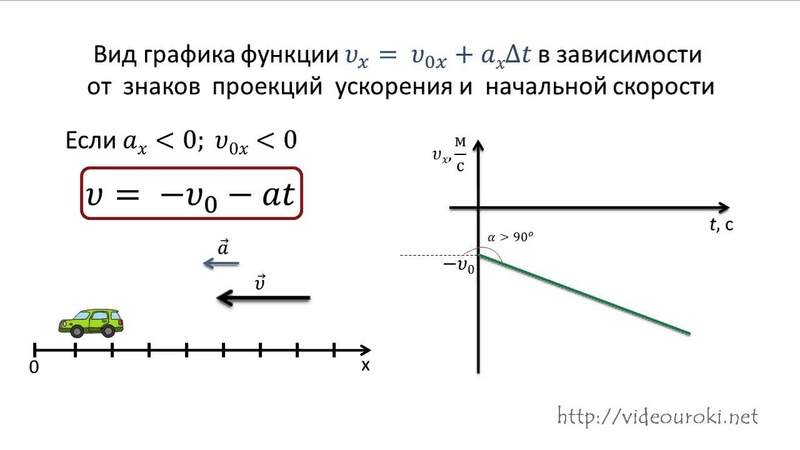
20 м = (26 м / с) t + 1 / 2 (- 9.8 м / с 2 ) т 2
20 м = (26 м / с) t — (4,9 м / с 2 ) t 2
20 = 26 т — 4,9 т 2
4,9 т 2 — 26 т + 20 = 0
Решите это из квадратного уравнения:
t 1 = 0,9 ст 2 = 4,4 с
Что означают эти два раза? t 1 есть время, когда скала на своем пути пересекает уровень плато вверх .t 2 — время, когда скала находится на плато на свой путь вниз ; t 2 — это когда он приземляет на плато. Это то время, которое мы хотим. Как далеко он продвинулся по горизонтали за это время?
X макс = v xo t 2X макс = (15 м / с) (4,4 с)
X макс. = 66 м
= 66 м
Формулы движения снаряда
Снаряд — это объект, которому задана начальная скорость, и на который действует сила тяжести.Путь, по которому следует объект, определяется этими эффектами (без учета сопротивления воздуха). Этот путь и есть траектория объекта. Траектория имеет горизонтальную (x) и вертикальную (y) компоненты. Скорость — это вектор (у нее есть величина и направление), поэтому общую скорость объекта можно найти с помощью векторного сложения компонентов x и y: v 2 = v x 2 + v y 2 . Единицы измерения горизонтального и вертикального расстояний — метры (м).Горизонтальная и вертикальная скорости выражаются в метрах в секунду (м / с).
Расстояние по горизонтали
горизонтальное расстояние = (начальная горизонтальная скорость) (время)
x = v xo т
Расстояние по вертикали
Горизонтальная скорость
горизонтальная скорость = начальная горизонтальная скорость
v x = v xo
Вертикальная скорость
вертикальная скорость = начальная вертикальная скорость — (ускорение свободного падения) (время)
v y = v год — gt
x = горизонтальное расстояние (м)
y = расстояние по вертикали (м)
v = скорость (комбинированные компоненты, м / с)
v x = горизонтальная скорость (м / с)
v y = вертикальная скорость (м / с)
v xo = начальная горизонтальная скорость (м / с)
v yo = начальная вертикальная скорость (м / с)
t = время (с)
г = ускорение свободного падения (9. 80 м / с 2 )
80 м / с 2 )
Формулы движения снаряда Вопросы:
1) Ребенок сбивает футбольный мяч с вершины холма. Начальная скорость мяча 15,0 м / с по горизонтали. Какова величина скорости мяча через 5,00 с?
Ответ: Скорость мяча через 5,00 с имеет две составляющие. Как только эти два компонента найдены, их необходимо объединить с помощью векторного сложения, чтобы найти конечную скорость. Мяч был нанесен горизонтально, поэтому v xo = 15.0 м / с, и v лет = 0,0 м / с. Компонент x скорости после 5,00 с:
v x = v xo
, а компонент y:
v y = v год — gt
v y = (0,0 м / с) — (9,80 м / с 2 ) (5,00 с)
v y = -49,0 м / с
В задачах о движении снаряда вверх определяется как положительное направление, поэтому компонент y имеет величину 49.0 м / с по направлению вниз.
Чтобы найти величину скорости, необходимо сложить компоненты x и y с векторным сложением:
v 2 = v x 2 + v y 2
v 2 = (15,0 м / с) 2 + (-49,0 м / с) 2
v 2 = 2626 (м / с) 2
∴ v = 51.24 м / с
Величина скорости 51,24 м / с.
Хотя в вопросе этого не требовалось, также можно найти направление скорости в виде угла. Если горизонтальное направление равно 0,0 радиана, угол можно найти с помощью уравнения:
tanθ = -3,267
∴
θ = -1,274 радиан
θ = -72,98 °
Следовательно, скорость (величина и направление) мяча после 5.00 с было 51,24 м / с, -72,98 ° вниз от горизонтали.
2) Игрушечная ракета запускается в плоском поле, направленном под углом 60,0 ° вверх от горизонтальной оси (x). Его начальная скорость составляет 20,0 м / с. Сколько времени игрушечная ракета проводит в воздухе и как далеко от точки старта она приземляется в поле?
Его начальная скорость составляет 20,0 м / с. Сколько времени игрушечная ракета проводит в воздухе и как далеко от точки старта она приземляется в поле?
Ответ: Первое, что необходимо найти для решения этой проблемы, — это начальная скорость в направлениях x и y. Приведенная скорость имеет компоненты x и y, потому что она имеет направление 60.0 ° вверх от горизонтального (x) направления. Начальная скорость может быть разбита с помощью уравнения, связывающего синус и косинус:
1 = cos 2 θ + sin 2 θ
Умножаем обе части на квадрат начальной скорости v o 2 :
( v o 2 ) (1) = ( v o 2 ) ( cos 2 θ ) + ( v o ) ( sin 2 θ )
v o 2 = ( v o cosθ ) 2 + ( v o sinθ ) 2
Уравнение векторного сложения начальных компонент скорости:
v o 2 = v xo 2 + v лет 2
Итак, компоненты скорости можно установить равными частям приведенного выше уравнения:
v xo 2 = ( v o cosθ ) 2
∴ v xo = v o cosθ
и v лет 2 = ( v o sinθ ) 2
∴ v лет = v o sinθ
Итак, начальная скорость в направлении x v xo составляет:
v xo = v o cosθ
v xo = (20. 0 м / с) (cos60 °)
0 м / с) (cos60 °)
v xo = 10,0 м / с
, а начальная скорость в направлении y:
v лет = v o sinθ
v лет = (20,0 м / с) (sin60 °)
v лет = 17,32 м / с
Чтобы определить, как долго игрушечная ракета находилась в воздухе, используйте уравнение для вертикального расстояния для ракеты:
Поле ровное, поэтому ракета снова ударится о землю при y = 0.00 мин. Итак, установите левую часть уравнения равной этой высоте:
(-4,90 м / с 2 ) t 2 + (17,32 м / с) t + 0,00 м = 0
Это имеет форму квадратного уравнения с t в качестве переменной:
Если на 2 + bt + c = 0,.
Есть два решения для t, в зависимости от того, выбрано положительное или отрицательное значение в символе ±. Решаем для каждого:
т + = 0.

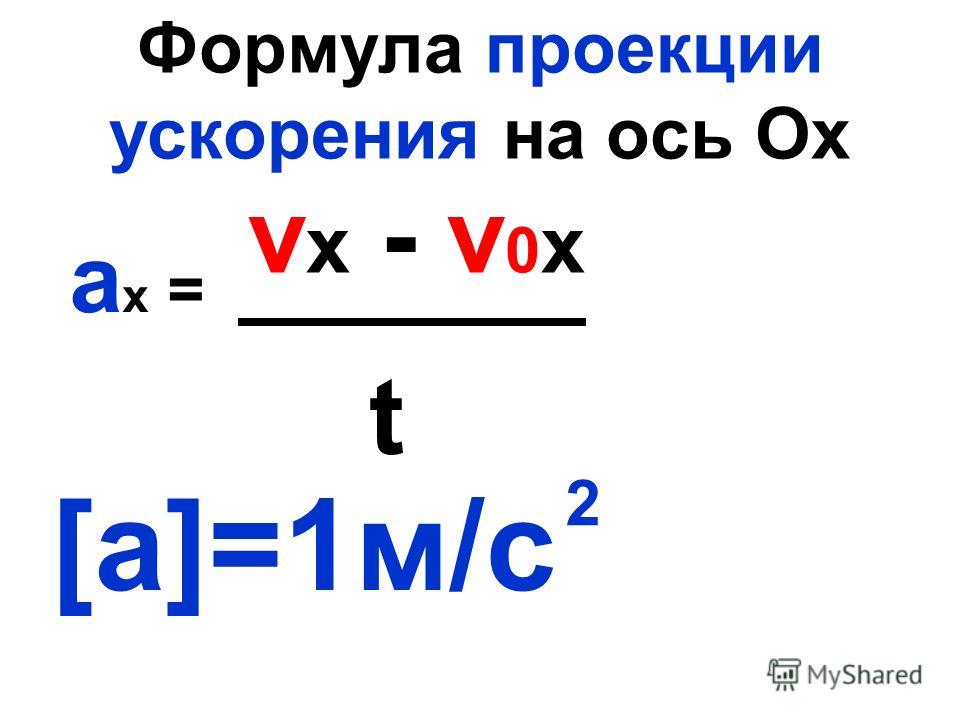 Например,
Например,  В этом случае искомые интервалы времени или расстояния удобно находить как разность интервалов времени или расстояний, отсчитанных от начала движения. Например, зависимость координаты автомобиля от времени в задаче 2.2.5 дается соотношением
В этом случае искомые интервалы времени или расстояния удобно находить как разность интервалов времени или расстояний, отсчитанных от начала движения. Например, зависимость координаты автомобиля от времени в задаче 2.2.5 дается соотношением

 По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось
По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось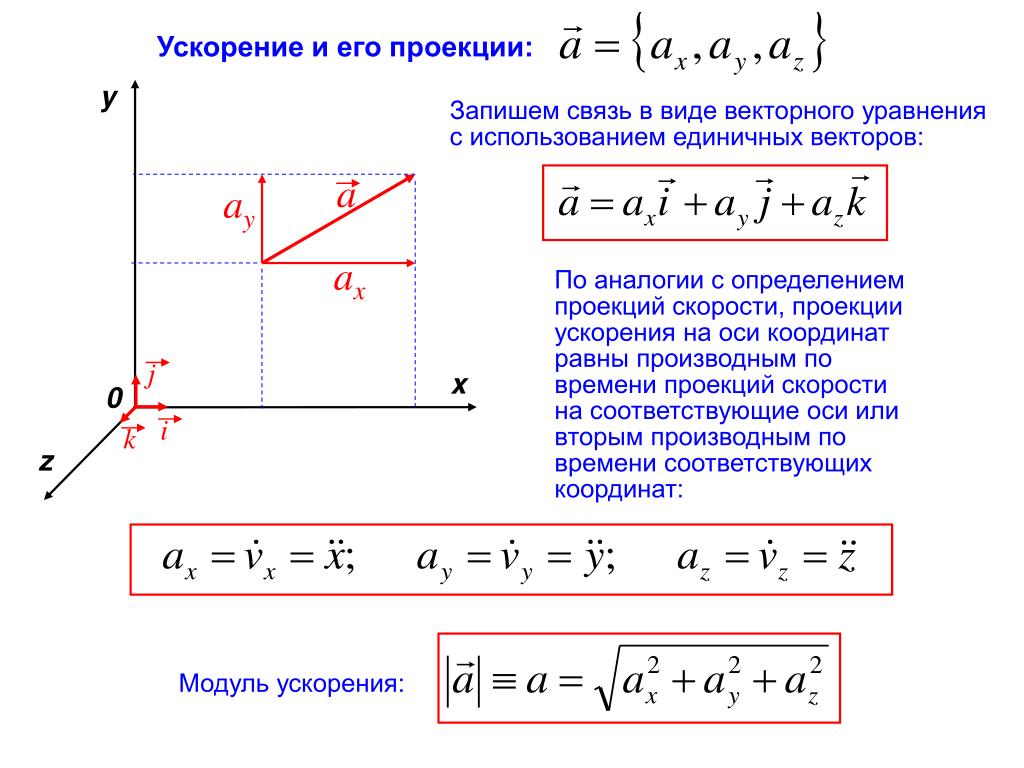 В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение
В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус.
Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус. Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.


 Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления шара.
Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления шара.
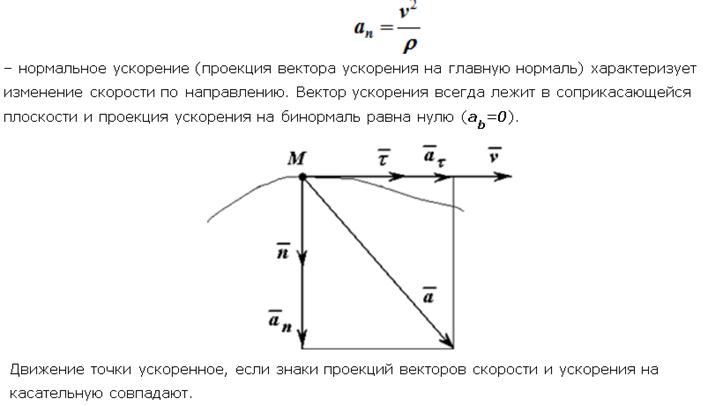
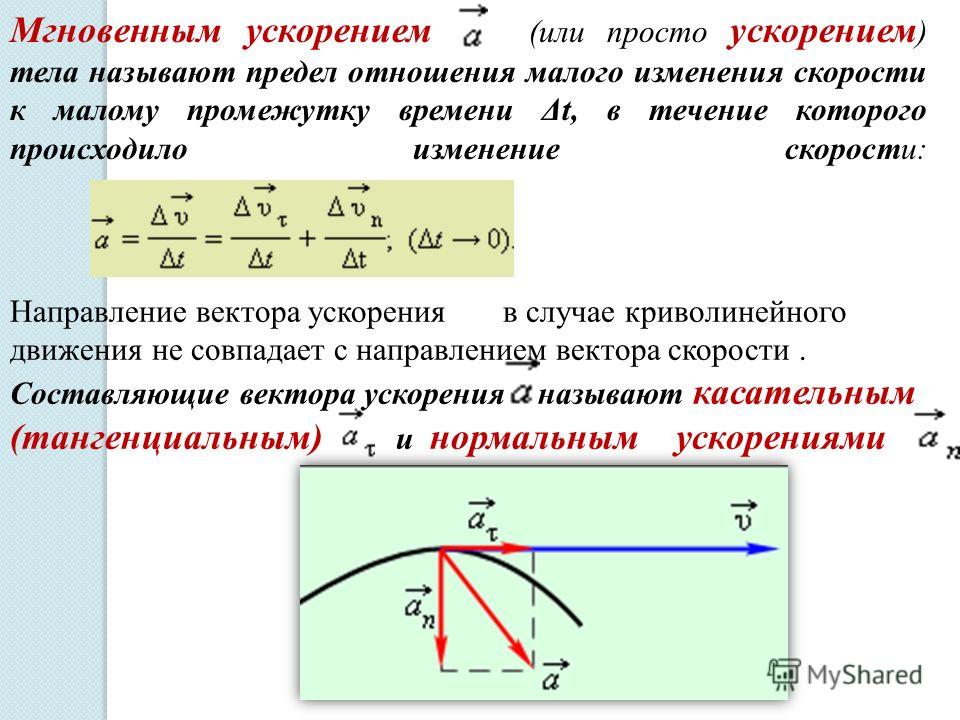 8
ОБЗОР КОНЦЕПЦИИ При движении снаряда горизонтальная или x-составляющая ускорения равна нулю, а вертикальная или y-составляющая ускорения — это ускорение свободного падения. На этой покадровой фотографии кошка демонстрирует движение снаряда в воздухе, предполагая, что эффекты сопротивления воздуха можно игнорировать.(© Стивен Далтон / Фотоисследователи).
8
ОБЗОР КОНЦЕПЦИИ При движении снаряда горизонтальная или x-составляющая ускорения равна нулю, а вертикальная или y-составляющая ускорения — это ускорение свободного падения. На этой покадровой фотографии кошка демонстрирует движение снаряда в воздухе, предполагая, что эффекты сопротивления воздуха можно игнорировать.(© Стивен Далтон / Фотоисследователи).
 Следовательно, для обозначения направления с каждым из них должен стоять алгебраический знак (+ или -).
Следовательно, для обозначения направления с каждым из них должен стоять алгебраический знак (+ или -). Автомобиль движется вправо с постоянной скоростью. Как показано на рис. 3.11, вы наводите винтовку прямо вверх и стреляете из нее. Где бы пуля приземлилась при отсутствии сопротивления воздуха — позади вас, впереди вас или в стволе винтовки?
Автомобиль движется вправо с постоянной скоростью. Как показано на рис. 3.11, вы наводите винтовку прямо вверх и стреляете из нее. Где бы пуля приземлилась при отсутствии сопротивления воздуха — позади вас, впереди вас или в стволе винтовки? При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость автомобиля в качестве своей начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не изменяется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате, пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается непосредственно под плоскостью.
При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость автомобиля в качестве своей начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не изменяется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате, пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается непосредственно под плоскостью. Моделирование также отображает графики положения и скорости как функции времени.
Моделирование также отображает графики положения и скорости как функции времени.

 Таким образом,
Таким образом, 5 м
5 м  Однако эта траектория отличалась от того, что было бы на Земле, потому что ускорение свободного падения на Луне примерно в шесть раз меньше, чем на Земле. Рассмотрим тот же шар на земле, запущенный под тем же углом и с одинаковой скоростью. Найдите отношение (а) максимальной высоты лунного шара к максимальной высоте земного шара и (б) расстояния между лунным шаром и земным шаром.
Однако эта траектория отличалась от того, что было бы на Земле, потому что ускорение свободного падения на Луне примерно в шесть раз меньше, чем на Земле. Рассмотрим тот же шар на земле, запущенный под тем же углом и с одинаковой скоростью. Найдите отношение (а) максимальной высоты лунного шара к максимальной высоте земного шара и (б) расстояния между лунным шаром и земным шаром. Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается к своей исходной высоте; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью.
Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается к своей исходной высоте; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью.
Leave A Comment