Ускорение свободного падения — формулы, примеры и определение
Покажем, как применять знание физики в жизни
Начать учиться
138.2K
Чем отличается яблоко, упавшее в Алматы, от такого же яблока в Осло? Тем, что в этих городах разное ускорение свободного падения! Что это такое и как его вычислить — отвечаем в статье.
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
Сила тяжести — сила, с которой Земля притягивает все тела.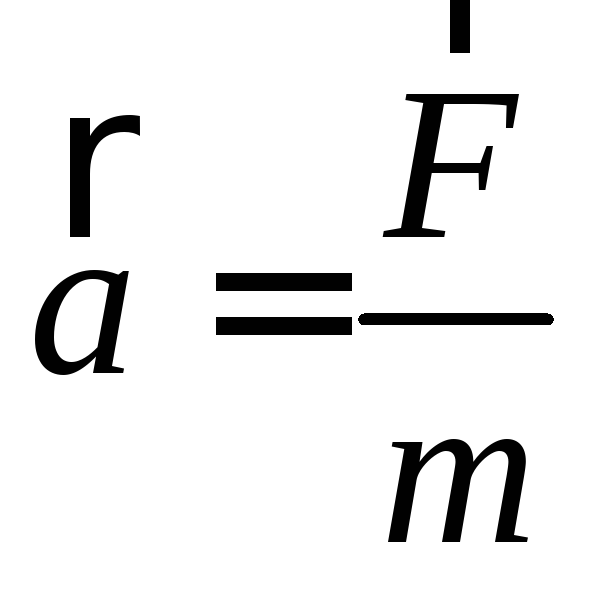
Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] |
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору или подвес. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается.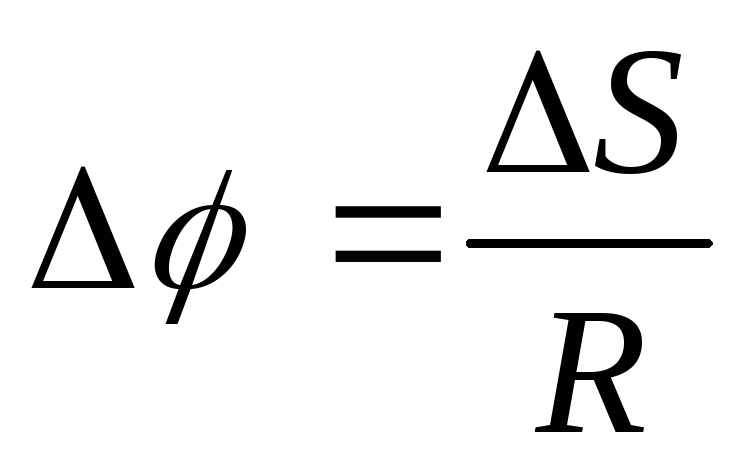 Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу тела левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
g — ускорение свободного падения [м/с2] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2 |
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
- Гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2 - Масса Земли
M = 5,97 × 1024 кг - Радиус Земли
R = 6371 км
Подставим значения в формулу:
Есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с
В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 м/с2, в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело | Диаметр, км | Расстояние до Солнца, миллионы км | Масса, кг | Соотношение с массой Земли | |
|---|---|---|---|---|---|
Меркурий | 4 878 | 58 | 3,3×1023 | 0,055 | |
Венера | 8,87 | 12 103 | 108 | 4,9×1024 | 0,82 |
Земля | 9,8 | 12 756,28 | 150 | 6,0×1024 | 1 |
Марс | 3,7 | 6 794 | 228 | 6,4×1023 | 0,11 |
Юпитер | 24,8 | 142 984 | 778 | 1,9×1027 | 317,8 |
Сатурн | 10,4 | 120 536 | 1 427 | 5,7×1026 | 95,0 |
Уран | 8,87 | 51 118 | 2 871 | 8,7×1025 | 14,4 |
Нептун | 10,15 | 49 532 | 4 498 | 1,02×1026 | 17,1 |
Плутон | 0,66 | 2 390 | 5 906 | 1,3×1022 | 0,0022 |
Луна | 1,62 | 3 473,8 | 0,3844 (до Земли) | 7,35×1022 | 0,0123 |
Солнце | 274,0 | 1 391 000 | 0 | 2,0×1030 | 332 900 |
Ускорение свободного падения на Земле в разных местах
Сюрприз-сюрприз! В разных городах ускорения свободного падения тоже различаются. Это происходит из-за того, что Земля имеет форму геоида — приплюснутого шара, и в разных точках у нее различается радиус. Если подставить эти радиусы в формулу ускорения свободного падения, получатся разные значения. Ниже представлены некоторые из них.
Это происходит из-за того, что Земля имеет форму геоида — приплюснутого шара, и в разных точках у нее различается радиус. Если подставить эти радиусы в формулу ускорения свободного падения, получатся разные значения. Ниже представлены некоторые из них.
Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
Алматы | 76,85 в. д. | 43,22 с. | 786 | 9,78125 |
Берлин | 13,40 в. д. | 52,50 с. ш. | 40 | 9,81280 |
Будапешт | 19,06 в. д. | 47,48 с. ш. | 108 | 9,80852 |
Вашингтон | 77,01 з. д. | 38,89 с. ш. | 14 | 9,80188 |
Вена | 16,36 в. | 48,21 с. ш. | 183 | 9,80860 |
Владивосток | 131,53 в. д. | 43,06 с. ш. | 50 | 9,80424 |
Гринвич | 0,0 в. д. | 51,48 с. ш. | 48 | 9,81188 |
Каир | 31,28 в. д. | 30,07 с. | 30 | 9,79317 |
Киев | 30,30 в. д. | 50,27 с. ш. | 179 | 9,81054 |
Мадрид | 3,69 в. д. | 40,41 с. ш. | 667 | 9,79981 |
Минск | 27,55 в. д. | 53,92 с. ш. | 220 | 9,81347 |
Москва | 37,61 в. | 55,75 с. ш. | 151 | 9,8154 |
Нью-Йорк | 73,96 з. д. | 40,81 с. ш. | 38 | 9,80247 |
Одесса | 30,73 в. д. | 46,47 с. ш. | 54 | 9,80735 |
Осло | 10,72 в. д. | 59,91 с. | 28 | 9,81927 |
Париж | 2,34 в. д. | 48,84 с. ш. | 61 | 9,80943 |
Прага | 14,39 в. д. | 50,09 с. ш. | 297 | 9,81014 |
Рим | 12,99 в. д. | 41,54 с. ш. | 37 | 9,80312 |
Стокгольм | 18,06 в. | 59,34 с. ш. | 45 | 9,81843 |
Токио | 139,80 в. д. | 35,71 с. ш. | 18 | 9,79801 |
Например, ускорение свободного падения в Алматы меньше, чем в Осло. Значит, если два яблока упадут с одинаковой высоты в этих городах, то к концу падения яблоко в Осло наберет большую скорость, чем яблоко в Алматы.
Но разве это не зависит еще и от массы предмета?
Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Карина Хачатурян
К предыдущей статье
Электроемкость конденсатора
К следующей статье
Удельная теплота сгорания
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Понятие и формула силы натяжения нити в физике
Оглавление
Время чтения: 3 минуты
1 253
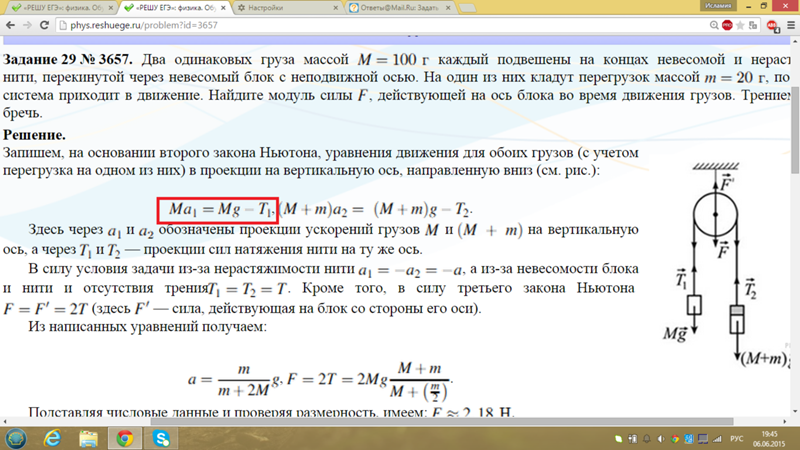
Понятие силы натяжения
Под силой натяжения понимают силу, приложенную к концам объекта и образующую внутри него упругую деформацию.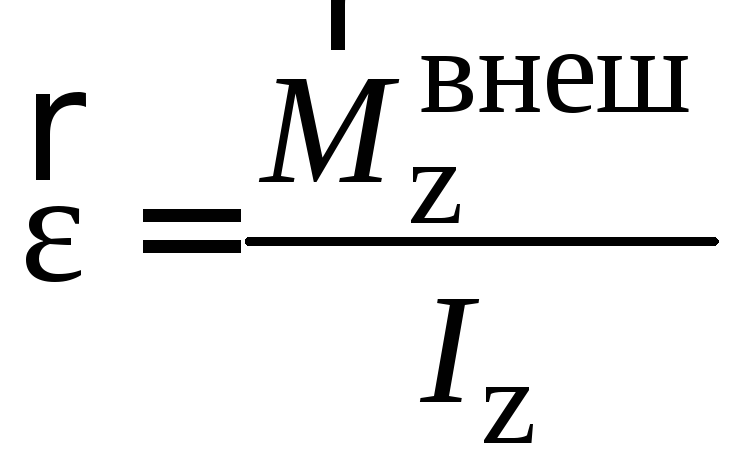 Длина данного объекта обычно в несколько раз превышает его толщину (нить, веревка, проволока, бечева, трос, шнур и другие похожие объекты).
Длина данного объекта обычно в несколько раз превышает его толщину (нить, веревка, проволока, бечева, трос, шнур и другие похожие объекты).
Увидеть силу натяжения можно в различных областях жизнедеятельности, к примеру, альпинистское снаряжение, вытаскивание ведра из колодца, подвесной мост, ремень безопасности, гитара, буксировка автомобиля, перетягивание каната и в других.
Чему равна сила натяжения нити
Формула
Если в натянутой нити верхний конец крепко закреплен, а нижний находится под действием груза, то определение сила тяжести рассчитывается, как масса груза, умноженная на ускорение свободного падения:
\[\mathrm{F}=\mathrm{F}_{\text {тяж }}=\mathrm{m} \cdot \mathrm{g}\]
Где m — масса, g — ускорение свободного падения.
Если в натянутой нити верхний конец крепко закреплен, а нижний находится под действием груза, то определение сила тяжести рассчитывается, как масса груза, умноженная на ускорение свободного падения:
Существует и такой случай, когда нить находится под заданным углом, следовательно, формула силы натяжения примет такой вид:
\[\mathrm{F}_{\Pi}=\mathrm{m} \cdot \mathrm{g} \cdot \cos (\alpha)\], где α-угол отклонения нити. {2}}{\mathrm{r}}\]
{2}}{\mathrm{r}}\]
Вращение может производиться непосредственно в вертикальной площади, а значит, сила натяжения изменяется циклическим образом. При приближении к земле, ее значение увеличивается, а при отдалении от нее, уменьшается. Главным образом, напряжение внутри нити связано с углом отклонения от вертикали (см. пример).
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример задачи на силу натяжения нити
Пример
Маятник длиной 2 метра отклонен от вертикального положения на двадцать градусов и движется со скоростью 2
м/с. Найти силу натяжения нити маятника с массой подвешенного груза 3 кг.
На груз, который подвешен к маятнику, действуют 2 силы:
- сила притяжения;
- центробежная сила.
Поэтому необходимо найти сумму этих сил, чтобы решить данную задачу.
Силу притяжения рассчитаем по формуле: \[\mathrm{F}_{\Pi}=\mathrm{m} \cdot \mathrm{g} \cdot \cos (\alpha)\]
Где m — масса, g — ускорение свободного падения, α — угол отклонения. {2}}{2}=6 H\]
{2}}{2}=6 H\]
\[\Sigma=27,93 \mathrm{H}+6 \mathrm{H}=33,93 \mathrm{H}\]
Ответ: сила натяжения нити маятника равна 33,93Н.
Оценить статью (45 оценок):
Поделиться
Как рассчитать ускорение — советы по линейному движению
By Danielle Collins Оставить комментарий
Как только вы узнаете, какой профиль движения используется, вам нужно знать, как рассчитать ускорение на основе общего расстояния перемещения и общего времени перемещения. При определении размера линейной системы большое внимание уделяется скорости, но влияние ускорения на систему и ее компоненты часто бывает более значительным, чем влияние скорости.
Ускорение больше всего связано с профилем движения и с тем, как наилучшим образом достичь требуемого перемещения за указанное время, но оно также вызывает дополнительные силы на систему и компоненты (вспомним второй закон Ньютона, F=ma), которые необходимо учитывать в размерах и выборе. Он также играет важную роль в определении того, какой крутящий момент требуется от двигателя для привода нагрузки.
Ускорение — это скорость изменения скорости: изменение скорости, деленное на изменение во времени. С точки зрения вычислений ускорение является производной скорости (dv/dt) и может быть определено путем вычисления наклона кривой профиля движения (скорости в зависимости от времени).
Первым шагом в расчете необходимого ускорения для перемещения является определение того, какой тип профиля движения будет использовать приложение — треугольный или трапециевидный.
Треугольный профиль движения имеет фазы ускорения и фазы замедления, которые обычно равны. Трапециевидный профиль движения имеет фазы ускорения, постоянной скорости и замедления. Время для каждой из трех фаз может быть одинаковым, но фаза постоянной скорости часто короче или длиннее, чем фазы ускорения и торможения.Изображения предоставлены: Womack Machine Supply Co.
Как рассчитать ускорение для треугольного профиля перемещения
Для треугольного профиля перемещения ускорение достигается за половину общего времени перемещения и половину общего расстояния перемещения. (Точно так же торможение занимает оставшуюся половину времени движения и половину расстояния перемещения.) Таким образом, время ускорения (t a ) равно 1/2 общего времени движения:
(Точно так же торможение занимает оставшуюся половину времени движения и половину расстояния перемещения.) Таким образом, время ускорения (t a ) равно 1/2 общего времени движения:
И расстояние ускорения (d a ) составляет 1/2 от общего расстояния перемещения.
Напомним, что ускорение — это скорость изменения скорости или скорость, деленная на время. Чтобы определить ускорение, нужно знать максимальную скорость. Для простоты начнем с определения средней скорости.
Средняя скорость — это просто общее расстояние перемещения, деленное на общее время перемещения:
Для треугольного профиля движения максимальная скорость в 2 раза превышает среднюю скорость, что может быть выражено как:
Ускорение – это максимальная скорость, деленная на время разгона:
Подставляя вместо v max и используя уравнение для t a сверху:
Как рассчитать ускорение для трапецеидального профиля движения
Чисто трапециевидный профиль движения использует 1/3 общего времени движения для ускорения, 1/3 для постоянной скорости и 1/3 для замедления: 1/3 при постоянной скорости и 1/3 при замедлении:
Как и для треугольного профиля движения, средняя скорость для треугольного профиля движения представляет собой просто общее расстояние перемещения, деленное на общее время движения:
Но максимальная скорость для трапециевидного профиля движения немного ниже, чем будет для того же движения, выполненного с треугольным профилем движения. Вместо того, чтобы максимальная скорость в два раза превышала среднюю скорость, максимальная скорость для трапециевидного профиля только в 1,5 раза превышает среднюю скорость. (Это можно увидеть, проанализировав геометрию трапеции, как описано в этом посте.)
Вместо того, чтобы максимальная скорость в два раза превышала среднюю скорость, максимальная скорость для трапециевидного профиля только в 1,5 раза превышает среднюю скорость. (Это можно увидеть, проанализировав геометрию трапеции, как описано в этом посте.)
Ускорение – это максимальная скорость, деленная на время разгона:
Подставляя v max и t на (и заменяя 1,5 дробью 3/2):
Упрощая, получаем:
Рубрики: Применение, Избранное, Линейные приводы (все), Линейные приводы (все), Направляющие + направляющие (все)
Основа техники: расчет времени разгона
Когда пользователю или оператору системы требуется время начала разгона двигателя? В первую очередь операторы используют время начала разгона как одну из многих записей в системе управления приводимым оборудованием. При первоначальной настройке системы управления оператор вводит расчетное время разгона, предоставленное производителем.
Затем, при запуске нового двигателя, наблюдаемое время начала разгона, вероятно, будет немного отличаться от первоначальной оценки, предоставленной производителем, из-за фактической нагрузки на месте и источника питания, поэтому измеренное значение ускорения будет использоваться для замены оценка в системе управления.
ИЗОБРАЖЕНИЕ 1: Кривая зависимости скорости от крутящего момента — профиль крутящего момента двигателя при напряжении полной нагрузки, отображаемый над требуемым крутящим моментом нагрузки приводимого оборудования в процентах от крутящего момента двигателя при полной нагрузке. (Изображения предоставлены Siemens)
Если время разгона не точно включено в управление пуском, двигатели могут перегреться, когда двигатель находится в состоянии остановки, или время разгона слишком велико. Такой перегрев может вызвать опасность в опасной среде и/или необратимое повреждение двигателя. Поставщики двигателей также оценивают время начала разгона, чтобы обеспечить соблюдение отраслевых стандартов.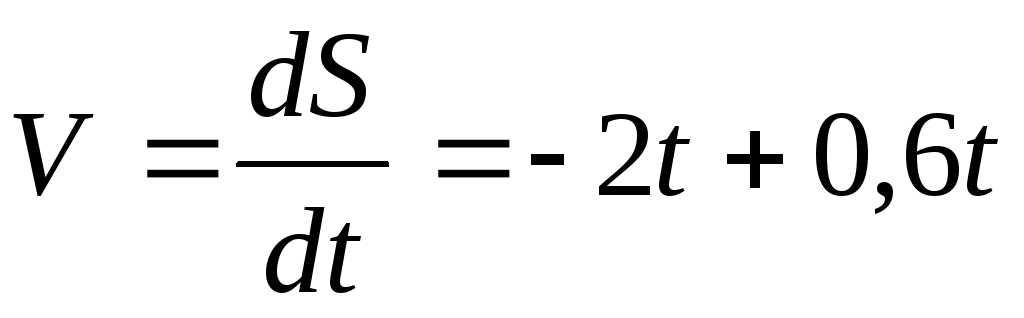 Например, стандарт 541 5-й редакции Американского института нефти (API) для двигателей премиум-класса требует, чтобы время горячего останова для
Например, стандарт 541 5-й редакции Американского института нефти (API) для двигателей премиум-класса требует, чтобы время горячего останова для
двигателей превышает 150 % времени начала разгона или должно быть на 5 секунд больше, чем время начала разгона.
Часто инженеры по эксплуатации нефтегазовых, химических и других горючих объектов (например, с содержанием угольной пыли, волокнистых частиц и т. д.) требуют, чтобы их производители соответствовали этому критерию или иным образом соответствовали аналогичным стандартам.
Расчет времени начала разгона (уравнение 1) должен быть частью исходных спецификаций, запрашиваемых у производителя двигателя. На этапе проектирования инженеры производителя могут предоставить расчетное время начала разгона для утверждения оператором.
Если время начала разгона требует регулировки, инженеры изготовителя могут сделать соответствующий выбор конструкции на этапе проектирования, но после изготовления двигателя время начала разгона не может быть легко отрегулировано.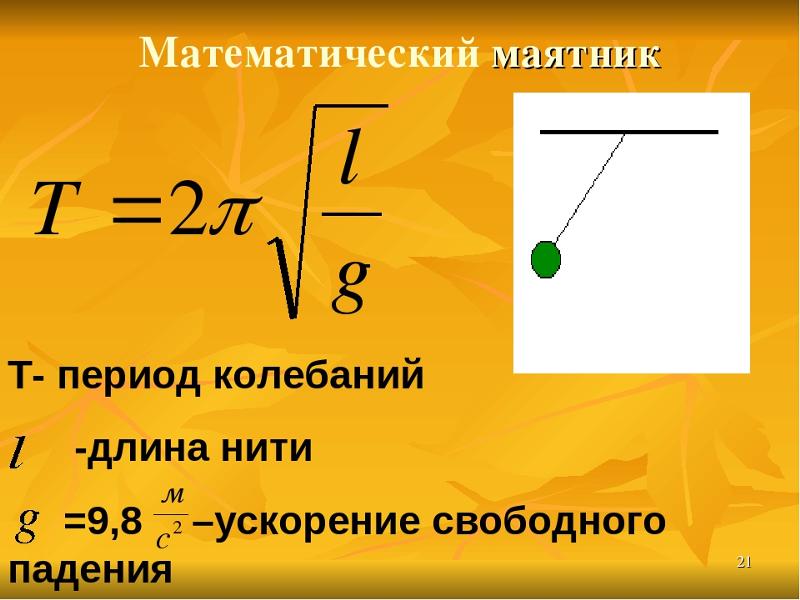
Инженеры регулярно интересуются основанием для определения времени начала ускорения. В этой статье объясняются детали, объясняется, почему оценки отличаются от измеренного времени начала, и когда инженеру может понадобиться использовать формулу.
Формула времени разгонаСредний доступный крутящий момент на приращение скорости (Ta) рассчитывается путем умножения крутящего момента при полной нагрузке (FLT) на ускоряющий крутящий момент (на единицу крутящего момента или PUT). Ускоряющий крутящий момент представляет собой среднее значение разницы между кривой крутящего момента нагрузки и кривой крутящего момента двигателя для заданного постепенного увеличения скорости. Другими словами, ускоряющий момент представляет собой процентную разницу между крутящим моментом двигателя и требованием момента нагрузки, измеренным для двух различных и последовательных значений оборотов в минуту (об/мин).
Как правило, сегменты, выбранные для приращений ∆rpm, пропорционально соответствуют кривым крутящего момента для системы. В нижней части диапазона оборотов на единицу (до 80%) можно выбрать приращение 10%, но по мере увеличения нагрузки приращение должно быть сужено.
В нижней части диапазона оборотов на единицу (до 80%) можно выбрать приращение 10%, но по мере увеличения нагрузки приращение должно быть сужено.
Различия между кривыми нагрузки становятся более изменчивыми при более высоких нагрузках, поэтому шаг 5 % или меньше фиксирует эту изменчивость в диапазоне высоких оборотов. Конкретные интервалы (10% и т. д.), выбранные для суммирования, могут варьироваться по усмотрению человека, вычисляющего время ускорения, с меньшими интервалами, повышающими точность, но увеличивающими сложность расчета.
ИЗОБРАЖЕНИЕ 2: Предоставленные производителем кривые скорость-момент помогают получить значения в этой таблице.
Чтобы лучше понять, как работает формула, рассмотрим следующий пример:
Мощность двигателя (л.с.) = 250
Скорость двигателя (об/мин) = 1787 кв.
Инерция нагрузки = 1016,7 фунто-футов на кв.
Суммарная инерция = 1104,7 фунто-футов на кв.
Производитель предоставляет кривые скорость-момент под нагрузкой вместе с двигателем, на которых изображена ожидаемая кривая нагрузки и выходной крутящий момент двигателя в процентах от крутящего момента при полной нагрузке двигателя, как показано выше. При использовании этой кривой создается таблица, показанная на Рисунке 2. Когда интервалы времени ускорения из таблицы суммируются, общее время ускорения отображается в уравнении 2.
При использовании этой кривой создается таблица, показанная на Рисунке 2. Когда интервалы времени ускорения из таблицы суммируются, общее время ускорения отображается в уравнении 2.
Формула требует оценки среднего крутящего момента, доступного для ускорения, и чувствительна к изменениям этого среднего крутящего момента. Любая ошибка, допущенная при оценке, приводит к соответствующей ошибке во времени ускорения. Формула также требует комбинированной инерции двигателя (предоставляемой производителем) и оценки нагрузки. Отсутствие учета обоих приводит к занижению времени ускорения, а ошибка в любом из них приводит к пропорциональной ошибке в расчете времени запуска.
Наконец, формула чувствительна к ошибкам вычислений. Хотя все формулы остаются уязвимыми для сценариев «мусор в мусоре», огромное количество вычислений, необходимых для ручной оценки, дает множество шансов на то, что одна ошибка исказит результаты.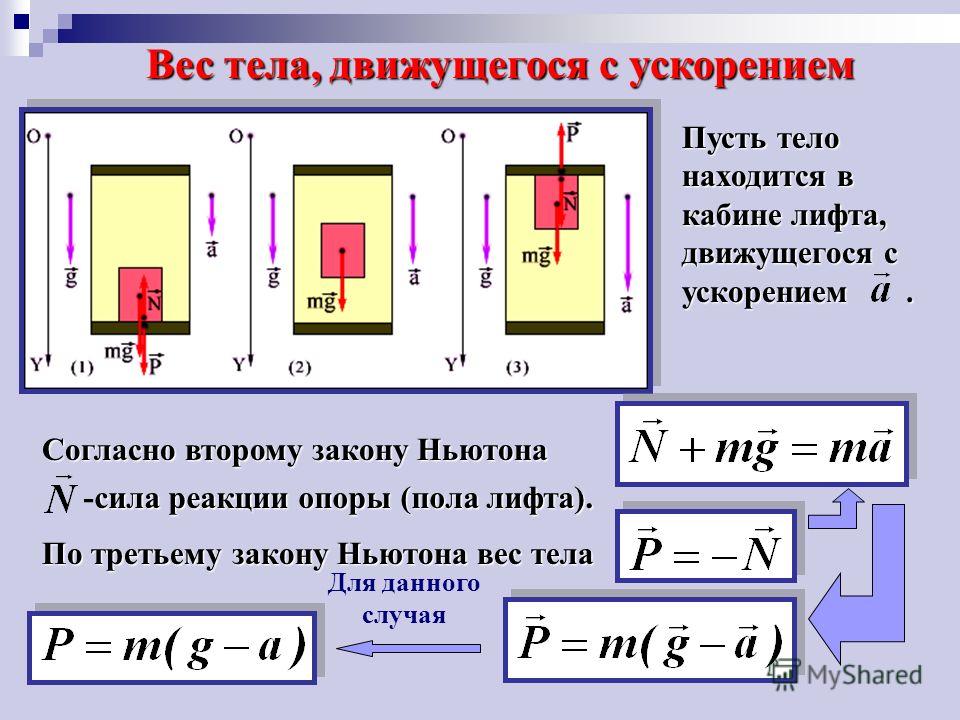 Всегда полезно работать в команде, чтобы несколько пар глаз могли проверить цифры.
Всегда полезно работать в команде, чтобы несколько пар глаз могли проверить цифры.
Формула времени разгона не применяется к двигателям с частотно-регулируемым приводом (ЧРП), поскольку ускорение определяет программное обеспечение, а не двигатель. Формула применима ко всем устройствам с постоянной нагрузкой и двигателям, таким как насосы, вентиляторы, компрессоры и т. д.
Если двигатель перемотать, его производительность может незначительно измениться, что также может повлиять на расчет времени начала разгона; новая кривая может быть предоставлена производителем, выполняющим перемотку.
Двигатели с измененной номинальной мощностью могут предлагаться с различной номинальной мощностью для различных пользователей и областей применения. Однако после приобретения для конкретного применения производитель может предоставить оценку времени начала разгона двигателя.
Хотя пользователи обычно выбирают конкретное приложение и не рассматривают другие номинальные мощности после установки, бывают ситуации, когда в аварийной ситуации может потребоваться срочное развертывание двигателя для новой цели. В случае чрезвычайной ситуации, такой как эта, пользователи могут извлечь спецификации, чтобы рассчитать новое потенциальное время ускорения с новой нагрузкой, другим напряжением и т. д.
В случае чрезвычайной ситуации, такой как эта, пользователи могут извлечь спецификации, чтобы рассчитать новое потенциальное время ускорения с новой нагрузкой, другим напряжением и т. д.
Если пользователи понимают основу расчета времени разгона, они могут уверенно использовать кривые, предоставленные производителем, для выполнения необходимых расчетов.
Реальное время начала разгонаЭта формула применима ко всем приложениям с двигателями с постоянной скоростью вращения, так зачем ее корректировать в полевых условиях? Расчеты основаны на оценках — оценках числа оборотов в минуту, оценках нагрузки и т. д. Даже хорошие оценки содержат небольшие отклонения, влияющие на фактическое время разгона.
Например, небольшое отклонение в подаваемом напряжении может замедлить время запуска на аналогичную величину. Кроме того, в то время как новые двигатели среднего напряжения изготавливаются по индивидуальному заказу для конкретного применения, двигатели с измененными характеристиками могут обладать более высокими характеристиками, чем это необходимо для номинального применения, и смещать кривые нагрузки.

 ш.
ш. д.
д. ш.
ш. д.
д. ш.
ш.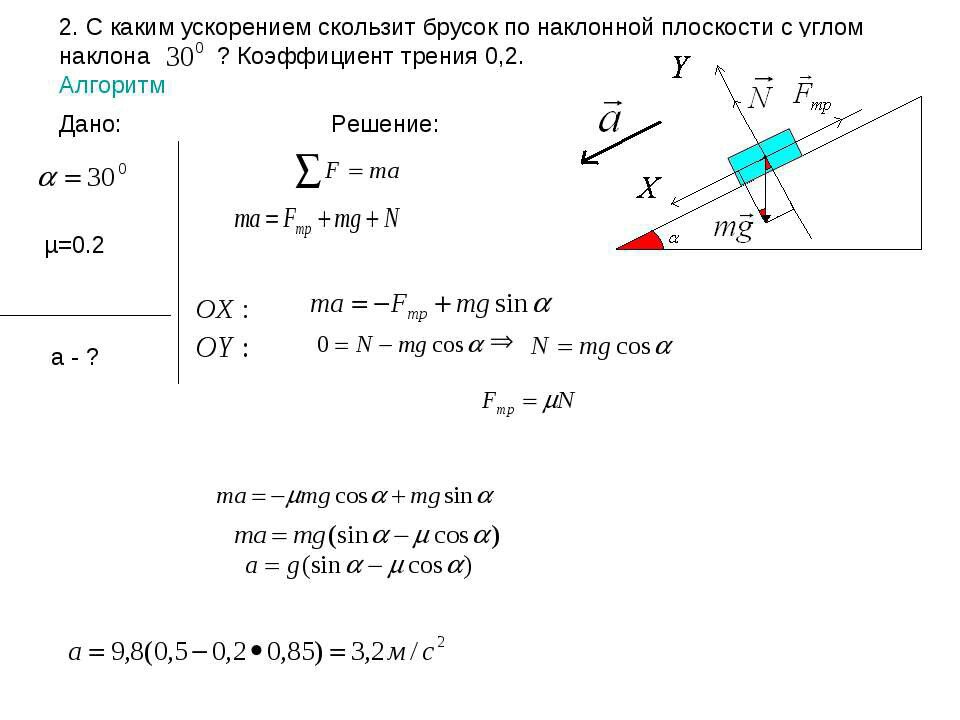 д.
д.
Leave A Comment