Формула средней скорости при равноускоренном прямолинейном движении
Из первого уравнения системы (1) имеем:
\[a_x=\frac{v_x-v_{0x}}{t}\left(7\right).\]
Величину ускорения из уравнения (7) подставим в формулу (5) получим, что перемещение по оси X равно:
\[\Delta x=\frac{v_x+v_{0x}}{2}t\left(8\right).\]
Найдем проекцию средней скорости на ось X из определения средней скорости движения:
\[{\left\langle v\right\rangle }_x=\frac{\Delta x}{t}\left(9\right).\]
Разделим правую и левую части выражения (8) на время движения тела. Получим, что средняя скорость при рассматриваемом движении равна:
\[\frac{\Delta x}{t}=\frac{v_x+v_{0x}}{2}={\left\langle v\right\rangle }_x\left(10\right).\]
Примеры задач с решением
Пример 1
Задание. 2}$
2}$
Читать дальше: формулы свободного падения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Равнопеременное движение. Ускорение. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Равнопеременное движение. Ускорение.
| Равнопеременное движение. Ускорение. | ||
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. | ||
Обозначим: — вектор начальной скорости, — изменение скорости, а Δt — промежуток времени. Пусть Δt1= Δt2=Δt3=…, тогда по определению | ||
Следовательно,
Т.о., это характеристика движения. | ||
Если t0=0, то | ||
УСКОРЕНИЕ — физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло. | ||
Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ — м/с2. | Например, ускорение равно 5 м/с2 — это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения. | |
В случае не равнопеременного движения: | ||
| тогда мгновенное ускорение | ||
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает. | Условие р.у.д. —. | |
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается. | Условие р.з.д. — . | |
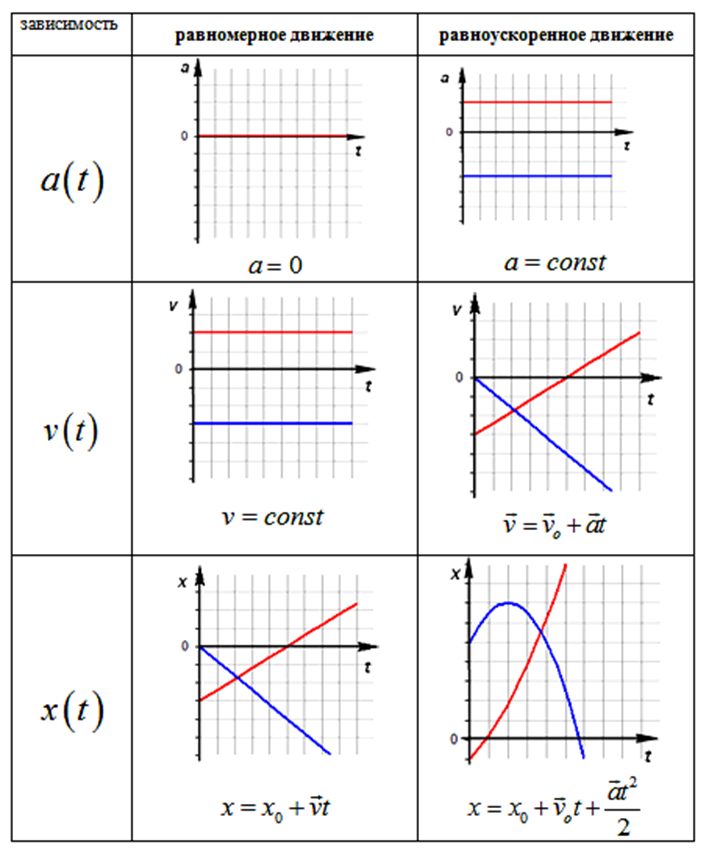
Графики равнопеременного движения. | ||
или — в проекциях; или – через модули. | ||
Линейная функция. График — прямая. | ||
Движения, совпадающие с направлением координатной оси: 1. равноускоренноес начальной скоростью 2. равноускоренное без начальной скорости 3. равнозамедленное
4. равнозамедленное 5. равноускоренное без начальной скорости 6. равноускоренное с начальной скоростью | ||
Перемещение при равнопеременном движении. | ||
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению. | ||
Решение основной задачи механики для р.у.д. : | ||
Графики перемещения и координаты. | ||
Функции и — квадратичные. | ||
Теги:
конспект
Скорость при движении с постоянным ускорением. Прямолинейное движение с постоянным ускорением
О данном уроке, тема которого: «Уравнение движения с постоянным ускорением. Поступательное движение», вспомним, что такое движение, как оно происходит. Также вспомним, что такое ускорение, рассмотрим уравнение движения с постоянным ускорением и как с его помощью определить координаты движущегося тела. Рассмотрим пример задачи на закрепление материала.
Основная задача кинематики — определить положение тела в любой момент времени. Тело может отдохнуть, тогда его положение не изменится (см. рис. 1).
Рис. 1. Тело в покое
Тело может двигаться прямолинейно с постоянной скоростью. Тогда его перемещение будет изменяться равномерно, т. е. одинаково через равные промежутки времени (см. рис. 2).
Рис.
Движение, скорость умноженная на время, это мы давно умеем делать. Тело может двигаться с постоянным ускорением, рассмотрим такой случай (см. рис. 3).
Рис. 3. Движение тела с постоянным ускорением
Ускорение
Ускорение – это изменение скорости в единицу времени (см. рис. 4) : Рис. 4. Разгон Скорость является векторной величиной, следовательно, изменение скорости, т. е. разность между векторами конечной и начальной скорости, является вектором. Ускорение также является вектором, направленным в ту же сторону, что и вектор разности скоростей (см. рис. 5). Мы рассматриваем прямолинейное движение, поэтому можем выбрать ось координат вдоль прямой, вдоль которой происходит движение, и рассмотреть проекции векторов скорости и ускорения на эту ось: |
Тогда его скорость изменяется равномерно: (если его начальная скорость была равна нулю). Как теперь найти ход? Умножить скорость на время невозможно: скорость постоянно менялась; какой взять? Как определить, где будет находиться тело в любой момент времени при таком движении — сегодня мы решим эту задачу.
Как теперь найти ход? Умножить скорость на время невозможно: скорость постоянно менялась; какой взять? Как определить, где будет находиться тело в любой момент времени при таком движении — сегодня мы решим эту задачу.
Сразу определим модель: мы рассматриваем прямолинейное поступательное движение тела. В этом случае мы можем использовать материальную точку модели. Ускорение направлено по той же прямой, по которой движется материальная точка (см. рис. 6).
поступательное движение
Поступательное движение — это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое движение (см. рис. 7). Рис. 7. Движение вперед А как иначе? Помашите рукой и следуйте: видно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки возле оси почти не двигаются, а кабинки двигаются с разной скоростью и по разным траекториям (см. Рис. 8. Перемещение выбранных точек на колесе обозрения Посмотрите на движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным ( см. рис. 9). Рис. 9. Движение транспортных средств Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считается материальной точкой. Обратите внимание, что при движении вперед линия, соединяющая любые две точки тела при движении, остается параллельной самой себе (см. рис. 10). Рис. 10. Положение линии, соединяющей две точки |
Машина ехала прямо час. В начале часа его скорость была 10 км/ч, а в конце — 100 км/ч (см. рис. 11).
Рис. 11. Рисунок к задаче
Скорость изменялась равномерно. Сколько километров проехала машина?
Разберем условие задачи.
Скорость автомобиля изменялась равномерно, то есть его ускорение было постоянным на протяжении всего пути.
Автомобиль ехал прямолинейно, поэтому его движение можно рассматривать в проекции на одну ось координат:
Найдем ход.
Пример увеличения скорости
Орехи кладут на стол, по одному ореху в минуту. Понятно: сколько минут пройдет, столько и орехов будет на столе. Теперь представим, что скорость укладки гаек от нуля увеличивается равномерно: в первую минуту гайки не кладут, во вторую кладут одну гайку, затем две, три и так далее. Сколько орехов будет на столе через некоторое время? Понятно, что меньше, чем если бы максимальная скорость поддерживалась всегда. Причем хорошо видно, что она меньше чем в 2 раза (см. рис. 12). Рис. 12. Количество гаек при разных скоростях укладки То же самое и с равноускоренным движением: допустим, сначала скорость была равна нулю, в конце стала равной (см. рис. Рис. 13. Изменение скорости Если бы тело постоянно двигалось с такой скоростью, то его перемещение было бы равно, а так как скорость возрастает равномерно, то было бы в 2 раза меньше. |
Мы можем найти перемещение при РАВНОМЕРНОМ движении: . Как обойти эту проблему? Если скорость меняется не сильно, то движение можно приблизительно считать равномерным. Изменение скорости за короткий промежуток времени будет небольшим (см. рис. 14).
Рис. 14. Изменение скорости
Поэтому время в пути Т разобьем на N малых отрезков продолжительности (см. рис. 15).
Рис. 15. Разбиение отрезка времени
Рассчитаем смещение на каждом временном интервале. Скорость увеличивается на каждом интервале на:
На каждом отрезке движение будем считать равномерным, а скорость примерно равной начальной скорости на данном интервале времени. Посмотрим, не приведет ли наша аппроксимация к ошибке, если мы будем считать движение равномерным на малом интервале. Максимальная ошибка будет:
Максимальная ошибка будет:
и суммарная ошибка за весь путь -> . При больших N будем считать, что ошибка близка к нулю. Мы увидим это на графике (см. рис. 16): на каждом интервале будет ошибка, но суммарная ошибка для больших чисел интервалов будет пренебрежимо мала.
Рис. 16. Ошибка на интервалах
Таким образом, каждое следующее значение ускоряется на такое же значение больше, чем предыдущее. Из алгебры мы знаем, что это арифметическая прогрессия с разностью прогрессии:
Путь на участках (при равномерном прямолинейном движении (см. рис. 17) равен:
Рис. 17. Рассмотрение области движения тела
На втором участке:
На n-м участке путь:
Арифметическая прогрессия
Арифметической прогрессией называется такая числовая последовательность, в которой каждое следующее число отличается от предыдущего на одинаковую величину. Сумма первых членов арифметической прогрессии вычисляется по формуле: |
Просуммируем все пути. Это будет сумма первых N членов арифметической прогрессии:
Так как мы разбили движение на множество интервалов, то можно считать, что , то:
У нас было много формул, и чтобы не запутаться , мы не писали каждый раз индексы x, а считали все в проекции на ось координат.
Итак, мы получили основную формулу равноускоренного движения: движение с равноускоренным движением за время T, которую будем использовать вместе с определением ускорения (изменение скорости в единицу времени) для решения задач:
Мы работали над проблемой автомобиля. Подставляем числа в решение и получаем ответ: машина проехала 55,4 км.
Математическая часть решения задачи
С движением мы разобрались.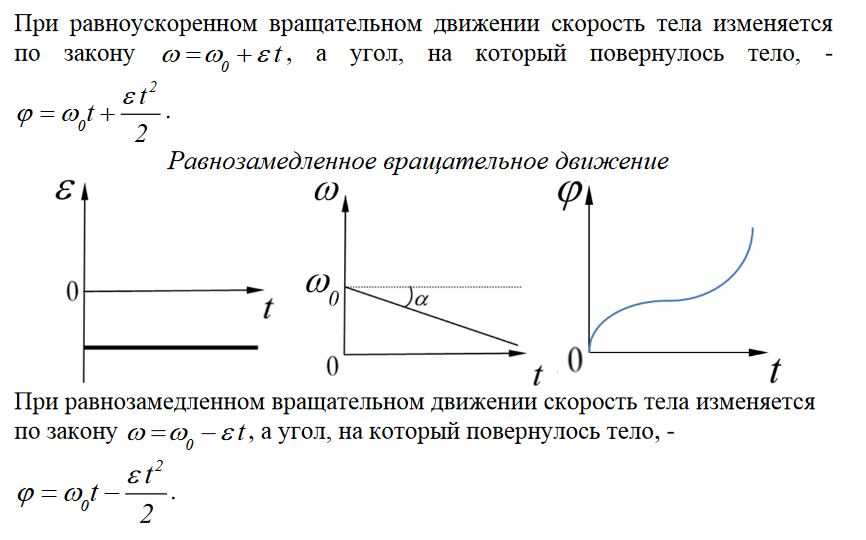 А как определить координату тела в любой момент времени?
А как определить координату тела в любой момент времени?
По определению движение тела во времени — это вектор, начало которого находится в начальной точке движения, а конец — в конечной точке, где тело будет находиться во времени. Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):
Рис. 18. Проекция движения
Выразим координату:
То есть координата тела в момент времени равна начальной координате плюс проекция движения, которое тело совершило за время. Проекцию перемещения при равноускоренном движении мы уже нашли, осталось подставить и записать:
Это уравнение движения с постоянным ускорением. Он позволяет в любой момент узнать координату движущейся материальной точки. Понятно, что мы выбираем момент времени в интервале работы модели: ускорение постоянное, движение прямолинейное.
Почему уравнение движения нельзя использовать для нахождения пути
В каких случаях движение по модулю можно считать равным пути? Когда тело движется прямолинейно и не меняет направления. При равноускоренном движении скорость изменяется. Если скорость и ускорение направлены в противоположные стороны (см. рис. 19), то модуль скорости уменьшается, и в какой-то момент он станет равным нулю и скорость изменит направление, то есть тело начнет двигаться в противоположном направлении. Рис. 19. Модуль скорости уменьшается И тогда, если в этот момент времени тело находится на расстоянии 3 м от начала наблюдения, то его перемещение равно 3 м, но если тело сначала прошло 5 м, затем развернулось и прошло еще 2 м, тогда путь будет 7 м. И как его найти, если вы не знаете этих цифр? Нужно только найти момент, когда скорость равна нулю, т. е. когда тело развернется, и найти путь в эту точку и из нее (см. рис. 20). Рис. 20. Момент когда скорость 0 |
Список литературы
- Соколович Ю.
 А., Богданова Г.С. Физика: Справочник с примерами решения задач. — Перераспределение 2-го издания. — Х.: Веста: Изд-во «Ранок», 2005. — 464 с.
А., Богданова Г.С. Физика: Справочник с примерами решения задач. — Перераспределение 2-го издания. — Х.: Веста: Изд-во «Ранок», 2005. — 464 с. - Ландсберг Г.С. Начальный учебник физики; т.1. Механика. Нагревать. Молекулярная физика- М.: Издательство «Наука», 1985.
- Интернет-портал «kaf-fiz-1586.narod.ru» ()
- Интернет-портал «Учись — Легко» ()
- Интернет-портал «Гипермаркет знаний» ()
Домашнее задание
- Что такое арифметическая прогрессия?
- Какое движение является поступательным?
- Что такое векторная величина?
- Запишите формулу ускорения через изменение скорости.
- Какое уравнение движения с постоянным ускорением?
- Вектор ускорения направлен в сторону движения тела. Как тело изменит свою скорость?
Среди различных движений с постоянным ускорением самым простым является прямолинейное движение. Если при этом модуль скорости увеличивается, то движение иногда называют равноускоренным, а если модуль скорости уменьшается, то равномерным замедлением.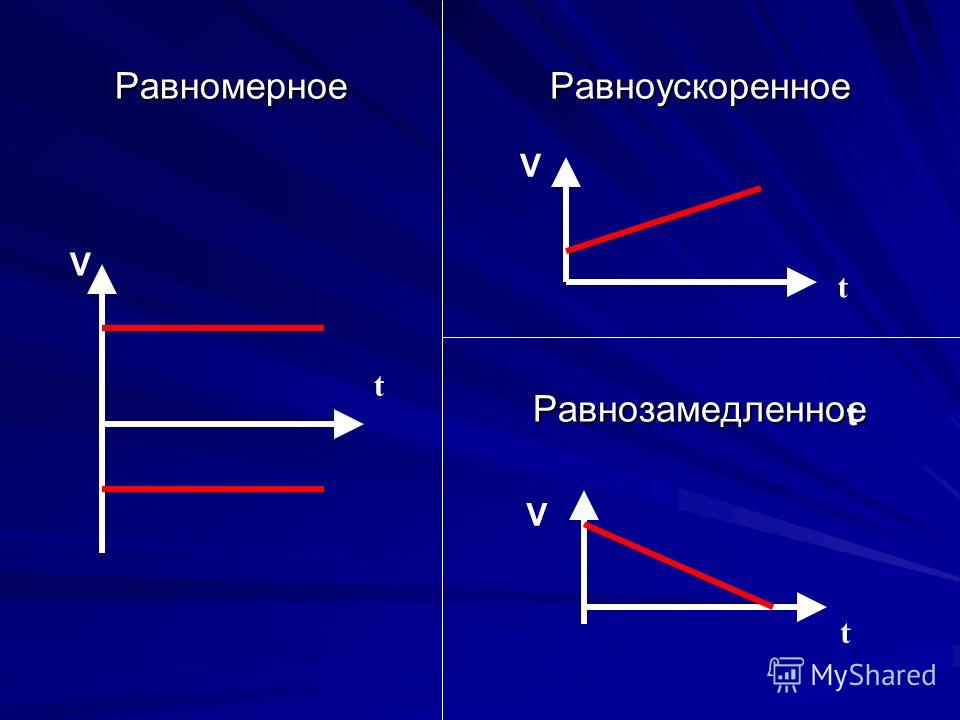 Такой вид движения совершает поезд, отправляющийся со станции или приближающийся к ней. Камень, брошенный вертикально вниз, движется с равномерным ускорением, а камень, брошенный вертикально вверх, движется одинаково медленно.
Такой вид движения совершает поезд, отправляющийся со станции или приближающийся к ней. Камень, брошенный вертикально вниз, движется с равномерным ускорением, а камень, брошенный вертикально вверх, движется одинаково медленно.
Для описания прямолинейного движения с постоянным ускорением можно обойтись одной осью координат (например, осью X), которая целесообразно направлена по траектории движения. В этом случае любая задача решается с помощью двух уравнений:
(1.20.1)
и
2? Проекция перемещения и пути при прямолинейном движении с постоянным ускорением
М2
Ах = v0xt +(1.20.3)
Если скорость тела (точки) не меняет своего направления, то путь равен проекции перемещения по модулю 9= v. Следовательно, при прямолинейном движении с постоянным ускорением t
проекция средней скорости на ось X равна:
!ar + Vr
vx=0x2 . (1.20.5)
Можно показать, что если какая-либо другая физическая величина находится в линейной зависимости от времени, то среднее по времени значение этой величины равно половине суммы ее наименьшего и наибольшего значений за этот промежуток времени.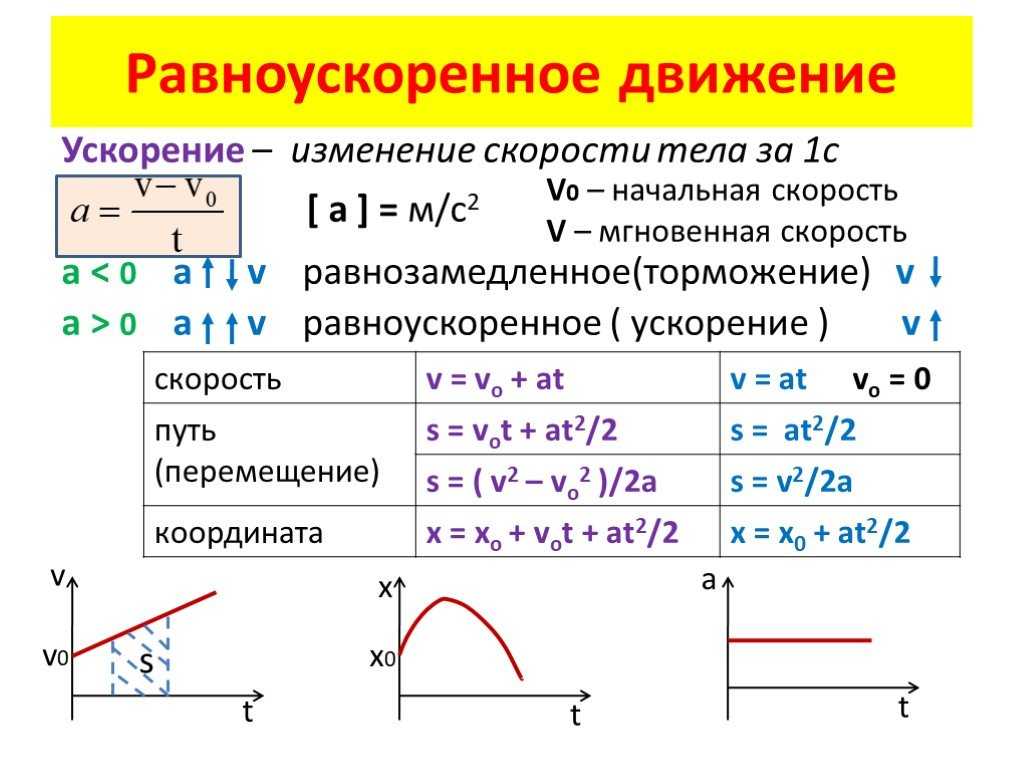
Если при прямолинейном движении с постоянным ускорением направление скорости не меняется, то средний модуль скорости равен половине суммы модулей начальной и конечной скоростей, т. е.
К* + vx\ v0 + v
Связь между проекциями начальной и конечной скоростей, ускорением и перемещением
По формуле (1.19.1)
Lx = ° * 2 xt. (1.20.7)
Время t выражается из формулы (1.20.1)
Vx~V0x ah
и подставляется в (1.20.7). Получаем:
Vx + V0x Vx — v0x V2X — i>jj
= 2ST» —257-
Отсюда
v2x = v Іx + 2a3Lx. (1.20.8)
Полезно запомнить формулу (1.20 .8) и выражение (1.20.6) для средней скорости Эти формулы могут понадобиться для решения многих задач.
? 1. Как направлено ускорение при выходе поезда со станции (ускорение)? При приближении к станции (торможение)?
Нарисуйте график пути при разгоне и торможении.
Докажите сами, что при равноускоренном прямолинейном движении без начальной скорости пути, пройденные телом за равные последовательные промежутки времени, пропорциональны последовательным нечетным числам:
Sj: S2* Sg .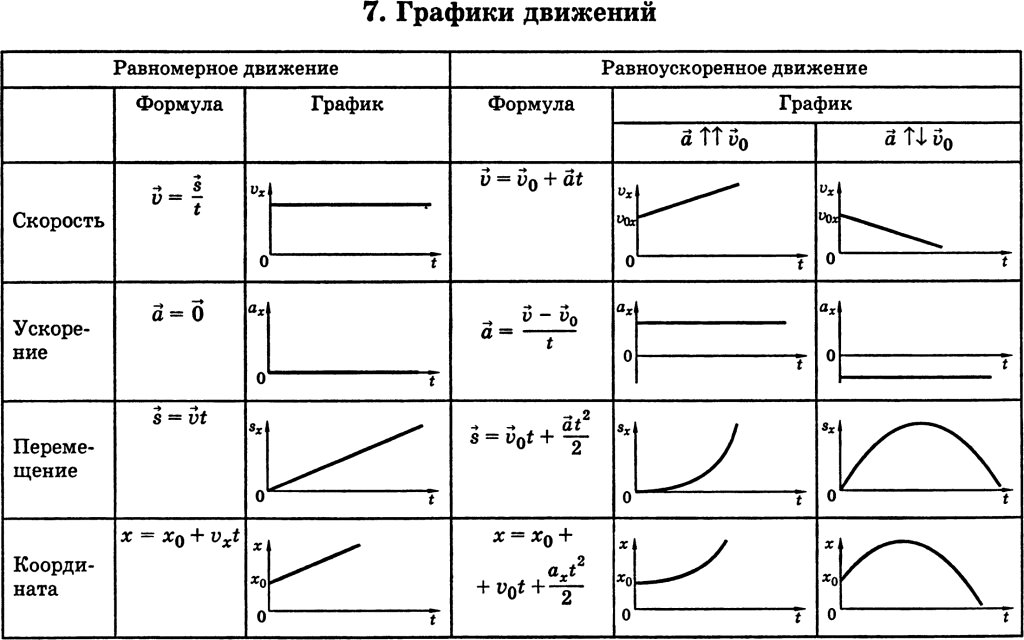 .. = 1:3:5: . .. . Впервые это доказал Галилей.
.. = 1:3:5: . .. . Впервые это доказал Галилей.
Еще по теме §1.20. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ:
- § 4.3. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТсчета, движущиеся прямолинейно с постоянным ускорением
- §1.18. ГРАФИК ЗАВИСИМОСТИ МОДУЛЬНО-ПРОЕКЦИОННОЙ СКОРОСТИ И МОДУЛЬНО-ПРОЕКЦИОННОЙ СКОРОСТИ ОТ ВРЕМЕНИ В ДВИЖЕНИИ С ПОСТОЯННЫМ УСКОРЕНИЕМ
Ускорение. Прямолинейное движение с постоянным ускорением. Мгновенная скорость.
Ускорение показывает, как быстро изменяется скорость тела.
t 0 = 0c v 0 = 0 м/с Скорость изменилась на v = v 2 — v 1 в течение
t 1 = 5c v 1 = 2 м/с интервал времени = t 2 — t 1. Значит за 1 с скорость
t 2 = 10c v 2 = 4 м/с тела будет увеличить на =.
t 3 = 15c v 3 = 6 м/с = или =. (1 м/с 2)
Ускорение — векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
физический смысл : а = 3 м/с 2 — это значит, что за 1 с модуль скорости изменяется на 3 м/с.
Если тело ускоряется а > 0, если замедляется а
At = ; = + at – мгновенная скорость тела в любой момент времени. (Функция v(t)).
Движение с равноускоренным движением. Уравнение движения
D
la равномерное движение S=v*t, где v и t — стороны прямоугольника под графиком скорости. Те. водоизмещение = площадь фигуры под графиком скорости.
Аналогично можно найти перемещение при равноускоренном движении. Нужно просто найти отдельно площади прямоугольника, треугольника и сложить их. Площадь прямоугольника равна v 0 t, площадь треугольника равна (v-v 0) t/2, где делаем замену v — v 0 = at . Получаем s = v 0 t + при 2/2
s = v 0 t + at 2/2
Формула движения при равноускоренном движении
Учитывая, что вектор s = x-x 0, получим x-x 0 = v 0 t + at 2/2 или переместим начальная координата вправо x = x 0 + v 0 t + at 2/2
x = x 0 + v 0 t + at 2/2
По этой формуле можно найти координату ускоренно движущегося тело в любой момент времени
При равномерно-замедленном движении перед буквой «а» в формулах знак + можно заменить на —
Движение с постоянным ускорением — это движение, при котором вектор ускорения остается постоянным как по величине, так и по направлению.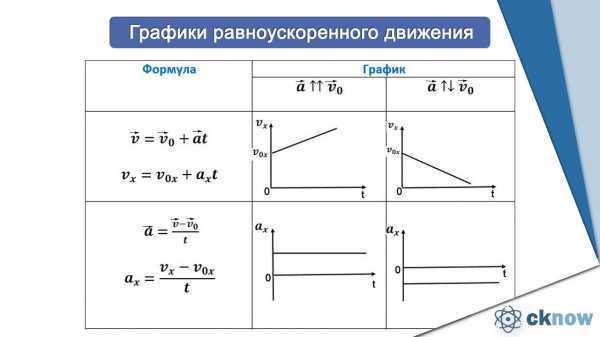 Примером этого вида движения является движение точки в поле силы тяжести (как по вертикали, так и под углом к горизонту).
Примером этого вида движения является движение точки в поле силы тяжести (как по вертикали, так и под углом к горизонту).
Используя определение ускорения, получаем следующее соотношение
После интегрирования имеем равенство
.
Учитывая, что вектор мгновенной скорости здесь равен
, получим следующее выражение
Интегрирование последнего выражения дает следующее отношение
. Откуда получаем уравнение движения точки с постоянным ускорением
.
Примеры векторных уравнений движения материальной точки
Равномерное прямолинейное движение (
):
. (1.7)
Движение с постоянным ускорением (
):
. (1.8)
Зависимость скорости от времени при движении точки с постоянным ускорением имеет вид:
. (1.9)
Вопросы для самоконтроля.
Сформулируйте определение механического движения.
Определить материальную точку.
Как определяется положение материальной точки в пространстве при векторном способе описания движения?
В чем суть векторного метода описания механического движения? Какие характеристики используются для описания этого движения?
Дайте определения векторов средней и мгновенной скорости. Как определяется направление этих векторов?
Как определяется направление этих векторов?
Определите вектор среднего и мгновенного ускорения.
Какое из соотношений является уравнением движения точки с постоянным ускорением? Какое соотношение определяет зависимость вектора скорости от времени?
§1.2. Координатный способ описания движения
В координатном методе для описания движения выбирается система координат (например, декартова). Опорная точка жестко фиксируется с выбранным телом ( опорное тело ). Пусть
ортов направлены в положительные стороны осей OX, OY и OZ соответственно. Положение точки задается координатами
.
Мгновенный вектор скорости определяется следующим образом:
где
проекций вектора скорости на оси координат, а
производных координат по времени.
Длина вектора скорости связана с его проекциями соотношением:
. (1.11)
Для вектора мгновенного ускорения верно соотношение:
где
проекций вектора ускорения на оси координат, а
производных по времени от проекций вектора скорости.
Длина вектора мгновенного ускорения находится по формуле:
. (1.13)
Примеры уравнений движения точки в декартовой системе координат
. (1.14)
Уравнения движения:
. (1,15)
Зависимости проекций вектора скорости на оси координат от времени:
(1.16)
Вопросы для самоконтроля.
В чем суть координатного метода описания движения?
Какое соотношение определяет мгновенный вектор скорости? По какой формуле вычисляют модуль вектора скорости?
Какое соотношение определяет вектор мгновенного ускорения? По какой формуле вычисляют модуль вектора мгновенного ускорения?
Какие соотношения называются уравнениями равномерного движения точки?
Какие соотношения называются уравнениями движения с постоянным ускорением? По каким формулам вычисляют проекции мгновенной скорости точки на оси координат?
«Ускорение. Прямолинейное движение с постоянным ускорением
В этом уроке, тема которого: «Уравнение движения с постоянным ускорением.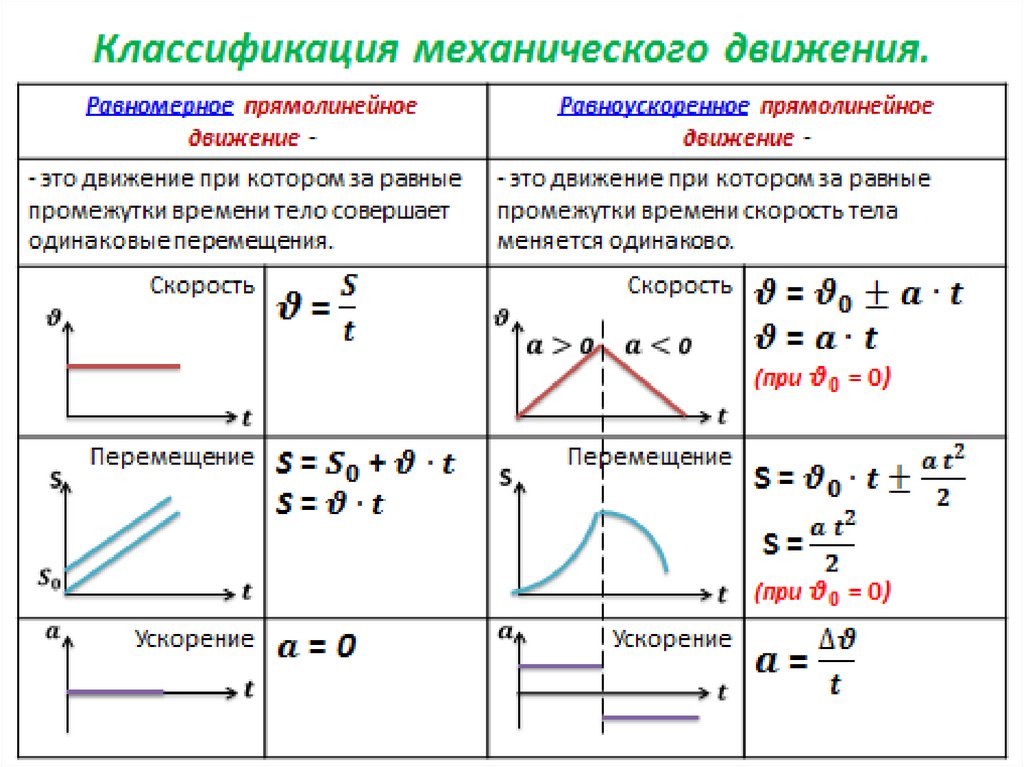 Поступательное движение», вспомним, что такое движение, как оно происходит. Также вспомним, что такое ускорение, рассмотрим уравнение движения с постоянным ускорением и как с его помощью определить координаты движущегося тела. Рассмотрим пример задачи на закрепление материала.
Поступательное движение», вспомним, что такое движение, как оно происходит. Также вспомним, что такое ускорение, рассмотрим уравнение движения с постоянным ускорением и как с его помощью определить координаты движущегося тела. Рассмотрим пример задачи на закрепление материала.
Основной задачей кинематики является определение положения тела в любой момент времени. Тело может отдохнуть, тогда его положение не изменится (см. рис. 1).
Рис. 1. Тело в покое
Тело может двигаться прямолинейно с постоянной скоростью. Тогда его перемещение будет изменяться равномерно, т. е. одинаково через равные промежутки времени (см. рис. 2).
Рис. 2. Движение тела при движении с постоянной скоростью
Движение, скорость умноженная на время, это мы давно умеем делать. Тело может двигаться с постоянным ускорением, рассмотрим такой случай (см. рис. 3).
Рис. 3. Движение тела с постоянным ускорением
Ускорение
Ускорение – это изменение скорости в единицу времени (см. Рис. 4. Разгон Скорость является векторной величиной, следовательно, изменение скорости, т. е. разность между векторами конечной и начальной скорости, является вектором. Ускорение также является вектором, направленным в ту же сторону, что и вектор разности скоростей (см. рис. 5). Мы рассматриваем прямолинейное движение, поэтому можем выбрать координатную ось вдоль прямой, вдоль которой происходит движение, и рассмотреть проекции векторов скорости и ускорения на эту ось: |
Тогда его скорость изменяется равномерно: (если его начальная скорость была равна нулю). Как теперь найти ход? Умножить скорость на время невозможно: скорость постоянно менялась; какой взять? Как определить, где будет находиться тело в любой момент времени при таком движении — сегодня мы решим эту задачу.
Сразу определим модель: мы рассматриваем прямолинейное поступательное движение тела. В этом случае мы можем применить модель материальной точки. Ускорение направлено по той же прямой, по которой движется материальная точка (см. рис. 6).
В этом случае мы можем применить модель материальной точки. Ускорение направлено по той же прямой, по которой движется материальная точка (см. рис. 6).
поступательное движение
Поступательное движение — это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое движение (см. рис. 7). Рис. 7. Движение вперед А как иначе? Помашите рукой и следуйте: видно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки возле оси почти не двигаются, а кабинки двигаются с разной скоростью и по разным траекториям (см. рис. 8). Рис. 8. Перемещение выбранных точек на колесе обозрения Посмотрите на движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным ( см. Рис. 9. Движение транспортных средств Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считается материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной самой себе (см. рис. 10). Рис. 10. Положение линии, соединяющей две точки |
Машина ехала прямо час. В начале часа его скорость была 10 км/ч, а в конце — 100 км/ч (см. рис. 11).
Рис. 11. Рисунок к задаче
Скорость изменялась равномерно. Сколько километров проехала машина?
Разберем условие задачи.
Скорость автомобиля изменялась равномерно, то есть его ускорение было постоянным на протяжении всего пути. Ускорение по определению равно:
Автомобиль ехал прямолинейно, поэтому его движение можно рассмотреть в проекции на одну ось координат:
Найдем ход.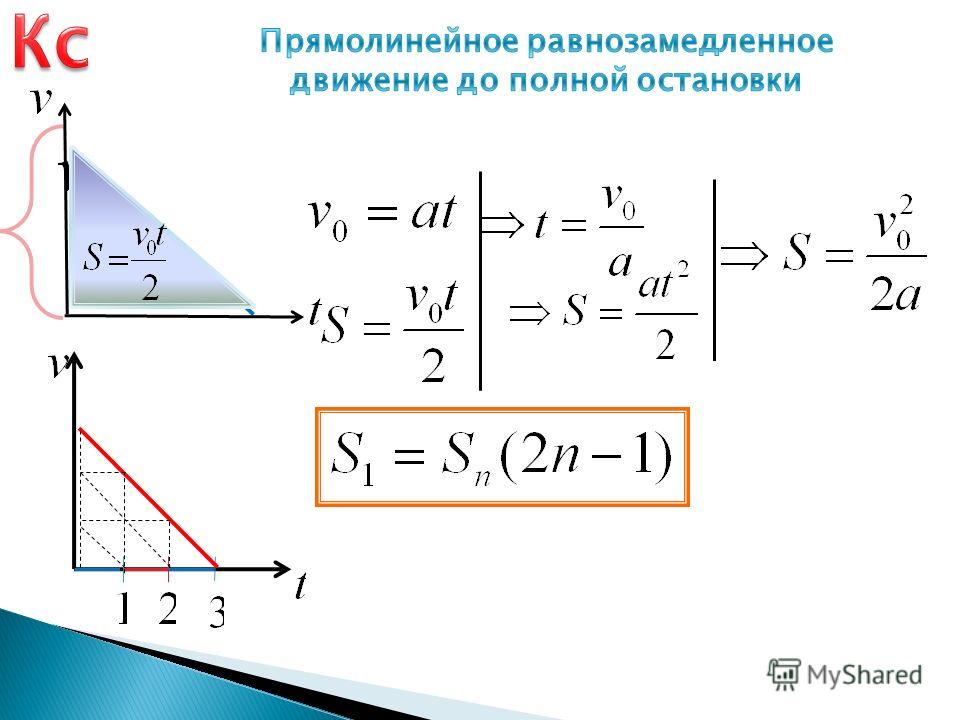
Пример увеличения скорости
Орехи кладут на стол, по одному ореху в минуту. Понятно: сколько минут пройдет, столько и орехов будет на столе. Теперь представим, что скорость укладки гаек от нуля увеличивается равномерно: в первую минуту гайки не кладут, во вторую кладут одну гайку, затем две, три и так далее. Сколько орехов будет на столе через некоторое время? Понятно, что это меньше, чем если бы всегда сохранялась максимальная скорость. Причем хорошо видно, что она меньше чем в 2 раза (см. рис. 12). Рис. 12. Количество гаек при разных скоростях укладки То же самое и с равноускоренным движением: допустим, сначала скорость была равна нулю, в конце стала равной (см. рис. 13). Рис. 13. Изменение скорости Если бы тело постоянно двигалось с такой скоростью, то его перемещение было бы равно, а так как скорость возрастает равномерно, то было бы в 2 раза меньше. |
Мы можем найти перемещение при РАВНОМЕРНОМ движении: . Как обойти эту проблему? Если скорость меняется не сильно, то движение можно приблизительно считать равномерным. Изменение скорости за короткий промежуток времени будет небольшим (см. рис. 14).
Рис. 14. Изменение скорости
Поэтому время в пути Т разобьем на N малых отрезков продолжительности (см. рис. 15).
Рис. 15. Разбиение отрезка времени
Рассчитаем смещение на каждом временном интервале. Скорость увеличивается на каждом интервале на:
На каждом отрезке движение будем считать равномерным, а скорость примерно равной начальной скорости на данном интервале времени. Посмотрим, не приведет ли наша аппроксимация к ошибке, если мы будем считать движение равномерным на малом интервале. Максимальная ошибка будет:
и суммарная ошибка за весь путь -> . При больших N будем считать, что ошибка близка к нулю. Мы увидим это на графике (см.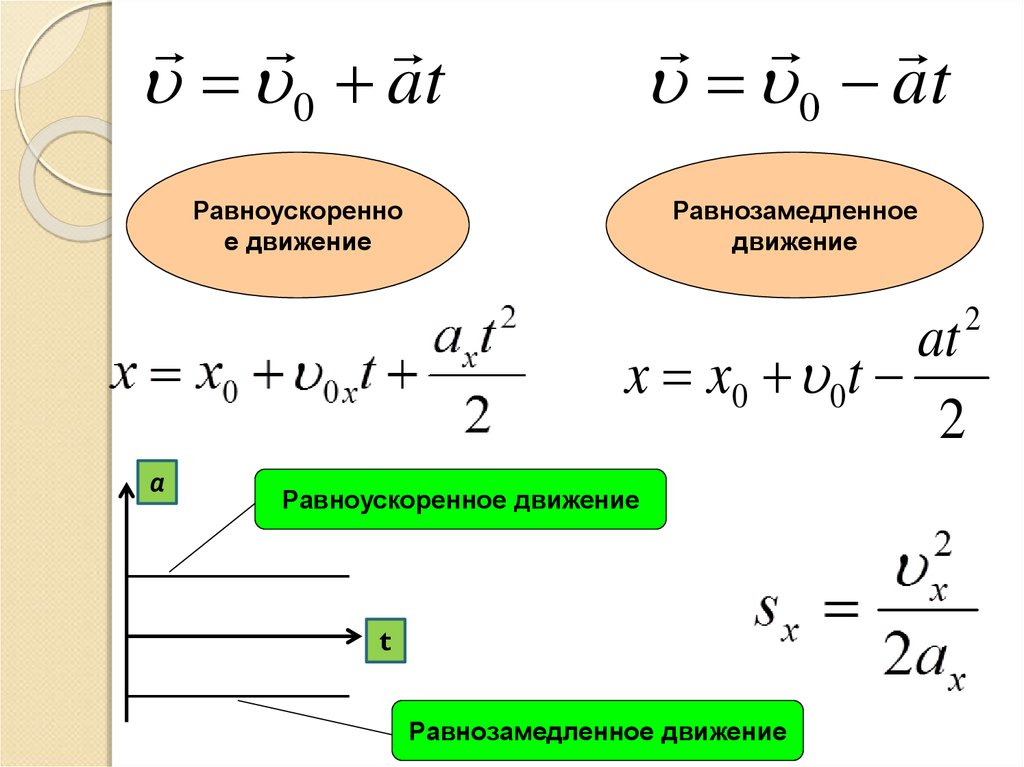 рис. 16): на каждом интервале будет ошибка, но суммарная ошибка для достаточно большого количества интервалов будет пренебрежимо мала.
рис. 16): на каждом интервале будет ошибка, но суммарная ошибка для достаточно большого количества интервалов будет пренебрежимо мала.
Рис. 16. Ошибка на интервалах
Итак, каждое следующее значение скорости на одну и ту же величину больше предыдущего. Из алгебры мы знаем, что это арифметическая прогрессия с разностью прогрессии:
Путь на участках (при равномерном прямолинейном движении (см. рис. 17) равен:
Рис. 17. Рассмотрение площади движения тела
На втором участке:
На n-м участке путь равен:
Арифметическая прогрессия
Арифметической прогрессией называется такая числовая последовательность, в которой каждое последующее число отличается от предыдущего на одинаковую величину. Арифметическая прогрессия задается двумя параметрами: начальным членом прогрессии и разностью прогрессии. Тогда последовательность записывается так: Сумма первых членов арифметической прогрессии вычисляется по формуле: |
Просуммируем все пути. Это будет сумма первых N членов арифметической прогрессии:
Это будет сумма первых N членов арифметической прогрессии:
Так как мы разбили движение на множество интервалов, то можно считать, что , то:
У нас было много формул, и чтобы не запутаться , мы не писали каждый раз индексы x, а считали все в проекции на ось координат.
Итак, мы получили основную формулу равноускоренного движения: перемещение при равноускоренном движении за время Т, которую мы вместе с определением ускорения (изменения скорости в единицу времени) будем использовать для решения задач:
Мы работали над проблемой автомобиля. Подставляем числа в решение и получаем ответ: машина проехала 55,4 км.
Математическая часть решения задачи
С движением мы разобрались. А как определить координату тела в любой момент времени?
По определению движение тела во времени — это вектор, начало которого находится в начальной точке движения, а конец — в конечной точке, где тело будет находиться во времени. Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):
Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):
Рис. 18. Проекция движения
Выразим координату:
То есть координата тела в момент времени равна начальной координате плюс проекция движения, которое тело совершило за время. Проекцию перемещения при равноускоренном движении мы уже нашли, осталось подставить и записать:
Это уравнение движения с постоянным ускорением. Он позволяет в любой момент узнать координату движущейся материальной точки. Понятно, что мы выбираем момент времени в интервале работы модели: ускорение постоянное, движение прямолинейное.
Почему уравнение движения нельзя использовать для нахождения пути
В каких случаях движение по модулю можно считать равным пути? Когда тело движется прямолинейно и не меняет направления. Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, находим ли мы путь или движение, они все же совпадают. При равноускоренном движении скорость изменяется. Если скорость и ускорение направлены в противоположные стороны (см. рис. 19), то модуль скорости уменьшается, и в какой-то момент он станет равным нулю и скорость изменит направление, то есть тело начнет двигаться в противоположном направлении. Рис. 19. Модуль скорости уменьшается И тогда, если в этот момент времени тело находится на расстоянии 3 м от начала наблюдения, то его перемещение равно 3 м, но если тело сначала прошло 5 м, затем развернулось и прошло еще 2 м, тогда путь будет 7 м. И как его найти, если вы не знаете этих цифр? Нужно только найти момент, когда скорость равна нулю, т. е. когда тело развернется, и найти путь в эту точку и из нее (см. рис. 20). Рис. 20. Момент когда скорость 0 |
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. — Перераспределение 2-го издания.
 — Х.: Веста: Изд-во «Ранок», 2005. — 464 с.
— Х.: Веста: Изд-во «Ранок», 2005. — 464 с. - Ландсберг Г.С. Начальный учебник физики; т.1. Механика. Нагревать. Молекулярная физика — М.: Изд-во «Наука», 1985.
- Интернет-портал «kaf-fiz-1586.narod.ru» ()
- Интернет-портал «Учись — Легко» ()
- Интернет-портал «Гипермаркет знаний» ()
Домашнее задание
- Что такое арифметическая прогрессия?
- Какое движение является поступательным?
- Что такое векторная величина?
- Запишите формулу ускорения через изменение скорости.
- Какое уравнение движения с постоянным ускорением?
- Вектор ускорения направлен в сторону движения тела. Как тело изменит свою скорость?
«Круто! Физика» движется от «народа»!
«Круто! Физика» — сайт для тех, кто любит физику, изучает себя и учит других.
«Круто! Физика» — всегда рядом!
Интересные материалы по физике для школьников, учителей и всех любознательных.
Оригинальный сайт «Класс! Физика» (class-fizika.narod.ru) с 2006 года включен в выпуски каталога «Образовательные ресурсы сети Интернет для основного общего и среднего (полного) общего образования», утвержденного Министерством Министерства образования и науки Российской Федерации, Москва.
Читайте, учитесь, исследуйте!
Мир физики интересен и увлекателен, он приглашает всех любознательных путешествовать по страницам Крутого! Сайт физики.
А для начала — наглядная карта физики, на которой показано, откуда они берутся и как взаимосвязаны между собой разные области физики, что изучают и для чего нужны.
Карта физики создана на основе видеоролика Доминика Вилиммана «Карта физики» канала «Область науки».
Физика и тайны художников
Тайны мумий фараонов и изобретения Ребрандта, подделки шедевров и тайны папирусов Древнего Египта — искусство скрывает множество тайн, но современные физики, с помощью новых методов и устройств, найти объяснения все большему количеству удивительных тайн прошлого.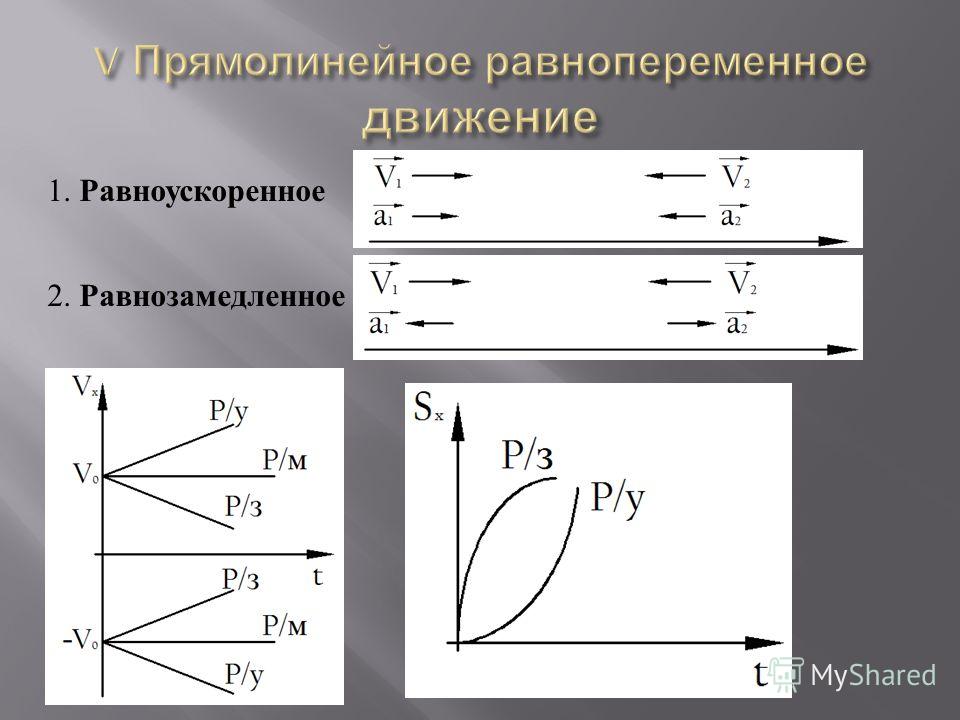 …….. читать
…….. читать
Азбука физики
Всемогущее трение
Оно есть везде, но куда же без него ?
А вот и три героя-помощника: графит, молебденит и тефлон. Эти удивительные вещества с очень высокой подвижностью частиц в настоящее время используются в качестве отличной твердой смазки……… читать
Аэронавтика
«Так поднимитесь к звездам!» — начертано на эмблеме основоположников воздухоплавания братьев Монгольфье.
Знаменитый писатель Жюль Верн летал на воздушном шаре всего 24 минуты, но это помогло ему создать самые завораживающие произведения искусства…….. читать
паровые машины
«Этот могучий великан был трехметрового роста: великан легко тянул фургон с пятью пассажирами. На голове у Парового Человека была труба дымохода, из которой валил густой черный дым… все, даже лицо, было из железа, и все это постоянно скрежетало и грохотало…» О ком это? Для кого эти похвалы? ……… читать
Тайны магнита
Фалес Милетский наделил его душой, Платон сравнил его с поэтом, Орфей нашел его подобным жениху.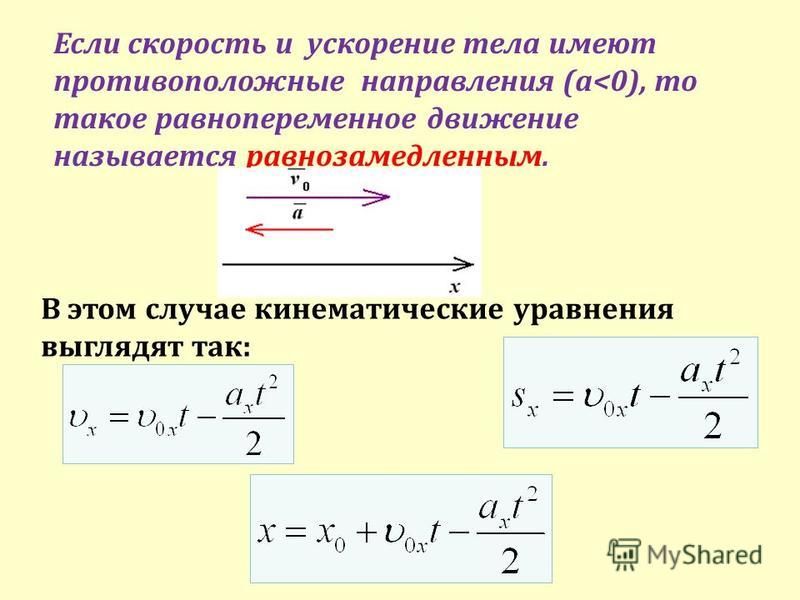 .. В эпоху Возрождения магнит считали отражением неба и приписывали ему способность искривлять пространство. Японцы верили, что магнит — это сила, которая поможет повернуть к вам фортуну……… читать
.. В эпоху Возрождения магнит считали отражением неба и приписывали ему способность искривлять пространство. Японцы верили, что магнит — это сила, которая поможет повернуть к вам фортуну……… читать
По ту сторону зеркала
Знаете, сколько интересных открытий может подарить «зеркало»? У изображения вашего лица в зеркале правая и левая половины поменялись местами. Но лица редко бывают полностью симметричными, поэтому окружающие видят вас совсем другими. Вы думали об этом? ……… читать
Тайны обычного волчка
«Осознание того, что чудесное было рядом с нами, приходит слишком поздно.» — А. Блок.
Знаете ли вы, что малайцы могут часами зачарованно наблюдать за вращением вершины. Однако, чтобы правильно его крутить, требуется немалая сноровка, ведь вес малайской волчки может достигать нескольких килограммов………читать
Изобретения Леонардо да Винчи
«Хочу творить чудеса!» — сказал он и спросил себя: — А скажи мне, ты хоть что-нибудь сделал? Леонардо да Винчи писал свои трактаты по криптографии с помощью обычного зеркала, поэтому его зашифрованные манускрипты впервые удалось прочесть лишь три столетия спустя.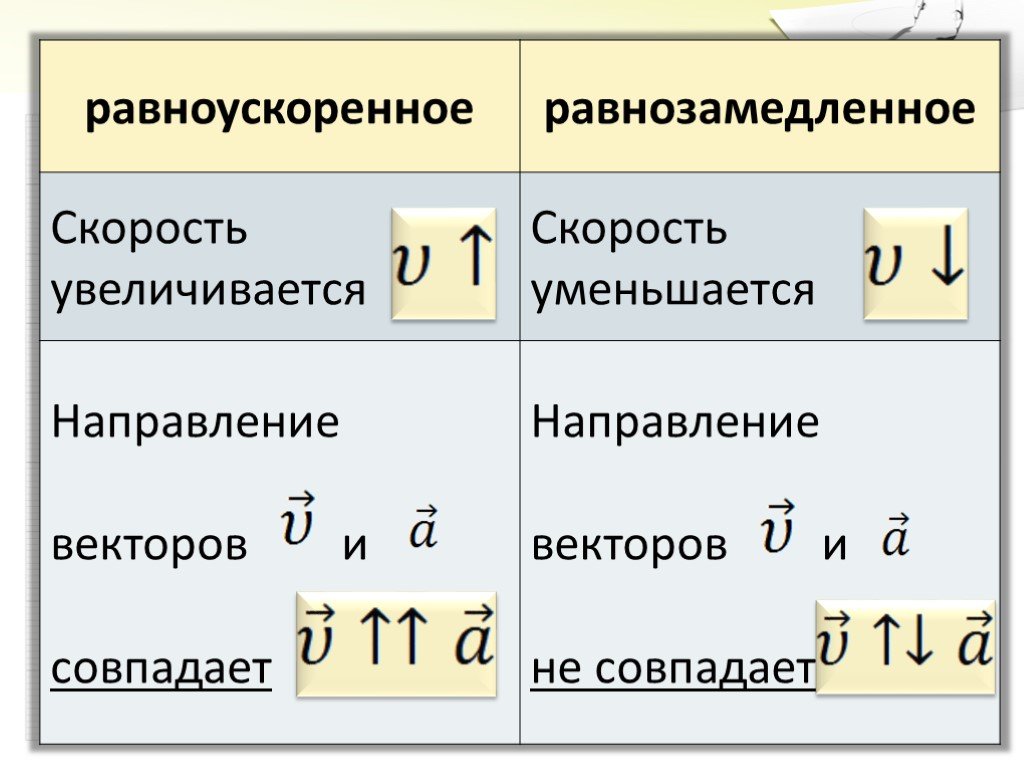 ……..
……..
Движение с постоянным ускорением — это движение, при котором ускорение вектор остается постоянным как по величине, так и по направлению. Примером этого вида движения является движение точки в поле силы тяжести (как по вертикали, так и под углом к горизонту).
Используя определение ускорения, получаем следующее соотношение
После интегрирования имеем равенство
.
Учитывая, что вектор мгновенной скорости равен
, мы получим следующее выражение
Интегрирование последнего выражения дает следующее соотношение
. Откуда получаем уравнение движения точки с постоянным ускорением
.
Примеры векторных уравнений движения материальной точки
Равномерное прямолинейное движение (
):
. (1.7)
Движение с постоянным ускорением (
):
. (1.8)
Зависимость скорости от времени при движении точки с постоянным ускорением имеет вид:
. (1.9)
Вопросы для самоконтроля.

Сформулируйте определение механического движения.
Определить материальную точку.
Как определяется положение материальной точки в пространстве при векторном способе описания движения?
В чем суть векторного метода описания механического движения? Какие характеристики используются для описания этого движения?
Дайте определения векторов средней и мгновенной скорости. Как определяется направление этих векторов?
Определите вектор среднего и мгновенного ускорения.
Какое из соотношений является уравнением движения точки с постоянным ускорением? Какое соотношение определяет зависимость вектора скорости от времени?
§1.2. Координатный способ описания движения
В координатном методе для описания движения выбирается система координат (например, декартова). Опорная точка жестко фиксируется с выбранным телом ( опорное тело ). Пусть
ортов направлены в положительные стороны осей OX, OY и OZ соответственно. Положение точки задается координатами
Положение точки задается координатами
.
Мгновенный вектор скорости определяется следующим образом:
где
проекций вектора скорости на оси координат и
производных координат по времени.
Длина вектора скорости связана с его проекциями соотношением:
. (1.11)
Для вектора мгновенного ускорения справедливо соотношение:
где
проекций вектора ускорения на оси координат, а
производных по времени от проекций вектора скорости.
Длина вектора мгновенного ускорения находится по формуле:
. (1.13)
Примеры уравнений движения точки в декартовой системе координат
. (1.14)
Уравнения движения:
. (1.15)
Зависимости проекций вектора скорости на оси координат от времени:
(1.16)
Вопросы для самоконтроля.
В чем суть координатного метода описания движения?
Какое соотношение определяет мгновенный вектор скорости? По какой формуле вычисляют модуль вектора скорости?
Какое соотношение определяет вектор мгновенного ускорения? По какой формуле вычисляют модуль вектора мгновенного ускорения?
Какие соотношения называются уравнениями равномерного движения точки?
Какие соотношения называются уравнениями движения с постоянным ускорением? По каким формулам вычисляют проекции мгновенной скорости точки на оси координат?
Кинематика — это изучение классического механического движения в физике. В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В этой статье мы рассмотрим, что такое ускорение и движение с постоянным ускорением.
В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В этой статье мы рассмотрим, что такое ускорение и движение с постоянным ускорением.
Понятие об ускорении
При движении тела в пространстве за некоторое время оно преодолевает определенный путь, равный длине траектории. Для расчета этого пути используйте понятия скорости и ускорения.
Скорость как физическая величина характеризует скорость изменения во времени пройденного пути. Скорость направлена по касательной к траектории в направлении движения тела.
Ускорение — несколько более сложная величина. Короче говоря, он описывает изменение скорости в данный момент времени. Математика выглядит так:
Чтобы лучше понять эту формулу, приведем простой пример: предположим, что за 1 секунду движения скорость тела увеличилась на 1 м/с. Эти цифры, подставленные в вышеприведенное выражение, приводят к результату: ускорение тела за эту секунду равно 1 м/с 2 .
Направление ускорения полностью не зависит от направления скорости. Его вектор совпадает с вектором равнодействующей силы, вызывающей это ускорение.
Следует отметить важный момент в приведенном выше определении ускорения. Эта величина характеризует изменение не только скорости по модулю, но и направления. Последний факт следует учитывать в случае криволинейного движения. Далее в статье будет рассматриваться только прямолинейное движение.
Скорость при движении с постоянным ускорением
Ускорение является постоянным, если оно сохраняет свой модуль и направление во время движения. Такое движение называется равномерно ускоренным или равномерно замедленным — все зависит от того, приводит ли ускорение к увеличению скорости или к ее уменьшению.
В случае движения тела с постоянным ускорением скорость можно определить по одной из следующих формул:
Первые два уравнения характеризуют равноускоренное движение. Отличие между ними в том, что второе выражение применимо для случая ненулевой начальной скорости.
Третье уравнение представляет собой выражение для скорости равномерно медленного движения с постоянным ускорением. Ускорение направлено против скорости.
Графики всех трех функций v(t) представляют собой прямые линии. В первых двух случаях прямые имеют положительный наклон относительно оси абсцисс, в третьем случае этот наклон отрицательный.
Формулы расстояний
Для пути в случае движения с постоянным ускорением (ускорение a = const) нетрудно получить формулы, если вычислить интеграл скорости по времени. Проделав эту математическую операцию над тремя вышеприведенными уравнениями, мы получим следующие выражения для пути L:
L = v 0 * t + a * t 2 / 2;
L = v 0 *t — a*t 2 / 2.
Графики всех трех функций времени пути представляют собой параболы. В первых двух случаях правая ветвь параболы увеличивается, а для третьего функция постепенно достигает некоторой постоянной, которая соответствует пройденному пути до полной остановки тела.
Решение проблемы
Двигаясь со скоростью 30 км/ч, автомобиль начал ускоряться. За 30 секунд он прошел дистанцию 600 метров. Каково было ускорение автомобиля?
Прежде всего, переведем начальную скорость из км/ч в м/с:
v 0 = 30 км/ч = 30000/3600 = 8,333 м/с.
Теперь запишем уравнение движения:
L = v 0 *t + a*t 2 /2.
Из этого равенства выразим ускорение, получим:
а = 2*(L — v 0 *t)/t 2 .
Все физические величины в этом уравнении известны из условий задачи. Подставляем их в формулу и получаем ответ: а ≈ 0,78 м/с 2 . Таким образом, двигаясь с постоянным ускорением, автомобиль увеличивал свою скорость на 0,78 м/с каждую секунду.
Также посчитаем (для интереса), какую скорость он приобрел через 30 секунд ускоренного движения, получим:
v = v 0 + a * t = 8,333 + 0,78 * 30 = 31,733 м/с.
Полученная скорость 114,2 км/ч.
Цели урока:
Образовательные:
Проявление:
Вос питательный
Тип урока : Комбинированный урок.
Посмотреть содержание документа
Тема урока: «Ускорение. Прямолинейное движение с постоянным ускорением.
Подготовила — учитель физики МБОУ «СОШ № 4» Погребняк Марина Николаевна
Класс -11
Занятие 5/4 Тема урока: «Ускорение. Прямолинейное движение с постоянным ускорением ».
Цели урока:
Образовательный: Познакомить учащихся с характерными чертами прямолинейного равноускоренного движения. Дайте понятие ускорения как основной физической величины, характеризующей неравномерное движение. Введите формулу определения мгновенной скорости тела в любой момент времени, вычислите мгновенную скорость тела в любой момент времени,
для улучшения умения учащихся решать задачи аналитическим и графическим способами.
Проявление: развитие теоретического, творческого мышления у школьников, формирование операционального мышления, направленного на выбор оптимальных решений
Вос питательный : воспитывать сознательное отношение к обучению и интерес к изучению физики.
Тип урока : Комбинированный урок.
Демонстрации:
1. Равноускоренное движение мяча по наклонной плоскости.
2. Мультимедийное приложение «Основы кинематики»: фрагмент «Равномерно ускоренное движение».
Рабочий процесс.
1. Организационный момент .
2. Проверка знаний : Самостоятельная работа («Движение». «Графики прямолинейного равномерного движения») — 12 мин.
3. Изучение нового материала.
План подачи нового материала:
1. Мгновенная скорость.
2. Ускорение.
3. Скорость при прямолинейном равноускоренном движении.
1. Мгновенная скорость. Если скорость тела изменяется со временем, то для описания движения необходимо знать, какова скорость тела в данный момент времени (или в данной точке траектории). Эта скорость называется мгновенной скоростью.
Можно также сказать, что мгновенная скорость — это средняя скорость за очень небольшой интервал времени. При движении с переменной скоростью средняя скорость, измеренная за разные промежутки времени, будет разной.
Однако если при измерении средней скорости брать все меньшие и меньшие интервалы времени, то значение средней скорости будет стремиться к какому-то определенному значению. Это мгновенная скорость в данный момент времени. В дальнейшем, говоря о скорости тела, мы будем иметь в виду его мгновенную скорость.
2. Ускорение. При неравномерном движении мгновенная скорость тела переменная; она различна по модулю и (или) по направлению в разные моменты времени и в разных точках траектории. Все автомобильные и мотоциклетные спидометры показывают нам только мгновенный модуль скорости.
Если мгновенная скорость неравномерного движения изменяется неодинаково за одни и те же промежутки времени, то рассчитать ее очень сложно.
Такие сложные неравномерные движения в школе не изучают. Поэтому мы будем рассматривать только простейшее неравномерное движение — равноускоренное прямолинейное движение.
Прямолинейное движение, при котором мгновенная скорость изменяется одинаково за любые равные промежутки времени, называется равноускоренным прямолинейным движением.
Если скорость тела изменяется по мере его движения, возникает вопрос: какова «скорость изменения скорости»? Эта величина, называемая ускорением, играет важнейшую роль во всей механике: мы вскоре увидим, что ускорение тела определяется силами, действующими на это тело.
Ускорение есть отношение изменения скорости тела к интервалу времени, в течение которого это изменение произошло.
Единица ускорения в СИ: м/с 2 .
Если тело движется в одном направлении с ускорением 1 м/с 2 , его скорость меняется каждую секунду на 1 м/с.
Термин «ускорение» используется в физике, когда речь идет о любом изменении скорости, в том числе когда модуль скорости уменьшается или когда модуль скорости остается неизменным и скорость изменяется только в направлении.
3. Скорость при прямолинейном равноускоренном движении.
Из определения ускорения следует, что v = v 0 + at.
Если направить ось x вдоль прямой, по которой движется тело, то в проекциях на ось x получим v x = v 0 x + a x t.
Таким образом, при прямолинейном равноускоренном движении проекция скорости линейно зависит от времени. Это означает, что график v x (t) представляет собой отрезок прямой.
Формула движения:
График скорости автомобиля:
График скорости автомобиля
4. Закрепление нового материала.
Какова мгновенная скорость камня, брошенного вертикально вверх в верхней точке траектории?
О какой скорости — средней или мгновенной — идет речь в следующих случаях:
а) поезд шел между станциями со скоростью 70 км/ч;
б) скорость молота при ударе 5 м/с;
в) спидометр электровоза показывает 60 км/ч;
г) пуля вылетает из винтовки со скоростью 600 м/с.



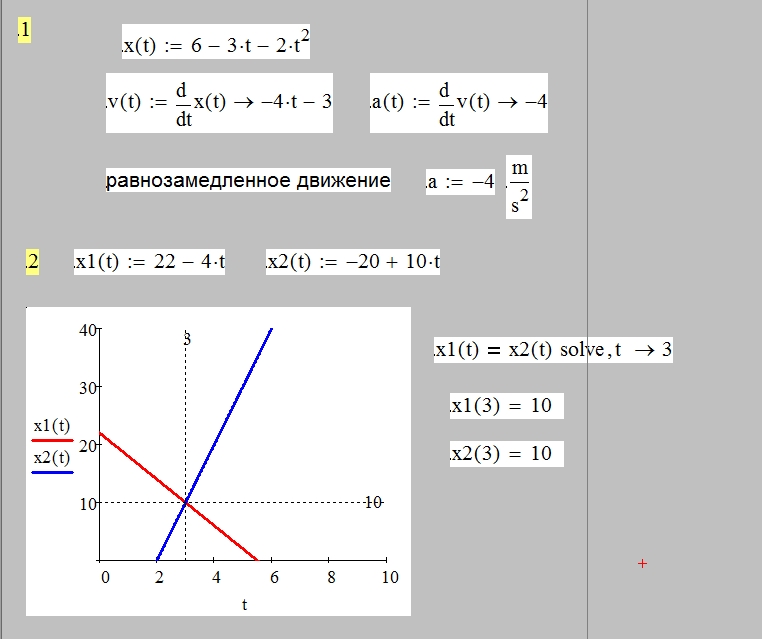
 13).
13). Арифметическая прогрессия задается двумя параметрами: начальной прогрессией членов и разницей прогрессии. Тогда последовательность записывается так:
Арифметическая прогрессия задается двумя параметрами: начальной прогрессией членов и разницей прогрессии. Тогда последовательность записывается так: Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, находим ли мы путь или движение, они все же совпадают.
Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, находим ли мы путь или движение, они все же совпадают.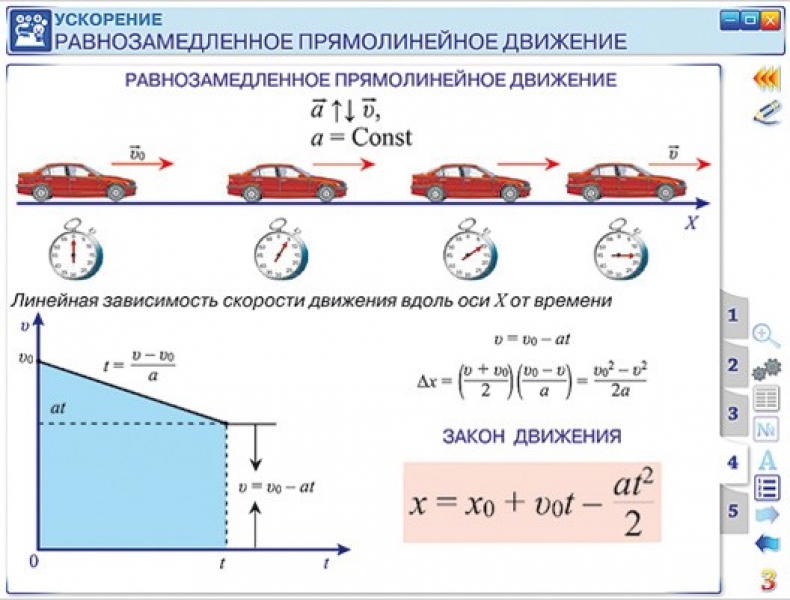 А., Богданова Г.С. Физика: Справочник с примерами решения задач. — Перераспределение 2-го издания. — Х.: Веста: Изд-во «Ранок», 2005. — 464 с.
А., Богданова Г.С. Физика: Справочник с примерами решения задач. — Перераспределение 2-го издания. — Х.: Веста: Изд-во «Ранок», 2005. — 464 с. рис. 4) :
рис. 4) :  рис. 9).
рис. 9).

 — Х.: Веста: Изд-во «Ранок», 2005. — 464 с.
— Х.: Веста: Изд-во «Ранок», 2005. — 464 с.
Leave A Comment