Физика 9 кл. Перемещение при прямолинейном равноускоренном движении
- Подробности
- Просмотров: 77
1.Как доказать, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ?
Отрезок АС — график проекции вектора скорости тела, движущегося с постоянным ускорением а при начальной скорости v0.
При прямолинейном равномерном движении проекция вектора перемещения, совершенного телом, определяется по той же формуле, что и площадь прямоугольника, заключенного под графиком проекции вектора скорости.
Поэтому проекция вектора перемещения численно равна площади этого прямоугольника.
Докажем, что и в случае прямолинейного равноускоренного движения проекцию sx вектора перемещения можно определять по той же формуле, что и площадь фигуры, заключенной под графиком скорости (АС).
За промежуток времени db скорость тела меняется от Vах до Vcх.
За этот малый промежуток времени проекция вектора скорости меняется очень незначительно.
Поэтому движение тела на этом промежутке времени мало отличается от равномерного.
Тогда участок ас графика можно считать горизонтальным, а полоску acbd — прямоугольником.
Значит, площадь этой полоски численно равна проекции вектора перемещения за время db.
На такие полоски можно разбить всю площадь фигуры ОАСВ, являющейся трапецией.
Тогда проекция sx вектора перемещения за времени, равное ОВ, численно равна площади трапеции ОАСВ и определяется по той же формуле, что и эта площадь.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Основаниями трапеции ОАСВ являются отрезки OA = Vox и ВС = Vх, а высота равна ОВ = t.
Тогда:
Так как :
Получаем:
2. Как выглядит формула для определения проекции вектора перемещения тела при его прямолинейном равноускоренном движении?
Формула для расчёта проекции вектора перемещения при равноускоренном движении:
По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью (при торможении тела), только в этом случае векторы скорости и ускорения будут направлены в противоположные стороны, поэтому их проекции будут иметь разные знаки.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
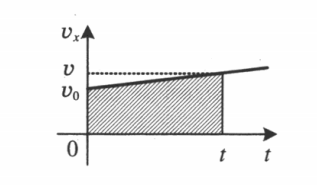

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Формула перемещения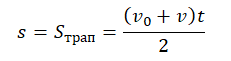
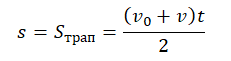
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
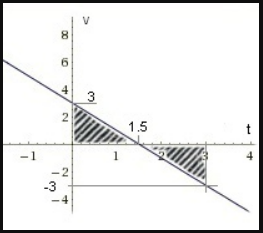

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
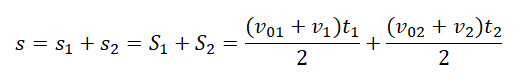
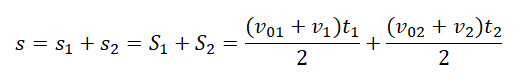
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещенияКонечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
v = v0 ± at
В итоге получается формула:
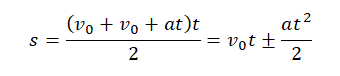
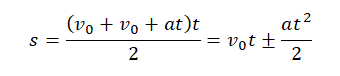
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает вид:
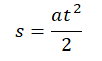
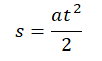
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
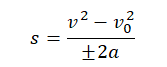
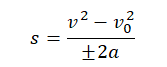
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
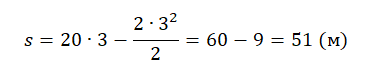
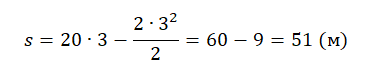
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
t1 = t – t2
Когда тело тормозит, через некоторое время t1 оно останавливается. Поэтому скорость в момент времени t1 равна 0:
0 = v01 – at1
При торможении перемещение s1 равно:
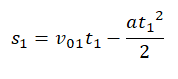
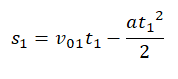
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
t2 = t – t1
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
v = at2
При разгоне перемещение s2 равно:
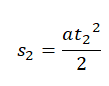
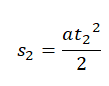
При этом модуль перемещения в течение всего времени движения равен:
s = |s1 – s2|
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
l = s1 + s2
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с2. Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
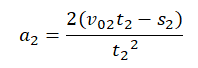
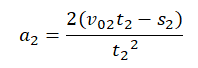
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
v02 = v01 + a1t1 = a1t1 (так как v01 = 0)
Подставляем выраженные величины в формулу:
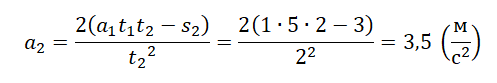
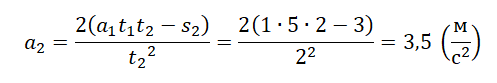
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
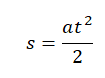
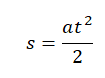
За первую секунду тело переместится на расстояние, равное:
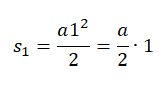
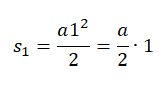
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
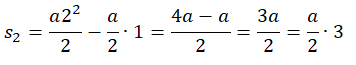
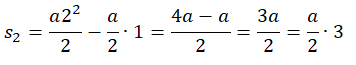
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
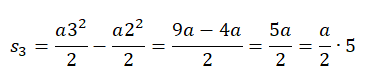
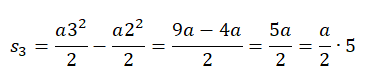
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:


Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду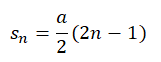
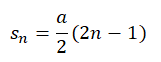
Пример №4. Автомобиль разгоняется с ускорением 3 м/с2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
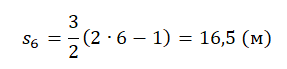
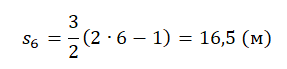
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
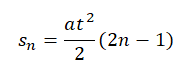
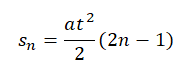
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с2. Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
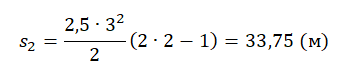
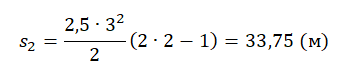
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:
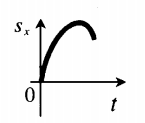
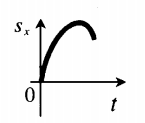
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
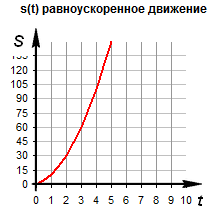

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
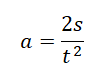
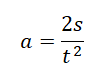
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
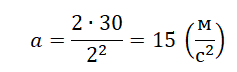
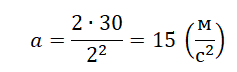
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
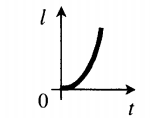
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
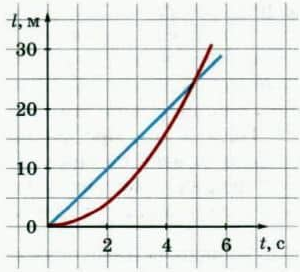

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
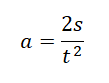
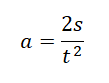
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:
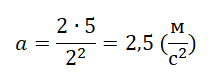
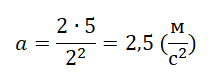

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
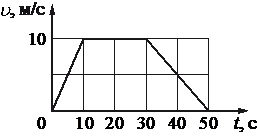
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
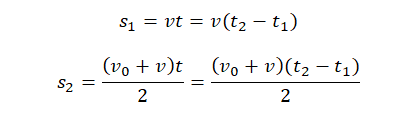
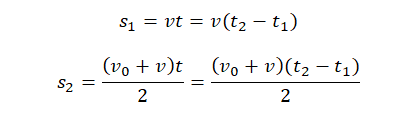
Теперь рассчитаем пути s1 и s2, а затем сложим их:
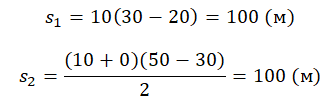
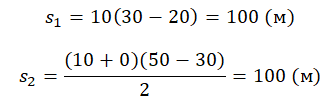
s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17957 За 10 секунд скорость автомобиля, движущегося равноускоренно по прямой дороге, увеличилась от 0 до 20 м/с. Пройденный автомобилем путь равен…Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения пути при равноускоренном прямолинейном движении.
- Определить недостающие исходные данные.
- Найти искомую величину.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Конечная скорость v = 20 м/с.
- Время изменения скорости t = 10 с.
Формула для вычисления пути при равноускоренном прямолинейном движении:
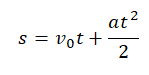
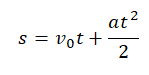
Так как начальная скорость равна нулю, формула принимает вид:
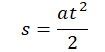
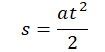
Нам неизвестно ускорение, но его можно вычислить по формуле:
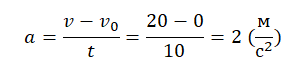
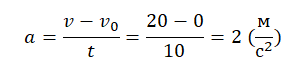
Вычисляем путь:
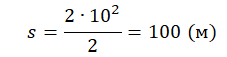
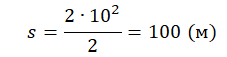
Ответ: 100
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22776

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.


Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор | оценить
Физика 9 кл. Перемещение тела при прямолинейном равноускоренном движении без начальной скорости
- Подробности
- Просмотров: 84
1. По каким формулам рассчитываются проекция и модуль вектора перемещения тела при его равноускоренном движении из состояния покоя?
Исходная расчетная формула проекции вектора перемещения тела, движущегося равноускоренно:
Проекция вектора перемещения тела, движущегося равноускоренно, если его начальная скорость v0 равна нулю:
Модуль вектора перемещения при прямолинейном равноускоренном движении без начальной скорости прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено:
2. Каковы закономерности равноускоренного движения без начальной скорости ?
а)
ОА : ОВ : ОС : OD : 0E = 1 : 4 : 9 : 16 : 25
т. е. при увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.
б)
OA : AB : BC : CD : DE = 1 : 3 : 5 : 7 : 9
т. е. модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени (каждый из которых равен t
3. Во сколько раз увеличится модуль вектора перемещения тела при увеличении времени его движения из состояния покоя в n раз?
При увеличении в n раз времени движения, отсчитываемого от момента начала движения, перемещение увеличивается в n2 раз.
4. Как относятся друг к другу модули векторов перемещений тела, движущегося равноускоренно из состояния покоя, при увеличении времени его движения в целой число раз по сравнению с t1?
При увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t
5. Как относятся друг к другу модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, если это тело движется равноускоренно из состояния покоя?
Модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, относятся как ряд последовательных нечётных чисел.
6. С какой целью можно использовать эти закономерности?
ОА : ОВ : ОС : OD : ОЕ = 1 : 4 : 9 : 16 : 25
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
Вышеуказанные закономерности присущи
Ими можно пользоваться, если необходимо определить, является движение равноускоренным или нет.
Например:
Задача.
Определим, было ли равноускоренным движение улитки, которая:
—
за первые 20 с движения переместилась на 0,5 см,
—
за вторые 20 с — на 1,5 см,
—
за третьи 20 с — на 2,5 см.
Для этого найдём, во сколько раз перемещения, совершённые за второй и третий промежутки времени, больше, чем за первый:
Значит, 0,5 см : 1,5 см : 2,5 см = 1 : 3 : 5.
Поскольку эти отношения представляют собой ряд последовательных нечётных чисел, то движение тела было равноускоренным.
Равноускоренный характер движения был выявлен на основании закономерности:
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
«Прямолинейное равноускоренное движение»
Код ОГЭ 1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении
Прямолинейное равноускоренное движение — прямолинейное движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени.
Основные величины, характеризующие движение:
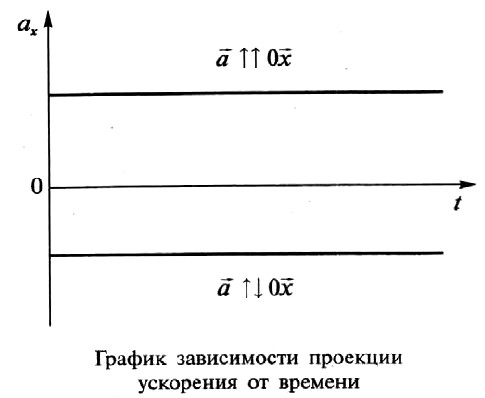
- Ускорение. Не меняется, то есть постоянно по величине и направлению:

Физический смысл: ускорение численно равно изменению скорости за 1 с. Например, ускорение равно 5 м/с2 — это значит, что скорость тела изменяется на 5 м/с за каждую секунду своего движения.
- Мгновенная скорость. Меняется равномерно, увеличиваясь или уменьшаясь одинаково за равные промежутки времени.
Уравнение, описывающее изменение скорости с течением времени: 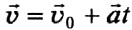 , в проекциях ʋx = ʋ0x + axt.
, в проекциях ʋx = ʋ0x + axt.
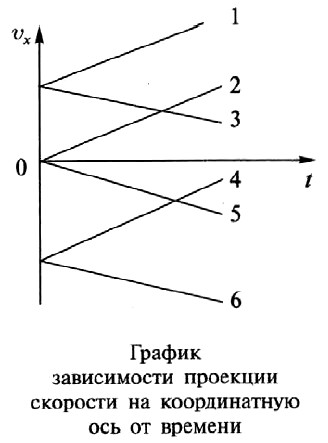 На графике изображены следующие случаи движения.
На графике изображены следующие случаи движения.
1) Проекция начальной скорости больше нуля.
то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью.
2) Проекция начальной скорости равна нулю.
то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью.
3) Проекция начальной скорости больше нуля,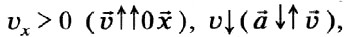
то есть тело движется в направлении координатной оси с уменьшающейся по модулю скоростью.
4) Проекция начальной скорости меньше нуля.
то есть тело движется в направлении, противоположном направлению координатной оси, с уменьшающейся по модулю скоростью.
5) Проекция начальной скорости равна нулю.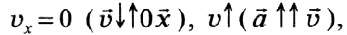
то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью.
6) Проекция начальной скорости отрицательна.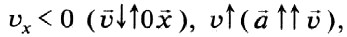
то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью.
- Перемещение. Зависимость перемещения от времени описывается квадратичной функцией:
 . В проекциях на координатную ось:
. В проекциях на координатную ось:  .
.
Иногда удобно пользоваться другими формулами для расчёта перемещения, которые получаются из исходной и уравнения зависимости проекции скорости от времени: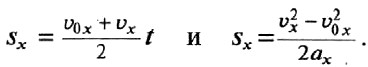
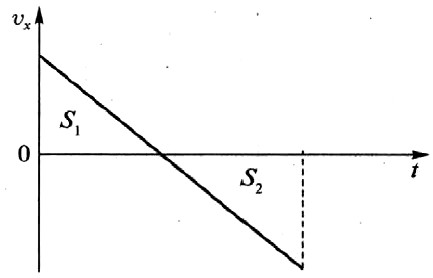 Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени.
Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени.
В случае, изображённом на рисунке: sx = S1 – S2, где S1, и S2 — числовые значения площадей треугольников.
- Координата. Поскольку х = х0 + sx, зависимость координаты от времени тоже описывается квадратичной функцией:

Если использовать другие варианты расчёта ускорения при равноускоренном движении, получаем: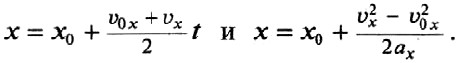 .
.
- Путь. Если направление движения не меняется, то l = s. Если направление движения меняется, то
l = s1 +s2, где s1 — модуль вектора перемещения до остановки, s2 — модуль вектора перемещения при движении в обратном направлении. Внимание! Путь не может быть отрицательным!

Конспект урока по физике для 9 класса «Прямолинейное равноускоренное движение».
Следующая тема: «Свободное падение». (код ОГЭ по физике 1.4)
Попытаемся вывести формулу для нахождения проекции вектора перемещения тела, которое двигается прямолинейно и равноускоренно, за любой промежуток времени.
Для этого обратимся к графику зависимости проекции скорости прямолинейного равноускоренного движения от времени.
График зависимости проекции скорости прямолинейного равноускоренного движения от времени
Ниже на рисунке представлен график, для проекции скорости некоторого тела, которое движется с начальной скорость V0 и постоянным ускорением а.
Если бы у нас было равномерное прямолинейное движение, то для вычисления проекции вектора перемещения, необходимо было бы посчитать площадь фигуры под графиком проекции вектора скорости.
Теперь докажем, что и в случае равноускоренного прямолинейного движения проекция вектора перемещения Sx будет определяться таким же образом. То есть проекция вектора перемещения будет равняться площади фигуры под графиком проекции вектора скорости.
Найдем площадь фигуры ограниченную осью оt, отрезками АО и ВС, а также отрезком АС.
Выделим на оси ot малый промежуток времени db. Проведем через эти точки перпендикуляры к оси времени, до их пересечения с графикос проекции скорости. Отметим точки пересечения a и c. За этот промежуток времени скорость тела поменяется от Vax до Vbx.
Если взять этот промежуток достаточно малым, то можно считать что скорость остается практически неизменной, а следовательно мы будем иметь на этом промежутке дело с равномерным прямолинейным движением.
Тогда можно считать отрезок ac горизонтальным, а abcd – прямоугольником. Площадь abcd будет численно равна проекции вектора перемещения, за промежуток времени db. Мы можем разбить на такие малые промежутки времени всю площадь фигуры OACB.
То есть мы получили, что проекция вектора перемещения Sx за промежуток времени, соответствующий отрезку ОВ, будет численно равна площади S трапеции ОACB, и будет определяться по той же формуле, что и эта площадь.
Следовательно,
Так как Vx=V0x+ax*t и S=Sx, полученная формула примет следующий вид:
Мы получили формулу, с помощью которой можем рассчитать проекцию вектора перемещения при равноускоренном движении.
В случае равнозамедленного движения формула примет следующий вид:
Нужна помощь в учебе?
Предыдущая тема: Скорость прямолинейного равноускоренного движения: график скорости
Следующая тема:   Перемещение при прямолинейном равноускоренном движении без начальной скорости
Все неприличные комментарии будут удаляться.
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для класса 4 Maths
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Математика
- Решения NCERT для класса 6 Наука
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Класс 11 Бизнес-учебный план
- Класс 11 Экономический учебный план
- Класс 12 Бухгалтерский учебный план
- Класс 12 бизнес-учебный план
- 0 91818001818000 ,Равномерно ускоренное движение — IB Physics Stuff
Определение символов IB:
u начальная скорость
v конечная скорость
a ускорение (постоянное)
т пройденное время
с пройденное расстояние2.1.7 Вывести уравнения для равномерно ускоренного движения
Ускорение определяется как скорость изменения скорости относительно времени в заданном направлении.Единицами ускорения СИ являются мс -2 . Это будет означать, что если объект имеет ускорение 1 мс -2 , он будет увеличивать свою скорость (в заданном направлении) на 1 мс -1 каждую секунду, когда он ускоряется. Если мы напишем определение для ускорения в математических терминах:
(1)\ begin {align} a = {v-u \ over t} \ end {align}
Тогда решите v:
(2)\ begin {уравнение} v = u + at \ end {уравнение}
Это дает нам конечную скорость объекта с точки зрения ускорения, начальной скорости и времени ускорения объекта.В графической форме уравнение представляет собой прямую линию с u в качестве вертикального пересечения, a в качестве наклона и t в качестве независимой переменной.
Мы можем вывести еще одно уравнение, если посмотрим на график зависимости скорости от времени для объекта с ненулевой начальной скоростью.
Мы знаем, что площадь под кривой равна расстоянию
(3)\ begin {уравнения} Площадь = красный + желтый \ конец {уравнение}
(4)\ begin {align} s = ut + {(v-u) \ over 2} t \ end {align}
(5)\ begin {align} s = ut + {1 \ over 2} vt — 1 {\ over 2} ut \ end {align}
(6)\ begin {align} s = {u + v \ over 2} t \ end {align}
Теперь, когда мы объединяем два уравнения, которые мы получили, мы можем создать другое уравнение:
(7)\ begin {align} s = {u + u + at \ over 2} t \ end {align}
(8)\ begin {align} s = ut + {1 \ over 2} в ^ 2 \ end {align}
Теперь, если мы вернемся к определению ускорения (1) и умножим на t и разделим на:
(9)\ begin {align} t = {v-u \ over a} \ end {align}
Если подставить это выражение для времени в 3-е уравнение и решить для v:
(10)\ begin {align} s = u \ left [{v-u \ over a} \ right] + {1 \ over 2} a \ left [{v-u \ over a} \ right] ^ 2 \ end {align}
(11)\ begin {align} s = {uv -u ^ 2 \ over a} + {v ^ 2 + u ^ 2 -2uv \ over 2a} \ end {align}
(12)\ begin {уравнение} 2as = 2uv -2u ^ 2 + v ^ 2 + u ^ 2 -2uv \ end {уравнение}
(13)\ begin {уравнения} 2as = v ^ 2 -u ^ 2 \ end {уравнения}
(14)\ begin {уравнение} v ^ 2 = u ^ 2 + 2as \ end {уравнение}
Так что у нас есть? У нас есть четыре уравнения, которые описывают равномерно ускоренное движение:
Уравнение (2) предоставляет способ вычисления конечной скорости с точки зрения начальной скорости, ускорения и времени ускорения объекта.
Уравнение (6) предоставляет способ вычисления расстояния (смещения) объекта с точки зрения начальной скорости, конечной скорости и времени, в течение которого объект находился в движении.
Уравнение (8) дает нам пройденное расстояние без необходимости знать конечную скорость объекта. В обмен на знание конечной скорости мы должны знать ускорение объекта.
Уравнение (14) связывает начальную скорость, конечную скорость и ускорение объекта без времени! Иногда это очень полезно.
Очень важно отметить, что эти уравнения применяются ТОЛЬКО, если рассматриваемый объект испытывает равномерное ускорение , что означает, что ускорение является постоянным или может быть аппроксимировано как постоянное.
2.1.8 Опишите вертикальное движение объекта в однородном гравитационном поле
Равномерное гравитационное поле просто означает, что сила тяжести не изменяется или существенно не изменяется. Если вы остаетесь около поверхности Земли (в километре или двух), гравитационное поле можно считать постоянным (по крайней мере, для целей физики IB).
Если гравитационное поле постоянно, то объект в этом поле будет испытывать постоянную силу и, следовательно, постоянное ускорение. Это означает, что уравнения, полученные выше, являются достоверным описанием движения объекта в однородном гравитационном поле (без учета других сил).
Если объект удерживается в постоянном гравитационном поле, он упадет. Это будет сделано с равномерным ускорением. У поверхности земли ускорение составляет около 9.8 мс -2 . Это означает, что каждую секунду, когда объект падает, его скорость увеличивается на 9,8 мс -1 . Таким образом, через одну секунду объект имеет скорость 9,8 мс -1 , через 5 секунд он будет иметь скорость 47,5 мс -1 и т. Д. Поскольку скорость движения объекта увеличивается каждую секунду, это, естественно, означает, что расстояние до него покрывает каждую секунду, также увеличивается …
Что произойдет, если объект брошен? Ускорение еще вниз. Если объект брошен с начальной скоростью 30 мс -1 , через одну секунду он будет подниматься только на 20 мс -1 , через 2 секунды он будет подниматься только на 10 мс -1 , после 3 секунды объект будет иметь нулевую скорость! Даже если скорость объекта равна нулю, ускорение не равно нулю.
Вертикальное движение в гравитационном поле будет обсуждаться более подробно, когда мы перейдем к движению снаряда.
2.1.9 Опишите влияние сопротивления воздуха падающего объекта
Когда объект падает, он испытывает сопротивление или силу трения из-за воздуха, мы называем эту силу сопротивлением воздуха. Эта сила сопротивления всегда находится в противоположном направлении движения. Когда объект движется медленно, сила сопротивления пропорциональна скорости движения объекта. По мере увеличения скорости объекта сопротивление пропорционально квадрату скорости, что означает, что сила сопротивления очень быстро увеличивается.В какой-то момент сила сопротивления увеличится до величины силы тяжести на объекте. Когда две силы равны, они не будут являться чистой силой на объект, и он больше не будет ускоряться, то есть теперь он будет двигаться с постоянной скоростью. Эта конечная максимальная скорость называется конечной скоростью. Сопротивление и, следовательно, конечная скорость определяются формой объекта, его массой и поперечным сечением объекта.
Люди пережили падение с самолетов и воздушных шаров, это случается не часто, но это случается время от времени.Многие падают на пару минут, прежде чем упасть на землю, где они на самом деле подпрыгивают. Бывает, что падающее человеческое тело довольно быстро достигает своей конечной скорости (около 200-300 км / ч), поэтому, хотя они могут падать в течение длительного периода времени, они падают на землю с относительно низкой скоростью. Низкая по сравнению со скоростью, с которой они столкнулись бы, если бы воздух не уменьшал их ускорение.
Хотите добавить или прокомментировать эти заметки? Сделай это ниже.
,Калькулятор равномерного ускорения движения
Использование калькулятора
Калькулятор Uniformly Accelerated Motion использует уравнения движения для решения вычислений движения, включающих постоянное ускорение в одном измерении — прямую линию. Он может определить начальную скорость u, конечную скорость v, смещение s, ускорение a и время t.
Выберите расчет, чтобы найти неизвестные переменные, и введите переменные, указанные в вашей задаче.Этот калькулятор рассчитает неизвестные значения и предоставит производные уравнения, которые были использованы для поиска решения. Уравнения решения выводятся из приведенных ниже уравнений движения с равномерным ускорением.
Обратите внимание, что при поиске нескольких переменных обычно существует несколько способов решения ваших неизвестных. Вы можете получить более одного набора уравнений для решения вашей проблемы различными способами.
Уравнения равномерного ускорения движения
\ (s = \ dfrac {1} {2} (v + u) t \ tag {1} \)
\ (v = u + at \ tag {2} \)
\ (v ^ 2 = u ^ 2 + 2as \ tag {3} \)
\ (s = ut + \ dfrac {1} {2} в ^ 2 \ tag {4} \)
Где:
- u = начальная скорость
- v = конечная скорость
- = ускорение
- с = смещение
- т = время
Используйте стандартную гравитацию, а = 9.80665 м / с 2 , для уравнений, использующих гравитационную силу Земли в качестве скорости ускорения объекта.
Уравнения с 1 по 4 являются ключевыми уравнениями, используемыми для поиска переменных в этом калькуляторе, однако иногда вы увидите различное количество Уравненно ускоренных уравнений движения в зависимости от ресурса. Вы обнаружите, что уравнение 1 происходит от подстановки уравнения 1b в уравнение 1а ниже.
\ (s = \ overline {v} t \ tag {1a} \)
\ (\ overline {v} = \ dfrac {1} {2} (v + u) \ tag {1b} \)
,равномерно ускоренного движения — PDF скачать бесплатноГлава 3 Практический тест
Дополнительная информация Глава 3 Практический тест с множественным выбором Определите, какой вариант лучше всего дополняет утверждение или отвечает на вопрос.1. Что из следующего является физической величиной, имеющей как величину, так и направление?
Глава 3 Практический тест с множественным выбором Определите, какой вариант лучше всего дополняет утверждение или отвечает на вопрос.1. Что из следующего является физической величиной, имеющей как величину, так и направление?ГЛАВА 6 РАБОТА И ЭНЕРГИЯ
Дополнительная информация ГЛАВА 6 КОНЦЕПТУАЛЬНЫЕ ВОПРОСЫ ПО РАБОТЕ И ЭНЕРГИИ. ПРИЧИНА И РЕШЕНИЕ Работа, проделанная F для перемещения коробки через смещение s, равна W = (F cos 0) s = Fs. Работа, выполняемая F: W = (F cos θ). с
ГЛАВА 6 КОНЦЕПТУАЛЬНЫЕ ВОПРОСЫ ПО РАБОТЕ И ЭНЕРГИИ. ПРИЧИНА И РЕШЕНИЕ Работа, проделанная F для перемещения коробки через смещение s, равна W = (F cos 0) s = Fs. Работа, выполняемая F: W = (F cos θ). с1 из 7 05.09.2009 18:12
Дополнительная информация 1 из 7 05.09.2009 18:12 Глава 2 Домашнее задание, которое необходимо выполнить: 9:00 во вторник, 8 сентября 2009 г. Примечание. Чтобы понять, как начисляются баллы, ознакомьтесь с политикой аттестации вашего инструктора.[Вернуться к стандартному виду назначения]
1 из 7 05.09.2009 18:12 Глава 2 Домашнее задание, которое необходимо выполнить: 9:00 во вторник, 8 сентября 2009 г. Примечание. Чтобы понять, как начисляются баллы, ознакомьтесь с политикой аттестации вашего инструктора.[Вернуться к стандартному виду назначения]Глава 6 Работа и энергия
Дополнительная информация Глава 6 РАБОТА И ОБЗОР ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, через которое он действует. Когда работа выполняется в системе или системой, энергия этой системы
Глава 6 РАБОТА И ОБЗОР ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, через которое он действует. Когда работа выполняется в системе или системой, энергия этой системыЛабораторная работа 8: Баллистический маятник
Дополнительная информация Лабораторная работа 8: Оборудование для баллистического маятника: устройство для баллистического маятника, линейка 2 метра, линейка 30 см, чистый лист бумаги, копировальная бумага, липкая лента, шкала.Осторожно! В этом эксперименте стальной шар проецируется горизонтально.
Лабораторная работа 8: Оборудование для баллистического маятника: устройство для баллистического маятника, линейка 2 метра, линейка 30 см, чистый лист бумаги, копировальная бумага, липкая лента, шкала.Осторожно! В этом эксперименте стальной шар проецируется горизонтально.PHY121 # 8 Среднесрочный I 3.06.2013
Дополнительная информация PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Экзамен Вопросы с множественным выбором # 1 # 4 1. Когда показанная выше система без трения ускоряется под действием силы величины F, натяжение
PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Экзамен Вопросы с множественным выбором # 1 # 4 1. Когда показанная выше система без трения ускоряется под действием силы величины F, натяжениеСвободно падающие предметы
Дополнительная информация Физика свободно падающих предметов 1425 Лекция 3 Майкл Фаулер, УВА.Темы сегодняшнего дня В предыдущей лекции мы анализировали одномерное движение, определяя смещение, скорость и ускорение и находя
Физика свободно падающих предметов 1425 Лекция 3 Майкл Фаулер, УВА.Темы сегодняшнего дня В предыдущей лекции мы анализировали одномерное движение, определяя смещение, скорость и ускорение и находя1. Масса, сила и гравитация
Дополнительная информация Введение в STE Physics Name 1. Масса, сила и гравитация Прежде чем пытаться понять силу, нам нужно взглянуть на массу и ускорение. а) Что измеряет масса? Количество вещества (атомов) б) Что такое
Введение в STE Physics Name 1. Масса, сила и гравитация Прежде чем пытаться понять силу, нам нужно взглянуть на массу и ускорение. а) Что измеряет масса? Количество вещества (атомов) б) Что такоеЗадача V Решения
Дополнительная информация Задача V Решения.Рассмотрим массы m, m 2, m 3 в точке x, x 2, x 3. Найдите X, координату C, найдя X 2, C массы и 2 и комбинируя ее с m 3. Показать, что это дает то же самое результат как 3
Задача V Решения.Рассмотрим массы m, m 2, m 3 в точке x, x 2, x 3. Найдите X, координату C, найдя X 2, C массы и 2 и комбинируя ее с m 3. Показать, что это дает то же самое результат как 3РАБОТА, ВЫПОЛНЕННАЯ ПОСТОЯННЫМИ СИЛАМИ
Дополнительная информация РАБОТА, ВЫПОЛНЕННАЯ ПОСТОЯННОЙ СИЛЕЙ Определение работы W, когда постоянная сила (F) направлена в направлении смещения (d), равно W = Fd. Единица СИ — ньютон-метр (Нм) = Джоуль, J. Если вы приложите сила
РАБОТА, ВЫПОЛНЕННАЯ ПОСТОЯННОЙ СИЛЕЙ Определение работы W, когда постоянная сила (F) направлена в направлении смещения (d), равно W = Fd. Единица СИ — ньютон-метр (Нм) = Джоуль, J. Если вы приложите силаФизика Секция 3.2 Free Fall
Дополнительная информация Раздел физики 3.2 Свободное падение Аристотель Аристотель учил, что вещества, составляющие Землю, отличаются от вещества, составляющего небеса. Он также учил этой динамике (раздел физики
Раздел физики 3.2 Свободное падение Аристотель Аристотель учил, что вещества, составляющие Землю, отличаются от вещества, составляющего небеса. Он также учил этой динамике (раздел физикиПроект: НАРУЖНЫЕ ЗАБОРЫ
Дополнительная информация 1 Проект: ОПИСАНИЕ НАРУЖНЫХ ЗАБОРОВ: В этом проекте вы будете работать с уравнениями движения снаряда и использовать математические модели для анализа задачи проектирования.Два софтбольных поля в Ролла, штат Миссури
1 Проект: ОПИСАНИЕ НАРУЖНЫХ ЗАБОРОВ: В этом проекте вы будете работать с уравнениями движения снаряда и использовать математические модели для анализа задачи проектирования.Два софтбольных поля в Ролла, штат МиссуриОдномерное и двухмерное движение
Дополнительная информация PHYS-101 LAB-02 Одномерное и двумерное движение 1. Цель Цели этого эксперимента: измерить ускорение силы тяжести с использованием одномерного движения, чтобы продемонстрировать независимость
PHYS-101 LAB-02 Одномерное и двумерное движение 1. Цель Цели этого эксперимента: измерить ускорение силы тяжести с использованием одномерного движения, чтобы продемонстрировать независимостьПростые гармонические колебания
Дополнительная информация Простое гармоническое движение 1 Объект Чтобы определить период движения объектов, которые выполняют простое гармоническое движение, и проверить теоретическое предсказание таких периодов.2 аппарата разных весов
Простое гармоническое движение 1 Объект Чтобы определить период движения объектов, которые выполняют простое гармоническое движение, и проверить теоретическое предсказание таких периодов.2 аппарата разных весовГлава 6. Работа и энергия
Дополнительная информация Глава 6 Работа и энергия Концепция сил, действующих на массу (один объект), тесно связана с концепцией производства или хранения энергии. Масса, ускоренная до ненулевой скорости, несет энергию
Глава 6 Работа и энергия Концепция сил, действующих на массу (один объект), тесно связана с концепцией производства или хранения энергии. Масса, ускоренная до ненулевой скорости, несет энергиюКЕ =? v o. Страница 1 из 12
Дополнительная информация Страница 1 из 12 CTEnergy-1.Масса m находится на конце легкого (безмассового) стержня длины R, другой конец которого имеет шарнир без трения, так что стержень может качаться в вертикальной плоскости. Стержень изначально горизонтальный
Страница 1 из 12 CTEnergy-1.Масса m находится на конце легкого (безмассового) стержня длины R, другой конец которого имеет шарнир без трения, так что стержень может качаться в вертикальной плоскости. Стержень изначально горизонтальныйПреобразования энергии
Дополнительная информация Энергетические преобразования Цели. Описать примеры энергетических преобразований. Продемонстрировать и применить закон сохранения энергии к системе, включающей вертикальную пружину и массу.Разработка и внедрение
Энергетические преобразования Цели. Описать примеры энергетических преобразований. Продемонстрировать и применить закон сохранения энергии к системе, включающей вертикальную пружину и массу.Разработка и внедрениеРешение старых проблем экзамена 1
Дополнительная информация Решение старых проблем экзамена 1 Привет студентам! Я помещаю эту старую версию моего обзора в первый промежуточный обзор, место и время которого будут объявлены. Проверьте наличие обновлений на веб-сайте, какие разделы
Решение старых проблем экзамена 1 Привет студентам! Я помещаю эту старую версию моего обзора в первый промежуточный обзор, место и время которого будут объявлены. Проверьте наличие обновлений на веб-сайте, какие разделыУскорение силы тяжести
Дополнительная информация Ускорение за счет силы тяжести 1 Объект Определение ускорения за счет силы тяжести различными методами.2 Аппаратные весы, шарикоподшипники, зажимы, электрические таймеры, счетчик, бумажные полоски, точность
Ускорение за счет силы тяжести 1 Объект Определение ускорения за счет силы тяжести различными методами.2 Аппаратные весы, шарикоподшипники, зажимы, электрические таймеры, счетчик, бумажные полоски, точностьУниверситет штата Теннесси
Дополнительная информация Физико-математический факультет Университета штата Теннесси PHYS 2010 CF SU 2009 Название 30% Время составляет 2 часа. Обман даст вам F-класс. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР.
Физико-математический факультет Университета штата Теннесси PHYS 2010 CF SU 2009 Название 30% Время составляет 2 часа. Обман даст вам F-класс. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР.Гистограммы Work-Energy
Дополнительная информация Название: Графики рабочей энергии. Читайте на занятии 2 главы «Работа, энергия и энергия» в классе физики: http: // www.PhysicsClassroom.com/class/energy/u5l2c.html MOP Связь: работа и энергия:
Название: Графики рабочей энергии. Читайте на занятии 2 главы «Работа, энергия и энергия» в классе физики: http: // www.PhysicsClassroom.com/class/energy/u5l2c.html MOP Связь: работа и энергия:Ньютон с Законом Викторина Обзор
Дополнительная информация , Час обзора по обзору законов Ньютона Название Чтобы быть правильно подготовленным к этой викторине, вы должны быть в состоянии сделать следующее: 1) изложить каждый из трех законов движения Ньютона 2) выбрать примеры трех законов из
Час обзора по обзору законов Ньютона Название Чтобы быть правильно подготовленным к этой викторине, вы должны быть в состоянии сделать следующее: 1) изложить каждый из трех законов движения Ньютона 2) выбрать примеры трех законов из

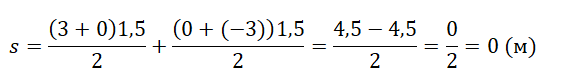
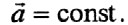
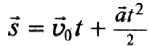 . В проекциях на координатную ось:
. В проекциях на координатную ось:  .
.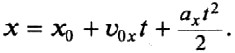
 Глава 3 Практический тест с множественным выбором Определите, какой вариант лучше всего дополняет утверждение или отвечает на вопрос.1. Что из следующего является физической величиной, имеющей как величину, так и направление?
Глава 3 Практический тест с множественным выбором Определите, какой вариант лучше всего дополняет утверждение или отвечает на вопрос.1. Что из следующего является физической величиной, имеющей как величину, так и направление? ГЛАВА 6 КОНЦЕПТУАЛЬНЫЕ ВОПРОСЫ ПО РАБОТЕ И ЭНЕРГИИ. ПРИЧИНА И РЕШЕНИЕ Работа, проделанная F для перемещения коробки через смещение s, равна W = (F cos 0) s = Fs. Работа, выполняемая F: W = (F cos θ). с
ГЛАВА 6 КОНЦЕПТУАЛЬНЫЕ ВОПРОСЫ ПО РАБОТЕ И ЭНЕРГИИ. ПРИЧИНА И РЕШЕНИЕ Работа, проделанная F для перемещения коробки через смещение s, равна W = (F cos 0) s = Fs. Работа, выполняемая F: W = (F cos θ). с 1 из 7 05.09.2009 18:12 Глава 2 Домашнее задание, которое необходимо выполнить: 9:00 во вторник, 8 сентября 2009 г. Примечание. Чтобы понять, как начисляются баллы, ознакомьтесь с политикой аттестации вашего инструктора.[Вернуться к стандартному виду назначения]
1 из 7 05.09.2009 18:12 Глава 2 Домашнее задание, которое необходимо выполнить: 9:00 во вторник, 8 сентября 2009 г. Примечание. Чтобы понять, как начисляются баллы, ознакомьтесь с политикой аттестации вашего инструктора.[Вернуться к стандартному виду назначения] Глава 6 РАБОТА И ОБЗОР ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, через которое он действует. Когда работа выполняется в системе или системой, энергия этой системы
Глава 6 РАБОТА И ОБЗОР ЭНЕРГИИ Работа — это скалярное произведение силы, действующей на объект, и смещения, через которое он действует. Когда работа выполняется в системе или системой, энергия этой системы Лабораторная работа 8: Оборудование для баллистического маятника: устройство для баллистического маятника, линейка 2 метра, линейка 30 см, чистый лист бумаги, копировальная бумага, липкая лента, шкала.Осторожно! В этом эксперименте стальной шар проецируется горизонтально.
Лабораторная работа 8: Оборудование для баллистического маятника: устройство для баллистического маятника, линейка 2 метра, линейка 30 см, чистый лист бумаги, копировальная бумага, липкая лента, шкала.Осторожно! В этом эксперименте стальной шар проецируется горизонтально. PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Экзамен Вопросы с множественным выбором # 1 # 4 1. Когда показанная выше система без трения ускоряется под действием силы величины F, натяжение
PHY11 # 8 Midterm I 3.06.013 AP Physics — Законы Ньютона AP Экзамен Вопросы с множественным выбором # 1 # 4 1. Когда показанная выше система без трения ускоряется под действием силы величины F, натяжение Физика свободно падающих предметов 1425 Лекция 3 Майкл Фаулер, УВА.Темы сегодняшнего дня В предыдущей лекции мы анализировали одномерное движение, определяя смещение, скорость и ускорение и находя
Физика свободно падающих предметов 1425 Лекция 3 Майкл Фаулер, УВА.Темы сегодняшнего дня В предыдущей лекции мы анализировали одномерное движение, определяя смещение, скорость и ускорение и находя Введение в STE Physics Name 1. Масса, сила и гравитация Прежде чем пытаться понять силу, нам нужно взглянуть на массу и ускорение. а) Что измеряет масса? Количество вещества (атомов) б) Что такое
Введение в STE Physics Name 1. Масса, сила и гравитация Прежде чем пытаться понять силу, нам нужно взглянуть на массу и ускорение. а) Что измеряет масса? Количество вещества (атомов) б) Что такое Задача V Решения.Рассмотрим массы m, m 2, m 3 в точке x, x 2, x 3. Найдите X, координату C, найдя X 2, C массы и 2 и комбинируя ее с m 3. Показать, что это дает то же самое результат как 3
Задача V Решения.Рассмотрим массы m, m 2, m 3 в точке x, x 2, x 3. Найдите X, координату C, найдя X 2, C массы и 2 и комбинируя ее с m 3. Показать, что это дает то же самое результат как 3 РАБОТА, ВЫПОЛНЕННАЯ ПОСТОЯННОЙ СИЛЕЙ Определение работы W, когда постоянная сила (F) направлена в направлении смещения (d), равно W = Fd. Единица СИ — ньютон-метр (Нм) = Джоуль, J. Если вы приложите сила
РАБОТА, ВЫПОЛНЕННАЯ ПОСТОЯННОЙ СИЛЕЙ Определение работы W, когда постоянная сила (F) направлена в направлении смещения (d), равно W = Fd. Единица СИ — ньютон-метр (Нм) = Джоуль, J. Если вы приложите сила Раздел физики 3.2 Свободное падение Аристотель Аристотель учил, что вещества, составляющие Землю, отличаются от вещества, составляющего небеса. Он также учил этой динамике (раздел физики
Раздел физики 3.2 Свободное падение Аристотель Аристотель учил, что вещества, составляющие Землю, отличаются от вещества, составляющего небеса. Он также учил этой динамике (раздел физики 1 Проект: ОПИСАНИЕ НАРУЖНЫХ ЗАБОРОВ: В этом проекте вы будете работать с уравнениями движения снаряда и использовать математические модели для анализа задачи проектирования.Два софтбольных поля в Ролла, штат Миссури
1 Проект: ОПИСАНИЕ НАРУЖНЫХ ЗАБОРОВ: В этом проекте вы будете работать с уравнениями движения снаряда и использовать математические модели для анализа задачи проектирования.Два софтбольных поля в Ролла, штат Миссури PHYS-101 LAB-02 Одномерное и двумерное движение 1. Цель Цели этого эксперимента: измерить ускорение силы тяжести с использованием одномерного движения, чтобы продемонстрировать независимость
PHYS-101 LAB-02 Одномерное и двумерное движение 1. Цель Цели этого эксперимента: измерить ускорение силы тяжести с использованием одномерного движения, чтобы продемонстрировать независимость Простое гармоническое движение 1 Объект Чтобы определить период движения объектов, которые выполняют простое гармоническое движение, и проверить теоретическое предсказание таких периодов.2 аппарата разных весов
Простое гармоническое движение 1 Объект Чтобы определить период движения объектов, которые выполняют простое гармоническое движение, и проверить теоретическое предсказание таких периодов.2 аппарата разных весов Глава 6 Работа и энергия Концепция сил, действующих на массу (один объект), тесно связана с концепцией производства или хранения энергии. Масса, ускоренная до ненулевой скорости, несет энергию
Глава 6 Работа и энергия Концепция сил, действующих на массу (один объект), тесно связана с концепцией производства или хранения энергии. Масса, ускоренная до ненулевой скорости, несет энергию Страница 1 из 12 CTEnergy-1.Масса m находится на конце легкого (безмассового) стержня длины R, другой конец которого имеет шарнир без трения, так что стержень может качаться в вертикальной плоскости. Стержень изначально горизонтальный
Страница 1 из 12 CTEnergy-1.Масса m находится на конце легкого (безмассового) стержня длины R, другой конец которого имеет шарнир без трения, так что стержень может качаться в вертикальной плоскости. Стержень изначально горизонтальный Энергетические преобразования Цели. Описать примеры энергетических преобразований. Продемонстрировать и применить закон сохранения энергии к системе, включающей вертикальную пружину и массу.Разработка и внедрение
Энергетические преобразования Цели. Описать примеры энергетических преобразований. Продемонстрировать и применить закон сохранения энергии к системе, включающей вертикальную пружину и массу.Разработка и внедрение Решение старых проблем экзамена 1 Привет студентам! Я помещаю эту старую версию моего обзора в первый промежуточный обзор, место и время которого будут объявлены. Проверьте наличие обновлений на веб-сайте, какие разделы
Решение старых проблем экзамена 1 Привет студентам! Я помещаю эту старую версию моего обзора в первый промежуточный обзор, место и время которого будут объявлены. Проверьте наличие обновлений на веб-сайте, какие разделы Ускорение за счет силы тяжести 1 Объект Определение ускорения за счет силы тяжести различными методами.2 Аппаратные весы, шарикоподшипники, зажимы, электрические таймеры, счетчик, бумажные полоски, точность
Ускорение за счет силы тяжести 1 Объект Определение ускорения за счет силы тяжести различными методами.2 Аппаратные весы, шарикоподшипники, зажимы, электрические таймеры, счетчик, бумажные полоски, точность Физико-математический факультет Университета штата Теннесси PHYS 2010 CF SU 2009 Название 30% Время составляет 2 часа. Обман даст вам F-класс. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР.
Физико-математический факультет Университета штата Теннесси PHYS 2010 CF SU 2009 Название 30% Время составляет 2 часа. Обман даст вам F-класс. Другие инструкции будут даны в зале. МНОЖЕСТВЕННЫЙ ВЫБОР. Название: Графики рабочей энергии. Читайте на занятии 2 главы «Работа, энергия и энергия» в классе физики: http: // www.PhysicsClassroom.com/class/energy/u5l2c.html MOP Связь: работа и энергия:
Название: Графики рабочей энергии. Читайте на занятии 2 главы «Работа, энергия и энергия» в классе физики: http: // www.PhysicsClassroom.com/class/energy/u5l2c.html MOP Связь: работа и энергия: Час обзора по обзору законов Ньютона Название Чтобы быть правильно подготовленным к этой викторине, вы должны быть в состоянии сделать следующее: 1) изложить каждый из трех законов движения Ньютона 2) выбрать примеры трех законов из
Час обзора по обзору законов Ньютона Название Чтобы быть правильно подготовленным к этой викторине, вы должны быть в состоянии сделать следующее: 1) изложить каждый из трех законов движения Ньютона 2) выбрать примеры трех законов из
Leave A Comment