Центральные и Вписанные углы. Как найти?
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол угол ABC равен половине угла AOC.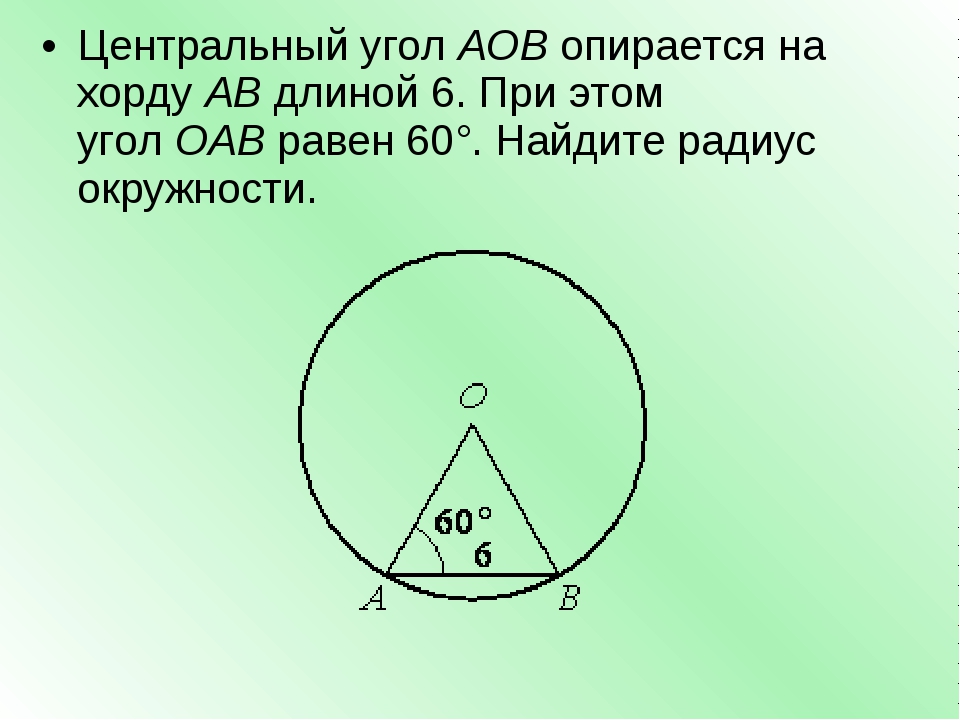
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
ㄥAOB = ◡ AB
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB угол равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
- Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается и половине градусной меры центрального угла, опирающегося на эту же дугу.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу. ㄥACB = ?
Как решаем: окружность 360° — AC — CB = 360 — 200 — 80 = 80
По теореме: вписанный угол равен дуге ½.
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360 = 72°
Вписанный угол равен половине дуги, поэтому CAB = ½ от CB = 72/36 = 36°
Еще больше примеров и задачек на уроках математики в онлайн-школе Skysmart. Наши преподаватели объяснят любую, даже самую остроугольную тему.
Записывайтесь на бесплатный вводный урок математики и занимайтесь в удовольствие!
8 класс. Геометрия. Окружность. Вписанный угол. Центральный угол. — Теорема о вписанном угле.
Комментарии преподавателяТеорема о вписанном угле
Напомним некоторые определения
Определение:
Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R (см. Рис. 1).
Рис. 1
Часть окружности называется дугой.
Дуга имеет угловое измерение.
Градусная мера дуги равна градусной мере соответствующего центрального угла :
Рассмотрим примеры:
Рис.
2
Определение
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным.
Рис. 3
Задана окружность с центром О, вершина А лежит на окружности, стороны АВ и АС угла пересекают окружность в точках В и С, угол называется вписанным. Он опирается на дугу , эта дуга расположена внутри угла (см. Рис. 3).
Вписанный угол измеряется половиной дуги, на которую он опирается (см. Рис. 4).
Рис. 4
Доказательство:
Рассмотрим несколько случаев.
Случай 1: точка О принадлежит лучу АС (см. Рис. 5).
Рис. 5
Доказать, что
Обозначим угол через , тогда угол также будет равен , так как треугольник равнобедренный, его стороны ОВ и ОА равны как радиусы окружности. Угол является внешним для треугольника , внешний угол равен сумме двух других углов, не смежных с ним, получаем: , то есть угловое измерение дуги есть .
Случай 2: точка О лежит внутри вписанного угла (см. Рис. 6).
Рис. 6
Доказать, что
Доказательство сводится к предыдущему случаю. Проведем диаметр AD, обозначим угол за и тогда дуга равна (объяснение см. случай 1). Угол за , тогда дуга равна (объяснение см. случай 1). Вся дуга равна:
Угол в свою очередь, равен .
Таким образом, мы доказали, что вписанный угол равен половине дуги, на которую он опирается.
Случай 3: точка О находится вне вписанного угла (см. Рис. 7).
Рис. 7
Доказать, что
Доказательство снова сводится к первому случаю. Проведем диаметр AD, обозначим угол через , тогда дуга (объяснение см. случай 1). Угол обозначим через , тогда дуга равна (объяснение см. случай 1).
Дуга является разностью большой дуги и дуги :
Вписанный угол равен . Таким образом, мы доказали, что вписанный угол равен половине дуги, на которую он опирается.
Итак, теорема полностью доказана, все случаи рассмотрены. И теперь из этого вытекают важные следствия.
Следствие 1:
Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой (см. Рис. 8).
Рис. 8
Угол равен , он вписанный и опирается на дугу , значит, дуга равна . Но на эту же дугу опираются много других углов, например, углы и , данные углы измеряются половиной градусной меры дуги, значит, они равны , как и угол.
Таким образом, получаем:
Следствие 2
Вписанные углы, опирающиеся на диаметр, прямые (см. Рис. 9).
Рис. 9
Теорема о вписанном угле является ключом к доказательству многих других теорем и к решению многих задач.
Произведение отрезков каждой из двух пересекающихся хорд есть величина постоянная.
Рис. 10
Доказать, что
Доказательство:
Рассмотрим треугольники и (см. Рис. 10). Данные треугольники подобны по равенству двух углов: равны вертикальные углы и ; вписанные углы и опираются на одну и ту же дугу . Выпишем соотношение подобия:
Применим свойство пропорции и преобразуем выражение:
, что и требовалось доказать.
Итак, мы рассмотрели понятие вписанного угла и теорему о вписанном угле. В следующем уроке мы рассмотрим свойства биссектрисы угла и серединного перпендикуляра к отрезку.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/okruzhnost/teorema-o-vpisannom-ugle
http://www.youtube.com/watch?v=v-udmw0gZIo
http://www.
youtube.com/watch?v=jdGg3_gYImQ
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/112-test-po-geometrii-8-klass-tema-tsentralnye-i-vpisannye-ugly-variant-1.html
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/113-test-po-geometrii-8-klass-tema-tsentralnye-i-vpisannye-ugly-variant-2.html
http://klassnoedelo.ru/upload/iblock/78d/78d9db552be4b537618cdef1c61fb4cd.jpg
Центральные и вписанные углы окружности. Вписанный угол
Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла. Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Теперь необходимая теория.
Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:
Центральным углом в окружности называется плоский угол с вершиной в ее центре .
Часть окружности, расположенная внутри плоского угла, называется дугой окружности.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.
Отрезок соединяющий две точки окружности называется хордой . Самая большая хорда проходит через центр окружности и называется диаметр.
Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:
1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.
2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.
5. Все вписанные углы, опирающиеся на диаметр, прямые.
Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.
Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:
Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).
Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.
Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.
Как правило, половина задач на вписанный угол даётся с эскизом, но без обозначений. Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать. Рассмотрим задачи:
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Построим центральный угол для заданного вписанного угла, обозначим вершины:
По свойству вписанного в окружность угла:
Угол АОВ равен 60 0 , так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 60 0 .
Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.
Таким образом, вписанный угол АСВ равен 30 0 .
Ответ: 30
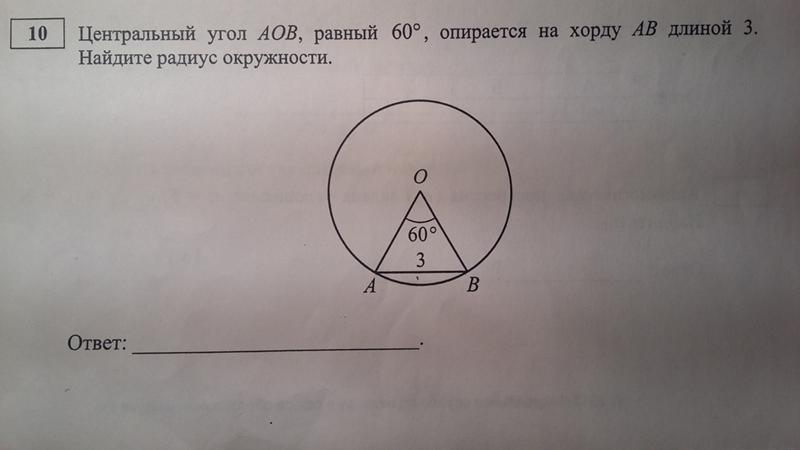
Найдите хорду, на которую опирается угол 30 0 , вписанный в окружность радиуса 3.
Это по сути обратная задача (предыдущей). Построим центральный угол.
Он в два раза больше вписанного, то есть угол АОВ равен 60 0 . От сюда можно сделать вывод, что треугольник АОВ равносторонний. Таким образом, хорда равна радиусу, то есть трём.
Ответ: 3
Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Построим центральный угол:
Зная радиус и хорду мы можем найти центральный угол АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно, второй центральный угол равен 360 0 – 90 0 = 270 0 .
Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.
Ответ: 135
Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса корень из трёх.
Соединим точки А и В с центром окружности. Обозначим её как О:
Нам известен радиус и вписанный угол АСВ. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.
По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен 360 0 – 240 0 = 120 0 .
По теореме косинусов:
Ответ:3
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.
Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 360 0 . *Окружность это угол в 360 градусов. Значит,
Таким образом, вписанный угол АСВ равен 36 градусам.
Ответ: 36
Дуга окружности AC , не содержащая точки B , составляет 200 градусов. А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.
Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.
Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет: 360 0 – 200 0 – 80 0 = 80 0 .
Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.
Ответ: 40
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Сегодня мы рассмотрим очередной тип задач 6 — на этот раз с окружностью. Многие ученики не любят их и считают сложными. И совершенно напрасно, поскольку такие задачи решаются элементарно , если знать некоторые теоремы. Или не решаются вообще, если их не знать.
Прежде чем говорить об основных свойствах, позвольте напомнить определение:
Вписанный угол — тот, у которого вершина лежит на самой окружности, а стороны высекают на этой окружности хорду.
Центральный угол — это любой угол с вершиной в центре окружности. Его стороны тоже пересекают эту окружность и высекают на ней хорду.
Итак, понятия вписанного и центрального угла неразрывно связаны с окружностью и хордами внутри нее. А теперь — основное утверждение:
Теорема. Центральный угол всегда в два раза больше вписанного, опирающегося на ту же самую дугу.
Несмотря на простоту утверждения, существует целый класс задач 6, которые решаются с помощью него — и никак иначе.
Задача. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
Пусть AB — рассматриваемая хорда, O — центр окружности. Дополнительное построение: OA и OB — радиусы окружности. Получим:
Рассмотрим треугольник ABO . В нем AB = OA = OB — все стороны равны радиусу окружности. Поэтому треугольник ABO — равносторонний, и все углы в нем по 60°.
Пусть M — вершина вписанного угла. Поскольку углы O и M опираются на одну и ту же дугу AB , вписанный угол M в 2 раза меньше центрального угла O . Имеем:
M = O : 2 = 60: 2 = 30
Задача. Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Введем обозначения:
- AB — хорда окружности;
- Точка O — центр окружности, поэтому угол AOB — центральный;
- Точка C — вершина вписанного угла ACB .
Поскольку мы ищем вписанный угол ACB
, обозначим его ACB
= x
.
Тогда центральный угол AOB
равен x
+ 36. С другой стороны, центральный угол в 2 раза больше вписанного. Имеем:
AOB
= 2 · ACB
;
x
+ 36 = 2 · x
;
x
= 36.
Вот мы и нашли вписанный угол AOB — он равен 36°.
Окружность — это угол в 360°
Прочитав подзаголовок, знающие читатели, наверное, сейчас скажут: «Фу!» И действительно, сравнивать окружность с углом не совсем корректно. Чтобы понять, о чем речь, взгляните на классическую тригонометрическую окружность:
К чему эта картинка? А к тому, что полный оборот — это угол в 360 градусов. И если разделить его, скажем, на 20 равных частей, то размер каждой из них будет 360: 20 = 18 градусов. Именно это и требуется для решения задачи B8.
Точки A , B и C лежат на окружности и делят ее на три дуги, градусные меры которых относятся как 1: 3: 5. Найдите больший угол треугольника ABC .
Для начала найдем градусную меру каждой дуги. Пусть меньшая из них равна x
.
На рисунке эта дуга обозначена AB
. Тогда остальные дуги — BC
и AC
— можно выразить через AB
: дуга BC
= 3x
; AC
= 5x
. В сумме эти дуги дают 360 градусов:
AB
+ BC
+ AC
= 360;
x
+ 3x
+ 5x
= 360;
9x
= 360;
x
= 40.
Теперь рассмотрим большую дугу AC , которая не содержит точку B . Эта дуга, как и соответствующий центральный угол AOC , равна 5x = 5 · 40 = 200 градусов.
Угол ABC — самый большой из всех углов треугольника. Это вписанный угол, опирающийся на ту же дугу, что и центральный угол AOC . Значит, угол ABC в 2 раза меньше AOC . Имеем:
ABC = AOC : 2 = 200: 2 = 100
Это и будет градусная мера большего угла в треугольнике ABC .
Окружность, описанная вокруг прямоугольного треугольника
Эту теорему многие забывают. А зря, ведь некоторые задачи B8 без нее вообще не решаются. Точнее, решаются, но с таким объемом вычислений, что вы скорее уснете, чем дойдете до ответа.
Теорема. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Что следует из этой теоремы?
- Середина гипотенузы равноудалена от всех вершин треугольника. Это прямое следствие теоремы;
- Медиана, проведенная к гипотенузе, делит исходный треугольник на два равнобедренных. Как раз это и требуется для решения задачи B8.
В треугольнике ABC провели медиану CD . Угол C равен 90°, а угол B — 60°. Найдите угол ACD .
Поскольку угол C равен 90°, треугольник ABC — прямоугольный. Получается, что CD — медиана, проведенная к гипотенузе. Значит, треугольники ADC и BDC — равнобедренные.
В частности, рассмотрим треугольник ADC . В нем AD = CD . Но в равнобедренном треугольнике углы при основании равны — см. «Задача B8: отрезки и углы в треугольниках ». Поэтому искомый угол ACD = A .
Итак, осталось выяснить, чему равен угол A . Для этого снова обратимся к исходному треугольнику ABC . Обозначим угол A = x . Поскольку сумма углов в любом треугольнике равна 180°, имеем:
A
+ B
+ BCA
= 180;
x
+ 60 + 90 = 180;
x
= 30.
Разумеется, последнюю задачу можно решить по-другому. Например, легко доказать, что треугольник BCD — не просто равнобедренный, а равносторонний. Значит, угол BCD равен 60 градусов. Отсюда угол ACD равен 90 − 60 = 30 градусов. Как видите, можно использовать разные равнобедренные треугольники, но ответ всегда будет один и тот же.
Инструкция
Если известны радиус (R) круга и длина дуги (L), соответствующая искомому центральному углу (θ), рассчитать его можно как в градусах, так и в радианах. Полная определяется формулой 2*π*R и соответствует центральному углу в 360° или двум числам Пи, если вместо градусов использовать радианы. Поэтому исходите из пропорции 2*π*R/L = 360°/θ = 2*π/θ. Выразите из нее центральный угол в радианах θ = 2*π/(2*π*R/L) = L/R или градусах θ = 360°/(2*π*R/L) = 180*L/(π*R) и рассчитайте по полученной формуле.
По длине хорды (m), соединяющей точки , которые определяет центральный угол (θ), его величину тоже можно рассчитать, если известен радиус (R) круга.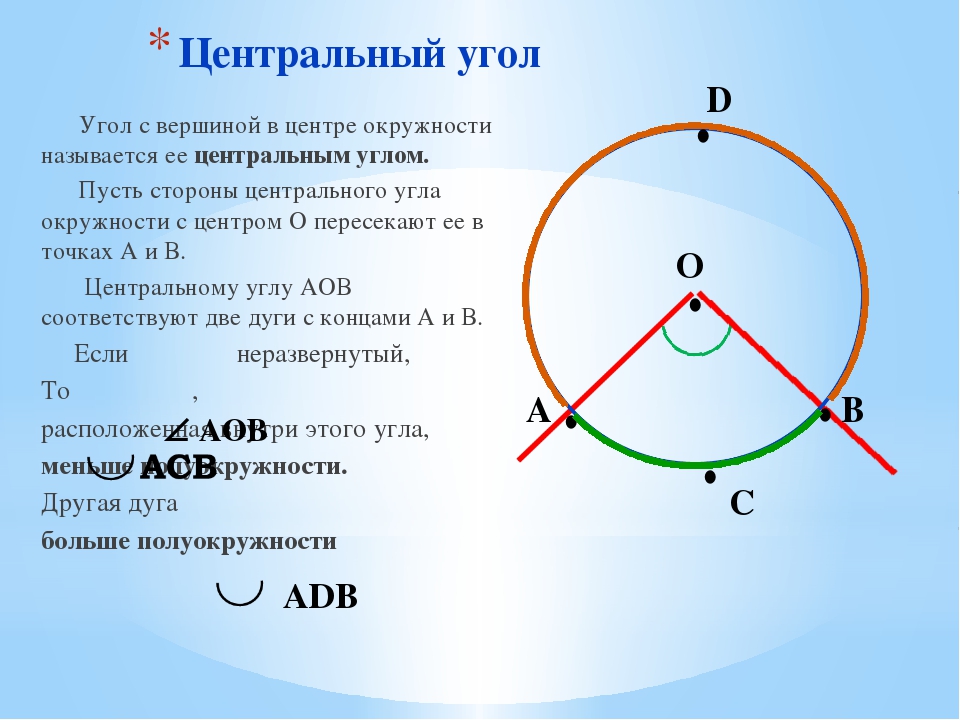
Для этого рассмотрите треугольник, образованный двумя радиусами и . Это равнобедренный треугольник, все известны, а найти нужно угол, лежащий напротив основания. Синус его половины равен отношению длины основания — хорды — к удвоенной длине боковой стороны — радиуса. Поэтому используйте для вычислений обратную синусу функцию — арксинус: θ = 2*arcsin(½*m/R).
Центральный угол может быть задан и в долях оборота или от развернутого угла. Например, если нужно найти центральный угол, соответствующей четверти полного оборота, разделите 360° на четверку: θ = 360°/4 = 90°. Эта же величина в радианах должна быть 2*π/4 ≈ 3,14/2 ≈ 1,57. Развернутый угол равен половине полного оборота, поэтому, например, центральный угол, соответствующий четверти от него будет вдвое меньше рассчитанных выше значений как в градусах, так и в радианах.
Обратная синусу тригонометрическая функция называется арксинусом . Она может принимать значения, лежащие в пределах половины числа Пи как в положительную, так и в отрицательную стороны при измерении в радианах.
При измерении в градусах эти значения будут находиться, соответственно, в диапазоне от -90° до +90°.
Инструкция
Некоторые «круглые» значения не обязательно вычислять, проще их запомнить. Например:- если аргумент функции равен нулю, то значение арксинуса от него тоже равно нулю;- от 1/2 равен 30° или 1/6 Пи, если измерять ;- арксинус от -1/2 равен -30° или -1/6 от числа Пи в ;- арксинус от 1 равен 90° или 1/2 от числа Пи в радианах;- арксинус от -1 равен -90° или -1/2 от числа Пи в радианах;
Для измерения значений этой функции от других аргументов проще всего воспользоваться стандартным калькулятором Windows, если под рукой есть . Чтобы запустить раскройте главное меню на кнопке «Пуск» ( или нажатием клавиши WIN), перейдите в раздел «Все программы», а затем в подраздел «Стандартные» и щелкните пункт «Калькулятор».
Переключите интерфейс калькулятора в тот режим работы, который позволяет вычислять тригонометрические функции. Для этого откройте в его меню раздел «Вид» и выберите пункт «Инженерный» или «Научный» (в зависимости от используемой операционной системы).
Введите значение аргумента, от которого надо вычислить арктангенс. Это можно делать, щелкая кнопки интерфейса калькулятора мышкой, или нажимая клавиши на , или скопировав значение (CTRL + C) и затем вставив его (CTRL + V) в поле ввода калькулятора.
Выберите единицы измерения, в которых вам нужно получить результат вычисления функции. Ниже поля ввода помещены три варианта, из которых вам нужно выбрать (щелкнув его мышкой) одни — , радианы или рады.
Поставьте отметку в чекбоксе, который инвертирует функции, указанные на кнопках интерфейса калькулятора. Рядом с ним стоит короткая надпись Inv.
Щелкните кнопку sin. Калькулятор инвертирует привязанную к ней функцию, произведет вычисление и представит вам результат в заданных единицах измерения.
Видео по теме
Одной из распространенных геометрических задач является вычисление площади кругового сегмента — части круга, ограниченной хордой и соответствующей хорде дугой окружности.
Площадь кругового сегмента равна разности площади соответствующего кругового сектора и площади треугольника, образованного радиусами соответствующего сегменту сектора и хордой, ограничивающей сегмент.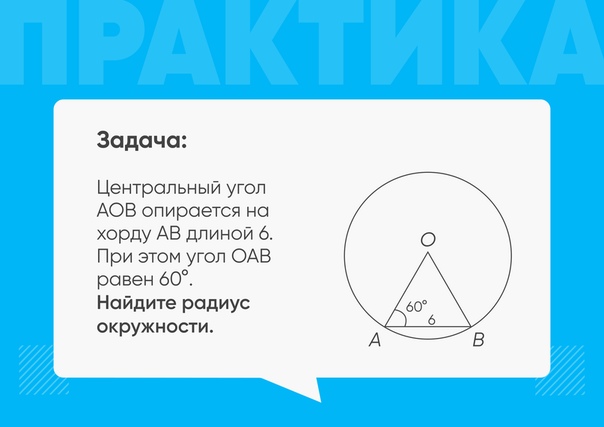
Пример 1
Длина хорды, стягивающей окружность равна величине а. Градусная мера дуги, соответствующей хорде, равна 60°. Найти площадь кругового сегмента.
Решение
Треугольник, образованный двумя радиусами и хордой, является равнобедренным, поэтому высота, проведенная из вершины центрального угла на сторону треугольника, образованную хордой, будет также являться биссектрисой центрального угла, поделив его пополам и медианой, поделив пополам хорду. Зная, что синус угла в равен отношению противолежащего катета к гипотенузе, можно вычислить величину радиуса:
Sin 30°= a/2:R = 1/2;
Sc = πR²/360°*60° = πa²/6
S▲=1/2*ah, где h — высота, проведенная из вершины центрального угла к хорде. По теореме Пифагора h=√(R²-a²/4)= √3*a/2.
Соответственно, S▲=√3/4*a².
Площадь сегмента, вычисляемая как Sсег = Sc — S▲, равна:
Sсег = πa²/6 — √3/4*a²
Подставив числовое значение вместо величины a, можно с легкостью вычислить числовое значение площади сегмента.
Пример 2
Радиус окружности равен величине а. Градусная мера дуги, соответствующей сегменту, равна 60°. Найти площадь кругового сегмента.
Решение:
Площадь сектора, соответствующего заданному углу можно вычислить по следующей формуле:
Sc = πа²/360°*60° = πa²/6,
Площадь соответствующего сектору треугольника вычисляется следующим образом:
S▲=1/2*ah, где h — высота, проведенная из вершины центрального угла к хорде. По теореме Пифагора h=√(a²-a²/4)= √3*a/2.
Соответственно, S▲=√3/4*a².
И, наконец, площадь сегмента, вычисляемая как Sсег = Sc — S▲, равна:
Sсег = πa²/6 — √3/4*a².
Решения в обоих случаях практически идентичны. Таким образом можно сделать вывод, что для вычисления площади сегмента в простейшем случае достаточно знать величину угла, соответствующего дуге сегмента и один из двух параметров — либо радиус окружности, либо длину хорды, стягивающей дугу окружности, образующую сегмент.
Источники:
- Сегмент — геометрия
Чаще всего процесс подготовки к ЕГЭ по математике начинается с повторения основных определений, формул и теорем, в том числе и по теме «Центральный и вписанный в окружность угол».
Как правило, данный раздел планиметрии изучается еще в средней школе. Неудивительно, что многие учащиеся сталкиваются с необходимостью повторения базовых понятий и теорем по теме «Центральный угол окружности». Разобравшись с алгоритмом решения подобных задач, школьники смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена.
Как легко и эффективно подготовиться к прохождению аттестационного испытания?
Занимаясь перед сдачей единого государственного экзамена, многие старшеклассники сталкиваются с проблемой поиска нужной информации по теме «Центральный и вписанный углы в окружности». Далеко не всегда школьный учебник имеется под рукой. А поиск формул в Интернете порой отнимает очень много времени.
«Прокачать» навыки и улучшить знания в таком непростом разделе геометрии, как планиметрия, вам поможет наш образовательный портал. «Школково» предлагает старшеклассникам и их преподавателям по-новому выстроить процесс подготовки к сдаче единого госэкзамена.
Весь базовый материал представлен нашими специалистами в максимально доступной форме. Ознакомившись с информацией в разделе «Теоретическая справка», учащиеся узнают, какими свойствами обладает центральный угол окружности, как найти его величину и т. д.
Затем для закрепления полученных знаний и отработки навыков мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий на нахождение величины угла, вписанного в окружность, и других параметров представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.
Готовиться к ЕГЭ, практикуясь в выполнении упражнений, к примеру, на нахождение величины центрального угла и длины дуги окружности, старшеклассники могут в онлайн-режиме, находясь в любом российском регионе.
При необходимости выполненное задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и еще раз разобрать принцип его решения.
Угол ABC — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (рис. 330).
Теорема . Вписанный угол измеряется половиной дуги, на которую он опирается.
Это надо понимать так: вписанный угол содержит столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд содержится в половине дуги, на которую он опирается.
При доказательстве этой теоремы надо рассмотреть три случая.
Первый случай. Центр круга лежит на стороне вписанного угла (рис. 331).
Пусть ∠ABC — вписанный угол и центр круга О лежит на стороне BC. Требуется доказать, что он измеряется половиной дуги AC.
Соединим точку A с центром круга. Получим равнобедренный \(\Delta\)AOB, в котором АО = OB, как радиусы одного и того же круга. Следовательно, ∠A = ∠B.
∠AOC является внешним по отношению к треугольнику AOB, поэтому ∠AOC = ∠А + ∠В, а так как углы А и В равны, то ∠В составляет 1 / 2 ∠AOC.
Но ∠AOC измеряется дугой АС, следовательно, ∠В измеряется половиной дуги АС.
Например, если \(\breve{AC}\) содержит 60°18’, то ∠В содержит 30°9’.
Второй случай. Центр круга лежит между сторонами вписанного угла (рис. 332).
Пусть ∠ABD — вписанный угол. Центр круга О лежит между его сторонами. Требуется доказать, что ∠ABD измеряется половиной дуги АD.
Для доказательства проведём диаметр BC. Угол ABD разбился на два угла: ∠1 и ∠2.
∠1 измеряется половиной дуги АС, а ∠2 измеряется половиной дуги СD, следовательно, весь ∠АВD измеряется 1 / 2 \(\breve{AC}\) + 1 / 2 \(\breve{CD}\), т. е. половиной дуги АD.
Например, если \(\breve{AD}\) содержит 124°, то ∠В содержит 62°.
Третий случай. Центр круга лежит вне вписанного угла (рис. 333).
Пусть ∠MAD — вписанный угол. Центр круга О находится вне угла. Требуется доказать, что ∠MAD измеряется половиной дуги MD.
Для доказательства проведём диаметр AB. ∠MAD = ∠MAB — ∠DAB. Но ∠MAB измеряется 1 / 2 \(\breve{MB}\), а ∠DAB измеряется 1 / 2 \(\breve{DB}\).
Следовательно, ∠MAD измеряется 1 / 2 (\(\breve{MB} — \breve{DB})\), т. е. 1 / 2 \(\breve{MD}\).
Например, если \(\breve{MD}\) содержит 48° 38″, то ∠MAD содержит 24° 19’ 8″.
Следствия
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги (рис. 334, а).
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности. Половина окружности содержит 180 дуговых градусов, значит, угол, опирающийся на диаметр, содержит 90 угловых градусов (рис. 334, б).
Центральные и вписанные углы 8 класс онлайн-подготовка на Ростелеком Лицей
Центральные и вписанные углы
Угол с вершиной в центре окружности называется ее центральным углом.
Центральный угол – угол между двумя радиусами.
Центральному углу АОВ соответствуют две дуги с концами А и В.
Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360°-∠AOB.
Центральный угол измеряется дугой, на которую опирается.
Сумма градусных мер дуг окружности с общими концами равна 3600.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
При этом говорят, что вписанный угол ABC опирается на дугу AC.
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство.
Пусть ∠АВС – вписанный угол окружности с центром О, опирающийся на дугу АС. Докажем, что ∠АВС=12AC. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
-
Луч ОВ совпадает с одной из сторон угла АВС, например со стороной ВС. В этом случае дуга АС меньше полуокружности, поэтому центральный угол АОС равен дуге АС. Так как угол АОС – внешний угол равнобедренного треугольника АВО, а углы 1 и 2 при основании равнобедренного треугольника равны, то ∠АОС=∠1+∠2=2·∠1.
Отсюда следует, что удвоенный ∠1 равен дуге АС или ∠АВС=∠1=12AC.
-
Луч ВО делит угол АВС на два угла. В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC.
-
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла. Этот случай доказывается аналогично двум предыдущим.
Из теоремы о вписанном угле следует два утверждения:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
Докажем еще одну теорему, которая пригодится для решения задач.
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Пусть хорды АВ и СD пересекаются в точке Е. Докажем, что АЕ·ВЕ = СЕ·DE.
Рассмотрим треугольники ADE и CBE. В этих треугольниках углы 1 и 4 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 2 и 3 равны как вертикальные. По первому признаку подобия треугольников △ADE ∼△CBE. Отсюда следует, что АЕСЕ=DEBE, или AE·BE = CE·DE.
Решим задачу, используя изученные свойства центральных и вписанных углов.
Центральный угол на 17° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Пусть центральный угол равен х, а вписанный угол, опирающийся на ту же дугу, равен у:
Мы знаем, что х = 2у. Отсюда 2у = 17+у; у = 17.
Ответ: 17.
Центральные и вписанные углы
Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.
Определение 1
Угол, вершина которого лежит в центре окружности называется центральным углом (рис. 1).
Рисунок 1. Центральный угол
Замечание 1
Отметим, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Введем теперь понятие вписанного угла.
Определение 2
Угол, вершина которого лежит на окружности и стороны которого пересекают эту же окружность, называется вписанным углом (рис. 2).
\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
Рисунок 4.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр — прямой.
0\]
Из следствия 2 сразу получаем, что искомый угол — прямой.
Чему равен вписанный угол | Треугольники
Выясним, чему равен вписанный угол окружности и как его величина связана с величиной центрального угла.
Теорема
(О вписанном угле)
Вписанный угол равен половине соответствующего ему центрального угла.
Дано: окружность (O; R),
∠ABС — вписанный,
∠AOС — центральный.
Доказать:
Доказательство:
1) Рассмотрим частный случай, когда одна из сторон угла проходит через центр окружности.
В треугольнике AOB OA=OB (как радиусы). Значит, треугольник AOB — равнобедренный с основанием AB. Следовательно, у него углы при основании равны:∠ABO=∠BAO.
∠AOC — внешний угол треугольника AOB. Внешний угол равен сумме двух внутренних углов, не смежных с ним:
∠AOC=∠ABO+∠BAO=2∙∠ABO. Отсюда,
2) Если центр окружности лежит между сторонами угла.
Проведем из вершины вписанного угла ABC диаметр BF.
Аналогично, ∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и
∠FOC — внешний угол при вершине O равнобедренного треугольника BCO и
3) Если центр окружности лежит вне угла.
Проведем диаметр BF.
∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и
∠СOF — внешний угол при вершине O равнобедренного треугольника BCO и
Что и требовалось доказать.
Замечание.
Дугу окружности можно измерять в градусах. Если центральный угол AOC меньше либо равен 180º, то градусная мера дуги AC равна градусной мере центрального угла AOC:
Если центральный угол AOC больше 180º, то градусная мера дуги AC равна 360º-∠AOC.
Таким образом, сумма градусных мер двух дуг окружности с общими концами равна 360º.
Другая формулировка теоремы о вписанном угле:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Центральные и вписанные углы в задании 6
Сегодня мы рассмотрим очередной тип задач 6 — на этот раз с окружностью. Многие ученики не любят их и считают сложными. И совершенно напрасно, поскольку такие задачи решаются элементарно, если знать некоторые теоремы. Или не решаются вообще, если их не знать.
Прежде чем говорить об основных свойствах, позвольте напомнить определение:
Вписанный угол — тот, у которого вершина лежит на самой окружности, а стороны высекают на этой окружности хорду.
Центральный угол — это любой угол с вершиной в центре окружности. Его стороны тоже пересекают эту окружность и высекают на ней хорду.
Итак, понятия вписанного и центрального угла неразрывно связаны с окружностью и хордами внутри нее.
А теперь — основное утверждение:
Теорема. Центральный угол всегда в два раза больше вписанного, опирающегося на ту же самую дугу.
Несмотря на простоту утверждения, существует целый класс задач 6, которые решаются с помощью него — и никак иначе.
Задача. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
Пусть AB — рассматриваемая хорда, O — центр окружности. Дополнительное построение: OA и OB — радиусы окружности. Получим:
Рассмотрим треугольник ABO. В нем AB = OA = OB — все стороны равны радиусу окружности. Поэтому треугольник ABO — равносторонний, и все углы в нем по 60°.
Пусть M — вершина вписанного угла. Поскольку углы O и M опираются на одну и ту же дугу AB, вписанный угол M в 2 раза меньше центрального угла O. Имеем:
M = O : 2 = 60 : 2 = 30
Задача. Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности.
Найдите вписанный угол.Введем обозначения:
- AB — хорда окружности;
- Точка O — центр окружности, поэтому угол AOB — центральный;
- Точка C — вершина вписанного угла ACB.
Поскольку мы ищем вписанный угол ACB, обозначим его ACB = x. Тогда центральный угол AOB равен x + 36. С другой стороны, центральный угол в 2 раза больше вписанного. Имеем:
AOB = 2 · ACB;
x + 36 = 2 · x;
x = 36.
Вот мы и нашли вписанный угол AOB — он равен 36°.
Окружность — это угол в 360°
Прочитав подзаголовок, знающие читатели, наверное, сейчас скажут: «Фу!» И действительно, сравнивать окружность с углом не совсем корректно. Чтобы понять, о чем речь, взгляните на классическую тригонометрическую окружность:
К чему эта картинка? А к тому, что полный оборот — это угол в 360 градусов. И если разделить его, скажем, на 20 равных частей, то размер каждой из них будет 360 : 20 = 18 градусов. Именно это и требуется для решения задачи B8.
Точки A, B и C лежат на окружности и делят ее на три дуги, градусные меры которых относятся как 1 : 3 : 5. Найдите больший угол треугольника ABC.
Для начала найдем градусную меру каждой дуги. Пусть меньшая из них равна x. На рисунке эта дуга обозначена AB. Тогда остальные дуги — BC и AC — можно выразить через AB: дуга BC = 3x; AC = 5x. В сумме эти дуги дают 360 градусов:
AB + BC + AC = 360;
x + 3x + 5x = 360;
9x = 360;
x = 40.
Теперь рассмотрим большую дугу AC, которая не содержит точку B. Эта дуга, как и соответствующий центральный угол AOC, равна 5x = 5 · 40 = 200 градусов.
Угол ABC — самый большой из всех углов треугольника. Это вписанный угол, опирающийся на ту же дугу, что и центральный угол AOC. Значит, угол ABC в 2 раза меньше AOC. Имеем:
ABC = AOC : 2 = 200 : 2 = 100
Это и будет градусная мера большего угла в треугольнике ABC.
Окружность, описанная вокруг прямоугольного треугольника
Эту теорему многие забывают.
А зря, ведь некоторые задачи B8 без нее вообще не решаются. Точнее, решаются, но с таким объемом вычислений, что вы скорее уснете, чем дойдете до ответа.
Теорема. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Что следует из этой теоремы?
- Середина гипотенузы равноудалена от всех вершин треугольника. Это прямое следствие теоремы;
- Медиана, проведенная к гипотенузе, делит исходный треугольник на два равнобедренных. Как раз это и требуется для решения задачи B8.
В треугольнике ABC провели медиану CD. Угол C равен 90°, а угол B — 60°. Найдите угол ACD.
Поскольку угол C равен 90°, треугольник ABC — прямоугольный. Получается, что CD — медиана, проведенная к гипотенузе. Значит, треугольники ADC и BDC — равнобедренные.
В частности, рассмотрим треугольник ADC. В нем AD = CD. Но в равнобедренном треугольнике углы при основании равны — см.
«Задача B8: отрезки и углы в треугольниках». Поэтому искомый угол ACD = A.
Итак, осталось выяснить, чему равен угол A. Для этого снова обратимся к исходному треугольнику ABC. Обозначим угол A = x. Поскольку сумма углов в любом треугольнике равна 180°, имеем:
A + B + BCA = 180;
x + 60 + 90 = 180;
x = 30.
Разумеется, последнюю задачу можно решить по-другому. Например, легко доказать, что треугольник BCD — не просто равнобедренный, а равносторонний. Значит, угол BCD равен 60 градусов. Отсюда угол ACD равен 90 − 60 = 30 градусов. Как видите, можно использовать разные равнобедренные треугольники, но ответ всегда будет один и тот же.
Смотрите также:
- Задача B8: отрезки и углы в треугольниках
- Работа с формулами в задаче B12
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Пробный ЕГЭ 2012 от 7 декабря. Вариант 4 (без логарифмов)
- Метод коэффициентов, часть 2
- Задача B4: расчет времени в пути
Как найти центральный угол
Представьте, что вы стоите в центре идеально круглой арены.
Вы смотрите на толпу по краям арены и замечаете своего лучшего друга на одном месте и учителя математики в средней школе через пару секций. Какое расстояние между ними и вами? Как далеко вам придется пройти, чтобы добраться от места друга до места учителя? Каковы размеры углов между вами? Это все вопросы, связанные с центральными углами.
Центральный угол — это угол, который образуется при проведении двух радиусов от центра круга к его краям. В этом примере два радиуса — это две линии вашего взгляда от вас, в центре арены, до вашего друга и ваша линия обзора до учителя. Угол, который образуется между этими двумя линиями, и есть центральный угол. Это угол, ближайший к центру круга.
Ваш друг и ваш учитель сидят вдоль окружности или краев круга.Путь вдоль арены, который их соединяет, представляет собой дугу .
Найдите центральный угол по длине дуги и окружности
Есть несколько уравнений, которые вы можете использовать, чтобы найти центральный угол.
Иногда получается длина дуги , расстояние по окружности между двумя точками. (В этом примере это расстояние, которое вам нужно будет пройти по арене, чтобы добраться от друга до учителя.) Соотношение между центральным углом и длиной дуги составляет:
(длина дуги) ÷ окружность = (центральный угол ) ÷ 360 °
Центральный угол будет в градусах.
Эта формула имеет смысл, если вдуматься. Длина дуги из общей длины по окружности (окружности) равна той же пропорции, что и угол дуги из общего угла в окружности (360 градусов).
Чтобы эффективно использовать это уравнение, вам необходимо знать длину окружности круга. Но вы также можете использовать эту формулу, чтобы найти длину дуги, если вы знаете центральный угол и длину окружности. Или, если у вас есть длина дуги и центральный угол, вы можете найти окружность!
Найдите центральный угол по длине дуги и радиусу
Вы также можете использовать радиус окружности и длину дуги, чтобы найти центральный угол.
Назовем меру центрального угла θ. Тогда:
θ = s ÷ r , где s — длина дуги, а r — радиус. θ измеряется в радианах.
Опять же, вы можете изменить это уравнение в зависимости от имеющейся информации. Вы можете найти длину дуги по радиусу и центральному углу. Или вы можете найти радиус, если у вас есть центральный угол и длина дуги.
Если вам нужна длина дуги, уравнение выглядит следующим образом:
s = θ * r , где s — длина дуги, r — радиус, а θ — центральный угол в радианах.
Теорема о центральном угле
Давайте добавим поворот к вашему примеру, где вы находитесь на арене со своим соседом и учителем. Теперь на арене есть третий человек, которого вы знаете: ваш ближайший сосед. И еще одно: они позади вас. Вы должны обернуться, чтобы увидеть их.
Ваш сосед находится примерно через арену от вашего друга и вашего учителя. С точки зрения вашего соседа, есть угол, образованный их линией взгляда на друга и их линией взгляда на учителя.
Это называется вписанным углом. Вписанный угол — это угол, образованный тремя точками на окружности окружности.
Теорема о центральном угле объясняет взаимосвязь между размером центрального угла, образованного вами, и вписанным углом, образованным вашим соседом. Теорема о центральном угле утверждает, что центральный угол вдвое больше вписанного угла . (Предполагается, что вы используете одни и те же конечные точки. Вы оба смотрите на учителя и друга, а не на кого-то еще).
Вот еще способ записать. Давайте назовем место вашего друга A, место вашего учителя B и место вашего соседа C. Вы, в центре, можете быть O.
Итак, для трех точек A, B и C по окружности круга и точки O на В центре центральный угол ∠AOC вдвое больше вписанного угла ABC.
То есть ∠AOC = 2∠ABC.
В этом есть смысл. Вы ближе к другу и учителю, поэтому они смотрят на вас дальше (под большим углом).Вашему соседу с другой стороны стадиона они выглядят намного ближе друг к другу (меньший угол).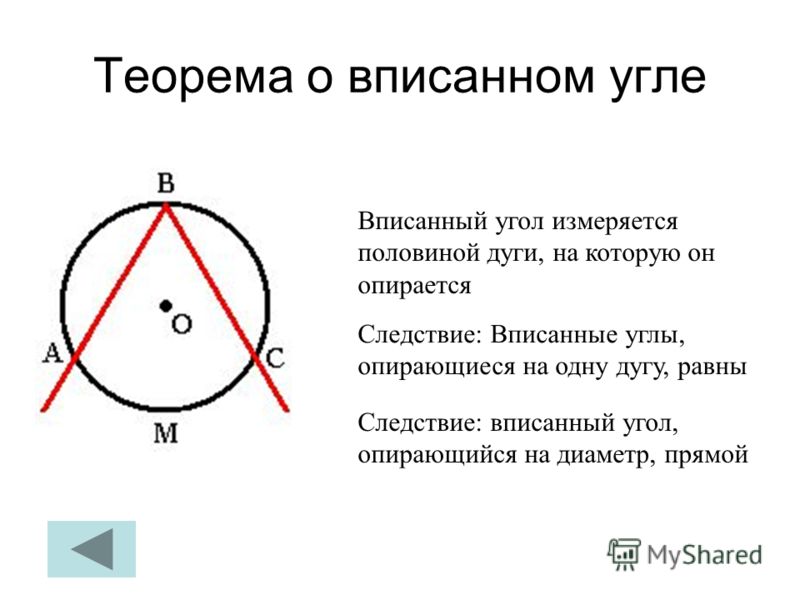
Исключение из теоремы о центральном угле
Теперь давайте сдвинемся с места. Ваш сосед на дальней стороне арены начинает двигаться! У них все еще есть линия обзора для друга и учителя, но линии и углы продолжают изменяться по мере движения соседа. Угадайте, что: до тех пор, пока сосед остается вне дуги между другом и соседом, теорема о центральном угле остается верной!
Но что происходит, когда сосед перемещает между другом и учителем? Теперь ваш сосед находится внутри малой дуги , относительно небольшого расстояния между другом и учителем по сравнению с большим расстоянием вокруг остальной арены.Тогда вы получите исключение из теоремы о центральном угле.
Исключение из теоремы о центральном угле гласит, что когда точка C, соседняя, находится внутри малой дуги, вписанный угол является дополнением половины центрального угла. (Помните, что угол и его дополняют в сумме 180 градусов.
)
Итак: вписанный угол = 180 — (центральный угол ÷ 2)
Или: ∠ABC = 180 — (∠AOC ÷ 2)
Visualize
Math Open Reference имеет инструмент для визуализации теоремы о центральном угле и ее исключения.Вы можете перетащить «соседа» во все разные части круга и наблюдать, как меняются углы. Попробуйте, если вы хотите получить визуальную или дополнительную практику!
Теорема о центральном угле. В геометрии изображен центральный угол… | Войцех Вечорек | Cantor’s Paradise
В геометрии центральный угол, образованный дугой, вдвое больше любого вписанного угла той же дуги.
Если бы ваш учитель математики начал урок с вопроса о ваших ассоциациях с теоремой о центральном угле, вы бы ответили, говоря о теореме Фалеса? Если да, то ответом будет: «Да, но только в одной трети».Причина в том, что дуга, на которую можно положить вписанный угол, может иметь полукруг, большую или меньшую длину.
Полукруглый известен как теорема Фалеса. И сначала мы начнем с его объяснения; но непосредственно перед началом, для удобства чтения, давайте познакомимся с определениями, которые мы собираемся использовать.
Вершина: точка, где встречаются две линии (в нашем случае).
Диаметр: Любой отрезок прямой линии, проходящий через центр окружности и конечные точки которого лежат на окружности.Есть бесконечное количество возможностей его нарисовать.
Хорда: отрезок прямой линии, соединяющий любые две точки на окружности, диаметр которой является самым длинным.
Дуга: часть длины окружности.
Центральный угол: угол в центре окружности между двумя радиусами.
Вписанный угол: угол вершины на окружности между ее хордами.
Угол, образованный дугой: Вершина, концы хорды которой охватывают данную дугу.
Когда диаметр проходит через центр окружности, тогда центральный угол, образованный дугой полукруга, будет просто 180 ° , без сомнения.
И, если теория верна, любой вписанный угол, концы хорд которого находятся на соответствующих концах этого диаметра, должен быть вдвое меньше — он должен быть 90 ° . Итак, у нас получился прямоугольный треугольник, в котором диаметр — гипотенуза.
Обозначим конечные точки диаметров как A, и A ’, , их углы как α и α’, и вершину этого вписанного угла, ß , как B. Соединив их, мы получили треугольник. Более того, это был бы прямоугольный треугольник, поскольку вписанный угол является прямым углом; с диаметром, являющимся его гипотенузой.
Это выглядит так:
Готовы? Устойчивый? Идти! Для доказательства этой чрезвычайно полезной теоремы.
Геометрическое доказательство для удобства
Обратите внимание, что отрезки от центра O окружности до вершин являются ее радиусами. И они делят треугольник AA’B на два других, но не на какие-либо треугольники.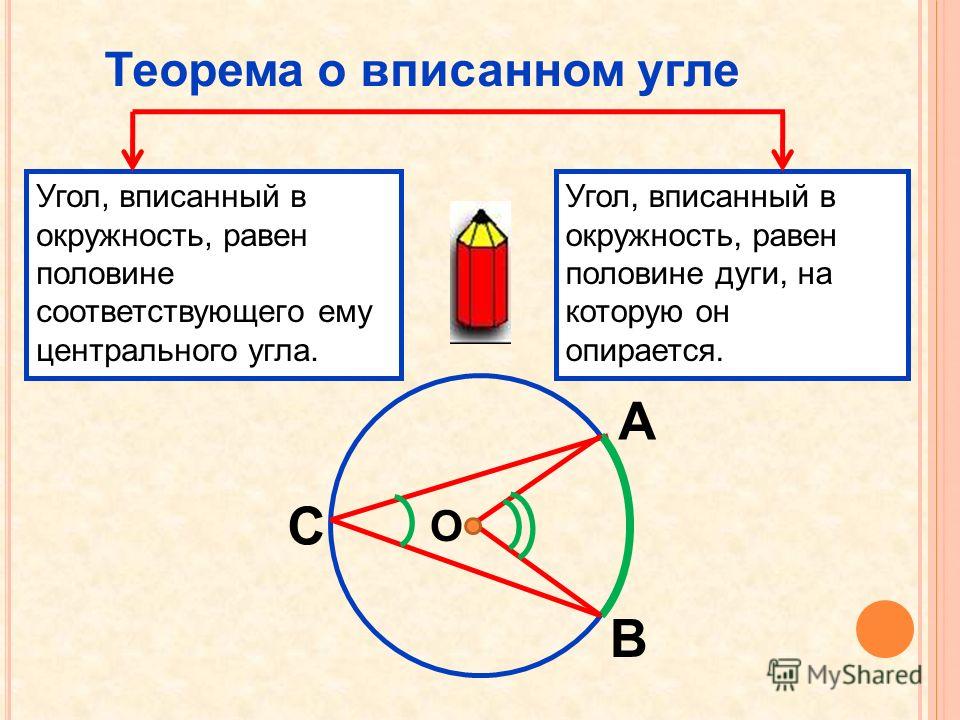
Они должны быть равнобедренными, потому что у каждого есть две равные стороны, равные радиусу нашего круга.
Тем не менее, оба угла между сторонами радиуса и 3-ей опорой должны быть одинаковыми; следовательно, ß = α + α ’.
И мы знаем, что сумма углов в треугольнике равна 180 ° . Складывая их все из треугольника AA’B , мы получаем:
Итак, действительно ß — прямой угол.
qed
Пифагорейское доказательство для небольшого развлечения
Изначально я назвал этот раздел «Пифагорейское доказательство», но мне так понравилось писать его, что пришлось добавить дополнительное «для небольшого развлечения» здесь.
Предположим, что вписанный угол ∠ABA ’, вдвое меньше центрального, является правильным. Если это так, то должна выполняться теорема Пифагора.
Не беспокойтесь об угле θ ; это будет объяснено чуть позже, но сначала давайте применим формулу, чтобы показать то, что мы пытаемся доказать, а именно:
Это θ — это просто угол, на который линия наклонена от начала координат.
Это все.
Имея это, мы можем разложить нашу линию на составляющие по оси.И с небольшой помощью тригонометрии мы могли вычислить их: компонентов, записанных таким образом, известны как полярные координаты.
Вернемся к самому доказательству. Нам нужно разложить стороны по прямому углу на x, y -компоненты, а затем, применив теорему Пифагора, сложить обе их длины.
Длина AB :
Обратите внимание, что компонент x- складывается из r и r ⋅ cosθ .В то время как y состоит из одного значения.
Длина A’B :
Здесь стоит упомянуть длину x-компоненты, в отличие от той же самой ранее, вынуждающей нас вычесть из r r ⋅ cosθ . Также посмотрите и сравните y-компоненты: они равны. Что, если подумать, не должно быть сюрпризом.
Теперь мы можем вернуться к нашей исходной формуле, подставить эти значения и проверить, равны ли ее стороны или нет.
Как видно, все правильно — так и будет.
q.e.d
Что отличает большой (и второстепенный) корпус от корпуса Thales, так это то, что теперь радиусы не образуют диаметра. Эти радиусы создают больший центральный угол, чем 180 ° . Это означает, что если теорема все еще верна, любой вписанный угол вдвое меньше, чем 90 ° .
Это выглядит так:
Геометрическое доказательство
Для доказательства этого (и следующего) случая необходимы три вещи.Два из них нам уже известны: отрезки от центра круга до каждой вершины — это радиусы. И они делят нашу фигуру на два равнобедренных треугольника. Но что есть третье?
Если мы «скопируем» OB, и повернем его вокруг перпендикулярной оси, отметив противоположную точку на окружности как B ’, мы получим диаметр.
Теперь, нарисовав один дополнительный аккорд от B ’ к каждому A и A’ , мы могли бы разделить всю эту проблему на две, скажем, левую и правую.
Там, где оба могут быть исследованы по теореме Фалеса, поскольку BB ’ — это диаметр, центральный угол составляет 180 ° , а вписанный угол ∠BAB’ и ∠BA’B ’ равен 90 ° . Конечно, ABB ’, A’BB’ — это прямоугольные треугольники.
Левый выглядит так:
Найдя угол ∠AOB ’, мы узнаем, какова левая часть центрального угла. Что это могло быть? Угол ∠BAB ‘ равен 90 ° , но поскольку его верхняя часть равна α , нижняя часть должна быть 90 ° -α , а угол ∠AB’O должен быть таким же. ! Итак, суммируя углы в нижнем треугольнике, мы получаем:
Таким образом, левая часть центрального угла действительно вдвое больше, чем α.
Разложенная правая часть выглядит так:
И мы делаем все так же, как и с левой частью, получая:
Таким образом, действительно, центральный угол вдвое больше любого вписанного угла, подведенного той же дугой.
q.e.d
Последний случай, когда центральный угол меньше 180 ° . Все шаги идентичны основному случаю. Но сначала давайте посмотрим, как это выглядит:
Геометрическое доказательство
Что мы делаем, так это предоставляем диаметр BB ’, который снова разделит нашу проблему на левую и правую.
Левый:
Угол ∠BAB ’ составляет 90 ° , а его верхняя часть равна α . Таким образом, нижняя часть должна быть 90 ° -α. Угол ∠AB’O должен быть точно таким же. Таким образом, сумма углов в нижнем треугольнике равна:
После применения ситуация выглядит следующим образом:
Правый:
И в последний раз вписанный угол ∠BA’B ‘ равен 90 ° . Поскольку его верхняя часть равна α ’, нижняя должна быть равна 90 ° -α’ .Также угол ∠A’B’O такой же по размеру.
Суммируя углы в нижнем треугольнике, мы получаем:
, что дает:
Итак, в этом случае теорема о центральном угле также работает.
q.e.d
Узнайте о центральных и вписанных углах
В этом видео мы рассмотрим центральный и вписанный углы:
- Как определить центральные углы
- Как определить вписанные углы
- Соотношение между центральными углами и пересеченной дугой
- Взаимосвязь между вписанными углами и пересеченной дугой
Центральные углы: Углы с вершиной, расположенной в центре окружности.Мера центрального угла такая же, как мера дуги, которую он пересекает.
Например:
Если размер центрального угла равен, то размер пересекаемой дуги также равен.
Вписанные углы: Углы, вершина которых расположена на окружности круга.
Размер вписанного угла составляет половину меры дуги, которую он пересекает.
Например:
Если размер дуги равен, то измеряется только вписанный угол.
Если центральный угол и вписанный угол пересекают одну и ту же дугу, то центральный угол вдвое больше вписанного угла, а вписанный угол составляет половину центрального угла.
Стенограмма видеоурока
В этом уроке мы собираемся рассмотреть центральные и вписанные углы.
Здесь у нас есть круг с центром.
Нарисуем радиус от центра до края круга.
Мы могли бы заметить, что если мы полностью обойдем круг внутри круга, то получится.
Основываясь на том факте, что мы можем войти внутрь круга, мы можем связать это с окружностью. Вся окружность будет равна, а любая часть окружности будет составлять некоторую долю от.
Доля окружности связана с центральным углом.
Если мы должны нарисовать другой радиус и полученный угол равен.
Тогда дуга тоже.
Это представляет собой целое. Длина дуги также равна общей окружности.
Центральный угол называется центральным, потому что вершина находится в центре.Какой бы ни была мера этого угла, равняется измерению пересекаемой дуги в градусах.
Теперь посмотрим на вписанный угол.
Вписанные углы имеют вершину на окружности. Нарисованный угол — это вписанный угол.
Допустим, длина дуги равна. Затем с этим связана мера вписанного угла.
Углы вписаны в точку пересечения дуги.
Если мы можем посмотреть, как связаны центральный угол и вписанный угол.
Снова нарисуем центральный угол. Мера этого угла такая же, как у точки пересечения дуги, а размер вписанного угла равен половине меры дуги, которую он пересекает.
Просто сфокусируйтесь на вписанном угле. Его размер составляет половину длины дуги в градусах. Пока он вписан и пересекает эту дугу.
Например, у нас может быть угол в другом месте.
Этот угол вписан, потому что его вершина находится на окружности, и он также пересекает дугу, которая измеряет вписанный угол.
Если мы начертили вписанный угол здесь, то это также потому, что он пересекает ту же дугу с.
Под перехватом я подразумеваю, что если мы продолжим линии под углом, между ними будет дуга. О какой дуге мы говорим.
То же самое и с другими строками. Это перехваченная дуга.
Итак, какой бы размер дуги ни был, вписанный угол равен половине.
Мера центрального угла равна измеренной длине дуги.
Вы можете видеть, что если центральный угол и вписанный угол пересекают одну и ту же дугу, центральный угол будет вдвое больше вписанных углов.
Точно так же вписанный угол составляет половину центрального угла.
As8dspark
As8dsparkпо
Дэвид С. Парк
Теорема о центральном угле очень полезна при решении вопросов, касающихся углов внутри окружностей. Использование этой теоремы часто упрощает сложную ситуацию до довольно простой.
😉 для изучения.
Теорема: теорема о центральном угле
Теорема о центральном угле утверждает, что центральный угол из двух выбранных точек A и B на окружности всегда вдвое больше вписанного угла из этих двух точек. Вписанный угол может быть определен любой точкой вдоль внешней дуги AB и двумя точками A и B.
Теорема о центральном угле
Примечание: Теорема о центральном угле гласит, что вписанный угол APB может иметь точку P в любом месте на внешней дуге AB, и соотношение углов сохраняется.
Все вписанные углы одной дуги AB равны по размеру
Для тех, кто хочет проверить, так ли это на самом деле, вы можете проверить теорему о центральном угле с помощью этого файла GSP: НАЖМИТЕ ЗДЕСЬ. (Файл измеряет вписанный угол и центральный угол для любого положения точек P, A и B.)
Доказательство теоремы о центральном угле:Упражнение: Задача № 13 Задания 8
Следующее упражнение использует теорему о центральном угле и является хорошим примером для понимания этой теоремы.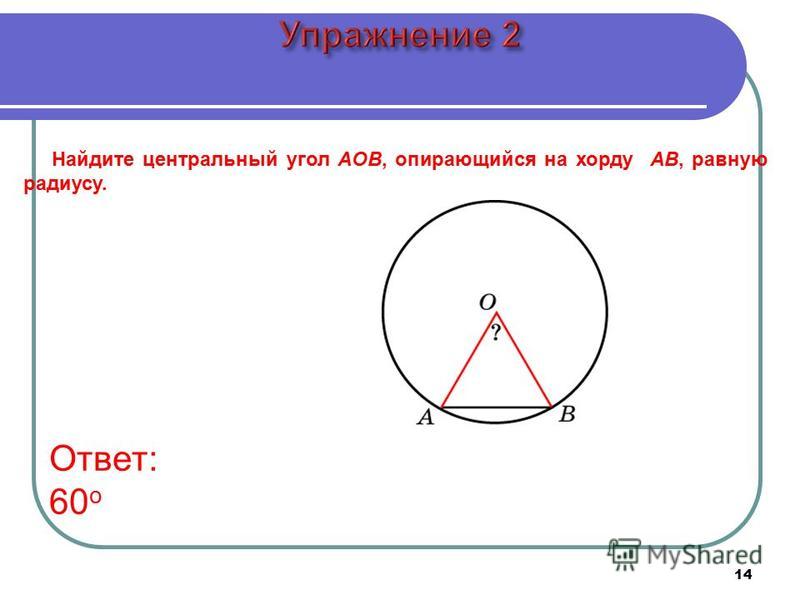
Задача № 13 : Биссектрисы внутреннего угла треугольника ABC продолжаются до пересечения с описанной окружностью в точках L, M и N соответственно. Найдите углы треугольника LMN через углы A, B и C. Верен ли ваш результат только для острых треугольников?
Проблема № 13
Решение :
Поскольку каждый угол A, B и C делятся пополам удлиненными линиями, обозначим каждый разделенный пополам угол буквами a, b и c.
Обозначение каждого угла пополам
Давайте посмотрим на Arc BL на нижнем левом рисунке.По теореме о центральном угле вписанный угол BAL равен вписанному углу BML. Это потому, что эти два вписанных угла имеют одни и те же две базовые точки B и L вдоль дуги. Аналогично, от базовой дуги CL на правой диаграмме угол LAC = угол LNC.
Основная дуга BL слева и основная дуга CL справа
Если мы продолжим тот же процесс для дуг AM, MC, AN и NB, то мы получим следующую угловую зависимость.
Применение теоремы о центральном угле для дуг AM, MC, AN и NB
Теперь мы можем выразить три угла L, M и N через A, B и C.
Конец решения!
*** Решение не зависело от того, был ли треугольник острым или тупым. Такое же соотношение углов будет справедливо и для тупого треугольника.
Вернуться в дом Давида
Перехваченная дуга — объяснение и примеры
Теперь, когда мы изучили все основные части круга. Давайте перейдем к чему-нибудь сложному. Речь идет о перехваченной дуге , , которая образуется в окружности за счет внешних линий .Если вы действительно хорошо разбираетесь в углах, то этот урок не должен стать для вас проблемой.
Мы уже видели все основные определения частей окружностей, такие как диаметр, хорда, вершина и центральный угол; если нет, просмотрите предыдущие уроки, потому что эти части используются в этом уроке.
Из этой статьи вы узнаете:
- Определение перехваченной дуги,
- как найти перехваченную дугу и формулу
- перехваченной дуги.
Что такое перехваченная дуга?
Напомним, дуга — это часть окружности круга. Таким образом, перехваченная дуга может быть определена как дуга, образованная, когда одна или две разные хорды или линейные сегменты пересекают окружность и встречаются в общей точке, называемой вершиной.
Важно отметить, что линии или хорды могут встречаться либо в середине круга, либо на другой стороне круга, либо даже вне круга.
Или мы также можем определить пересеченную дугу, как когда две прямые пересекают окружность в двух разных точках, часть окружности между точками пересечения образует пересеченную дугу.
Как найти перехваченную дугу?
Существует несколько интересных соотношений между перехваченной дугой и вписанным центральным углом круга. В геометрии вписанный угол — это угол, образованный между хордами или линиями, пересекающими круг.
Центральный угол — это угол, образованный двумя радиусами, которые соединяют концы хорды с центром окружности . Эти отношения между различными перехваченными дугами и соответствующими им вписанными углами образуют формулу перехваченной дуги.
Давайте посмотрим.
Формула перехваченной дуги
- Формула перехваченной дуги для линий, пересекающихся в середине круга
Центральный угол = мера перехваченной дуги
- Формула перехваченной дуги для хорд, пересекающихся на другой стороне круг.
Вписанный угол = 1/2 × пересеченная дуга
Или
2 × вписанный угол = пересеченная дуга
Пересекающиеся хорды:
Для пересекающихся хорд пересекаемая дуга задается ,
Вписанный угол = половина суммы пересеченных дуг.
Внешний вписанный угол:
Размер угла при вершине вне окружности = 1/2 × (разность перехваченных дуг)
Разработаны примеры перехваченной дуги.
Пример 1
Найдите угол ABC в окружности, показанной ниже.
Решение
Учитывая, что пересеченная дуга = 150 °
Центральный угол = пересеченная дуга
Следовательно, ∠ ABC = 150 °
Пример 2
Определить значение x в кружке, показанном ниже.
Решение
Центральный угол = пересеченная дуга
60 ° = (3x + 15) °
Simplify
60 ° = 3x + 15 °
Вычесть 15 ° с обеих сторон.
45 ° = 3x
Разделим обе стороны на 3
x = 15 °
Итак, значение x равно 15 °.
Пример 3
Найдите значение перехваченной дуги на диаграмме, показанной ниже.
Решение
Дано,
Вписанный угол = 15 °
По формуле
Вписанный угол = ½ × пересеченная дуга
15 ° = ½ x пересеченная дуга
Следовательно перехваченной дуги составляет 30 °.
Пример 4
Если пересекаемая дуга на диаграмме ниже 160 °, определите значение x.
Решение
Дано,
Перехваченная дуга = 160 °
Вписанный угол = ½ × отрезанная дуга
Вписанный угол = ½ x 160 °
= 80 °
Итак, мы имеем ,
2 (4x + 21) ° = 80 °
8x + 42 ° = 80 °
Вычтем 42 ° с обеих сторон.
8x = 38 °
Разделите обе стороны на 8, чтобы получить.
x = 4,75 °
Таким образом, значение x равно 4,75 °
Пример 5
Найдите значение вписанного угла на следующей диаграмме.
Решение
Вписанный угол равен половине суммы пересеченных дуг.
= ½ x (170 ° + 50 °)
= ½ x 220 °
= 110 °
Итак, вписанный угол составляет 110 °.
Пример 6
Найдите значение x на диаграмме, показанной ниже.
Решение
Даны перехваченные дуги 62 ° и 150 °
Вписанный угол = половине суммы перехваченных дуг.
Вписанный угол = ½ (62 ° + 150 °)
= ½ x 212 °
= 106 °
Теперь решите относительно x.
(2x + 10) ° = 106 °
Упростить.
2x + 10 ° = 106 °
Вычтите 10 ° с обеих сторон.
2x = 96
Разделив обе стороны на 2, мы получим
x = 48 °
Следовательно, значение x равно 48 градусам.
Пример 7
Найдите угол внешней вершины на диаграмме, показанной ниже.
Решение
Теперь вам нужно вспомнить свойства, которые мы изучили выше.
Размер угла при вершине вне окружности = 1/2 × (разность пересеченных дуг)
Угол при вершине = ½ (140 ° — 40 °)
= ½ x 100 °
= 50 °
Итак , мера угла с вершиной вне окружности — 50 °.
youtube.com/embed/F77BrIfYbqE?rel=0;controls=0;showinfo=0;theme=light» frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Геометрические гипотезы: вписанные углы
Геометрические гипотезы: вписанные углыПояснение:
Вписанный угол — это угол, образованный двумя хордами в окружности, имеющими общую конечную точку. Эта общая конечная точка образует вершину вписанного угла. Две другие конечные точки определяют то, что мы называем перехваченной дугой на окружности.Перехваченную дугу можно рассматривать как часть круга, которая находится «внутри» вписанного угла. (См. Розовую часть круга на картинке выше.) Центральный угол — это любой угол, вершина которого находится в центре окружности. Центральный угол обязательно проходит через две точки на окружности, которые, в свою очередь, делят окружность на две дуги: большая дуга и малая дуга .
Малая дуга — меньшая из двух дуг, а большая дуга — больше.Мы определяем угол дуги как меру центрального угла, который его пересекает.
Гипотеза о вписанном угле I дает соотношение между измерениями вписанного угла и угла пересечения дуги. В нем говорится, что размер перехваченной дуги равен удвоенным , чем вписанный угол.
Точные формулировки гипотез приведены ниже. С каждой гипотезой связана демонстрация Sketch Pad, чтобы проиллюстрировать ее истинность (доказательство — Sketch Pad от Geometer!).Связанный список мероприятий также включает указания для дальнейших «практических» расследований, связанных с этими гипотезы, а также геометрические задачи, использующие их результаты.
Точное изложение домыслов:
Гипотеза ( Гипотеза о вписанных углах I ): В круге размер вписанного угла составляет половину меры центрального угла с той же пересеченной дугой.
Следствие ( Гипотеза о вписанных углах II ): В круге два вписанных угла с одной и той же пересеченной дугой совпадают.
Проба: Измерение каждого вписанного угла составляет ровно половину меры его пересеченной дуги. Поскольку они имеют одинаковую перехваченную дугу, они имеют одинаковую меру.
Следствие ( Гипотеза о вписанных углах III ): Любой угол, вписанный в полукруг, — это прямой угол.
Проба: Перехватываемая дуга для угла, вписанного в полукруг, составляет 180 градусов. Следовательно, угол должен составлять половину 180 или 90 градусов.Другими словами, угол — это прямой угол.
Leave A Comment