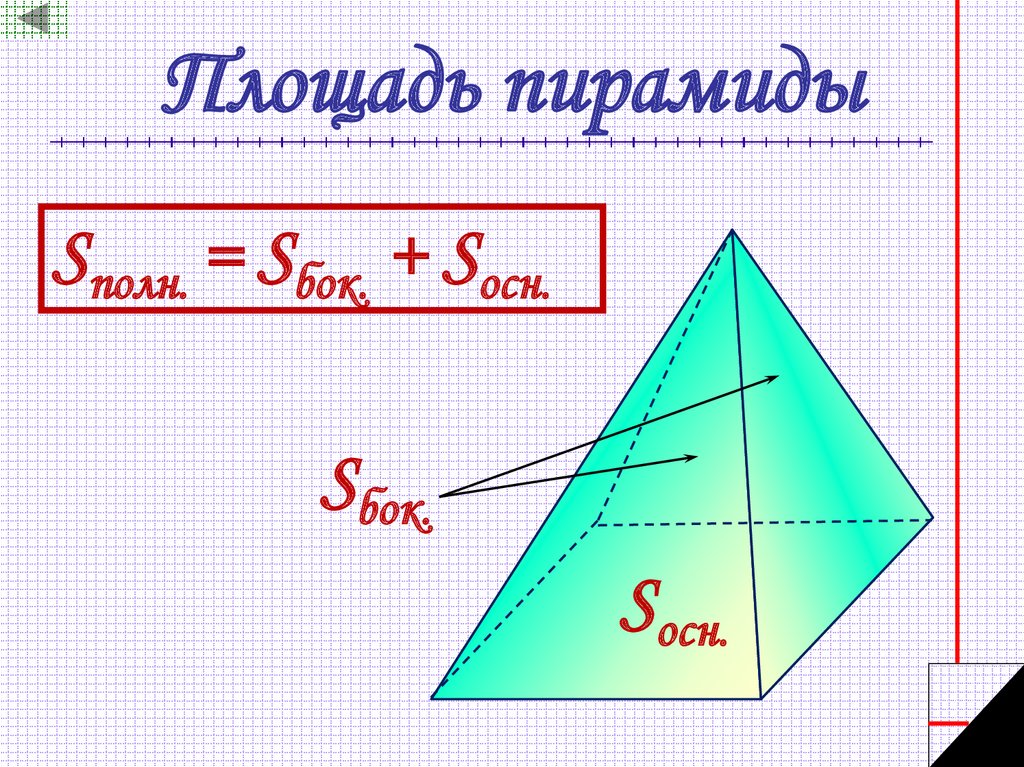
Площадь поверхности пирамиды
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-03-21
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
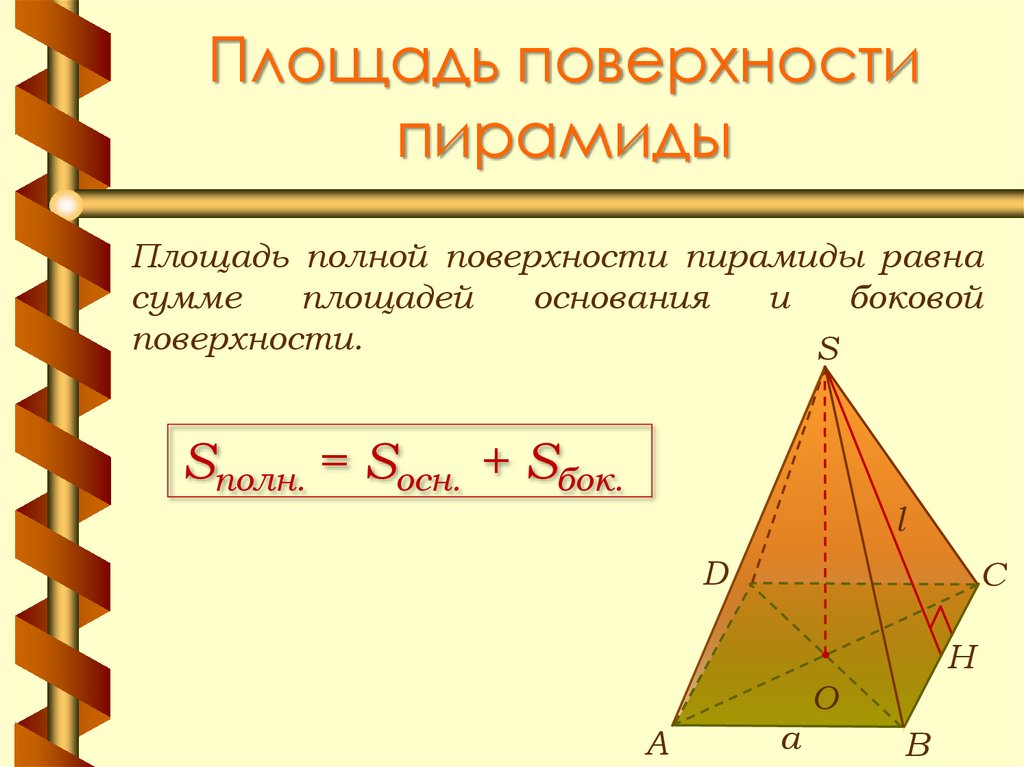
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами. Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПИРАМИДЫ | ЕГЭ-№2Площадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Площадь поверхности правильной пирамиды формулы и калькулятор
{S_{полн} = \dfrac{1}{2}PL + S}
Найти площадь
полной поверхностибоковой поверхности
Тип пирамиды
правильнаяправильная треугольнаяправильная четырехугольнаяправильная шестиугольная
Через
периметр, площадь и апофемусторону основания и высоту
Периметр основания P
ммсмдммкмдюймы (in)футы (ft)
Апофема L
ммсмдммкмдюймы (in)футы (ft)
Площадь основания S
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды.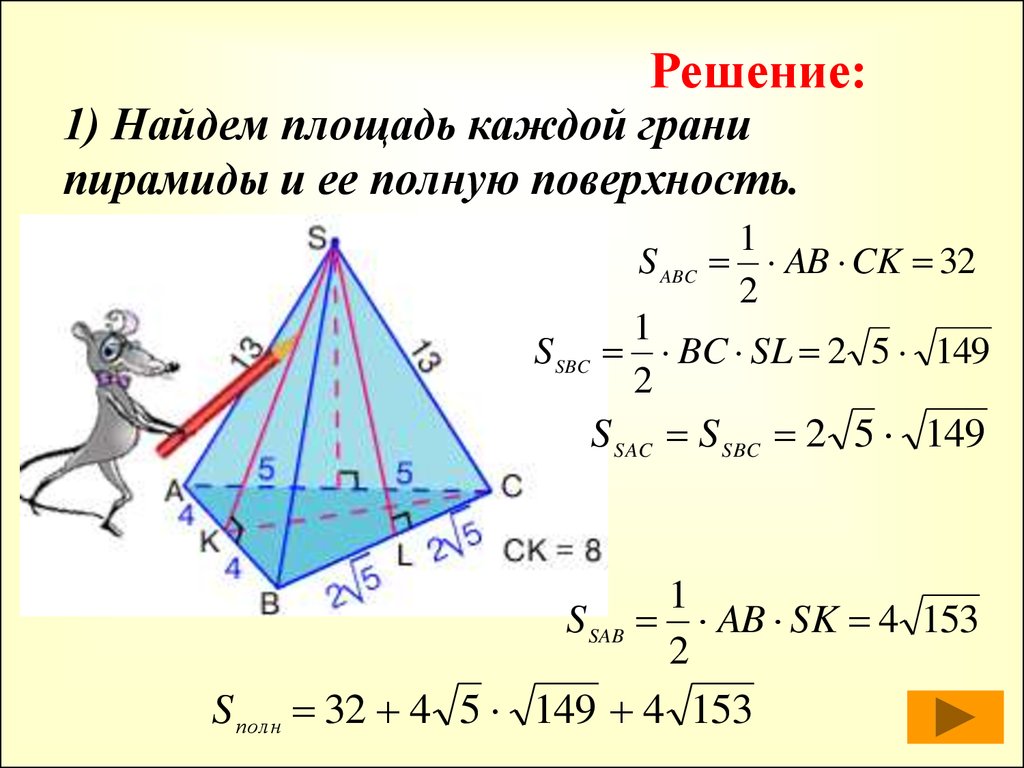 Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.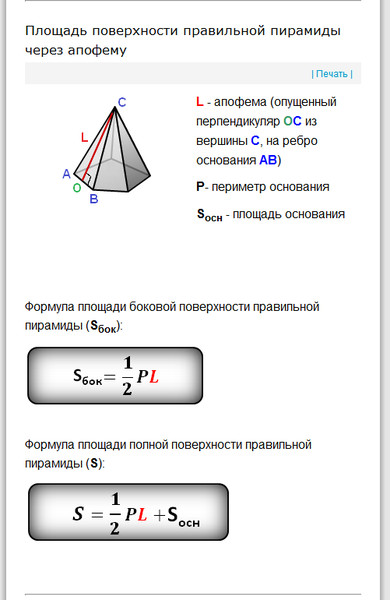
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = \dfrac{1}{2}PL+S}
P — периметр основания пирамиды
S — площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = \dfrac{na}{2} {\Bigg( \dfrac{a}{2 \\tg ( \dfrac{180°}{n})} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \\tg ( \dfrac{180°}{n})} \Bigg) ^2} \Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = \dfrac{a^2 \sqrt{3}+6aL}{4}}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = \dfrac{a^2 \sqrt{3}+6a \sqrt{b^2 — \dfrac{a^2}{4}}}{4}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = \dfrac{3a}{2} {\Bigg( \dfrac{a}{2 \tg ( 60°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 60°)} \Bigg) ^2} \Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a \sqrt{b^2- \dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {\Bigg( \dfrac{a}{2 \tg ( 45°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 45°)} \Bigg) ^2} \Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = \dfrac{3\sqrt{3}a^2}{2}+3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = \dfrac{3\sqrt{3}a^2}{2}+3a\sqrt{b^2-\dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {\Bigg( \dfrac{a}{2 \tg ( 30°)} + \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 30°)} \Bigg) ^2} \Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = \dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = \dfrac{na}{2} \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( \dfrac{180°}{n})} \Bigg) ^2} }
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = \dfrac{3}{2}aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = \dfrac{3a \sqrt{b^2 — \dfrac{a^2}{4}}}{2}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = \dfrac{3a}{2} \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 60°)} \Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =\dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a \sqrt{b^2 — \dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 45°)} \Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3a\sqrt{b^2-\dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 30°)} \Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. 2} = 60 \: см²
2} = 60 \: см²
Ответ: 60 см²
Проверка .
Нахождение объема и площади поверхности пирамиды (видео и практика)
Привет и добро пожаловать на это видео о пирамидах! В этом видео мы рассмотрим различные типы пирамид и способы расчета их объема и площади поверхности. Давайте узнаем о пирамидах!
Нельзя говорить о пирамидах, не упомянув самые известные пирамиды в мире, расположенные в Египте и построенные как усыпальницы египетских царей. Хотя пирамиды не совсем распространены, их форма настолько поразительна, что кажется, что они используются для того, чтобы сделать заявление, возможно, именно поэтому египетские цари использовали их в качестве своих гробниц. Лувр в Париже, который является крупнейшим художественным музеем в мире, также имеет форму пирамиды. Как видно из изображений египетских пирамид, 9Пирамида 0005 представляет собой трехмерную фигуру с треугольными сторонами, которые встречаются по краям и наверху, образуя вершину , и имеет многоугольник в качестве основания.
Многоугольное основание определяет тип пирамиды. Здесь вы видите пирамиду с треугольником в основании — треугольную пирамиду, пирамиду с прямоугольником в основании — прямоугольную пирамиду, а пирамиду с пятиугольником в основании — пятиугольную пирамиду. У нас также есть шестиугольные пирамиды и семиугольные пирамиды, и так далее.
Давайте на минутку вспомним, что означают объем и площадь поверхности трехмерной фигуры.
объем трехмерной фигуры является мерой того, сколько она может вместить, и измеряется в кубических единицах.
Площадь поверхности трехмерной фигуры является мерой общей площади, которую покрывает поверхность фигуры, и измеряется в квадратных единицах.
Прежде чем мы сможем вычислить объем и площадь поверхности пирамиды, мы должны знать разницу между высотой и наклонной высотой. высота пирамиды — длина перпендикуляра от вершины до основания, а наклонная высота — длина от вершины до середины нижнего края одной из треугольных граней.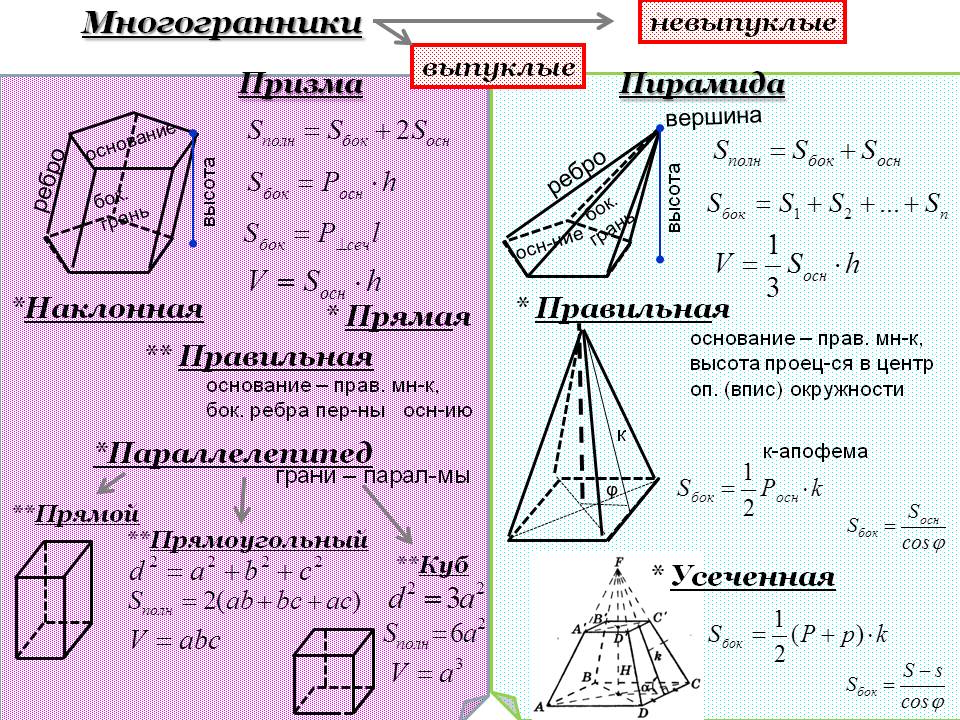
Вот формулы объема и площади поверхности любой пирамиды.
\(V=\frac{1}{3}Bh\)
\(SA=B+\frac{1}{2}ps\)
Для расчета объема и площади поверхности любой пирамиды нам нужно B, который представляет площадь основания, и p, который представляет периметр основания. Важно отметить, что, поскольку основанием пирамиды может быть любой многоугольник, мы будем использовать наши предварительные знания о нахождении площади и периметра различных многоугольников для вычисления объема и площади поверхности пирамиды.
\(V=\frac{1}{3}Bh\)
\(SA=B+\frac{1}{2}ps\)
\(B\) = площадь основания
\( h\) = высота пирамиды
\(p\) = периметр основания
\(s\) = наклонная высота
Рассмотрим пример.
Треугольная пирамида имеет в основании равносторонний треугольник с длинами сторон 6 дюймов и высотой 8 дюймов. Каковы объем и площадь поверхности пирамиды?
Чтобы найти площадь поверхности пирамиды, мы используем формулу \(SA=B+\frac{1}{2}ps\), где \(B\) — площадь основания, \(p\) — периметр основания, а \(s\) — наклонная высота.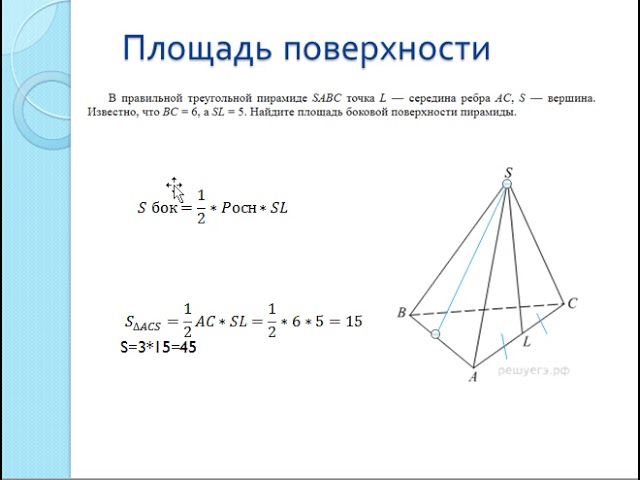 {3}\) 9{3}\)
{3}\) 9{3}\)
Тогда, если мы подставим это в калькулятор, мы получим, что это примерно равно 91,67 кубических сантиметров.
Но когда нам это понадобится в реальной жизни? Что ж, я рад, что вы спросили! Взгляните на следующий пример и попробуйте сами.
Крыша деревянного коттеджа имеет форму пирамиды с квадратным основанием. Длина сторон квадратного основания 22 фута, а высота треугольной грани 14 футов. Питер хочет покрасить крышу своего деревянного коттеджа и должен определить, сколько краски ему нужно купить. Предположим, что 1 пинта краски покрывает 400 квадратных футов. Сколько краски нужно купить Петру?
Крыша коттеджа не включает основание пирамиды. Следовательно, нам нужно только найти площадь 4-х треугольных граней. Это так называемая боковая зона. Таким образом, площадь боковой поверхности равна площади поверхности минус площадь основания. Итак, все, что нам нужно, это:
\(LA=\frac{1}{2}ps\)
Периметр нашего квадрата в 4 раза больше длины стороны.
\(LA=\frac{1}{2}(4\times 22)(14)\)
Что мы можем вставить в калькулятор, чтобы получить: 9{2}\)
Таким образом, нам потребуется 616 квадратных футов для покрытия.
Если 1 пинта краски покрывает 400 квадратных футов, нам нужно разделить 616 на 400, чтобы вычислить, сколько краски нам нужно. Итак:
\(616\div 400=1.54\)
Итак, Петру нужно будет купить 2 пинты краски, чтобы покрыть крышу коттеджа, потому что 1 пинту не хватит, и вы не сможете получить 0,54 пинты. Таким образом, 2 литра краски покроют всю крышу.
Надеюсь, это видео о нахождении объема и площади поверхности пирамиды было полезным! Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Как найти объем пирамиды?
A
Чтобы найти объем пирамиды, мы умножаем площадь ее основания на высоту пирамиды и делим на \(3\). Выразим это произведение формулой \(V=\frac{1}{3}\times B\times h\), где \(B\) — площадь основания пирамиды, а \(h\) это его высота. 2\). 92)\times h\), где \(h\) — высота пирамиды.
2\). 92)\times h\), где \(h\) — высота пирамиды.
Q
Как найти общую площадь поверхности пирамиды?
A
Чтобы найти общую площадь поверхности пирамиды, нам нужно сложить площади каждой стороны, включая основание. Для треугольных пирамид будет три боковых панели; для квадратных и прямоугольных пирамид их будет четыре; и так далее.
Q
Какова формула площади поверхности треугольной пирамиды?
A
Чтобы найти общую площадь поверхности, нам нужно сложить площади основания и трех других сторон. \(SA=B+\frac{1}{2}(P\times l)\), где \(B\) — площадь основания пирамиды, \(P\) — периметр основания, \(l\) — наклонная высота пирамиды. Мы можем найти \(B\), используя формулу \(\frac{1}{2}bh\) для площади треугольника. \(P\) можно легко определить, сложив длины сторон базового треугольника. Наклонную высоту \(l\) можно найти по теореме Пифагора, где \(l\) — длина гипотенузы.
Q
Какова общая площадь поверхности квадратной пирамиды?
A
Чтобы найти общую площадь поверхности квадратной пирамиды, мы суммируем площадь основания с площадью четырех сторон. Поскольку четыре боковые панели идентичны, нам просто нужно найти эту площадь один раз и умножить ее на четыре.
Поскольку четыре боковые панели идентичны, нам просто нужно найти эту площадь один раз и умножить ее на четыре.
\(SA=A_{основание}+(4\times A_{сторона})\)
Пример. Найдите общую площадь поверхности квадратной пирамиды, длина сторон основания которой равна \(8\text{см}\) , а высота равна \(3\text{см}\). Начнем с вычисления площади поверхности основания. 92\).
Практические вопросы
Вопрос №1:
Вычислите площадь поверхности следующей квадратной пирамиды.
95 см 2
100 см 2
105 см 2
110 см 2
SHOW
9000. ANTAR {1}{2}pl\) можно использовать для вычисления площади поверхности квадратной пирамиды.
\(B\) представляет собой площадь основания.
\(p\) представляет собой периметр основания.
\(l\) представляет наклонную высоту.
Когда в формулу подставляются соответствующие значения, \(SA=B+\frac{1}{2}pl\) становится \(SA=25+\frac{1}{2}(20)(8)\) что упрощается до 105 см 2 . Площадь поверхности квадратной пирамиды равна 105 см 2 .
Скрыть ответ
Вопрос №2:
Вычислите площадь поверхности следующей равносторонней треугольной пирамиды.
357 в 2
350 в 2
257 в 2
332 в 2
Покажите ответ
Ответ:
. к формуле квадратной пирамиды. Единственная разница возникает при определении площади базовой формы. Формула \(SA=B+\frac{1}{2}pl\) по-прежнему будет применяться, но B будет рассчитываться путем умножения \(\frac{1}{2}bh\). Это можно подставить в формулу для 92\).
Скрыть ответ
Вопрос №3:
Вычислите объем пирамиды.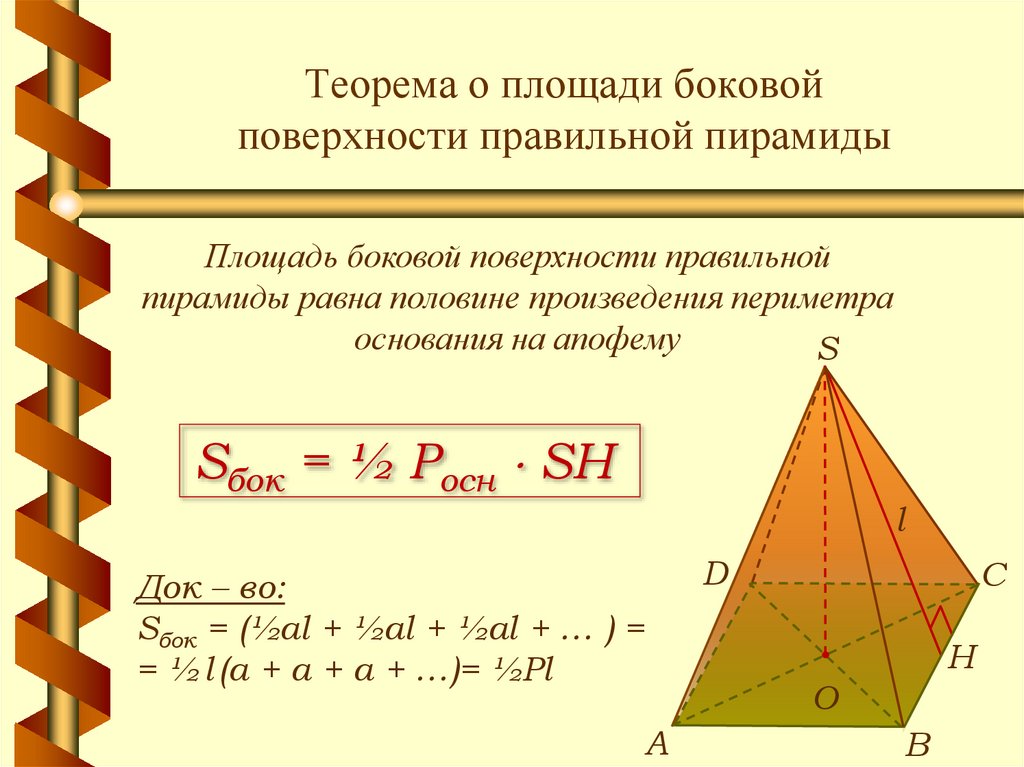
2 670 в 3
3 670 в 3
4,670 в 3
5 670 в 3
Show
908908 96303030303030303030303908 96303908 9085 9000 3908 9000 39. 1}{3}Bh\) можно использовать для вычисления объема пирамиды.B представляет площадь базовой формы.
h представляет собой высоту пирамиды (не высоту наклона). Когда в формулу подставляются соответствующие значения, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(2{,}130)(27)\) что упрощается до \(V=5{,}670\). Объем пирамиды равен 5670 3 .
Скрыть ответ
Вопрос № 4:
У Лео есть треугольная стеклянная пирамида, которую он надеется заполнить небольшим количеством пляжного песка. Во время своего отпуска во Флориде он собирает 6,5 см .3 песка. Треугольник в основании стеклянной пирамиды имеет площадь 5 см 2 , а высота пирамиды 6 см. Если он соберет 6,5 см 3 песка, будет ли пирамида достаточно большой, чтобы вместить весь песок?
Если он соберет 6,5 см 3 песка, будет ли пирамида достаточно большой, чтобы вместить весь песок?
Да, пирамида достаточно большая
Нет, пирамида слишком маленькая.
Показать Ответ
Ответ:
Объем пирамиды с треугольным основанием можно рассчитать по формуле \(V=\frac{1}{3}Bh\), где B — площадь основания треугольника, а h — высота пирамиды. Когда B и h подключены, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(5)(6)\), что упрощает до \(V=10\). Объем пирамиды составляет 10 см 3 , что достаточно для 6,5 см 3 песка.
Скрыть ответ
Вопрос № 5:
Некоторые из первых эскизов парашютов Леонардо да Винчи имели форму пирамид с квадратным основанием. Для конструкции парашюта с прямоугольным основанием, длиной сторон шести футов и восьми футов и высотой семь футов, сколько воздуха будет захвачено пирамидой после ее полного развертывания?
112 FT 3
109 FT 3
115 FT 3
118 FT 3
SHOW ANSTER
9000 9000. 6. 6. 6. 6. 1}{3}Bh\) можно использовать для вычисления объема пирамиды. B представляет площадь основания фигуры, а h представляет высоту пирамиды. Когда в формулу подставляются соответствующие значения, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(48)(7)\), что упрощается до \ (V=112\). Объем полностью развернутого парашюта составит 112 футов 9 дюймов.0329 3 .
6. 6. 6. 6. 1}{3}Bh\) можно использовать для вычисления объема пирамиды. B представляет площадь основания фигуры, а h представляет высоту пирамиды. Когда в формулу подставляются соответствующие значения, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(48)(7)\), что упрощается до \ (V=112\). Объем полностью развернутого парашюта составит 112 футов 9 дюймов.0329 3 .Скрыть ответ
Площадь поверхности пирамиды – формула, определение и примеры
Площадь поверхности пирамиды получается сложением площадей всех ее граней. Пирамида — это трехмерная фигура, основанием которой является многоугольник, а боковые грани (треугольники) сходятся в точке, называемой вершиной (или вершиной). Перпендикулярное расстояние от вершины до центра основания называется высотой или высотой пирамиды. Длина перпендикуляра, проведенного от вершины к основанию треугольника (боковой грани), называется «наклонной высотой». Давайте узнаем больше о площади поверхности пирамиды вместе с ее формулой, несколькими решенными примерами и практическими вопросами.
Давайте узнаем больше о площади поверхности пирамиды вместе с ее формулой, несколькими решенными примерами и практическими вопросами.
| 1. | Какова площадь поверхности пирамиды? |
| 2. | Площадь поверхности пирамиды Формула |
| 3. | Доказательство площади поверхности пирамиды Формула |
| 4. | Часто задаваемые вопросы о площади поверхности пирамиды |
Какова площадь поверхности пирамиды?
площадь поверхности пирамиды является мерой общей площади, занимаемой всеми ее гранями. Посмотрите на приведенную ниже пирамиду, чтобы увидеть все ее грани и другие части, такие как вершина, высота, наклонная высота и основание.
Площадь поверхности пирамиды представляет собой сумму площадей ее граней и, следовательно, измеряется в квадратных единицах, таких как м 2 , см 2 , дюймы 2 , футы 2 и т. д. Пирамида имеет два типа площадей поверхности: площадь боковой поверхности (LSA) и общая площадь поверхности (TSA).
д. Пирамида имеет два типа площадей поверхности: площадь боковой поверхности (LSA) и общая площадь поверхности (TSA).
- Площадь боковой поверхности (LSA) пирамиды = сумма площадей боковых граней (треугольников) пирамиды.
- Общая площадь поверхности (TSA) пирамиды = LSA пирамиды + площадь основания
В целом, площадь поверхности пирамиды без каких-либо указаний относится к общей площади поверхности пирамиды.
Площадь поверхности пирамиды Формула
Площадь поверхности пирамиды можно вычислить, найдя площади каждой из ее граней и сложив их. Если пирамида правильная (т. Е. Пирамида, основание которой представляет собой правильный многоугольник, а высота проходит через центр основания), есть некоторые специальные формулы для нахождения площади боковой поверхности и общей площади поверхности. Рассмотрим правильную пирамиду, периметр основания которой равен «P», площадь основания — «B», а наклонная высота (высота каждого треугольника) — «l». Затем
Затем
- Площадь боковой поверхности пирамиды (LSA) = (1/2) Pl
- Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
Обратите внимание, что здесь мы будем использовать формулы площади полигонов для расчета базовых площадей. Теперь давайте посмотрим, как вывести формулы площади поверхности пирамиды.
Доказательство площади поверхности пирамиды Формула
Площадь поверхности пирамиды включает периметр и наклонную высоту. Давайте разберемся с формулами LSA и TSA пирамиды на примере конкретной пирамиды. Рассмотрим квадратную пирамиду, длина основания которой равна «а», а высота наклона равна «l».
Затем,
- Площадь основания (площадь квадрата) пирамиды, B = a 2
- Периметр основания (периметр квадрата) пирамиды равен, P = 4a
- Площадь каждой из боковых граней (площадь треугольника) = (1/2) × основание × высота = (1/2) × (a) × l
Следовательно, сумма всех боковых граней (сумма всех 4-х треугольных граней) = 4 [(1/2) × (a) × l] = (1/2) × (4a) × l = (1/2 ) пл. (Здесь мы заменили 4a на P, который представляет его периметр.)
(Здесь мы заменили 4a на P, который представляет его периметр.)
Следовательно, площадь боковой поверхности пирамиды (LSA) = (1/2) Pl
Мы знаем, что общая площадь поверхности пирамиды (TSA) получается путем сложения площадей основания и боковой поверхности. Таким образом,
Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
Используя эти две формулы, мы можем вывести формулы площади поверхности различных типов пирамид.
Площадь поверхности пирамиды с указанием высоты
Площадь поверхности пирамиды можно рассчитать, если известна ее высота. Обратите внимание на приведенный ниже рисунок, который показывает, что треугольник, образованный половиной длины стороны основания (a/2), наклонной высоты (l) и высоты (h), является прямоугольным треугольником. Следовательно, мы можем применить теорему Пифагора и узнать наклонную высоту, если известны высота и длина основания. Таким образом, л 2 = h 2 + (a/2) 2
Таким образом, мы можем рассчитать наклонную высоту по формуле l 2 = h 2 + (a/29) 2 90 . Теперь, когда у нас есть наклонная высота, длина основания и высота, мы можем найти площадь поверхности пирамиды, используя формулу Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
Теперь, когда у нас есть наклонная высота, длина основания и высота, мы можем найти площадь поверхности пирамиды, используя формулу Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
☛ Связанные статьи
- Площадь поверхности прямоугольного параллелепипеда
- Площадь поверхности цилиндра
- Площадь поверхности призмы
- Площадь поверхности конуса
- Площадь поверхности сферы
- Разница между площадью и площадью поверхности
- Формулы площади поверхности
- Площадь поверхности куба
Примеры площади поверхности пирамиды
Пример 1: Рассчитайте площадь боковой поверхности квадратной пирамиды, если длина стороны основания составляет 14 дюймов, а наклонная высота пирамиды составляет 20 дюймов.
Решение:
Длина стороны основания, a = 14 дюймов
Тогда периметр основания (квадрата) равен P = 4a = 4(14) = 56 дюймов.

Наклонная высота, l = 20 дюймов
Площадь боковой поверхности квадратной пирамиды,
Площадь боковой поверхности (LSA) = (1/2) Pl
= (1/2) × (56) × 20
= 560 в 2
Следовательно, площадь боковой поверхности данной пирамиды равна 560 в 2 .
Пример 2: Укажите истинное или ложное значение.
а.) Площадь поверхности любой пирамиды можно вычислить, найдя площади каждой из ее граней и сложив их.
b.) Общая площадь поверхности (TSA) пирамиды = площадь боковой поверхности (LSA) пирамиды
Решение:
a.) Действительно, площадь поверхности любой пирамиды можно рассчитать, найдя области каждой из его граней и их сложение.
b.) Неверно, общая площадь поверхности (TSA) пирамиды = площадь боковой поверхности (LSA) пирамиды + площадь основания
Пример 3: Рассчитайте общую площадь поверхности квадратной пирамиды, если сторона основания равна 14 дюймам, а высота пирамиды равна 24 дюймам.

Решение:
Дана сторона основания a = 14 дюймов, а высота пирамиды h = 24 дюйма.
Пусть его наклонная высота будет ‘l’.
По теореме Пифагора, l 2 = (a/2) 2 + h 2
l 2 = (14/2) 2 + 24 2 = 625
Таким образом, l = 25 дюймов.
Периметр основания равен P = 4a = 4(14) = 56 дюймов.
Базовая площадь, B = 14 2 = 196 квадратных дюймов.
Общая площадь поверхности квадратной пирамиды равна,
TSA = (1/2) Pl + B, где B = 196, P = 56, l = 25 25] + 196 = 896 квадратных дюймов
Следовательно, TSA данной пирамиды = 896 квадратных дюймов.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности пирамиды
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности пирамиды
Что такое определение площади поверхности пирамиды?
Площадь поверхности пирамиды определяется как сумма площадей всех ее граней. Существует два типа площадей поверхности: общая площадь поверхности (TSA), представляющая собой сумму площадей всех граней, и площадь боковой поверхности (LSA), представляющая собой сумму площадей сторон. лица.
Существует два типа площадей поверхности: общая площадь поверхности (TSA), представляющая собой сумму площадей всех граней, и площадь боковой поверхности (LSA), представляющая собой сумму площадей сторон. лица.
Какова общая площадь поверхности пирамиды?
Общая площадь поверхности пирамиды получается путем сложения площадей всех ее граней (и основания, и боковых граней). Общая площадь поверхности пирамиды, периметр основания которой равен «P», площадь основания — «B», а наклонная высота — «l», рассчитывается по формуле TSA = (1/2) Pl + B.
Какова площадь боковой поверхности пирамиды?
Площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней (треугольников). Площадь боковой поверхности пирамиды рассчитывается по формуле LSA = (1/2) Pl, где P — периметр основания, а l — наклонная высота.
Какова формула площади поверхности пирамиды?
Существует два типа площадей поверхности пирамиды: общая площадь поверхности и площадь боковой поверхности.
- Общая площадь поверхности = (1/2) Pl + B
- Площадь боковой поверхности = (1/2) Pl
, где «B» — площадь основания, «l» — высота наклона, а «P» — периметр основания.
Как найти площадь поверхности пирамиды с наклонной высотой?
Формула, используемая для определения площади поверхности пирамиды, может быть рассчитана с использованием наклонной высоты. Его общую площадь поверхности можно рассчитать по формуле (1/2) Pl + B. Рассмотрим пирамиду, высота наклона которой равна «l», периметр основания равен «P», а площадь основания равна «B». Площадь основания можно найти, применяя формулы площади многоугольника.
Как найти площадь поверхности пирамиды с высотой (или высотой)?
Площадь поверхности пирамиды можно рассчитать, если известна высота. Рассмотрим пирамиду, основание которой представляет собой правильный многоугольник со стороной «а», наклонная высота пирамиды равна «l», а высота равна «h».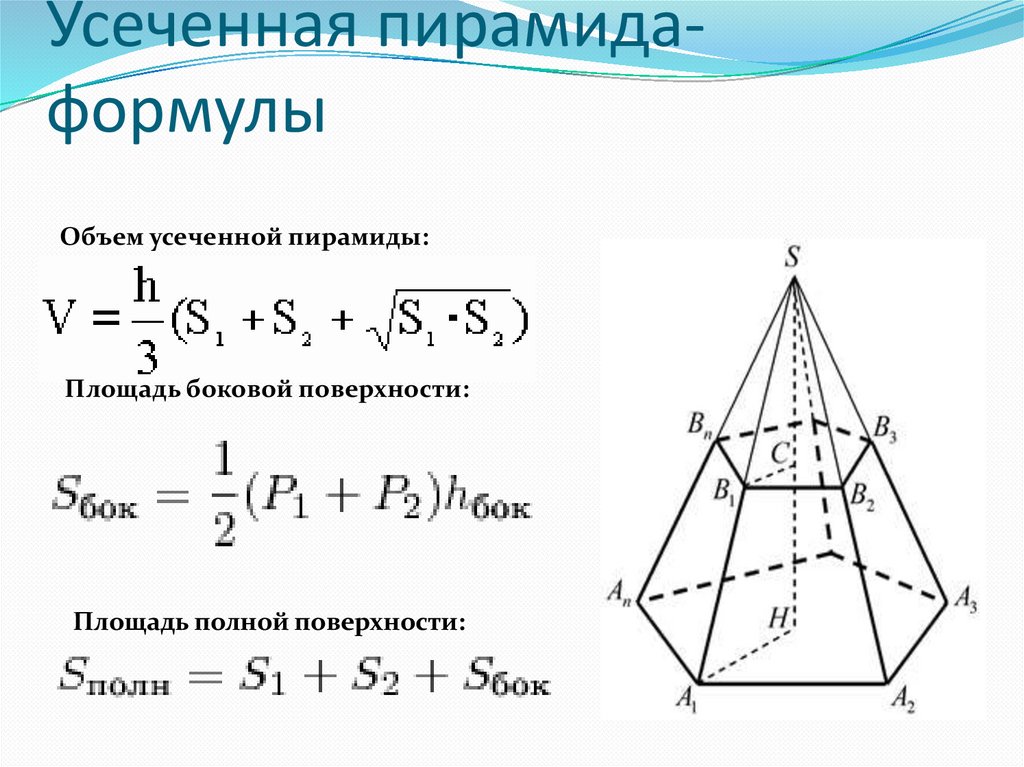

Leave A Comment