как найти через высоту, формула с доказательством
Содержание:
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Содержание
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Окружность, вписанная в треугольник — как найти радиус
Определение
Вписанной в треугольник окружностью
В таком случае грани треугольника представляют собой касательные к этой окружности. Сама геометрическая фигура с тремя углами считается описанной вокруг рассматриваемой окружности.
Источник: people-ask.ruСвойства вписанной в треугольник окружности
Окружность, которую вписали в треугольник, обладает определенными свойствами. Основные из них можно записать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Центр окружности, которую вписали в треугольник, совпадает с точкой пересечения биссектрис этой геометрической фигуры.
- Во внутреннее пространство любого треугольника можно вписать лишь одну окружность.
- Формула радиуса окружности, который вписали во многоугольник с тремя углами, будет иметь такой вид:
В представленной формуле радиуса окружности использованы следующие величины:
- S – является площадью треугольника;
- р – представляет собой полупериметр геометрической фигуры;
- a, b, c – являются сторонами треугольника.
Перечисленные свойства необходимо доказать.
Первое свойство
Требуется доказать, что центр окружности, которую вписали в фигуру с тремя углами, совпадает с точкой пересечения биссектрис.
Доказательство построено в несколько этапов:
- Необходимо опустить из центральной точки окружности перпендикулярные прямые OL, OK и OM, которые опускаются на стороны треугольника АВС. Из вершин треугольника следует провести прямые, соединяющие их с центром фигуры OA, OC и OB.
- Далее можно рассмотреть пару треугольников AOM и AOK. Можно отметить, что они являются прямоугольными, так как OM и OK являются перпендикулярами к сторонам AC и AB. Гипотенуза OA является общей для пары этих фигур.
- Исходя из того, что касательная к окружности является перпендикуляром к радиусу, который проведен в точку касания, согласно свойству касательной к окружности, то катеты OМ и OК представляют собой радиусы окружности и, следовательно, равны.
- Согласно полученным утверждениям, можно сделать вывод о равенстве прямоугольных треугольников AOМ и AOК по гипотенузе и катету. Таким образом, углы OAМ и OAК тоже равны. Получается, что OA является биссектрисой угла BAC.
- Аналогично можно доказать, что OC является биссектрисой угла ACB, а OB – биссектрисой угла ABC.
- Таким образом, биссектрисы треугольника совпадают в одной точке, которая представляет собой центр вписанной окружности.
Данное свойство окружности доказано.
Второе свойство
Необходимо представить доказательства свойства окружности, согласно которому в любой треугольник можно вписать окружность, причем только одну.
Доказательство состоит из нескольких этапов:
- Окружность получится вписать в треугольник в том случае, когда существует точка, удаленная на равные расстояния от сторон геометрической фигуры.
- Можно построить пару биссектрис ОА и ОС. Из точки, в которой они пересекаются, необходимо опустить перпендикулярные прямые OK, OL и OM ко всем граням многоугольника с тремя углами ABC.
- Затем следует рассмотреть пару треугольников AOK и AOM.
- Эти фигуры обладают общей гипотенузой АО. Углы OAK и OAM равны, так как OA является биссектрисой угла KAM. Углы OKA и OMA прямые, то есть также равны, так как OK и OM являются перпендикулярами к сторонам AB и AC.
- Исходя из того, что две пары углов равны, можно сделать вывод о равенстве третьей пары AOM и AOK.
- Таким образом, получилось подтвердить равенство треугольников AOK и AOM по стороне AO и двум углам, которые к ней прилегают.
- Удалось определить равенство сторон ОМ и ОК, то есть они удалены на одинаковое расстояние от сторон геометрической фигуры АС и АВ.
- Аналогично можно доказать, что OM и OL равны, то есть равноудалены от граней AC и BC.
- Таким образом, точка равноудалена от сторон треугольника, что делает ее центром окружности, которая вписана в этот многоугольник.
- Аналогичным способом можно определить точку во внутреннем пространстве любой геометрической фигуры с тремя углами, которая будет удалена на равные расстояния от его сторон, и представляет собой центр окружности, вписанной в этот треугольник.
- Исходя из вышесказанного, можно сделать вывод о том, что в любой треугольник можно вписать окружность.
- Необходимо заметить, что центральная точка окружности совпадает с точкой, в которой пересекаются биссектрисы треугольника.
- Можно допустить ситуацию, при которой в геометрическую фигуру с тремя углами можно вписать две и более окружности.
- Необходимо провести три прямые из вершин геометрической фигуры к центральной точке окружности, вписанной в нее, и опустить перпендикулярные прямые к каждой грани треугольника. Таким образом, будет доказано, что рассматриваемая окружность лежит на пересечении биссектрис треугольника, согласно доказательству ее первого свойства.
- Получим совпадение центральной точки окружности и центра первой окружности, которая уже была вписана в этот треугольник, а ее радиус соответствует перпендикуляру, опущенному на сторону треугольника так же, как и в первом случае. Можно сделать вывод о совпадении этих окружностей.
- Аналогично любая другая окружность, вписанная в геометрическую фигуру с тремя углами, будет совпадать с первой окружностью.
- Таким образом, в треугольник получается вписать лишь одну окружность.
Можно сделать вывод о совпадении этих окружностей.Свойство доказано.
Третье свойство
Требуется доказать, что радиус окружности, которую вписали в геометрическую фигуру с тремя углами, представляет собой отношение площади треугольника к полупериметру:
Источник: people-ask.ruКроме того, необходимо представить доказательства следующему равенству:
Источник: people-ask.ruДоказательство:
Источник: people-ask.ru- Следует рассмотреть произвольный треугольник АВС, стороны которого соответствуют a, b и c. Для расчета полупериметра данного треугольника целесообразно использовать формулу:
- Центральная точка окружности совпадает с точкой пересечения биссектрис геометрической фигуры с тремя углами. Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.
Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.- Исходя из того, что площадь какого-либо треугольника представляет собой половину произведения его основания на высоту, а высота треугольников AOC, COB, BOA рассчитывается, как радиус окружности r, то площади треугольников AOC, COB и BOA можно определить по формулам:
- Далее необходимо представить площадь S геометрической фигуры АВС, как сумму площадей нескольких треугольников:
- Следует отметить, что второй множитель является полупериметром геометрической фигуры с тремя углами АВС, что можно записать в виде равенства:
ru- Таким образом, доказано равенство радиуса вписанной окружности и отношения площади треугольника к полупериметру.
- Можно записать формулу Герона, смысл которой заключается в следующем: площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c)
- Далее следует преобразовать формулу для расчета радиуса:
Свойство окружности доказано.
Формулы вычисления радиуса вписанной окружности
Параметры окружности, которую вписали в геометрическую фигуру с тремя углами, можно рассчитать с помощью стандартных формул. Радиус окружности будет определен в зависимости от типа треугольника.
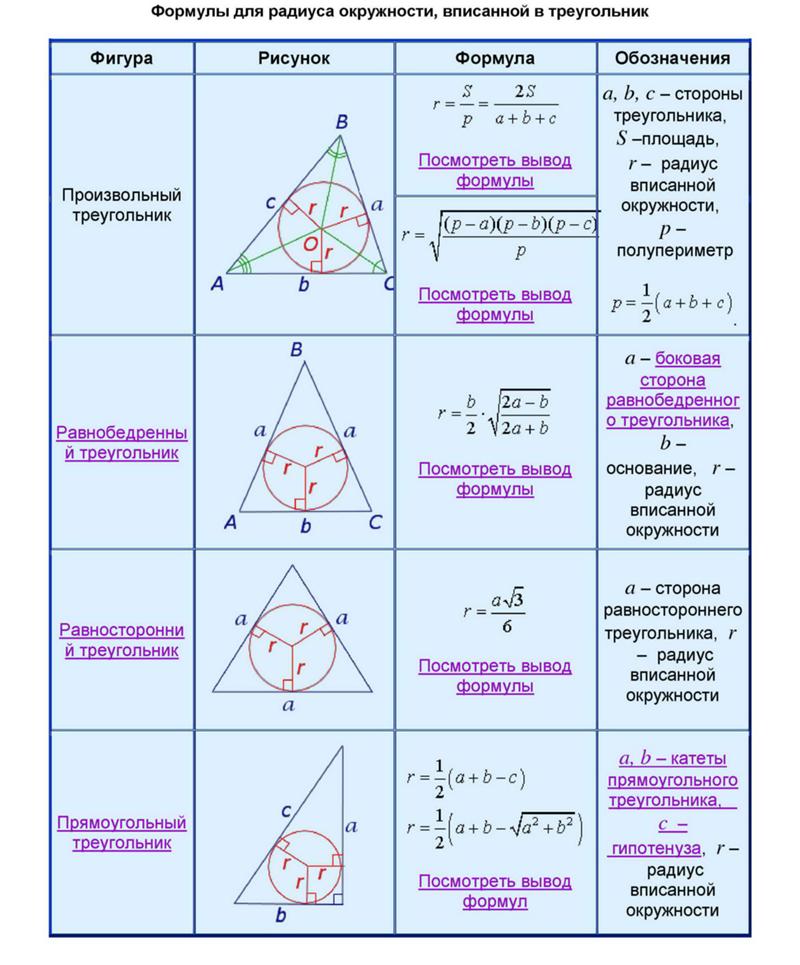
Произвольный треугольник
Определить радиус окружности, которая вписана в какой-либо треугольник, можно, как удвоенную площадь треугольника, поделенную на его периметр.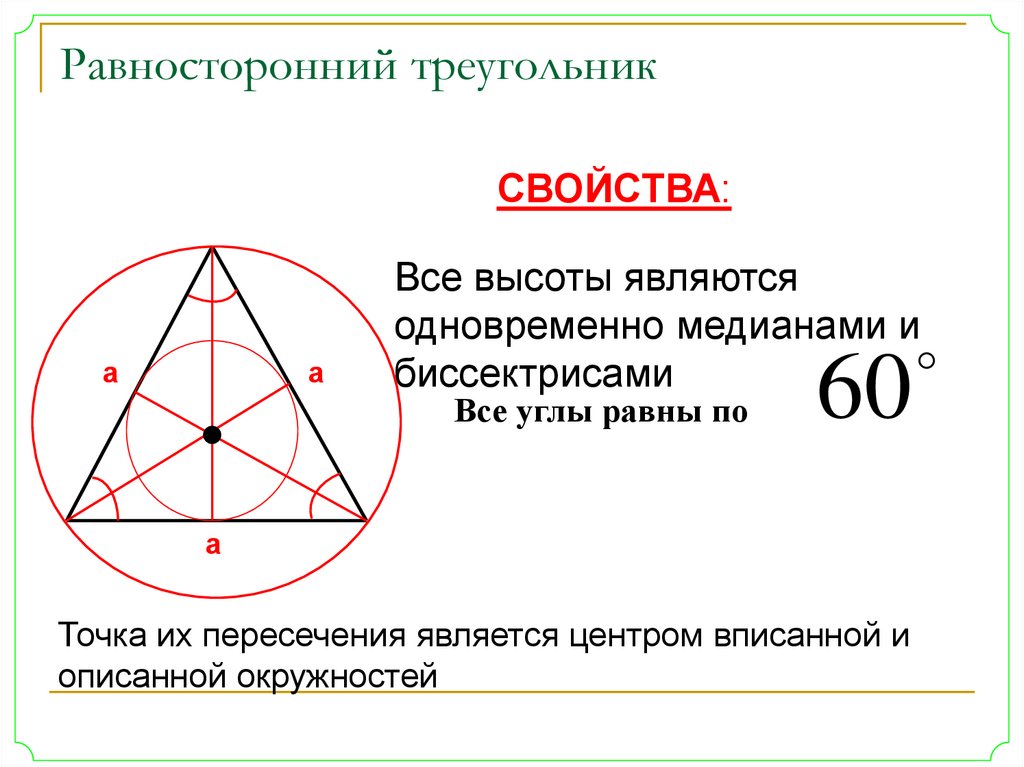
В данном случае, a, b, c являются сторонами геометрической фигуры с тремя углами, S – ее площадь.
Прямоугольный треугольник
Радиус окружности, которую вписали в треугольник с прямым углом, представляет собой дробь с числителем в виде суммы катетов за минусом гипотезы и знаменателем, равным числу 2.
Источник: microexcel.ruВ формуле a и b являются катетами, c – гипотенузой треугольника.
Равнобедренный треугольник
Радиус окружности, которая вписана в равнобедренный треугольник, определяют по формуле:
Источник: microexcel.ruВ этом случае a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Расчет радиуса окружности, которая вписана в правильный или равносторонний треугольник, выполняют по формуле:
Источник: microexcel.ruгде a – сторона геометрической фигуры с тремя углами.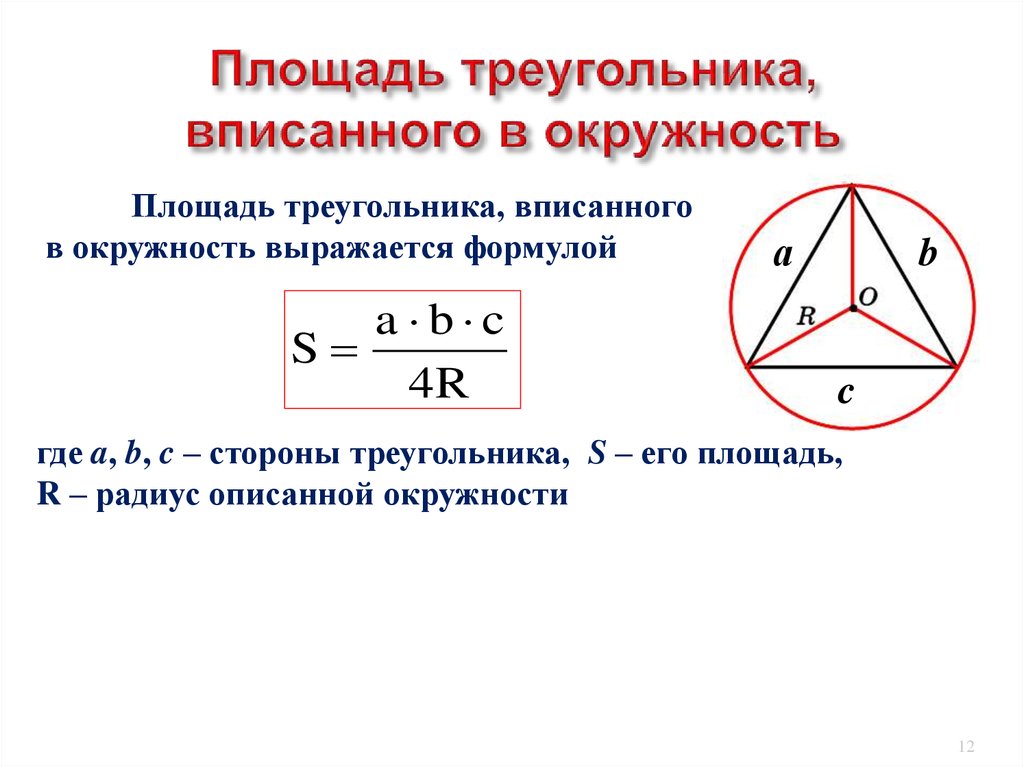
Как найти через высоту или стороны, примеры решения
Задача 1
Имеется геометрическая фигура с тремя углами, стороны которой составляют 5, 7 и 10 см. Требуется определить радиус окружности, которая вписана в этот треугольник.
Решение
В первую очередь необходимо определить, какова площадь треугольника. Для этого можно воспользоваться формулой Герона:
Источник: microexcel.ruЗатем применим формулу для расчета радиуса круга:
Источник: microexcel.ruОтвет: радиус окружности составляет примерно 1,48 см.
Задача 2
Необходимо рассчитать радиус окружности, которая вписана в равнобедренный треугольник. Боковые стороны геометрической фигуры составляют 16 см, а основание равно 7 см.
Решение
Следует использовать подходящую формулу для расчета радиуса, подставив в нее известные величины:
Источник: microexcel.ruОтвет: радиус окружности примерно равен 2,8 см.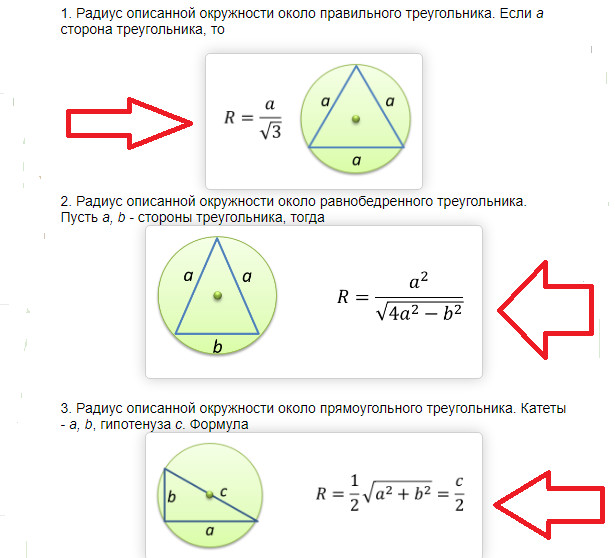
Насколько полезной была для вас статья?
Рейтинг: 3.50 (Голосов: 2)
Поиск по содержимому
решение / Справочник :: Бингоскул
Площадь круга, вписанного в равносторонний треугольник: решениедобавить в закладки удалить из закладок
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
Окружность, касающаяся всех сторон треугольника, называется вписанной в него, а сам 3-угольник – описанным. Перпендикуляры EO, DO, FO, берущие начало в центре сторон треугольника, пересекаются в общей точке.
Последняя находится на одинаковом удалении от них. Отсюда следует, что перпендикуляры имеют одинаковую длину EO = DO = FO.
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr2.
a, где:
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
.
В задачах могут давать длину сторон, тогда
Выражение для равностороннего треугольника можно записать в виде так как 3-угольник равносторонний. С иной стороны – это полупериметр рассматриваемой геометрической фигуры – p.
Зная это, формула записывается в виде: S = r * p.
Задачи
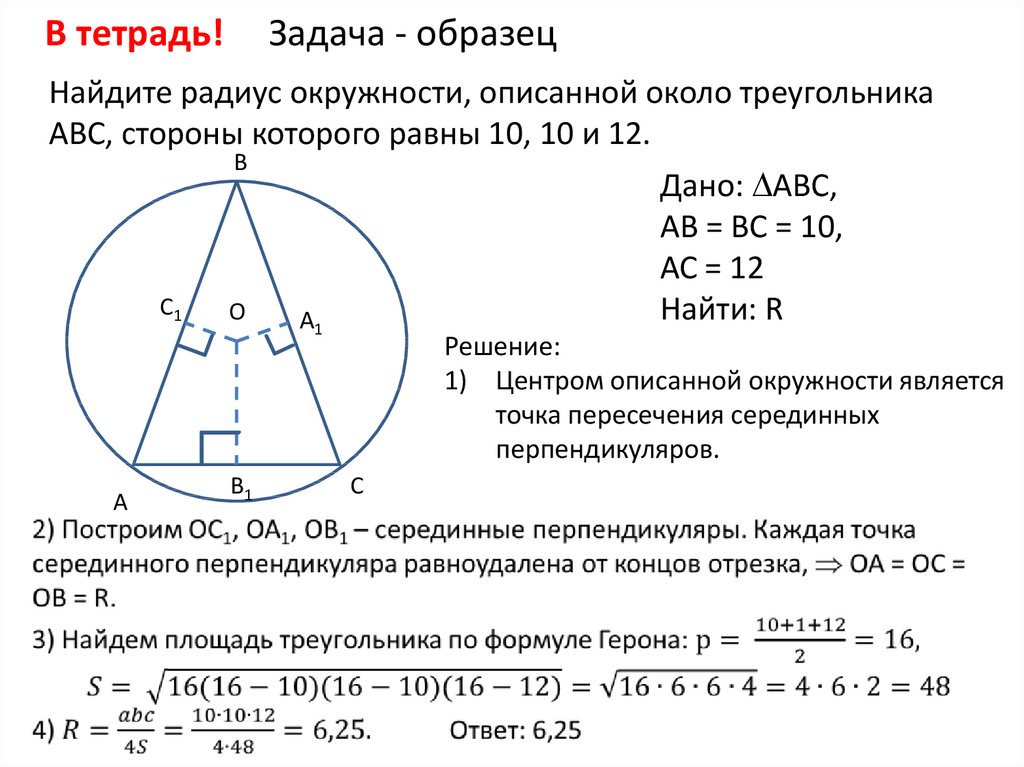
Найдите площадь круга, вписанного в равносторонний треугольник, если известна его сторона: a = 12 см.
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
Для вычислений необходимо найти радиус r.
Известно, что он определяется по формуле:
После преобразований выражение упрощается до .
– полупериметр.
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
p = 30/2 = 15 см.
Проверим по упрощённой формуле:
Всё известно, финальный этап.
Поделитесь в социальных сетях:
14 октября 2021, 20:39
Геометрия
Could not load xLike class!
Калькулятор формул для уравнений равностороннего треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.
| Периметр | |
| Semiperimeter | |
| Area | |
| Area | |
| Base | |
| Height | |
| Angle Bisector of side a | |
| Angle Bisector of сторона b | |
| Биссектриса угла стороны c | |
| Медиана стороны a | |
| Медиана стороны b0018 | |
| Median of side c | |
| Altitude of side a | |
| Altitude of side b | |
| Altitude of side c | |
| Circumscribed Circle Radius | |
| Радиус вписанной окружности |
Закон косинусов
| Длина стороны a | |
Эквиласторный треугольник:
Все три стороны имеют одинаковую длину
.
Right Triangle:
One angle is equal to 90 degrees
Right Triangle Equations
| Pythagorean Theorem | ||
| Периметр | ||
| Полупериметр | ||
| Площадь | ||
| Altitude of a | ||
| Altitude of b | ||
| Altitude of c | ||
| Angle Bisector of a | ||
| Angle Bisector of b | ||
| Angle Бискектор C | ||
| Медиана | ||
| Медиана B | ||
| Медиан из C | ||
| Median of C | из C | 9|
. 0018 | Inscribed Circle Radius | |
| Circumscribed Circle Radius |
Isosceles Triangle:
Two sides have equal length
Two angles are equal
Isosceles Triangle Equations
| Perimeter | |
| Полупериметр | |
| Площадь | |
| Высота сторон а и с | |
| Altitude of side b | |
| Median of sides a and c | |
| Median of side b | |
| Angle Bisector of sides a and c | |
| Angle Bisector стороны b | |
| Радиус описанной окружности | |
| Радиус вписанной окружности |
9017 P
6
Справочник — Книги: 1) Макс А.
Собель и Норберт Лернер. 1991. Предварительная математика. Прентис Холл. 4-е изд.
В равносторонний треугольник вписана окружность. Найдите периметр этого треугольника, если длина его окружности равна 1 см.
РЕШЕНИЕ: В равносторонний треугольник вписана окружность. Найдите периметр этого треугольника, если длина его окружности равна 1 см.Алгебра -> Настраиваемые средства решения задач Word -> Разное -> РЕШЕНИЕ: В равносторонний треугольник вписана окружность. Найдите периметр этого треугольника, если длина его окружности равна 1 см. Войти
|
Найдите периметр этого треугольника, если длина его окружности равна 1 см. 
Leave A Comment