Внутреннее сопротивление источника тока — формула
Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.
Зависимость напряжения между его выводами от тока источника
Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.
У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.
Измерение сопротивления петли фаза-нуль
Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза».
Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.
Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.
На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль.
- заменяются участки провода, не отвечающие требованиям по диаметру сечения;
- перекручиваются болтовые соединения с обязательной установкой врезных шайб;
- вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
- при необходимости в контур защитного заземления добавляются дополнительные элементы;
- исключается последовательное подключение корпусов устройств к общей шине заземления.
После выполнения комплекса мероприятий измерения проводятся повторно.
Проверка сопротивления петли «фаза – ноль»
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.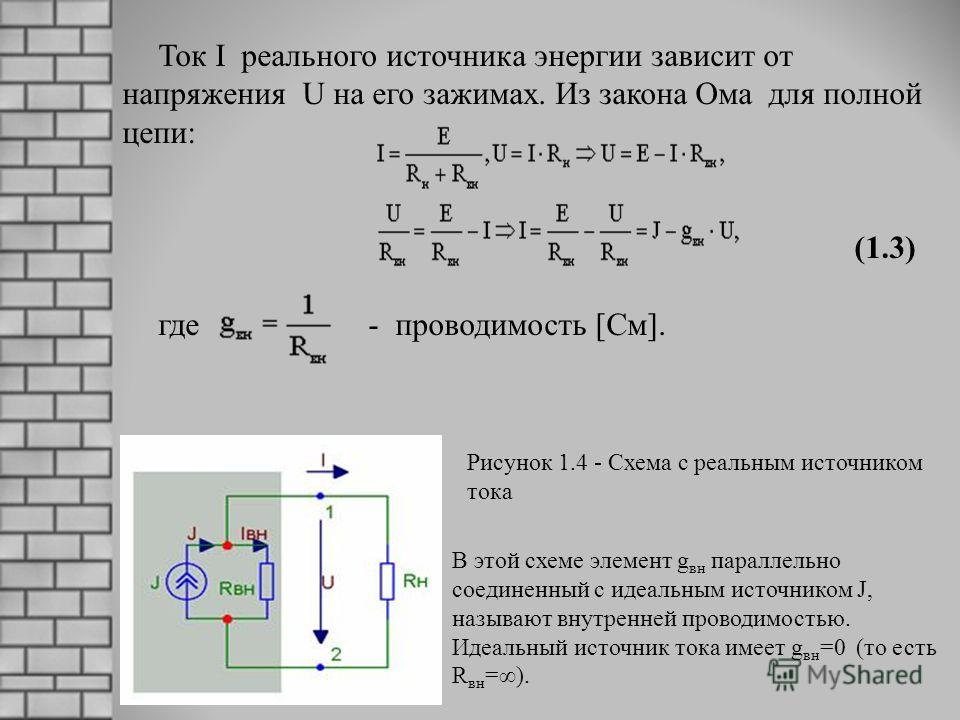
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
I = ε / (r + R).
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
r = (ε / I) – R,
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода.
Внутреннее сопротивление источника тока
Малое внутреннее сопротивление
Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.
Реактивное внутреннее сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Большое внутреннее сопротивление
Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала.
Внутреннее сопротивление и импеданс
Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.
Слагаемые полного сопротивления – импеданса
Двухполюсник и его эквивалентная схема
Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:
- цепи, содержащие источник тока или напряжения;
- двухполюсники, не являющиеся источниками.
Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.
Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.
Влияние внутреннего сопротивления на свойства двухполюсника
Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:
PR = E2/(r+R)2*R,
где:
- E – напряжение ЭДС;
- R – сопротивление нагрузки;
- r – активное внутреннее сопротивление двухполюсника.
Формула применима к двухполюсникам, не отдающим энергию.
К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.
Разрядная ёмкость автомобильного аккумулятора
Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Видео
Закон Ома для полной цепи
1. Источник тока
При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).
В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2.
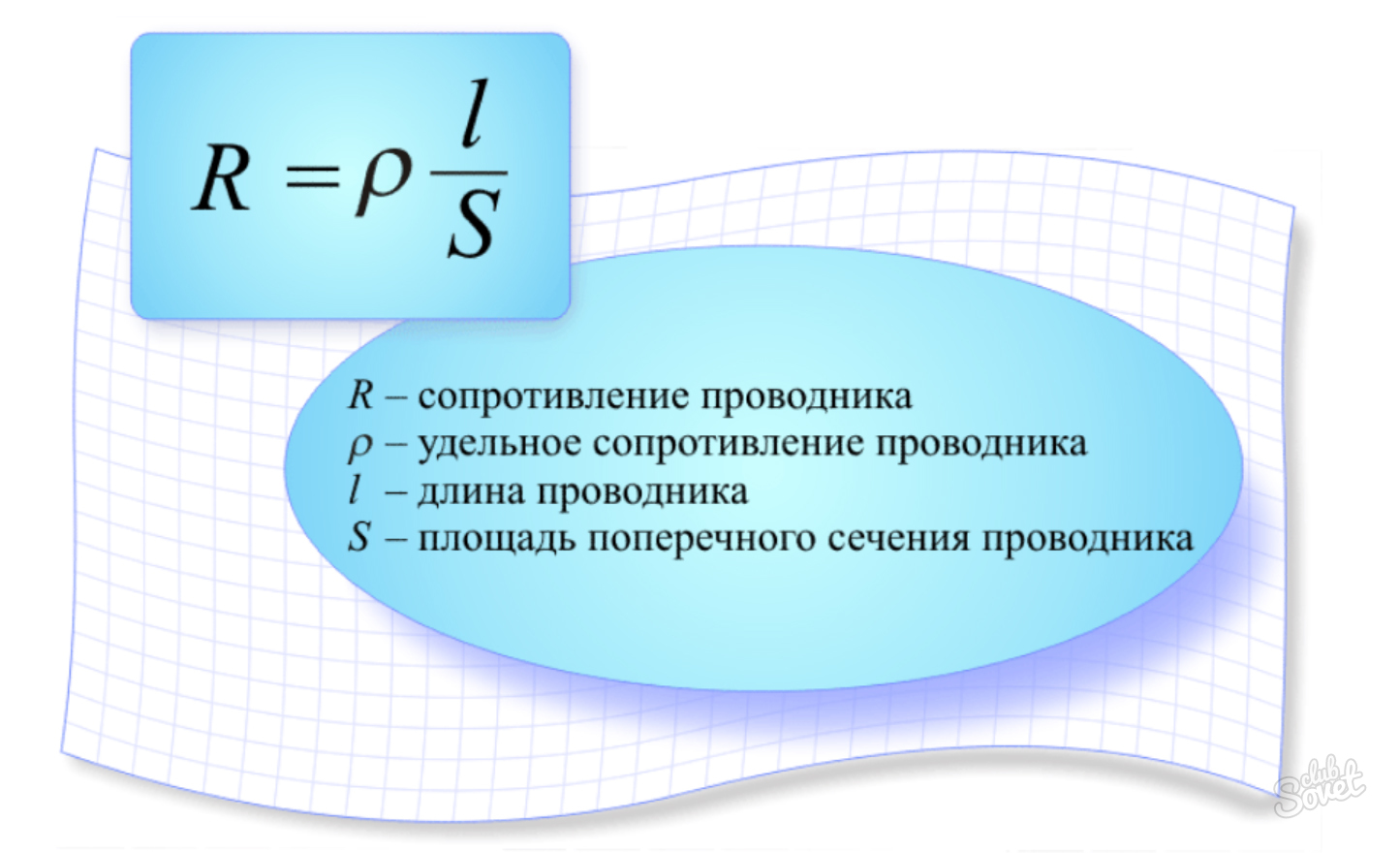 Закон Ома для полной цепи
Закон Ома для полной цепиЕсли сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
а внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
где r – сопротивление источника, которое называют его внутренним сопротивлением.
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) – (5) следует:
I = ξ / (R + r). (6)
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?
? 3.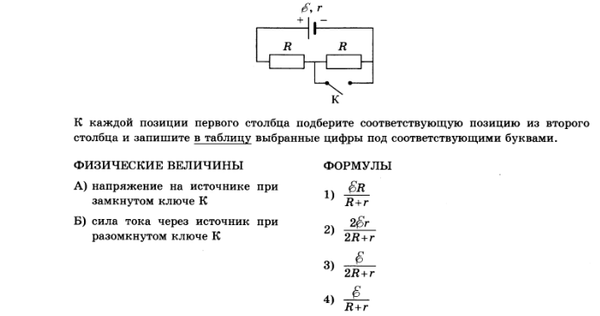 При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ – Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.
а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5.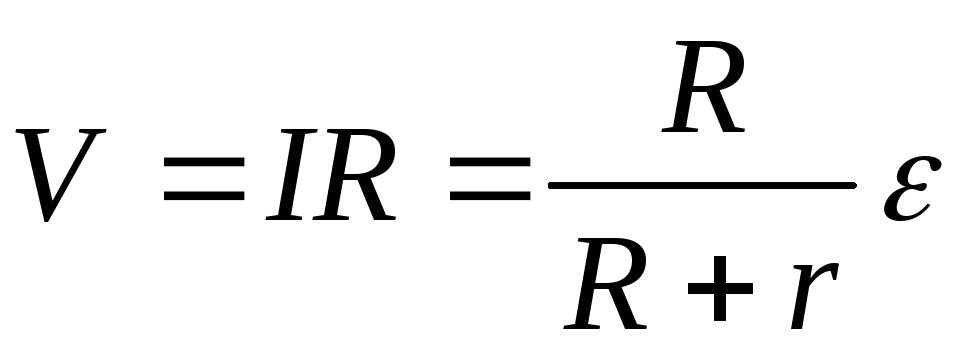 Покажите, что сила тока короткого замыкания выражается формулой
Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
получаем для отношения полезной работы к работе сторонних сил:
η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).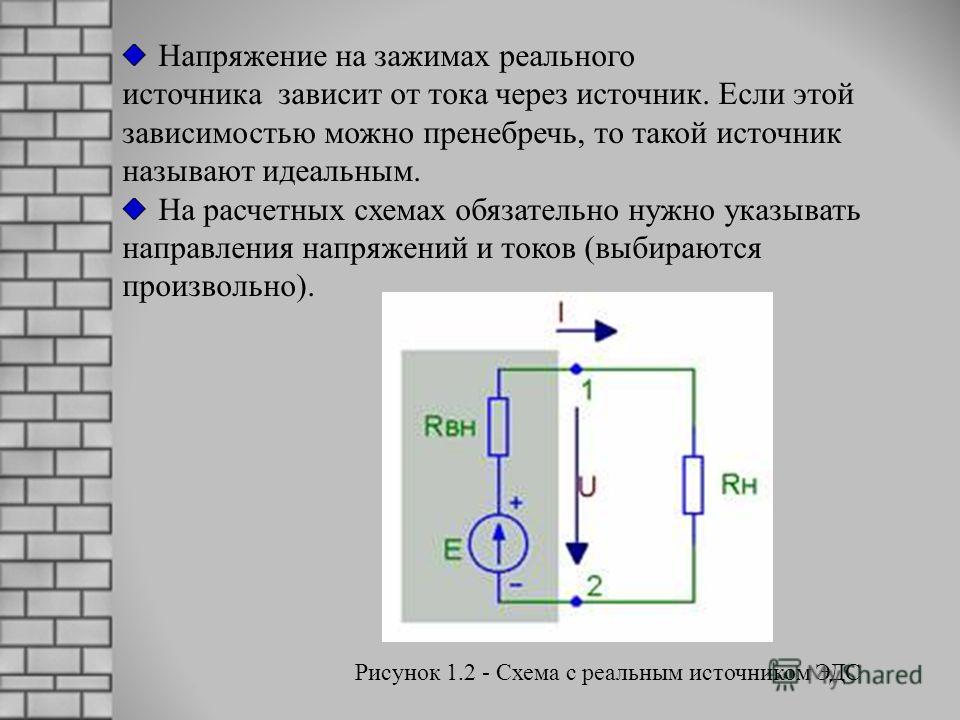
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
ЭДС и напряжение. Внутреннее сопротивление источников питания.
РадиоКот >Обучалка >Аналоговая техника >Основы электроники >ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Несмотря на то, что многие из посетителей этого сайта являются продвинутыми радиокотами
и уже успешно занимаются программированием и конструированием, существуют еще отдельные
котята, у которых возникают иногда вопросы, связанные с азами радио- (или даже электро) техники.
Итак, вернемся к азам… По азу- я всех везу! Ой! Это из другой оперы…
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили.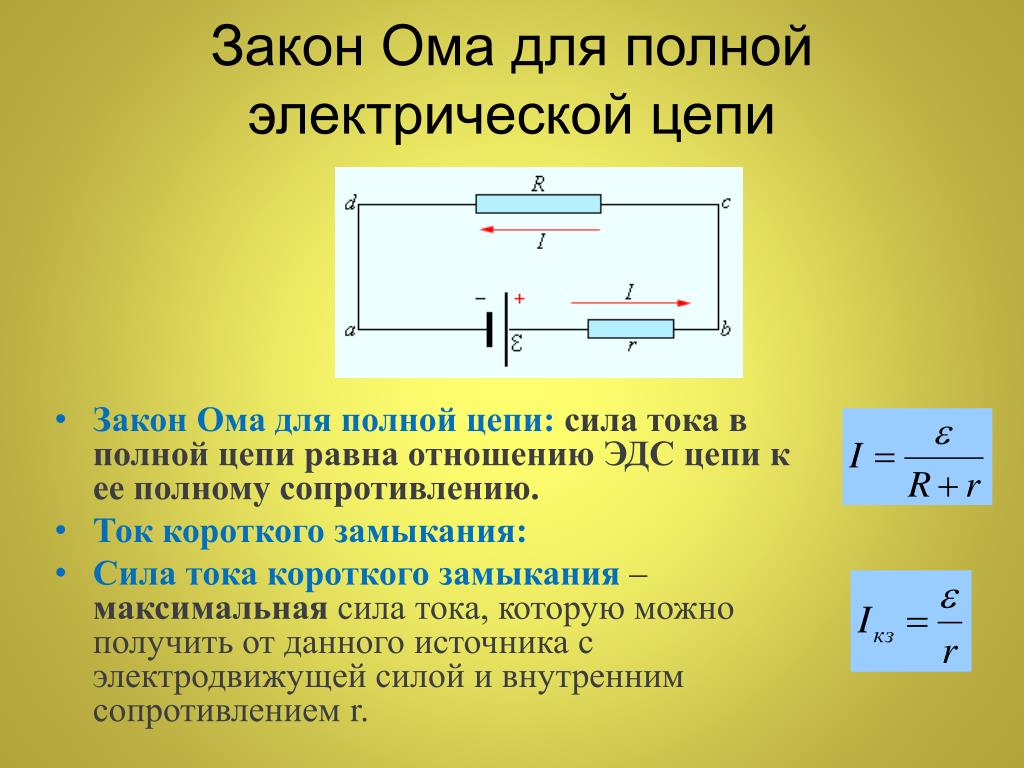 Поговорим еще раз — с несколько иной стороны.
Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (
электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Поговорим еще раз — с несколько иной стороны.
Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (
электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:
I=E/R
где:
I — сила тока,
E — Э.Д.С. — электродвижущая сила
R — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.
Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято
считать бесконечно малым.
В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):
I=U/R
где:
U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с.
и включенного последовательно с ним некоего резистора, который будет олицетворять собой
внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр.
Его входное сопротивление значительно больше внутреннего сопротивления батарейки,
но не бесконечно большое — то есть, через него потечет ток.
Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с.
как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.
Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:
U(бат)=E-U(внутр)
Так как со временем у всех элементов питания внутреннее сопротивление увеличивается,
то и падение напряжения на внутреннем сопротивлении тоже увеличивается.
При этом напряжение на клеммах батарейки уменьшается. Мяу!
Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи,
чтобы на каком-нибудь из них получить напряжение,
уменьшенное, по сравнению с исходным, во сколько угодно раз.
Простейший делитель напряжения состоит из двух резисторов.
Чем меньшую часть исходного напряжения мы хотим получить и передать в нагрузку,
тем меньше должно быть сопротивление резистора, с которого оно снимается.
Кроме того, сопротивление этого резистора должно быть значительно меньше,
чем сопротивление нагрузки, иначе подключение нагрузки изменит сопротивление всего участка,
и напряжение на нем изменится.
Частенько вместо одного из резисторов делителя используют саму нагрузку. В этом случае второй резистор, на котором гасится избыток напряжения, называют гасящим сопротивлением.
Подключив резистор параллельно нагрузке, можно уменьшить идущий через нее ток. Резистор, который включается для ответвления лишнего тока, порядочные коты называют шунтом (ШУНТ в переводе на русский — обходной путь).
Нормальные герои всегда идут шунтом! (Шутка!)
Чем меньше сопротивление шунта, тем большая часть тока пойдет через него и меньшая через нагрузку.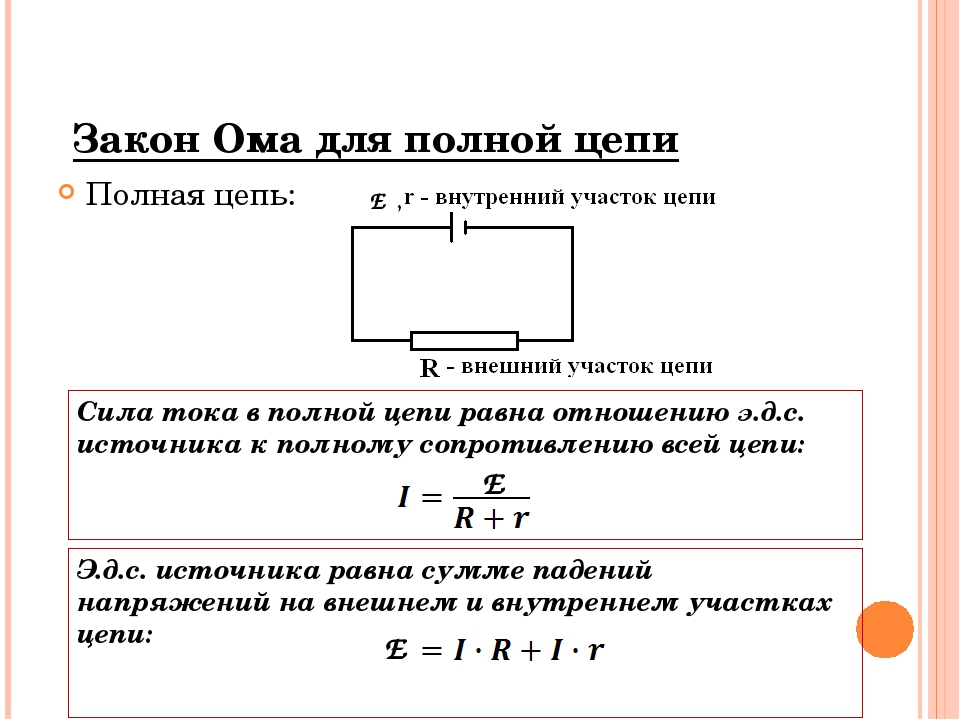
Уф! Запарилась писать такие объемы на своей КПКошке…
Вопросы есть? Будут — пишите. Может, чего еще из школьной программы вспомню.
<<—Вспомним пройденное—-Поехали дальше—>>
Как вам эта статья? | Заработало ли это устройство у вас? |
| Электродвижущая сила. | |
Роль источника тока: разделить заряды за счет совершения работы сторонними силами. Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называютсторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами) | |
ЭДС — энергетическая характеристика источника. Измеряется в вольтах (В). | |
Еще одна характеристика источника — внутреннее сопротивление источника тока: r. |
|
Закон Ома для полной цепи. | |
Энергетические преобразования в цепи: — закон сохранения энергии (А — работа сторонних сил; Авнеш.— работа тока на внешнем участке цепи сопротивлением R; Авнутр.— работа тока на внутреннем сопротивлении источникаr.) | |
Закон Ома: Сила тока в цепи постоянного тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению электрической цепи. | |
Следствия: |
|
1. Если R>>r, то ε=U. Измеряют e высокоомным вольтметром при разомкнутой внешней цепи. | |
2.Если R<<r, то ток — максимальный ток для данной цепи (ток короткого замыкания). Опасно, т.к. — возрастает | e= U1+U2 |
3. На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. A=Aвнутр+ Aвнеш. Тогда: εq=U1q+U2q. Следовательно: ε= U1+U2 ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи. |
|
4. Если R растет, то I уменьшается. — при уменьшении силы тока в цепи напряжение увеличивается! |
|
5. Мощность: а) Полная.. б) Полезная. . в) Теряемая. . г) КПД . |
|
Соединение источников тока. | |
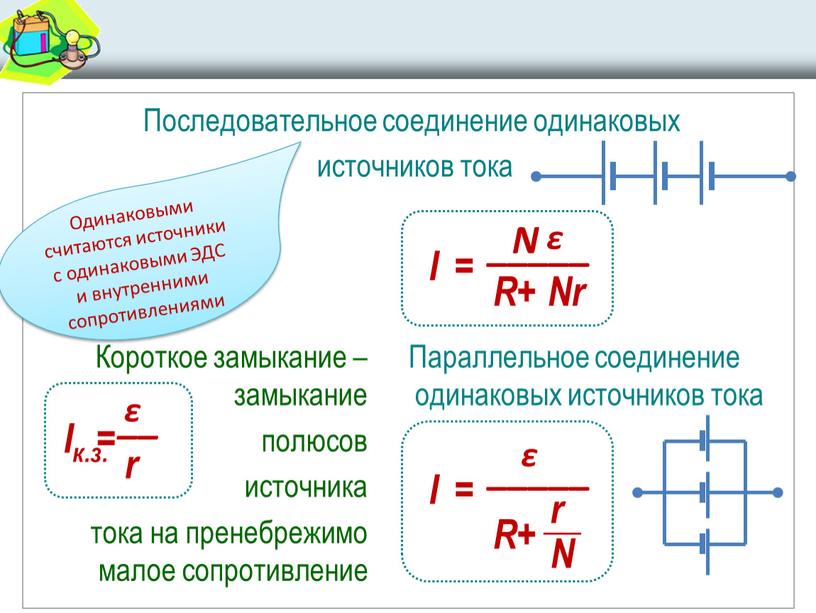
1. Последовательное соединение источников: полная ЭДС цепи равнаалгебраической сумме ЭДС отдельных источников, полное внутреннее сопротивление равно сумме внутренних сопротивлений всех источников тока. Если все источники одинаковы и включены в одном направлении, то . Тогда з-н Ома запишется в виде: | |
2. Если все источники одинаковы , то закон Ома запишется в виде:. | |
Закон Ома для неоднородного участка цепи . | |
— знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем. | |
Правила Кирхгофа. | |
1. Алгебраическая сумма сил токов в каждом узле (точке разветвления) равна 0. — следствие закона сохранения электрического заряда. | |
2. В любом замкнутом контуре цепи алгебраическая сумма произведений сил токов в отдельных участках на их сопротивления равна алгебраической сумме ЭДС источников в этих контурах. — следствие закона Ома для неоднородного участка цепи. | |
Направление токов выбирают произвольно. Если после вычислений значение силы тока отрицательно, то направление противоположно. Замкнутый контур обходят в одном направлении. Если направление обхода совпадает с направлением тока, то IR>0. Если при обходе приходят к «+» источника, то его ЭДС отрицательна. В полученную систему уравнений должны входить все ЭДС и все сопротивления. Т.о. система должна состоять из одного уравнения для токов и k-1 — го уравнения для ЭДС (k — количество замкнутых контуров). |
|
Закон Ома для полной (замкнутой) цепи
Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.
Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.
Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.
Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.
Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивление электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.
Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а сопротивление самого источника тока — внутренним сопротивлением. Внутреннее сопротивление обозначается буквой r.
Внутреннее сопротивление обозначается буквой r.
Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно закону Ома между ее концами должна существовать разность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.
Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E=I*r+I*R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E=I(r+R)
или
I=E/(r+R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональна ЭДС в цепи и обратно пропорциональна общему сопротивлению цепи.
Под общим сопротивлением подразумевается сумма внешнего и внутреннего сопротивлений.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Т. Закон Ома — PhysBook
Закон Ома для замкнутой цепи
Замкнутая цепь (рис. 2) состоит из двух частей — внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя — различные потребители, соединительные провода, приборы и т.д. Общее сопротивление внешней части обозначается R. Тогда полное сопротивление цепи равно r + R.
Рис. 2
По закону Ома для внешнего участка цепи 1 → 2 имеем:
\(~\varphi_1 — \varphi_2 = IR .\)Внутренний участок цепи 2 → 1 является неоднородным. Согласно закону Ома, \(~\varphi_2 — \varphi_1 + \varepsilon = Ir\). Сложив эти равенства, получим
\(~\varepsilon = IR + Ir . \qquad (1)\)
\qquad (1)\)Отсюда
\(~I = \frac{\varepsilon}{R + r} . \qquad (2)\)Последняя формула представляет собой закон Ома для замкнутой цепи постоянного тока. Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи.
Так как для однородного участка цепи разность потенциалов есть напряжение, то \(~\varphi_1 — \varphi_2 = IR = U\) и формулу (1) можно записать:
\(~\varepsilon = U + Ir \Rightarrow U = \varepsilon — Ir .\)Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением силы тока в цепи при ε = const.
Подставим в последнюю формулу силу тока (2), получим
\(~U = \varepsilon \left( 1 — \frac{r}{R + r} \right) .\)Проанализируем это выражение для некоторых предельных режимов работы цепи.
а) При разомкнутой цепи (R → ∞) U = ε, т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.
На этом основана возможность приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого много больше внутреннего сопротивления источника тока (\(~R_v \gg r\)). Для этого вольтметр подключают к клеммам источника тока.
Для этого вольтметр подключают к клеммам источника тока.
б) Если к клеммам источника тока подключить проводник, сопротивление которого \(~R \ll r\), то R + r ≈ r, тогда \(~U = \varepsilon \left( 1 — \frac{r}{r} \right) = 0\) , а сила тока \(~I = \frac{\varepsilon}{r}\) — достигает максимального значения.
Подключение к полюсам источника тока проводника с ничтожно малым сопротивлением называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания:
\(~I_{kz} = \frac{\varepsilon}{r} .\)У источников с малым значением r (например, у свинцовых аккумуляторов r = 0,1 — 0,01 Ом) сила тока короткого замыкания очень велика. Особенно опасно короткое замыкание в осветительных сетях, питаемых от подстанций (ε > 100 В), Ikz может достигнуть тысячи ампер. Чтобы избежать пожаров, в такие цепи включают предохранители.
Запишем закон Ома для полной цепи в случае последовательного и параллельного соединения источников тока в батарею. При последовательном соединении источников «-» одного источника соединяется с «+» второго, «-» второго с «+» третьего и т.д. (рис. 3, а). Если ε1 = ε2 = ε3 а r1 = r2 = r3 то εb = 3ε1, rb = 3r1. В этом случае закон Ома для полной цепи имеет вид\[~I = \frac{\varepsilon_b}{R + r_b} = \frac{3 \varepsilon_1}{R + 3r_1}\], или для n одинаковых источников \(~I = \frac{n \varepsilon_1}{R + nr_1}\).
При последовательном соединении источников «-» одного источника соединяется с «+» второго, «-» второго с «+» третьего и т.д. (рис. 3, а). Если ε1 = ε2 = ε3 а r1 = r2 = r3 то εb = 3ε1, rb = 3r1. В этом случае закон Ома для полной цепи имеет вид\[~I = \frac{\varepsilon_b}{R + r_b} = \frac{3 \varepsilon_1}{R + 3r_1}\], или для n одинаковых источников \(~I = \frac{n \varepsilon_1}{R + nr_1}\).
Рис. 3
Последовательное соединение применяют в том случае, когда внешнее сопротивление \(~R \gg nr_1\), тогда \(~I = \frac{n \varepsilon_1}{R}\) и батарея может дать силу тока, в n раз большую, чем сила тока от одного источника.
При параллельном соединении источников тока все «+» источников соединены вместе и «-» источников — также вместе (рис. 3, б). В этом случае
\(~\varepsilon_b = \varepsilon_1 ; \ r_b = \frac{r_1}{3}. \)
\)Откуда \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{3}}\) .
Для n одинаковых источников \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{n}}\) .
Параллельное соединение источников тока применяют тогда, когда нужно получить источник тока с малым внутренним сопротивлением или когда для нормальной работы потребителя электроэнергии в цепи должен протекать ток. больший, чем допустимый ток одного источника.
Параллельное соединение выгодно, когда R невелико по сравнению с r.
Иногда применяют смешанное соединение источников.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 262-264.
Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:
где:
- I [А] – сила тока в цепи,
- ε [В] – ЭДС источника напряжения,
- R [Ом] – сопротивление всех внешних элементов цепи,
- r [Ом] – внутреннее сопротивление источника напряжения
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|---|---|
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
| Дано: | Решение: |
|---|---|
|
|
»Электроника
Простейшей формой источника тока является резистор, но активные источники тока, использующие транзисторы, могут обеспечивать гораздо более постоянный ток или управляемый ток.
Типы транзисторных цепей включают:
Типы транзисторных цепей
Общий эмиттер
Эмиттер-повторитель
Общая база
Пара Дарлингтона
Пара Шиклай
Текущее зеркало
Длиннохвостая пара
Источник постоянного тока
Множитель емкости
Двухтранзисторный усилитель
Фильтр высоких частот
См. Также: Конструкция транзисторной схемы
Активные источники постоянного тока часто используются в проектировании электронных схем.Некоторые цепи постоянного тока могут быть изготовлены с использованием очень небольшого количества электронных компонентов, но другие, обеспечивающие лучшую производительность, могут использовать несколько больше.
В простейшем источнике постоянного тока используется один электронный компонент: резистор, но часто в источниках постоянного тока используются транзисторы, хотя можно также использовать полевые транзисторы и, где это применимо, вакуумные настройки термоэмиссионных клапанов.
Можно сделать активный источник постоянного тока, используя один транзистор и пару резисторов, хотя также доступны более полные конструкции с использованием нескольких дополнительных электронных компонентов.
Обозначения цепи источника токаЧто такое источник постоянного тока
Базовым элементом является источник тока, а это элемент или блок в цепи, функция которого заключается в обеспечении тока, при этом основное внимание уделяется обеспечению тока, а не напряжения.
Более полезным элементом с точки зрения обеспечения тока является то, что называется источником постоянного тока. Этот объект обеспечивает заданный уровень тока независимо от импеданса нагрузки, на которую он направляет ток.
Теоретический источник постоянного тока сможет обеспечить постоянный ток полностью независимо от импеданса. Проблемы могут возникнуть, когда встречаются очень высокие уровни импеданса или даже разомкнутые цепи, потому что для достижения требуемых уровней тока могут потребоваться очень высокие напряжения.
В связи с этим у реальных источников постоянного тока есть ограничения на диапазон уровней импеданса, при которых они могут обеспечивать постоянный ток.
В зависимости от графика I-V выхода источника постоянного тока характеристика представлена прямой линией.
Есть два типа источников постоянного тока:
Независимый источник тока: Для этой формы источника тока ток не зависит от какой-либо переменной в цепи. Другими словами, он производит фиксированный ток.
Контролируемый источник тока: Эта форма устройства постоянного тока вырабатывает уровень тока, которым можно управлять с помощью внешнего фактора, такого как управляющее напряжение, но оно может обеспечивать требуемый уровень тока независимо от Загрузка.

Применения активного источника тока
Источники тока необходимы в различных областях проектирования электронных схем.
Источники тока могут использоваться для смещения транзисторов, а также могут использоваться в качестве активной нагрузки для каскадов усилителей с высоким коэффициентом усиления. Они также могут использоваться в качестве источников излучения для дифференциальных усилителей — например, они могут использоваться в паре транзисторов с длинными хвостами.
Они также могут использоваться в качестве повышающих звеньев с широким диапазоном напряжения в источниках питания и других цепях с широким диапазоном напряжений.Если бы использовались обычные резисторы, то ток значительно варьировался бы в диапазоне напряжений.
Одним из распространенных примеров использования источников тока является управление стабилитроном в цепи регулятора. Поддержание постоянного тока независимо от тока, потребляемого последовательным транзистором в цепи, помогает поддерживать гораздо лучший уровень регулирования.
Отдельные источники тока также необходимы в различных процессах, включая электрохимию и электрофорез.
Таким образом, можно увидеть, что источник постоянного тока является важным схемным блоком, используемым в самых разных областях проектирования электронных схем.
Схема простого резисторного источника тока
В простейшей форме цепи постоянного тока используется единственный электронный компонент: резистор. Если напряжение источника намного выше, чем напряжение, при котором требуется ток, то выходной ток будет почти не зависеть от нагрузки.
Для идеального источника постоянного тока источник напряжения должен иметь бесконечное напряжение, а резистор — бесконечное сопротивление.
Для практических применений напряжение и сопротивление должны позволять току быть достаточно постоянным в требуемом диапазоне нагрузки.
Простой источник постоянного тока, состоящий из источника высокого напряжения и резистора высокого номинала. Для приведенной выше схемы ток можно очень легко рассчитать, так как он приблизительно равен I = V / R, потому что Vload (напряжение на нагрузке) намного меньше, чем V (напряжение источника).
Эта простая форма источника тока имеет множество ограничений:
- Высокие значения сопротивления, необходимые для рассеивания мощности, делают цепи неэффективными.
- Необходимы источники высокого напряжения, которые не всегда легко доступны.
- Изменения нагрузки могут вызвать некоторые колебания тока, если недоступны достаточно высокие значения напряжения источника.
Ввиду этих ограничений этот простой источник постоянного тока не используется широко там, где требуется истинный постоянный ток.
Для достижения лучшей производительности с источником более низкого напряжения и меньшей рассеиваемой мощностью, хотя и с несколькими дополнительными электронными компонентами, активная цепь постоянного тока более широко используется и обеспечивает лучшую общую производительность для большинства практических требований.
Основы транзисторного активного источника постоянного тока
Простое использование транзистора позволяет создать гораздо более эффективный источник тока, используя всего несколько дополнительных электронных компонентов, включая транзистор, несколько резисторов и несколько простых уравнений для конструкции электронной схемы.
Источник тока работает из-за того, что ток коллектора в схеме транзистора в раз больше тока базы. Это не зависит от напряжения коллектора, при условии, что имеется достаточное напряжение для пропускания тока через нагрузочное устройство в коллекторе.
Активный источник тока с одним транзистором
В этой схеме ток коллектора в β раз больше тока базы. Обычно β велико, и поэтому можно предположить, что ток эмиттера, который в (β + 1) раз больше тока базы, и ток коллектора, который в β раз больше тока базы, одинаковы.
Ввиду этого спроектировать схему для заданного тока несложно.
Ie = (β + 1) IbIload = Ic = βIb
Iload = β Ve (β + 1) Re
Iload = Vb — 0.6Re
Примечание: здесь предполагается использование кремниевого транзистора, поскольку падение напряжения на базе эмиттера составляет 0,6 В
Установкой резисторов R1 и R2 можно установить базовое напряжение. Напряжение эмиттера будет на 0,6 вольт меньше, если предположить, что это кремниевый транзистор. Зная напряжение эмиттера, можно рассчитать ток эмиттера, просто зная закон Ома.
Зная напряжение эмиттера, можно рассчитать ток эмиттера, просто зная закон Ома.
Схема простого стабилизированного активного источника тока
Чтобы устранить любые колебания тока, возникающие из-за изменений напряжения питания, очень просто добавить некоторую регулировку в основную схему, заменив несколько электронных компонентов.Это достигается заменой R2 на стабилитрон или опорный диод напряжения.
Транзистор активного источника тока с использованием стабилитрона для улучшения стабильностиТех же уравнения применяются, как и раньше, но с той лишь разницей, что напряжение базы удерживается на более постоянный уровне в результате присутствия Зенера, опорное напряжение диода.
Температурная зависимость активного источника тока
Одним из основных недостатков основного активного источника тока является то, что он в определенной степени зависит от температуры.Для многих приложений это может быть не важно, но там, где требуются очень строго контролируемые условия, температурные характеристики могут быть очень важны.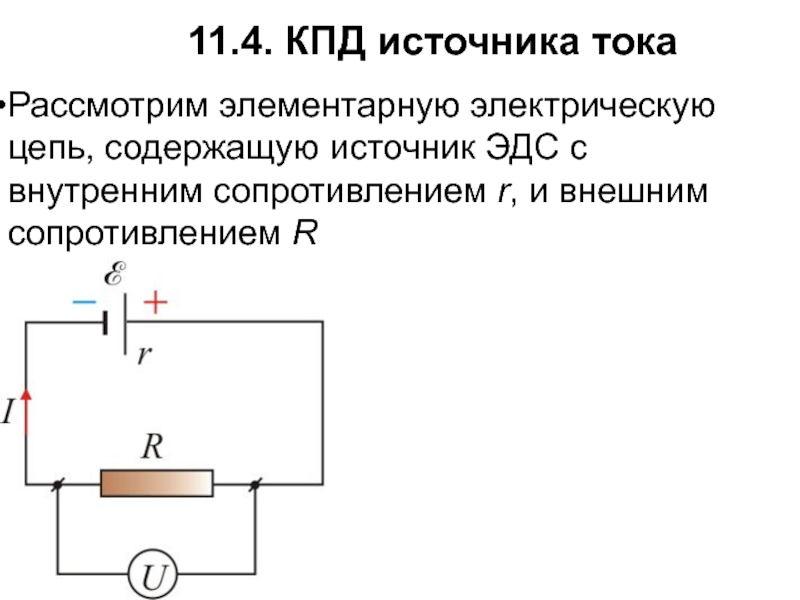
Есть два основных варианта:
- Изменения Vbe в зависимости от температуры Эффекты изменения Vbe, вызванные температурой, составляют приблизительно -2 мВ / ° C. Это приводит к изменению Vce. Можно рассчитать приблизительное соотношение: ΔVbe примерно равно -0.0001ΔVce.
Это можно минимизировать, выбрав достаточно большое сопротивление эмиттера, чтобы гарантировать, что изменения напряжения эмиттера в десятки милливольт будут составлять лишь небольшую часть от общего напряжения эмиттера. Однако необходимо следить за тем, чтобы между коллектором и шиной оставалось достаточное напряжение, чтобы пропускать ток через нагрузку и компенсировать любые изменения напряжения питания.
- Вариации β в зависимости от температуры Это может не быть серьезной проблемой, и любые отклонения можно минимизировать, выбрав транзистор с высоким значением / Hfe.Таким образом, вклад базового тока в ток эмиттера сводится к минимуму, а отклонения уменьшаются, насколько это возможно.

Цепи активного источника тока с хорошей температурной стабильностью
Можно разработать схемы транзисторных активных источников тока, у которых внутренняя температурная стабильность лучше, чем у простых схем, приведенных выше.
Одна из простейших схем — использовать схему, в которой используются транзисторы NPN и PNP. В показанной схеме изменения падения напряжения Vbe в TR1 компенсируются соответствующими изменениями в TR2.В этой схеме следует отметить, что R3 является подтягивающим резистором для коллектора TR1, потому что база TR2 может принимать ток, но не обеспечивать его.
Транзисторный источник активного тока с температурной компенсацией Все схемы включают транзисторы, но также могут использоваться другие активные электронные компоненты, включая полевые транзисторы и даже вакуумные лампы / термоэлектронные клапаны. При использовании других электронных компонентов в качестве активного устройства в источнике тока, устройства и схема смещения должны учитывать тот факт, что и полевые транзисторы, и клапаны / лампы управляются напряжением, а не током. Тем не менее их можно использовать так же эффективно.
Тем не менее их можно использовать так же эффективно.
Транзисторные активные источники тока используются во многих областях, особенно в интегральных схемах и некоторых зарядных устройствах. Они позволяют подавать фиксированный или контролируемый ток независимо от напряжения (в определенных пределах) и поэтому очень полезны.
Другие схемы и схемотехника:
Основы операционных усилителей
Схемы операционных усилителей
Цепи питания
Конструкция транзистора
Транзистор Дарлингтона
Транзисторные схемы
Схемы на полевых транзисторах
Условные обозначения схем
Вернуться в меню «Конструкция схемы».. .
Анализ схем с помощью преобразования источника
В этой статье используются примеры, объясняющие технику преобразования источника.
Справочное исследование
Электрическая сеть может состоять из источников и пассивных элементов. Источники — это компоненты схемы, которые обладают собственной энергией и могут передавать эту энергию другим элементам схемы.
Есть два основных типа источников: источники напряжения и источники тока.Они могут быть далее классифицированы как независимые или зависимые. В случае независимых источников напряжение или ток фиксированы. Если источник является зависимым, значение напряжения или тока зависит от величины тока или напряжения в другом месте цепи.
Пассивные компоненты не имеют собственной энергии. В результате они считаются раковинами. Однако они влияют на величину тока или напряжения в данной части цепи. Резисторы, конденсаторы и катушки индуктивности являются пассивными компонентами.
Анализ электрических сетей
Сложность электрических сетей варьируется от очень простых, например, делитель напряжения, до очень сложных, например, внутренней структуры интегральной схемы (IC).
Ожидается, что хороший проектировщик электрики хорошо разбирается в системе в целом, независимо от ее сложности. Это абсолютно необходимо, когда возникает проблема обновления или устранения неполадок системы.
Здесь важно отметить, что анализ электрической цепи иногда бывает простым и понятным, занимая всего пару минут.Иногда, однако, это может потребовать большого количества тяжелой работы (или, скорее, умной работы), и это может даже заставить анализатор прибегнуть к помощи программного обеспечения. Тем не менее, способ анализа основан на определенных основных правилах и теоремах.
Вот список важных теорем с кратким объяснением:
- Теорема суперпозиции: помогает найти ток и напряжение в цепи, имеющей несколько источников; эффекты, производимые каждым из источников по отдельности, можно суммировать.
- Теорема Тевенина: помогает в упрощении схемы; несколько источников и сопротивлений могут быть представлены эквивалентной схемой с одним источником напряжения и одним резистором.
- Теорема Нортона: помогает в упрощении схемы; несколько источников и сопротивлений могут быть представлены эквивалентной схемой только с одним источником тока и одним резистором.

- Теорема Миллмана: метод упрощения, включающий схемы с параллельными ветвями.
Здесь следует отметить, что все эти теоремы основаны на основных правилах, регулирующих область электроники, а именно на законе Ома и законах Кирхгофа.
Кроме того, иногда мы можем найти схему, в которой резисторы подключены по схеме треугольник / пи или звезда / треугольник. В таких случаях мы можем использовать преобразование звезда-треугольник или дельта-звезда при анализе схемы.
Преобразование источника для независимых источников
Рассмотрим схему, показанную на рисунке 1; цель состоит в том, чтобы найти ток (обозначенный i) через центральный резистор 5 Ом.Здесь невозможно применить анализ сетки (закон напряжения Кирхгофа, KVL), потому что в схеме есть ответвление с источником тока. Таким образом, нам нужно разработать метод, с помощью которого мы можем исключить этот источник тока из нашей схемы. Однако при этом мы должны позаботиться о том, чтобы ток и напряжение в цепи оставались неизменными.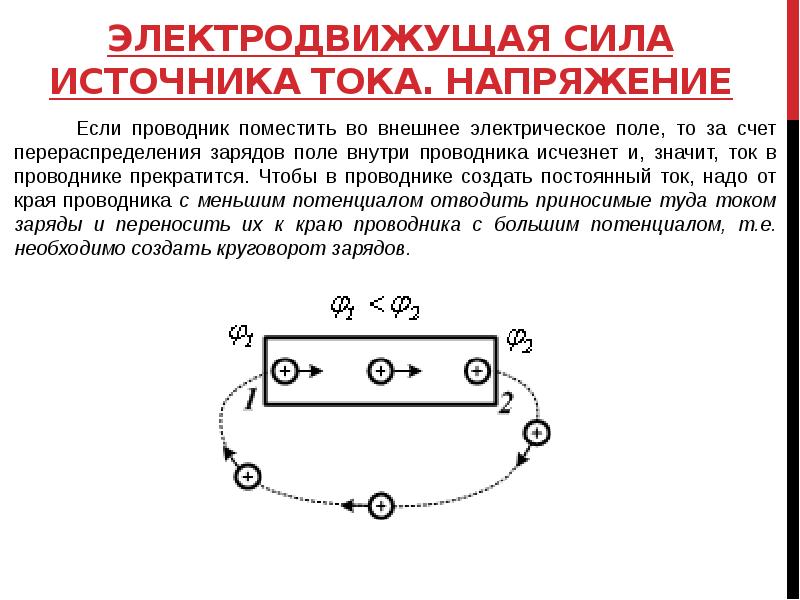
Вспомните закон Ома, который гласит, что $$ I = \ frac {V} {R} $$.
Шаг 1. Преобразование источника тока в напряжение
Еще раз посмотрев на схему (рис. 1), мы увидим, что источник тока 1 А имеет параллельно включенный резистор 10 Ом. Давайте теперь заменим эту комбинацию источником напряжения V = 1 A × 10 Ω = 10 V и последовательным резистором 10 Ω. Вы можете увидеть, как это выглядит на рисунке 2. Обратите внимание, что положительный вывод источника напряжения помещен слева, потому что стрелка источника тока указывала влево.Эти две схемы (рисунок 1 и рисунок 2) считаются эквивалентными: ток 1 А, входящий в узел X из узла Y, не изменился.
Рисунок 2 Выполняемый здесь процесс называется преобразованием источника. Мы преобразовали существующий источник тока с параллельным резистором в эквивалентный источник напряжения с последовательным резистором.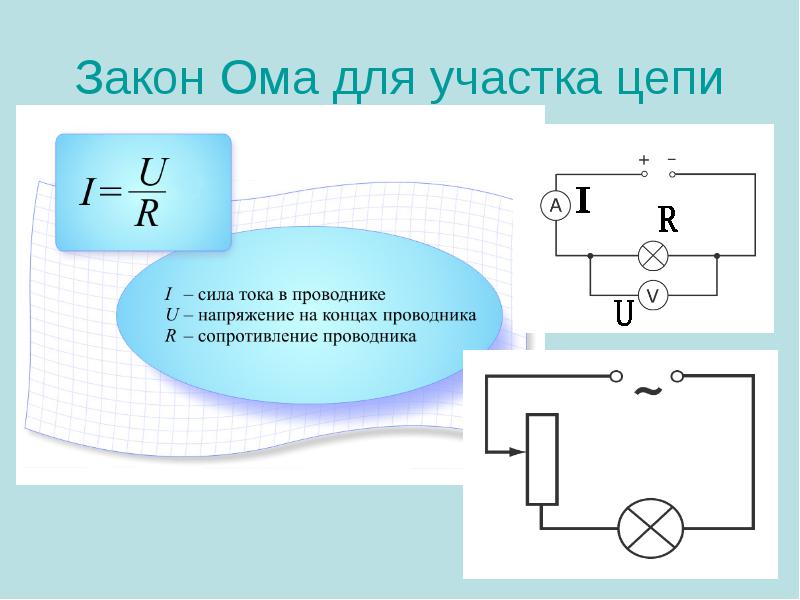
Шаг 2: Преобразование источника напряжения в ток
Схема на Рисунке 2 может быть дополнительно упрощена, поскольку в ней последовательно соединены резистор 10 Ом и резистор 5 Ом.Их можно заменить эквивалентным резистором 15 Ом (= 10 Ом + 5 Ом). Упрощенная схема показана на рисунке 3 (а).
Теперь мы можем легко применить анализ сетки для решения стоящей перед нами проблемы. Однако есть также гораздо более простой графический способ добиться этого: снова применить преобразование источника!
Ранее мы преобразовали источник тока с помощью параллельного резистора, но мы также можем применить преобразование источника к источнику напряжения с последовательным резистором. У нас есть два таких устройства, как показано на рисунке 3 (b).Эта схема эквивалентна схеме, показанной на рисунке 3 (а).
Рисунок 3 Итак, здесь мы применим преобразование источника напряжения в ток, которое очень похоже на преобразование источника тока в напряжение. Процесс включает в себя замену источника напряжения V последовательно на резистор R на эквивалентную сеть, в которой источник тока $$ I = \ frac {V} {R} $$ параллелен резистору R. Источник тока ориентирован таким образом стрелка указывает на положительный вывод заменяемого источника напряжения (см. Рисунок 4).
Процесс включает в себя замену источника напряжения V последовательно на резистор R на эквивалентную сеть, в которой источник тока $$ I = \ frac {V} {R} $$ параллелен резистору R. Источник тока ориентирован таким образом стрелка указывает на положительный вывод заменяемого источника напряжения (см. Рисунок 4).
Таким образом, для крайней левой ветви у нас есть источник тока $$ I = \ frac {10} {5} = 2 \ A $$, подключенный параллельно резистору 5 Ом. Аналогично для самой правой ветви мы получаем $$ I = \ frac {10} {15} = \ frac {2} {3} \ A $$, подключенную параллельно резистору 15 Ом. Полученная схема показана на рисунке 4.
Схема на Рисунке 4 имеет два источника тока, направленных в одном направлении, и, следовательно, их можно заменить одним источником тока, значение которого равно их сумме, то есть $$ \ frac {8} {3} \ A $ $.
Рисунок 4 Имеется три резистора: два резистора 5 Ом и один резистор 15 Ом, все подключенные параллельно.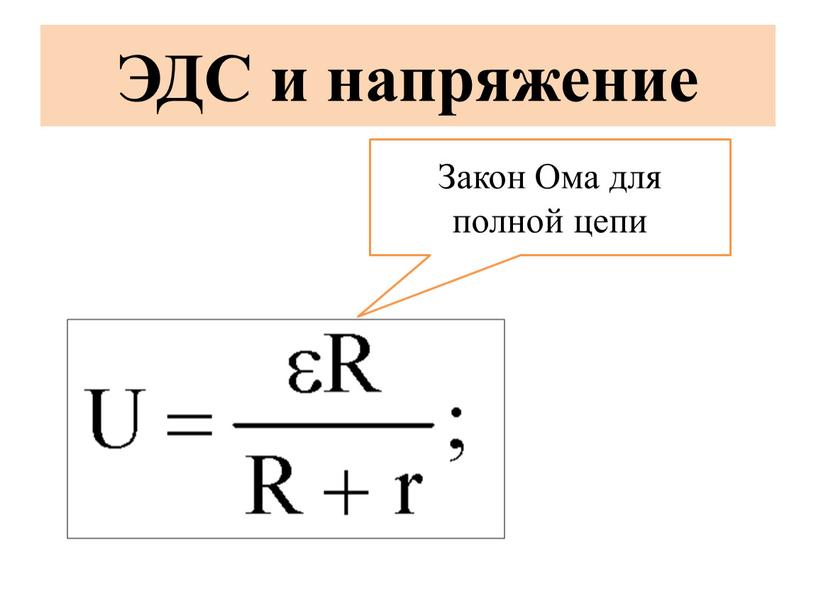 Мы могли бы заменить все три из них эквивалентным сопротивлением (R EQ ), но наша цель — найти ток через резистор 5 Ом, поэтому мы объединим только два других.
Мы могли бы заменить все три из них эквивалентным сопротивлением (R EQ ), но наша цель — найти ток через резистор 5 Ом, поэтому мы объединим только два других.
$$ R_ {EQ} = \ frac {5 × 15} {5 + 15} = \ frac {5 × 15} {20} = \ frac {15} {4} \ \ Omega $$
Внеся эти изменения, мы получаем схему, показанную на рисунке 5.
Рисунок 5Шаг 3: Преобразование источника тока в напряжение (снова)
Теперь давайте снова применим преобразование источника тока в напряжение для комбинации, показанной на рисунке 5.
Здесь источник напряжения будет иметь значение $$ V = \ frac {8} {3} \ times \ frac {15} {4} = 10 \ V $$, с положительной клеммой к узлу X, последовательно с резистором $$ \ frac {15} {4} \ \ Omega $$.
Результирующая схема показана на рисунке 6.
Рисунок 6На рисунке 6 мы можем легко применить KVL для получения тока через резистор 5 Ом:
$$ 10 — \ frac {15} {4} i — 5i = 0 $$
$$ 10 — \ frac {35} {4} i = 0 $$
$$ 10 = \ frac {35} {4} i $$
$$ i = 10 \ times \ frac {4} {35} = \ frac {8} {7} \ A $$
Преобразование исходного кода для зависимых источников
Преобразование источника применимо даже для цепей с зависимыми источниками. Рассмотрим схему, показанную на рисунке 7 (а).
Рассмотрим схему, показанную на рисунке 7 (а).
Здесь необходимо прибегнуть к смещению источника для источника тока 3 А перед применением преобразования источника. Это дает схему, показанную на рисунке 7 (б).
Рисунок 7Шаг 1. Преобразование источника тока в напряжение
Теперь применим преобразование источника тока в напряжение для элементов схемы, показанных на рисунке 7 (b).
Для верхней части мы имеем V = 3 × 1 = 3 В с положительной клеммой, направленной вниз, последовательно с резистором 1 Ом.Точно так же для нижней части мы получаем V = 3 × 2 = 6 В, направленное вниз, последовательно с резистором 2 Ом. Это приводит к схеме, показанной на рисунке 8 (а).
Рисунок 8 Схема может быть дополнительно уменьшена: верхняя сетка имеет резистор 1 Ом последовательно с резистором 2 Ом, образуя эквивалентное сопротивление 3 Ом, а нижняя сетка имеет резистор 2 Ом последовательно с резистором 3 Ом, который может быть заменен одним резистором 5 Ом.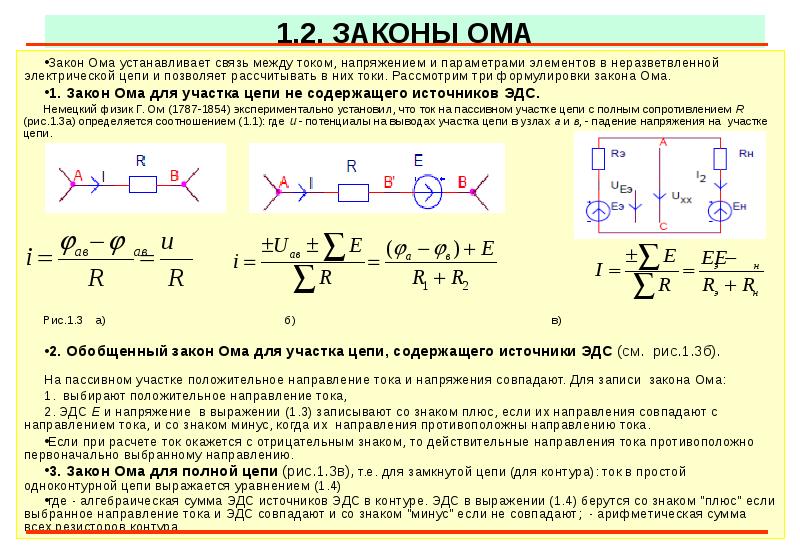 В результате получается схема, показанная на рисунке 8 (b).
В результате получается схема, показанная на рисунке 8 (b).
Шаг 2: Преобразование источника напряжения в ток
Посмотрев на рисунок 8 (b), вы можете увидеть, что нам нужно применить преобразование напряжения в ток источника три раза (по одному разу для каждой комбинации источник-плюс-резистор).
Корпус 1: Для источника 3 В последовательно с 3 Ом
$$ I = \ frac {3} {3} = 1 \ A $$ параллельно резистору 3 Ом, направленному влево.
Случай 2: Для 5i 1 зависимый источник напряжения последовательно с 5 Ом
$$ I = \ frac {5i_ {1}} {5} = 1i_ {1} \ A $$ параллельно с резистором 5 Ом, направленным вправо.
Корпус 3: Для источника 6 В последовательно с 5 Ом
$$ I = \ frac {6} {5} \ A $$ параллельно с резистором 5 Ом, направленным вправо.
Эти шаги приводят к схеме, показанной на Рисунке 9.
Рисунок 9 Здесь два независимых источника тока ориентированы в противоположных направлениях и, таким образом, могут быть заменены одним источником тока, значение которого определяется как $$ I = \ frac {6} {5} -1 = \ frac {1} {5 } \ A $$, направлено вправо.
Затем мы можем выразить значение зависимого источника тока как $$ I = \ frac {1} {5} + 1i_ {1} = \ frac {1 + 5i_ {1}} {5} \ A $$, вправо.
Нам нужно найти ток, протекающий через резистор 5 Ом (тот, что посередине). Поэтому мы оставим все как есть и заменим два других (т. Е. Резисторы 3 Ом и 5 Ом сверху и снизу) эквивалентным сопротивлением: R = 5 || 3 = $$ \ frac {5 \ times 3} {5 + 3} = \ frac {15} {8} \ \ Omega $$.
Теперь схему можно изобразить следующим образом:
Рисунок 10Шаг 3: Преобразование источника тока в напряжение (снова)
Наконец, мы можем преобразовать зависимый источник тока в зависимый источник напряжения со значением
$$ V ‘= \ frac {1 + 5i_1} {5} × \ frac {15} {8} = \ frac {3 + 15i_1} {8} \ V $$
Он будет включен последовательно с резистором $$ \ frac {15} {8} \ \ Omega $$ и будет иметь положительный вывод справа.
Рисунок 11Теперь KVL можно использовать для вычисления i 1 :
$$ \ frac {3 + 15i_1} {8} — \ frac {15} {8} \ times i_1-5i_1 = 0 $$
$$ \ frac {3} {8} + \ frac {15i_1} {8} — \ frac {15} {8} \ times i_1-5i_1 = 0 $$
$$ \ frac {3} {8} -5i_1 = 0 $$
$$ \ frac {3} {8} = 5i_1 $$
$$ i_1 = \ frac {3} {40} \ A $$
Преобразование источника для цепей с индукторами и конденсаторами
Обратите внимание, что преобразование источника также применимо для цепей с индукторами и конденсаторами. Однако в этом сценарии необходимо проанализировать схему в частотной области.
Однако в этом сценарии необходимо проанализировать схему в частотной области.
Давайте посмотрим на схему, показанную на рисунке 12 (а).
Рисунок 12Здесь, если принять ω равным 50 рад / с, то
- Импеданс конденсатора 2 мФ = -j / ωC = -j / (50 × 2 × 10 -3 ) = -j / (100 × 10 -3 ) = -10j
- Импеданс индуктора 40 мГн = jωL = j × 50 × 40 × 10 -3 = 2j
Теперь предположим, что нам нужно найти напряжение на катушке индуктивности 40 мГн.
Когда мы смотрим на принципиальную схему, становится очевидным, что этот процесс станет проще, если мы преобразуем источник тока 2 А, подключенный параллельно с сопротивлением -10j, в источник напряжения. Этот процесс дает V = 2 × (-10j) = -20j, направленное вниз, последовательно с импедансом -10j .
Результирующая схема показана на рисунке 13.
Рисунок 13 Теперь применим KVL к схеме, чтобы определить ток I, протекающий через нее.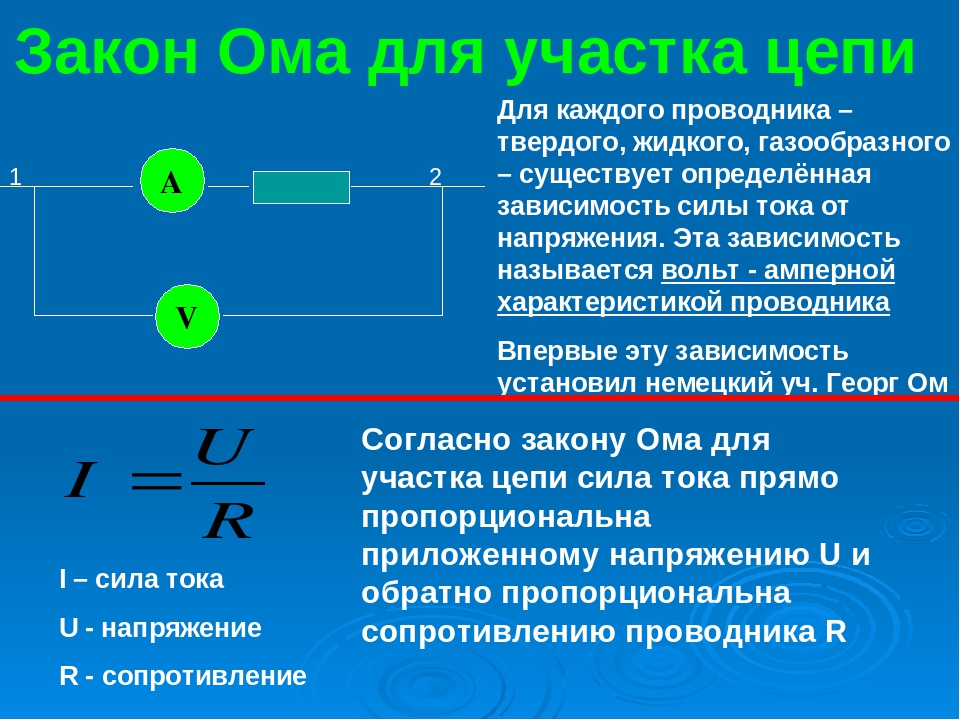
$$ 5-2jI + 10jI-20j = 0 $$
$$ \ влево (10j-2j \ вправо) I = 20j-5 $$
$$ 8jI = 20j-5 $$
$$ I = \ frac {20j-5} {8j} = \ left (2,5 + 0,625j \ right) \ A $$
Таким образом, напряжение на дросселе V L будет
$$ 5-V_L + 10jI-20j = 0 $$
$$ 5-V_L + (10j) \ times (2,5 + 0,625j) -20j = 0 $$
$$ 5 + \ влево (-6,25 + 25j \ вправо) -20j = V_L $$
$$ V_L = \ left (-1.25 + 5j \ right) \ V $$
Заключение
Анализ трансформации источников, представленный в этой статье, можно свести к следующим трем пунктам:
1.Преобразование источника, выполняемое в соответствии с правилами, показанными на рисунке 14, можно использовать для упрощения схем и облегчения анализа сетки.
Рисунок 142. Зависимые источники могут быть преобразованы так же, как и независимые источники (Рисунок 15).
Рисунок 15 3.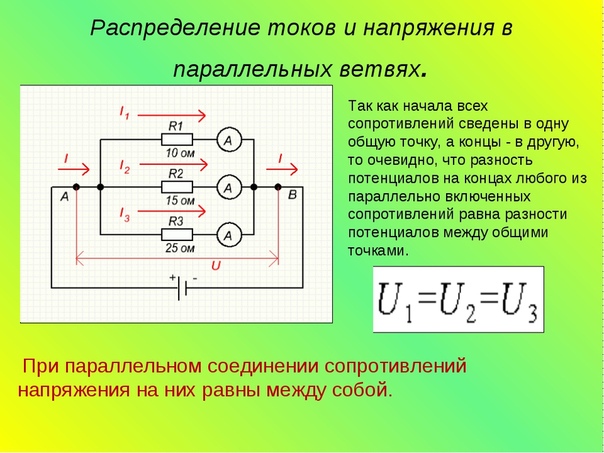 Технику преобразования источника можно использовать даже для анализа цепей, имеющих конденсаторы и катушки индуктивности, при условии, что мы анализируем их в частотной области.
Технику преобразования источника можно использовать даже для анализа цепей, имеющих конденсаторы и катушки индуктивности, при условии, что мы анализируем их в частотной области.
Я надеюсь, что эта статья дала вам лучшее понимание преобразования исходного кода.
Как использовать теорему Тевенина | EAGLE
Существует множество доступных методов анализа сложных электрических цепей, таких как анализ сетки, узловой анализ или законы Кирхгофа для цепей. Проблема в том, что при проектировании сети постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развития процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей вашей цепи каждый раз при изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина.В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Тевенина, чтобы быстро рассчитать ток и напряжение. Давай начнем.
Давай начнем.
Что такое теорема Тевенина?
Как и все другие математические и научные теории / законы, теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином, французским телеграфным инженером, родившимся в Мо, Франция. После службы в корпусе инженеров-телеграфистов Тевенин был назначен инспектором по обучению в Высшей школе телеграфии в 1882 году.Именно здесь он заинтересовался измерением электрических цепей с использованием двух доступных в то время методов — законов Кирхгофа и закона Ома.
Леон Шарль Тэвенин (Источник изображения)
Стремясь упростить анализ сложных схем для каждого инженера, Тевенин разработал свою теперь известную теорему Тевенина, которая сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.
Эта теорема утверждает, что можно взять любую линейную схему, которая может содержать несколько ЭДС и резистивных компонентов, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.

Упрощенная эквивалентная схема Тевенина с одним источником напряжения и сопротивлением. (Источник изображения)
В данном случае линейная цепь — это цепь, которая включает в себя пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако, если вы работаете со схемой, которая включает газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина не для этого годилась. Так зачем использовать эту теорему для анализа линейных цепей?
- Эффективность .Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, которая меняет значение в процессе анализа. Эта теорема обеспечивает эффективный способ вычисления напряжения и тока, протекающих через нагрузку, без необходимости заново рассчитывать всю схему.
- Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы.
 Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.
Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.
Посмотрите на пример схемы ниже. Здесь в качестве нагрузки используется резистор R2. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкие методы анализа, такие как Branch Current, Mesh Current и т. Д., Каждый раз, когда значение резистора нагрузки изменяется.
(Источник изображения)
Чтобы упростить эту задачу, мы можем использовать теорему Тевенина, чтобы удалить сопротивление нагрузки и напряжения. Затем мы упрощаем остальную часть схемы как единый источник напряжения и последовательное сопротивление.В этой упрощенной схеме Тевенина два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенные напряжение и сопротивление будут работать так же, как и наша исходная схема.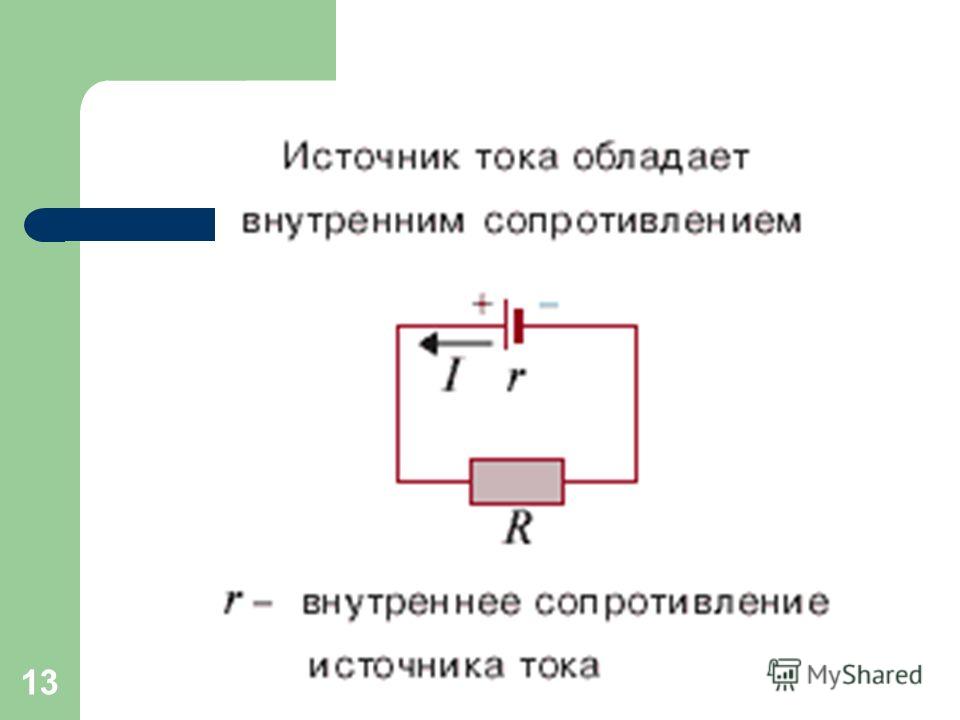 Теперь у нас есть только две простые переменные, с которыми мы будем работать в наших расчетах.
Теперь у нас есть только две простые переменные, с которыми мы будем работать в наших расчетах.
(Источник изображения)
Теорема Тевенина в действии
Давайте посмотрим на пример схемы и вычислим ток, протекающий через нагрузочный резистор между двумя выводами.Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:
- Найдите сопротивление Тевенину, удалив все источники напряжения и нагрузочный резистор.
- Найдите напряжение Thevenin, подключив напряжение.
- Используйте сопротивление и напряжение Тевенина, чтобы найти ток, протекающий через нагрузку.
Вот пример схемы, с которой мы будем работать:
(Источник изображения)
Шаг 1 — Thevenin Resistance
Сначала нам нужно снять нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения.Это даст нам разомкнутую цепь при нулевом напряжении, в результате чего останется только два резистора, подключенных последовательно.![]()
(Источник изображения)
Чтобы вычислить общее сопротивление тевенину, мы можем использовать следующий процесс:
Шаг 2 — Напряжение Thevenin
Затем мы можем использовать закон Ома для вычисления полного тока, протекающего по цепи, следующим образом:
Поскольку эти резисторы соединены последовательно, они будут иметь одинаковый 0.33 ампера. Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:
Шаг 3 — Ток нагрузки
Теперь, когда у нас есть сопротивление и напряжение Тевенина, мы можем соединить эквивалентную схему Тевенина с нашим исходным нагрузочным резистором, как показано ниже.
Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:
Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!
Запомните трехэтапный процесс:
- Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузку.

- Найдите напряжение Thevenin, повторно подключив источники напряжения.
- Используйте сопротивление и напряжение Тевенина, чтобы найти полный ток, протекающий через нагрузку.
Сохраняйте простоту
Планируете разработать схему питания постоянного тока? Скорее всего, вы включите нагрузку, значение которой изменится во время анализа схемы. Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, которая упрощает вашу работу.
Эта теорема позволяет вам взять любую сложную линейную схему с множеством резистивных компонентов и ЭДС и упростить ее до эквивалентной схемы Тевенина. С помощью этой упрощенной схемы вы можете легко рассчитать полный ток и напряжение, протекающие через нагрузку. Это огромная экономия времени для любого инженера, которому необходимо эффективно анализировать схемы для силовых схем и других сложных приложений.
Тем из вас, кто изучает визуальное / кинестетическое мышление, обязательно посмотрите видео ниже, в котором показано, как использовать теорему Тевенина шаг за шагом.
Готовы спроектировать свою первую силовую цепь? Попробуйте Autodesk EAGLE бесплатно сегодня!
Источник напряженияи источник тока — идеальный вариант по сравнению с практичным
Источник — это устройство, преобразующее механическую, химическую, тепловую или другую форму энергии в электрическую. Типы источников, доступных в электрической сети, — это источник напряжения и источник тока . Источник напряжения используется для подачи напряжения на нагрузку, а источник тока используется для подачи тока.
Источник напряжения
Источник напряжения — это устройство, которое обеспечивает постоянное напряжение для нагрузки в любой момент времени и не зависит от тока, потребляемого от него. Этот тип источника известен как идеальный источник напряжения. Практически невозможно сделать идеальный источник напряжения.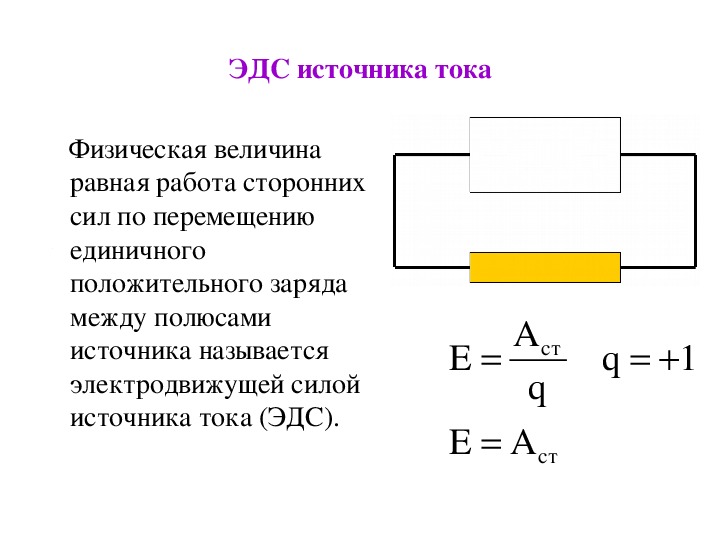 У него нулевое внутреннее сопротивление. Обозначается этим символом.
У него нулевое внутреннее сопротивление. Обозначается этим символом.
Обозначение источника напряжения
Идеальный источник напряжения
График представляет изменение напряжения источника напряжения во времени.Он постоянен в любой момент времени.
Источники напряжения, имеющие некоторое внутреннее сопротивление, известны как практические источники напряжения. Из-за этого внутреннего сопротивления происходит падение напряжения. Если внутреннее сопротивление велико, на нагрузку будет подаваться меньшее напряжение, а если внутреннее сопротивление меньше, источник напряжения будет ближе к идеальному источнику напряжения. Таким образом, практический источник напряжения обозначается последовательным сопротивлением, которое представляет внутреннее сопротивление источника.
Практический источник напряжения
График отображает напряжение источника напряжения в зависимости от времени. Это непостоянно, но с течением времени продолжает уменьшаться.
Источник тока
Источник тока — это устройство, которое обеспечивает постоянный ток для нагрузки в любое время и не зависит от напряжения, подаваемого в цепь. Этот тип тока известен как идеальный источник тока; практически идеального источника тока также нет. У него бесконечное сопротивление.Обозначается этим символом.
Символ источника тока
Идеальный источник тока
График представляет изменение силы тока источника тока во времени. Он постоянен в любой момент времени.
Почему идеальный источник тока имеет бесконечное сопротивление?
Источник тока используется для питания нагрузки, так что нагрузка включается. Стараемся подавать 100% мощности на нагрузку. Для этого мы подключаем некоторое сопротивление для передачи 100% мощности на нагрузку, потому что ток всегда идет по пути наименьшего сопротивления.Итак, чтобы ток пошел по пути наименьшего сопротивления, мы должны подключить сопротивление выше нагрузки. Вот почему у нас есть идеальный источник тока с бесконечным внутренним сопротивлением. Это бесконечное сопротивление не повлияет на источники напряжения в цепи.
Вот почему у нас есть идеальный источник тока с бесконечным внутренним сопротивлением. Это бесконечное сопротивление не повлияет на источники напряжения в цепи.
Практический источник тока
На практике источники тока не имеют бесконечного сопротивления, но имеют конечное внутреннее сопротивление. Таким образом, ток, подаваемый практическим источником тока, непостоянен и также в некоторой степени зависит от напряжения на нем.
Практический источник тока представляет собой идеальный источник тока, подключенный параллельно с сопротивлением.
Практический источник тока
График показывает зависимость тока источника тока от времени. Это непостоянно, но со временем продолжает уменьшаться.
Примеры источников тока и напряжения
Примерами источников тока являются солнечные элементы, транзисторы, а примерами некоторых источников напряжения являются батареи и генераторы переменного тока.
Речь шла об идеальных и практичных источниках энергии. Идеальные источники очень полезны для теоретических расчетов, но поскольку идеальные источники практически невозможны, в практических схемах используются только практические источники. Батареи, которые мы используем, являются практическим источником энергии, а напряжение и ток уменьшаются по мере их использования. Таким образом, оба они полезны для нас по-своему.
Идеальные источники очень полезны для теоретических расчетов, но поскольку идеальные источники практически невозможны, в практических схемах используются только практические источники. Батареи, которые мы используем, являются практическим источником энергии, а напряжение и ток уменьшаются по мере их использования. Таким образом, оба они полезны для нас по-своему.
LM317 — Калькулятор
Регулируемый регулятор напряжения LM317 может поставить 1.5 А при выходном напряжении 1,2 … 37 В.В отличие от стабилизаторов постоянного напряжения семейства 78xx, где эталонный напряжение U r связано с землей, U r на LM317 выходное напряжение U , выход . Это дает возможность с всего три разъема и установите выходное напряжение с помощью двух резисторов (см.
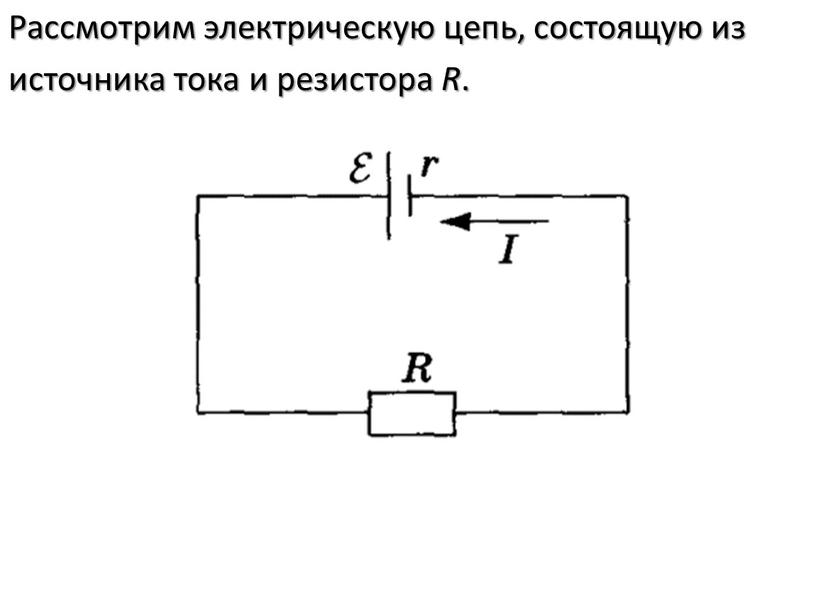 схему ниже).
схему ниже).Поскольку U r для LM317 всегда 1,25 В, применяется к выходному напряжению. U выход = 1,25 * (1 + R2 / R1)
R1 должен иметь значение 240 Ом. Маркированный диод 1N4001 защищает регулятор, если то Выходное напряжение должно быть выше входного (например, при переключении выключен, когда Выходная сторона «толстых» конусов в схеме).DIode также можно не указывать. Регулятор напряжения
Для регулировки выходного напряжения требуются только два внешних резистора. Пожалуйста, выберите, хотите ли вы рассчитать U OUT или резистор Р2 .
В качестве альтернативы опорный вывод нормально-заземленного стабилизатора постоянного напряжения также может быть
переключенный делитель напряжения «поднят» и, следовательно, также с фиксированным регулятором напряжения отличается от напряжения, чем
печатные генерируются. Чтобы избежать колебаний, конденсатор можно подключить параллельно R2.
(также с LM317). Также примите во внимание возникающую потерю мощности (охлаждение).
регулятора напряжения.
Чтобы избежать колебаний, конденсатор можно подключить параллельно R2.
(также с LM317). Также примите во внимание возникающую потерю мощности (охлаждение).
регулятора напряжения.
Код 404 страница не найдена. К сожалению, страница отсутствует или перемещена.Ниже приведены основные подразделы этого сайта.
»Главная
» Электронное письмо
»Пожертвовать
» Преступление
»Электроника для хобби »Архив 1
»Архив 2
»Архив 3
»Архив 4
»Архив 5 Веб-сайт Авторские права Льюис Лофлин, Все права защищены. |
% PDF-1.2
%
73 0 объект
>
endobj
xref
73 54
0000000016 00000 н.
0000001428 00000 н.
0000001582 00000 н.
0000001653 00000 н.
0000001708 00000 н. 0000001763 00000 н.
0000001824 00000 н.
0000001883 00000 н.
0000001944 00000 н.
0000001999 00000 н.
0000002565 00000 н.
0000002837 00000 н.
0000002929 00000 н.
0000003021 00000 н.
0000003113 00000 п.
0000003205 00000 н.
0000003296 00000 н.
0000003387 00000 н.
0000003478 00000 н.
0000003570 00000 н.
0000003662 00000 н.
0000003754 00000 н.
0000003846 00000 н.
0000004034 00000 п.
0000004538 00000 п.
0000004717 00000 н.
0000004903 00000 н.
0000005090 00000 н.
0000005541 00000 н.
0000006079 00000 п.
0000006260 00000 н.
0000006282 00000 п.
0000006938 00000 п.
0000006960 00000 н.
0000007545 00000 н.
0000007567 00000 н.
0000008191 00000 п.
0000008213 00000 н.
0000008950 00000 н.
0000008972 00000 н.
0000009328 00000 н.
0000009441 00000 п.
0000009586 00000 н.
0000010032 00000 п.
0000010229 00000 п.
0000010894 00000 п.
0000010916 00000 п.
0000011571 00000 п.
0000011593 00000 п.
0000012152 00000 п.
0000012174 00000 п.
0000012253 00000 п.
0000002055 00000 н.
0000001763 00000 н.
0000001824 00000 н.
0000001883 00000 н.
0000001944 00000 н.
0000001999 00000 н.
0000002565 00000 н.
0000002837 00000 н.
0000002929 00000 н.
0000003021 00000 н.
0000003113 00000 п.
0000003205 00000 н.
0000003296 00000 н.
0000003387 00000 н.
0000003478 00000 н.
0000003570 00000 н.
0000003662 00000 н.
0000003754 00000 н.
0000003846 00000 н.
0000004034 00000 п.
0000004538 00000 п.
0000004717 00000 н.
0000004903 00000 н.
0000005090 00000 н.
0000005541 00000 н.
0000006079 00000 п.
0000006260 00000 н.
0000006282 00000 п.
0000006938 00000 п.
0000006960 00000 н.
0000007545 00000 н.
0000007567 00000 н.
0000008191 00000 п.
0000008213 00000 н.
0000008950 00000 н.
0000008972 00000 н.
0000009328 00000 н.
0000009441 00000 п.
0000009586 00000 н.
0000010032 00000 п.
0000010229 00000 п.
0000010894 00000 п.
0000010916 00000 п.
0000011571 00000 п.
0000011593 00000 п.
0000012152 00000 п.
0000012174 00000 п.
0000012253 00000 п.
0000002055 00000 н.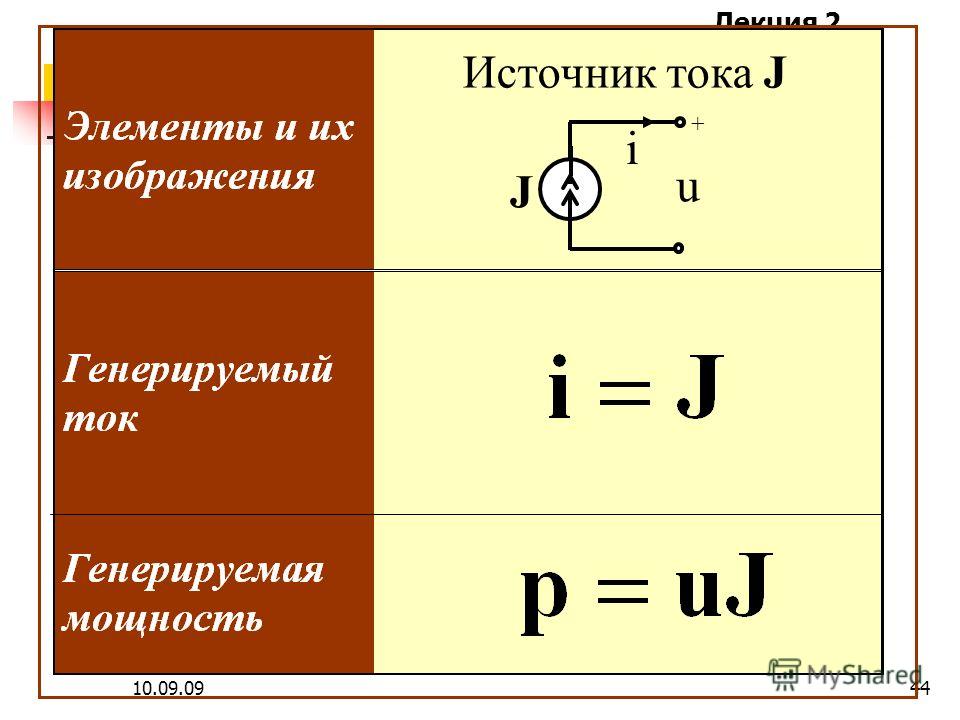

 Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду:
Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: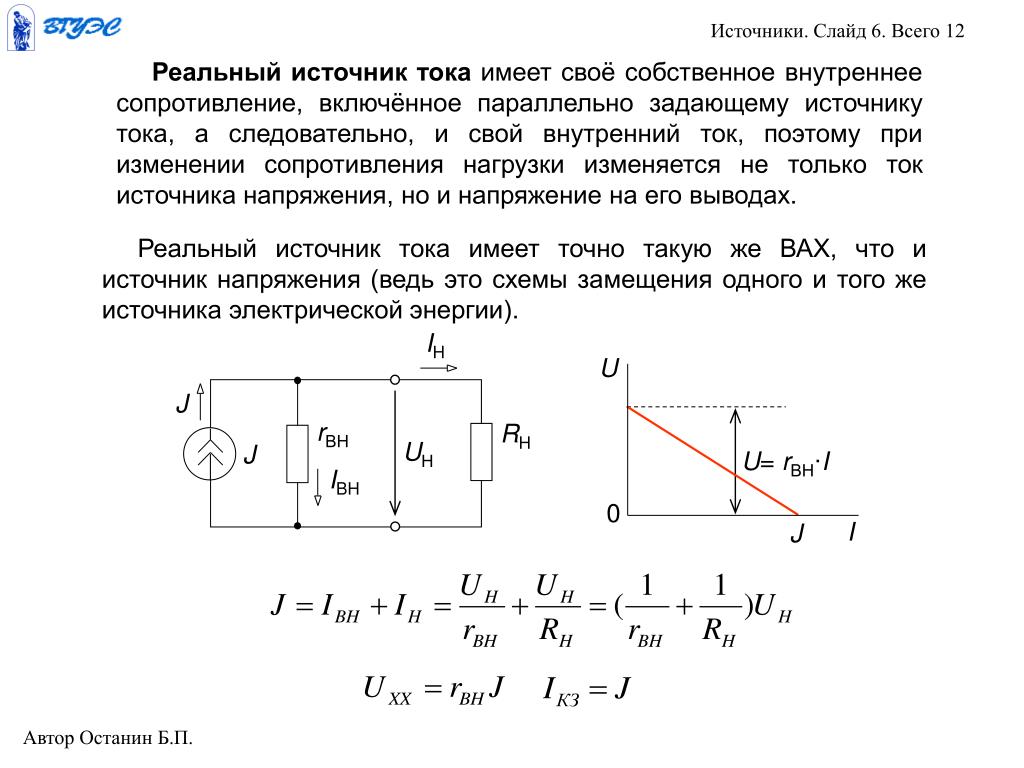
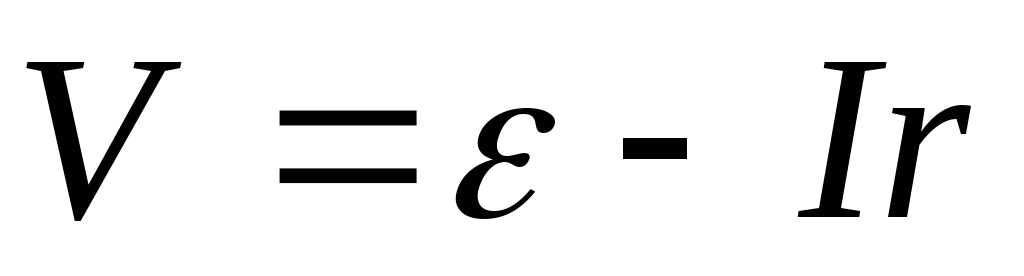
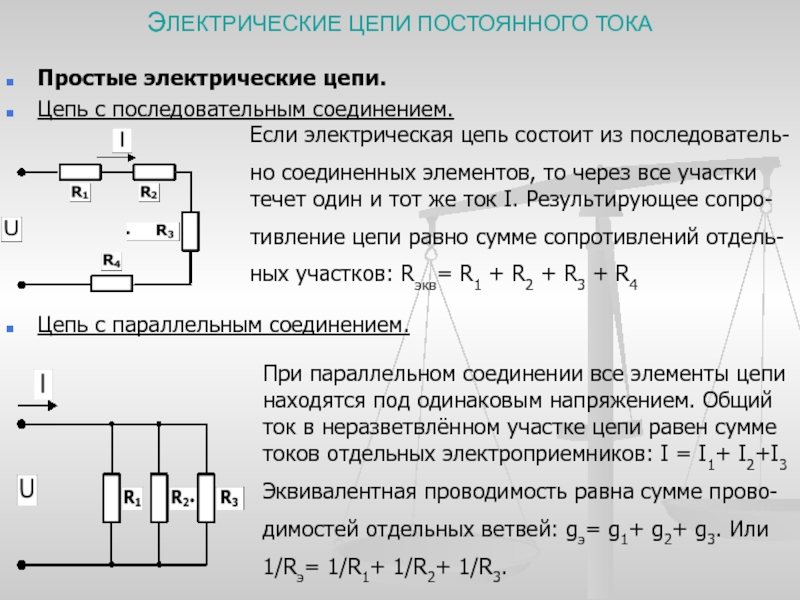
 Параллельное соединение источников: один из источников (с наибольшейЭДС) работает как источник, остальные — как потребители (на этом принципе основана зарядка аккумулятора). Расчет по правилам Кирхгофа (см.).
Параллельное соединение источников: один из источников (с наибольшейЭДС) работает как источник, остальные — как потребители (на этом принципе основана зарядка аккумулятора). Расчет по правилам Кирхгофа (см.).



 Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.
Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.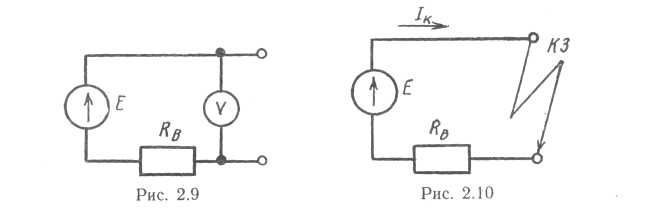
 :
:
Leave A Comment