Как найти радиус описанной около треугольника abc окружности
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
- Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
- Примеры задач
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами.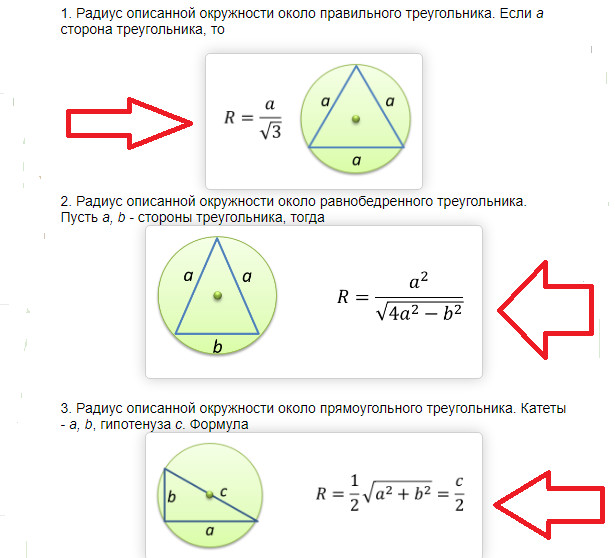
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Все формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
, , — стороны треугольника
— полупериметр
— центр окружности
Формула радиуса описанной окружности треугольника ( R ) :
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
— сторона треугольника
— высота
— радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.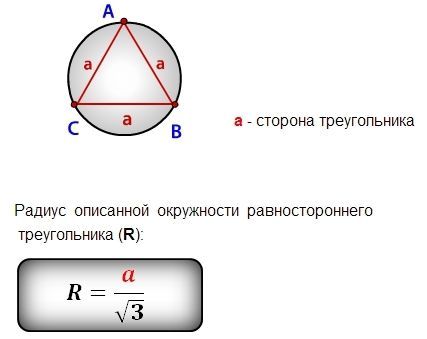
a, b — стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
p — полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
a — сторона квадрата
d — диагональ
Формула радиуса описанной окружности квадрата (R):
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
Формула радиуса описанной окружности прямоугольника (R):
Радиус описанной окружности правильного многоугольника
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
Радиус описанной окружности правильного шестиугольника
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
геометрия — Нахождение центра и радиуса описанного треугольника
спросил
Изменено 5 лет, 9 месяцев назад
Просмотрено 4к раз
$\begingroup$
Пусть $u=(6,7), v=(-2, 3), w=(7,0)$. Найдите центр и радиус описанной окружности треугольника $[u,v,w]$.
Найдите центр и радиус описанной окружности треугольника $[u,v,w]$.
Мой подход выглядел бы так:
(1) Определить углы треугольника $[u,v,w]$ с помощью скалярных произведений.
(2) Если провести три линии из центра $o$ окружности к трем вершинам, треугольник $[u,v,w]$ будет состоять из трех равносторонних треугольников. Тогда мы можем легко найти из (1) все девять углов трех треугольников.
(3) Определите высоты трех вписанных треугольников, которые будут одинаковыми для всех трех и которые будут радиусом $r$ вписанной окружности.
(4) Тогда мы можем опустить перпендикуляр из $o$, скажем, в $[v,w]$, чтобы найти координаты $o$.
Но есть ли гораздо менее утомительный способ решить эту проблему? И вы считаете мой подход правильным?
- геометрия
- векторы
- аналитическая геометрия
- круги
- треугольники
$\endgroup$
$\begingroup$ 92=25$$
$\endgroup$
$\begingroup$
Пусть $(h,k)$ — координаты центра описанной окружности, а $r$ — радиус описанной окружности.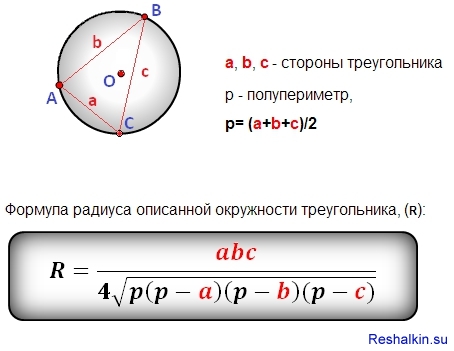
Центр описанной окружности — это точка пересечения серединных перпендикуляров.
Вам нужны только два из них, любые два.
- Отрезок $uv$ имеет наклон $\frac{1}{2}$ и середину $(2,5)$.
- Отрезок $vw$ имеет наклон $-\frac{1}{3}$ и середину $(\frac{5}{2},\frac{3}{2})$ 92) + Bx + Cy + D = 0$$ и график такого уравнения обычно представляет собой окружность.
- Во-вторых, если подставить координаты одной из заданных точек $u$, $v$ или $w$, определитель равен $0$ (поскольку полученная матрица состоит из двух одинаковых строк), поэтому график, который мы получаем проходит через точки $u,v,w$.
- геометрия
- тригонометрия
- треугольники
Метод изящно завершается ошибкой при неверном вводе: мы получаем линию вместо окружности, когда три точки лежат на одной прямой, а определитель равен $0$ для любого $(x,y)$, когда три точки не все различны.
В отличие от всех других методов, этот легко обобщается для нахождения сферы через четыре точки (см. эту страницу, где я впервые узнал об этом) и, возможно, для многих других подобных задач.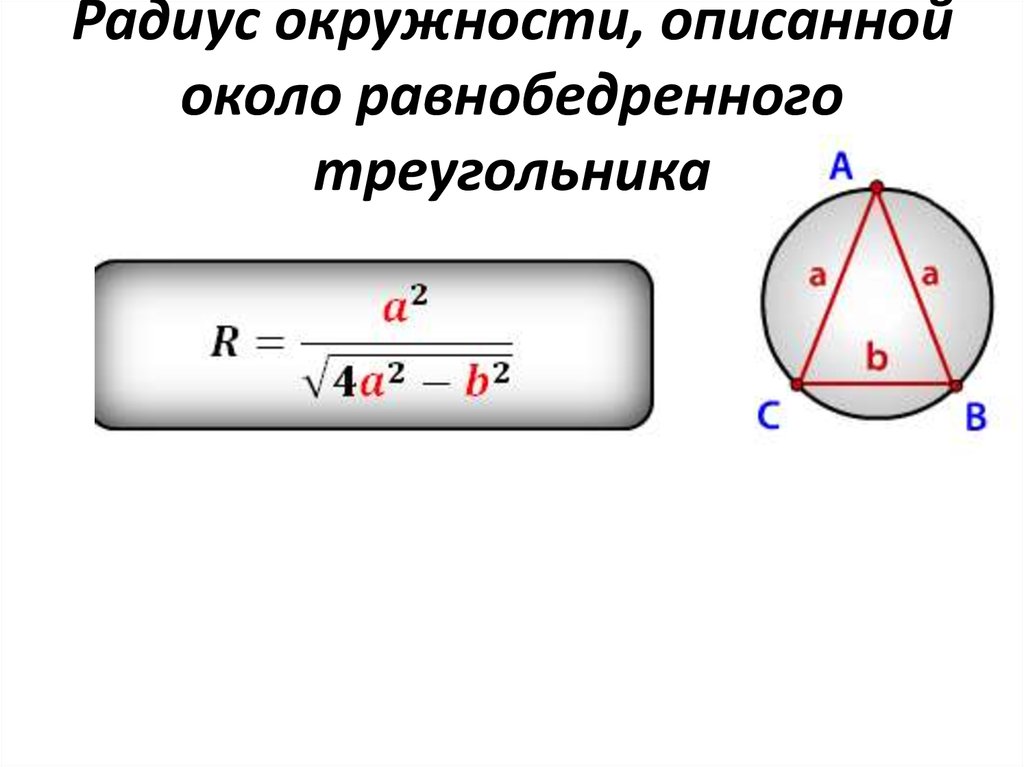
$\endgroup$
2
геометрия — Радиус описанной окружности равнобедренного треугольника
спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 3к раз
$\begingroup$
Дан равнобедренный треугольник $ABC$ $(AC=BC).$ Периметр $\треугольника ABC$ равен $2p$, угол при основании равен $\alpha.$ Найти радиус описанной окружности $R $.
$$R=\frac{p}{2\sin\alpha(1+\cos\alpha)}$$
Пусть $CD=2R.$ Треугольник $BCD$ прямоугольный и $\угол BAC=\угол ABC=\угол BDC=\alpha.$
Я не знаю, как подойти к проблема. Мне очень сложно решать такие проблемы. Можете ли вы дать мне подсказку и некоторые мысли по проблеме?
Мне очень сложно решать такие проблемы. Можете ли вы дать мне подсказку и некоторые мысли по проблеме?
$\endgroup$
5
$\begingroup$
Еще один простой подход. Пусть $x=AC=BC$. Тогда
$$2p=AC+BC+2AH\\=2x+2x\cos\alpha$$
и
$$R=\frac 12 CD=\frac 12 \frac{BC}{ \sin \ alpha} = \frac{x}{2 \sin \alpha}$$
Теперь вы можете завершить решение простой подстановкой.
$\endgroup$
2
$\begingroup$
Подсказка: Используйте следующую формулу: 92}$$ по теореме Пифагора, так как $\угол CBD$ вписан в полуокружность, значит угол прямой.
Теперь, используя тригонометрические свойства, выведите, что $$BH = BD \sin \alpha,$$ и $$BH = BC \cos \alpha.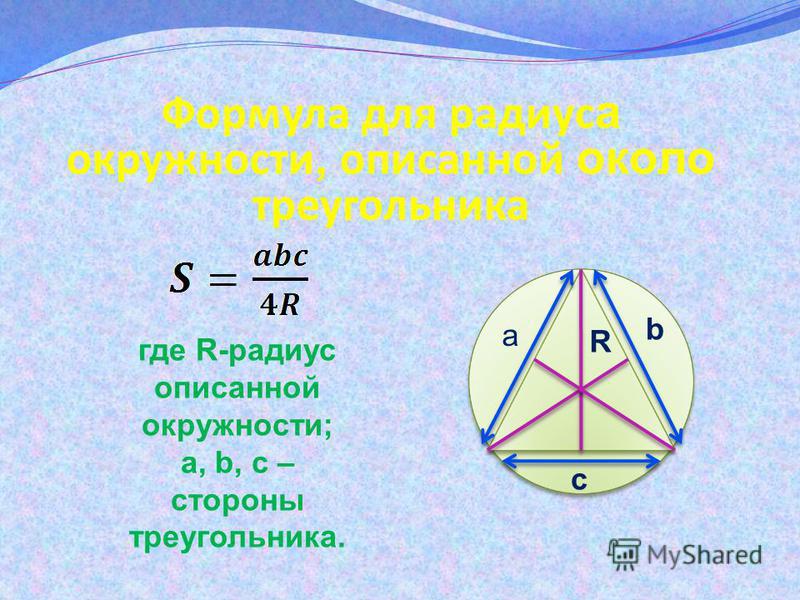

Leave A Comment