Импульс тела, силы. Изменение и направление вектора, единицы измерения. Связь с законом Ньютона. Примеры

Тестирование онлайн

  • Импульс тела, импульс силы. Основные понятия

  • Импульс тела, импульс силы

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание!

Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Средняя равнодействующая сила

Импульс тела | Все Формулы

    \[ \]

Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость

    \[\Large p=m\upsilon\]

Каждое тело, которое имеет массу и скорость, так же имеет и импульс.

Пусть на тело массой m в течение некоторого малого промежутка времени

    \[Δt\]

действовала сила F. Под действием этой силы скорость тела изменилась на

    \[\Delta \upsilon =\vec\upsilon _2-\vec\upsilon _1\]

. Следовательно, тело на промежутке

    \[Δt\]

двигалось с ускорением

    \[\Large \vec a=\frac{\Delta \vec\upsilon }{\Delta t}=\frac{\vec \upsilon _2-\vec\upsilon_1}{\Delta t}\]

На основе Второго закон Ньютона

    \[\Large \vec F=m \vec a=m\frac{(\vec \upsilon _2-\vec\upsilon _1)}{\Delta t}\]

А если немного преобразовать, то у нас получится:

    \[\Large \vec F\Delta t=m\vec \upsilon _2-m\vec\upsilon _1=m\Delta \vec\upsilon=\Delta (m\upsilon)\]

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела

    \[m\upsilon\]

. А физическая величина, равная произведению силы на время ее действия, называется импульсом силы

    \[F\Delta t\]

.

Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с)

В Формуле мы использовали :

p — Импульс тела

m — Масса тела

    \[\upsilon\]

— Скорость тела

Модуль силы, скорости, импульса. Что это?!

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!
модуль

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.

Сила и модуль силы

В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.

Что такое модуль силы?

модуль силы

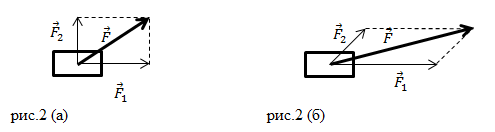
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.

Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.

Модуль равнодействующих двух сил определяется по формулам:

  • F=F1 + F2 (в случае сил с одинаковым направлением)
  • F=F1 — F2 (силы с разным направлением)

Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.

Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).

Что это модуль скорости?

модуль скорости

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.

Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это

модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.

Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:

v = S/t = (x — x0)/t.

Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.

Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:

  1. Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
  2. Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

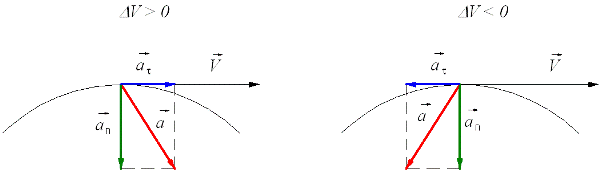
модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.

Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Импульс системы тел 1


Импульсом тела называется произведение его массы на скорость. Также импульс называют количеством движения. Импульс является векторной величиной. Направление его совпадает с направлением скорости.

    \[\vec{p}=m \vec{\upsilon}\]

Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует:

    \[\Delta \vec{p}= \vec{F} \Delta t\]

Здесь \Delta \vec{p}=\vec{p_2}-\vec{p_1} – изменение импульса за время \Delta t. Произведение силы на время ее действия называют импульсом силы. Сила здесь может быть и равнодействующей всех сил, действующих на тело.

Закон сохранения импульса – следствие второго и третьего законов Ньютона. Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.

В замкнутой системе суммарный импульс системы тел остается постоянным при любых взаимодействиях тел в системе между собой.

Система тел может быть не замкнута вдоль одной из осей, а вдоль другой – замкнута. Тогда закон сохранения импульса будет работать в такой системе вдоль этой оси. Например, если рассматривать столкновение лодок на озере и не принимать в расчет трение, то такая система может считаться замкнутой вдоль горизонтальной оси, и вдоль этой оси работает закон сохранения импульса. Вдоль вертикальной оси действует сила тяжести, и система не замкнута.

Также при решении задач, связанных с импульсом, очень важны такие понятия, как абсолютно упругий и абсолютно неупругий удары. При абсолютно упругом ударе  тело отскакивает от другого тела, сохраняя модуль импульса, и «угол падения равен углу отражения». При абсолютно неупругом ударе тела слипаются, образуя новое тело, масса которого равна сумме их масс. То, что  удар был неупругим  можно понять, например, если тело отскочило под углом, не равным углу падения, если о неупругом ударе специально не сказано в задаче.

Рассмотрим сначала простые задачи, где движение тел происходит вдоль одной прямой.

 

Задача 1. Тело массой m=1 кг движется равномерно по окружности, со скоростью \upsilon=2 м/с. Определить изменение импульса тела после того, как оно пройдет четверть окружности, половину окружности.

Импульс

Изменение импульса

После того, как тело пройдет четверть окружности, вектор его скорости повернется на 90 градусов, как показано на рисунке  – \upsilon_2. Изменение скорости можно определить как \Delta \upsilon=\upsilon_2-\upsilon_1=\upsilon_2+(-\upsilon_1), поэтому разворачиваем вектор скорости \upsilon_1, чтобы получить вектор -\upsilon_1, и складываем его с \upsilon_2 по правилу параллелограмма. Зеленым показан вектор изменения скорости \Delta \upsilon. По теореме Пифагора можно найти его длину – он будет равен \sqrt{2} \upsilon_1=2\sqrt{2} м/с, тогда изменение импульса тела в этом случае m \Delta \upsilon =1 \cdot 2\sqrt{2}=2\sqrt{2} кг*м/с.

Импульс

Вектора импульсов тел системы

Импульс

Вектора импульсов и их сложение

Когда тело пройдет половину окружности, вектор его скорости развернется в противоположную сторону – \upsilon_3. Точно так же изменение скорости можно определить как \Delta \upsilon=\upsilon_3-\upsilon_1=\upsilon_3+(-\upsilon_1), поэтому разворачиваем вектор скорости \upsilon_1, чтобы получить вектор -\upsilon_1, и складываем его с \upsilon_3 по правилу многоугольника. Зеленым показан вектор изменения скорости \Delta \upsilon. Видно, что \Delta \upsilon=-2\upsilon_1=-4 м/с.

Изменение импульса тела в этом случае m \Delta \upsilon =2 \cdot 2=4 кг*м/с.

Ответ: 2\sqrt{2} кг*м/с, 4 кг*м/с.

 

Задача 2. Снаряд массой m=10 кг  вылетает из ствола орудия со скоростью \upsilon=800 м/с. Зная, что время движения снаряда внутри ствола равно \Delta t=0,008 с, определить среднюю силу давления пороховых газов.

 

На вылете из ствола пушки снаряд обладает импульсом, равным p_{sn}=m \upsilon=10 \cdot 800=8000 кг*м/с. Так как на систему не действуют никакие внешние силы, то импульс системы сохраняется, а до выстрела он был нулевым. После выстрела суммарный импульс системы также нулевой, а это значит, что импульс снаряда равен по модулю и противоположен по направлению изменению импульса пороховых газов в стволе. Таким образом, газы будут давить с силой F=\frac{\Delta p}{\Delta t}=\frac{ m \upsilon }{\delta t}=\frac{8000}{0,008}=1000 кН

Ответ: 1000 кН

 

Задача 3. На тело в течение времени \Delta t=10 с действовала сила F=50 Н. Найти массу тела, если изменение скорости тела в результате действия силы равно \Delta \upsilon=5 м/с.

 

Изменение импульса равно произведению изменения скорости на массу тела. Импульс силы равен \Delta p= F {\Delta t}, масса тела тогда  m=\frac{ F \Delta t}{\dDelta \upsilon }=\frac{ 50 \cdot10}{5}=100 кг.

Ответ: 100 кг

 

Задача 4. Скорость реактивного самолета равна \upsilon=900 км/ч. На пути самолета оказалась птица массой m=2 кг.  Определить среднюю силу удара птицы о стекло кабины летчика, если длительность удара \Delta t=0,001 с. Каково среднее давление на стекло при ударе, если площадь соприкосновения птицы со стеклом S=1000 см^2?

 

Среднюю силу удара можно определить так: F=\frac{\Delta p}{\Delta t}=\frac{ m \upsilon }{\Delta t}

Скорость самолета выразим в единицах СИ – метрах в секунду. 900 км/ч=\frac{900 000}{3600}=250 м/с

    \[F=\frac{ m \upsilon }{\Delta t}=\frac{ 2 \cdot 250}{0,001}=500 000\]

Или 500 кН. Можно теперь определить среднее давление на стекло при ударе, только прежде представить площадь в м^2:

S=1000 см^2=0,1 м^2

    \[p=\frac{F}{S}=\frac{500 000}{0,1}=5 \cdot10^6\]

Паскалей или 50 атмосфер.

Ответ: p=5 \cdot10^6 Па или 50 атмосфер.

Задача 5. Падающий вертикально шарик массой m=0,2 кг ударился о пол и подпрыгнул на высоту 0,4 м. Найти среднюю силу, действующую со стороны пола на шарик, если длительность удара \Delta t=0,01 с, к моменту удара о пол скорость шарика \upsilon_0=5 м/с.

 

Шарик двигается равноускоренно, поэтому, когда он соприкоснется с полом, его вес будет больше силы тяжести. А его вес – это, собственно, и есть сила его давления на пол.

При равноускоренном движении вес можно вычислить:

    \[P=m(g+a)\]

Определим ускорение шарика. Здесь a – мера изменения скорости шарика, a=\frac{\Delta \upsilon}{\Delta t}

Так как шарик взлетел на высоту 0,4 метра, то определим его скорость при отрыве от пола по формуле:

    \[2aS=\upsilon^2-\upsilon_1^2\]

Скорость шарика в наивысшей точке равна 0, поэтому:

    \[-2gS=-\upsilon_1^2\]

    \[\upsilon_1=\sqrt{2gS}\]

    \[\upsilon_1=\sqrt{2\cdot9,8 \cdot0,4}=2,8\]

Тогда изменение скорости

    \[\Delta \upsilon=2,8-(-5)=7,8\]

a=\frac{\Delta \upsilon}{\Delta t}=\frac{7,8}{0,01}=780

    \[F=m(g+a)=0,2 \cdot 790=158\]

Ответ: 158 Н

 

Задача 6. Шарик летит навстречу стенке со скоростью \upsilon. Стенка движется навстречу шарику со скоростью u. Какой станет скорость шарика после упругого удара о стенку?

 

Сначала рассмотрим полет шарика относительно стенки. Тогда (если мы представим себе, что смотрим от стенки, и вместе с ней двигаемся со скоростью u, не замечая этого) нам будет казаться, что шарик летит на нас со скоростью u+\upsilon. Тогда после отскока шарик изменит свою скорость на такую же по модулю, но противоположную по направлению: -u-\upsilon – это мы его от стенки наблюдаем. А вот теперь мы покинули движущуюся стенку и смотрим с  неподвижной земли – и тогда шарик летит уже со скоростью -2u-\upsilon – минус показывает противоположное, относительно первоначального, направление полета.

 

Задача 7. Мальчик массой 22 кг, бегущий со скоростью 2,5 м/c, вскакивает сзади на платформу массой 12 кг. Чему равна скорость платформы с мальчиком?

 

Импульс системы тел будет сохраняться вдоль горизонтальной оси. Поэтому суммарный импульс тележки (0) и мальчика (m\upsilon_1) будет равен суммарному импульсу тележки с мальчиком на ней после прыжка:

    \[0+ m\upsilon_1=(m+M)\upsilon_2\]

    \[\upsilon_2=\frac{m}{m+M}\cdot\upsilon_1=\frac{22}{22+12}\cdot\2,5=1,62\]

Ответ: 1, 62 м/с

 

Задача 8. Два неупругих шара с массами 4 и 6 кг движутся со скоростями 8 м/с и 3 м/с соответственно, направленными вдоль одной прямой. С какой скоростью они будут двигаться после абсолютно неупругого удара, если первый догоняет второй? Если они двигаются навстречу?

 

Запишем закон сохранения в первом случае:

    \[m_1\upsilon_1+ m_2\upsilon_2=(m_1+m_2)\upsilon_3\]

Все слагаемые с плюсами, так как тела движутся в одну сторону.

    \[4\cdot 8+ 6\cdot 3=(4+6)\upsilon_3\]

    \[32+ 18=(4+6)\upsilon_3\]

    \[\upsilon_3=\frac{50}{10}=5\]

Теперь тела двигаются навстречу друг другу:

    \[m_1\upsilon_1- m_2\upsilon_2=(m_1+m_2)\upsilon_3\]

    \[4\cdot 8- 6\cdot 3=(4+6)\upsilon_3\]

    \[32- 18=(4+6)\upsilon_3\]

    \[\upsilon_3=\frac{14}{10}=1,4\]

Ответ: 5 м/с, 1,4 м/с

 

Задача 9. Тележка с песком катится со скоростью 1 м/с по горизонтальному пути без трения. Навстречу тележке летит шар массой 2 кг с горизонтальной скоростью 7 м/с.  Шар после попадания в песок застревает в нем.  В какую сторону и с какой скоростью покатится тележка после столкновения с шаром? Масса тележки 10 кг.

 

Записываем уравнение сохранения импульса системы тел вдоль горизонтальной оси: примем m_1 – масса камня, \upsilon_1 – скорость камня, m_2 – масса тележки, \upsilon_2 – скорость тележки.

    \[m_1\upsilon_1+ m_2\upsilon_2=(m_1+m_2)\upsilon_3\]

За положительное направление примем направление полета камня, тогда скорость тележки будет со знаком «минус»

    \[2\cdot 7- 10\cdot 1=(2+10)\upsilon_3\]

    \[14 - 10=12\upsilon_3\]

    \[\upsilon_3=\frac{4}{12}=2\]

Получили скорость тележки с камнем со знаком «плюс» – это значит, что она после «поимки» камня поедет в противоположную сторону.

Ответ: 2 м/c

 

Задача 10. Средневековая пушка массой 200 кг установлена у края плоской крыши  высокой башни. Пушка выпускает ядро массой 5 кг горизонтально, оно приземляется на расстоянии 300 м от стены башни. Пушка, двигаясь без трения, откатывается назад и падает на землю.  На каком расстоянии от основания башни она упадет?

 

Предположим, что высота стены башни H. Ядро пушка выпустила горизонтально, и его полет подобен телу, брошенному горизонтально: по горизонтали ядро перемещается с постоянной скоростью, а по вертикали падает, то есть движется равноускоренно.

Тогда ядро будет падать с этой высоты в течение времени, которое можно установить из формулы: H=\frac{gt^2}{2}

    \[t=\sqrt{2gH}\]

Все это время ядро летит горизонтально с постоянной скоростью, и пролетает 300 метров. Тогда его скорость по горизонтали равна:

    \[\upsilon_1=\frac{S_1}{t}=\frac{S_1}{\sqrt{2gH}}=\frac{300}{\sqrt{2gH}}\]

Импульс ядра равен импульсу пушки, поэтому пушка откатится назад со скоростью:

    \[m_1\upsilon_1= m_2\upsilon_2\]

Здесь m_1 – масса ядра, \upsilon_1 – его скорость, m_2 – масса пушки, \upsilon_2 – ее скорость.

    \[5\cdot \frac{300}{\sqrt{2gH}}= 200 \cdot\upsilon_2\]

Найдем горизонтальную скорость пушки:

    \[\upsilon_2=\frac{5\cdot \frac{300}{\sqrt{2gH}}}{200}\]

    \[\upsilon_2=7,5{\sqrt{2gH}}\]

Пушка падает ровно столько же времени, как и ядро, так как все тела на Земле падают вниз с одним и тем же ускорением, поэтому пушка пролетит за время t=\sqrt{2gH} расстояние от стены до места падения, равное: S_2=\upsilon_2 t=7,5 м

Ответ: 7,5 м

Импульс тела — методическая рекомендация. Физика, 9 класс.

1. Импульс тела 1 вид — рецептивный лёгкое 1 Б. Отработка навыка нахождения модуля импульса тела по формуле импульса.
2. Проекция импульса тела на ось 1 вид — рецептивный лёгкое 2 Б. Отработка навыка нахождения проекции вектора импульса тела на горизонтальную ось при движении данного тела вдоль и против оси.
3. Скорость тела 1 вид — рецептивный лёгкое 2 Б. Отработка навыка нахождения скорости движения тела по известной массе и импульсу тела.
4. Масса тела 2 вид — интерпретация среднее 2 Б. Отработка навыка нахождения массы тела по известной скорости движения и импульсу тела.
5. Изменение импульса тела при изменении его скорости 2 вид — интерпретация среднее 2 Б. Отработка навыка нахождения изменения модуля импульса тела при изменении модуля скорости движения тела.
6. Изменение импульса тела при изменении его массы и скорости 2 вид — интерпретация среднее 3 Б. Отработка навыка нахождения изменения модуля импульса движущегося тела при изменении массы и модуля скорости движения тела.
7. Изменение импульса тела при движении по окружности 3 вид — анализ сложное 4 Б. Отработка навыка нахождения изменения импульса тела при движении тела по окружности.
8. Импульс равноускоренно движущегося тела 3 вид — анализ сложное 4 Б. Отработка навыка нахождения импульса равноускоренно движущегося тела.
9. Изменение импульса тела, летящего под углом к горизонту 3 вид — анализ сложное 5 Б. Отработка навыка нахождения изменения импульса тела, летящего под углом к горизонту.
10. Изменение импульса тела при ударе 3 вид — анализ сложное 5 Б. Отработка навыка нахождения изменения импульса тела при ударе тела о горизонтальную гладкую поверхность во время свободного падения.

Импульс тела. Закон сохранения импульса – FIZI4KA

1. Опыты и наблюдения свидетельствуют о том, что результат действия силы (взаимодействия) зависит от времени её действия. Так, если к штативу на нити подвесить
тяжёлую гирю, к которой привязана ещё одна нить снизу, и резко дернуть нижнюю нить, то она оборвётся, а верхняя нить останется целой. Если же теперь медленно потянуть
нижнюю нить, то оборвётся верхняя нить. Поэтому для характеристики действия силы вводят величину, называемую импульсом силы.

Импульсом силы называют векторную величину, равную произведению силы и времени её действия ​\( (\vec{F}t) \)​. Импульс силы является мерой действия силы за некоторый промежуток времени.

Единица импульса силы ​\( [\,F\cdot t\,] \)​ = 1 Н · с.

2. С другой стороны, результат действия силы зависит и от характеристик тела, на которое эта сила действует.

Зависимость результата действия силы от массы тела можно проиллюстрировать с помощью следующего простого примера. Летящий с некоторой скоростью футбольный мяч, ударяясь о пустую картонную коробку, сдвинет её с места, а, ударяясь о такую же коробку, заполненную металлическими предметами, скорее всего, отскочит от неё, а коробка при этом останется неподвижной.

Пуля, летящая со скоростью 2 м/с, при попадании в деревянную стенку в лучшем случае оставит на ней вмятину, а пуля, летящая со скоростью 200 м/с, стенку пробьёт. Таким образом, результат действия силы зависит от массы и скорости взаимодействующих тел.

3. Величину, равную произведению массы тела и его скорости, называют импульсом тела, ​\( \vec{p}=m\vec{v} \)​ — импульс тела (или просто импульс). Единица импульса ​\( [\,p\,] \)​ = 1 кг · м/с2.

Импульс — величина векторная, поскольку масса — величина скалярная, а скорость — векторная.

Импульс — величина относительная, его значение зависит от выбора системы отсчёта, поскольку относительной величиной является скорость.

4. Импульс силы и изменение импульса тела связаны между собой.

Запишем второй закон Ньютона: ​\( \vec{F}=m\vec{a} \)​.

Подставим в формулу выражение для ускорения ​\( \vec{a}=\frac{\vec{v}-\vec{v}_0}{t} \)​, \( \vec{F}=\frac{m(\vec{v}-\vec{v}_0)}{t} \)​ или \( \vec{F}t=m\vec{v}-m\vec{v}_0 \)​.

В левой части равенства стоит импульс силы; в правой части — разность конечного и начального импульсов тела, т.е. изменение импульса тела. ​\( \vec{F}t=\Delta(m\vec{v}) \)​.

Таким образом, импульс силы равен изменению импульса тела.

Это иная формулировка второго закона Ньютона. Именно в таком виде сформулировал свой закон Ньютон.

5. Взаимодействующие между собой тела образуют систему тел. Между телами системы действуют силы взаимодействия: на одно тело — сила ​\( \vec{F}_1 \)​, на другое тело — сила \( \vec{F}_2 \). При этом сила равна силе и направлена противоположно ей: ​\( \vec{F}_1=-\vec{F}_2 \)​ (рис. 41).

Силы, с которыми тела системы взаимодействуют между собой, называют внутренними силами.

Помимо внутренних сил, на тела системы действуют внешние силы. Так взаимодействующие тела притягиваются к Земле. Сила тяготения является в данном случае внешней силой. Если тела движутся, то на них действует сила сопротивления воздуха, сила трения. Они тоже являются внешними силами по отношению к системе, которая в данном случае состоит из двух тел. Ни Земля, ни воздух в эту систему тел не входят.

Внешними силами называются силы, которые действуют на тела системы со стороны других тел.

Будем рассматривать такую систему тел, на которую не действуют внешние силы.

Замкнутой системой тел называют систему тел, взаимодействующих между собой и не взаимодействующих с другими телами. В замкнутой системе действуют только внутренние силы, внешние силы на неё не действуют.

6. Рассмотрим взаимодействие двух тел, составляющих замкнутую систему. Масса первого тела ​\( m_1 \),​ его скорость до взаимодействия ​\( \vec{v}_{01} \)​, после взаимодействия \( \vec{v}_{1} \). Масса второго тела \( m_1 \), его скорость до взаимодействия \( \vec{v}_{02} \), после взаимодействия \( \vec{v}_{2} \). Для этих тел справедливо равенство:

\[ m_1\vec{v}_{01}+m_1\vec{v}_{02}=m_1\vec{v}_{1}+m_1\vec{v}_{2} \]

В левой части равенства стоит сумма импульсов тел до взаимодействия, в правой части — сумма импульсов тел после взаимодействия. Как видно, импульс каждого тела при взаимодействии изменился, а сумма импульсов осталась неизменной.

Геометрическая сумма импульсов тел, входящих в замкнутую систему, остаётся постоянной при любых взаимодействиях тел этой системы между собой.

В этом состоит закон сохранения импульса.

7. Замкнутая система — это идеализация. В реальном мире нет таких систем, на которые не действовали бы внешние силы. Однако в ряде случаев реальные системы взаимодействующих тел можно рассматривать как замкнутые. Это возможно, когда внутренние силы много больше внешних сил, или когда время взаимодействия мало, или когда внешние силы уравновешивают друг друга. Кроме того, в ряде случаев равна нулю проекция внешних сил на какое-либо направление. В этом случае закон сохранения импульса выполняется для проекций импульсов взаимодействующих тел на это направление.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Тело двигалось под действием силы 10 Н в течение 5 с. Чему равно изменение импульса тела?

1) 2 Н/с
2) 5 Н·с
3) 50 Н·с
4) нельзя дать ответ, т.к. неизвестны масса и скорость тела

2. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся в ту же сторону с той же скоростью?

1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с

3. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся с той же скоростью, но в противоположную сторону?

1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с

4. На графике показаны изменения скорости велосипедиста с течением времени. Чему равно изменение импульса велосипедиста через 4 с после начала движения, если его масса 50 кг?

1) 200 кг·м/с
2) 2500 кг·м/с
3) 2000 кг·м/с
4) 2500 кг·м/с

5. Тело движется в положительном направлении оси ​\( Ox \)​. На рисунке представлен график зависимости от времени ​\( t \)​ проекции силы ​\( F_x \)​, действующей на тело. В интервале времени от 0 до 5 с проекция импульса тела на ось ​\( Ox \)​

1) уменьшается на 5 кг·м/с
2) не изменяется
3) увеличивается на 10 кг·м/с
4) увеличивается на 5 кг·м/с

6. Два шара массой ​\( m_1 \)​ и ​\( m_2 \)​ движутся в одном направлении со скоростями соответственно ​\( x_1 \)​ и \( x_2 \) по гладкому горизонтальному столу (см. рисунок). Полный импульс ​\( p \)​ системы шаров равен по модулю

1) ​\( p=m_2x_2-m_1x_1 \)​ и направлен налево ←
2) \( p=m_1x_1-m_2x_2 \) и направлен вправо →
3) \( p=m_1x_1+m_2x_2 \) и направлен налево ←
4) \( p=m_1x_1-m_2x_2 \) и направлен вправо →

7. Два шарика массой 50 г и 100 г движутся со скоростью 0,6 м/с и 0,4 м/с соответственно. Направления движения шариков составляют угол 90°. Модуль суммарного импульса шариков равен

1) 0,15 кг·м/с
2) 0,07 кг·м/с
3) 0,05 кг·м/с
4) 0,01 кг·м/с

8. Снаряд, импульс которого ​\( \vec{p} \)​ был направлен вертикально вверх, разорвался на два осколка. Импульс одного осколка \( \vec{p}_1 \) в момент взрыва был направлен горизонтально (рис. 1). Какое направление имел импульс \( \vec{p}_2 \) второго осколка (рис. 2)?

1) 1
2) 2
3) 3
4) 4

9. Масса мальчика в 3 раза меньше массы лодки. В момент прыжка с неподвижной лодки скорость мальчика равна 1,5 м/с. При этом лодка приобретает скорость, равную

1) 4,5 м/с
2) 2 м/с
3) 0,5 м/с
4) 0 м/с

10. Закон сохранения импульса справедлив:

А. Для замкнутой системы тел
Б. Для любой системы тел.

Правильный ответ

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

11. Установите соответствие между физическими величинами (в левом столбце таблицы) и их единицами (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами

ВЕЛИЧИНА
A. Импульс
Б. Скорость
B. Ускорение

ЕДИНИЦА
1) метр/секунда (1 м/с)
2) ньютон (1 Н)
3) метр/секунда2 (1 м/с2)
4) джоуль (1 Дж)
5) ньютон·секунда (1 Н·с)

12. Из приведённого перечня выберите 2 правильных утверждения и запишите их номера в таблицу.

1) Закон сохранения импульса справедлив для любой системы тел.
2) Импульс тела — величина скалярная.
3) Закон сохранения импульса справедлив для замкнутой системы тел.
4) Изменение импульса тела равно импульсу силы.
5) Закон сохранения импульса не применим к незамкнутой системе тел ни при каких условиях.

Часть 2

13. Снаряд летит горизонтально и разрывается на два осколка массой 2 кг и 3 кг. С какой скоростью летел снаряд, если первый осколок в результате разрыва приобрёл скорость 50 м/с, второй 40 м/с? Скорости осколков направлены горизонтально в противоположную сторону.

Ответы

Импульс тела. Закон сохранения импульса

Оценка

Импульс силы | Все Формулы

    \[ \]

Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.

    \[\Large p=Ft=m\upsilon-m\upsilon_0\]

Векторную величину Ft, равную произведению силы на время ее действия, называют импульсом силы. Векторную величину р=mv, равную произведению массы тела на его скорость, называют импульсом тела.

Формула для нахождения импульса тела вытекает из всем извесного Второго закона Ньютона

    \[\Large F=ma \]

А ускорение найдем через разность скоростей на время.

    \[\Large F=m(\frac{\upsilon -\upsilon _0}{t})\]

Отсюда и получается, что импульс силы

    \[\large Ft=m\upsilon-m\upsilon_0\]

Из импульса силы вытекает закон сохранения импульса

    \[\Large m_1\upsilon_1+m_2\upsilon _2=m_1\upsilon _1^

Так же есть:

Импульс тела

    \[\Large p=m\upsilon\]

В Формуле мы использовали :

p=Ft — Импульс силы

m — Масса тела

F — Сила приложенная к телу

t — Время действия силы

    \[\upsilon\]

— Конечная скорость тела

    \[\upsilon_0\]

— Начальная скорость тела

Импульсная амплитудная модуляция

— схема, определение, преимущества, типы

    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 11-12
    • КОНКУРЕНТНЫЙ ЭКЗАМЕН
      • BNAT 000 NC
        • BNAT 000 Книги
          • Книги NCERT для класса 5
          • Книги NCERT для класса 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • Книги NCERT для класса 11
          • Книги NCERT для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11
          • NCERT Exemplar Class 11
          • NCERT 9000 9000
          • NCERT
            • Решения RS Aggarwal, класс 12
            • Решения RS Aggarwal, класс 11
            • Решения RS Aggarwal, класс 10
              • 90 003 Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • Решения RD Sharma
            • RD Sharma Class 6 Решения
            • Решения RD Sharma
            • Решения RD Sharma класса 8
            • Решения RD Sharma класса 9
            • Решения RD Sharma класса 10
            • Решения RD Sharma класса 11
            • Решения RD Sharma класса 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Теорема Пифагора
            • 000
            • 00030003000300030004
            • Простые числа
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убыток
            • Полиномиальные уравнения
            • Деление фракций
          • 000
          • 000
          • 000
          • 000
          • 000 BIOG3000
                FORMULAS
                • Математические формулы
                • Алгебраные формулы
                • Тригонометрические формулы
                • Геометрические формулы
              • КАЛЬКУЛЯТОРЫ
                • Математические калькуляторы
                • 000 PBS4000
                • 000
                • 000 Физические калькуляторы
                • 000
                • 000
                • 000 PBS4000
                • 000
                • 000 Калькуляторы для химии
                  • Класс 6
                • Образцы документов CBSE для класса 7
                • Образцы документов CBSE для класса 8
                • Образцы документов CBSE для класса 9
                • Образцы документов CBSE для класса 10
          90 004
        .

        Формула объемного модуля упругости

        Когда к телу действует сила во всех направлениях и приводит к деформации всего объема, коэффициент упругости называется объемным модулем. Отношение изменения давления к дробному объему сжатия:

        Объемный модуль = (изменение напряжения давления) / (относительный объем) = (изменение давления) / (изменение объема / исходный объем)

        Уравнение

        B = ΔP / (ΔV / V)

        У нас:

        B: Модуль объемной упругости

        ΔP: изменение давления или силы, приложенной к единице площади материала

        ΔV: изменение объема материала из-за сжатия

        V: Начальный объем материала

        Уравнение объемного модуля упругости Вопросы:

        1) Каков объемный модуль упругости тела, которое испытало изменение давления на 5 * 10 4 Н / м 2 и его объем увеличился с 4 см 3 до 3.9 см 3 ?.

        Ответ: Модуль объемной упругости рассчитывается по формуле

        B = ΔP / (ΔV / V)

        B = (5 * 10 4 Н / м 2 ) / ((4 см 3 — 3,9 см 3 ) / 4 см 3 ) = 0,125 * 10 4 Н / м 2

        B = 1,25 * 10 4 Н / м 2

        2) Сфера радиусом 10 мм растягивается из своего первоначального объема до половины с помощью силы 100 Н. Каков объемный модуль упругости системы?

        Ответ: Модуль объемной упругости находится из уравнения:

        B = ΔP / (ΔV / V)

        Объем рассчитывается с использованием V = 4/3 π (r) 3 , где r равно 10 мм, тогда V равно

        A = 4/3 π (10 мм) 3 = 4/3 π (0.01 м) 3 = 4,2 * 10 (-6) м 3

        , подставив значение объема в

        ΔV = Vf — Vi = 4,2 * 10 (-6) м 3 — 1,1 * 10 (-6) м 3 = 1,1 * 10 (-6) м 3

        Разделив на V, получим дробный объем,

        ΔV / V = ​​1,1 * 10 (-6) м 3 / 4,2 * 10 (-6) м 3 = 0,26.

        Чтобы найти давление, мы используем формулу ΔP = F / A, где A — площадь сферы A = 4 π r 2 = 4 π (0.01 м) 2 = 1,26 * 10 (-3) м 2

        Тогда ΔP = 100 Н / 1,26 * 10 (-3) м 2 = 79300 Н / м 2 .

        Наконец, модуль объемной упругости равен

        .

        B = (79300 Н / м 2 ) / (0,26) = 305000 Н / м 2

        .

        Объемный модуль упругости и эластичность жидкости

        Объемный модуль упругости — или объемный модуль — это свойство материала, характеризующее сжимаемость жидкости — насколько легко можно изменить единицу объема жидкости при изменении давления, действующего на нее.

        Объемный модуль упругости можно рассчитать как

        K = — dp / (dV / V 0 )

        = — ( p 1 — p 0 ) / ((V 1 — V 0 ) / V 0 ) (1)

        где

        K = объемный модуль упругости (Па, Н / м 2 )

        dp = перепад давления на объект (Па, Н / м 2 )

        dV = перепад изменения объема объекта (м 3 )

        V 0 = начальный объем объекта (м 3 )

        p 0 = начальное давление ( Па, Н / м 2 )

        p 1 = конечное давление ( Па, Н / м 2 900 15)

        V 1 = конечный объем ( м 3 )

        Объемный модуль упругости можно также выразить как

        K = dp / (dρ / ρ 0 )

        = ( p 1 — p 0 ) / (( ρ 1 — ρ 0 ) / ρ 0 ) (2)

        где

        dρ = дифференциальное изменение плотности объекта (кг / м 3 )

        ρ 0 = начальная плотность объекта (кг / м 3 )

        ρ 1 = конечная плотность объекта ( кг / м 3 )

        Увеличение по давлению уменьшится объем (1). Уменьшение объема увеличивает плотность (2) .

        • Единица измерения объемного модуля упругости в системе СИ составляет Н / м 2 (Па)
        • Британская система мер (BG) составляет фунтов f / дюйм 2 (psi)
        • 1 фунт f / дюйм 2 (psi) = 6,894 10 3 Н / м 2 (Па)

        Большой модуль объемного сжатия указывает на относительную несжимаемость жидкости.

        Модуль объемной упругости для некоторых распространенных жидкостей:

        Жидкость Модуль объемной упругости
        — K —
        Британские единицы — BG
        ( 10 5 psi14 / фунт / дюйм фунт / кв. Дюйм) 2 )         		Единицы СИ
        ( 10 9 Па, Н / м 2 )
        Ацетон 1.34 0,92
        Бензол 1,5 1,05
        Тетрахлорид углерода 1,91 1,32
        Спирт этиловый 602 902 902 902 902 604 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902
        Глицерин 6,31 4,35
        Минеральное масло ISO 32 2,6 1.8
        Керосин 1,9 1,3
        Ртуть 41,4 28,5
        Парафиновое масло 2,41 1,66 1,66 1,66
        Эфир фосфорной кислоты 4,4 3
        Масло SAE 30 2,2 1,5
        Морская вода 3.39 2,34
        Серная кислота 4,3 3,0
        Вода 3,12 2,15
        Вода — гликолевая 902 902 902 902 902 3,3 2,3

        Нержавеющая сталь с модулем объемной упругости 163 10 9 Па составляет прибл. в 80 раз сложнее сжимать, чем воду с модулем объемной упругости 2.15 10 9 Па .

        Пример — Плотность морской воды в Марианской впадине

        — самая глубокая из известных точек в Мировом океане — 10994 м .

        Mariana Trench

        Гидростатическое давление в Марианской впадине можно рассчитать как

        p 1 = (1022 кг / м 3 ) (9,81 м / с 2 ) (10994 м)

        = 110 10 6 Па (110 МПа)

        Начальное давление на уровне моря составляет 10 5 Па , а плотность морской воды на уровне моря составляет 1022 кг / м 3 .

        Плотность морской воды на глубине можно рассчитать, изменив (2) на

        ρ 1 = ( ( p 1 — p 0 ) ρ 0 + K ρ 0 ) / K

        = (((110 10 6 Па) — (1 10 5 Па)) (1022 кг / м 3 ) + (2.34 10 9 Па) (1022 кг / м 3 )) / ( 2,34 10 9 Па )

        = 1070 кг / м 3

        Примечание! — поскольку плотность морской воды меняется в зависимости от глубины, расчет давления можно было бы сделать более точным, рассчитав интервалы глубины.

        .Формула модуля сдвига

        | Пример и практический вопрос

        Формула модуля сдвига

        СМОТРЕТЬ БОЛЬШЕ

        Модуль сдвига показывает, насколько эффективно тело будет сопротивляться силам, приложенным для изменения его формы.Когда к телу прикладывается поперечная сила, которая приводит к его поперечной деформации, коэффициент упругости называется модулем упругости при сдвиге. Он измеряет жесткость тела. Концептуально это отношение напряжения сдвига к деформации сдвига в теле.
        Пусть при приложении силы F по касательной к верхней поверхности коробки, закрепленной внизу, верхняя поверхность смещается на x, а плоскость, перпендикулярная силе, поворачивается на угол \ [\ theta \], как показано.

        Затем напряжение сдвига: \ [\ sigma = \ frac {F} {A} \]
        Деформация сдвига: \ [\ theta = \ frac {x} {L} \] (Как \ [\ theta \] очень-очень мало, \ [\ tan \ theta = \ theta \])
        L — перпендикулярное расстояние (в плоскости, перпендикулярной силе) до слоя, который смещается на величину x от фиксированного слоя.
        Тогда модуль сдвига: \ [G = \ frac {{shear \, \, \, stress}} {{shear \, \, \, напряжения}} = \ frac {{F / A}} {{x / L}} = \ frac {{FL}} {{Ax}} \]
        Единица модуля сдвига: Нм –2 или паскаль (Па).
        Пример 1
        Тонкая квадратная пластина размером 80 см × 80 см × 0,5 см закреплена вертикально на одной из ее меньших поверхностей. На него действует срезающая сила 2,8 × 10 4 Н. Верхняя грань куба смещена на 0,16 мм относительно нижней поверхности.{10}} Па \]

        Практический вопрос
        О приложении усилия сдвига 8 кН к кубу с ребром 4 см, изготовленному из материала с модулем сдвига 2 × 10 9 Па, верхней грани куба куб смещается на:
        (a) 0,1 мм (b) 0,1 см (c) 0,4 мм (d) 0,2 см
        Ans (a)

        ,