Таблица степеней 2 (двойки)
Приведенная таблица кроме степени двойки показывает максимальные числа, которые может хранить компьютер для заданного числа бит. Причем как для целых так и чисел со знаком.
Исторически сложилось, что компьютеры используют двоичную систему счисления, а, соответственно, и хранения данных. Таким образом, любое число можно представить как последовательность нулей и единиц (бит информации). Существует несколько способов представления чисел в виде двоичной последовательности.
Рассмотрим наиболее простой из них — это целое положительное число. Тогда чем больше число нам нужно записать, тем более длинная последовательность бит нам необходима.
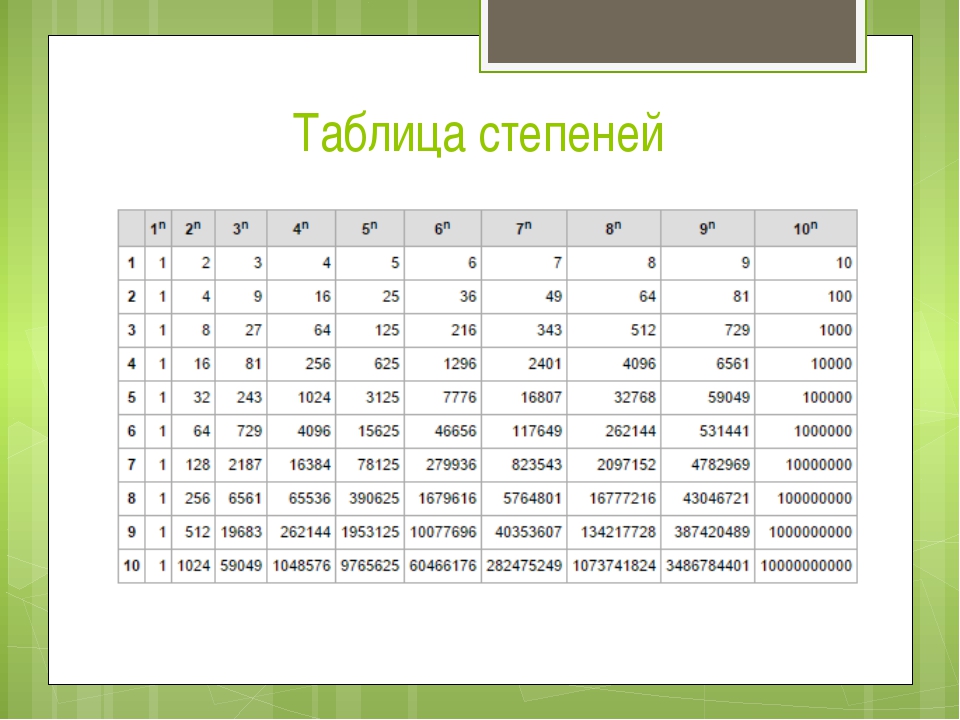
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.Как пользоваться
таблицей степеней числа два?Первый столбец — это степень двойки
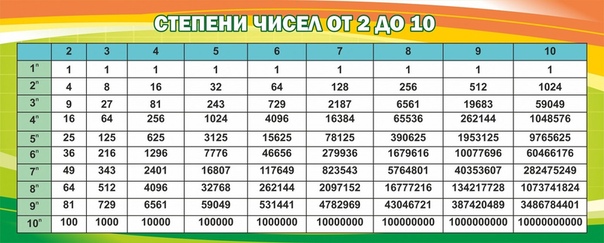
Второй столбец — значение двойки в соответствующей степени (n).
Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) — это 128
Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).
Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 2
| Степень двойки (n) |
Значение степени двойки 2n |
Максимальное число без знака, записанное с помощью n бит |
|
| 0 | 1 | - | - |
| 1 | 2 | 1 | - |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 131 072 | 131 071 | 65 535 | |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 33 554 431 | |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Необходимо принять во внимание, что не все числа в компьютере представлены таким образом.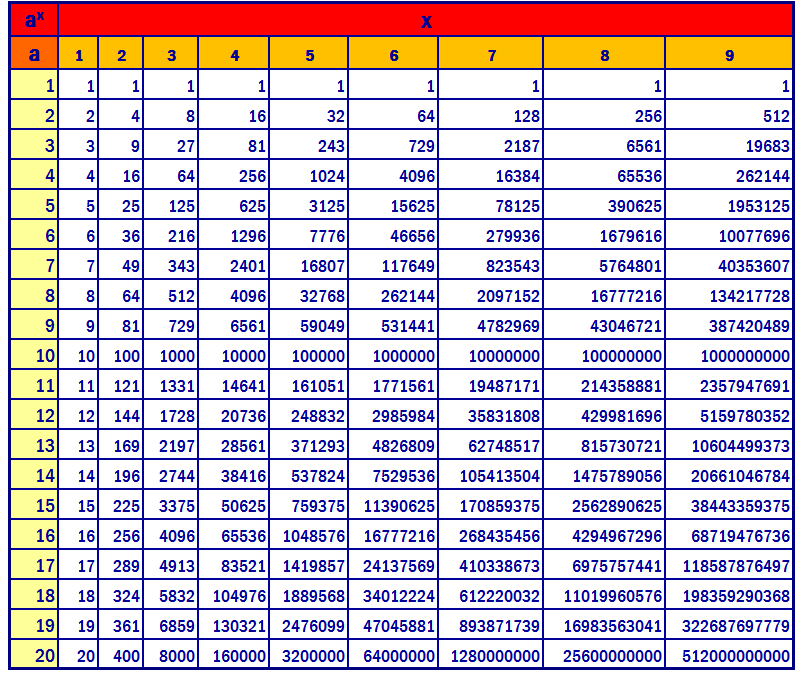 Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Для этого же самого примера
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048.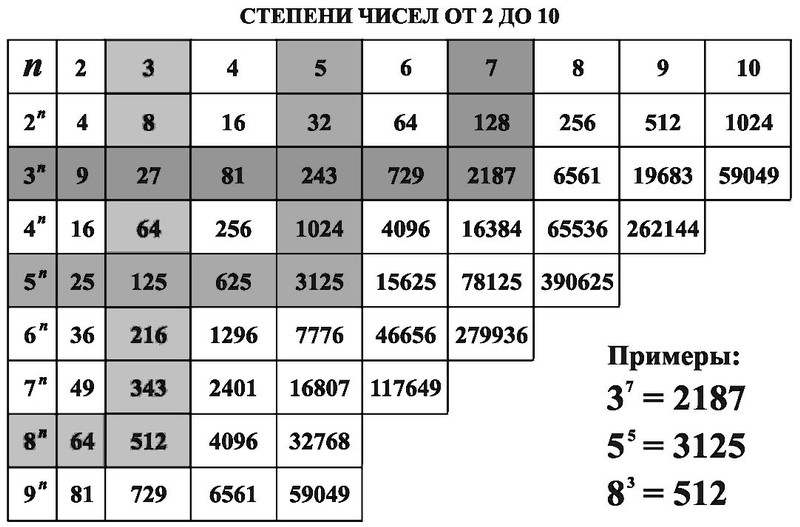
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072
Хранение и кодирование информации | Описание курса | Использование электронных таблиц Excel
Оценка риска возникновения остеопоротических переломов позвонков 2–3-й степени у женщин репродуктивного возраста и мужчин до 50 лет с сахарным диабетом 1-го типа | Водянова
1. Shah VN, Shah CS, Snell-Bergeon JK. Type 1 diabetes and risk of fracture: meta-analysis and review of the literature. Diabet Med. 2015;32(9): 1134–42. doi: 10.1111/ dme.12734.
2. Vestergaard P, Rejnmark L, Mosekilde L. Diabetes and its complications and their relationship with risk of fractures in type 1 and 2 diabetes. Calcif Tissue Int. 2009;84(1): 45–55. doi: 10.1007/s00223-008-9195-5.
3. Wang J, You W, Jing Z, Wang R, Fu Z, Wang Y. Increased risk of vertebral fracture in patients with diabetes: a meta-analysis of cohort studies. Int Orthop. 2016;40(6): 1299–307. doi: 10.1007/s00264-016-3146-y.
4. Zhukouskaya VV, Eller-Vainicher C, Vadzianava VV, Shepelkevich AP, Zhurava IV, Korolenko GG, Salko OB, Cairoli E, Beck-Peccoz P, Chiodini I. Prevalence of morphometric vertebral fractures in patients with type 1 diabetes. Diabetes Care. 2013;36(6): 1635–40. doi: 10.2337/ dc12-1355.
5. Ялочкина ТО, Белая ЖЕ, Рожинская ЛЯ, Анциферов МБ, Дзеранова ЛК, Мельниченко ГА. Переломы костей при сахарном диабете 2 типа: распространенность и факторы риска. Сахарный диабет. 2016;19(5): 359–65. doi: 10.14341/DM7796.
6. Vestergaard P. Discrepancies in bone mineral density and fracture risk in patients with type 1 and type 2 diabetes – a meta-analysis. Osteoporos Int. 2007;18(4): 427–44. doi: 10.1007/s00198-006-0253-4.
Vestergaard P. Discrepancies in bone mineral density and fracture risk in patients with type 1 and type 2 diabetes – a meta-analysis. Osteoporos Int. 2007;18(4): 427–44. doi: 10.1007/s00198-006-0253-4.
7. Crans GG, Genant HK, Krege JH. Prognostic utility of a semiquantitative spinal deformity index. Bone. 2005;37(2): 175–9. doi: 10.1016/j. bone.2005.04.003.
8. Lindsay R, Silverman SL, Cooper C, Hanley DA, Barton I, Broy SB, Licata A, Benhamou L, Geusens P, Flowers K, Stracke H, Seeman E. Risk of new vertebral fracture in the year following a fracture. JAMA. 2001;285(3): 320–3. doi: 10.1001/jama.285.3.320.
9. Melton LJ 3rd, Atkinson EJ, Cooper C, O’Fallon WM, Riggs BL. Vertebral fractures predict subsequent fractures. Osteoporos Int. 1999;10(3): 214–21. doi: 10.1007/ s001980050218.
doi: 10.1007/ s001980050218.
10. Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF 3rd, Feldman HI, Kusek JW, Eggers P, Van Lente F, Greene T, Coresh J; CKDEPI (Chronic Kidney Disease Epidemiology Collaboration). A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150(9): 604–12. doi: 10.7326/0003-4819-150-9-200905050-00006.
11. The International Society for Clinical Densitometry. Official Positions 2015 ISCD Combined: Adult and Pediatric [Internet]. 2015. 24 p. Доступно на: https://iscd.app.box. com/v/OP-ISCD-2015-Adult. Дата обращения: 15.05.2017.
12. Реброва ОЮ. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. М.: Медиа Сфера; 2002. 312 с.
13. Zhukouskaya VV, Shepelkevich AP, Chiodini I. Bone health in type 1 diabetes: where we are now and how we should proceed. Advances in Endocrinology. 2014;2014:982129. doi: 10.1155/2014/982129.
Zhukouskaya VV, Shepelkevich AP, Chiodini I. Bone health in type 1 diabetes: where we are now and how we should proceed. Advances in Endocrinology. 2014;2014:982129. doi: 10.1155/2014/982129.
14. Genant HK, Wu CY, van Kuijk C, Nevitt MC. Vertebral fracture assessment using a semiquantitative technique. J Bone Miner Res. 1993;8(9): 1137–48. doi: 10.1002/jbmr.5650080915.
15. Genant HK, Jergas M, Palermo L, Nevitt M, Val-entin RS, Black D, Cummings SR. Comparison of semiquantitative visual and quantitative morphometric assessment of prevalent and incident vertebral fractures in osteoporosis The Study of Osteoporotic Fractures Research Group. J Bone Miner Res. 1996;11(7): 984–96. doi: 10.1002/jbmr.5650110716.
16. Шепелькевич АП, Кабак СЛ, Рогов ЮИ, Кабак НС, Лебедь ОА. Морфологические изменения костной ткани при сахарном диабете 1-го типа. Военная медицина. 2011;(4): 68–73.
Морфологические изменения костной ткани при сахарном диабете 1-го типа. Военная медицина. 2011;(4): 68–73.
17. Трухачева НВ. Математическая статистика в медико-биологических исследованиях с применением пакета STATISTICA. М.: ГЭОТАР-Медиа; 2013. 384 с.
Степень с натуральным показателем
Предварительные навыкиЧто такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
Число, которое повторяется называют основанием степени. В выражении 53 основанием степени является число 5.
А число, которое надписано над числом 5 называют показателем степени. В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 25
Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5.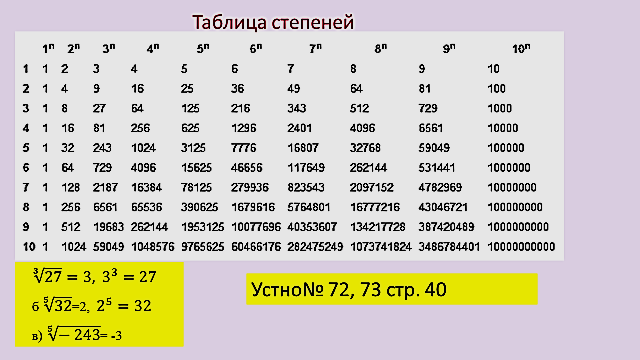 Выполнить умножение x × x
Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице.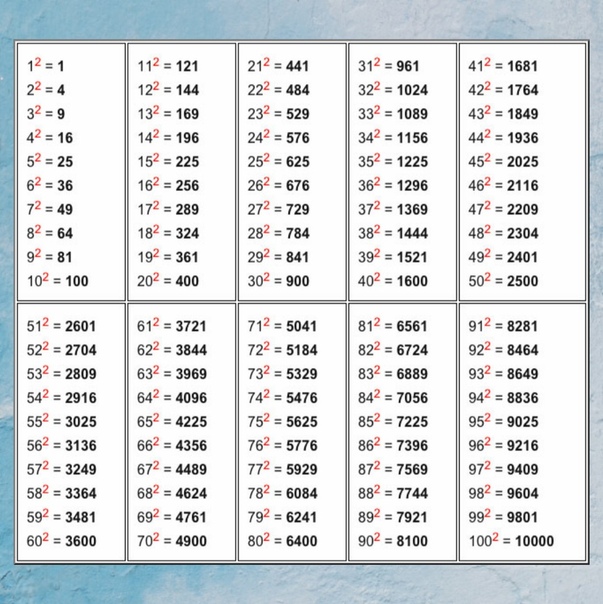 Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3.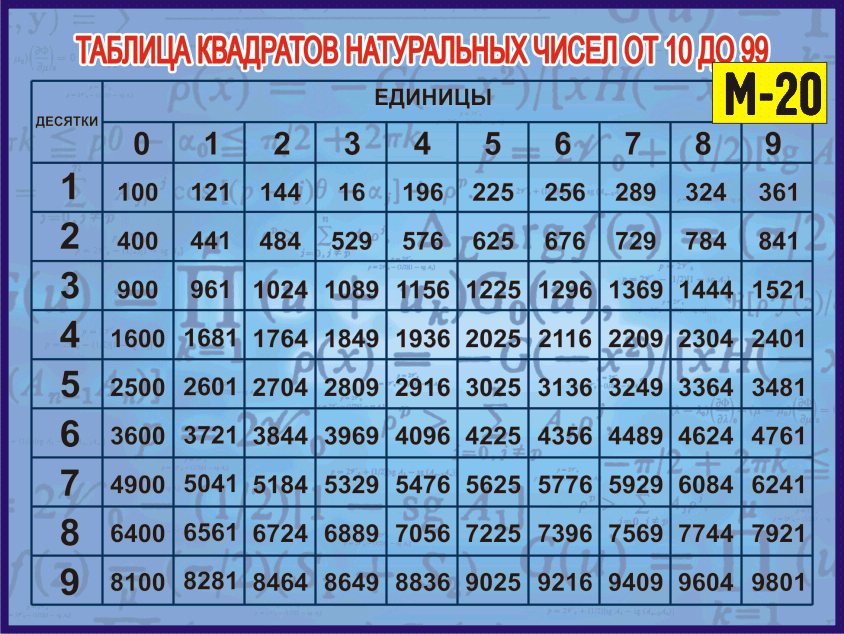 Возьмём в скобки данное произведение и в качестве показателя укажем 2
Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27.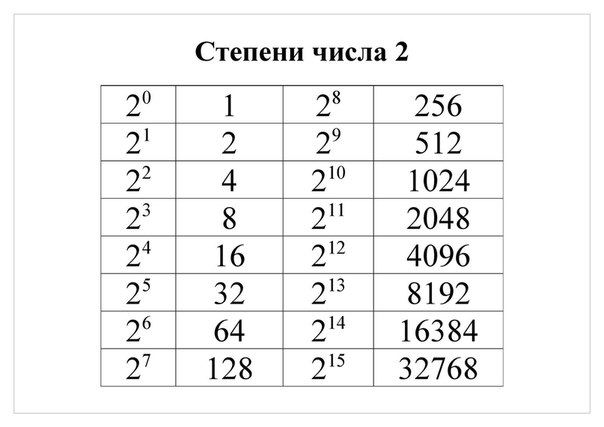 Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n.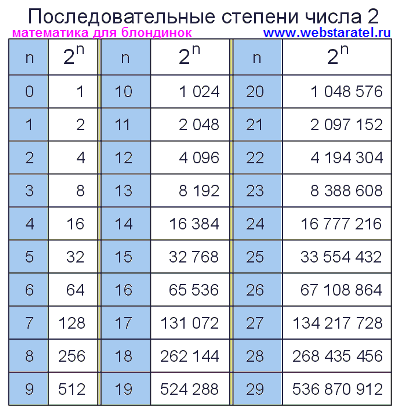 То есть левая и правая часть равенства поменялись местами.
То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8.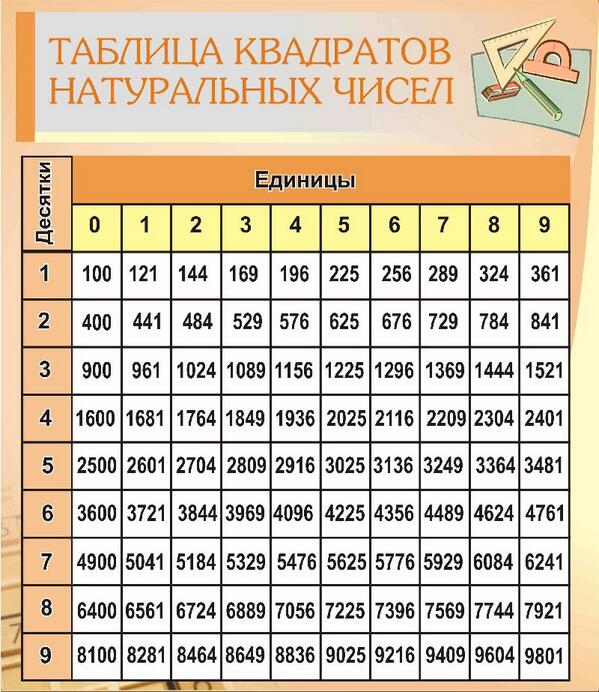 Буквенная часть останется без изменений:
Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26.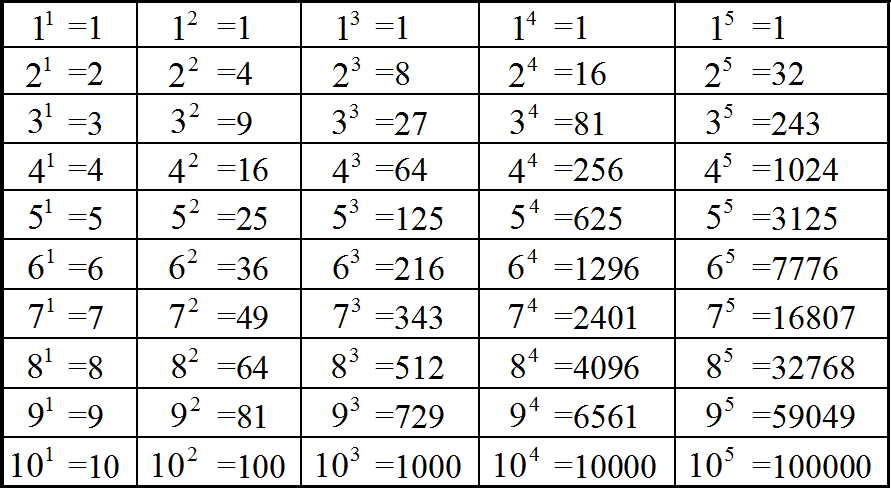 Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3.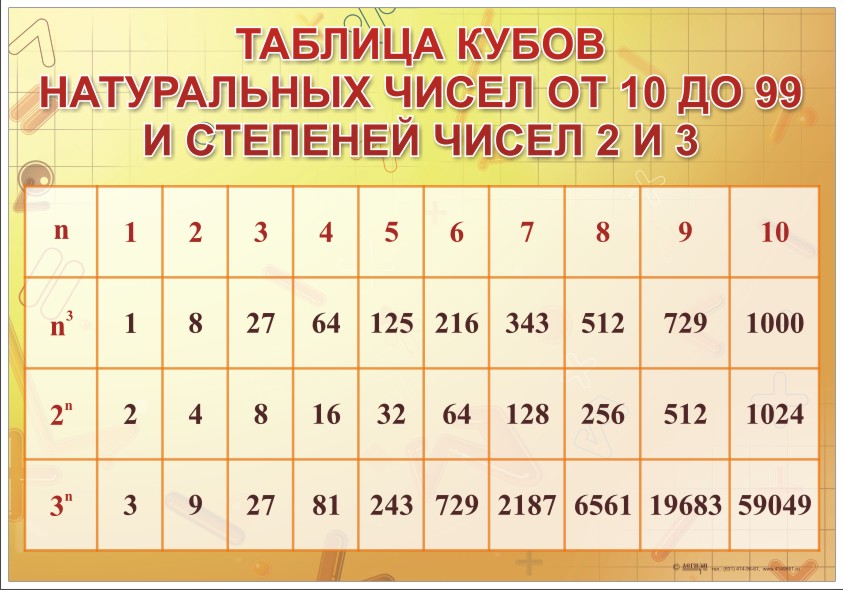 Представить частное x3 : x в виде степени с основанием x
Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x.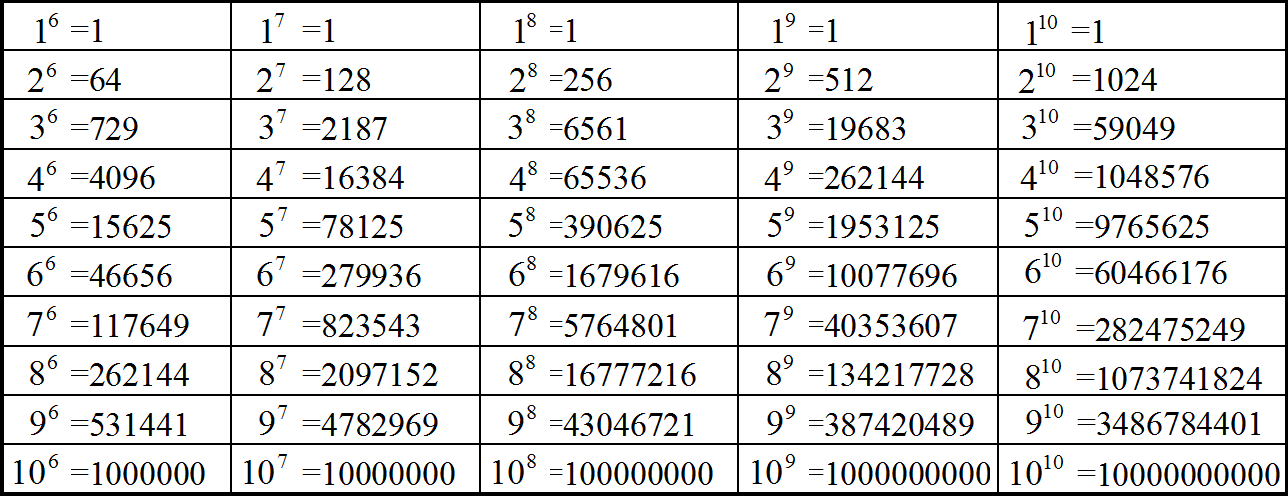 Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь на x2 нужно числитель и знаменатель дроби разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения равно 28. Запишем решение полностью:
Запишем решение полностью:
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь на c¹Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Действительно ли 2 + 2 равно 4? Получение степени бакалавра в муниципальном колледже
×
В наших усилиях по доставке хорошего контента как можно большему количеству людей текст этой статьи был переведен на машину, поэтому, пожалуйста, извините за любые ошибки. Спасибо!
Спасибо!
Кэти Э Ван Вик — Общественный колледж Такомы
Для получения традиционной степени бакалавра в США требуется четыре года, и студентам всего мира сказали, что для получения этой степени они должны сдать TOEFL или IELTS, получить высокий средний балл, набрать 1400+ на SAT и поступить на экзамен Университет. Но это не так!
Степень бакалавра 2 + 2 существует с конца 1800-х годов, когда в США были созданы общественные и младшие колледжи. По оценкам, почти половина всех студентов, получивших сегодня четырехлетнюю степень, посещали двухгодичные учебные заведения или общественные колледжи. . Это 50%! Однако в глобальном масштабе мы обнаруживаем недостаток знаний о том, что такое общественный колледж и каковы преимущества получения там степени. Вот краткий список:
- Иностранные студенты сэкономят около 50 000 долларов США, начав обучение в общественном колледже.
- Прием открыт и не требует стандартных тестов, таких как SAT или ACT.

- Классы меньше, больше взаимодействия с преподавателями
- Курсовая работа может быть общей, для изучения специальностей или специфической для интересов студента.
- График гибкий, часто с меньшим количеством курсов в любой момент времени и возможностью посещать занятия ночью или днем.
Я слышу большой вопрос: действительно ли я закончу учебу через четыре года, если начну учиться в общественном колледже?
Давайте посмотрим на несколько дел студентов, чтобы увидеть…
Студент А закончил Общественный колледж Такомы весной 2018 года со степенью младшего специалиста по психологии. В штате Вашингтон Вашингтонский университет в Сиэтле является не только самым высоко оцененным учебным заведением, но и ведущим университетом. Студент A подал заявление о приеме в UW-Seattle и был зачислен на осень 2018 года. После завершения двухлетней курсовой работы он заканчивает учебу со степенью бакалавра психологии весной 2020 года.
2 года Tacoma Community College + 2 года UW-Сиэтл = 4 года бакалавриата
Студент B мечтал работать в авиакосмической компании, такой как Boeing, и начал учиться в Tacoma Community College в области инженерии. Весной 2018 года студент B решил продолжить учебу в Университете штата Вашингтон благодаря рекомендациям профессоров Tacoma Community College и гарантированной схеме приема. Весной 2020 года студент B получает степень бакалавра в области машиностроения.
2 года Tacoma Community College + 2 года Вашингтонского государственного университета = 4 года бакалавриата
Итак, мой вопрос … Действительно ли 2 + 2 равно 4? И ответ ДА!
Что удивительно в выборе общественного колледжа, так это то, что студенты не только экономят деньги и получают дополнительную поддержку, но и имеют больше времени, чтобы сделать лучший выбор университета. Поскольку средний студент трижды меняет специализацию во время учебы в бакалавриате, общественный колледж позволяет им изучать разные специальности и сделать лучший выбор университета на третьем году получения степени бакалавра, а не в старшей школе.
Преимущества пути 2 + 2 очевидны, и, как мы видели выше, математика складывается. Поэтому я рекомендую вам добавить общественный колледж в ваш следующий поиск в Интернете и присоединиться к 50% американцев, которые получают университетскую степень в общественном колледже.
* Ориентировочная экономия затрат. Фактическая экономия может быть значительно выше или, возможно, ниже, в зависимости от учреждения.
Узнайте больше о муниципальном колледже Такомы .
Show More
Кэти Ван Вик — помощник директора по глобальной работе в муниципальном колледже Такомы . Она имеет степень бакалавра математики и степень магистра. в управлении по делам студентов.
| | Адрес этой страницы (вложенность) в справочнике dpva. ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица степеней степеней. Степени натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней. ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица степеней степеней. Степени натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Наименование олимпиады |
№ в перечне |
Предмет |
Профиль |
Уровень |
|
Олимпиада «Высшая проба» |
5 |
дизайн |
дизайн |
1 |
|
Олимпиада «Высшая проба» |
5 |
культурология |
культурология |
1 |
|
Всероссийская олимпиада школьников «Нанотехнологии — прорыв в будущее!» |
7 |
химия, физика, математика, биология |
нанотехнологии |
1 |
|
Московская олимпиада школьников |
36 |
искусство |
история искусств |
1 |
|
Олимпиада по комплексу предметов «Культура и искусство» |
46 |
дизайн, графика, монументально-декоративное искусство, декоративно-прикладное искусство и народные промыслы, технология художественной обработки материалов, искусство костюма и текстиля, конструирование изделий легкой промышленности, технологии и проектирование текстильных изделий, технология изделий легкой промышленности, информационные системы и технологии, технология полиграфического и упаковочного производства, прикладная информатика, профессиональное обучение (по отраслям) |
академический рисунок, живопись, композиция, история искусства и культуры |
1 |
|
Олимпиада по комплексу предметов «Культура и искусство» |
46 |
декоративно-прикладное искусство и народные промыслы, технология художественной обработки материалов, искусство костюма и текстиля, конструирование изделий легкой промышленности, технологии и проектирование текстильных изделий, технология изделий легкой промышленности, информационные системы и технологии, технология полиграфического и упаковочного производства, прикладная информатика, профессиональное обучение |
технический рисунок и декоративная композиция |
1 |
|
Олимпиада школьников «Ломоносов» |
50 |
история |
история российской государственности |
1 |
|
Олимпиада школьников «Ломоносов» |
50 |
история |
международные отношения и глобалистика |
1 |
|
Олимпиада СПбГУ |
59 |
иностранный язык |
китайский язык |
1 |
|
Олимпиада СПбГУ |
59 |
лечебное дело, стоматология, психология, клиническая психология, психология служебной деятельности |
медицина |
1 |
|
Олимпиады МГХПА имени С. |
74 |
искусство, дизайн |
рисунок, живопись, скульптура, дизайн |
1 |
|
Южно-Российская межрегиональная олимпиада школьников «Архитектура и искусство» |
2 |
рисунок, живопись, композиция, черчение |
искусство, черчение |
2 |
|
Всероссийская олимпиада учащихся музыкальных училищ и колледжей |
4 |
искусство концертного исполнительства (концертные народные инструменты) |
инструменты народного оркестра |
2 |
|
Всероссийская олимпиада учащихся музыкальных училищ и колледжей |
4 |
музыковедение, музыкознание и музыкально-прикладное искусство (музыкальная журналистика и редакторская деятельность в средствах массовой информации) |
теория и история музыки |
2 |
|
Всероссийская олимпиада учащихся музыкальных училищ и колледжей |
4 |
дирижирование (дирижирование академическим хором) |
хоровое дирижирование |
2 |
|
Олимпиада «Высшая проба» |
5 |
востоковедение и африканистика |
востоковедение |
2 |
|
Олимпиада «Высшая проба» |
5 |
иностранный язык |
восточные языки |
2 |
|
Олимпиада «Высшая проба» |
5 |
история |
история мировых цивилизаций |
2 |
|
Олимпиада «Высшая проба» |
5 |
инфокоммуникационные технологии и системы связи, информатика и вычислительная техника |
электроника и вычислительная техника |
2 |
|
Герценовская олимпиада школьников |
19 |
педагогическое образование, психолого-педагогическое образование, педагогическое образование (с двумя профилями подготовки), специальное (дефектологическое) образование |
педагогические науки и образование |
2 |
|
Межрегиональная олимпиада имени В. |
27 |
искусство |
графика |
2 |
|
Межрегиональная олимпиада имени В. Е. Татлина |
27 |
искусство |
композиция |
2 |
|
Межрегиональная олимпиада школьников им. И. Я. Верченко |
28 |
информационная безопасность |
компьютерная безопасность |
2 |
|
Межрегиональная олимпиада школьников им. |
28 |
математика, криптография |
математика |
2 |
|
Московская олимпиада школьников |
36 |
искусство |
изобразительное искусство |
2 |
|
Олимпиада школьников «Основы православной культуры» |
38 |
теология, история |
основы православной культуры |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, авиационная и ракетно-космическая техника, аэронавигация и эксплуатация авиационной и ракетно-космической техники, управление в технических системах |
беспилотные авиационные системы |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, электроника, радиотехника и системы связи, машиностроение, управление в технических системах |
водные робототехнические системы |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, электроника, радиотехника и системы связи, машиностроение, управление в технических системах |
интеллектуальные робототехнические системы |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
физика и астрономия, химия, биологические науки, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, химические технологии, технологии материалов, нанотехнологии и наноматериалы |
наносистемы и наноинженерия |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
прикладная математика и информатика, математическое обеспечение и администрирование информационных систем, прикладная информатика, фотоника, приборостроение, оптические и биотехнические системы и технологии, управление в технических системах, психология |
нейротехнологии и когнитивные науки |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
прикладная математика и информатика, фундаментальная информатика, компьютерные и информационные науки, информатика и вычислительная техника |
разработка приложений виртуальной и дополненной реальности |
2 |
|
Олимпиада Национальной технологической инициативы |
44 |
компьютерные и информационные науки, информатика и вычислительная техника, информационная безопасность, электроника, радиотехника и системы связи, управление в технических системах |
технологии беспроводной связи |
2 |
|
Олимпиада школьников «Ломоносов» |
50 |
геология |
геология |
2 |
|
Олимпиада школьников «Ломоносов» |
50 |
фундаментальная математика и механика |
космонавтика |
2 |
|
Олимпиада школьников «Ломоносов» |
50 |
почвоведение, экология и природопользование |
экология |
2 |
|
Олимпиада «Шаг в будущее» |
55 |
механика, компьютерные и информационные науки, информатика и вычислительная техника, информационная безопасность, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, электро- и теплоэнергетика, ядерная энергетика и технологии, машиностроение, физико-технические науки и технологии, оружие и системы вооружения, техносферная безопасность и природоустройство, технологии материалов, техника и технологии наземного транспорта, авиационная и ракетно-космическая техника, управление в технических системах, нанотехнологии и наноматериалы |
инженерное дело |
2 |
|
Сибирская олимпиада «Архитектурно-дизайнерское творчество» |
73 |
архитектура, дизайн, дизайн архитектурной среды, градостроительство |
архитектура, изобразительные и прикладные виды искусств |
2 |
|
Всероссийская олимпиада учащихся музыкальных училищ и колледжей |
4 |
музыкознание и музыкально-прикладное искусство (музыкальная педагогика) |
музыкальная педагогика и исполнительство |
3 |
|
Всероссийская олимпиада учащихся музыкальных училищ и колледжей |
4 |
искусство концертного исполнительства (концертные струнные инструменты) |
струнные инструменты |
3 |
|
Олимпиада «Высшая проба» |
5 |
менеджмент, государственное и муниципальное управление |
основы бизнеса |
3 |
|
Межрегиональная олимпиада «Архитектура и искусство» по комплексу предметов |
23 |
рисунок, композиция |
искусство |
3 |
|
Московская олимпиада школьников |
36 |
естественные и инженерные науки |
предпрофессиональня |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
прикладная математика и информатика, компьютерные и информационные науки, науки о земле, биологические науки, информатика и вычислительная техника, прикладная геология, горное дело, нефтегазовое дело и геодезия, управление в технических системах |
анализ космических снимков и геопространственных данных |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, электроника, радиотехника и системы связи, машиностроение, управление в технических системах |
аэрокосмические системы |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
экология и природопользование, биологические науки, фотоника, приборостроение, оптические и биотехнические системы и технологии, физико-технические науки и технологии, химические технологии, промышленная экология и биотехнологии, техносферная безопасность и природообустройство, агроинженерия, ветеринария и зоотехния |
инженерные биологические системы |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
компьютерные и информационные науки, информатика и вычислительная техника, информационная безопасность, электроника, радиотехника и системы связи, электро — и теплоэнергетика, управление в технических системах |
интеллектуальные энергетические системы |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
прикладная математика и информатика, механика и математическое моделирование, математика и компьютерные науки, прикладные математика и физика, строительство, информатика и вычислительная техника, информационные системы и технологии, прикладная информатика, программная инженерия, машиностроение, прикладная механика, автоматизация технологических процессов и производств, мехатроника и робототехника |
передовые производственные технологии |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, информационная безопасность |
программная инженерия финансовых технологий |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, физико-технические науки и технологии, прикладная геология, горное дело, нефтегазовое дело и геодезия, авиационная и ракетно-космическая техника, аэронавигация и эксплуатация авиационной и ракетно-космической техники, управление в технических системах |
системы связи и дистанционного зондирования Земли |
3 |
|
Олимпиада Национальной технологической инициативы |
44 |
информатика и вычислительная техника, информационная безопасность, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, электро — и теплоэнергетика, электроника и автоматика физических установок, техносферная безопасность и природообустройство, технологии материалов, управление в технических системах |
умный город |
3 |
|
Олимпиада школьников «Ломоносов» |
50 |
фундаментальные математика и механика |
механика и математическое моделирование |
3 |
|
Олимпиада школьников «Надежда энергетики» |
51 |
информатика |
комплекс предметов (физика, информатика, математика) |
3 |
|
Олимпиада «Шаг в будущее» |
55 |
механика, компьютерные и информационные науки, информатика и вычислительная техника, электроника, радиотехника и системы связи, фотоника, приборостроение, оптические и биотехнические системы и технологии, электро- и теплоэнергетика, ядерная энергетика и технологии, машиностроение, физико-технические науки и технологии, оружие и системы вооружения, техносферная безопасность и природоустройство, технологии материалов, техника и технологии наземного транспорта, авиационная и ракетно-космическая техника, управление в технических системах, нанотехнологии и наноматериалы |
компьютерное моделирование и графика |
3 |
|
Олимпиада СПбГУ |
59 |
прикладная математика и информатика, механика и математическое моделирование, прикладные математика и физика, радиофизика, системный анализ и управление, химия, физика и механика материалов |
инженерные системы |
3 |
| 1 | Вычислить | 6^3-4^3-7^2 | |
| 2 | Найти медиану | 11 , 13 , 5 , 15 , 14 | , , , , |
| 3 | Найти объем | сфера (5) | |
| 4 | Преобразовать в десятичную форму | 3/8 | |
| 5 | Преобразовать в десятичную форму | 5/8 | |
| 6 | Найти длину окружности | окружность (5) | |
| 7 | Вычислить | 10^2 | |
| 8 | График | y=2x | |
| 9 | Найти площадь | окружность (5) | |
| 10 | Найти площадь | окружность (6) | |
| 11 | Вычислить | 3^4 | |
| 12 | Вычислить | 5^3 | |
| 13 | Вычислить | 2^4 | |
| 14 | Найти площадь | окружность (4) | |
| 15 | Разложить на простые множители | 360 | |
| 16 | Вычислить | 3^-2 | |
| 17 | Вычислить | 2+2 | |
| 18 | Преобразовать в десятичную форму | 1/3 | |
| 19 | Преобразовать в десятичную форму | 3/5 | |
| 20 | Вычислить | pi | |
| 21 | Вычислить | -3^2 | |
| 22 | Вычислить | 2^3 | |
| 23 | Вычислить | (-3)^3 | |
| 24 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 25 | Преобразовать в десятичную форму | 3/4 | |
| 26 | Преобразовать в десятичную форму | 2/3 | |
| 27 | Найти площадь | окружность (3) | |
| 28 | Вычислить | 3^2 | |
| 29 | Вычислить | -9^2 | |
| 30 | Преобразовать в десятичную форму | 2/5 | |
| 31 | Найти объем | сфера (3) | |
| 32 | Вычислить | 2^5 | |
| 33 | Множитель | x^2-4 | |
| 34 | Вычислить | -8^2 | |
| 35 | Вычислить | -6^2 | |
| 36 | Вычислить | -7^2 | |
| 37 | Вычислить | -3^4 | |
| 38 | Вычислить | (-2)^3 | |
| 39 | Множитель | x^2-9 | |
| 40 | Найти объем | сфера (6) | |
| 41 | Найти площадь | окружность (8) | |
| 42 | Преобразовать в десятичную форму | 1/4 | |
| 43 | Преобразовать в смешанную дробь | 5/2 | |
| 44 | Преобразовать в десятичную форму | 1/2 | |
| 45 | Множитель | x^2-16 | |
| 46 | Вычислить | 5^2 | |
| 47 | Вычислить | 4^-2 | |
| 48 | Вычислить | 8^2 | |
| 49 | Преобразовать в смешанную дробь | 13/4 | |
| 50 | Найти длину окружности | окружность (4) | |
| 51 | Найти площадь | окружность (7) | |
| 52 | Найти объем | сфера (2) | |
| 53 | График | y=3x | |
| 54 | Найти объем | сфера (4) | |
| 55 | Найти длину окружности | окружность (6) | |
| 56 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 57 | Вычислить | 4^3 | |
| 58 | Вычислить | 2^-3 | |
| 59 | Вычислить | 2^2 | |
| 60 | Вычислить | -(-3)^3 | |
| 61 | Вычислить | 3^3 | |
| 62 | Найти длину окружности | окружность (3) | |
| 63 | Преобразовать в смешанную дробь | 10/3 | |
| 64 | Преобразовать в десятичную форму | 2/5 | |
| 65 | Разложить на простые множители | 36 | |
| 66 | Вычислить | (-7)^2 | |
| 67 | Множитель | x^2+5x+6 | |
| 68 | Вычислить | (-4)^3 | |
| 69 | Вычислить | (-5)^3 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | 6^2 | |
| 72 | Вычислить | 1+1 | |
| 73 | Преобразовать в смешанную дробь | 20/3 | |
| 74 | Преобразовать в десятичную форму | 1/6 | |
| 75 | Преобразовать в десятичную форму | 1/5 | |
| 76 | Преобразовать в десятичную форму | 1/8 | |
| 77 | Преобразовать в десятичную форму | 4/5 | |
| 78 | Вычислить | -2^2 | |
| 79 | Вычислить | (-4)^2 | |
| 80 | Вычислить | (-3)^2 | |
| 81 | Вычислить | 5+5 | |
| 82 | Вычислить | (-8)^2 | |
| 83 | Множитель | x^2+6x+9 | |
| 84 | Найти длину окружности | окружность (7) | |
| 85 | Преобразовать в смешанную дробь | 17/2 | |
| 86 | Разложить на простые множители | 45 | |
| 87 | Разложить на простые множители | 60 | |
| 88 | График | y=4x | |
| 89 | Найти длину окружности | окружность (8) | |
| 90 | Разложить на простые множители | 18 | |
| 91 | Разложить на простые множители | 30 | |
| 92 | Преобразовать в смешанную дробь | 43/5 | |
| 93 | Преобразовать в десятичную форму | 5/6 | |
| 94 | Преобразовать в десятичную форму | 7/9 | |
| 95 | Множитель | x^2-10x+25 | |
| 96 | Множитель | x^2-4 | |
| 97 | Множитель | x^2-6x+9 | |
| 98 | Преобразовать в упрощенную дробь | 0. 2 2 |
|
| 100 | Вычислить | 7*7 |
степеней 10
степеней 10Далее: Научная нотация Up: ES 10 Дополнительный Раздаточный материал 1 Предыдущее: ES 10 Дополнительный раздаточный материал 1
Степени 10
Десятичная система, основанная на числе 10, является используемой системой счисления. больше всего в мире. Другие системы счисления, с которыми вы знакомы, являются двоичными. числа, основанные на нуле и единице и используемые в компьютерах, и время, который делится (в основном) на единицы, кратные 60 — есть Например, 60 секунд в минуте и 60 минут в часе.Поскольку десятичная система и степень 10 так важны в науке, что я немного расскажу о них здесь.
1.1 Что такое 10
x ? Не паникуйте по поводу словосочетания « степени десяти » — вы уже привыкли использовать
их, даже если вы об этом не подозреваете. Быстро — что такое 10 × 10? 100, из
курс. А что такое 10 × 1/10? Это 1. Это простые примеры, чтобы показать
что вы уже знаете, как это работает.
Быстро — что такое 10 × 10? 100, из
курс. А что такое 10 × 1/10? Это 1. Это простые примеры, чтобы показать
что вы уже знаете, как это работает.
Степени десяти записываются как 10 х , где x — мощность, о которой я говорю, и называется « экспонента ».10 x означает « 10 × 10, x раз. » 10 -x означает « 1/10 × 1/10, x раз ». По математике, а не по словам, это выглядит так
Вот пара примеров, чтобы было понятнее:
Таблица 1 перечисляет числа как в общепринятой, так и в математической нотации. Некоторые степени десяти часто используются в науке и имеют специальные « префиксы », которые перечислены также. Кроме того, некоторым степеням десяти были даны имена, некоторые из которых сомнение знакомо вам; Я поместил имена в таблицу.
Если вы посмотрите на Таблицу 1,
вы можете заметить кое-что полезное: показатель степени для каждой записи в таблице
равно количеству нулей в соответствующем числе, написанном « нормально ».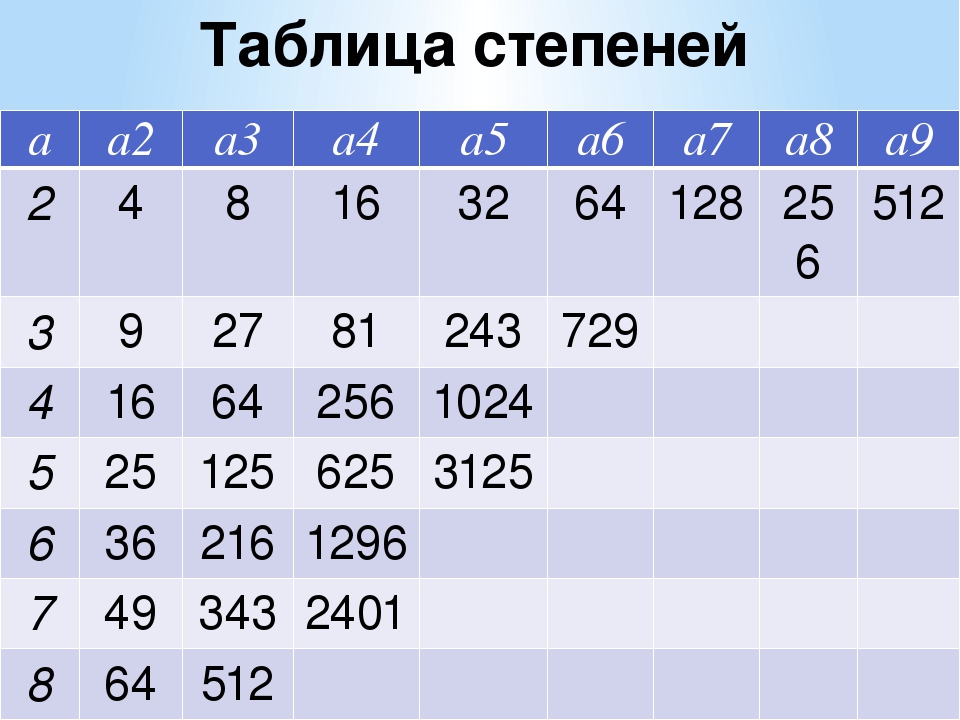 Это позволяет легко запомнить, что такое данная степень десяти, когда написано в
обычный способ. Вы также можете понять, почему ученые и инженеры предпочитают
писать такие вещи как
10 20 , г.
вместо того, чтобы записывать 1 с 20 нулями (100 000 000 000 000 000 000)
— короче. Подробнее о научной стенографии мы поговорим позже, когда
мы говорим о научных обозначениях .
Это позволяет легко запомнить, что такое данная степень десяти, когда написано в
обычный способ. Вы также можете понять, почему ученые и инженеры предпочитают
писать такие вещи как
10 20 , г.
вместо того, чтобы записывать 1 с 20 нулями (100 000 000 000 000 000 000)
— короче. Подробнее о научной стенографии мы поговорим позже, когда
мы говорим о научных обозначениях .
« Префикс » в пятом столбце в Таблица 1 используется как сокращение, когда говорят о количестве вещей. Например, память компьютера обычно измеряется в мегабайтах или миллионах байтов, и хранилище на жестком диске компьютера теперь часто измеряется в гигабайтах или миллиардах байтов. Кроме того, вы можете получить рецепт на лекарство от простуды, которое, например, 20 миллиграммов какого-то лекарства. Это сокращенный способ сказать 20 тысячных грамма.
Таблица 1: Числа и степени 10Вернуться к началу
1.2 Умножение и деление 10
Возможно, вы не уверены, что уметь писать числа в
степени десяти. Что ж, степени десяти полезны и при выполнении математических расчетов.
Скажем, я спрашиваю вас: « Сколько будет 10 умножить на 1000? »
сделка — это всего 10 тысяч. Но что, если я спрошу вас: « Сколько триллион раз
один квадриллион? »
Что ж, степени десяти полезны и при выполнении математических расчетов.
Скажем, я спрашиваю вас: « Сколько будет 10 умножить на 1000? »
сделка — это всего 10 тысяч. Но что, если я спрошу вас: « Сколько триллион раз
один квадриллион? »
Оказывается, умножение действительно больших чисел легко с помощью степеней десять. Все, что вам нужно сделать, это сложить экспоненты, и все готово.Давайте использовать пример, который я вам только что привел. Сколько один триллион умножить на квадриллион? Во-первых, используя таблицу 1, вы можете увидеть один триллион это 10 12 , г. и один квадриллион 10 15 . Итак, ответ 10 27 . что является действительно большим числом — и вы можете увидеть это почти сразу, без нужен калькулятор или лист бумаги, чтобы сделать это от руки. Вот еще несколько Примеры:
Деление работает аналогично, за исключением того, что из вычитается экспонент.Сколько будет триллион делить на квадриллион? Ну это
10 12 ÷
10 15 , г.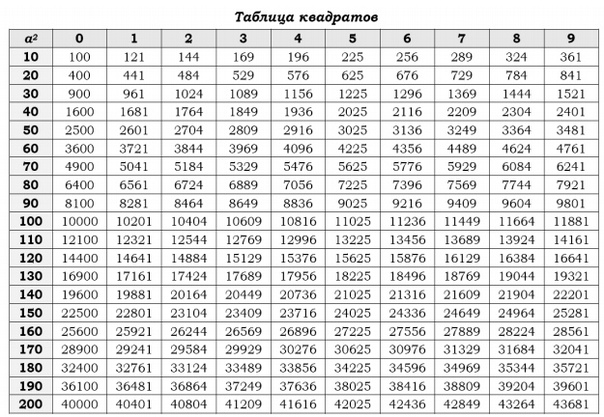 так что ответ будет 10 -3 , или одна тысячная. Здесь
еще несколько примеров:
так что ответ будет 10 -3 , или одна тысячная. Здесь
еще несколько примеров:
Опять же, хотя это может показаться бесполезным для небольших чисел, представьте себе деление один триллион триллионов триллионов, что составляет 10 36 , г. на один миллиард миллиардов, что 10 18 , г. от руки. Это займет у вас время. (Кстати, ответ 10 18 .)
Вернуться к началу
1.3 Что насчет « журналов »?
Вам может быть интересно, есть ли противоположность степени 10; что нибудь
например, как деление противоположно умножению или вычитанию,
противоположность сложению. Оказывается, есть как раз такая штука:
логарифмы, или « журналы ». Раньше журналы были действительно важны для
умножение
и деление, и все время использовались при выполнении арифметических операций с использованием правил скольжения.
Теперь, когда ручные калькуляторы стали обычным явлением, использование логарифмов
для основных расчетов исчезает, но все еще может быть стоящим. И хотя использование логарифмов для простой арифметики — редкость, есть и другие
используются для логарифмов во многих областях науки, и мы можем увидеть некоторые из них
использует позже в классе.
И хотя использование логарифмов для простой арифметики — редкость, есть и другие
используются для логарифмов во многих областях науки, и мы можем увидеть некоторые из них
использует позже в классе.
Логарифм (журнал) числа, записанного как степень десяти, легко вычислить. Это просто показатель степени. Так, например, журнал 10 3 равно 3. Журнал 10 -2 это всего -2. И поменять местами это также просто: если я скажу вам, что журнал какого-то числа равен 6, все, что вам нужно сделать, это сказать номер 10 6 , или один миллион.Еще несколько примеров:
Где действительно полезны журналы, так это при умножении и делении
числа. Из предыдущего раздела вы знаете, что умножать числа, которые
являются степенями десяти, вы складываете экспоненты и, чтобы разделить такие числа, вы
вычесть экспоненты. Ну, поскольку журнал числа, который является степенью
10 — это просто показатель степени, чтобы произвести умножение, вы просто добавляете
журналы.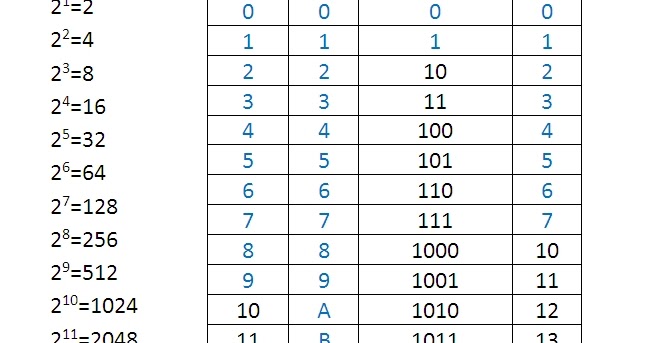 Чтобы сделать деление, просто вычтите бревна. Пример:
Чтобы сделать деление, просто вычтите бревна. Пример:
Вы могли видеть ответ из раздела 1.2, но вы можете видеть, насколько легко это сделать с помощью журналов. И так вы, наверное, можете понять, почему еще до появления мощных компьютеров логарифмы усложняли вычисления проще. Как я уже сказал, так мало кто умножает больше, но это можно сделать.
Вернуться к началу
1.4 Делаем все это на вашем калькуляторе
Если у вас есть базовый научный калькулятор, на нем будет кнопка.
где-то вроде « 10 x ».
Это кнопка для получения степени 10.Вы просто вводите число, скажем 5, и
нажмите кнопку « 10 x », и номер
вы получите обратно будет 10 5 или 100 000. В некоторых
случаев, если вы введете большое число, например 50, и нажмете
10 x кнопка, вы не увидите 1, за которым следует
50 нулей, но что-то вроде « 1 E 50 » или « 1 EE 50 ». Не надо
паника — это просто версия вашего калькулятора в научном представлении ,
о котором мы поговорим в следующем разделе.
Также на научных калькуляторах вы найдете кнопку для ведения журналов — это обычно пишется как « журнал » и часто находится очень близко к кнопке для выполнения 10 x .Вы просто набираете номер, скажем, 1000000, и нажимаете кнопку « журнал », и вы получите журнал миллиона, который равен 6.
Вернуться к началу
Вернуться к раздаточному материалу Содержание
Вернуться на страницу раздаточных материалов
Вернуться на главную страницу ES 10 Грег Андерсон
[email protected]
Вт, 6 января, 16:39:23 PST 1998
Два в сотой степени: удивительный ответ
(двойка в сотой степени)
Щелкните здесь, чтобы прочитать вопросОтвет:
Что ж… & nbsp, прежде чем я дам вам ответ, вам нужно немного справочная информация … Длина городского квартала вам наверняка знакома
с. & nbsp Представьте, что вы идете на длину блока. & nbsp Это занимает
около 3 минут.
Представьте себе 100 сквозных блоков. & Nbsp Это длина такой большой город, как Миннеаполис, в котором я живу. 20 минут езды от одного конца города до другого, если не было движения и не было красных светофора, чтобы ждать.& nbsp Прогулка расстояние займет 5 часов.
Свет, однако, может пройти из одного конца Миннеаполиса в другой. менее десятитысячной секунды. & nbsp Light — самый быстрый вещь есть. Ничего нет быстрее.
Расстояние через Соединенные Штаты примерно в 200 раз превышает длину
по городу, поэтому безостановочная прогулка, даже без перерыва на горшок, займет
1000 часов или почти 42 дня. & Nbsp Свет пересекает это расстояние за
чуть больше 1/100 секунды.& nbsp Страна очень большая,
но свет очень, очень быстро.
Расстояние от Земли до Луны почти в 100 раз больше ширины
Соединенные Штаты. Чтобы добраться до
Луна. Свет переходит с Земли на Луну менее чем за 1,3 секунды.
По сравнению с любым расстоянием на Земле, Луна ужасно далеко. & Nbsp Но свет преодолевает расстояние в мгновение ока.
Плутон — самая далекая известная планета в нашей солнечной системе: подробнее
более чем в 15 000 раз дальше от Земли, чем Луна.& nbsp Это
гораздо больший скачок в масштабе, чем любой из предыдущих увеличений. & nbsp Это
Чтобы добраться до Плутона, потребуется 167000 лет. & nbsp Ухх! & nbsp Думаю, я
Лети! Даже свету нужно 5,5 часов, чтобы достичь Плутона. По крайней мере,
— это хорошо знакомый период времени. Но по сравнению с
1,3 секунды, чтобы свет достиг Луны, Плутон ужасно далек.
Ближайшая к нашей солнечной системе звезда — Проксима Центавра. & Nbsp Это
На расстоянии 4,2 световых года, а это значит, что ее свет занимает 4 секунды.2 года до
добраться сюда. Это в 6700 раз дальше, чем Плутон. Еще один огромный
скачок в масштабе — намного больше, чем, например, 200-кратный скачок от
ширины города до ширины Соединенных Штатов. Вы можете довольно
легко подождать 5,5 часов, пока свет перейдет от Солнца к
Плутон, но ждет 4,2 года, пока свет доберется сюда. Проксима требует гораздо большего терпения. & Nbsp Даже самые близкие
звезда невероятно далеко.
Проксима требует гораздо большего терпения. & Nbsp Даже самые близкие
звезда невероятно далеко.
Звезды тонко разбросаны по большей части нашей галактики, Млечной Путь.& nbsp Хотя ближайшая к Земле звезда находится на расстоянии 4,2 световых лет, среднее расстояние между ближайшими соседними звездами около 10 световых лет. Так как в мире насчитывается не менее 300 миллиардов звезд Млечный Путь, галактика должна быть невообразимо большой. & Nbsp На самом деле, галактика диаметр видимого диска оценивается в 100 000 световых лет. & nbsp Это более чем в 20 000 раз больше расстояния до Проксимы.
Самый крупный скачок в масштабе.
Вы можете подождать 4,2 года, пока свет достигнет Земли от Проксимы
Центавра, но 100000 лет намного дольше, чем люди были
выращивание продовольственных культур или строительство постоянных убежищ.& nbsp Это длина
времени, которое невозможно пережить, и, вероятно, действительно не может быть
осмыслил. & nbsp Это говорит о том, что расстояние через Млечный Путь
тоже за гранью понимания.
Ближайшая к нам большая галактика — это знаменитая Галактика Андромеды. & Nbsp Он очень похож по размеру и форме на Млечный Путь и является другой важный компонент Местной группы галактик. & nbsp Это самая далекая вещь, которую можно увидеть невооруженным глазом. & nbsp Свет от Андромеды прошла 3 миллиона световых лет, чтобы добраться до нас.& nbsp Это в 30 раз больше диаметра Млечного Пути. & Nbsp При свете звезд из Андромеды, которую мы видим сейчас, начали свое путешествие на Землю, люди еще не существовало. Наши предки еще не научились делать каменные инструменты.
Самая далекая галактика, которую когда-либо видели напрямую (открыта в 1999 г.)
красное смещение 6,68, что указывает на то, что его свет излучался, когда
Возраст Вселенной составлял всего 5% от своего нынешнего возраста. & Nbsp Если Вселенная сейчас
13,7 миллиарда лет, свет пролетел 13 миллиардов световых лет.
чтобы добраться до нас.& nbsp Это в 4300 раз больше расстояния до Андромеды.
Галактика. Еще один огромный скачок в масштабах.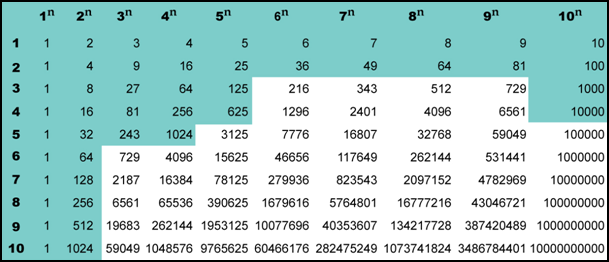 13 миллиардов лет назад
облако пыли и газа, из которого должна была образоваться наша Солнечная система, действительно
еще не существует.
13 миллиардов лет назад
облако пыли и газа, из которого должна была образоваться наша Солнечная система, действительно
еще не существует.
Максимально возможное расстояние — это расстояние, на которое свет может путешествовать с момента возникновения Вселенной во время Большого взрыва. & nbsp Все свет от этого события был немедленно поглощен (и повторно испущен, и многократно впитывалась снова), но через 380 000 лет температура выпала достаточно для образования атомов водорода, в результате чего Вселенная стать прозрачным.& nbsp Это позволило свету беспрепятственно перемещаться. & nbsp Свет из горячей молодой Вселенной достигает нас сейчас, сильно смещенный в красный цвет, как космическое микроволновое фоновое излучение.
Фоновая радиация прошла почти 13,7 миллиарда световых лет, или в 4600 раз больше расстояния до Галактики Андромеды.
Хорошо. Теперь ответ на вопрос.
Вы помните вопрос:
& nbsp & nbsp & nbsp & nbsp & nbsp Какой толщины будет стопка бумаги после того, как
& nbsp & nbsp & nbsp & nbsp & nbsp разрезать ее пополам и сложить стопкой 100 раз?
Каждый раз, когда вы разрезаете стопку бумаги на две части, количество
парные: 2 х 2 х 2. .. & nbsp сто раз, или два до
100-я степень, обозначенная как 2 100 .
.. & nbsp сто раз, или два до
100-я степень, обозначенная как 2 100 .
Два в сотой степени равны 1,267,650,600,228,229,401,496,703,205,376.
В системе присвоения номеров США это один нониллион 267 октиллион, 650 септиллионов, 600 секстиллионов, 228 квинтиллионов, 229 квадриллионов, 401 трлн, 496 млрд, 703 млн, 205 тыс., 376.
С помощью калькулятора, который показывает достаточное количество цифр, вы можете получить это число просто умножив два вместе менее чем за минуту.
Умножение на толщину бумаги в миллиметрах (0,1 мм) дает высоту стопки в миллиметрах. Деление результата на 1000 дает высоту штабеля в метрах. & nbsp Разделив это на количество метров в световом году (9 460 536 000 000 000) дает высота стопки в световых годах.
Начиная с листа бумаги толщиной 0,1 миллиметра, удваивая
толщина в сто раз приводит к стеку 13,4 миллиарда
световых лет в высоту. & nbsp Он достигнет Земли за пределы
самая далекая галактика, которую мы видим в самые мощные телескопы —
почти до края наблюдаемой Вселенной.
Часть дальнего поля космического телескопа Хаббла — Север. & Nbsp Почти каждое пятно света — это галактика.
Если вам трудно поверить, что всего 100 разрезов бумаги
заставит стек вырасти до такой высоты, вот способ визуализировать силы
два , а также другие факты и информация.
На мою домашнюю страницу «Космос и наука»
Джефф Рут
18 августа 2003 г.
Re: Теломеры [HAPP-L]
Re: Теломеры [HAPP-L][Предыдущая дата] [Следующая дата] [Предыдущая тема] [Следующая тема] [Указатель даты] [Указатель темы]
Считается, что уменьшение длины теломер с каждым делением клетки объясняет: для максимального количества делений, которым клетки в культуре подвергнутся до старение (предел Хейфлика - около 50 делений).Бессмертные клетки в культуре и раковые клетки, по-видимому, включили ген теломеразы, который восстанавливает укороченные теломеры. Биогеронтологи находят это очень интересным, но на самом деле им трудно связывают это со старением, поскольку большинство клеток в организме не достигают 50 делений.(Вес типичного элемента, умноженного на 2 в пятидесятой степени, превышает две тонны.) Клетки в культуре, выращенной от очень старых особей, не делятся столько раз, сколько от более молодых людей - значит, происходит потеря теломер, но может и не быть критический.Некоторые клетки, которые продолжают делиться, могут производить теломеразу для восстановления утраченного теломеры. (кишечный эпителий?). Теломеры явно связаны со старением клеток в культуре, но может иметь мало отношения к старению всего организма. Недавно была выдвинута гипотеза, что теломеры объясняют хирроз печени. Нормальный здоровая печень способна к значительной регенерации, но после многих лет хронического вируса инфекция, воздействие токсинов, алкоголь и т. д. клетки печени не работают. Согласно этому гипотеза, что реакция печени на этот хронический инсульт будет продолжать производить новые клетки.Постепенно теломеры исчезают, деление прекращается, и печень терпит неудачу. Джон Гвинн Биология Университет Акрона BKOPEC1@aol.
com написал: > Всем привет, > > Недавний выпуск журнала Scientific American "Frontiers" на тему старения. > был один сегмент на теломерах и то, как, по их мнению, они функционируют в ограничении > продолжительность жизни клетки. Несколько моих учеников задали вопрос > на который я, кажется, не могу найти ответа. Я читал, что это больше всего > клетки человека имеют максимум около 50 клеточных циклов (делений), которые они могут пройти > до того, как теломеры «закончатся» и клетки умрут.Кажется > Чтобы подразумевать, что у нас должна быть продолжительность жизни намного короче, чем у нас. Как может > 50 делений на клетку составляют 70-, 80-, 90-летние особи > особенно в свете текста Кэмпбелла, предполагающего, что «человеческие клетки > Теломеразы вообще не хватает, за исключением половых клеток »? > > Пожалуйста, ответьте напрямую, если вы считаете, что эта тема не интересует > Остальные листсервы. > > [email protected] > > Заранее благодарим за помощь.> > Брюс Копек > Средняя школа Плейнфилда > Центральная деревня, CT 06332 > > =========== ВЕБ-САЙТ HAPS НА http://www.
hapsweb.org ====== > **** Отказаться от подписки **** > отправьте электронное письмо по адресу [email protected] > В ТЕЛЕ сообщения в начале > в первой строке ставьте ТОЛЬКО одно слово UNSUBSCRIBE > ------------------------------------------------- --- > Отправленное письмо является обязанностью > оригинальный автор: ХАПС и Колледж Империал Вэлли, попечители, > администрация, факультет и т. д.отказываемся от любых обязательств. =========== ВЕБ-САЙТ HAPS НА http://www.hapsweb.org ====== **** Отписаться**** отправьте электронное письмо на [email protected] В ТЕЛЕ сообщения в начале первая строка помещает ТОЛЬКО одно слово UNSUBSCRIBE -------------------------------------------------- - Выраженная почта является обязанностью оригинальный автор: ХАПС и Колледж Империал Вэлли, попечители, Администрация, факультет и т. д. не несут ответственности.
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е.е., для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой .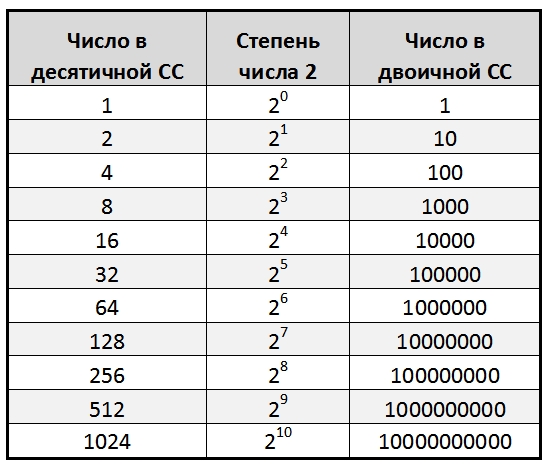 , и они автоматически конвертируются в дроби — то есть 1,45 .
, и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого числа и дроби: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в словесных задачах:
следующие математические задачи »
Как далеко вы можете достичь ?. Достигните луны, сложив лист бумаги 42 раза. | Равитея Говиндараджу
Достигните луны, сложив лист бумаги 42 раза.
Полный текст сообщения можно прочитать здесь: http://designthoughts.co/reach-moon-by-folding-a-paper-42-times/
Недавно я прочитал последний роман Дэна Брауна «Ад». Хотя мне не нравились слишком длинные описания мест, мне понравилась центральная тема, вокруг которой была построена история: перенаселенность является основной причиной всех проблем.
Хотя мне не нравились слишком длинные описания мест, мне понравилась центральная тема, вокруг которой была построена история: перенаселенность является основной причиной всех проблем.
В частности, одна сцена, которая происходит между антагонистом Бертрана Зобриста и Элизабет Сински , действительно очаровала меня.
«Если бы я взял этот лист бумаги и разорвал его на две части…» — он остановился у стола, взял лист бумаги и громко разорвал его пополам.«А затем, если бы я положил две половинки друг на друга…» Он сложил две половинки друг на друга. «А потом, если бы я повторил процесс…» Он снова разорвал бумаги, складывая их стопкой. «Я делаю стопку бумаги, которая теперь в четыре раза толще оригинала, верно?» Его глаза, казалось, тлели в темноте комнаты.
«Гипотетически говоря, — продолжил он, придвигаясь еще ближе, — если исходный лист бумаги имеет толщину всего одну десятую миллиметра, и я должен повторить этот процесс… скажем, пятьдесят раз… вы знаете, какой высоты?» этот стек будет? »
Елизавета ощетинилась.
«Я знаю», — ответила она с большей враждебностью, чем предполагала. «Это будет одна десятая миллиметра, умноженная на два в пятидесятой степени. Это называется геометрической прогрессией. Могу я спросить, что я здесь делаю? »
Мужчина ухмыльнулся и впечатленно кивнул. «Да, и вы можете догадаться, как может выглядеть это фактическое значение? Одна десятая миллиметра умножить на два в пятидесятой степени? Вы знаете, какой высоты стала наша стопка бумаги? » Он остановился всего на мгновение. «Наша стопка бумаги, после пятидесяти удвоений, теперь достигает почти полностью….-7 км.
Если вы сбросите 50 раз, подставив n = 50, вы получите 112589990,684 км.
Расстояние между солнцем и землей = D = 149,600,000 км
Расстояние от поверхности земли до поверхности солнца = D — (радиус земли) — (радиус солнца) = 149600000 — 6371 — 695500 = 148898129 км
т.е. вы почти дошел до солнца. Если быть точным, вы прошли 75,61% дистанции.
Я провел еще несколько расчетов, которые вы можете найти здесь: http://designthoughts.
co/reach-moon-by-folding-a-paper-42-times/
Итак, в следующий раз, когда кто-нибудь спросит вас, как далеко это <место>, скажите им, что это примерно
складок бумаги;) Порядковые числа | Словарь | Английский Клуб
Мы используем порядковые номера , чтобы говорить о «порядке» вещей или определять положение вещей в ряду.
пихта ул 1 ул seco nd 2 nd thi rd 3 ряд четыре th 4 -й пятая 5-я шестой 6-й седьмой 7-я восьмой 8-й девятый 9-я десятый 10-я одиннадцатый 11-я двенадцатая 12-й тринадцатый 13-й четырнадцатый 14-й пятнадцатый 15-й шестнадцатый 16-й семнадцатый 17-я восемнадцатый 18-я девятнадцатый 19-я двадцатая 20-й двадцать пихта ул 21 ул двадцать секо nd 22 nd двадцать девять рд 23 ряд двадцать четвертая 24-я тридцатая 30-я Тридцать Пихта ул 31 ул сороковая 40-й пятидесятая 50-я шестидесятые 60-я семидесятые 70-я восьмидесятые 80-я девяностые 90-я сотых 100-я сотка ул 101 ул сто пятьдесят сек nd 152 nd двухсотый 200-я тысячная 1000-е миллионная 1000000-е миллиардная 1,000,000,000-е трлн. 1,000,000,000,000-я Обратите внимание, что после цифры или цифры мы пишем последние две буквы слова.Например, мы берем последние две буквы , первые и добавляем их к цифре 1 , чтобы получить 1-е .
Расшифровка стенограммы :
Ну, я сделал ставку на лошадь
и надеялся, что она выиграет
Я был прикован к телевизору
, наблюдая за скачкамиНо это не было 1-м (первым) или 2-м (вторым)
3-й (третий) или 4-й (четвертый)
5-й (пятый), 6-й (шестой)
7-й (седьмой) курс
8-й (восьмой)
9 (девятый)
10-й (десятый)
11-й (одиннадцатый)
12-й (двенадцатый) )
13 (тринадцатый)
14 (четырнадцатый)
15 (пятнадцатый)или 16 (шестнадцатый)
17 (семнадцатый)
18 (восемнадцатый)
19 (девятнадцатый)
20 (двадцатый)
21 (двадцать первый)
22-я (двадцать вторая)
23-я (двадцать третья)
24-я (двадцать четвертая)
25-я (двадцать пятая)
26-я (двадцать шестая)
27-я (двадцать седьмая)
28-я (двадцать восьмая)
29-е (двадцать девятое)
30-е (тридцатое)Даже не 31-е (тридцать первое)!
Нигде не видно32-й (тридцать второй)
33-й (тридцать третий)
34 (тридцать четвертый)
35-й (тридцать пятый)
36-й (тридцать шестой)
37-й (тридцать седьмой)
38-й (тридцать восьмой)
39-й (тридцать девятый)
40-й (сороковой)Угу.
..
Продолжу отсчет41 (сорок первый)
42 (сорок второй)
43 (сорок третий)
44 (сорок четвертый)
45 (сорок пятый)
46 (сорок третий) шестой)
47-й (сорок седьмой)
48-й (сорок восьмой)
49-й (сорок девятый)
50-й (пятидесятый)
Нигде не видно60-й (шестидесятый)
70-й (семидесятый)
80-й (восьмидесятый)
90 (девяносто)
100 (сотое)
101 (сто первое)Нет, я пришел последним
Английский клуб : Учить английский : Словарный запас : Тематический словарь: Числа: Порядковые номера
152 (сто пятьдесят второе)
Что за осел!50-й закон от 50 Cent
Лучший из всех.Гораздо более применимо к вашей жизни, чем другие.Ничего не бойся.
Цитаты:
«Поймите: никто не рождается таким. Это неестественно, не испытывайте страха. Это процесс, требующий испытаний и испытаний. Что разделяет тех, кто погибает, и тех, кто преодолевает вышеуказанные невзгоды, — это то, что сила их воли и их жажда власти «.
«Самый большой страх людей — это быть самими собой. Они хотят быть 50 Cent или кем-то еще. Они делают то, что делают все остальные, даже если это не соответствует тому, где и кем они являются.Но так вы никуда не денетесь; ваша энергия слаба, и никто не обращает на вас внимания. Вы убегаете от того, чем владеете — от того, что отличает вас от других. Я потерял этот страх. И как только я почувствовал силу, которой обладаю, показав миру, что меня не волнует, что я похож на других людей, я уже не смогу вернуться назад ».
« Ключ к обладанию этой высшей силой — принять активный режим работы с ваши страхи. Это означает выход на те самые арены, которых вы обычно избегаете: принятие очень трудных решений, которых вы избегали, противостояние людям, которые играют с вами в силовые игры, думание о себе и о том, что вам нужно, вместо того, чтобы доставлять удовольствие другим, заставляя себя изменить направление. вашей жизни, даже если такие изменения — это как раз то, чего вы боитесь.
«
» Поймите: вам не нужно расти в Саутсайд Квинс или быть целью убийцы, чтобы развить такое отношение. Все мы сталкиваемся с проблемами, соперниками и неудачами. Мы предпочитаем игнорировать или избегать их из страха. Важна не физическая реальность вашего окружения, а ваше психическое состояние, то, как вы приходите к преодолению невзгод, которые являются частью жизни на всех уровнях. 50. пришлось противостоять своим страхам; вы должны выбрать «
» Когда вы работаете на других, вы находитесь в их власти.Им принадлежит ваша работа; они владеют тобой. Ваш творческий дух подавлен. В таких положениях вас удерживает страх утонуть или плыть по выигранному вами. Вместо этого вы должны больше бояться того, что с вами случится, если вы останетесь зависимым от других в своей власти. Ваша цель в каждом жизненном маневре должна заключаться в том, чтобы владеть собой, работая уголком для себя. Когда это твое, ты можешь проиграть — ты более мотивирован, более креативен, более жив. Высшая сила в жизни — быть полностью самостоятельным, полностью самим собой.
«
» Они испугались и устали от работы. Они хотели комфорта и безопасности зарплаты. И это станет образцом на всю оставшуюся жизнь — боясь жизненных трудностей, они станут зависеть от помощи других людей. Возможно, они могли бы продолжать так в течение нескольких лет, но слово расплаты придет, когда не будет больше работы и они разучатся заботиться о себе ».
« Вы пришли в эту жизнь с единственной реальной собственностью, которая когда-либо была материя — ваше тело, время, которое у вас есть, ваша энергия, мысли и идеи, уникальные для вас, и ваша автономия.Но с годами вы склонны все это раздавать. Вы проводите годы, работая на других — они владеют вами в течение этого периода. Вы напрасно увлекаетесь играми и битвами людей, тратите энергию и время, и никогда не вернетесь. Вы все меньше и меньше начинаете уважать собственные идеи, прислушиваясь к мнению экспертов, придерживаясь общепринятых мнений. Не осознавая этого, вы растрачиваете свою независимость, все, что делает вас творческой личностью ».
« Если вы не владеете собой в первую очередь, вы будете постоянно зависеть от людей и обстоятельств, глядя вовне вместо того, чтобы полагаться на себя и свое остроумие. .«
» Вы более одиноки, чем вы думаете. Это должно быть источником не страха, а свободы ».
« Пока не стало слишком поздно, вы должны двигаться в противоположном направлении. Вы не можете получить эту необходимую внутреннюю силу из книг, гуру или каких-либо таблеток. Это может исходить только от вас ».
« Наша задача как взрослого человека — полностью овладеть той автономией и индивидуальностью, с которой мы родились. Это окончательно преодолеть зависимую фазу в детстве и стать самостоятельными. Мы должны рассматривать желание вернуться к этой фазе как регрессивное и опасное.Это происходит из-за страха — быть ответственным за наш успех и неудачу, действовать самостоятельно и принимать трудные решения. Мы часто упаковываем это как противоположное: работая для других, проявляя послушание, вписываясь в группу или подчиняя себя группе, мы становимся хорошим человеком.
Но это наш страх говорит и вводит нас в заблуждение. «
» Помните: ваши начальники предпочитают держать вас в зависимых положениях. В их интересах, чтобы вы не полагались на собственные силы, и поэтому они будут склонны накапливать информацию.Вы должны тайно бороться с этим и использовать эту информацию для себя ».
« Поймите: вы единственный в своем роде. Черты вашего характера — это своего рода химическая смесь, которая никогда не повторится в истории. Есть идеи, уникальные для вас, определенный ритм и точка зрения, которые являются вашими сильными сторонами, а не вашими слабостями. Вы не должны бояться своей уникальности, и вы должны все меньше и меньше заботиться о том, что люди думают о вас ».
« Каждый негатив — это позитив. плохие вещи, которые случаются со мной, я как-то делаю хорошими.Это означает, что вы не можете ничего сделать, чтобы причинить мне боль. «
» Мысленное представление негативного события как замаскированного благословения облегчает вам продвижение вперед.
Это своего рода ментальная алхимия, превращающая дерьмо в сахар ».
« Может показаться, что сильные чувства любви, ненависти или гнева могут быть использованы, чтобы подтолкнуть вас к какому-то проекту, но это иллюзия. Такие эмоции дают вам прилив энергии, который быстро падает и оставляет вас таким же низким, как и высоким. Скорее, вы хотите более сбалансированной эмоциональной жизни, с меньшим количеством взлетов и падений.Это не только помогает вам двигаться и преодолевать мелкие препятствия, но также влияет на восприятие вас людьми. Они начинают видеть в вас человека, у которого есть грация под давлением, твердая рука, и они обратятся к вам как к лидеру. Поддержание такой устойчивости будет поддерживать этот позитив в движении. «
» Это должно быть вашей моделью в любом предприятии, в котором участвуют группы людей. Вы предоставляете основу, основанную на ваших знаниях и опыте, но вы позволяете этому проекту формироваться участниками.Они мотивированы и креативны, помогая придать проекту больше потока и силы.
Вы не заходите слишком далеко в этом процессе; вы задаете общее направление и тон. Вы просто отпускаете эту пугающую потребность заставлять людей делать именно то, что вы хотите. В конечном итоге вы обнаружите, что ваша способность мягко направлять энергию людей в свое русло дает вам более широкий диапазон контроля над формой и результатом проекта. «
» Мы работаем, чтобы отложить или избежать конфликтов, а также когда они дошли до точки, когда мы больше не можем играть в такую пассивную игру, нам не хватает опыта и привычки встречать их лицом к лицу.«
» То, что обнаружил Райт, было простым: когда вы в духе подчиняетесь агрессорам или несправедливой и невозможной ситуации, вы не покупаете себе настоящего мира. Вы побуждаете людей идти дальше, принимать вас в большей форме, использовать вас в своих целях. Они чувствуют ваше неуважение к себе и считают, что плохо с вами обращаются ».
« Так бывает в жизни для всех: люди будут брать у вас все, что могут. Если они почувствуют, что вы относитесь к типу людей, которые принимают и подчиняются, они будут давить и толкать, пока не установят с вами эксплуататорские отношения.
«
» Группе нужна центростремительная сила, чтобы придать ей единство и сплоченность, но недостаточно, чтобы это были вы и сила вашей личности. Вместо этого это должно быть причиной, которую вы бесстрашно воплощаете. «
» Овладейте инструментом, овладейте музыкой, а затем забудьте все это дерьмо и играйте «.
» В большинстве случаев было лучше спорить по пунктам узкой процедуры. чем на грандиозных концепциях. «
» Часто, когда вы начинаете какой-либо проект, он идет не с того конца.Вы склонны думать в первую очередь о том, чего хотите достичь, представляя себе славу и деньги, которые это принесет вам в случае успеха. Затем вы приступаете к воплощению этой концепции в жизнь. Но продвигаясь вперед, вы часто теряете терпение, потому что маленькие шаги, которые нужно сделать для этого, не так увлекательны, как амбициозные видения в вашей голове. Вместо этого вы должны попробовать противоположный подход, который может привести к совсем другим результатам. У вас есть проект, который вы хотите воплотить в жизнь, но вы начинаете с погружения в детали предмета или области.
Вы изучаете материалы, с которыми приходится работать, вкусы вашей целевой аудитории и последние технические достижения в этой области. Вы получаете удовольствие все глубже и глубже разбираться в этих тонких моментах — ваши исследования интенсивны. На основе этих знаний вы формируете сам проект, обосновывая его реальностью, а не воздушными концепциями в своей голове. Такой способ работы поможет вам замедлить свой ум и развить терпение для кропотливой работы, необходимый навык для овладения любым ремеслом. «
» Он собирался создать бизнес-империю, и он хотел взять их все с собой.Он обеспечил бы все, чего бы они ни пожелали, при условии, что они будут надежными и разделяют его чувство цели. Они могли быть рэперами звукозаписывающего лейбла, который он основал, или гастрольными менеджерами его туров; или они могут пойти в колледж и получить степень — он заплатит за все ».
« Вы можете перестать черпать свое чувство идентичности и самооценки от других. Вы можете поэкспериментировать и выйти за рамки установленных для вас ограничений.
Вы можете предпринять действия, отличные от их ожиданий.Но это означает риск. Вы ведете себя нестандартно, возможно, немного странно в глазах тех, кто вас знает. Вы могли потерпеть неудачу в этом действии и подвергнуться насмешкам. Соответствовать ожиданиям людей безопаснее и удобнее, даже если это заставляет вас чувствовать себя несчастным и ограниченным. По сути, вы боитесь себя и того, кем вы могли бы стать ».
« Однако есть совершенно другое понятие свободы. Это не то, что люди дают нам как привилегию или право. Это состояние ума, над достижением которого мы должны работать и удерживать — прилагая много усилий.Это что-то активное, а не пассивное. Это происходит от проявления свободы воли. «
» Поймите: в день вашего рождения вы стали вовлеченными в борьбу, которая продолжается и по сей день и определит ваш успех или неудачу в жизни. Вы — личность, обладающая идеями и навыками, которые делают вас уникальными. Но люди постоянно пытаются вписать вас в узкие категории, которые делают вас более предсказуемыми и более легкими в управлении.


 Введите свой запрос:
Введите свой запрос:
 Г. Строганова
Г. Строганова Е. Татлина
Е. Татлина И. Я. Верченко
И. Я. Верченко (Вес типичного элемента, умноженного на 2 в пятидесятой степени, превышает две тонны.)
Клетки в культуре, выращенной от очень старых особей, не делятся столько раз, сколько
от более молодых людей - значит, происходит потеря теломер, но может и не быть
критический.Некоторые клетки, которые продолжают делиться, могут производить теломеразу для восстановления утраченного
теломеры. (кишечный эпителий?). Теломеры явно связаны со старением клеток
в культуре, но может иметь мало отношения к старению всего организма.
Недавно была выдвинута гипотеза, что теломеры объясняют хирроз печени. Нормальный
здоровая печень способна к значительной регенерации, но после многих лет хронического вируса
инфекция, воздействие токсинов, алкоголь и т. д. клетки печени не работают. Согласно этому
гипотеза, что реакция печени на этот хронический инсульт будет продолжать производить
новые клетки.Постепенно теломеры исчезают, деление прекращается, и печень
терпит неудачу.
Джон Гвинн
Биология
Университет Акрона
BKOPEC1@aol.
(Вес типичного элемента, умноженного на 2 в пятидесятой степени, превышает две тонны.)
Клетки в культуре, выращенной от очень старых особей, не делятся столько раз, сколько
от более молодых людей - значит, происходит потеря теломер, но может и не быть
критический.Некоторые клетки, которые продолжают делиться, могут производить теломеразу для восстановления утраченного
теломеры. (кишечный эпителий?). Теломеры явно связаны со старением клеток
в культуре, но может иметь мало отношения к старению всего организма.
Недавно была выдвинута гипотеза, что теломеры объясняют хирроз печени. Нормальный
здоровая печень способна к значительной регенерации, но после многих лет хронического вируса
инфекция, воздействие токсинов, алкоголь и т. д. клетки печени не работают. Согласно этому
гипотеза, что реакция печени на этот хронический инсульт будет продолжать производить
новые клетки.Постепенно теломеры исчезают, деление прекращается, и печень
терпит неудачу.
Джон Гвинн
Биология
Университет Акрона
BKOPEC1@aol. com написал:
> Всем привет,
>
> Недавний выпуск журнала Scientific American "Frontiers" на тему старения.
> был один сегмент на теломерах и то, как, по их мнению, они функционируют в ограничении
> продолжительность жизни клетки. Несколько моих учеников задали вопрос
> на который я, кажется, не могу найти ответа. Я читал, что это больше всего
> клетки человека имеют максимум около 50 клеточных циклов (делений), которые они могут пройти
> до того, как теломеры «закончатся» и клетки умрут.Кажется
> Чтобы подразумевать, что у нас должна быть продолжительность жизни намного короче, чем у нас. Как может
> 50 делений на клетку составляют 70-, 80-, 90-летние особи
> особенно в свете текста Кэмпбелла, предполагающего, что «человеческие клетки
> Теломеразы вообще не хватает, за исключением половых клеток »?
>
> Пожалуйста, ответьте напрямую, если вы считаете, что эта тема не интересует
> Остальные листсервы.
>
>
com написал:
> Всем привет,
>
> Недавний выпуск журнала Scientific American "Frontiers" на тему старения.
> был один сегмент на теломерах и то, как, по их мнению, они функционируют в ограничении
> продолжительность жизни клетки. Несколько моих учеников задали вопрос
> на который я, кажется, не могу найти ответа. Я читал, что это больше всего
> клетки человека имеют максимум около 50 клеточных циклов (делений), которые они могут пройти
> до того, как теломеры «закончатся» и клетки умрут.Кажется
> Чтобы подразумевать, что у нас должна быть продолжительность жизни намного короче, чем у нас. Как может
> 50 делений на клетку составляют 70-, 80-, 90-летние особи
> особенно в свете текста Кэмпбелла, предполагающего, что «человеческие клетки
> Теломеразы вообще не хватает, за исключением половых клеток »?
>
> Пожалуйста, ответьте напрямую, если вы считаете, что эта тема не интересует
> Остальные листсервы.
>
>  hapsweb.org ======
> **** Отказаться от подписки ****
> отправьте электронное письмо по адресу
hapsweb.org ======
> **** Отказаться от подписки ****
> отправьте электронное письмо по адресу 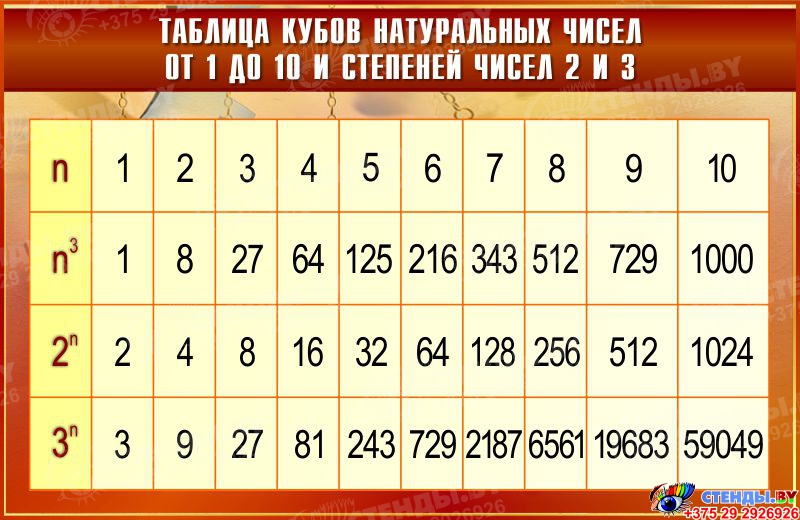 «Я знаю», — ответила она с большей враждебностью, чем предполагала. «Это будет одна десятая миллиметра, умноженная на два в пятидесятой степени. Это называется геометрической прогрессией. Могу я спросить, что я здесь делаю? »
«Я знаю», — ответила она с большей враждебностью, чем предполагала. «Это будет одна десятая миллиметра, умноженная на два в пятидесятой степени. Это называется геометрической прогрессией. Могу я спросить, что я здесь делаю? » co/reach-moon-by-folding-a-paper-42-times/
co/reach-moon-by-folding-a-paper-42-times/
 ..
.. 
 «
«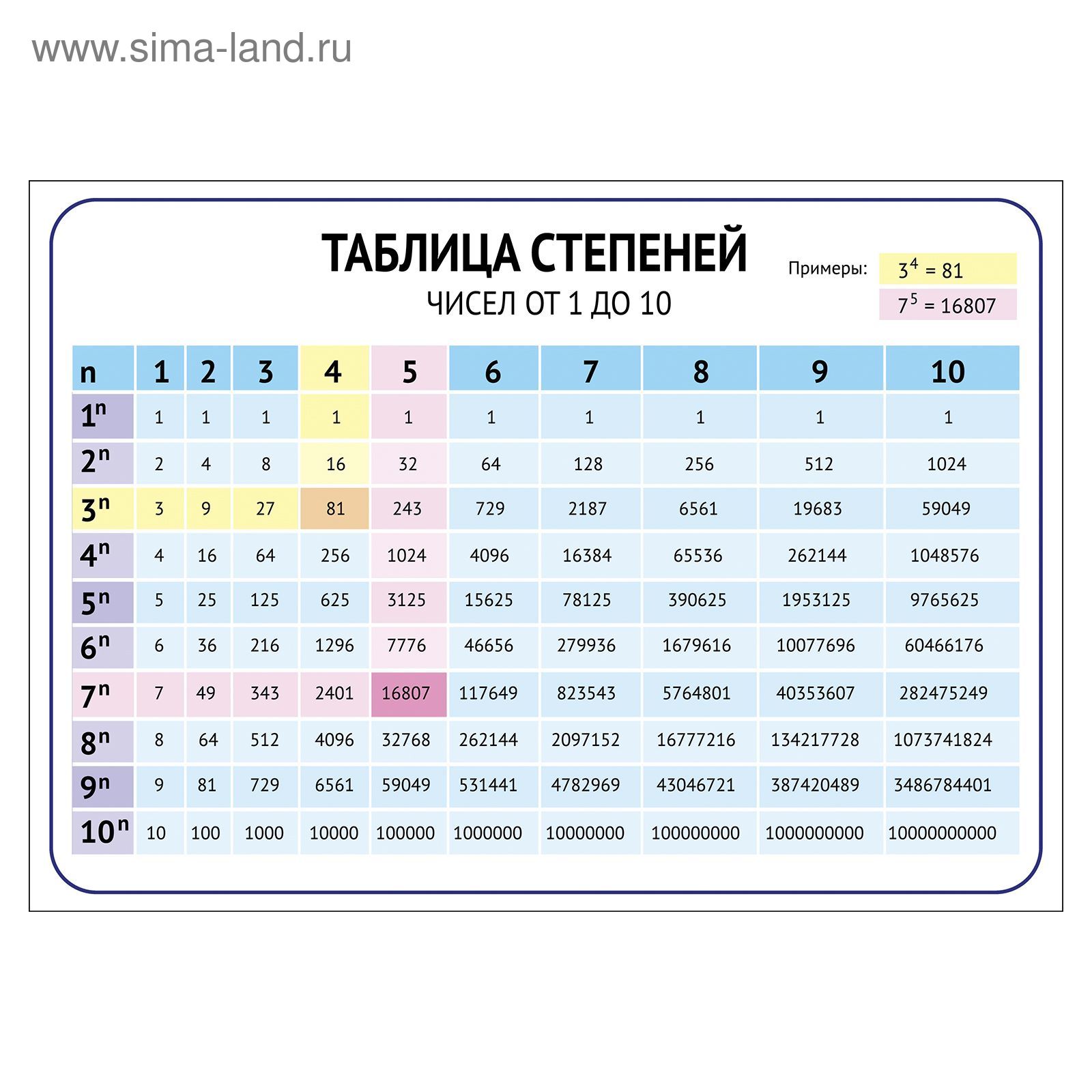 «
«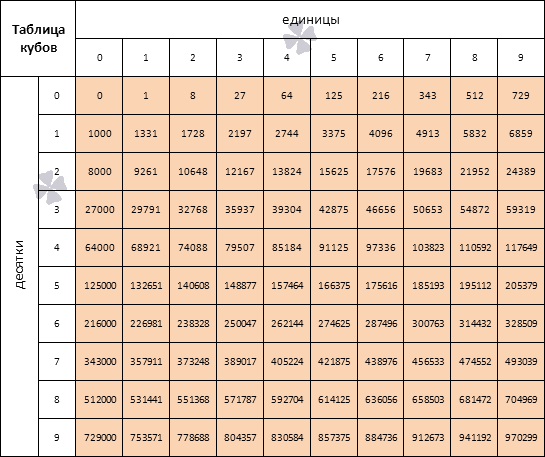 Но это наш страх говорит и вводит нас в заблуждение. «
Но это наш страх говорит и вводит нас в заблуждение. «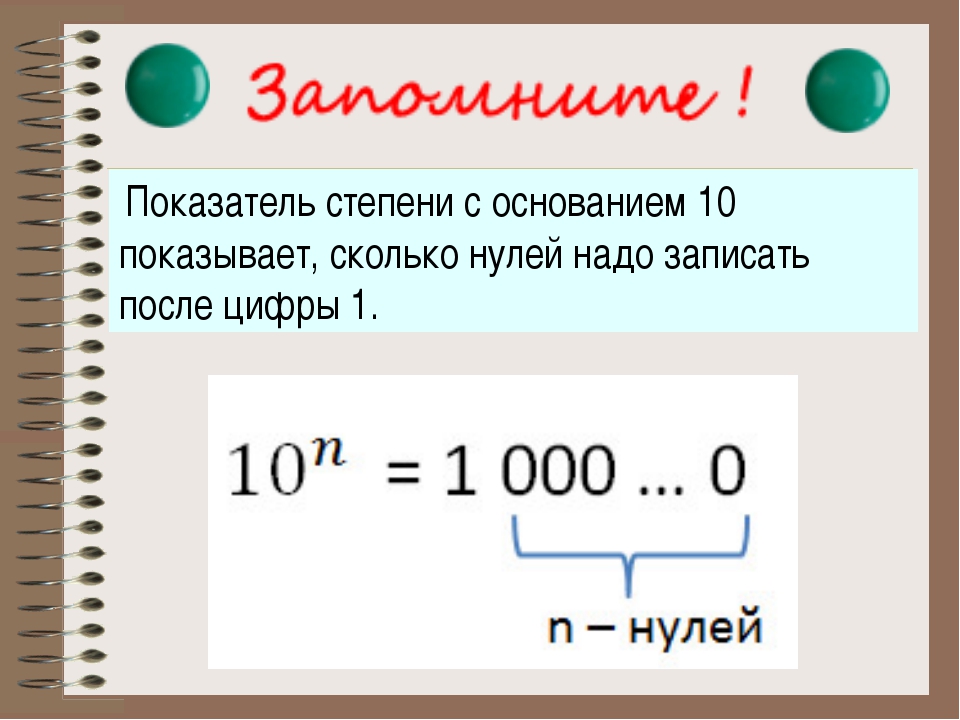 Это своего рода ментальная алхимия, превращающая дерьмо в сахар ».
Это своего рода ментальная алхимия, превращающая дерьмо в сахар ». Вы не заходите слишком далеко в этом процессе; вы задаете общее направление и тон. Вы просто отпускаете эту пугающую потребность заставлять людей делать именно то, что вы хотите. В конечном итоге вы обнаружите, что ваша способность мягко направлять энергию людей в свое русло дает вам более широкий диапазон контроля над формой и результатом проекта. «
Вы не заходите слишком далеко в этом процессе; вы задаете общее направление и тон. Вы просто отпускаете эту пугающую потребность заставлять людей делать именно то, что вы хотите. В конечном итоге вы обнаружите, что ваша способность мягко направлять энергию людей в свое русло дает вам более широкий диапазон контроля над формой и результатом проекта. « «
« Вы изучаете материалы, с которыми приходится работать, вкусы вашей целевой аудитории и последние технические достижения в этой области. Вы получаете удовольствие все глубже и глубже разбираться в этих тонких моментах — ваши исследования интенсивны. На основе этих знаний вы формируете сам проект, обосновывая его реальностью, а не воздушными концепциями в своей голове. Такой способ работы поможет вам замедлить свой ум и развить терпение для кропотливой работы, необходимый навык для овладения любым ремеслом. «
Вы изучаете материалы, с которыми приходится работать, вкусы вашей целевой аудитории и последние технические достижения в этой области. Вы получаете удовольствие все глубже и глубже разбираться в этих тонких моментах — ваши исследования интенсивны. На основе этих знаний вы формируете сам проект, обосновывая его реальностью, а не воздушными концепциями в своей голове. Такой способ работы поможет вам замедлить свой ум и развить терпение для кропотливой работы, необходимый навык для овладения любым ремеслом. « Вы можете предпринять действия, отличные от их ожиданий.Но это означает риск. Вы ведете себя нестандартно, возможно, немного странно в глазах тех, кто вас знает. Вы могли потерпеть неудачу в этом действии и подвергнуться насмешкам. Соответствовать ожиданиям людей безопаснее и удобнее, даже если это заставляет вас чувствовать себя несчастным и ограниченным. По сути, вы боитесь себя и того, кем вы могли бы стать ».
Вы можете предпринять действия, отличные от их ожиданий.Но это означает риск. Вы ведете себя нестандартно, возможно, немного странно в глазах тех, кто вас знает. Вы могли потерпеть неудачу в этом действии и подвергнуться насмешкам. Соответствовать ожиданиям людей безопаснее и удобнее, даже если это заставляет вас чувствовать себя несчастным и ограниченным. По сути, вы боитесь себя и того, кем вы могли бы стать ».
Leave A Comment