Открытая Физика. Сила упругости. Закон Гука
Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Её называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Fx = Fупр = –kx.
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жёсткостью тела.
ε=1Eσ.
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например,

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
Упругую силу
N→,
действующую на тело со стороны опоры (или подвеса), называют
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация
аренда автомобиля в санкт петербурге цены см. тут тут |
| naprokat78.ru |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
Закон Гука, сила упругости — определение, формулы
Покажем, как применять знание физики в жизни
Начать учиться 214.9KЕсли вы возьмете резиновый шарик и шар из камня и начнете кидать в стену (скучный день выдался, мало ли) — заметите, что они отталкиваются совершенно по-разному. Про силу упругости, которая объясняет этот процесс — в этой статье.
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит.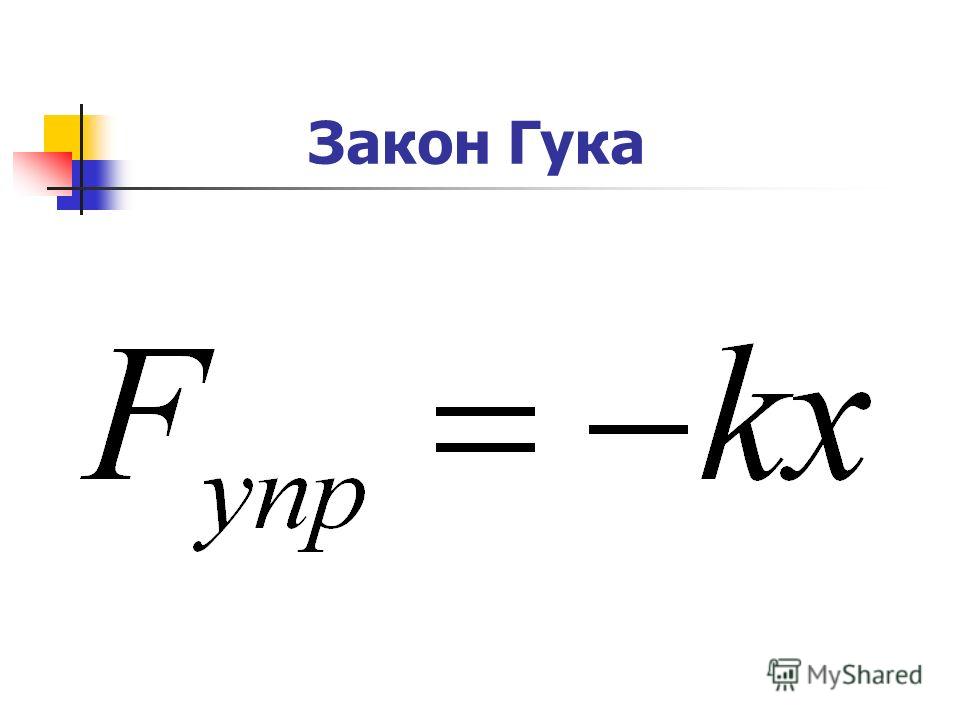 Причиной любого действия или взаимодействия является сила.
Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Деформация
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Деформация растяжения
Деформация сжатия
Деформация сдвига
Деформация при кручении
Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
—сила упругости [Н] k — коэффициент жесткости [Н/м] х — изменение длины (деформация) [м] |
Важно раз
Изменение длины может обозначаться по-разному в различных источниках.
Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Важно два
Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Вспомним закон Гука:
И выразим из него модуль удлинения лески:
Так как одна сила уравновешивает другую, мы можем их приравнять:
Подставим числа, жесткость лески при этом выражаем в ньютонах:
= 0,01 м = 1 см
Ответ: удлинение лески равно 1 см.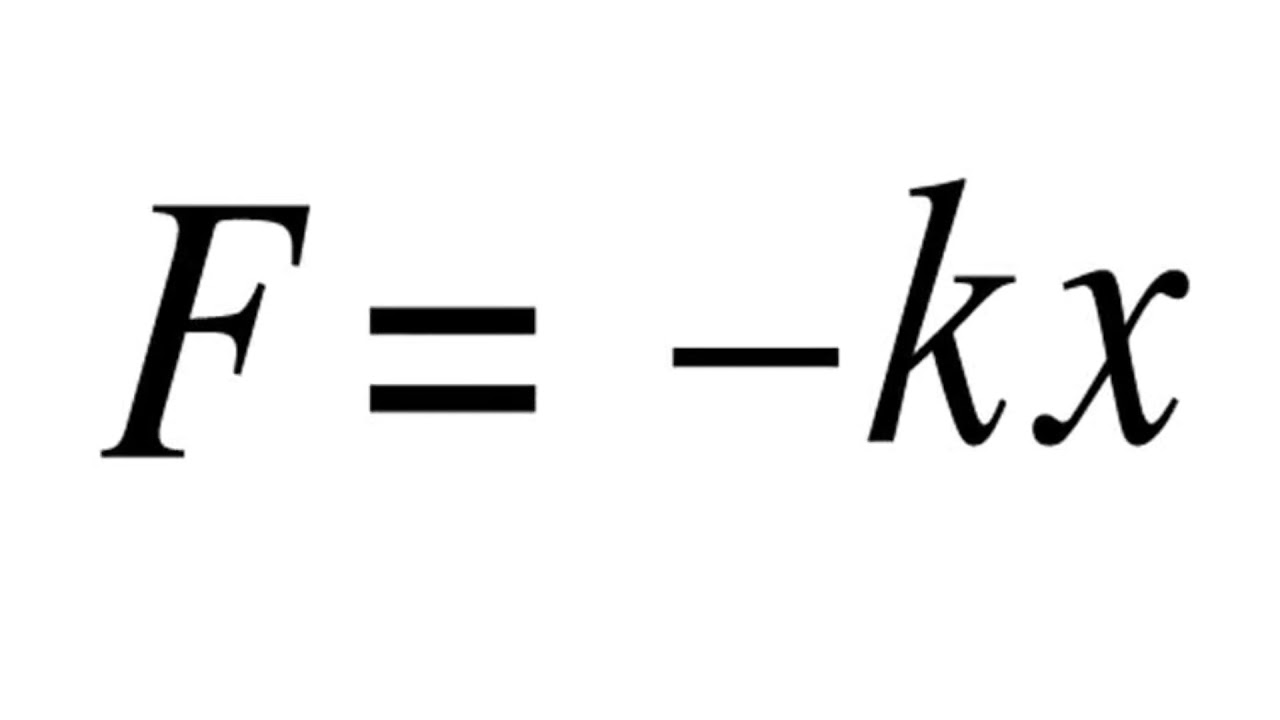
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Задачка
Какова жесткость системы из двух пружин, жесткости которых k1 = 100 Н/м, k2 = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
66,7 Н/м
Очень-очень важно!
Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
F = kx
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры:
2 см = 0,02 м
И подставим в формулу:
=100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Карина Хачатурян
К предыдущей статье
209.7KЗакон cохранения импульса
К следующей статье
203.7KЗакон электромагнитной индукции
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Формула закона Гука — определение, вывод, примеры решения и часто задаваемые вопросы в поле физики, которая утверждает, что смещение или изменение положения пружины относительно ее пропорции покоя прямо пропорционально нагрузке, приложенной к пружине.
 Так, при снятии нагрузки при заданных условиях предмет снова возвращается к своей первоначальной форме и размерам. Тот факт, что эти незначительные смещения молекул компонентов, атомов или ионов материалов происходят из нормальных положений и пропорциональны силе, вызывающей смещение, иллюстрирует упругое поведение твердых тел в соответствии с уравнением закона Гука.
Так, при снятии нагрузки при заданных условиях предмет снова возвращается к своей первоначальной форме и размерам. Тот факт, что эти незначительные смещения молекул компонентов, атомов или ионов материалов происходят из нормальных положений и пропорциональны силе, вызывающей смещение, иллюстрирует упругое поведение твердых тел в соответствии с уравнением закона Гука.Вывод закона Гука
Чтобы объяснить закон Гука с точки зрения математики, было выведено следующее уравнение, которое состоит из следующих членов:
F = kx
Здесь F — сила, которую мы прикладываем, и она постоянна. в этом уравнении, в то время как K обозначает постоянную, равную k-кратному смещению или изменению длины объекта, обозначенного x
Где
F = приложенная сила
k = постоянная смещения
x = удлинение в объект
Природа материала объекта, его размер и форма влияют на постоянную упругости k, и когда прилагается существенно большая сила, упругий материал деформируется намного больше, чем величина, указанная законом Гука. Материал, однако, по-прежнему остается эластичным и возвращается к своему первоначальному размеру при снятии приложенной силы, а также сохраняет свою форму при прекращении действия силы. Уравнение закона Гука иногда можно представить следующим образом:
Материал, однако, по-прежнему остается эластичным и возвращается к своему первоначальному размеру при снятии приложенной силы, а также сохраняет свою форму при прекращении действия силы. Уравнение закона Гука иногда можно представить следующим образом:
Возвращающая сила пружины равна постоянной пружины, умноженной на смещение пружины от ее нормального положения
F = -kx
Где,
Здесь F называется возвращающей силой пружины (Ньютоны, Н)
k = жесткость пружины (Н/м)
x = смещение пружины (м)
Знак минус относится к направлению приложенной силы.
По соглашению в F= -kx присутствует знак минус или минус.
Возвращающая сила F пропорциональна смещению x в соответствии с законом Гука.
При сжатии пружины координата смещения x отрицательна.
Нуль, когда пружина имеет нормальную длину.
Положительный, когда пружина растянута.
Пример закона Гука
Пример 1. Пружина растянута на 22 см и имеет силовую постоянную 6 см/дин. Определить приложенную силу.
Решение:
Даны параметры:
Силовая константа k равна 6 см/дин,
Расширение x = 22 см.
Формула закона Гука имеет вид
F = – k x
= – 6 × 22 см
= – 132 Н
Пр.2. Определите постоянную силы, если сила 200 Н растягивает пружину на 1,8 м.
Решение:
Заданы параметры:
Сила F = 200 Н,
Удлинение, x = 1,8 м.
Формула закона Гука:
Упр.3. Жесткая амортизирующая пружина была сжата на расстояние 3,00 см под действием силы 1500 Н. Каково значение постоянной силы k этой пружины?
Решение:
Сила, действующая на пружину, имеет величину 1200 Н. Это означает, что пружина оказывает равную (по величине) и противоположную (по знаку) восстанавливающую силу -1200 Н. Пружина сжимается на расстоянии 3,00 см. Чтобы найти значение жесткости пружины в единицах Н/м, расстояние необходимо преобразовать в метры:
Это означает, что пружина оказывает равную (по величине) и противоположную (по знаку) восстанавливающую силу -1200 Н. Пружина сжимается на расстоянии 3,00 см. Чтобы найти значение жесткости пружины в единицах Н/м, расстояние необходимо преобразовать в метры:
x = 3,00 см
x = (3,00)(1/100)
x = 0,03 м
Значение силовой постоянной можно найти, переставив формулу закона Гука,
F = -kx → k = -F/x
k = -(-1200 Н)/0,03 м
k = 1200 Н/0,03 м
k = 40000 Н/м
Значение жесткости пружины амортизирующая пружина 40 000 Н/м.
Дата последнего обновления: 27 мая 2023 г. 116 Формула трансформатора — КПД, Передаточное отношение, Шаг вверх и Шаг вниз
Формула радиоактивного распада– значение, уравнение, период полураспада и часто задаваемые вопросы
Электрические формулы — объяснение, примеры решений и часто задаваемые вопросы
Формула тепловой нагрузки — значение, расчет, примеры решений и часто задаваемые вопросы
Формула фотонной энергии — уравнения, графики, приложения и часто задаваемые вопросы
Формула цилиндрического конденсатора — определение. Пример решения и часто задаваемые вопросы
Пример решения и часто задаваемые вопросы
Формула трансформатора — эффективность, коэффициент трансформации, повышение и понижение
Формула радиоактивного распада — значение, уравнение, период полураспада и часто задаваемые вопросы
Электрические формулы — объяснение, примеры решения и часто задаваемые вопросы
Формула тепловой нагрузки – значение, расчет, примеры решений и часто задаваемые вопросы
Формула фотонной энергии – уравнения, графики, приложения и часто задаваемые вопросы
Формула цилиндрического конденсатора – определение. Решенный Пример и часто задаваемые вопросы
Актуальные темы
Работа и энергия
Работа и энергияСколько работы совершается, когда мы растягиваем пружинит на расстояние x от положения равновесия?
Во-первых, нам нужно знать об общем характеристики пружины.
Опытным путем находим
Это известно как закон Гука
Мы могли бы записать это в виде уравнения как F = к х.
Однако сила, действующая на пружину , всегда в направлении, противоположном растяжению (или сжатию) весны. Поэтому запишем закон Гука как
Ф = — к х Это сила, действующая на пружина . внешняя сила мы прикладываем к весна F доб = + к х .
Константа пропорциональности k известна как жесткость пружины и описывает, насколько жесткой является пружина. является.
Теперь мы снова готовы спросить
«Какая работа выполняется, когда мы растягиваем прыгнуть на расстояние x от своего положения равновесия?»
Мы умеем обращаться с постоянной силой. Для постоянной силы мы знаем
Ш = Ж д Сила пружины у нас разная, но мы можем думать его как (почти) постоянного по мере того, как мы движемся через (очень) маленький расстояние,
Работа, совершаемая переменной силой, равна область под «кривой» на графике сила-расстояние.

 Однако сила, действующая на пружину , всегда
в направлении, противоположном растяжению (или сжатию)
весны. Поэтому запишем закон Гука как
Однако сила, действующая на пружину , всегда
в направлении, противоположном растяжению (или сжатию)
весны. Поэтому запишем закон Гука как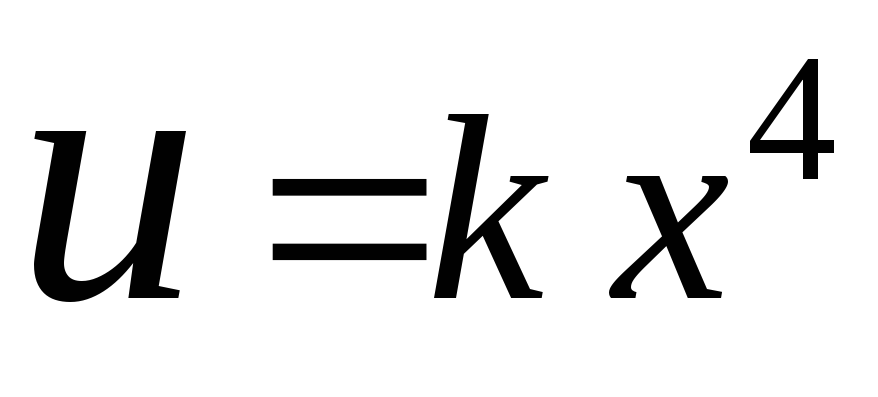
Leave A Comment