Если угол равен 47 то смежный с ним равен 153: Укажите номера верных утверждений. 1) Если угол равен 47°, то смежный с ним равен 153°. 2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны. 3) Через любую точку проходит ровно одна прямая.

1: Задание 13

1. B 10 № 67. Укажите номера верных утверждений.

 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2

2. B 10 № 93. Укажите номера верных утверждений.

 1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 3

3. B 10 № 119. Укажите номера верных утверждений.

 1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 3

4. B 10 № 145. Укажите номера верных утверждений.

 1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 3

5. B 10 № 171. Укажите номера верных утверждений.

 1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 3

6. B 10 № 197. Укажите номера верных утверждений.

 1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2

7. B 10 № 169915. Какие из следующих утверждений верны?

 1) Если угол равен 45°, то вертикальный с ним угол равен 45°.

2) Любые две прямые имеют ровно одну общую точку.

3) Через любые три точки проходит ровно одна прямая.

4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1

8. B 10 № 169916. Какие из следующих утверждений верны?

 1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 3

9. B 10 № 169917. Какие из следующих утверждений верны?

 1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2;3;4

10. B 10 № 169922. Какие из следующих утверждений верны?

 1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.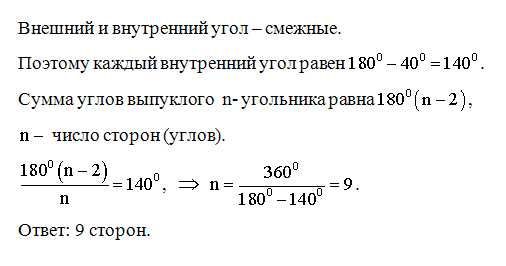

2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3; 4

11. B 10 № 169923. Какие из следующих утверждений верны?

 1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2; 4

12. B 10 № 169924. Какие из следующих утверждений верны?

 1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3

13. B 10 № 169926. Какие из следующих утверждений верны?

 1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.

4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.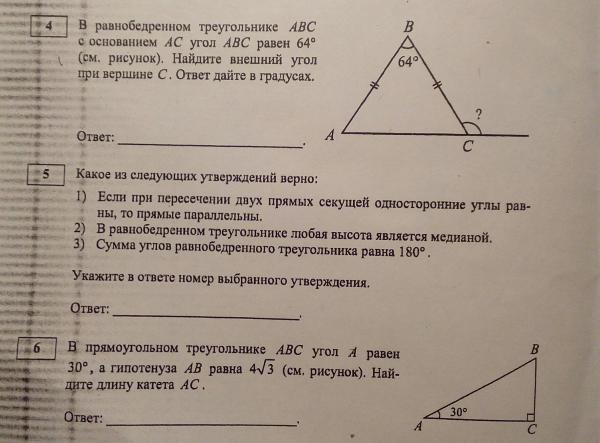

Ответ: 1; 2; 4

14. B 10 № 169928. Какие из следующих утверждений верны?

 1) Около всякого треугольника можно описать не более одной окружности.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2

15. B 10 № 169929. Какие из следующих утверждений верны?

 1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2; 3

16. B 10 № 169930. Какие из следующих утверждений верны?

 1) Окружность имеет бесконечно много центров симметрии.

2) Прямая не имеет осей симметрии.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Квадрат не имеет центра симметрии.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3

17. B 10 № 169931. Какие из следующих утверждений верны?

 1) Правильный шестиугольник имеет шесть осей симметрии.

2) Прямая не имеет осей симметрии.

3) Центром симметрии ромба является точка пересечения его диагоналей.

4) Равнобедренный треугольник имеет три оси симметрии.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 3

18. B 10 № 169932. Какие из следующих утверждений верны?

 1) Центром симметрии прямоугольника является точка пересечения диагоналей.

2) Центром симметрии ромба является точка пересечения его диагоналей.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2; 3

19. B 10 № 169933. Какие из следующих утверждений верны?

 1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1

20. B 10 № 169934. Какие из следующих утверждений верны?

 1) Любые два прямоугольных треугольника подобны.

2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

3) Стороны треугольника пропорциональны косинусам противолежащих углов.

4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 4

21. B 10 № 169935. Какие из следующих утверждений верны?

 1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 3; 4

22. B 10 № 169936. Какие из следующих утверждений верны?

 1) Если площади фигур равны, то равны и сами фигуры.

2) Площадь трапеции равна произведению суммы оснований на высоту.

3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.

4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 4

23. B 10 № 169938. Какие из следующих утверждений верны?

 1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.

2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.

3) Площадь трапеции меньше произведения суммы оснований на высоту.

4) Площадь прямоугольного треугольника меньше произведения его катетов.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 3; 4

24. B 10 № 311406. На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке  

2)

3)

4) прямая    пересекает график в точках    и  

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2

25. B 10 № 311684. Укажите номера верных утверждений.

 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 3

26. B 10 № 311763. Укажите номера верных утверждений.

 1) Через любую точку проходит не менее одной прямой.

2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1;2

27. B 10 № 311851. Укажите номера верных утверждений.

 1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.

2) Через любые три точки проходит не более одной прямой.

3) Сумма вертикальных углов равна 180°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2

28. B 10 № 311915. Укажите номера верных утверждений.

 1) Площадь трапеции равна половине высоты, умноженной на разность оснований.

2) Через любые две точки можно провести прямую.

3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2; 3

29. B 10 № 311959. Укажите номера верных утверждений.

 1) В любую равнобедренную трапецию можно вписать окружность.

2) Диагональ параллелограмма делит его углы пополам.

3) Площадь прямоугольного треугольника равна половине произведения его катетов.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3

30. B 10 № 314814. Какие из данных утверждений верны? Запишите их номера.

 1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.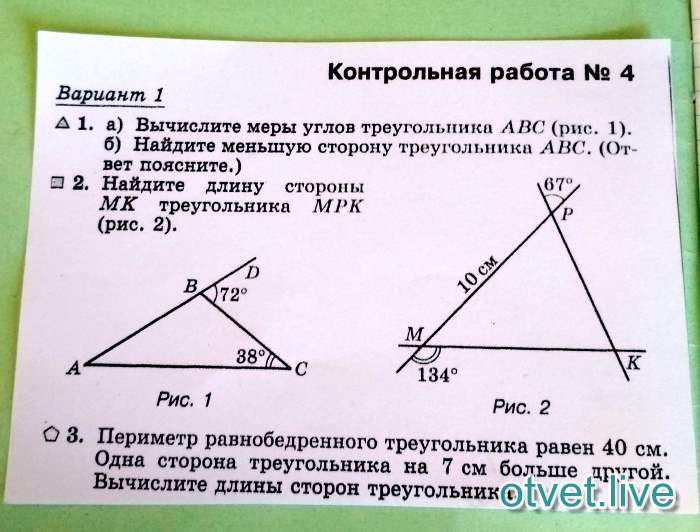

Ответ: 1;2;3

31. B 10 № 314818. Какие из данных утверждений верны? Запишите их номера.

 1) Каждая из биссектрис равнобедренного треугольника является его медианой.

2) Диагонали прямоугольника равны.

3) У любой трапеции боковые стороны равны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 2

32. B 10 № 314894. Какие из данных утверждений верны? Запишите их номера.

 1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.

2) Диагональ трапеции делит её на два равных треугольника.

3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1;3

33. B 10 № 316233. Укажите номера верных утверждений.

 1) Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3

34. B 10 № 316286. Укажите номера верных утверждений.

 1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

Ответ: 2

35. B 10 № 316323. Укажите номера верных утверждений.

 1) Любые три прямые имеют не более одной общей точки.

2) Если угол равен 120°, то смежный с ним равен 120°.

3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 3

36. B 10 № 316349. Укажите номера неверных утверждений.

 1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

2) Диагонали ромба перпендикулярны.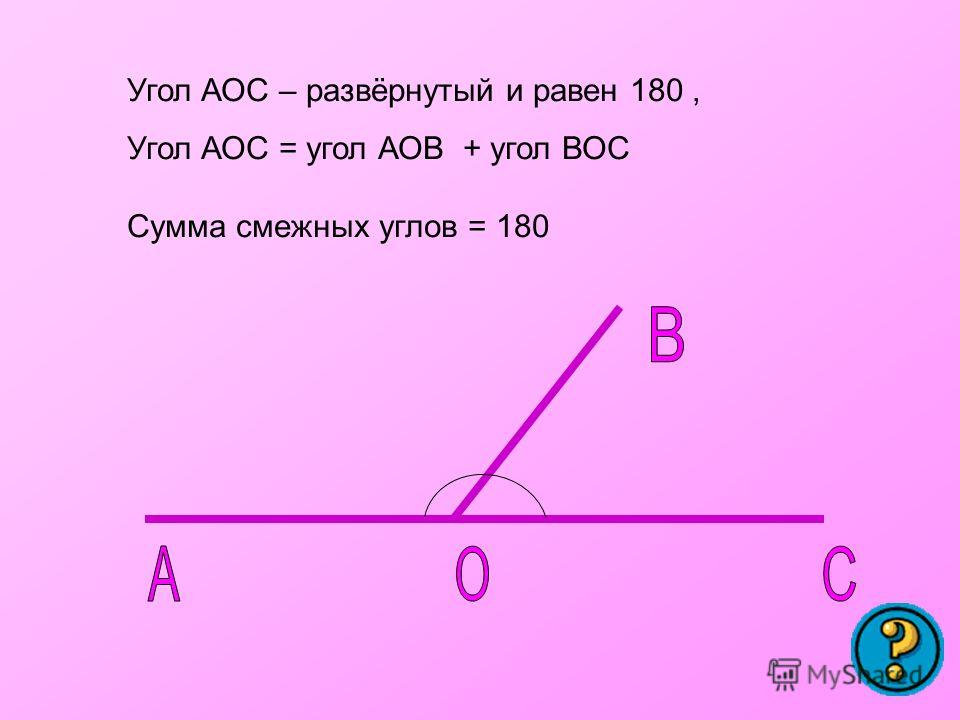

3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1;3

37. B 10 № 333015. Какие из следующих утверждений верны?

1) Через точку, не лежащую на данной прямой, можно провести прямую,

параллельную этой прямой.

2) Если диагонали параллелограмма равны, то это ромб.

3) Для точки, лежащей на окружности, расстояние до центра окружности

равно радиусу.

Ответ: 13

38. B 10 № 333094. Какие из следующих утверждений верны?

1) Любой прямоугольник можно вписать в окружность.

2) Все углы ромба равны.

3) Треугольник со сторонами 1, 2, 4 существует.

Ответ: 1

39. B 10 № 333120. Какие из следующих утверждений верны?

1) Площадь треугольника меньше произведения двух его сторон.

2) Средняя линия трапеции равна сумме её оснований.

3) Если два угла одного треугольника равны двум углам другого треуголь-

ника, то такие треугольники подобны.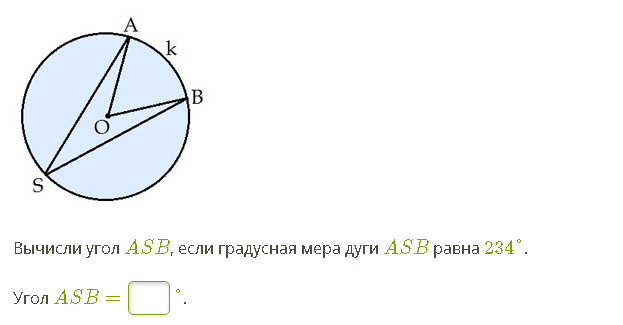

Ответ: 13

40. B 10 № 333147. Какие из следующих утверждений верны?

1) Средняя линия трапеции равна сумме её оснований.

2) Диагонали ромба перпендикулярны.

3) Площадь треугольника меньше произведения двух его сторон.

Ответ: 23

Зачет по заданиям ОГЭ №19

Зачет по заданиям
ОГЭ № 19 по математике

Оглавление

Вариант 1. 3

Вариант 2. 7

Форма для заполнения. 11

Ответы к тесту. 12

Источник. 13

1. Какие из данных утверждений верны? Запишите их номера.

1)  Через две различные точки на плоскости проходит единственная прямая.

2)  В любом прямоугольнике диагонали взаимно перпендикулярны.

3)  У равностороннего треугольника три оси симметрии.

2. Какое из следующих утверждений верно?

1.  Всегда один из двух смежных углов острый, а другой тупой.

2.  Площадь квадрата равна произведению двух его смежных сторон.

3.  Все хорды одной окружности равны между собой.

В ответ запишите номер выбранного утверждения.

3. Укажите номера верных утверждений.

1)  Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.

2)  Сумма смежных углов равна 180°.

3)  Любая медиана равнобедренного треугольника является его биссектрисой.

4. Укажите номера верных утверждений.

1)  Диаметр делит окружность на две равные дуги.

2)  Параллелограмм имеет две оси симметрии.

3)  Площадь треугольника равна его основанию, умноженному на высоту.

5. Какое из следующих утверждений верно?

1)  Любой прямоугольник можно вписать в окружность.

2)  Все углы ромба равны.

3)  Треугольник со сторонами 1, 2, 4 существует.

6. Какие из следующих утверждений верны?

1)  Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

2)  Средняя линия трапеции параллельна её основаниям.

3)  Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

7. Укажите номера верных утверждений.

1)  Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2)  Сумма смежных углов равна 180°.

3)  Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их номера в порядке возрастания.

8. Укажите номера верных утверждений.

1)  Если угол равен 47°, то смежный с ним равен 153°.

2)  Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3)  Через любую точку проходит ровно одна прямая.

Если утверждений несколько, запишите их номера в порядке возрастания.

9. Укажите номера верных утверждений.

1)  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2)  Треугольник со сторонами 1, 2, 4 существует.

3)  Если в ромбе один из углов равен 90°, то такой ромб  — квадрат.

4)  В любом параллелограмме диагонали равны.

10. Укажите номера верных утверждений.

1)  Через любую точку проходит не менее одной прямой.

2)  Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

3)  Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Если утверждений несколько, запишите их номера в порядке возрастания.

11. Какие из следующих утверждений верны?

1)  Все высоты равностороннего треугольника равны.

2)  Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.

3)  В любой ромб можно вписать окружность. 

Если утверждений несколько, запишите их номера в порядке возрастания.

12. Какие из следующих утверждений верны?

1)  Один из углов треугольника всегда не превышает 60 градусов.

2)  Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

3)  Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

13. Какие из следующих утверждений верны?

1)  Существуют три прямые, которые проходят через одну точку.

2)  Боковые стороны любой трапеции равны.

3)  Сумма углов равнобедренного треугольника равна 180 градусам.  

Если утверждений несколько, запишите их номера в порядке возрастания.

14. Какие из следующих утверждений верны?

1)  Треугольника со сторонами 1, 2, 4 не существует.

2)  Сумма углов любого треугольника равна 360 градусам.

3)  Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

15. Какое из следующих утверждений верно?

1)  Все углы ромба равны.

2)  Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3)  Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

В ответ запишите номер выбранного утверждения.

16. Какие из следующих утверждений верны?

1)  Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2)  В тупоугольном треугольнике все углы тупые.

3)  Средняя линия трапеции равна полусумме её оснований.

Если утверждений несколько, запишите их номера в порядке возрастания.

17. Какое из следующих утверждений верно?

1)  Диагонали параллелограмма равны.

2)  Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3)  Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

18. Укажите номера верных утверждений.

1)  Площадь трапеции равна половине высоты, умноженной на разность оснований.

2)  Через любые две точки можно провести прямую.

3)  Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

19. Какое из следующих утверждений верно?

1)  Точка касания двух окружностей равноудалена от центров этих окружностей.

2)  В параллелограмме есть два равных угла.

3)  Площадь прямоугольного треугольника равна произведению длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

20. Какие из следующих утверждений верны?

1)  Каждая сторона треугольника меньше разности двух других сторон.

2)  В равнобедренном треугольнике имеется не более двух равных углов.

3)  Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.

4)  В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.

21. Какие из следующих утверждений верны?

1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

2.Площадь трапеции равна произведению основания трапеции на высоту.

3.Треугольника со сторонами 1, 2, 4 не существует

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

22. Укажите номера верных утверждений.

1)  Смежные углы равны.

2)  Любые две прямые имеют ровно одну общую точку.

3)  Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их номера в порядке возрастания.

23. Какие из следующих утверждений верны?

1)  Окружность имеет бесконечно много центров симметрии.

2)  Прямая не имеет осей симметрии.

3)  Правильный пятиугольник имеет пять осей симметрии.

4)  Квадрат не имеет центра симметрии.

Если утверждений несколько, запишите их номера в порядке возрастания.

24. Какие из данных утверждений верны? Запишите их номера.

1)  Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.

2)  Диагональ трапеции делит её на два равных треугольника.

3)  Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.

25. Укажите номера верных утверждений.

1)  Если угол острый, то смежный с ним угол также является острым.

2)  Диагонали квадрата взаимно перпендикулярны.

3)  В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

26. Какое из следующих утверждений верно?

1)  Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2)  Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3)  Смежные углы равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

27. Какие из следующих утверждений верны?

1)  Треугольника со сторонами 1, 2, 4 не существует.

2)  Смежные углы равны.

3)  Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

28. Укажите номера верных утверждений.

1)  Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.

2)  Через любые три точки проходит не более одной прямой.

3)  Сумма вертикальных углов равна 180°.

Если утверждений несколько, запишите их номера в порядке возрастания.

29. Укажите номера неверных утверждений.

1)  При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

2)  Диагонали ромба перпендикулярны.

3)  Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.

Если утверждений несколько, запишите их номера в порядке возрастания.

30. Укажите номера верных утверждений.

1)  В любую равнобедренную трапецию можно вписать окружность.

2)  Диагональ параллелограмма делит его углы пополам.

3)  Площадь прямоугольного треугольника равна половине произведения его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

31. Какие из следующих утверждений верны?

1)  Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.

2)  Диагонали ромба перпендикулярны.

3)  Существуют три прямые, которые проходят через одну точку.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

32. Какие из данных утверждений верны? Запишите их номера.

1)  Площадь квадрата равна произведению его диагоналей.

2)  Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.

3)  Вокруг любого параллелограмма можно описать окружность.

33. Какое из следующих утверждений верно?

1)  Все равнобедренные треугольники подобны.

2)  Существует прямоугольник, диагонали которого взаимно перпендикулярны.

3)  Сумма углов прямоугольного треугольника равна 90 градусам.

34. Укажите номера верных утверждений.

1)  Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2)  Существует квадрат, который не является ромбом.

3)  Сумма углов любого треугольника равна 180° .

Если утверждений несколько, запишите их номера в порядке возрастания.

35. Укажите номера верных утверждений.

1)  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2)  Треугольник со сторонами 1, 2, 4 существует.

3)  Если в ромбе один из углов равен 90°, то такой ромб  — квадрат.

4)  Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их номера в порядке возрастания.

36. Какие из следующих утверждений верны?

1)  Около любого правильного многоугольника можно описать не более одной окружности.

2)  Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3)  Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4)  Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

37. Какие из данных утверждений верны? Запишите их номера.

1)  Вокруг любого треугольника можно описать окружность.

2)  Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм  — квадрат.

3)  Площадь трапеции равна произведению средней линии на высоту.

Если утверждений несколько, запишите их номера в порядке возрастания.

38. Какие из данных утверждений верны? Запишите их номера.

1)  Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.

2)  В любой треугольник можно вписать окружность.

3)  Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

39. Какие из следующих утверждений верны?

1)  Если две стороны треугольника равны 3 и 5, то его третья сторона больше 3.

2)  Внешний угол треугольника равен сумме двух его внутренних углов.

3)  Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны.

4)  Если две стороны треугольника равны 3 и 4, то его третья сторона меньше 7.

40. Укажите номера верных утверждений.

1)  Любые три прямые имеют не более одной общей точки.

2)  Если угол равен 120°, то смежный с ним равен 120°.

3)  Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их номера в порядке возрастания.

41. Укажите номера верных утверждений.

1)  Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2)  В любом прямоугольнике диагонали взаимно перпендикулярны.

3)  Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их номера в порядке возрастания.

42. Какие из следующих утверждений верны?

1)  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2)  Треугольник со сторонами 1, 2, 4 существует.

3)  В любом параллелограмме есть два равных угла.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

43. Какие из следующих утверждений верны?

1)  В треугольнике против меньшего угла лежит большая сторона.

2)  Если один угол треугольника больше 120°, то два других его угла меньше 30°.

3)  Если все стороны треугольника меньше 1, то и все его высоты меньше 1.

4)  Сумма острых углов прямоугольного треугольника не превосходит 90°.

44. Какие из следующих утверждений верны?

1.  Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

2.  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

3.  Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

45. Какое из следующих утверждений верно?

1)  Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.

2)  Вписанные углы окружности равны.

3)  Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

4)  Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.

46. Какие из данных утверждений верны? Запишите их номера.

1)  У равнобедренного треугольника есть ось симметрии.

2)  Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм  — квадрат.

3)  Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.

47. Укажите номера верных утверждений.

1)  Существует квадрат, который не является прямоугольником.

2)  Если два угла треугольника равны, то равны и противолежащие им стороны.

3)  Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

48. Какое из следующих утверждений верно?

1)  Отношение площадей подобных треугольников равно коэффициенту подобия.

2)  Диагонали прямоугольника точкой пересечения делятся пополам.

3)  Биссектриса треугольника делит пополам сторону, к которой она проведена.

В ответе запишите номер выбранного утверждения.

49. Укажите номера верных утверждений.

1)  Если один из углов треугольника прямой, то треугольник прямоугольный.

2)  Диагонали квадрата точкой пересечения делятся пополам.

3)  Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.

50. Какие из следующих утверждений верны?

1)  Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник  — параллелограмм.

2)  Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

3)  Сумма двух противоположных углов четырехугольника не превосходит 180°.

4)  Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.

1. Материал взят с сайта РЕШУ ОГЭ https://oge.sdamgia.ru/

Справка по базовой геометрии

Студенты, нуждающиеся в помощи по основам геометрии, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по базовой геометрии. Имея под рукой обязательные концепции изучения и актуальные практические вопросы, вы быстро получите массу помощи по базовой геометрии. Получите помощь сегодня с нашей обширной коллекцией важной информации по базовой геометрии.

Геометрия является наиболее распространенным математическим предметом в средней школе США. По оценкам Института педагогических наук, в 2009 году 88 процентов учащихся средних школ США прошли курс геометрии. Этот раздел математики знакомит учащихся со свойствами и взаимосвязями углов, линий, поверхностей и других элементов основных форм. Предмет, который большинство учащихся могут освоить к 10-му классу, является обязательным для любого студента колледжа, который хочет изучать математику, а также междисциплинарные области, такие как физика и инженерия. Независимо от планов учащегося на будущее, изучение основ геометрии обеспечит необходимые строительные блоки для более сложных математических концепций как в старшей школе, так и в колледже. Нужна ли вам репетиторство по геометрии в Атланте, репетиторство по геометрии в Миннеаполисе или репетиторство по геометрии в Остине, работа один на один с экспертом может стать именно тем стимулом, в котором нуждается ваша учеба.

Справка по основам геометрии, доступная с помощью бесплатного инструмента обучения Varsity Tutors «Learn by Concept Learning Tool», охватывает множество тем для студентов, плохо знакомых с предметом. Студенты, которым нужна учеба, помогут получить ее, ответив на ряд примеров вопросов на веб-сайте Varsity Tutors Learning Tools. Темы организованы как учебная программа класса, с несколькими общими разделами и серией подтем. В каждом примере вопроса вам дается проблема и несколько возможных ответов. Вы решаете задачу и выбираете правильный ответ, а затем проверяете, правильно ли вы его поняли. Varsity Tutors предлагает такие ресурсы, как бесплатные практические тесты по базовой геометрии, которые помогут вам в самостоятельном обучении, или вы можете рассмотреть возможность найма репетитора по геометрии.

Что еще более важно, Learn by Concept выходит за рамки простого предоставления проблем и решений, сосредоточив внимание на процессе решения проблем. Каждый образец вопроса содержит подробное объяснение того, как прийти к правильному ответу. Каждое релевантное понятие или формула отмечены, и каждый отдельный шаг описан в этих объяснениях. Если существует несколько правильных методов решения проблемы, то каждый метод включается. Если вы дали неправильный ответ, вы можете повторить свои шаги, чтобы точно определить, где вы сбились с пути и как вернуться. Если вы ответили правильно, вы можете проверить свою работу и убедиться, что процесс был правильным, а не просто повезло с ответом. В дополнение к разделу справки по основам геометрии и урокам геометрии вы также можете рассмотреть некоторые из наших карточек по основам геометрии.

Любой учащийся, планирующий изучать высшую математику в колледже или просто желающий хорошо учиться в старшей школе, может использовать инструмент «Учиться по понятиям» в качестве учебного пособия по основам геометрии. Инструмент охватывает основные темы кругов, линий, четырехугольников и треугольников. Каждая подтема структурирована как «Как сделать», например «Как найти диаметр». Количество вопросов варьируется в зависимости от предмета: некоторые подтемы содержат более 50 вопросов, а другие относятся к младшим подросткам.

На веб-сайте учебных материалов Varsity Tutors также можно найти дополнительные материалы для изучения геометрии. Наряду с инструментом «Изучение концепций» вы можете пройти один из нескольких бесплатных полноразмерных практических тестов по базовой геометрии, чтобы определить, какие концепции вы понимаете, а на каких следует сосредоточить внимание при изучении. Существуют также сотни практических тестов, посвященных конкретным областям, которые позволяют вам определить, в чем вам нужна помощь.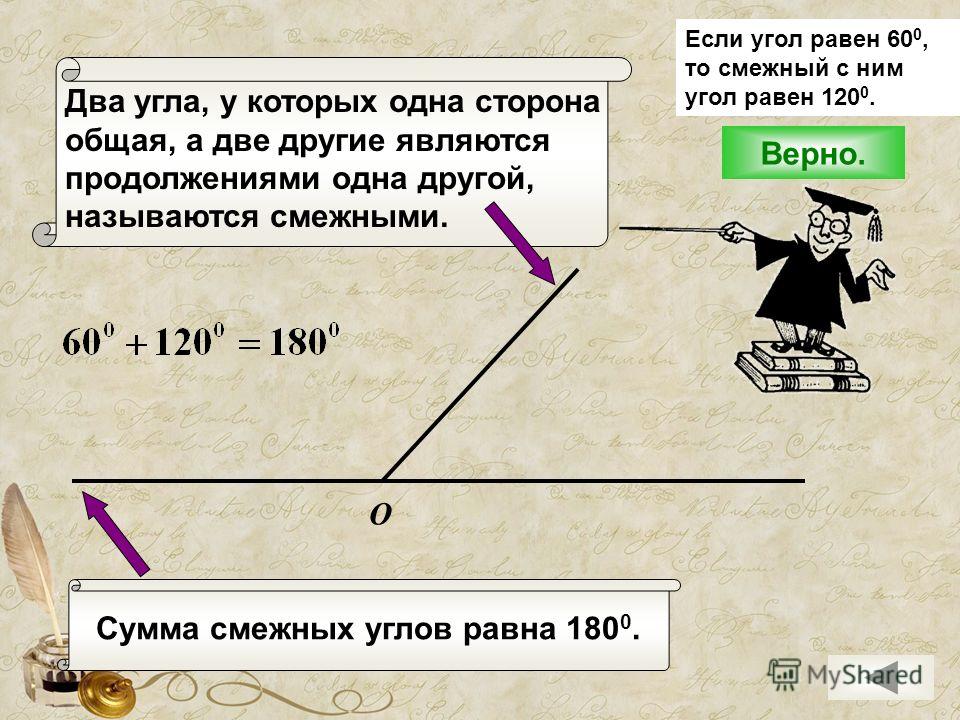 Изучив бесплатные примеры вопросов «Учитесь по концепции», вы также можете использовать карточки для обучения по инструментам обучения преподавателей Varsity Tutors, чтобы проверить себя по тем же темам. Карточки можно сортировать по категориям или настраивать в соответствии с вашими конкретными потребностями. Инструмент «Вопрос дня» рандомизирует вопросы из всех основных тем и концепций геометрии, чтобы помочь вам проверить свои общие знания по предмету. Используйте инструменты обучения Varsity Tutors, чтобы оставаться сосредоточенным, когда вы изучаете базовую геометрию и начинаете переходить к более продвинутым концепциям.

• Базовая геометрия

• Плоская геометрия

• Круги

• Математика часов

• Как найти угол часовых стрелок

• Как найти расстояние между стрелками часов

• Диаметр

• Как найти длину диаметра

• Как найти соотношение диаметра и длины окружности

• Радиус

• Как найти длину окружности

• Как найти площадь круга

• Как найти длину радиуса

• строки

• Как найти луч

• Как найти угол прямой

• Четырехугольники

• Прямоугольники

• Как определить, подобны ли прямоугольники

• Как найти площадь прямоугольника

• Как найти длину диагонали прямоугольника

• Как найти длину стороны прямоугольника

• Как найти периметр прямоугольника

• Квадраты

• Как найти площадь квадрата

• Как найти длину диагонали квадрата

• Как найти длину стороны квадрата

• Как найти периметр квадрата

• Треугольники

• 45/45/90 Прямоугольные равнобедренные треугольники

• Как найти площадь прямоугольного равнобедренного треугольника 45/45/90

• Как найти высоту прямоугольного равнобедренного треугольника 45/45/90

• Как найти длину гипотенузы прямоугольного равнобедренного треугольника 45/45/90 : теорема Пифагора

• Как найти длину стороны прямоугольного равнобедренного треугольника 45/45/90

• Как найти периметр 45/45/90 прямоугольный равнобедренный треугольник

• Прямоугольные треугольники

• Как найти угол в прямоугольном треугольнике

• Как определить конгруэнтность прямоугольных треугольников

• Как определить, подобны ли прямоугольные треугольники

• Как найти площадь прямоугольного треугольника

• Как найти высоту прямоугольного треугольника

• Как найти длину гипотенузы прямоугольного треугольника : Теорема Пифагора

• Как найти длину стороны прямоугольного треугольника

• Как найти периметр прямоугольного треугольника

Видео-вопрос: Использование тригонометрических соотношений для нахождения двух недостающих длин прямоугольного треугольника

Стенограмма видео

Найдите значения 𝑥 и 𝑦, дающие ответ с точностью до трех знаков после запятой.

В этом вопросе нам нужно определить значения двух неизвестных 𝑥 и 𝑦, и нам нужно дать ответ с точностью до трех знаков после запятой. Чтобы ответить на этот вопрос, сначала заметим, что значения 𝑥 и 𝑦 представляют длины сторон прямоугольного треугольника. И в этом прямоугольном треугольнике нам дан один из непрямых углов и одна из длин другой стороны. Следовательно, мы можем определить значения 𝑥 и 𝑦, используя тригонометрию прямоугольного треугольника.

Для этого нам сначала нужно обозначить размер этого прямоугольного треугольника. Мы всегда должны начинать с гипотенузы. Это самая длинная сторона прямоугольного треугольника, лежащая напротив прямого угла. Значит, в данном случае гипотенуза имеет длину 𝑦. Затем нам нужно пометить две другие стороны в зависимости от их положения относительно угла, который мы знаем. Это 47 градусов. Во-первых, мы можем заметить, что сторона длиной 28 сантиметров находится напротив угла 47 градусов. Итак, мы пометим эту сторону как противоположную сторону. Наконец, последняя сторона длины 𝑥 находится рядом с нашим углом 47 градусов, поэтому мы можем сказать, что она примыкает к этому углу. Назовем эту сторону соседней стороной.

Теперь мы можем вспомнить, что мы можем определить значения 𝑥 и 𝑦, используя тригонометрические соотношения. Чтобы помочь нам определить, какие тригонометрические отношения нам нужно использовать, мы вспомним следующую аббревиатуру: SOH CAH TOA. Нам нужно применить это дважды, чтобы определить значения 𝑥 и 𝑦 по отдельности. Начнем с определения значения 𝑥. Это означает, что нам нужно начать с использования нашей аббревиатуры, чтобы определить, какое тригонометрическое отношение поможет нам найти значение 𝑥.

Мы видим, что 𝑥 — сторона, примыкающая к нашему углу. И мы уже знаем значение стороны, противоположной нашему углу. И мы можем видеть в аббревиатуре, если мы знаем сторону, противоположную углу, и сторону, примыкающую к углу, то нам нужно использовать функцию тангенса. Мы знаем, что если 𝜃 является углом в прямоугольном треугольнике, то тангенс угла 𝜃 говорит нам об отношении длины противолежащей стороны к углу 𝜃, деленной на длину прилежащей стороны к углу 𝜃. В нашем прямоугольном треугольнике мы хотим использовать угол 𝜃, равный 47 градусам. Тогда прилежащая сторона имеет длину 𝑥, а противоположная сторона имеет длину 28 сантиметров.

Подставляя эти значения, получаем тангенс 47 градусов равен 28 делённому на 𝑥. Нам нужно решить это уравнение относительно 𝑥. Во-первых, мы умножим обе части нашего уравнения на 𝑥. Это дает нам, что 𝑥, умноженное на тангенс 47 градусов, равно 28. И теперь мы можем найти 𝑥, разделив обе части уравнения на тангенс 47 градусов. Получаем, что 𝑥 равно 28, деленному на тангенс 47 градусов. А теперь, вспомнив, что длины сторон этого треугольника измеряются в сантиметрах, и с помощью нашего калькулятора, где мы убедились, что наш калькулятор настроен на режим градусов, мы можем найти значение 𝑥. Это 26,1104, и это расширение продолжается в сантиметрах.

Наконец, вопрос требует, чтобы мы привели значения 𝑥 и 𝑦 к трем знакам после запятой. Итак, мы смотрим на четвертый десятичный знак, равный четырем, который, как мы знаем, меньше пяти. Итак, нам нужно округлить это в меньшую сторону. Следовательно, с точностью до трех знаков после запятой 𝑥 равно 26,110 сантиметра.

Точно так же мы можем найти значение 𝑦. Еще раз, мы будем использовать нашу аббревиатуру SOH CAH TOA, чтобы определить, какое тригонометрическое соотношение нам нужно использовать. На диаграмме нам известна длина противоположной стороны, и мы хотим определить 𝑦, которая является длиной гипотенузы. Поэтому нам нужно тригонометрическое отношение, связывающее противоположную сторону и гипотенузу. Это функция синуса. Затем мы можем вспомнить, если 𝜃 — угол в прямоугольном треугольнике, то sin 𝜃 равен длине стороны, противоположной углу 𝜃, деленной на длину гипотенузы.

Затем мы можем подставить наши значения из диаграммы. Получаем, что грех 47 градусов равен 28 делённому на 𝑦. Теперь все, что нам нужно сделать, это решить это уравнение для 𝑦. Мы умножаем обе части уравнения на 𝑦, а затем делим на грех 47 градусов. Получаем 𝑦 равно 28 делённому на грех 47 градусов.