Если угол острый то смежный с ним угол острый: Ука­жи­те но­ме­ра вер­ных утвер­жде­ний. 1) Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся…

Тесты 7 класс геометрия

Билет1.

1. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Через любые три точки про­хо­дит ровно одна пря­мая.

    2). Вер­ти­каль­ные углы равны.

    3). Любая бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его ме­ди­а­ной.

 

2. Ука­жи­те но­ме­ра невер­ных утвер­жде­ний.

    1). Через любую точку про­хо­дит более одной пря­мой.

    2). Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

    3). В равнобедренном треугольнике все стороны равны.

 

3.Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ведённая из вер­ши­ны, про­ти­во­ле­жа­щей      ос­но­ва­нию, делит ос­но­ва­ние на две рав­ные части.

    2). Любые две пря­мые имеют ровно одну общую точку.

    3.) Для точки, ле­жа­щей на окруж­но­сти, рас­сто­я­ние до цен­тра окруж­но­сти равно ра­ди­у­су.

 

4. Ука­жи­те но­ме­ра невер­ных утвер­жде­ний.

    1). Любые две пря­мые имеют не менее одной общей точки.

    2). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°, то эти две пря­мые па­рал­лель­ны.

    3). Сумма углов лю­бо­го тре­уголь­ни­ка равна 180° .

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся ост­рым.

    2). Любые три пря­мые имеют не менее одной общей точки.

    3). В плос­ко­сти все точки, рав­но­удалённые от за­дан­ной точки, лежат на одной окруж­но­сти.

 

 

Билет2.

1. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если угол равен 45°, то вер­ти­каль­ный с ним угол равен 45°.

    2). Сумма смеж­ных углов равна 180°.

    3). Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

 

2. Какие из сле­ду­ю­щих утвер­жде­ний не верны?

   1). Если две сто­ро­ны од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

   2). Длина ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше суммы длин его ка­те­тов.

  3). В треугольнике ABC, для которого  ,  ,  , угол В наибольший.

 

 

3. Какие из сле­ду­ю­щих утвер­жде­ний верны?

    1). Длина ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше суммы длин его ка­те­тов.

    2). В ту­по­уголь­ном тре­уголь­ни­ке все углы тупые.

    3). В равнобедренном треугольнике имеется не более двух равных углов.

 

 

4. Какие из сле­ду­ю­щих утвер­жде­ний не верны?

   1). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние на­крест ле­жа­щие углы со-­ став­ля­ют в сумме 90°, то эти две пря­мые па­рал­лель­ны.

   2). Через любую точку про­хо­дит не менее одной пря­мой

   3). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние од­но­сто­рон­ние углы равны  70° и 110°, то эти две пря­мые па­рал­лель­ны.

 

5.  Какие из сле­ду­ю­щих утвер­жде­ний верны?

     1). Через точку, не ле­жа­щую на дан­ной пря­мой, можно про­ве­сти пря­мую, па­рал­лель­ную этой пря­мой.

     2). Тре­уголь­ник со сто­ро­на­ми 1, 2, 4 су­ще­ству­ет.

     3). Сумма вер­ти­каль­ных углов равна 180°.

 

 

 

Билет3.

1.

Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если угол равен 60°, то смеж­ный с ним равен 120°.

    2.) Любые три пря­мые имеют не более одной общей точки.

    3). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние на­крест ле­жа­щие углы со­став­ля­ют в сумме 90°, то эти две пря­мые па­рал­лель­ны.

 

2. Ука­жи­те но­ме­ра невер­ных утвер­жде­ний 

     1). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 37°, то эти две пря­мые па­рал­лель­ны.

     2). Через любые три точки про­хо­дит не более одной пря­мой.

     3). Каж­дая из бис­сек­трис рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его ме­ди­а­ной.

 

3. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны.

    2). Через любые две точки можно про­ве­сти пря­мую.

    3). Через точку, не ле­жа­щую на дан­ной пря­мой, можно про­ве­сти един­ствен­ную пря­мую, пер­пен­ди­ку­ляр­ную дан­ной пря­мой.

 

4.  Ука­жи­те но­ме­ра невер­ных утвер­жде­ний.

    1). Смеж­ные углы равны.

    2). Любые две пря­мые имеют ровно одну общую точку.

    3). Если угол равен 47°, то смеж­ный с ним равен 153°.

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если угол равен 108°, то вер­ти­каль­ный с ним равен 108°.

    2). Если две пря­мые пер­пен­ди­ку­ляр­ны тре­тьей пря­мой, то эти две пря­мые па­рал­лель­ны.

    3). Через любую точку про­хо­дит ровно одна пря­мая.

 

Билет 4.

1. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

     1.) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°, то эти две пря­мые па­рал­лель­ны.

     2). Если угол равен 120°, то смеж­ный с ним равен 120°.

     3). Если две сто­ро­ны и угол од­но­го тре­уголь­ни­ка равны со­от­вет­ствен­но двум сто­ро­нам и углу дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

 

2. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

    1). При пе­ре­се­че­нии двух па­рал­лель­ных пря­мых тре­тьей пря­мой сумма на­крест ле­жа­щих углов равна 180°.

     2). Если при пересечении двух прямых третьей соответственные углы равны, то

   прямые перпендикулярны

    3). Каждая сторона треугольника меньше сумме двух других сторон.

 

3. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1).

При пе­ре­се­че­нии двух па­рал­лель­ных пря­мых тре­тьей пря­мой сумма на­крест ле­жа­щих углов равна 180°.

    2). Если при пересечении двух прямых третьей соответственные углы равны, то

    прямые перпендикулярны.

    3). В треугольнике против меньшей стороны лежит меньший угол.

 

4. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

   1). Если угол равен  54°, то вертикальный с ним угол равен  34°.

   2). Если угол равен 72°, то смежный с ним угол равен 108°.

   3). Все радиусы окруж­но­сти равны между собой.

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если два угла треугольника равны 36° и 64°, то третий угол равен 100°.  

    2). В треугольнике против меньшей стороны лежит меньший угол.

    3). Если три угла одного  треугольника равны  трем углам другого треугольника, то  такие треугольники равны.

Билет 5.

1. Ука­жи­те но­ме­ра ­вер­ных утвер­жде­ний.

    1). Каждая сторона треугольника равна сумме двух других сторон.

    2). Если угол равен 45°, то вертикальный с ним угол равен 45°.

    3). Катет,  лежащий   против угла   30°,  равен  гипотенузе.

 

2. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

    1). Длина ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше суммы длин его катетов.

    2). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°,

то эти две пря­мые параллельны.

    3). В тре­уголь­ни­ке про­тив мень­ше­го угла лежит боль­шая сторона.

 

3. Ука­жи­те но­ме­ра ­вер­ных утвер­жде­ний.

    1). Сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка не пре­вос­хо­дит 90°.

    2). Если один угол тре­уголь­ни­ка боль­ше 120°, то два дру­гих его угла мень­ше 30°.

    3). Катет,  лежащий   против угла  в 30°,  равен  половины гипотенузы.

 

4. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

    1). Треугольник со сторонами 1, 2, 3 не существует.

    2). В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.

    3). Если две стороны треугольника равны 3 и 5, то его третья сторона не меньше 3.

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны   и  , то эти две прямые параллельны.

    2). В равнобедренном прямоугольном треугольнике все стороны равны.

    3). Если две стороны треугольника равны 3 и 4, то его третья сторона меньше 7.

 

 

Билет 6.

1. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Внешний угол треугольника всегда тупой.

2) Внут­рен­ние на­крест ле­жа­щие углы, об­ра­зо­ван­ные двумя па­рал­лель­ны­ми пря­мы­ми и се­ку­щей, равны.

3)  В треугольнике против меньшего угла лежит большая сторона.

 

2. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.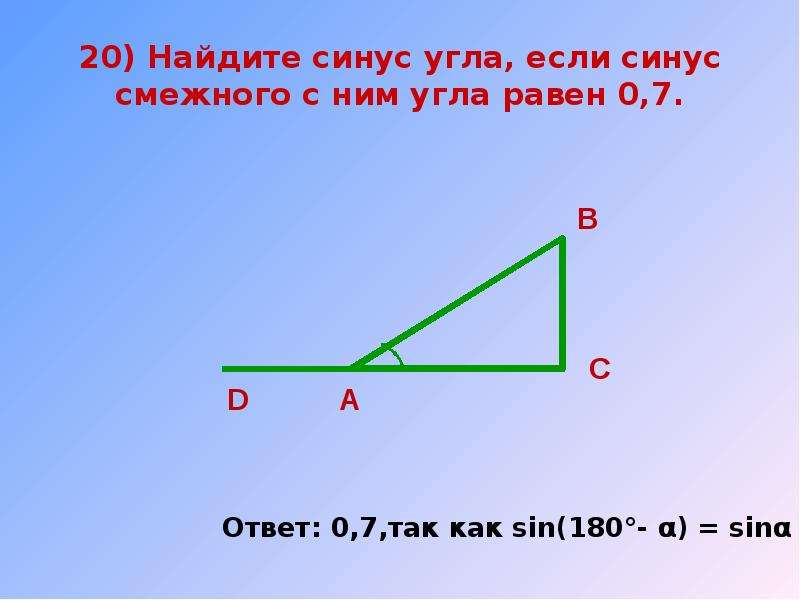

1. В треугольнике ABC, для которого  ,  ,  , угол С наименьший.

2.Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.

3. Биссектриса угла треугольника делит треугольник пополам.

 

3. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1). В треугольнике  , для которого  ,  ,  , угол   — наибольший.

2). Внешний угол треугольника больше не смежного с ним  внутреннего углов.

3)  В равнобедренном треугольнике все углы равны.

 

 

4. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

    1). Если все сто­ро­ны тре­уголь­ни­ка мень­ше 1, то и все его вы­со­ты мень­ше 1.

    2).  Каждая сторона треугольника не превосходит суммы двух других сторон.

    3). Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1).В треугольнике  , для которого  ,  ,  , сторона   — наименьшая.

    2). Через любые три точки про­хо­дит не более одной пря­мой.

    3).  Внешний угол треугольника равен сумме  его внутренних углов.

 

 

 

 

 

Билет 7.

1. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). В равнобедренном треугольнике имеется не менее двух равных углов.

    2). Если все сто­ро­ны тре­уголь­ни­ка мень­ше 3, то и все его вы­со­ты мень­ше 3.

    3).  В треугольнике против большего угла лежит меньшая сторона.

 

2. Ука­жи­те но­ме­ра невер­ных утвер­жде­ний.

    1). Через любую точку про­хо­дит более одной пря­мой.

    2). Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

    3).  В равнобедренном треугольнике все стороны равны

 

3. Какие из сле­ду­ю­щих утвер­жде­ний верны?

    1). Если две сто­ро­ны од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

    2). Длина ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше суммы длин его ка­те­тов.

    3). В треугольнике ABC, для которого  ,  ,  , угол В наибольший.

 

4. Ука­жи­те но­ме­ра невер­ных утвер­жде­ний.

     1). Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны.

     2). Через любые две точки можно про­ве­сти пря­мую.

     3). Через точку, не ле­жа­щую на дан­ной пря­мой, можно про­ве­сти един­ствен­ную пря­мую, пер­пен­ди­ку­ляр­ную дан­ной пря­мой.

 

5. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

    1). Если угол равен  54°, то вертикальный с ним угол равен  34°.

    2).Если угол равен 72°, то смежный с ним угол равен 108°.

    3). Все радиусы окруж­но­сти равны между собой.

 

 

 

 

 

 

 

 

 

Что такое смежные углы? Ответ на webmath.ru

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

• Определение смежных углов
• Следствия из теоремы о смежных углах
• Свойства (тригонометрические соотношения)

Определение смежных углов

Определение

Смежными углами называются два прилежащих угла, несовпадающие стороны которых образуют прямую (рис. {\circ}-\angle \beta$$

Так как $\angle \alpha \neq \angle \beta$, то и разности, стоящие в правых частях последних равенств также не равны, причем при равенстве уменьшаемого та разность меньше, где вычитаемое больше, следовательно $\angle \alpha_{1} < \angle \beta_{1}$.

Что и требовалось доказать.

Свойства (тригонометрические соотношения)

1. Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
2. Чтобы построить угол, смежный данному, надо одну из сторон рассматриваемого угла продлить за вершину (рис. 3).

Читать дальше: что такое острый угол.

острых углов | Определение, примеры, классификация, пары и викторина

Введение

В жизни мы сталкиваемся с геометрическими понятиями, даже не осознавая, что процесс моделируется с помощью геометрии. Например, при разрезании торта на шесть или восемь совершенно одинаковых кусков нам необходимо определить центральный угол каждого куска торта. Когда мы смотрим на некий предмет, наши глаза направляются по двум лучам, которые сходятся на этом предмете в одной точке и таким образом образуют угол. Приближаясь к объекту, угол увеличивается, удаляясь от объекта – угол уменьшается. А что уж говорить о таких важных областях нашей жизни, как архитектура, физика или механика, где без углов почти ничего не сделаешь. Так почему бы не описать математически то, что мы используем в жизни?

Определение острого угла

Угол определяется как фигура, образованная при пересечении двух лучей в одной точке. Угол обозначается символом ∠.

Каждый угол состоит из двух плеч и вершины:

• плечами угла являются те два луча, которые, соединяясь, образуют угол;
• вершина угла является общей конечной точкой, в которой встречаются два плеча.

Мы можем назвать угол, используя вершину и точку на каждом из плеч угла. Название угла представляет собой последовательность из трех букв, обозначающих эти точки, с вершиной посередине. Например, на диаграмме ниже показан ∠AOB с плечами $\overrightarrow{OA}$ и $\overrightarrow{OB}$ и вершиной O.

Обычно мы измеряем углы в градусах или радианах.

Градусов: Один полный оборот вокруг точки равен 360°.

Полный поворот{Изображение взято с бесплатного ресурса Pixabay}

Вы можете спросить, почему угол полного поворота равен 360°? Древние персидские астрономы считали, что год состоит из 360 дней. Наблюдая за вращением солнца, они заметили, что солнцу потребовалось ровно 360 дней, чтобы вернуться в исходное положение. Другими словами, каждый день солнце поворачивается на 1°. Другая историческая причина предполагает, что мера полного угла поворота исходит от вавилонян. Они использовали систему счисления с основанием 60, и число 360 было легко представить в этой системе счисления.

Вавилонская система счисления {Изображение взято из Викисклада}

Радиан: Один радиан — это угол, образуемый в центре круга дугой, длина которой равна радиусу круга. Полный круг имеет 2π радиан, поэтому существует простая связь между градусами и радианами.

Угол	Радианы	градусов
Полное вращение	2π	360 °
Полно.0038	π	180 °
Квартал полного вращения	$ \ frac {π} {4} $	90 °

равняется 180°. Например, $\frac{π}{3}$ радиан равно $\frac{180°}{3}$=60°.

Если вы хотите перевести градусы в радианы, то найдите, какую часть 180° составляет заданный угол. Например, 45° — это $\frac{1}{4}$ из 180°, поэтому 45° — это $\frac{1}{4}π=\frac{π}{4}$.

Мы можем измерять углы транспортиром. Нормальный транспортир измеряет углы от 0° до 180°.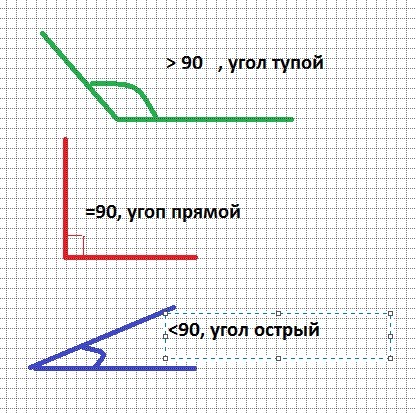 Например, мера угла ниже составляет 15 ° (правая сторона угла указывает на ноль, а левая сторона угла указывает на 15 °).

Используя обычный транспортир, мы можем измерять углы в обоих направлениях: по часовой стрелке и против часовой стрелки.

Существуют также транспортиры полного круга. Например, на диаграмме ниже показан угол с мерой 210°.

Определение: Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.

Примеры острых углов

Мы уже знаем, что острый угол меньше 90°. Примерами острых углов являются 12°, 35°, 61° или 89°, но углы 0°, 90°, 146° или 214° не являются острыми углами.

ПРИМЕР: Найдя величину каждого угла, определите, какой угол острый, а какой нет.

РЕШЕНИЕ:

а) В этом случае угол имеет градусную меру 60°, поэтому он острый (измеряйте этот угол против часовой стрелки).

b) Этот угол не является острым, поскольку его градусная мера больше 90° (измеряйте этот угол по часовой стрелке).

c) Правая сторона угла указывает на 75°, левая сторона угла указывает на 120°, поэтому величина угла 120°-75°=45°. Поскольку 45° меньше 90°, этот угол острый.

d) Показанный угол не является острым, его мера 270° даже больше, чем 180°.

Классификация углов

Углы можно классифицировать по их величинам:

• если градусная мера угла точно равна 0°, угол равен нулю угла;
• если градусная мера угла больше 0° и меньше 90°, угол является острым;
• если градусная мера угла точно равна 90°, то угол прямой;
• если градусная мера угла больше 90° и меньше 180°, то угол является тупым;
• если градусная мера угла точно равна 180°, то угол прямой;
• , если градусная мера угла больше 180° и меньше 360°, угол является рефлекторным;
• если градусная мера угла равна точно 360°, то угол является полным углом.

Покажем это с помощью следующей таблицы.

Тип угла	Диаграмма	Диапазон измерений
Zero		Мера = 0 °
. 0°
right		Measure =90°
obtuse		90°< Measure <180°
straight		Measure =180°
reflex		180°< мера <360°
полный		мера =360°

или полный угол:

• Полный угол — это полный угол поворота. Если данный угол ограничивает менее четверти полной окружности, то это острый угол.
• Прямой угол равен половине полного угла. Если данный угол ограничивает менее половины прямого угла, то это острый угол. Если пределы данного угла близки к половине или больше половины прямого угла, то он не является острым углом.
• Прямой угол составляет четверть полного угла. Если пределы данного угла меньше прямого угла, то это острый угол.

Например, на приведенной ниже диаграмме показан угол, который ограничивает большую часть окружности, чем одна четверть, поэтому этот угол не является острым.

Часто возникают следующие вопросы об углах: 

• «Острый ли угол с мерой 0°?», «Острый ли угол с мерой 90°?» Теперь вы знаете, что углы с размерами 0° и 90° не являются острыми, это нулевой и прямой углы соответственно.
• «Нулевой угол и полный угол — это одно и то же?» Нет, эти углы имеют разную меру.

Примеры острых углов из жизни

I) « Где в жизни можно увидеть нулевой угол? »

Вы наверняка видели часы с циферблатом и стрелками. Итак, стрелки часов, указывающие на определенный час, образуют угол с вершиной в центре часов.

Теперь рассмотрим пример, часы показывают время 2 часа ночи. Какой угол образуют обе стрелки часов? Является ли этот угол острым?

Сначала найдите угол между двумя последовательными числами на часах. На часах 12 чисел, поэтому мера угла между двумя последовательными числами равна $\frac{360°}{12}$=30°.

Теперь, если часы показывают, что время 2 часа, то более длинная стрелка указывает на 12, а более короткая стрелка указывает на 2. Между этими двумя числами находятся два угла по 30°, следовательно, мера неизвестного угла равна 2⋅30°=60°. Поскольку 60°<90°, угол с градусной мерой 60° является острым углом.

II) “ Где в реальной жизни я могу видеть полный угол? ”

Наматывая нить на катушку каждый раз, когда возвращаемся в исходную точку, проходим полный угол.

III) « Где в реальной жизни я могу увидеть прямой угол? ”

Когда бы вы ни поехали кататься, вы можете увидеть прямой угол на дороге. Более того, на Т-образном перекрестке можно увидеть два прямых угла.

IV) « Где в жизни можно увидеть острый угол? »

В реальной жизни очень часто встречаются острые углы: бока раскрытых ножниц, кусочек пиццы, угол между двумя пальцами, вешалка для одежды, крыша дома и даже пасть крокодила. В повседневной жизни мы видим множество углов – нужно только иметь немного воображения, чтобы их увидеть и понять: «О, я вижу угол, и он острый!»

Пары углов

• Смежные углы: углы, имеющие одну вершину и одно общее плечо.
• Линейная пара углов: два смежных угла, которые вместе образуют прямой угол;
• Дополнительные углы: пара углов, которые вместе образуют прямой угол, другими словами, их сумма составляет 90º.
• Дополнительные углы: пара углов, которые вместе образуют прямой угол, другими словами, сумма этих углов равна 180º.
• Вертикальные углы: вертикальные углы — это два противоположных угла, образованных при пересечении двух линий.
• Односторонние внутренние углы: односторонние внутренние углы представляют собой пару углов, образованных при пересечении одной прямой двух параллельных прямых. Внутренние углы с одной стороны в сумме составляют 180°.
• Альтернативные внутренние углы: альтернативные внутренние углы представляют собой пару углов, образованных при пересечении одной прямой двух параллельных прямых. Альтернативные внутренние углы всегда равны друг другу.
• Альтернативные внешние углы: альтернативные внешние углы представляют собой пару углов, образованных при пересечении одной прямой двух параллельных прямых. Альтернативные внешние углы — это просто вертикальные углы альтернативных внутренних углов. Альтернативные внешние углы равны.
• Односторонние внешние углы: односторонние внутренние углы представляют собой пару углов, образованных при пересечении одной прямой двух параллельных прямых. Односторонние внешние углы — это просто вертикальные углы односторонних внутренних углов. Внешние углы с одной стороны в сумме составляют 180°.
• Соответствующие углы: соответствующие углы представляют собой пару углов, образованных при пересечении прямой парой параллельных прямых. Соответствующие углы также равны между собой.

Пусть параллельные прямые a и b пересекаются секущей c. Вот пример каждой пары углов:

• смежные углы: ∠1 и ∠2;
• дополнительные уголки: ∠1 и ∠2;
• вертикальные углы: ∠1 и ∠3;
• Уголки внутренние односторонние: ∠3 и ∠5;
• альтернативные внутренние углы: ∠3 и ∠6;
• Уголки наружные односторонние: ∠1 и ∠7;
• альтернативные внешние углы: ∠1 и ∠8;
• соответствующие углы: ∠1 и ∠6.

Учитывая все описанные определения и свойства пар углов, посмотрим, какие из них могут быть острыми.

• В паре смежных углов может быть два острых, один острый или нет острых углов.
• Каждая пара дополнительных углов состоит из двух острых углов.
• Каждая пара непрямых углов состоит из одного острого и одного тупого угла.
• При пересечении двух неперпендикулярных прямых одна пара вертикальных углов состоит из двух конгруэнтных острых углов, а другая пара вертикальных углов состоит из двух конгруэнтных тупых углов.
• При пересечении двух параллельных прямых неперпендикулярными секущими один из односторонних внутренних углов всегда острый.
• Когда две параллельные прямые пересекаются неперпендикулярной секущей, одна пара альтернативных внутренних углов состоит из двух конгруэнтных острых углов, а другая пара альтернативных внутренних углов состоит из двух конгруэнтных тупых углов.
• При пересечении двух параллельных прямых неперпендикулярными секущими один из односторонних внешних углов всегда острый.
• При пересечении двух параллельных прямых неперпендикулярной секущей одна пара альтернативных внешних углов состоит из двух конгруэнтных острых углов, а другая пара альтернативных внешних углов состоит из двух конгруэнтных тупых углов.
• При пересечении двух параллельных прямых неперпендикулярными секущими образуются четыре пары соответствующих углов. Две пары состоят из двух конгруэнтных острых углов, а две другие пары состоят из двух конгруэнтных тупых углов.

Треугольники с острыми углами

Все треугольники можно классифицировать по углам или сторонам.

Классификация треугольников по углам:

• остроугольный треугольник – все углы треугольника острые;
• прямоугольный треугольник – есть один прямой угол;
• тупоугольный треугольник – есть один тупой угол.

В остроугольных треугольниках все три угла острые, в то же время в прямоугольном и тупоугольном треугольниках по два острых угла.

Классификация треугольников по сторонам:

• разносторонний треугольник – все три стороны разной длины;
• равнобедренный треугольник – две стороны равны;
• равносторонний треугольник – все три стороны равны.

Разносторонние и равнобедренные треугольники могут быть остроугольными, прямоугольными и тупоугольными. Однако у равнобедренного треугольника не может быть двух тупых углов при основании. Равносторонний треугольник также является равноугольным треугольником, все его острые углы равны и равны 60°.

В остроугольном треугольнике сумма квадратов двух сторон треугольника больше, чем квадрат наибольшей стороны,

a ² +b ² >c ²

: В остроугольном треугольнике ABC длины двух меньших сторон равны 5 см и 12 см. Каков диапазон всех возможных длин наибольшей стороны в треугольнике ABC?

РЕШЕНИЕ: В остроугольном треугольнике ABC длина наибольшей стороны c удовлетворяет неравенству

5 ² +12 ² > C ²

C ² <25 +144

C ² <169

C <13

. Чтобы найти наименьшую возможную длину c, примените неравенство треугольника:

c+5>12

c>7

Следовательно, диапазон всех возможных длин наибольшей стороны в остроугольном треугольнике ABC равен

7 см< c<13 см

Часто задаваемые вопросы

1. Почему полный оборот составляет 360°, а не 100° или 1000°, например?

Древнеперсидские астрономы считали, что год состоит из 360 дней. Наблюдая за вращением солнца, они заметили, что солнцу потребовалось ровно 360 дней, чтобы вернуться в исходное положение. Другими словами, каждый день солнце вращается по градусу. Другая историческая причина предполагает, что мера полного угла поворота исходит от вавилонян. Они использовали систему счисления с основанием 60, и число 360 было легко представить в этой системе счисления. 9о$.

Если вы хотите перевести градусы в радианы, то найдите, какую долю составляет 180 ^o данного угла. Например, 45 ^o  равно $\frac{1}{4}$ из 180 ^o , поэтому 45 ^o равно $\frac{1}{4}π=\frac{π}{4}$ .

3. Существует ли треугольник с одним острым углом?

Нет, если треугольник имеет только один острый угол, то два других угла имеют меры не менее 90 ^o  и сумма мер всех внутренних углов треугольника будет больше 180 ^или .

4. Какое наибольшее и какое наименьшее количество острых углов в произвольном треугольнике?

Наибольшее количество острых углов в треугольнике равно трем, наименьшее количество острых углов в треугольнике равно двум.

5. Является ли угол с мерой 0° острым?

Нет, этот угол известен как нулевой угол.

6. Является ли угол с мерой 90° острым?

Нет, этот угол прямой.

7. Нулевой угол и полный угол — это одно и то же?

Нет, у них разные размеры.

8. Где в жизни можно увидеть нулевой угол?

На часы или ножницы.

Викторина

1. В каждом случае определите, является ли данный угол острым. Если это не острый угол, то каков его тип? Объясните свои рассуждения.

а) 13°;

б) 125°;

в) 90°;

г) 78°;

д) 180°;

е) 66°;

г) 0°;

h) 330°.

и) 360°.

РЕШЕНИЕ : 

а) 0°<13°<90°, тогда угол с мерой 13° является острым углом.

б) Поскольку 90°<125°<180°, угол с мерой 125° не является острым углом, этот угол тупой.

в) Угол 90° прямой, значит, этот угол не острый.

г) 0°<78°<90°, тогда угол с мерой 78° является острым углом.

д) Угол 180° прямой, поэтому этот угол не острый.

е) 0°<66°<90°, тогда угол с мерой 66° является острым углом.

g) Угол 0° является нулевым углом, поэтому этот угол не является острым.

з) Поскольку 180°<330°<360°, угол с мерой 330° не является острым углом, этот угол рефлекторный.

i) Угол 360° — это полный угол, поэтому этот угол не является острым.

2. Найдя величину каждого угла, определите, какой угол острый, а какой нет.

РЕШЕНИЕ: а) Правая сторона угла указывает на угол 45°, левая сторона угла указывает на угол 150°, поэтому величина угла 150°-45°=105°. Поскольку 105° больше 90°, этот угол не является острым.

б) Правая сторона угла указывает на 15°, левая сторона угла указывает на 75°, поэтому величина угла 75°-15°=60°. Поскольку 60° меньше 90°, этот угол острый.

ОТВЕТ: а) не острый угол б) острый угол

3. В каждом случае сравнение заданного угла с прямым, прямым или полным углом определяет, является ли он острым.

РЕШЕНИЕ : а) На рисунке показан угол, который ограничивает больший угол, чем прямой угол, поэтому этот угол не является острым.

б) На рисунке показан угол, который ближе к прямому углу, чем к прямому. Это означает, что данный угол не является острым углом.

в) На рисунке показан угол, который ограничивает меньший угол, чем прямой угол, поэтому этот угол является острым.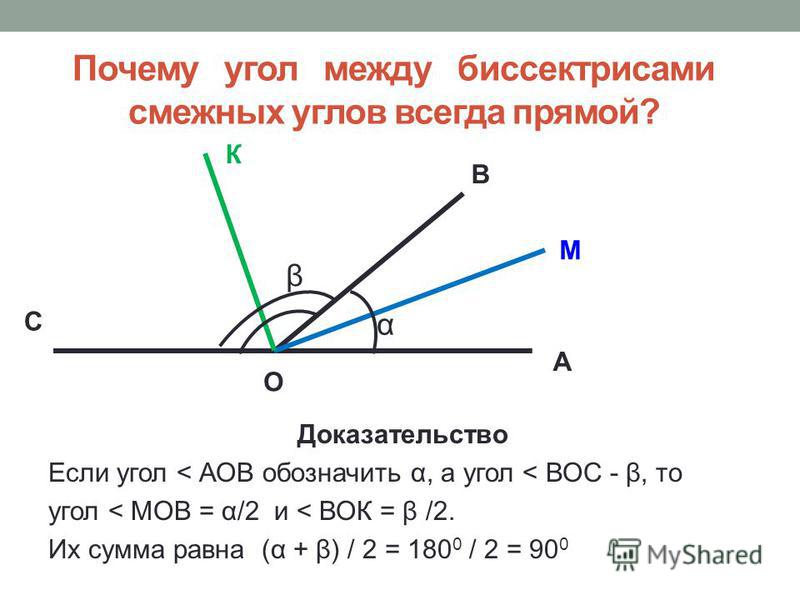

ОТВЕТ: а) не острый б) не острый в) острый

4. Какое из следующих утверждений верно? Объяснить, почему.

а) При пересечении двух параллельных прямых неперпендикулярными секущими внутренние углы с одной стороны равны.

б) При пересечении двух параллельных прямых перпендикулярной секущей один из внешних углов всегда острый.

в) При пересечении двух параллельных прямых неперпендикулярными секущими одна пара соответствующих углов всегда острая.

г) При пересечении двух прямых всегда имеется пара равных вертикальных острых углов.

РЕШЕНИЕ : а) При пересечении двух параллельных прямых секущими внутренние углы с одной стороны являются дополнительными. Два дополнительных угла равны только тогда, когда они оба прямые. Поскольку трансверсаль не перпендикулярна, внутренние углы с одной стороны не прямые, следовательно, они не равны, и это утверждение неверно.

b) При пересечении двух параллельных прямых перпендикулярной секущей противоположные внешние углы всегда прямые. Прямой угол не является острым углом, поэтому это утверждение неверно.

в) При пересечении двух параллельных прямых неперпендикулярными секущими образуются четыре пары соответствующих углов. Две пары состоят из двух конгруэнтных острых углов, а две другие пары состоят из двух конгруэнтных тупых углов. Итак, это утверждение верно.

г) При пересечении двух перпендикулярных прямых они образуют две пары вертикальных прямых углов. Если пересекающиеся прямые не перпендикулярны, это утверждение верно. Но в целом утверждение неверно.

ОТВЕТ : a) Неверно b) Неверно c) Верно d) Неверно

5. В остроугольном треугольнике ABC длины двух меньших сторон равны 8 см и 15 см. Чему равна натуральная длина наибольшей стороны треугольника ABC?

SOLUTION: In the acute triangle ABC, the length of the longest side c satisfies the inequality

8 ² +15 ² >c ²

c ² <64+225

в ² <289

c<17

Максимально возможная естественная длина наибольшей стороны равна 16 см.

ОТВЕТ: 16 см

Выводы

1. Каждый острый угол имеет размер меньше 90°.
2. Мы можем найти размеры углов, используя обычный транспортир или транспортир с полной окружностью.
3. Визуально мы можем сравнить углы с прямым углом, чтобы определить, острый он или нет.
4. Угол с величиной 0° не является острым углом.
5. В реальной жизни острые углы можно найти повсюду.
6. Каждый треугольник содержит не менее двух острых углов.

Острые углы (на тему спорта) Рабочие листы по математике
Острые треугольники (на тему города) Рабочие листы по математике
Углы (на тему архитектуры) Рабочие листы

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Пары углов в геометрии

Существует три основных типа углов: острые, прямые и тупые. Острые углы меньше 90 градусов, прямые углы ровно 90 градусов, а тупые углы больше 90 градусов, но меньше 180 градусов. Однако есть также два типа пар углов — комплементарные и добавочные. Дополнительные углы в сумме дают 90 градусов, а дополнительные углы в сумме составляют 180 градусов. Вот более подробный взгляд на каждый тип пары углов.

 

Дополнительные углы

Как мы только что упоминали, сумма дополнительных углов всегда равна 90 градусам. Это означает, что если вы знаете один угол в паре, вы всегда можете найти другой угол, вычитая известный угол из 90 градусов. Например, если угол A равен 30 градусам, то угол B должен быть равен 60 градусам, потому что 30 + 60 = 90.

 

Есть два особых случая, когда речь идет о дополнительных углах. Во-первых, когда один из углов прямой. В этом случае другой угол должен быть острым, потому что сумма острого угла и прямого угла всегда равна 9.0 градусов. Таким образом, если угол А прямой, то угол В должен быть меньше 90 градусов.

 

Второй частный случай имеет место, когда оба угла острые. В этом случае говорят, что два угла являются дополнительными смежными углами, потому что они имеют общую вершину и сторону. Дополнительные смежные углы всегда являются смежными (то есть имеют общую вершину), а их неразделенные стороны образуют прямую. Другими словами, они образуют прямую линию!

 

Дополнительные углы

Сумма дополнительных углов всегда составляет 180 градусов, но что произойдет, если один или оба угла тупые? Вот где все становится немного сложнее. Помните, что тупой угол больше 90 градусов, но меньше 180 градусов. Это означает, что если угол А тупой и мы знаем, что угол В является дополнительным к углу А, то угол В также должен быть тупым, потому что сумма двух тупых углов всегда больше 180 градусов, но меньше 360 градусов (полный оборот). . Однако, если только один угол тупой, то другой угол должен быть острым, потому что сумма острого угла и тупого угла всегда равна 180 градусам.

 

Вывод: 

Существует три основных типа углов — острые, прямые и тупые — и два основных типа пар углов — дополнительные и добавочные. Дополнительные углы всегда составляют в сумме 90 градусов, а дополнительные углы всегда в сумме составляют 180 градусов. Однако все может стать сложнее, когда один или оба угла в паре тупые, потому что сумма двух тупых углов всегда больше 180, но меньше 360 (полный оборот). Лучший способ запомнить всю эту информацию — попрактиковаться в определении различных типов пар углов в задачах по геометрии. При достаточной практике вы сможете идентифицировать их, даже не задумываясь об этом!

 

Часто задаваемые вопросы

Что такое пара углов в геометрии?

Пара углов – это два угла, которые каким-то образом связаны друг с другом. Существует три основных типа пар углов: дополнительные, дополнительные и смежные. Дополнительные углы в сумме дают 90 градусов, а дополнительные углы в сумме составляют 180 градусов. Смежные углы имеют общую вершину и сторону, но не обязательно имеют какое-либо математическое отношение.

 

Какие существуют 4 типа пар углов?

Существует четыре типа пар углов: дополнительные, дополнительные, смежные и вертикальные. Дополнительные углы в сумме дают 90 градусов, а дополнительные углы в сумме составляют 180 градусов. Смежные углы имеют общую вершину и сторону, но не обязательно имеют какое-либо математическое отношение. Вертикальные углы — это углы, лежащие друг против друга и имеющие общую вершину.

 

Сколько пар углов в геометрии?

Существует три основных типа пар углов — дополнительные, дополнительные и смежные. Дополнительные углы в сумме дают 90 градусов, а дополнительные углы в сумме составляют 180 градусов. Смежные углы имеют общую вершину и сторону, но не обязательно имеют какое-либо математическое отношение.

 

Какие 5 пар углов?

Существует пять пар углов: острые, прямые, тупые, комплементарные и добавочные.