Хело! Какие из утверждений верны? Вариант 6. Часть 1. Задание 13. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/класс
Хело! Какие из утверждений верны? Вариант 6. Часть 1. Задание 13. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Какие из следующих утверждений верны?

2) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
3) Если диагонали параллелограмма равны, то он является ромбом.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Олимпиады
Экзамены
Оценки
похожие вопросы 5
Вариант 1. Часть 2. Задание 26. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите найти АН.
На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АD (Подробнее…)
ГДЗМатематикаОГЭ9 классЯщенко И. В.
В.
Вариант 3. Часть 1. Задание 4. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите с корнями!
Решите уравнение х2- 5х = 14 .
ГДЗМатематикаОГЭ9 классЯщенко И.В.
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.
Здравствуйте! Помогите установить соответствие между величинами и их возможными значениями: к каждому элементу первого столбца (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ
Всем привет, поделитесь ответом на задание
Рассмотрите условные обозначения однородных членов. (Подробнее…)
ГДЗРусский языкКанакина В. П.Горецкий В.Г.4 класс
П.Горецкий В.Г.4 класс
А что интересного будет происходить в эти выходные? Куда сходить с учителем?
А что интересного будет происходить в эти выходные? Куда сходить с учителем?
9 класс
Свойство биссектрисы угла / Окружность / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Свойство биссектрисы угла
Теорема
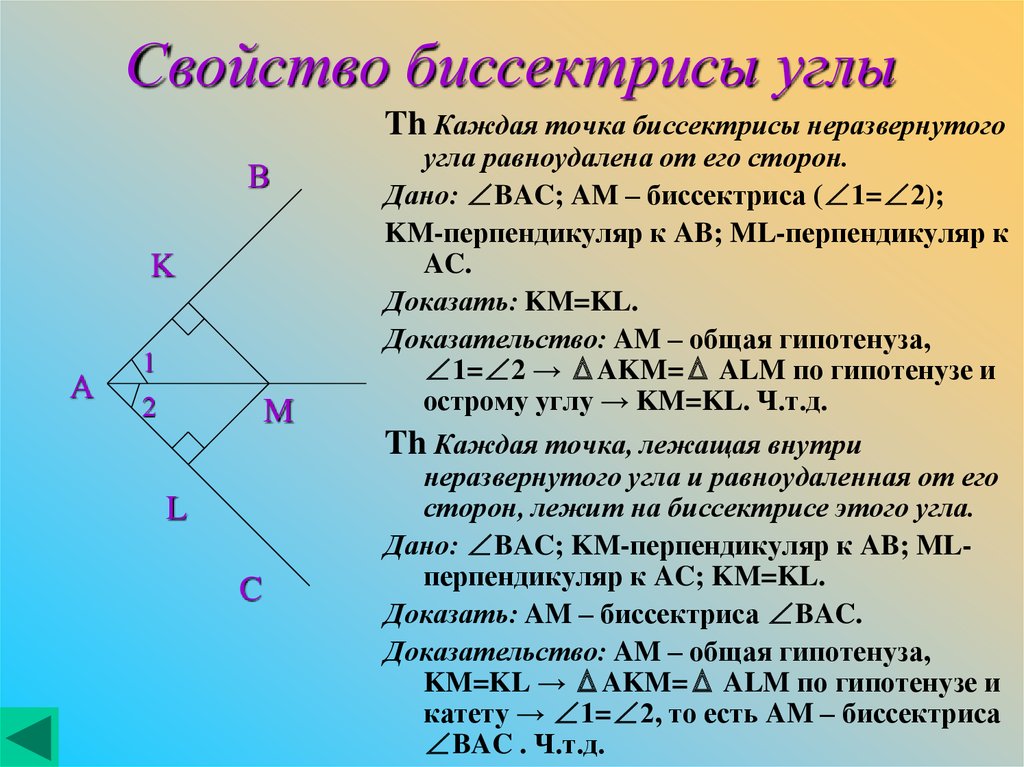
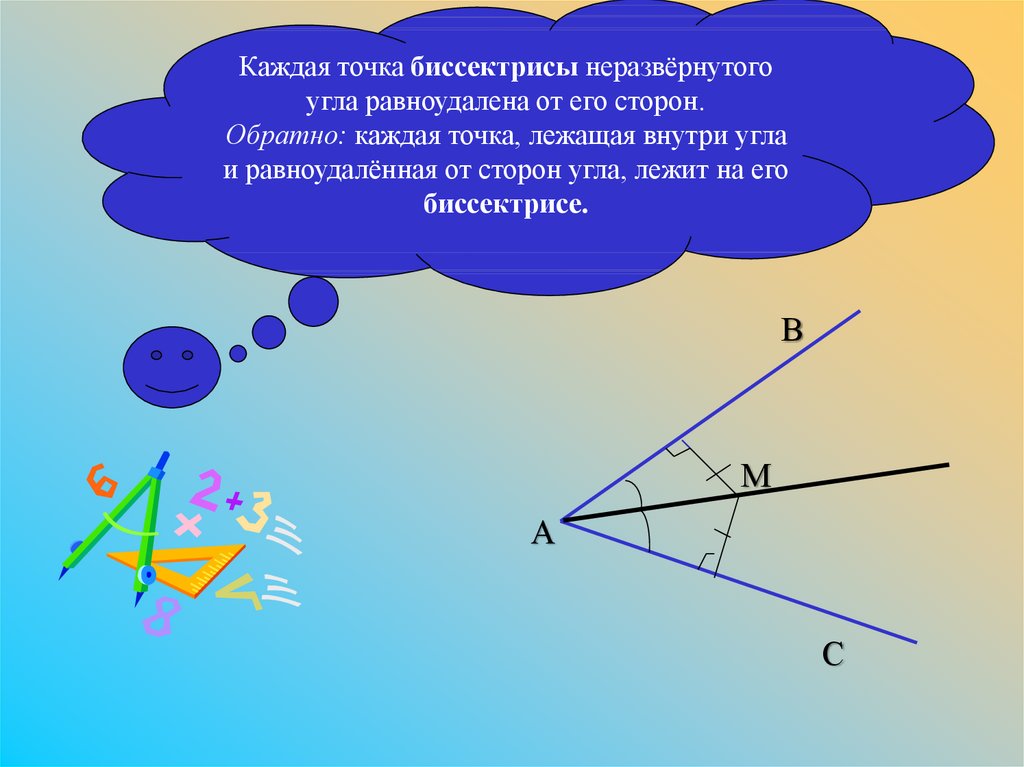
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. |
Доказательство
1) Дано: ВАС, АМ — биссектриса, МК АВ, MLАС.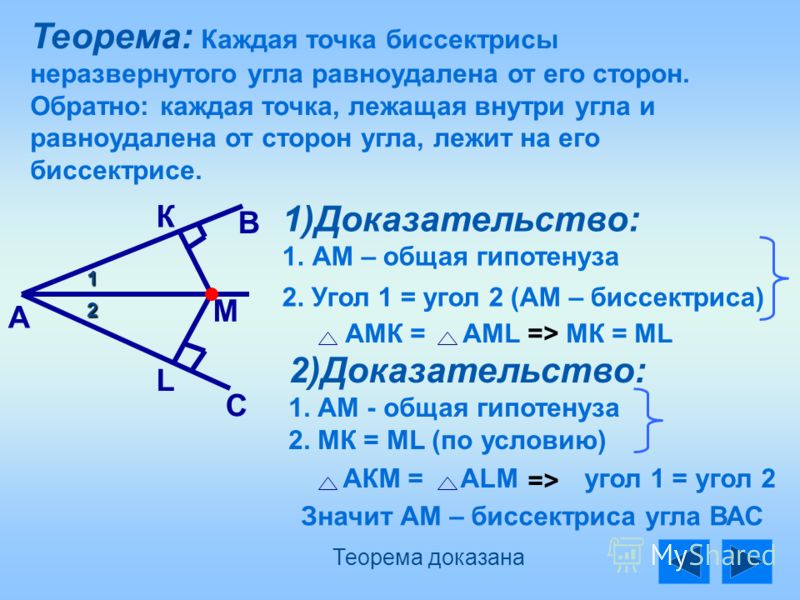
Доказать: MK =
Доказательство:
Рассмотрим АМК и AML: МКАВ, MLАС, поэтому рассматриваемые треугольники прямоугольные. АМ — общая гипотенуза, 1 = 2, т.к. луч АМ — биссектриса, следовательно, АМК = AML, по гипотенузе и острому углу, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому MK = ML.
2) Дано: ВАС, MK = ML, МК АВ, MLАС.
Доказать: АМ — биссектриса ВАС
Доказательство:
Рассмотрим АМК и AML: МКАВ, ML
Следствие 1
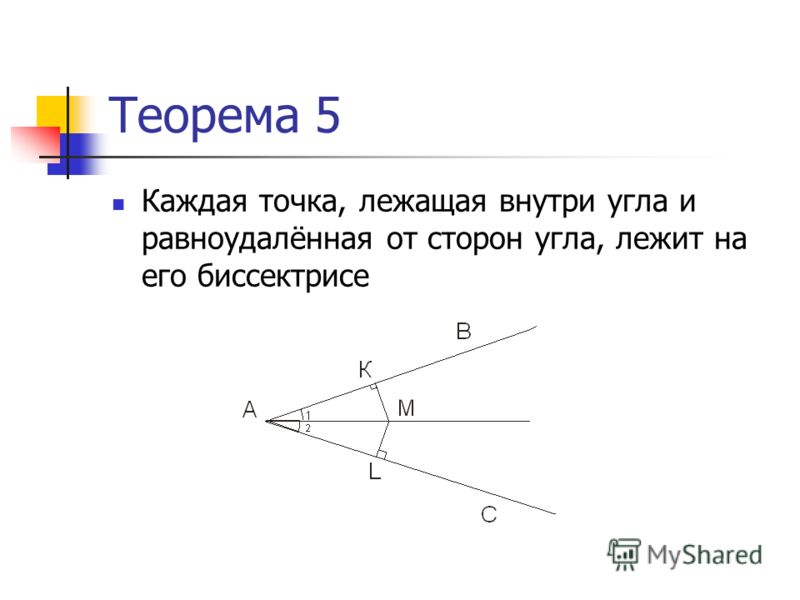
Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла. |
Следствие 2
| Биссектрисы треугольника пересекаются в одной точке. |
В самом деле, обозначим буквой О точку пересечения биссектрис АА1 и ВВ1 треугольника АВС и проведем перпендикуляры
По доказанной теореме ОК = ОМ и ОК = OL. Поэтому ОМ = OL, т.е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы треугольника
Следовательно, все три биссектрисы треугольника
Советуем посмотреть:
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 677, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 688, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 689, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 691, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 724, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 885, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1086, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1275, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
4.
 21: Биссектрисы углов в треугольниках
21: Биссектрисы углов в треугольниках- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4818
Построение и свойства биссектрисы, делящей углы пополам.
Биссектриса угла Теорема
Биссектриса угла делит угол ровно пополам. Одно важное свойство биссектрисы угла состоит в том, что если точка лежит на биссектрисе угла, то она равноудалена от сторон угла. Это называется теоремой биссектрисы угла.
Другими словами, если \(\overrightarrow{BD}\) делит пополам \(\угол ABC\), \(\overrightarrow{BA}\perp FD\overline{AB}\) и \(\overrightarrow {BC}\perp \overline{DG}\), затем \(FD=DG\).
Рисунок \(\PageIndex{1}\) Обратное утверждение этой теоремы также верно.
Теорема о биссектрисе угла Обратное : если точка находится внутри угла и равноудалена от сторон, то она лежит на биссектрисе этого угла.
Когда мы строим биссектрисы углов треугольника, они пересекаются в одной точке. Эта точка называется инцентром треугольника.
Рисунок \(\PageIndex{2}\)Что, если бы вам сказали, что \(\overrightarrow{GJ}\) является биссектрисой угла \(\angle FGH\)? Как бы вы нашли длину \(FJ\), зная длину \(HJ\)? 9{\circ}\).
Пример \(\PageIndex{3}\)
Находится ли \(Y\) на биссектрисе угла \(\angle XWZ\)?
Рисунок \(\PageIndex{4}\)Решение
Если \(Y\) лежит на биссектрисе угла, то \(XY=YZ\) и оба отрезка должны быть перпендикулярны сторонам угла . Из маркировки мы знаем \(\overline{XY}\perp \overrightarrow{WX}\) и \(\overline{ZY}\perp \overrightarrow{WZ}\). Во-вторых, \(XY=YZ=6\). Итак, да, \(Y\) лежит на биссектрисе угла \(\угол XWZ\).
Пример \(\PageIndex{4}\)
\(\overrightarrow{MO}\) — биссектриса угла \(\angle LMN\). Найдите меру \(х\).
Найдите меру \(х\).
Решение
\(LO=ON\) по теореме о биссектрисах угла.
\(\begin{align*} 4x−5&=23 \\ 4x&=28 \\ x&=7\end{align*} \)
Пример \(\PageIndex{5}\)
\(\ overrightarrow{AB}\) — биссектриса угла \(\angle CAD\). Найдите недостающую переменную.
Рисунок \(\PageIndex{6}\)Решение
\(CB=BD\) по теореме о биссектрисе угла, поэтому мы можем составить и решить уравнение для \(x\).
\(\begin{align*} x+7&=2(3x−4) \\ x+7&=6x−8 \\ 15x&=5 \\ x&=3\end{align*}\)
Обзор
В вопросах 1-4 \(\overrightarrow{AB}\) — это биссектриса угла \(\angle CAD\). Найдите недостающую переменную.
- Рисунок \(\PageIndex{7}\)
- Рисунок \(\PageIndex{8}\)
- Рисунок \(\PageIndex{9}\)
- Рисунок \(\PageIndex{10}\)
Достаточно ли информации, чтобы определить, является ли \(\overrightarrow{AB}\) биссектрисой угла \angle CAD? Почему или почему нет?
- Рисунок \(\PageIndex{11}\)
- Рисунок \(\PageIndex{12}\)
- В треугольнике какого типа все биссектрисы угла проходят через вершины треугольника?
- Как иначе называют биссектрисы углов, лежащих в вершинах квадрата?
- Начерти биссектрисы вершин квадрата.
 Сколько у тебя треугольников? Какие это треугольники?
Сколько у тебя треугольников? Какие это треугольники? - Заполните пропуски в обратной теореме о биссектрисе угла. Рисунок \(\PageIndex{13}\)
Даны : \(\overline{AD}\cong \overline{DC}\), такие, что \(AD\) и \(DC\) являются кратчайшими расстояниями до \(\overrightarrow{BA}\) и \(\overrightarrow{BC}\)
Докажите : \(\overrightarrow{BD} делит пополам \угол ABC\)
| Выписка | Причина |
|---|---|
| 1. | 1. |
| 2. | 2. Кратчайшее расстояние от точки до прямой перпендикулярно. |
| 3. Углы \(\угол DAB\) и \(\угол DCB\) прямые | 3. |
4. \(\угол DAB\конг \угол DCB\) \(\угол DAB\конг \угол DCB\) | 4. |
| 5. \(\overline{BD}\cong \overline{BD}\) | 5. |
| 6. \(\Delta ABD\cong \Delta CBD\) | 6. |
| 7. | 7. ЦПКТС |
| 8. \(\overrightarrow{BD}\) делит пополам \(\угол ABC\) | 8. |
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 5.3.
Ресурсы
youtube.com/embed/hb4hzQ5Ro1s?vq=hd1080″ frameborder=»0″ allowfullscreen=»true»>Словарь
| Срок | Определение |
|---|---|
| биссектриса угла | Биссектриса угла — это луч, который делит угол на два равных меньших угла. |
| Теорема о биссектрисе угла | Теорема о биссектрисе угла гласит, что если точка лежит на биссектрисе угла, то эта точка равноудалена от сторон угла. |
| Обратная теорема о биссектрисе угла | Обратная теорема о биссектрисе угла утверждает, что если точка находится внутри угла и равноудалена от сторон, то она лежит на биссектрисе этого угла. |
| в центре | Центр вписанной окружности — это точка пересечения биссектрис треугольника. |
Дополнительные ресурсы
Интерактивный элемент
ВИДЕО: Примеры: Решение для неизвестных значений с использованием свойств угла бисекторов
Активность: BiSectors. Практика: Биссектрисы углов в треугольниках
Реальный мир: биссектрисы перпендикуляра
Эта страница под названием 4.21: Биссектрисы углов в треугольниках распространяется под лицензией CK-12 и была создана, изменена и/или курирована CK-12 Foundation с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.

 Сколько у тебя треугольников? Какие это треугольники?
Сколько у тебя треугольников? Какие это треугольники?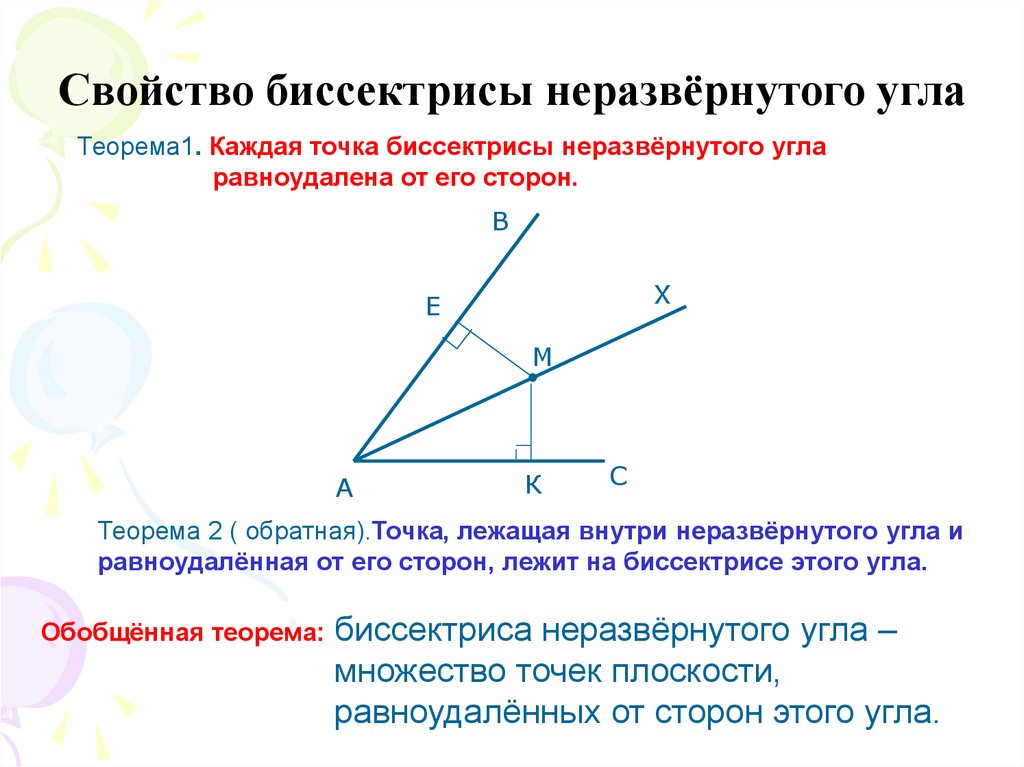 ck12.org/c/geometry
ck12.org/c/geometry

Leave A Comment